State Estimation and Detectability of Probabilistic Discrete Event Systems

Abstract

A probabilistic discrete event system (PDES) is a nondeterministic discrete event system where the probabilities of nondeterministic transitions are specified. State estimation problems of PDES are more difficult than those of non-probabilistic discrete event systems. In our previous papers, we investigated state estimation problems for non-probabilistic discrete event systems. We defined four types of detectabilities and derived necessary and sufficient conditions for checking these detectabilities. In this paper, we extend our study to state estimation problems for PDES by considering the probabilities. The first step in our approach is to convert a given PDES into a nondeterministic discrete event system and find sufficient conditions for checking probabilistic detectabilities. Next, to find necessary and sufficient conditions for checking probabilistic detectabilities, we investigate the “convergence” of event sequences in PDES. An event sequence is convergent if along this sequence, it is more and more certain that the system is in a particular state. We derive conditions for convergence and hence for detectabilities. We focus on systems with complete event observation and no state observation. For better presentation, the theoretical development is illustrated by a simplified example of nephritis diagnosis.

1. Introduction

When applying discrete event system theory (Cao, Lin, & Lin, 1997; Cassandras & Lafortune, 1999; Cieslak, Desclaux, Fawaz, & Varaiya, 1988; Heymann & Lin, 1994; Kumar & Shayman, 1998; Lafortune & Lin, 1991; Li, Lin, & Lin, 1998; Lin, & Wonham, 1988; Ozveren & Willsky, 1990; Ramadge, 1986; Ramadge & Wonham, 1987; Ramadge & Wonham, 1989; Thistle, 1996; Wonham & Ramadge, 1988), we often need to know the state of a system. Clearly, if the initial state of a system is unknown, or if the system is nondeterministic, then we may not know the current state. In general, the state estimation is based on observations of events and state outputs. For example, by observing a copy machine, we cab see a page being fed into the machine and its copy being made. But we may not be able to observe the movement of papers inside the copy machine. The events that can be seen are called observable events. Knowing what observable events have occurred can help us to determine the current state of the system. We may also observe some state outputs that can help us to obtain more information about the state of the system. For example, a signal warning that papers are jammed in the copy machine will tell us some papers are stuck in the paper path, but it may not tell us how many papers are stuck or where they are stuck.

State estimation is always an important problem in system and control theory. In classical control theory, the state estimation problem is investigated in terms of observability, while in discrete event systems, the problem is investigated in terms of detectability. Although the state estimation of discrete event system is investigated early in Ozveren & Willsky (1990), Ramadge (1986), the full-scale study has not been done until our previous work (Shu, Lin, & Ying, 2006; Shu, Lin, & Ying, 2007). We investigate the detectabilities of deterministic as well as nondeterministic discrete event systems in Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007). We say that a system is detectable if we can determine its state along some trajectories of the system. We say that a system is strongly detectable if we can determine its state along all trajectories of the system. We can check if a system is detectable or strongly detectable by constructing an observer, which summarizes the current estimate of the state of the system. In other words, by following the observer, we can say that after a sequence of observations, the system is in one among a set of possible states. If this set consists of only one state, then the state of the system is known exactly. By constructing the observer, we can not only know the current estimate of the state, but also check detectability and strong detectability of the system.

Although we have investigated the detectabilities of deterministic as well as nondeterministic discrete event systems in Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007), there are some limitations of the previous work in dealing with some practical applications, especially in biomedical applications, where transition probabilities are important. Let us take nephritis for example. If we want to know if one person has nephritis or if the person has recovered from nephritis, the effective way is to check the urine sample. For a previously healthy person, if his/her urine sample is positive, then the person has developed nephritis recently. It is more difficult to check if a patient has recovered from nephritis. If his/her urine sample is positive, then the person still has nephritis. But if his/her urine sample is negative, it is possible that the patient has recovered from nephritis (we assume the probability is 0.7); or the patient may still have nephritis (we assume the probability is 0.3) because only repeated negative tests can confirm that the patient has recovered from nephritis. In order to model this formally, we define two discrete states:

Normal (q₁): the person is healthy

Failure (q₂): the person has nephritis

and two events:

α̃: Urine test is negative

β̃: Urine test is positive

Now, it is not difficult to derive the following probabilistic discrete event system (PDES) model based on the reasons given above (a formal definition of PDES will be given shortly):

Since our goal is to determine whether a person is healthy or has nephritis; naturally, the problem can be translated into a state estimation problem of PDES.

Hence, in this paper, we consider the state estimation problem of probabilistic discrete event systems. We assume that a system is nondeterministic and assign probabilities to the nondeterministic transitions. The additional information on probabilities introduces more complexities as well as more opportunities to the state estimation problem. In particular, although we may never be 100% sure about the state of the system, we may be more and more certain about our estimation of the state as we observe more and more event occurrences. Therefore, a system may be undetectable in the non-probabilistic sense, but detectable in the probabilistic sense.

As one can expect, checking probabilistic detectabilities are much more complex than checking non-probabilistic detectabilities. Constructing an observer will not be sufficient for checking probabilistic detectabilities. We must study the asymptotical behavior of the system. Markov chains are similar but not identical, to probabilistic discrete event systems. The state estimation problem has been investigated in Markov chain (Doucet & Andrieu, 1999; Doucet, Logothetis, & Krishnamurthy, 2000; Evans & Evans, 1997; Evans & Krishnamurthy, 1999; Evans & Krishnamurthy, 2001; Ford & Moore, 1998; Habiballah, Ghosh-Roy, & Irving, 1998). However, the state estimation problems discussed in the literature of Markov chains are different from the estimation problem to be discussed in this paper, in at least the following two aspects: (1) While the observations in the estimation problems of Markov chains are some continuous variables and/or states, the observation in our estimation problem is the occurrence of events. Clearly, the observations in Markov chains are not event observations. In fact, the concept of events is not explicitly defined in Markov chains. Furthermore, observation noises are usually assumed in Markov chains but we do not have such an issue in our estimation problem. (2) States to be estimated are often not the states of the Markov chains but the state variables of some linear or nonlinear continuous systems built on the hidden Markov chains. To the best of our knowledge, the state estimation problem as defined in this paper has not been studied before.

We will first briefly review non-probabilistic discrete event systems and their detectabilities in Section 2, as our new results are built on the previous results in Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007). We will then define probabilistic discrete event systems and probabilistic detectabilities in Section 3. Again, two versions of detectabilities will be defined. The weak version requires the system be detectable for some trajectories of the system and the strong version requires the system be detectable for all trajectories of the system. To check detectability and strong detectability, in Section 4, we convert a probabilistic discrete event system into a non-probabilistic discrete event system, construct its observer, and investigate circular strings in the observer. For each circular string, we build its realizations to determine the system behavior along the string. By investigating the realizations, we can determine if the circular string converges or not. We can then determine the detectabilities of the system.

2. Non-Probabilistic Discrete Event Systems and Detectabilities

We first briefly review the results on non-probabilistic detectability of discrete event systems studied in Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007). We use an automaton (also called state machine or generator) to model a discrete event system (Cassandras & Lafortune, 1999; Ramadge & Wonham, 1987; Lin, & Wonham, 1988):

$$G=(Q,\mathrm{\sum },\delta ),$$

where Q is the set of discrete states, Σ is the set of events, and δ is the transition function describing what event can occur at one state and the resulting new state. We assume that the system is nondeterministic, that is, the transition function is given by δ: Q×Σ → 2^Q. Another equivalent way to define the transition function is to specify the set of all possible transitions: {(q,σ,q′): q′ ∈ δ(q,σ)}. With a slight abuse of notation, we will also use δ to denote the set of all possible transitions. We sometimes need to extend the definition of δ: Q×Σ → 2^Q to δ: 2^Q ×Σ → 2^Q: For a subset of states x ⊆ Q, the next set of possible states after σ is defined as $\delta (x,\sigma )=\underset{q\in x}{\cup }\delta (q,\sigma )$.

In this paper, we will assume that all events are observable and no states are observable. (In the terminologies of Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007), this means Σ_o = Σ and Y = φ.) We also assume that the system G = (Q,Σ,δ) is deadlock free, that is, for any state of the system, at least one event is defined at that state: (∀q ∈ Q)(∃ σ ∈ Σ)δ(q,σ) ≠ φ.

In Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007), the following state estimation problem is solved. Given a nondeterministic discrete event system, we do not know the initial state of G = (Q,Σ,δ). Under what conditions can we determine the current state of the system after a finite number of event observations?

Depending on whether we want to determine the current state for all trajectories or some trajectories and for all future times or some future times, we can define four types of detectabilities as shown in Table 1.

Table 1.

Four types of detectabilities

	For all trajectories	For some trajectories
For all future times	Strong Detectability	(Weak) Detectability
For some future times	Strong Periodic Detectability	(Weak) Periodic Detectability

For example, strong detectability requires that we can determine the current state and the subsequent states of the system after a finite number of event observations for all trajectories of the system. This is the strongest version of detectability and only a few practical systems will be detectable in this strong sense. The procedure to check strong detectability can be summarized as follows.

Step 1, we convert the nondeterministic automaton G = (Q,Σ,δ) into a deterministic automaton G_obs called observer using the standard method [1].

$$G_{\mathit{obs}}=(X,\mathrm{\sum },\xi ,x_o)=Ac(2^Q,\mathrm{\sum },\xi ,Q)$$

where X ⊆ 2^Q is the state space⁵, x_o = Q is the initial state, the transition function is given by ξ(x,σ) = {q ∈ Q: (∃q′∈ x)δ(q′,σ) = q}, and Ac denotes the accessible part. The automaton G_obs tells us which subset of states the system could be in after observing a sequence of events (that is, the state estimate).

Step 2, we mark the states in G_obs that contain a singleton state of Q.

$$X_m=\{x\in X:\mid x\mid =1\}$$

where |x| denotes the number of elements in x.

Step 3, we check if all loops in G_obs are entirely within X_m. If so, then the system can always reach X_m and stay within X_m after a finite number of observations (transitions). This is because of the assumption that the system is deadlock free. Therefore, the system is strongly detectable.

Procedures to check other detectabilities are similar and can be found in Shu, Lin, & Ying (2006), Shu, Lin, & Ying (2007).

The above defined detectabilities are non-probabilistic. They are independent of probabilities of event occurrences. Therefore, if a system is detectable, then we can determine the state of the system for sure after finite event observations. This version of detectabilities may be too restrictive because in many applications, especially in medical applications, we can never determine the state of the system for sure, but we can be more and more certain that the system is in a particular state. For such applications, we investigate probabilistic detectabilities. This requires the introduction of probabilistic discrete event systems. From now on, if it is clear from the context, we will call probabilistic detectabilities simply as detectabilities.

3. Probabilistic Discrete Event Systems and Detectabilities

To generalize the model of non-probabilistic discrete event systems to that of probabilistic discrete event systems, we first reformulate non-probabilistic automata G = (Q,Σ,δ) and represent states, events, and their transitions by vectors and matrices: We enumerate the states of G as k = 1,2,…n, where n = |Q|= the number of states in G. The current state of the system is represented by a vector

$$q={[p(q_k)]}_{1\times n}=[p(q_1)\dots p(q_n)],$$

where (q_k) ∈ {0,1} indicates whether the system is currently in state k, that is, {k: p(q_k) = 1} is the set of states the system may be in. Each event σ is represented by an event transition matrix

$$\sigma ={[{\sigma }_{ij}]}_{n\times n}=\left[\begin{array}{lll}{\sigma }_{11}\hfill & \dots \hfill & {\sigma }_{1n}\hfill \\ \dots \hfill & \hfill & \hfill \\ {\sigma }_{n1}\hfill & \dots \hfill & {\sigma }_{nn}\hfill \end{array}\right]$$

where σ_ij equals 1 if σ is defined from state i to state j; and equals 0 otherwise. In this way, if the current state of the system is q and σ occurs in the system, then the next state will be qσ in terms of matrix multiplication; that is, δ(q,σ) = qσ. Note that, with a slight abuse of notation, we use q to denote both a state and the vector representing the state. Similarly, we use σ to denote both an event and the matrix representing the event transition.

A probabilistic automaton is denoted by

$$\stackrel{\sim }{G}=(\stackrel{\sim }{Q},\mathrm{\sum }^{\sim },\stackrel{\sim }{\delta }),$$

where Q̃, Σ̃, and δ̃ are extensions of Q, Σ, and δ respectively. They are defined as follows. Q̃ ∈ Q̃ is a probabilistic state vector (representing the estimation of the state)

$$\stackrel{\sim }{q}={[p(q_k)]}_{1\times n}=[p(q_1)\dots p(q_n)],$$

where p(q_k) ∈ [0,1] with ${\displaystyle \sum _{k=1}^n}p(q_k)=1$ takes values between 0 and 1 and represents the probability for the system to be in state k. Equation ${\displaystyle \sum _{k=1}^n}p(q_k)=1$ states the sum of the probabilities in different states must be one. σ̃ ∈ Σ̃ is a probabilistic event transition matrix

$$\stackrel{\sim }{\sigma }={[{\stackrel{\sim }{\sigma }}_{ij}]}_{n\times n}=\left[\begin{array}{lll}{\stackrel{\sim }{\sigma }}_{11}\hfill & \dots \hfill & {\stackrel{\sim }{\sigma }}_{1n}\hfill \\ \dots \hfill & \hfill & \hfill \\ {\stackrel{\sim }{\sigma }}_{n1}\hfill & \dots \hfill & {\stackrel{\sim }{\sigma }}_{nn}\hfill \end{array}\right]$$

where σ̃_ij ∈ [0,1] with ${\displaystyle \sum _{j=1}^n}{\stackrel{\sim }{\sigma }}_{ij}=1$ or 0, for 1 ≤ i ≤ n, represents the probability for the system to transit from state i to state j when event σ̃ occurs. Therefore, if the current state vector is Q̃ and σ̃ occurs in the system, then the next state will be δ̃(Q̃,σ̃). Since some events may not be defined in some states, we allow ${\displaystyle \sum _{j=1}^n}{\stackrel{\sim }{\sigma }}_{ij}=0$ for some i. Note that stochastic automaton is discussed in details early in Paz, (1971), Rabin, (1963) and our probabilistic discrete event system is slight modification of stochastic automaton.

For a system modeled by a probabilistic automaton, our goal is to solve the following problem.

State Estimation Problem

Given a probabilistic discrete event system

$$\stackrel{\sim }{G}=(\stackrel{\sim }{Q},\mathrm{\sum }^{\sim },\stackrel{\sim }{\delta }),$$

we do not know the initial state of G̃ = (Q̃,Σ̃,δ̃), but we can observe event occurrences. Under what conditions can we obtain more and more accurate estimate of the current state of the system after more and more event observations?

By obtaining more and more accurate estimate of the current state of the system, we mean the following: Consider an infinite sequence of events s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k …, that is, s̃ is a string in an ω-language (s̃ ∈Σ̃^ω) representing a possible trajectory of the system (Thistle, & Wonham, 1994). Note that under the deadlock-free assumption, any (finite) sequence can be extended to an infinite sequence. Along the sequence s̃, the state estimation can be obtained as follows. Initially, we do not know which state the system is in. We assume that all states are equally likely initially; that is, Q̃_o = [1/n … 1/n]. After the occurrence and observation of σ̃₁, the likelihood of the system in each state is given by Q̃_oσ̃₁. However, the sum of elements in Q̃_oσ̃₁ may not be equal to 1, as the early state estimation may be wrong and hence may not be σ̃₁ defined at some state in the early estimation. To overcome this difficulty, we introduce a normalization operator N(.) as

$$N(v)=N([\begin{array}{llll}{v}_1\hfill & v_2\hfill & \dots \hfill & v_n\hfill \end{array}])=\{\begin{array}{ll}[\begin{array}{llll}{v}_1\hfill & v_2\hfill & \dots \hfill & v_n\hfill \end{array}]/T\hfill & \text{if}T=v_1+v_2+\dots +v_n\ne 0\hfill \\ \text{undefined}\hfill & \text{otherwise}\hfill \end{array}.$$

Then, the state estimation after σ̃₁ is N(Q̃_oσ̃₁). Note that the operator N(.) has the following property⁶:

$$N(N({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1){\stackrel{\sim }{\sigma }}_2)=N({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2).$$

In other words, it is sufficient to apply N(.) once. Using N(.), we can estimate the state of the system after observing a sequence of events t̃ = σ̃₁ σ̃₂…σ̃_k as

$$\stackrel{\sim }{q}=N({\stackrel{\sim }{q}}_o\stackrel{\sim }{t})=N({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k).$$

In other words, Q̃ = δ̃(Q̃_o, t̃) = N(Q̃_o t̃). If the maximal element in Q̃ approaches 1, then we are more and more certain that the system is in one particular state (corresponding to the maximum element). In this case, we say that s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k… converges.

Formally, an infinite sequence s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k… of G̃ converges if

$$maxN({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k)\to 1,\text{as}k\to \infty .$$

With this definition of convergence, we can define strong (probabilistic) detectability as follows.

Definition 1 (Strong Detectability)

A probabilistic discrete event system

$$\stackrel{\sim }{G}=(\stackrel{\sim }{Q},\mathrm{\sum }^{\sim },\stackrel{\sim }{\delta })$$

is strongly detectable if from the initial state ${\stackrel{\sim }{q}}_o=[\begin{array}{lll}1/n\hfill & \dots \hfill & 1/n\hfill \end{array}]$, all infinite sequences s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k … of G̃ converge.

Strong detectability requires all infinite sequences converge. If only some sequences converge, then we have (weak) detectability.

Definition 2 (Weak Detectability)

A probabilistic discrete event system

$$\stackrel{\sim }{G}=(\stackrel{\sim }{Q},\mathrm{\sum }^{\sim },\stackrel{\sim }{\delta })$$

is weakly detectable (or simply detectable) if from the initial state ${\stackrel{\sim }{q}}_o=[\begin{array}{lll}1/n\hfill & \dots \hfill & 1/n\hfill \end{array}]$, there exists at least one infinite sequence s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k… of G̃ that converges.

Before we derive conditions for checking detectability and strong detectability, let us first get some intuitions from the following example.

Example 1

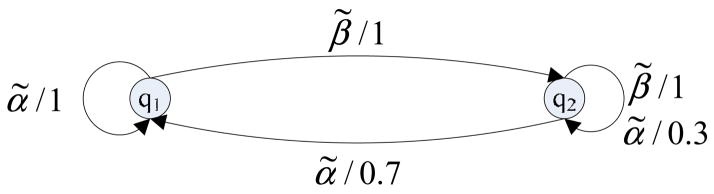
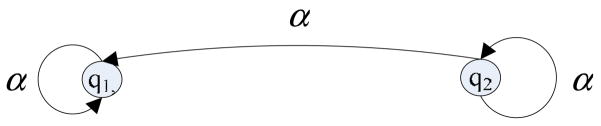
Let us first consider the nephritis diagnosis system shown in Figure 1. The system has two states and two events. The event transition matrices are

Figure 1.

The nephritis diagnosis system modeled by PDES

$$\stackrel{\sim }{\alpha }=\left[\begin{array}{cc}1& 0\\ 0.7& 0.3\end{array}\right],\stackrel{\sim }{\beta }=\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right].$$

Assuming ${\stackrel{\sim }{q}}_o=\left[\begin{array}{ll}0.5\hfill & 0.5\hfill \end{array}\right]$, we can estimate the probabilistic state vector after observing various sequences of events as follows.

$$\begin{array}{l}N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta })=\left[\begin{array}{ll}0\hfill & 1\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta }\stackrel{\sim }{\beta })=\left[\begin{array}{ll}0\hfill & 1\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta }\stackrel{\sim }{\beta }\stackrel{\sim }{\beta })=\left[\begin{array}{ll}0\hfill & 1\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.85\hfill & 0.15\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\alpha }\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.955\hfill & 0.045\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\alpha }\stackrel{\sim }{\alpha }\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.986\hfill & 0.014\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.7\hfill & 0.3\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha }\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.7\hfill & 0.3\hfill \end{array}\right]\\ N({\stackrel{\sim }{q}}_o\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha }\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha }\stackrel{\sim }{\beta }\stackrel{\sim }{\alpha })=\left[\begin{array}{ll}0.7\hfill & 0.3\hfill \end{array}\right]\end{array}$$

Hence, we are certain that the system is in State 2 (having nephritis) after observations of event β̃ (positive urine test) and we are more and more certain that the system is in State 1 after more and more observations of event α̃. On the other hand, if we keep observing string β̃α̃, then we are not sure about the current state the system. In other words, some infinite sequences converge but some others do not. Intuitively we know the system is detectable and not strongly detectable.

4. Checking Detectabilities

To check detectabilities, we first convert the probabilistic automaton G̃ = (Q̃, Σ̃, δ̃) into a non-probabilistic (and nondeterministic) automaton

$$\mathit{convert}(\stackrel{\sim }{G})=(Q,\mathrm{\sum },\delta )$$

where Q = {q₁, q₂, …, q_n}, Σ = {σ₁, σ₂,…, σ_|Σ̃|}, and δ are defined as follows.

$$(q_i,\sigma ,q_j)\in \delta \iff {\stackrel{\sim }{\sigma }}_{ij}>0.$$

In other words, transition (q_i, σ, q_j) is defined in convert(G̃) if and only if the probability of event σ̃ occurring at state q_i and leading to state q_j is non-zero. δ can be extended to a mapping δ: 2^Q × Σ → 2^Q as described before. After converting G̃ = (Q̃, Σ̃, δ̃), we can take G = convert(G̃) and follow the steps outlined in Section 2 to obtain the observer automaton G_obs = (X, Σ, ξ, x_o).

To see the connections between states and transitions of G̃ and G_obs, let us define, for a probabilistic state $\stackrel{\sim }{q}={[p(q_k)]}_{1\times n}=[\begin{array}{lll}p(q_1)\hfill & \dots \hfill & p(q_n)\hfill \end{array}]$, its corresponding non-probabilistic state convert(Q̃) = {q_i: p(q_i) ≠ 0}. Hence, for ${\stackrel{\sim }{q}}_o=[\begin{array}{lll}1/n\hfill & \dots \hfill & 1/n\hfill \end{array}]$, convert(Q̃_o) = Q = x_o.

Lemma 1

Starting from the initial state ${\stackrel{\sim }{q}}_o=[\begin{array}{lll}1/n\hfill & \dots \hfill & 1/n\hfill \end{array}]$, if a sequence of events t̃ = σ̃₁σ̃₂…σ̃_k is observed, then the set of possible states the system may be in is given by

$$x=\xi (x_o,t)=\mathit{convert}(\stackrel{\sim }{\delta }({\stackrel{\sim }{q}}_o,\stackrel{\sim }{t})),$$

where t = σ₁σ₂…σ_k is the corresponding sequence in convert(G̃).

Proof

From our discussion in Section 3, the state of the system after observing a sequence of events t̃ = σ̃₁σ̃₂…σ̃_k in G̃ is given by

$$N({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k)=N({\stackrel{\sim }{q}}_o\stackrel{\sim }{t})=\stackrel{\sim }{\delta }({\stackrel{\sim }{q}}_o,\stackrel{\sim }{t}).$$

Therefore, we only need to prove ξ(x_o, t) = convert(N(Q̃_ot̃)), which can be done by a simple induction on the length of t̃ = σ̃₁σ̃₂…σ̃_k.

Q.E.D.

Now we can present our first result.

Theorem 1

1. If G = convert(G̃) is non-probabilistically detectable, then G̃ is detectable.

2. If G = convert(G̃) is strongly non-probabilistically detectable, then G̃ is strongly detectable.

Proof

1. If G = convert(G̃) is non-probabilistically detectable, then by the definition, the current state and the subsequent states of the system can be determined after finite number of event observations for some trajectories of the system. In other words, there exists an infinite string σ₁σ₂…σ_k… such that for sufficiently large k, | ξ(x_o, σ₁σ₂…σ_k) |= 1. By Lemma 1,

$$\xi (x_o,{\sigma }_1{\sigma }_2\cdots {\sigma }_k)=\mathit{convert}(\stackrel{\sim }{\delta }({\stackrel{\sim }{q}}_o,{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k))=\mathit{convert}(N({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k)).$$

Therefore, |ξ (x_o, σ₁ σ₂…σ_k) | = 1 implies that there is only one element in N(Q̃_oσ̃₁σ̃₂…σ̃_k) that is non-zero and it must be 1. Hence max N(Q̃_oσ̃₁σ̃₂…σ̃_k) = 1 and G̃ is detectable

1. Similar proof but for all trajectories of the system.

Q.E.D.

To check if G = convert(G̃) is non-probabilistically detectable or strongly non-probabilistically detectable, the results of Shu, Lin, & Ying, (2006) can be used.

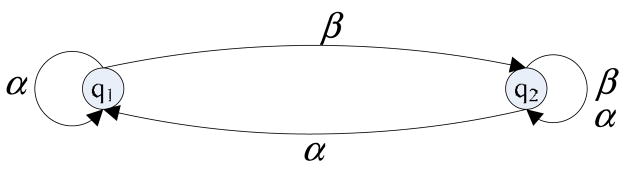
Example 2

For the probabilistic automaton G̃ shown in Figure 1, the converted nondeterministic automaton G = convert(G̃) is given in Figure 2.

Figure 2.

The converted non-probabilistic and nondeterministic discrete event system from Figure 1

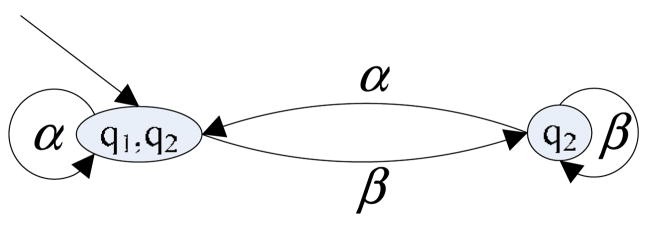
Using the procedure of Section 2, we can compute the observer automaton G_obs, which is shown in Figure 3.

Figure 3.

The observer of the nondeterministic discrete event system in Figure 2

From G_obs, we can see that G = convert(G̃) is (weak) non-probabilistically detectable but not strongly non-probabilistically detectable. By Theorem 1, G̃ is (weak) detectable. We do not know if it is strongly detectable because the conditions in Theorem 1 are only sufficient but not necessary. This can be seen as follows: From Figure 3, we know that the event sequence ααα··· does not lead to singleton state. However, the corresponding probabilistic event sequence α̃α̃α̃··· is convergent.

To obtain necessary and sufficient conditions for checking detectabilities, we need to consider infinite sequences generated by G_obs. These strings must form circles in G_obs. Let us define circular strings in G_obs that start and end at the same state x∈X as

$$L_c(G_{\mathit{obs}},x)=\{v\in {\mathrm{\sum }}^{\ast }:\xi (x,v)=x\}.$$

The set of all circular strings in G_obs are given by

$$L_c(G_{\mathit{obs}})=\underset{x\in X}{\cup }{L}_c(G_{\mathit{obs}},x).$$

We denote a circular string from x ∈ X, v = σ₁σ₂…σ_j ∈ L_c (G_obs, x) as a pair (x,v), its realization is a sequence

$$R(y_0,v)=(y_0\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }{y}_2\to \dots \dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j).$$

where y₀ ⊆ x ⊆ Q, y₁ = δ(y₀, σ₁), y₂ = δ(y₁, σ₂), …, y_j = δ (y_j−1, σ_j) such that y_j ⊆ y₀. A realization has the following property: if the system G = convert(G̃) starts within states y₀, then after the realization, the system remains within states y₀. A realization is nonblocking if for all i = 0,1, …, j−1 and for all q∈y_i, δ(q, σ_i+1) ≠ φ.

If we start from y₀ = x, then by the definition of G_obs, ξ(x,v) x. Therefore,

$$R(x,v)=(x\stackrel{{\sigma }_1}{\to }{x}_1\stackrel{{\sigma }_2}{\to }{x}_2\to \dots \dots x_{j-1}\stackrel{{\sigma }_j}{\to }{x}_j).$$

is a realization with x_j ⊆ x. However, R(x,v) may block. Also, it may not be minimal. A realization R(y,v) is a minimal realization if there exists no other realization R(y′,v) such that y′⊂y. To find realizations and minimal realizations, we construct a transition graph

$$TG(x,v)=(x,\mathit{Arc}(v,x))$$

for v ∈ L_c(G_obs, x) as follows. The nodes of TG(x,v) are x. For q₁, q₂ ∈ x, the arc (q₁, q₂) ∈ Arc(v, x) is defined if and only if q₂ ∈ δ(q₁,v). In other words, (q₁, q₂) ∈ Arc(v, x) means that starting from state q₁ ∈ x, it is possible for the system to end at state q₂ ∈ x. If the system starts at a subset of states y ⊆ x, then the set of possible states after v is

$$\mathit{Post}(y)=\{q_2\in x:(\exists q_1\in y)(q_1,q_2)\in \mathit{Arc}(v,x)\}.$$

From these definitions, we can check a realization and nonblocking realization as follows.

1. $R(y_0,v)=(y_0\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots \dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j)$ is a realization if and only if Post(y₀) ⊆y₀.

2. $R(y_0,v)=(y_0\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots \dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j)$ is a nonblocking realization if and only if it is a realization and for all i = 0,1,…, j−1 and for all q ∈ y_i, δ(q, σ_i+1) ≠ φ.

Checking minimal realization is more involved and needs the concept of strongly connected subgraphs. A subgraph with states y ⊆ x is strongly connected if and only if there exists a direct path from any state to any other state in y. For a subgraph with only one node, it is strongly connected if and only if the node has a self loop. Strongly connected subgraphs are related to minimal realizations as follows.

Lemma 2

R(y,v) is a minimal realization if and only if Post(y) ⊆ y and the subgraph of y is strongly connected.

Proof

If y has only one state, then the result is obvious. If y has more than one states, then we can partition states or remove states to prove the result as follows.

If the subgraph of y is not strongly connected, then we can partition it into two subgraphs y₁ and y₂ and there is no direct path from states in y₁ to states in y₂. We can remove states in y₂ and the remaining subgraph still satisfies Post(y₁) ⊆ y₁. Therefore, R(y₁, v) is a realization and R(y,v) is not a minimal realization.

On the other hand, if the subgraph of y is strongly connected, then removing any subset y′ from y will result in Post(y \ y′) ⊆ (y \ y′) no longer true.

Q.E.D.

Given a pair (x,v) with v = σ₁σ₂…σ_j ∈ L_c (G_obs, x), we say that it converges if it has a unique minimal and nonblocking realization

$$R(y,v)=(y\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j)$$

such that

$$\mid y\mid =\mid y_1\mid =\dots =\mid y_j\mid =1.$$

R(y,v) is called the convergent realization of (x,v) and denoted by R_c (y,v). Therefore, a pair (x,v) converges if and only if it has the (unique) convergent realization R_c (y,v).

Given a circular string v = σ₁σ₂…σ_j ∈L_c (G_obs), we say that v = σ₁σ₂…σ_j converges if there exists a convergent pair (x, v); and v = σ₁σ₂…σ_j strongly converges if all the pairs (x, v) are convergent.

Theorem 2

A PDES G̃ = (Q̃, Σ̃, δ̃) is detectable if and only if the corresponding G = convert(G̃) and G_obs have at least one convergent circular string v ∈ L_c (G_obs).

Proof

(IF) Assume that G = convert(G̃) and G_obs has a convergent circular string v = σ₁σ₂…σ_j ∈ L_c (G_obs, x) whose convergent realization is

$$R(y,v)=(y\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j)$$

By the definition, R(y,v) is the unique minimal and nonblocking realization of v ∈L_c (G_obs, x) and |y| =|y₁| = … =|y_j| = 1.

Let u ∈ Σ^* be a string such that ξ(x_o,u) = x (u exists because x is accessible). By Lemma 1, we have x = convert(δ̃ (Q̃_o, ũ)). Let Q̃ = (Q̃_o, ũ) and ṽ = σ̃₁σ̃₂… σ̃_j; that is, Q̃ and ṽ are state set and string in G̃ corresponding to x and v in G. We prove that when ṽ repeats infinitely, the infinite sequences s̃ = ũṽṽ … ṽ … of G̃ converge. Since | y | = 1, let us write y = {q_i}, that is, y is the ith state. Because R(y,v) is a nonblocking realization, p_i (N(Q̃ṽ^m)) ≥ p_i(Q̃) and lim_m→∞ p_i (N(Q̃ṽ^m)) ≥ p(q_i). Because y ⊆ x and there are no other minimal and nonblocking realizations, for all other states q_j, {q_j} ≠ y, lim_m→∞ p_j (N(Q̃ṽ^m)) = 0. Hence,

$${lim}_{m\to \infty }\frac{p_i(\stackrel{\sim }{q}{\stackrel{\sim }{v}}^m)}{{\displaystyle \sum _{k=1}^n}{p}_k(\stackrel{\sim }{q}{\stackrel{\sim }{v}}^m)}={lim}_{m\to \infty }\frac{p_i(\stackrel{\sim }{q}{\stackrel{\sim }{v}}^m)}{p_i(\stackrel{\sim }{q}{\stackrel{\sim }{v}}^m)}=1.$$

In other words,

$$maxN({\stackrel{\sim }{q}}_o\stackrel{\sim }{u}{\stackrel{\sim }{v}}^m)\to 1,\text{as}m\to \infty .$$

So G̃ = (Q̃, Σ̃, δ̃) is detectable. This proves the “IF” part.

(ONLY IF) Assume that G̃ = (Q̃, Σ̃, δ̃) is detectable. Then there exists an infinite sequence s̃ of G̃ that converges. Since the corresponding s is an infinite string in G = convert(G̃) and G_obs, it must visit some state x of G_obs infinitely often.

For a state q ∈x, let p^m(q) be the probability of G̃ being at q when s̃ visits x for the mth time. Since s̃ converges, there must exist a unique state q ∈ x such that p^m(q) →1 as m → ∞. Let m be sufficiently large and ε is sufficiently small and p^m+1(q) ≥ p^m (q) ≥1−ε. Let v = σ₁σ₂…σ_j be the substring of s between the mth and (m+1)st visit of x by G_obs. Clearly v ∈L_c (G_obs, x) is a circular string. We want to show that v converges and $R(\{q\},v)=(\{q\}\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots \dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j)$ is the convergent realization with y_j = {q}.

To do so, let us first show that R({q},v) is a realization; that is, y_j ⊆ {q} as follows. If y_j ⊆ {q}, then when the system starts at {q} and after the occurrence of v = σ₁σ₂…σ_j, it may move outside of {q}, hence the probability of returning to {q} after v is less, contradicting the assumption p^m+1(q) ≥ p^m (q) ≥1−ε. R({q},v) is minimal because {q} consists of only one state. Also, |y₁|= … =|y_j|= 1 must be true because s̃ converges. Also R({q},v) is nonblocking because any y_i is a singleton state. Furthermore, R({q},v) is the unique realization that is minimal and nonblocking, because otherwise, q ∈ x is not the unique state such that p^m(q) →1 as m→∞. All these facts together show that v ∈ L_c (G_obs, x) is a convergent circular string. This proves the “ONLY IF” part.

Q.E.D.

The above theorem gives a necessary and sufficient condition for checking (weak) detectability. Now let us present the following theorem for a necessary and sufficient condition for checking strong detectability.

Theorem 3

A PDES G̃ = (Q̃, Σ̃, δ̃) is strongly detectable if and only if all circular strings v ∈L_c (G_obs) of the corresponding G = convert(G̃) and G_obs strongly converge.

Proof

(IF) Assume that all circular strings v ∈ L_c (G_obs) of the corresponding G = convert(G̃) and G_obs strongly converge. Let us prove that G̃ = (Q̃, Σ̃, δ̃) is strongly detectable by contradiction. Suppose that G̃ = (Q̃, Σ̃, δ̃) is not strongly detectable. Then there exists an infinite sequence s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k… of G̃ that does not converge; that is,

$$maxN({\stackrel{\sim }{q}}_o{\stackrel{\sim }{\sigma }}_1{\stackrel{\sim }{\sigma }}_2\dots {\stackrel{\sim }{\sigma }}_k)\nrightarrow 1,\text{as}k\to \infty .$$

The infinite sequence s̃ = σ̃₁σ̃₂σ̃₃…σ̃_k… of G̃ must visit at least one state x of G_obs infinitely often. Let u∈ Σ^* be a string such that ξ (x_o,u) = x. By Lemma 1, we have x = convert(δ̃(Q̃_o,ũ)). The infinite sequence can be re-written as s̃ = ũα̃₁α̃₂…α̃_k…, where α̃_k ∈Σ̃. Because all circular strings strongly converge, there exists a nonblocking path

$$\{q_i\}\stackrel{{\alpha }_1}{\to }{y}_1\stackrel{{\alpha }_2}{\to }\dots y_{j-1}\stackrel{{\alpha }_j}{\to }{y}_j\dots$$

such that {q_i} = y₀ ⊆ x, y_j = δ(y_j−1, α_j), and |y₀|= | y₁|= … =| y_j| =… = 1. Denote by p(y_j) the probability for G̃ to be in state y_j along the sequence s̃ = ũα̃₁α̃₂…α̃_k…. Then clearly p(y_j) ≤ p(y_j+1). Furthermore, we can conclude that p(y_j) → 1 as j→ ∞ because otherwise, there exists a different nonblocking path

$$\{{q^{\prime }}_i\}\stackrel{{\alpha }_1}{\to }{y^{\prime }}_1\stackrel{{\alpha }_2}{\to }\dots {y^{\prime }}_{j-1}\stackrel{{\alpha }_j}{\to }{y^{\prime }}_j\dots$$

such that {q′_i} = y′₀⊆x, y′_j = δ(y′_j−1, α_j). From these two different infinite paths, we can obtain two different minimal and nonblocking realizations for some circular strings, which contradicts the assumption that all circular strings v ∈L_c (G_obs) of the corresponding G convert(G̃) and G_obs strongly converge. This proves the “IF” part.

(ONLY IF) Assume that G_obs has a circular string v = σ₁σ₂ …σ_j ∈ L_c(G_obs, x) that does not converge. Let u ∈ Σ^* be a string such that ξ(x_o,u) = x. By Lemma 1, we have x = convert(δ̃(Q̃_o,ũ)). Let us prove that the infinite sequences s̃ = ũṽṽ…ṽ… of G̃ does not converge by contradiction.

For a state q ∈x, let p^m(q) be the probability of G̃ = (Q̃, Σ̃, δ̃) being at q when s̃ visits x for the mth time. If s̃ converges, there must exist a unique state q ∈x such that p^m(q) →1 as m → ∞. Let m be sufficiently large and ε is sufficiently small and p^m+1(q) ≥ p^m(q) ≥1 − ε. Consider

$$R(\{q\},v)=(\{q\}\stackrel{{\sigma }_1}{\to }{y}_1\stackrel{{\sigma }_2}{\to }\dots \dots y_{j-1}\stackrel{{\sigma }_j}{\to }{y}_j).$$

If _{y j} ⊈{q}, then when the system starts at {q} and after the occurrence of v = σ₁σ₂ …σ_j, it may move outside of {q}, hence the probability of returning to {q} after v is less, contradicting the assumption p_m+1 (q) ≥ p_m(q). Therefore, y_j ⊆ {q} and R({q},v) is a realization. R({q},v) is minimal because {q} consists of only one state. R({q},v) is nonblocking because the system is strongly detectable. Furthermore, R({q},v) is the unique realization that is minimal and nonblocking, because otherwise, q ∈ x is not the unique state such that p_m(q) → 1 as m → ∞. Finally, |y₁|= … =|y_j|=1 must be true because s̃ converges. Therefore, v ∈ L_c(G_obs, x) is a convergent circular string, which contradicts the assumption that v = σ₁σ₂ …σ_j does not converge. This proves the “ONLY IF” part.

Q.E.D.

Example 3 (continued)

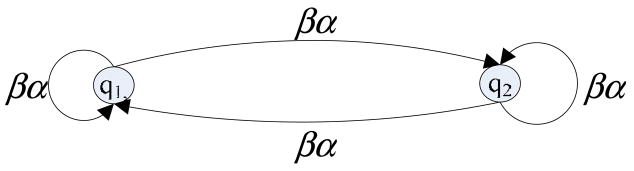
Let us check circular strings in Figure 3 and determine the detectability of the nephritis diagnosis system in Figure 1. For the pair ({q₁, q₂},βα), its transition graph TG(x,v) = TG({q₁, q₂},βα ) is as follows:

Clearly R({q₁, q₂},βα) is a minimal realization. Although it is nonblocking, it is not convergent. Therefore, the system is not strongly detectable.

For the pair ({q₁, q₂},α), we have its transition graph TG(x,v) TG = ({q₁, q₂},α) as follows:

The minimal realization is R({q₁},α). It is not difficult to see that it is a convergent realization. Hence the system is detectable.

5. Conclusion

In this paper, we considered detectabilities of probabilistic discrete event system. We defined (probabilistic) detectabilities both in a strong sense and in a weak sense. Compared with the detectabilities considered in our early work (Shu, Lin, & Ying, 2006; Shu, Lin, & Ying, 2007), the problem becomes much more complex because the transition probabilities must be taken into consideration. We defined the convergence for circular strings. Based on the definition of convergence for circular strings, we derived the necessary and sufficient conditions for (probabilistic) detectability and strong (probabilistic) detectability. All the results are illustrated by examples.

Figure 4.

the transition graph of the pair ({q₁, q₂},βα)

Figure 5.

the transition graph of the pair ({q₁, q₂},α)

Biographies

Shaolong Shu was born in Hubei, China, in 1980. He received his B.Eng. degree in automatic control, and his Ph.D. degree in control theory and control engineering from Tongji University, Shanghai, China, in 2003 and 2008, respectively.

From August, 2007 to February, 2008, he was a visiting scholar in Wayne State University, Detroit, MI, USA. He is now with Tongji University. His main research interests include discrete event system and robust control.

Feng Lin received his B.Eng. degree in electrical engineering from Shanghai Jiao-Tong University, Shanghai, China, in 1982, and his M.A.Sc. and Ph.D. degrees in electrical engineering from the University of Toronto, Toronto, Canada, in 1984 and 1988, respectively.

From 1987 to 1988, he was a postdoctoral fellow at Harvard University, Cambridge, MA. Since 1988, he has been with the Department of Electrical and Computer Engineering, Wayne State University, Detroit, Michigan, where he is currently a professor. His research interests include discrete-event systems, hybrid systems, robust control, and image processing. He was a consultant for GM, Ford, Hitachi and other auto companies.

Dr. Lin co-authored a paper with S. L. Chung and S. Lafortune that received a George Axelby outstanding paper award from IEEE Control Systems Society. He is also a recipient of a research initiation award from the National Science Foundation, an outstanding teaching award from Wayne State University, a faculty research award from ANR Pipeline Company, and a research award from Ford. He was an associate editor of IEEE Transactions on Automatic Control. He is the author of a book entitled “Robust Control Design: An Optimal Control Approach.”

Hao Ying received his Ph.D. degree in biomedical engineering from The University of Alabama, Birmingham, Alabama, in 1990. He is a Professor at Department of Electrical and Computer Engineering, Wayne State University, Detroit, Michigan, USA. He is also a Full Member of its Barbara Ann Karmanos Cancer Institute. He was on the faculty of The University of Texas Medical Branch at Galveston between 1992 and 2000. He was an Adjunct Associate Professor of the Biomedical Engineering Program at The University of Texas at Austin between 1998 and 2000. He has published one research monograph/advanced textbook entitled Fuzzy Control and Modeling: Analytical Foundations and Applications (IEEE Press, 2000), 87 peer-reviewed journal papers, and 117 conference papers.

Dr. Ying is an Associate Editor for six international journals and is on the editorial board of three other international journals. He was a Guest Editor for four journals. He is an elected board member of the North American Fuzzy Information Processing Society (NAFIPS). He served as Program Chair for The 2005 NAFIPS Conference as well as for The International Joint Conference of NAFIPS Conference, Industrial Fuzzy Control and Intelligent System Conference, and NASA Joint Technology Workshop on Neural Networks and Fuzzy Logic held in 1994. He served as the Publication Chair for the 2000 IEEE International Conference on Fuzzy Systems and as a Program Committee Member for 28 international conferences. He was invited to serve as reviewer for over 60 international journals, which are in addition to major international conferences, and book publishers.

Xinguang Chen currently holds an Associated Professor at Wayne State University, Michigan, United States. He received his MD degree from Wuhan Medical College, China in 1982, Masters of Public Health in Biostatistics from Tongji Medical University, China, in 1987, and PhD degree in Biostatistics/Epidemiology from the University of Hawaii, United States in 1993. His research focuses on analytical methodologies and their utilization in the study of etiology and prevention of health risk behavior among adolescents with transdisciplinary perspective. Dr. Chen has been well published in public health and behavioral science fields.