Computational prediction of small-molecule catalysts

Abstract

Most organic and organometallic catalysts have been discovered through serendipity or trial and error, rather than by rational design. Computational methods, however, are rapidly becoming a versatile tool for understanding and predicting the roles of such catalysts in asymmetric reactions. Such methods should now be regarded as a first line of attack in the design of catalysts.

Just 40 years ago, computational methods for simulating chemical reactions used in synthesis did not exist. Since then, the discovery of several computational principles and algorithms — together with the development of fast computers — has resulted in enormous leaps in the accuracy and speed of computational methods, and it is now feasible to model many synthetic reactions in this way. It was the release of Gaussian 70 (a general-purpose, ab initio computer program that has developed into today’s Gaussian 03 software)¹ and the advent of minicomputers, both in the 1970s, that brought the tools of quantum mechanics to organic chemists. The subsequent development of quantum-mechanical techniques such as density-functional-theory calculations² and high-accuracy ab initio computational methods proceeded at an ever-accelerating pace³. In addition, methods were devised to reduce the lengthy times required to model large systems (those containing thousands of atoms) or smaller systems with high accuracy, and these methods continue to be improved³

The cost of computation has also decreased enormously since the 1960s. Moore’s law — which states that the number of transistors on an integrated circuit doubles every two years — reflects the incredible rate at which computing power is increasing. But a more impressive figure involves the economics of computing: the cost of 1 gigaflops of computing power in the 1960s was about US$7.9 trillion in today’s currency, whereas the same computing power is available now for less than 20 cents (ref. ⁴ and see http://news.bbc.co.uk/2/hi/technology/4554025.stm).

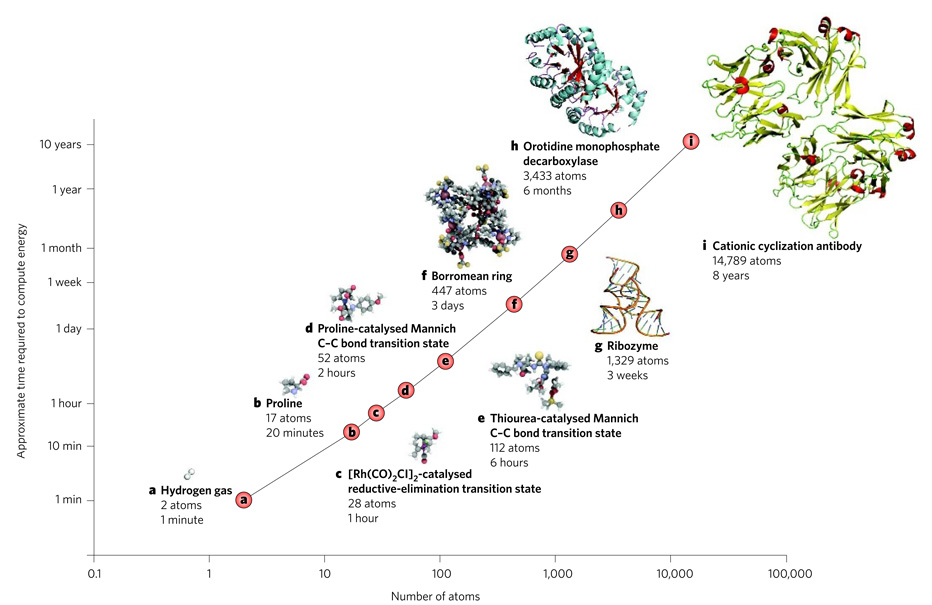
Today, there are computational methods for modelling molecules and reactions that can obtain results at almost any accuracy desired, as long as sufficient computer resources are available (Fig. 1). In practice, the energies of small molecular systems can be computed at greater accuracies (±1 kilocalorie per mol) than those achievable in most experiments. Larger systems are generally modelled at a lower accuracy so that results can be obtained within a reasonable time. The errors in absolute energies (typically ±5 kilocalories per mol) might therefore be larger than desired, but a much greater accuracy can be achieved when comparing several similar structures, for example the transition states of diastereomeric molecules.

Figure 1. Time required to compute molecular structures.

Shown is the approximate time taken to compute the structure of molecules of various sizes by using density functional theory and double-zeta basis sets on a modern desktop computer with appropriate memory and storage. The time required (shown on a log scale) increases exponentially with the size of the molecule. Structures were generated using PyMOL³⁵, QuteMol³⁶ or CYLview³⁷.

Computational methods are proving to be especially useful for modelling catalytic reactions. Such theoretical approaches readily provide insights into the mechanisms of catalytic processes and their selectivities for various products. Indeed, a theoretical approach is sometimes faster than an experimental one and is often the only way to attain the level of detail that chemists seek. Small chiral catalysts — either organic catalysts (organocatalysts; see page 304) or transition-metal complexes (organometallic catalysts; see page 314) — are ideal for computational modelling, because their size makes accurate simulations feasible, allowing detailed results to be generated and used to design new catalysts. Predicting how effective such catalysts will be in a specific reaction is still a daunting task, but several notable successes make it clear that computational design is becoming an increasingly powerful tool. We argue here that computational design is ready to take its place as an essential component of catalyst design.

The road to catalyst design

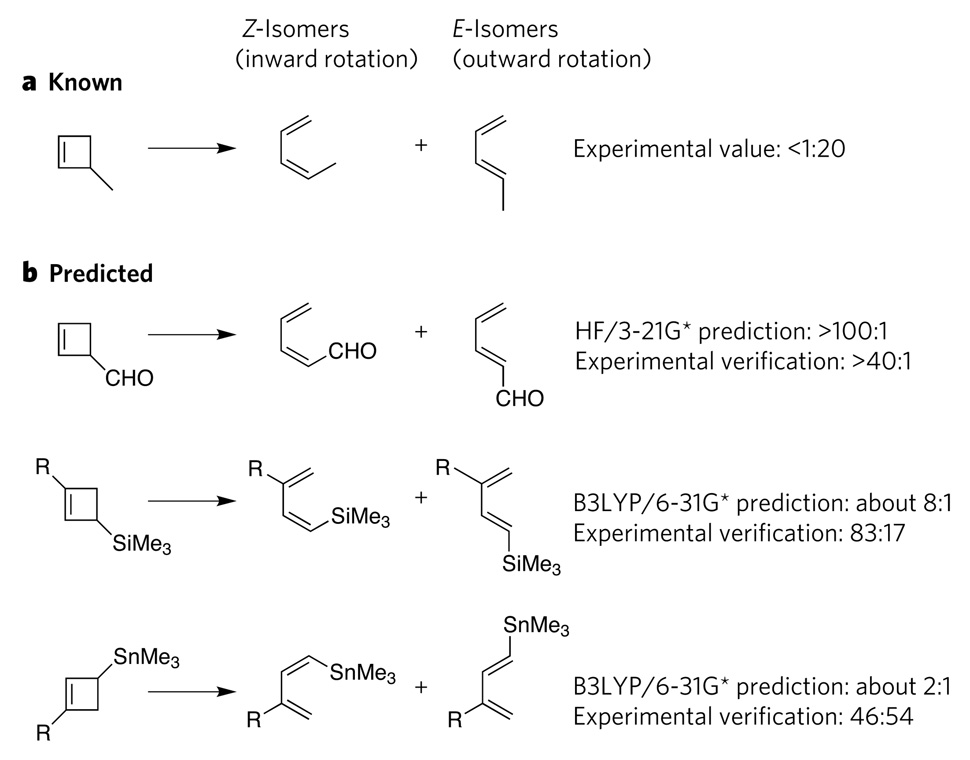
Most computational chemistry research involves the explanation of phenomena that are not well understood. Current quantum-mechanical methods have been successfully used for such rationalization of chemical phenomena. But, as quantum-mechanical methods have developed, it has become increasingly possible to make predictions (rather than rationalizations), and several predictions have now been confirmed experimentally. The first such predictions were for non-catalytic reactions involving small molecules. An example is the prediction and subsequent experimental verification of contra-steric stereochemistry in the products of the electrocyclic ring-opening of 3-formylcyclobutene⁵ (Fig. 2), a non-intuitive result that would not have been predicted by researchers on the basis of knowledge about reactions of the analogous molecule 3-methylcyclobutene. Subsequent to this prediction, Masahiro Murakami and colleagues predicted that, in cyclobutene ring-opening reactions, silyl groups and stannyl groups would also anomalously rotate inwards, and they then verified these predictions experimentally^6,7. Similarly, unexpected outcomes have been predicted computationally and verified experimentally for reactions commonly used in synthesis; for example, the stereoselectivity of hydride additions to cycloheptanones has been computed and confirmed in this way⁸.

Figure 2. Successful computational predictions of non-catalytic reactions.

a, In cyclobutene ring-opening reactions, 3-methylcyclobutene forms mainly the E-isomer of 1-methylbutadiene (as well as a small amount of the Z-isomer); the experimentally determined ratio is <1 Z-isomer to 20 E-isomers. b, Using this knowledge as a starting point, computations correctly predicted the stereochemical outcomes of three analogous reactions⁵–⁷, as verified by subsequent experiments, even though the products were mainly Z-isomers rather than E-isomers. In these reactions, the electron-withdrawing substituents favour inward rotation, whereas, in the original reaction, the electron-donating substituent favours outward rotation. HF/3-21G* is an ab initio computational method, and B3LYP/6-31G* is a density-functional-theory computational method. Me, methyl; R, CMe₂Ph.

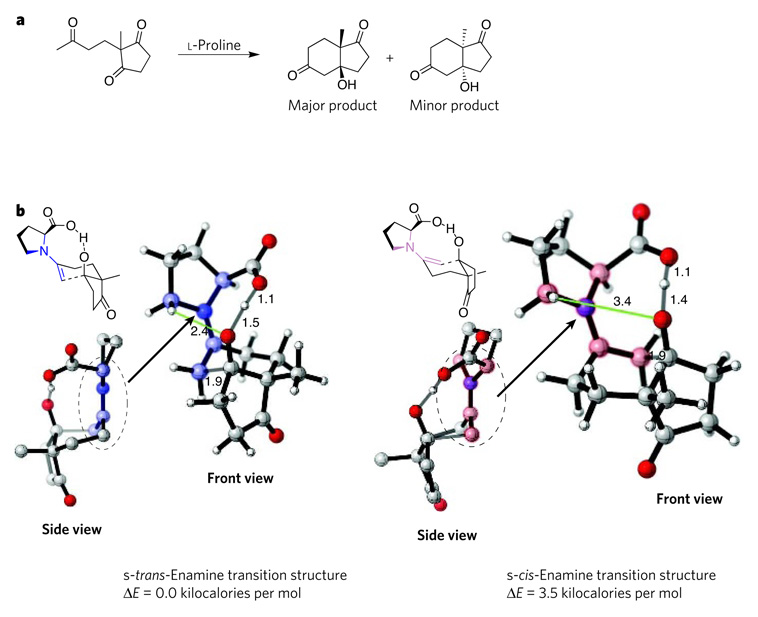
The first organocatalytic reaction to be studied computationally was the Hajos–Parrish reaction^9–11 (an asymmetric, intramolecular aldol reaction that is catalysed by l-proline), and this work was pivotal in showing the power of computational methods for studying and predicting catalytic reactions. Four mechanisms had been proposed for the Hajos–Parrish reaction. Of these, computations revealed a preference for the s-trans transition state (which has a vinyl group and a carboxylic acid in a trans arrangement across an enamine single bond), which leads to the experimentally observed product¹² (Fig. 3). The computed energy of 3.5 kilocalories per mol favouring the formation of the major stereoisomer corresponded well to the experimentally observed stereoselectivity of 95% enantiomeric excess, and could be explained by analysing the structural features that stabilize the s-trans transition structure rather than the s-cis form. Building on this precedent, computational studies of aldol reactions catalysed by proline derivatives have now been published¹³, including some predictions of new catalysts — although these have yet to be confirmed experimentally^14,15.

Figure 3. Transition structures of the Hajos–Parrish reaction.

The Hajos–Parrish reaction (a) was one of the first reported organocatalytic processes. Four possible transition states for this reaction were modelled¹² using the hybrid density-functionaltheory method B3LYP and the basis set 6-31G*. The computations revealed that the most favoured transition state involves the s-trans-enamine intermediate (b, left), which incorporates a shorter, and therefore more strongly stabilizing, electrostatic interaction (green) between a hydrogen atom in the pyrrolidine ring and the oxygen atom of the developing alkoxide than does the s-cis-enamine intermediate (b, right). The side view of the s-trans enamine shows that this intermediate is a stable, undistorted (planar) developing iminium ion, whereas the s-cis-enamine intermediate is an unstable, distorted (non-planar) developing iminium ion. The favoured transition state leads to the formation of the major product that is observed experimentally, whereas the other transition state leads to the minor product. The main structural differences between the two intermediates are shaded in pale blue (s-trans form) and pale pink (s-cis form). Carbon is shown in grey, hydrogen in white, oxygen in red and nitrogen in blue. Distances between atoms are indicated in angstroms. Structures were generated using CYLview³⁷. E, energy.

Designer organocatalysts realized

The first and most successful examples of the computational design of a stereoselective organocatalyst that was later experimentally validated came from studies of highly selective anti Mannich reactions¹⁶. Proline-catalysed Mannich reactions are selective for products in the syn orientation, but Carlos Barbas and his colleagues discovered that by using pipecolic acid (a proline analogue with a six-membered ring) as the catalyst, a mixture of syn and anti products resulted. The challenge then was whether further modifications could be made to the catalyst to result in reactions that were highly selective for the anti orientation.

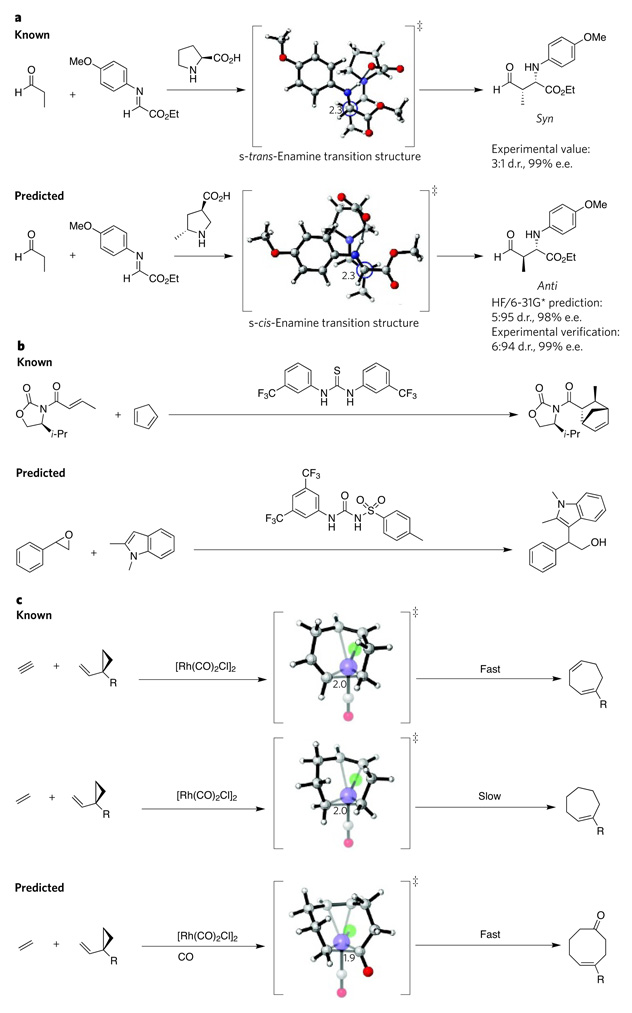
In collaboration with Barbas’s research group, we modelled the transition states of these reactions and found that selectivity for the anti orientation arises when the s-cis-enamine intermediate (formed from a reaction between the catalyst and the aldehyde reactant) attacks the imine starting material, rather than the alternative possibility in which the s-trans-enamine attacks¹⁷. On this basis, several potential catalysts that would favour the s-cis transition state were proposed, and computations were carried out to predict which of these molecules would be highly selective for the product in the anti orientation. The molecule shown in Fig. 4a was predicted to result in the anti product selectively (with 5% syn products and 95% anti products, and 98% enantiomeric excess). Subsequent experiments with this molecule by Barbas’s research group showed remarkable agreement with these predictions (6% syn and 94% anti, and 99% enantiomeric excess)¹⁶. Such in silico screening can be much quicker than making each potential catalyst and checking it experimentally, so these studies show how computational methods could be used to save time when designing catalysts.

Figure 4. Successful computational predictions of catalysts.

a, Most Mannich reactions catalysed by organocatalysts mainly yield products in the syn configuration (top). Chemists designed an organocatalyst selective for the anti configuration (bottom) based on computational analysis of information from a proline-catalysed Mannich reaction¹⁶. b, The design of an epoxide-activating urea catalyst (bottom) came from the computational analysis of known thiourea catalysts (top) that activate carbonyl-containing compounds¹⁹. c, Rhodium-catalysed [5 + 2]-cycloaddition reactions of vinylcyclopropanes with allenes (not shown) or alkynes (top) are fast, but the analogous reactions with alkenes (centre) are slow. Computational analysis of these reactions led to the design of an analogous [5 + 2 + 1]-multicomponent-cycloaddition reaction that yields cyclooctenones²³ (bottom). Carbon is shown in grey, hydrogen in white, oxygen in red, nitrogen in blue, chloride in green and rhodium in purple (large spheres). Critical carbon–carbon bond-forming distances in the transition structure are indicated in angstroms. Transition-state structures were generated using CYLview³⁷. d.r., diastereomeric ratio; e.e., enantiomeric excess; Et, ethyl; i-Pr, isopropyl; R, alkoxy, alkyl, siloxy; ‡, transition state.

Other types of organocatalysis have also proved amenable to computational predictions. Thioureas, for example, are effective catalysts for activating various substrates containing a carbonyl group¹⁸. But they are not as effective at activating epoxides. To tackle this problem, Stephen Connon, Isabel Rozas and their colleagues used computational methods to model the structures of analogues of thioureas and ureas in complex with epoxides¹⁹. On the basis of their results, they predicted that N-tosyl ureas would form stronger complexes with epoxides than would thioureas or ureas and therefore could catalyse epoxide ring-opening reactions. Subsequent experiments showed that this was the case —N-tosyl ureas successfully catalyse the addition of indoles to styrene oxides (Fig. 4b), whereas the previously known bis-(aryl)thiourea complexes are essentially inert.

These are examples of the state of the art in the computational design of catalysts. The greatest successes have involved modifying molecules that show some catalytic activity, through using the knowledge gleaned from computational models to design a second generation of catalysts. Given a well-understood candidate catalyst, chemists can use their intuition to suggest modified compounds that might work better or a diverse library of structurally related analogues to explore. Computations can then be used to determine which of these should be the best catalyst. This is akin to computational approaches to drug design, in which the activity of a compound is successfully optimized by starting with a ‘lead’ structure.

Designing organometallic reactions

Computational approaches are most accurate for predicting the catalytic activities of analogues of existing catalysts. But, in theory, these approaches should be able to make predictions about any class of compound, not just analogues of those used as a ‘training set’ for the computational model. Marisa Kozlowski and her colleagues have developed several computational tools to achieve this goal. They have created computational models for catalytic activity based on either the transition state for a particular reaction²⁰ (as calculated by quantum-mechanical methods) or the structures of the catalysts in their ground states²¹ (which are much easier to determine than transition states). Quantitative structure–selectivity relationships for catalysts can thus be developed. This method was used to predict new and effective β-aminoalcohols, ligands that help to catalyse enantioselective additions of diethylzinc to benzaldehyde.

Computational methods not only can help to design catalysts for known reactions but also can predict new catalytic reactions. Paul Wender and his colleagues have developed a series of reactions that are catalysed by the rhodium dimer [Rh(CO)₂Cl]₂, including several [5 + 2]-cycloaddition reactions of vinylcyclopropanes with alkynes or allenes²². Intriguingly, the analogous reactions with alkenes do not work. From this collaboration²² with Wender and one of us (K.N.H.), Zhi-Xiang Yu knew that the problem lay in the final step of the reaction mechanism (a reductive-elimination reaction). He speculated that an alternative alkene reaction — a [5 + 2 + 1]-multicomponent cycloaddition to form cyclooctenones — might occur if carbon monoxide was added to the reaction mixture. Yu computed the energies of the proposed new reaction and found that the [5 + 2 + 1]-cycloaddition was feasible²³. He and his coworkers then confirmed this prediction experimentally (Fig. 4c), showing that cyclooctenones form in the presence of carbon monoxide.

Speed versus accuracy

From the studies discussed here, it is clear that computational chemistry has proved its worth as a predictive tool for the development of catalysts. Methods for rapidly screening virtual libraries of catalysts have been developed²⁴, and leads from completed experimental screens can be modified in silico. Thus, only the most effective compounds need to be pursued in follow-up experiments. Nevertheless, highly accurate methods for modelling large molecular systems are lacking, and certain compromises must, inevitably, be made in terms of the accuracy of theoretical models. The development of techniques that allow reasonably accurate predictions in a short time is therefore a crucial strand of current research.

One example of such work has been reported by Ghislain Deslongchamps and his colleagues. They have developed a rapid computational method to screen transition structures of catalysed processes and have applied this method to various reactions, such as the TADDOL-catalysed hetero-Diels–Alder reaction²⁵. This useful method is based on molecular mechanics and assumes that the geometry of the substrate in the uncatalysed process is the same as in the catalysed one. However, this assumption might not always be accurate, so care must be taken in interpreting the results. Such methods sometimes predict transition states with relative energies that differ from those obtained using fully quantum-mechanical methods, owing to the approximate nature of the force-field method²⁶.

Experimental studies are usually carried out in solution, and the calculation of solvation energies is another factor that reduces the accuracy of computational methods. Most computational studies use polarizable continuum solvation models to compute solvation energies. These models use a polarizable continuum to compute the extent to which the solvent stabilizes the solute’s dipole, as well as surface and cavitation terms to describe the solute’s contact with the solvent²⁷. Specific individual interactions, such as hydrogen bonding, are overlooked in these models but can be captured by more elaborate models, such as explicit solvation dynamics²⁸. It should be noted that there are also pitfalls in using quantum-mechanical methods, such as the commonly used density-functional-theory calculations. These methods cannot accurately model dispersion forces (such as van der Waals interactions), which result from an electron-correlation effect. Although they have not been perfected, several recent theoretical advances are leading to more efficient and more accurate computations³.

Catalysts for all occasions

What is the prospect of predicting, from scratch, the efficacy of a catalyst for any arbitrary reaction? Is it even possible to predict accurately what occurs when a mixture of chemicals is placed in a solvent? These predictions are impractical at present, because of the numerous potential reactions that typically need to be studied to define any single system. It is clear, however, that computational chemistry is suited to predicting the activation energies and stereoselectivities of particular steps in a reaction pathway or even of whole catalytic cycles. For example, the complete catalytic cycles of proline-catalysed aldol reactions^10,11 and of transition-metal-catalysed cycloaddition reactions^23,29 have been studied computationally. But, in these cases, the overall reactions were known, so all of the potential competing reactions did not need to be computed.

Despite these issues, there have been some moderate successes in the a priori computational design of effective catalysts, such as the ‘theozyme’ approach. A theozyme is a theoretical catalyst, designed by computing the optimal geometry of functional groups to stabilize an uncatalysed transition state³⁰. Theozymes were originally devised to help to identify the catalytic residues of enzymes, but the same idea can be used to design catalysts. Hendrik Zipse and colleagues, for example, have used the computed transition structure for an uncatalysed amino lysis reaction³¹ to predict a host molecule that encapsulates and moderately stabilizes the transition state, leading to moderate catalysis³². Theozymes are also the starting point for the computational design of proteins that have folding properties and catalytic functions that differ from natural enzymes; two successful examples of this type have been reported, showing the power of computational design^33,34.

The de novo prediction of effective catalysts for any given reaction is a distant goal, but the computational prediction and design of more effective analogues of known catalysts is a reality. Similarly, during drug discovery, no one expects a drug to be designed from scratch using computational methods, but such techniques are invaluable for optimizing existing leads. At present, however, the use of computational methods for the design of catalysts is relatively rare, whereas it is an accepted — and some would say essential — part of drug discovery.

It is time for chemists’ perceptions of computational techniques to change. These techniques provide information about known catalytic reactions that is not available from experiments alone, but this information now extends beyond that obtained by mere rationalizations. As the examples discussed here show, computational techniques have become an invaluable tool for predicting the behaviour of catalysts and have earned their place as a standard tool for the design of catalysts.