Enzymatic Activity versus Structural Dynamics: The Case of Acetylcholinesterase Tetramer

Abstract

The function of many proteins, such as enzymes, is modulated by structural fluctuations. This is especially the case in gated diffusion-controlled reactions (where the rates of the initial diffusional encounter and of structural fluctuations determine the overall rate of the reaction) and in oligomeric proteins (where function often requires a coordinated movement of individual subunits). A classic example of a diffusion-controlled biological reaction catalyzed by an oligomeric enzyme is the hydrolysis of synaptic acetylcholine (ACh) by tetrameric acetylcholinesterase (AChEt). Despite decades of efforts, the extent to which enzymatic efficiency of AChEt (or any other enzyme) is modulated by flexibility is not fully determined. This article attempts to determine the correlation between the dynamics of AChEt and the rate of reaction between AChEt and ACh. We employed equilibrium and nonequilibrium electro-diffusion models to compute rate coefficients for an ensemble of structures generated by molecular dynamics simulation. We found that, for the static initial model, the average reaction rate per active site is ∼22–30% slower in the tetramer than in the monomer. However, this effect of tetramerization is modulated by the intersubunit motions in the tetramer such that a complex interplay of steric and electrostatic effects either guides or blocks the substrate into or from each of the four active sites. As a result, the rate per active site calculated for some of the tetramer structures is only ∼15% smaller than the rate in the monomer. We conclude that structural dynamics minimizes the adverse effect of tetramerization, allowing the enzyme to maintain similar enzymatic efficiency in different oligomerization states.

Introduction

Diffusion plays a critical role in a variety of biological processes, including in substrate-enzyme, antigen-antibody, and protein-nucleic acid associations (1,2). In diffusion-controlled processes, such as the termination of synaptic impulses, the rate of the initial diffusional encounter between the reacting particles determines or controls the overall rate of the reaction (3). Termination of neural signaling in the synapse requires a rapid breakdown of the neurotransmitter acetylcholine (ACh) into acetate and choline by the enzyme acetylcholinesterase (AChE) (4,5).

AChE is a serine hydrolase that exists as a monomer, dimer, or tetramer, the latter being the most important functional form under physiologic conditions (6,7). Three crystal structures of tetrameric AChE (AChEt) have been determined: two from Electrophorus electricus at 4.5 and 4.2 Å resolutions (PDB codes 1C2O and 1C2B) (8) and one from recombinant mouse at 2.9 Å resolution (PDB code 1MAA) (9). In all three structures, the tetramer is made up of two canonical homodimers aligned anti-parallel to each other (9). The arrangement of the individual subunits is such that 1MAA and 1C2O are compact whereas 1C2B is loose. Furthermore, 1MAA and 1C2B are pseudo-square planar whereas 12CO is not, suggesting the existence of AChEt in multiple conformations. Therefore, structural fluctuation was predicted to modulate substrate entry into, and product removal from, the active site gorges (8,10).

These structures lacked the C-terminal ∼40-residue tryptophan amphiphilic tetramerization (WAT) domain (11,12), which interacts with the proline-rich attachment domain (PRAD) of the collagenlike Q subunit. Therefore, a complete AChEt model was constructed by Zhang and McCammon (13) using 1C2O and the crystal structure of the PRAD/WAT complex (14). The resulting structure was found to be intermediate between 1C2O and 1C2B in terms of the assembly of the catalytic domains. Subsequent work based on this model, including normal mode analysis, coarse-grained (CG) Brownian dynamics (BD) and atomistic molecular dynamics (MD) simulations have shown that AChEt undergoes large scale intra- and intersubunit fluctuations (13,15). These multiscale simulations also found that the relative in-plane translation and out-of-plane rotational motions of the catalytic domains enable dynamic opening and closure of the peripheral anionic site (PAS) of the active site gorge (15), thus linking domain motion and substrate accessibility. Moreover, the motions were found to gate substrate-protein association and allow for the active center to be accessible for >80% of the time on average. The remaining outstanding question is the extent to which such structural fluctuations regulate catalytic efficiency.

An earlier computational work examined the consequence of tetramerization on the rate of ACh hydrolysis by comparing the reaction rates among individual active sites in the 1C2O and 1C2B tetramers, and between the tetramers and a monomer. It was found that the reaction rates differ for different individual active sites in the compact tetramer crystal structure (i.e., 1C2O); the rates are similar for different individual active sites in the loose (open) crystal structure (1C2B) (10). That work used a continuum diffusion model by solving the steady-state Smoluchowski equation (SMOL) (16). In this model, the ACh molecule is treated as a diffusing density of particles. The ACh diffusion is driven by the AChE-induced and solvent-mediated electrostatic field, which is calculated by solving the Poisson-Boltzmann equation (16). The time-dependent SMOL solver has been subsequently implemented and applied to the same systems (17,18). Because they used the same geometric mesh, reaction model, and electrostatic potential profile, the time-dependent and the steady-state diffusion models yielded nearly identical final reaction rates across a range of ionic strength values (10,17). Both studies concluded that, at physiological ionic strengths, the rates per active site for the compact tetramer are 67–75% of the rate for the monomer, whereas the corresponding rates for the open tetramer are comparable to the rate for the monomer (10,17). These studies thus suggested that structural dynamics may play an important role in the near diffusion-controlled hydrolysis of ACh by AChEt (19,20).

However, these calculations were performed only for two (1C2O and 1C2B) X-ray structures and an intermediate obtained by morphing between them. Thus they represent only three snapshots of a potentially diverse set of structures accessible to the enzyme. Furthermore, the tetramer structures lacked the WAT/PRAD domain, which may modulate function. Our current work extends the earlier efforts into a larger set of structures obtained from MD simulations of the complete tetramer representing, at least in part, a dynamic model of the enzyme under its physiologically most relevant oligomerization state. The current computational method also enhances and/or differs from the previous ones in several respects, such as in the reactive model, electrostatic solver, and mesh generation. For example, in both the steady-state and time-dependent implementations of SMOL, the chemical reaction was modeled by using a sink boundary condition on specified reactive molecular surface patch(es) around the active site gorge(s) (16). However, it is hard to reasonably define and track the reactive surface for a dynamic model of an enzyme using currently available mesh generation tools, because for each structure a new molecular surface mesh needs to be generated. To capture the gorge dynamics along with the enzyme conformational fluctuation, our model uses a reactive volume to model the chemical reactions in the active site gorge, rather than reactive surface patches used in the previous studies (10,16–18). The reactive volume is specified by the overlap of the gorges and a set of spheres with fixed radii (see the blue region in Fig. 1 formed by the union of these spheres). The positions of the spheres were determined by the location of residues that line the gorge, allowing them to move along with structural fluctuations. Therefore, the reactive volume more relevantly reflects the gorge opening and closure events and avoids the need of defining a reactive patch on the molecular surface mesh. This model was tested before (21).

Figure 1.

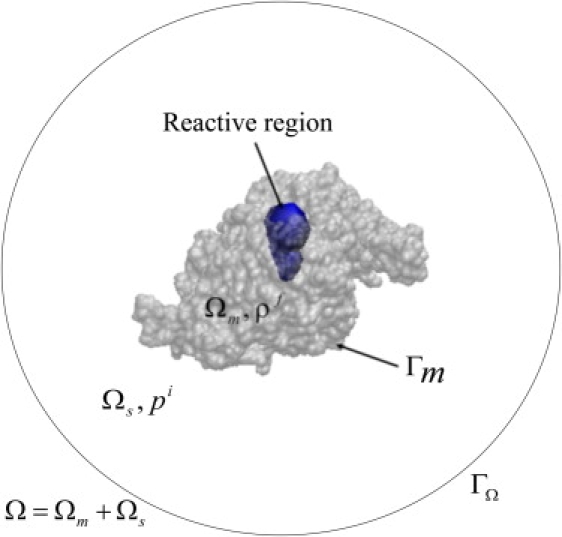
Schematic of the problem domain for a subunit of AChEt, highlighting the boundaries and volumes. Γ_m denotes the molecular boundary of the molecular domain Ω_m (shown by a transparent space-filling model of the molecule). The outer boundary Γ_Ω of the whole domain Ω is taken to be 3600 Å away from the molecular center, which is far enough as to mimic the bulk area. The blue region around the active site gorge represents the reactive region where the chemical reaction happens.

We use a recently developed hybrid numerical method and a fully continuum diffusion model for calculating both the electrostatic potentials and reaction rates (18). This hybrid method, termed FEM/BEM, employs combined finite element methods (FEM) and boundary element methods (BEM) to solve the Poisson-Boltzmann (PB) or the Poisson-Nernst-Planck (PNP) equations. With the same mesh resolution, BEM typically yields improved electrostatic potential in the vicinity of molecular surfaces where the reaction occurs, thus improving the rate prediction (18,22). When the PB solver is used for calculating the electrostatic potential, the method is equivalent to the SMOL method, which we refer to as an equilibrium method, since in this method the spectator ions are supposed to obey the Boltzmann distribution and the substrate concentration is not supposed to affect the electrostatic field. On the other hand, if the PNP solver is used, it allows coupling of the potential with the charged substrate flux that is caused by chemical reaction and breaks the equilibrium distribution of the full set of charges. Therefore, the FEM/BEM PNP model improves the diffusion description by taking into account the effect of nonequilibrium charge distribution on the electrostatic interactions of the whole diffusion-reaction system. In addition, all the meshes are consistently generated using recently developed software (23), and include both the molecular interior domain and exterior domain for each snapshot to meet the requirements of the FEM/BEM PNP hybrid numerical method (18).

Using this methodology and the MD-generated structures, we have investigated how the structural dynamics of AChEt modulates the rate of ACh hydrolysis. We show that, under both the equilibrium and nonequilibrium conditions, the average reaction rate per active site is ∼22–30% slower in the rigid initial tetramer than in the monomer. This effect of tetramerization is modulated by structural fluctuations, which either enhance or reduce substrate access to the active site via steric and/or electrostatic effects. The interplay between these two effects is complex, being complementary or antagonizing depending on the overall structure of the tetramer. Interestingly, the rate per active site calculated for some of the tetramer structures is only ∼15% slower than in the monomer, suggesting that the negative effect of tetramerization is significantly mitigated by the intrinsic mobility of the enzyme.

Methods

The diffusion-controlled reaction between ACh and AChEt can be measured by the reaction rate coefficient, k_on. Several methods have been developed to compute k_on based around continuum electrostatics and Brownian dynamics simulations (16,24). In these methods, the substrate (ACh) diffuses to the enzyme (AChEt) steered by the electrostatic field generated by the latter. Because the electrostatic field is calculated from the distribution of charges on the structures and the protein-solvent boundaries are defined by the molecular geometry, the choice (and dynamics) of the AChEt structure plays a crucial role. Therefore, below we discuss how the dynamic structural models of AChEt were prepared for the current calculations of k_on. Then the main ideas behind the computational models used to compute k_on are briefly discussed.

Preparation of dynamic models

Our previous analysis of an all-atom explicit solvent molecular dynamics (MD) and Cα-based coarse-grained (CG) implicit solvent Brownian dynamics (BD) trajectories found that intersubunit fluctuations modulate active site accessibility (15). The implication of this result was that dynamics modulates the enzymatic reaction rates. This prediction could only be fully tested by assessing the enzymatic efficiency for thousands of snapshots along the multiple μs-long CG trajectories, which is prohibitively expensive. In principle, a set of carefully selected snapshots might have been sufficient. However, lack of atomistic details required for molecular surface and mesh generation presents additional challenges; attempts to remap side chains onto Cα-based models have so far failed to yield reliable results. Nonetheless, we reasoned that the predicted correlation between the observed intersubunit fluctuations and enzymatic efficiency may be illustrated based on a few carefully selected conformers from the 20-ns-long atom-scale MD simulation (see (15) for simulation details). In other words, based only on ns-scale fluctuations, we sought to establish the link between dynamics and reaction rates, without attempting to directly capture or quantify the entire effect of dynamics. Therefore, 11 evenly-spaced snapshots representing various levels of opening/closure of the gorge, as measured by the occlusion number defined before (15), were used for computing k_on. The diffusion-reaction is calculated independently for each of these snapshots.

For the purpose of defining, visualizing, and measuring the gorge volume, we defined six overlapping spheres centered at the center-of-mass of the C_α and C atoms of the following residues:

• 203;

• 121, 448, 297, 447, 236;

• 83, 122, 295, 72, 236, 334, 447, 236;

• 82, 124, 297, 338, 295, 341;

• 286, 341, 72, 338, 342, 297, 80, 337, 294, 296;

• 286, 341, 74, 342, 80, 343, 293, 292, 368.

The radius of these spheres was 4.5, 5.0, 5.0, 6.0, 7.0, and 8.0, respectively. For each tetramer (and the corresponding monomer), coordinate files containing charges and radii (PQR files) were prepared by the program PDB2PQR (25,26); the radii of all polar hydrogen atoms was set to 1 Å.

Computational model

The continuum PNP model is used for the electrostatic potential and rate calculations of the electro-diffusion-reaction process. All the mobile charged species, including the substrate ACh, are treated as diffusing particles with continuous density distributions. The diffusion of the mobile particles is influenced by the electrostatic field generated by the macromolecule AChEt, as well as by all the mobile particles themselves. In this work, we have three diffusing species; two are salt ions (e.g., Cl⁻ and Na⁺) and the third is the substrate ACh. The following PNP equations describe the coupling of the electrostatic potential field with diffusion-reaction processes through the Nernst-Planck (NP) equation (Eq. 1), which describes the diffusion processes of the two ions and the substrate outside the biomolecule (Ω_s), and the Poisson equation (Eq. 2), which describes the electrostatic field for the whole system domain (Ω). The system is set up as in Fig. 1:

$$\nabla \cdot [D^{\text{i}}\nabla p^{\text{i}}\left(r\right)+D^{\text{i}}\beta q^{\text{i}}{p}^{\text{i}}\left(r\right)\nabla \varphi ]+{\alpha }^{\text{i}}{p}^{\text{i}}\left(r\right)=0,i=1\dots 3,r\in {\mathrm{\Omega }}_{\text{s}},$$ (1)

$$\nabla \cdot \varepsilon \left(r\right)\nabla \varphi \left(r\right)=-{\rho }^{\text{f}}\left(r\right)-\sum _{\text{i}}{q}^{\text{i}}{p}^{\text{i}}\left(r\right),r\in \mathrm{\Omega }\text{.}$$ (2)

In these equations, the density distribution function of the diffusing particles of the i^th species is represented by pⁱ(r), its diffusion coefficient by Dⁱ(r), and charge by qⁱ. The fixed source charge distribution on the biomolecule (usually the atomic charges) is denoted by ρ^f(r). β is the inverse Boltzmann energy, ɛ is the dielectric coefficient, ϕ is the electrostatic potential determined by the Poisson equation, and αⁱ is the intrinsic reaction rate constant that describes the chemical reaction in a reactive region around the active site (see Fig. 1). Because two of the diffusing species, the salt ions, are nonreactive, α¹ = α² = 0. In earlier studies, the last term of the left-hand side of Eq. 1 vanishes, and the reaction between the biomolecule and the diffusing particle was described via a sink boundary condition on the reactive molecular surface patch (10,16–18). In our model, reaction events occur in certain regions such that the intrinsic reaction rate for the reactive species ACh, α^ACh, is nonzero in a properly selected reactive region (see previous section) and zero otherwise. The intrinsic rate should be large in diffusion-controlled reaction processes. Different bulk densities are applied on the outer boundary (Γ_Ω; Fig. 1) as boundary conditions for different species, while maintaining the neutrality condition. In the NP equation, the reflecting boundary condition is applied on the whole molecular boundary (Γ_m; Fig. 1) for all species. In the PNP model, the ionic strength includes contributions from the bulk concentration of all three diffusive species. When solution is achieved, the reaction rate coefficient k_on of ACh, defined as the reaction rate divided by the bulk concentration, is thus calculated through

$$\frac{\int {\alpha }^{\text{ACh}}{p}^{\text{ACh}}\left(x\right)d{x}^3}{{\rho }_{\text{bulk}}^{\text{ACh}}}\text{.}$$

The intrinsic reaction rate constant α and the radii of the spheres used to define the reactive region (see above) were determined by extensive tests of equilibrium calculations in which these parameters were varied. The initial symmetric model, which is close to the crystal structure 1C2B with all four active sites open, was used for these test calculations. The calculated rate constant for each subunit was then compared with previous results (10). Values of α, and radii that yielded subunit k_on values whose relative magnitude among the four subunits is similar to those reported in Zhang et al. (10), were selected. A final value of 1.0 × 10⁵ s⁻¹ for α obtained in this manner was used for all calculations presented in this work.

Before numerical solution, it was necessary to generate the molecular surface and discretize the whole domain, which was done for each selected AChE tetramer structure using our recently developed mesh generation tool (23). All the atomic charges, radii, and mesh control parameters were kept the same among all structures. We then used the FEM/BEM hybrid method to solve both the equilibrium (SMOL) and the nonequilibrium (PNP) equations for each structure. The detailed numerical methods of such continuum models were given in Lu et al. (18) and Lu and McCammon (21), and some applications on AChE monomer and sphere cases were also shown to yield good results. However, we would like to mention some underlying limitations of this model for future considerations:

• The substrate size and geometry effects are highly reduced.

• The results are very sensitive to the molecular surface representation.

• Some parameters such as reactive region/patch and intrinsic reaction rate constant need to be fitted or parameterized according to existing experimental data.

• The enzyme dynamics is not coupled with the substrate diffusion-reaction process in the continuum model.

• The enzyme concentration effects are hard to include in the current model.

Results and Discussion

The dynamics of AChEt, which has been discussed in a previous publication (15), is exemplified here by the structures shown in Fig. 2. Reaction rate coefficients were calculated for 11 such structures. To facilitate comparison among multiple rate coefficients, we define the following terms: $k_{\text{on}}^{\text{m},\text{i}}$ represents the rate coefficient of monomer i whose structure is extracted from the tetramer, $k_{\text{on}}^{\text{s},\text{i}}$ is the rate coefficient for subunit i in the tetramer, and $k_{\text{on}}^{\text{t}}=\sum _{\text{i}=1}^4{k}_{\text{on}}^{\text{s},\text{i}}$ is the rate coefficient for the tetramer. In the following, we first probe (using a single structure) the effect of tetramerization on the reaction rate by comparing $k_{\text{on}}^{\text{t}}$ with the sum of $k_{\text{on}}^{\text{m}}$ over the four monomers ($\sum _1^4{k}_{\text{on}}^{\text{m},\text{i}}$). Then we discuss the modulation of $k_{\text{on}}^{\text{t}}$ by structural fluctuations, as well as the relative role of steric and electrostatic effects on the rate coefficients. Note that reaction rate coefficients were calculated for a number of ionic strength conditions. The dependence of the rate coefficients on the ionic strength was found to be very similar to previous reports (10,17). We therefore limit our discussion to a single ionic strength value of 150 mM.

Figure 2.

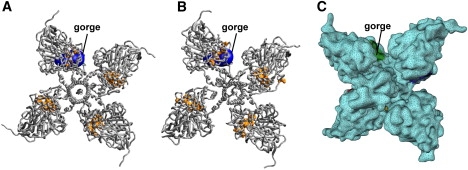
Cartoon and mesh representations of the acetylcholinesterase tetramer. (A) The initial symmetric model and (B) a snapshot after 10 ns of atomistic MD simulation; and (C) mesh representation of the structure in panel A. Selected residues (72, 82, 83, 121, 122, 124, 236, 295, 297, 334, 338, 341, 447, and 448) of the gorge are shown as surfaces (orange).

Reaction rates for monomeric and tetrameric AChE

Table 1 lists the reaction rate coefficients calculated for the complete tetramer, and monomers obtained by deleting the other three subunits and PRAD.

Table 1.

Rate coefficients for a complete tetrameric model of AChEt (× 10⁻¹¹ M⁻¹ min⁻¹)

		Subunits
Condition (solver)		1	2	3	4	Mean (±SD)	Sum
Equilibrium (SMOL)	$k_{\text{on}}^{\text{m}}$	2.36	2.19	2.21	2.51	2.32 (±0.15)	9.27
	$k_{\text{on}}^{\text{s}}$	2.11	1.52	1.81	1.76	1.80 (±0.24)	7.22
	$\Delta =k_{\text{on}}^{\text{m}}-k_{\text{on}}^{\text{s}}$	0.25	0.67	0.40	0.75	0.52 (±0.23)	2.05
	$\frac{\Delta }{k_{\text{on}}^{\text{m}}}\times 100$	10.6	30.6	18.1	29.9	22.3 (±9.68)	22.1
Nonequilibrium (PNP)	$k_{\text{on}}^{\text{m}}$	2.18	2.20	2.04	2.36	2.20 (±0.13)	8.78
	$k_{\text{on}}^{\text{s}}$	1.67	1.53	1.63	1.42	1.56 (±0.11)	6.25
	$\Delta =k_{\text{on}}^{\text{m}}-k_{\text{on}}^{\text{s}}$	0.51	0.73	0.41	0.94	0.65 (±0.23)	2.53
	$\frac{\Delta }{k_{\text{on}}^{\text{m}}}\times 100$	23.4	33.2	20.1	39.8	29.1 (±9.00)	25.7

The structure used for these calculations is the initial symmetric model in which all four active sites were open. This same structure was used to initiate the MD simulations. The data are for an ionic strength of 150 mM. The concentration of ACh in the PNP calculations was 100 mM.

The computed rate coefficients using the equilibrium SMOL method are 7.22 × 10¹¹ M⁻¹ min⁻¹ for the tetramer (i.e., $k_{\text{on}}^{\text{t}}$) at ionic strength of 150 mM, 2.19–2.51 × 10¹¹ M⁻¹ min⁻¹ for $k_{\text{on}}^{\text{m},\text{i}}$ and 1.52–2.11 × 10¹¹ M⁻¹ min⁻¹ for $k_{\text{on}}^{\text{s},\text{i}}$. Thus, $k_{\text{on}}^{\text{t}}$ is ∼78% of the sum of $k_{\text{on}}^{\text{m},\text{i}}$ ($\sum _1^4{k}_{\text{on}}^{\text{m},\text{i}}$ = 9.27 × 10¹¹ M⁻¹ min⁻¹). Furthermore, the change in the rate ($\Delta =k_{\text{on}}^{\text{m}}-k_{\text{on}}^{\text{s}}$) shows that tetramer formation reduces the rate per active site by 10–30%. This is interesting because all four active sites in the current tetramer are open (Fig. 2), and the structures of the monomers were directly extracted from the tetramer. These results thus indicate that even for a hypothetical case where tetramerization did not alter the structure of the assembled monomers, and even for relatively well open active sites, the presence of an opposing subunit reduces catalytic efficiency by ∼22%.

For the x-ray structure with two of the four active sites partially occluded (PDB code 1C2O), previous computations found that $k_{\text{on}}^{\text{t}}$ is ∼67–75% of that expected from four monomers (10,17). The average $k_{\text{on}}^{\text{m}}$ of the current calculations (2.32 ± 0.15 × 10¹¹ M⁻¹ min⁻¹) is close to what has been calculated for one of the fully open active sites in the 1C2B structure (∼1.94 × 10¹¹ M⁻¹ min⁻¹) (10,17). Overall, the current and previous results compare surprisingly well, given the different structure (the previous computations were carried out on the C-terminally truncated structures lacking the WAT/PRAD domain) and computational methods employed.

Table 1 also lists rate coefficients computed by the nonequilibrium PNP model at a substrate concentration of 100 mM. We can see that, although the magnitudes of the rates are generally lower due perhaps to ionic screening among ACh molecules, the overall trend remains similar to that computed by the equilibrium SMOL model. The reduction in the rate per active site due to tetramerization is between 20% and 40% (mean = 29%). Thus, irrespective of the reaction conditions, the rate for the tetramer is ∼70–80% of the corresponding rate for the four monomers.

Two additional lessons can be drawn form Table 1. The first is that differences in $k_{\text{on}}^{\text{m},\text{i}}$ (as well as $k_{\text{on}}^{\text{s},\text{i}}$) among subunits indicate attenuation of enzymatic efficiency by local structural fluctuations. This effect modulates the rates by ∼14% (estimated as (maximum–minimum)/mean) and can be caused by small differences around the active site, such as side-chain reorientations. The second important lesson is that if the monomers assemble into a tetramer with their structure unaltered, the reaction rate per active site reduces by 10–30% (SMOL) and 20–40% (PNP). This is solely the consequence of tetramerization, and arises from steric blockade and/or modulation of the active site electrostatic field by an opposing subunit. Because AChEt is a dynamic assembly of monomers that undergoes large-scale intersubunit fluctuations, the effect of tetramerization was predicted to be attenuated by the dynamic opening and closure of individual active sites (15). The following sections thus investigate the extent to which conformational fluctuation mitigates or enhances this negative effect of tetramer formation on reaction rate.

Dynamic rate coefficients at equilibrium: SMOL

Fig. 3 A displays the rate coefficients for 10 snapshots from a MD simulation and the initial model used to initiate the simulation (see Methods). The calculated $k_{\text{on}}^{\text{t}}$ values of 6.12–7.89 × 10¹¹ M⁻¹ min⁻¹ indicate that structural fluctuation modulates the reaction rate by ∼25% ((maximum–minimum)/mean). Notice that the rates for the individual subunits, $k_{\text{on}}^{\text{s},\text{i}}$, exhibit large variations. For example, for structure #5 (index starting from 0), $k_{\text{on}}^{\text{s},4}$ is only ∼50% of $k_{\text{on}}^{\text{s},3}$. On the other hand, the rates of these same subunits differ by ∼17% in structure #7. Interestingly, the rate fluctuations reflect the intersubunit fluctuations and PAS occlusions reported before (15). For instance, in almost all the structures, $k_{\text{on}}^{\text{s},4}$ represents the smallest calculated rate, which is consistent with subunit 4 being the most occluded in the simulations (see Fig. 4 of (15)). Furthermore, the $k_{\text{on}}^{\text{t}}$ values for structures #5 and 7 (Fig. 3 A) are only ∼15% smaller than the sum of the monomer $k_{\text{on}}^{\text{m}}$ values ($\sum _1^4{k}_{\text{on}}^{\text{m},\text{i}}$, Table 1). This result clearly shows that structural dynamics indeed mitigates the reduction in reaction rate upon tetramerization.

Figure 3.

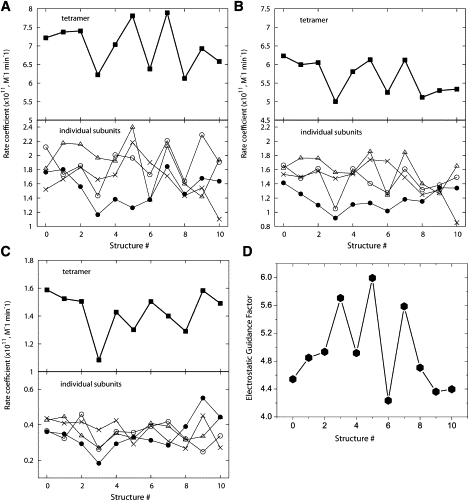
Calculated k_on values and the role of electrostatics. Results from SMOL and PNP methods are shown in panels A and B. In these calculations, the diffusing particle ACh was assigned a unit positive charge. (C) SMOL-calculated k_on with the charge on ACh turned off. (D) The electrostatic guidance enhancement factor (EGF) calculated as the ratio of the tetramer k_on values shown in panels A and C. Eleven structural models (the initial model plus 10 snapshots from MD simulation) were used. (Open circles) Subunit 1; (cross) subunit 2; (triangle) subunit 3; and (solid circles) subunit 4.

Figure 4.

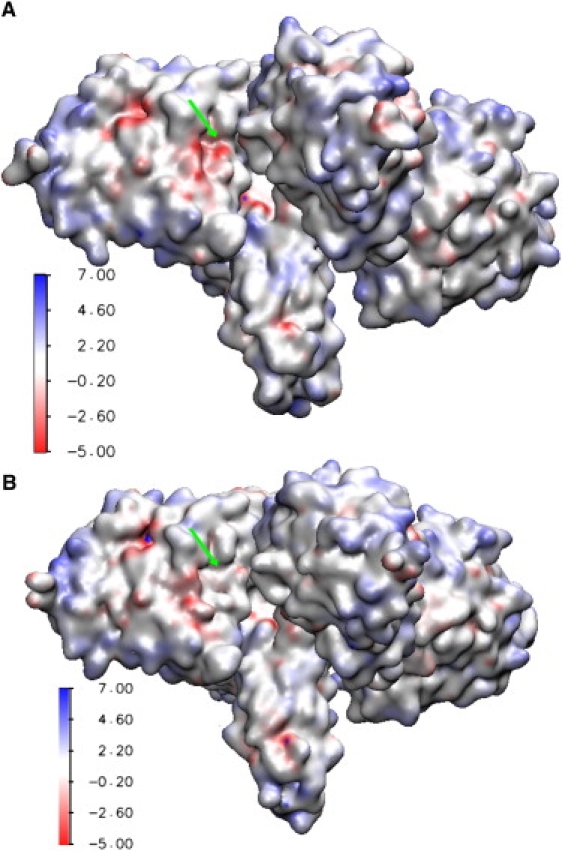
Electrostatic potential surfaces at ionic strength of 150 mM: (A) structure #5; (B) structure #6. The active site gorge for subunit 3 is indicated by arrow and is used to highlight the correlation between reaction rate and variation in the electrostatic steering force due to structure dynamics. We find from Fig 3A that $k_{\text{on}}^{\text{s},3}$ = 2.40 × 10¹¹ M⁻¹ min⁻¹ in structure #5 (A) and 1.37 × 10¹¹ M⁻¹ min⁻¹ in structure #6 (B), with the difference accounting for ∼69% of the difference in the overall reaction rate of $k_{\text{on}}^{\text{t}}$ = 7.80 × 10¹¹ M⁻¹ min⁻¹ (structure #5) and 6.30 × 10¹¹ M⁻¹ min⁻¹ (structure #6). The $k_{\text{on}}^{\text{t}}$ values calculated with the neutral ACh are reversed, being 1.30 × 10¹¹ M⁻¹ min⁻¹ and 1.50 ± 10¹¹ M⁻¹ min⁻¹ for structures #5 and 6, respectively. The higher rate coefficient in structure #5 is entirely due to the stronger electrostatic effect, as can be seen from the relative intensities of the negative electrostatic potentials in panels A and B.

It is noteworthy that large-scale spatiotemporal fluctuations, such as those sampled by our previous CG-BD simulations, allow opening of the active sites for ∼80% of the time. Assuming that the reaction rates for those open structures would be greater than or equal to those calculated for structures #5 and 7, the tetramer rate per active site would, on average, be at least 85% of the rate for the monomer. This conclusion is consistent with experimental data that suggest only small loss of catalytic efficiency upon tetramerization (27). Additionally, despite the occasional occlusion of some of the PAS in several of the structures considered here, the average $k_{\text{on}}^{\text{t}}$ (7.0 ± 0.61 × 10¹¹ M⁻¹ min⁻¹) is within error of the rate measured for the initial structure whose active sites are all open (Table 1).

Dynamic rate coefficients at nonequilibrium: PNP

The $k_{\text{on}}^{\text{t}}$ values calculated by the nonequilibrium PNP method (Fig. 3 B) are 5.00–6.23 × 10¹¹ M⁻¹ min⁻¹, indicating that structural fluctuations modulate $k_{\text{on}}^{\text{t}}$ by ∼22%, which is close to the value calculated by SMOL. Furthermore, similar to the SMOL results, the average $k_{\text{on}}^{\text{t}}$ (5.67 ± 0.47 × 10¹¹ M⁻¹ min⁻¹) is within error of the $k_{\text{on}}^{\text{t}}$ for the initial structure under the same condition (Table 1). Overall, the conclusions drawn from the SMOL method regarding the dependence of the reaction rate on structural dynamics also hold for PNP. That $k_{\text{on}}^{\text{t}}$ is modulated by roughly 25% in both methods further emphasizes the important role of dynamics on the efficiency of AChEt.

However, there are notable differences between the SMOL- and PNP-calculated reaction rate coefficients. The first is that the k_on values calculated by PNP are generally smaller than those calculated by SMOL. In SMOL, the calculated rate coefficients are not dependent on ACh bulk concentrations, as they are in the more complete PNP model. As noted above, this may suggest ionic screening among the 100 mM substrate molecules for binding to the active sites. In general, however, the ACh concentration flux can affect the electrostatic field in various ways, thereby influencing the reaction rates in ways that are difficult to predict; the conditions employed in the current PNP calculations clearly favor factors that lower the rates. The second, and perhaps most important, difference is that the relative rates among the 11 structures are different in the two methods. For example, the largest $k_{\text{on}}^{\text{t}}$ calculated by PNP is the one for the initial structure (structure #0). In contrast, the SMOL-calculated $k_{\text{on}}^{\text{t}}$ is highest for structures #5 and 7. This data suggests that subtle electrostatic interactions between ACh and AChEt, as well as intersubstrate interactions in the confined reactive regions, are captured by PNP but not by SMOL. The fact that the reaction rates and their dependence on structure vary with the specific representation of the diffusing particle and the model used to describe the reaction conditions has major implications for future studies and methods developments.

Role of electrostatics on rate coefficients

In our model, the overall reaction rate is dictated by the geometry and the electrostatic potential of the biomolecule. In the preceding sections, we discussed the role of tetramerization and its fluctuations on the reaction rates. We found that tetramerization reduces the reaction rate by an average of 22% and 29% in the SMOL and PNP methods. Moreover, we found that structural fluctuations modulate the reaction rate by ∼25% in both methods. Such a modulation of the reaction rate by structural fluctuations can arise from purely geometric (or steric) effects, electrostatic effects, or a combination of both.

Previous rate calculations on the available x-ray structures showed that, in the limit of zero salt, the reaction rates per active site for the tetramers are the same as that for the monomer, whereas at higher ionic strength, the rates per active site for the tetramers are 67–75% of the rate for the monomer (10). It was also found that electrostatic forces play an even more important role for the tetramers than for the monomer. It would be interesting to ask: what are the relative roles of geometry and electrostatics and how are they affected by structural fluctuations?

To address this issue, we considered the case where diffusion is not controlled by the electrostatic potential, i.e., the substrate diffuses freely, and repeated the rate calculations after turning off the single positive charge on ACh. The results are displayed in Fig. 3 C. As noted before (10), the reaction rates for the neutral substrate are much smaller than its charged counterpart; the $k_{\text{on}}^{\text{t}}$ for the uncharged substrate is 1.09–1.59 × 10¹¹ M⁻¹ min⁻¹ (mean = 1.43 ± 0.15 × 10¹¹ M⁻¹ min⁻¹), which is roughly six times smaller than that for the charged ACh. This is consistent with the expected electrostatic guidance of the charged substrate to the active site. To quantify the extent of the electrostatic guidance, and its modulation by structural fluctuations, we used the electrostatic guidance enhancement factor (EGF). EGF has been defined as the ratio between the rates of the charged (q = 1) and neutral (q = 0) substrate (10):

$$EGF=\frac{k_{\text{on}}\left(q=1\right)}{k_{\text{on}}\left(q=0\right)}\text{.}$$ (3)

The EGFs for the tetramer displayed in Fig. 3 D show that the dependence of the electrostatic guidance on structure is large and complex; in some cases, the effects of electrostatics and geometry are complimentary while in other cases either one of them predominates. To illustrate this point, let us consider structure #5, which has the highest EGF and hence the largest effect of electrostatics on the rate coefficient $k_{\text{on}}^{\text{t}}$, and structure #6, which exhibits the smallest EGF and hence the smallest effect of electrostatics on $k_{\text{on}}^{\text{t}}$. For the charged substrate, the $k_{\text{on}}^{\text{t}}$ for structure #5 is ∼1.21-times that for structure #6 (Fig. 3 A, upper panel). For the neutral ACh, however, the order is reversed with $k_{\text{on}}^{\text{t}}$ for structure #5 being only ∼0.87-times that for structure #6 (Fig. 3 C, upper panel). If the effect of electrostatics was similar in the two structures, the relative magnitude of the $k_{\text{on}}^{\text{t}}$ would have been the same in the charged and neutral ACh. Moreover, if there was no change in geometry, i.e., if steric effects were unaltered, the rate coefficients would have remained the same in the two structures―indeed in all the structures―for the neutral substrate. In general, the difference in the distribution of the rate coefficients calculated for the neutral and charged substrates and the fact that the EGF varies among structures demonstrate that intersubunit fluctuations modulate the rate of reaction both directly via steric hindrance of substrate access to the active site and indirectly by either enhancing or diminishing the electrostatic steering force.

A closer inspection of the data in Fig. 3 reveals additional insights into the role of dynamics in modulating the interplay between steric and electrostatic effects on the rate of reaction. For example, the steric effect in structure #5 substantially reduced the rate coefficient, but it is compensated for by the electrostatic effect. In contrast, in structure #6 the steric effect predominates over the electrostatic effect (Fig. 3, A, C, and D). Fig. 3 further shows that, from among the four subunits, subunit 3 (Fig. 3 A, triangles) has the highest rate coefficient in structure #5 ($k_{\text{on}}^{\text{s},3}$ = 2.40 × 10¹¹ M⁻¹ min⁻¹) but the lowest in structure #6 ($k_{\text{on}}^{\text{s},3}$ = 1.37 × 10¹¹ M⁻¹ min⁻¹); this difference accounts for ∼69% of the difference in the tetrameric rate coefficient ($k_{\text{on}}^{\text{t}}$) of the two structures. Interestingly, the $k_{\text{on}}^{\text{s},3}$ values calculated with the neutral ACh are reversed, being 0.33 × 10¹¹ M⁻¹ min⁻¹ and 0.42 × 10¹¹ M⁻¹ min⁻¹ for structures #5 and 6, respectively. These data clearly suggest that 1), the active site gorge of subunit 3 is more open in structure #6 than in structure #5; and 2), the faster reaction rate in subunit 3 of structure #5 is entirely due to the rate enhancement by electrostatics. The PB-calculated electrostatic potentials can be used to visualize the source of the electrostatic-dominated rate enhancement in structure #5 relative to structure #6 (Fig. 4). The electrostatic potential around the active site gorge of subunit 3 (indicated by arrow) is substantially more negative (red) in structure #5 than in structure #6. The stronger electrostatic attractive force generated by the more negative electrostatic field in structure #5 is able to more effectively steer the diffusing positively charged ACh substrate toward the active site gorge. In summary, the reaction rate of AChEt is modulated not only by the change in the shape of the active site gorge that occurs during dynamics, but also by the alteration in the intensity and distribution of the electrostatic field around the active site gorge.

Concluding Remarks

Interplay among dynamic, electrostatic, and steric effects on enzymatic efficiency

In an earlier work, we used a combination of coarse-grained and atomistic simulations to probe the dynamic modulation of substrate access to the active sites of AChEt (15). We found that AChEt exhibits long timescale intersubunit domain motions involving in-plane translation and out-of-plane rotations of the catalytic domains relative to one another. These motions lead to dynamic occlusions and openings of the peripheral sites. We predicted that these openings of the active sites would minimize the reduction in the reaction rate arising from tetramer formation. To test this prediction, one needs to directly assess the effect of dynamics on enzymatic efficiency. As noted in Methods, a more comprehensive test would require the use of many thousand structural models of the tetramer that represent all the statistically relevant conformational states and various degrees of active site opening. However, on the one hand, atomistic representation of the structures is necessary for the rate calculations, yet exhaustive sampling with atomistic techniques is not practical. On the other hand, Cα-based coarse-grained simulations can achieve the required level of sampling (15), but remapping side chains back onto the Cα-model would not be reliable; it would in fact introduce significant error on the rate calculation because the rate coefficients depend on the electrostatic field, which is dominated by charged side chains. We chose a compromise solution and sought to illustrate the correlation between reaction rate coefficients and enzyme dynamics using selected conformers from an atomistic MD simulation. The results were therefore not expected to unambiguously quantify the entire effect of dynamics on the enzymatic efficiency of AChEt. However, the correlation between dynamics and the rate coefficient is clear from our calculations, as the data in Table 1 and Fig. 3 illustrate. Therefore, below we briefly recapitulate the main findings in order to highlight how AChEt dynamics affects the reaction rate coefficients by modulating the electrostatic and steric characteristics of the enzyme.

Using our recently developed Poisson-Nernst-Planck solver for modeling the coupled electro-diffusion-reaction processes (18,28), we first explored the effect of tetramerization on the reaction rates of the full-length, tetrameric form of the enzyme (Table 1). We found that, under nonequilibrium conditions, the tetramer rate is ∼70% of the sum of the rates for the isolated monomers (the corresponding value under equilibrium conditions is 80%). These values compare well with similar previous calculations for the C-terminally truncated (i.e., lacking the WAT/PRAD) tetramer structures (10,17). Furthermore, we found that local structural fluctuations modulate enzymatic efficiency by ∼14%. However, the major effect (∼22–29%) of tetramerization on the reaction rate arises from alterations in steric and electrostatic properties of an active site due to the presence of an opposing subunit. These properties are bound to substantially vary with structural fluctuations in the tetramer (15).

Our next aim was therefore to assess the consequence of structural fluctuations on the (essentially interdependent) reaction rate and the steric and electrostatic features of the enzyme. We found that not only does the conformer-averaged reaction rate remain within error of the rate for the open initial structure, but also that the rates for some structures are ∼85% of the sum of the rates for the four isolated monomers. Note that only a small portion of the conformational space accessible to AChEt is accounted for in the current calculations. Given the large length and timescale motions inherent in AChEt (15), the rate for the cellular tetramer is likely to be at least 85% of the rate of four independent monomers. We conclude that structural dynamics mitigates the effect of tetramerization and allows the enzyme to maintain a similar level of efficiency in different oligomerization states.

In summary, we have shown that intersubunit fluctuations modulate the reaction rates via steric and electrostatic effects. The latter is coupled with charge density of the approaching substrate. The interplay between these two effects (steric and electrostatic) is complex, being complementary or antagonizing depending on the overall structure of the tetramer. This article thus shows that the near diffusion-controlled rate of hydrolysis of acetylcholine by tetrameric acetylcholinesterase involves an intricate interplay of dynamic, electrostatic, and steric effects. The implications of this result to biology include the following. The demonstration that there is a direct link between structural flexibility and enzyme kinetics helps us to further appreciate the crucial role of protein flexibility in function. Most importantly, that modulation of enzymatic activity by steric effects arising from oligomerization is mitigated by favorable electrostatic interactions underscores how biology might achieve higher effective local concentration through oligomerization without compromising the function of the individual components. This is an ingenious solution to the problem of molecular crowding that arises from the need for high concentration of reactive species and is particularly relevant for fast, diffusion-limited, biological processes.