Size of Bicelle Defects Probed via Diffusion Nuclear Magnetic Resonance of PEG

Abstract

Diffusion of various poly(ethylene glycol) (PEG) tracers of well-defined molecular weight and narrow polydispersity confined within the aqueous interstices between positively magnetically aligned bicelles was measured using pulsed-field-gradient ¹H nuclear magnetic resonance. The bicelles consisted of mixtures of dimyristoylphosphatidylcholine (DMPC), dimyristoylphosphatidylglycerol (DMPG), and dihexanoylphosphatidylcholine (DHPC) in the molar ratios q = [100 DMPC +5 DMPG]/[DHPC] = 3.5, 4.5, and 5.5, to which Yb³⁺ had been added in the ratio 1:75 Yb³⁺/phospholipid. The field gradients were applied such that diffusion was measured in the direction parallel to the normal to the bicelles' planar regions, thereby rendering the experiment sensitive to the ability of PEG to traverse lamellar defects within the bicelles. The pulsed-field-gradient nuclear magnetic resonance diffusive intensity decays were diffusion-time-independent in all cases, with diffusive displacements corresponding to many hundreds of bicellar lamellae. This permitted a description of such diffusive decays in terms of a mean behavior involving a combination of straight obstruction effects common to all PEG, with hindrance to diffusion proportional to the relative size of a given PEG with respect to the size of the lamellar defects. Across the range of PEG molecular weights (200–4600) and bicelle compositions examined, the apparent radial dimension of the lamellar defects decreased from 165 Å with q = 3.5 to 125 Å with q = 5.5. This is opposite to the trend predicted from static geometric models of either bicelle disks or perforated lamellae. Qualitatively, the observed trend suggests that mobility of the obstructions to diffusion will need to be considered to reconcile these differences.

Introduction

Bicelles, or bilayered micelles, are a model membrane system widely employed to study the conformation and dynamics of membrane-associating molecules (1–5). They consist of mixtures of short chain amphiphiles, typically 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC), and long chain amphiphiles, typically 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), combined in the molar ratio q = DMPC/DHPC. In the resulting self-assembled bicellar mixture DMPC forms a planar bilayer, stabilized by DHPC located at high curvature edge regions. Much of the popularity of bicelles stems from their ability to align in the magnetic field of a nuclear magnetic resonance (NMR) spectrometer. The resulting NMR spectrum is generally simplified even while providing orientation-dependent structural information. The spontaneous orientation direction, arising from the inherent negative magnetic susceptibility anisotropy of the bicelle assembly, leaves the normal to the planar lipid bilayer aligned perpendicular to the direction of the magnetic field, and is referred to as negative magnetic alignment. In the presence of additives having a positive magnetic susceptibility, such as surface-bound lanthanides, e.g., Tm⁺³, Yb⁺³, Er⁺³, or Eu⁺³ (6,7), or phosphatidylcholines containing a biphenyl group (8–10), or peptides having phenyl ring side chains (11), or membrane-associating aromatic amphiphiles (12), bicelles can orient with the normal to the planar bilayer aligned parallel to the magnetic field.

Originally, bicelles were considered to adopt only a discoidal morphology with a strict segregation of DMPC into a planar bilayer region, and of DHPC to regions of high curvature at the disk edges. This is now the accepted model only at low overall bicelle concentrations, or low q values (q < 2), or at temperatures below the DMPC gel-to-liquid-crystalline phase transition. At temperatures above the DMPC gel-to-liquid-crystalline phase transition, and at higher bicelle concentrations and q values, the preponderance of evidence from a combination of small angle x-ray scattering (13), small angle neutron scattering (SANS) (14–19), fluorescence (20), and electron microscopy (21,22) observations points to a nematic phase consisting of DMPC-rich lamellar regions perforated by DHPC-lined toroidal defects for negatively aligned bicelles. For positively magnetically aligned bicelles, SANS results indicate that the bicelles adopt a smectic arrangement of perforated lamellae (14,16,17).

These notions of bicelle morphology are not universally accepted, however. Specifically, electron microscopy results on both negatively (23) and positively magnetically aligned bicelles (10) have been interpreted to suggest a discoidal morphology.

³¹P NMR provides a convenient means to monitor bicelle alignment, to assess the mosaic spread of alignments and bicelle order parameters, and to readily differentiate negative from positive magnetic alignment (8–13,22–27). Recent ³¹P NMR results support a mixed bicelle model in which DHPC undergoes fast exchange between DMPC-rich and DHPC-rich regions (28). However, ³¹P NMR does not readily differentiate between disk-versus-perforated-lamellae (or other) potential bicelle morphologies.

NMR diffusion measurements, on the other hand, have long been used to provide fundamental morphological information on colloidal systems (for reviews, see (29–32)). These typically used the pulsed-field-gradient (PFG) NMR technique introduced by Stejskal and Tanner (33). In bicelles, PFG NMR measurements of lateral diffusion show unobstructed diffusion of bilayer partitioned species over long diffusion distances, which is inconsistent with a disk morphology and strongly supports a perforated lamellar model (34–37). Further, as noted by Gaemers and Bax (34), the fact that bicelles retain liquid crystalline order down to volume fractions as low as 3% is incompatible with the Onsager limit for liquid crystal formation unless bicelles are lamellar.

PFG NMR measurements of translamellar diffusion of water in bicelles reveal the fractional surface area of defects, and demonstrate that such diffusion increases directly with the amount of DHPC present in the bicelles (38); however, this alone does not yield any resolution of the disk-versus-perforated-lamellae controversy. Specifically, although the disk model dictates that increasing DHPC content produces smaller disks (39), for a smectic arrangement of circular disks, the total fractional surface area of defects will be independent of disk radius (40), other factors being constant. However, the gaps between such disks must decrease in size with decreasing disk radius. Conversely, the perforated lamellar model predicts a greater area fraction of toroidal defects with increasing DHPC content, as observed experimentally (38), but only assuming the size of an individual defect remains constant. Knowledge of the dimensions of bicellar defects spaces, whether of the gaps between bicelle disks, or of their lamellar toroidal perforations, is clearly required.

A popular tracer for size measurements is poly(ethylene glycol) (PEG), being highly water-soluble, nontoxic, available in a wide range of well-defined molecular weights, and overall intensely studied and well understood (41–43). Size-dependent PEG diffusion has been used to probe confinement dimensions in a variety of situations (44–56), including bicelles (57).

In this report we employ PFG NMR to examine the diffusion of various molecular weight PEG in the direction parallel to the bilayer normal in positively magnetically aligned bicelles where it is established that an ordered smectic phase occurs (14). Regardless of whether one assumes the disk or the perforated lamellar morphology, smaller PEG will diffuse through defects edged by DHPC, whereas larger PEG will be blocked, as shown schematically in Fig. 1. The molecular-weight dependence of PEG diffusion should reveal the defect dimensions. How these dimensions vary with the ratio q = DMPC/DHPC will be examined and compared with the predictions of idealized models of discoidal versus perforated lamellae bicellar morphologies.

Figure 1.

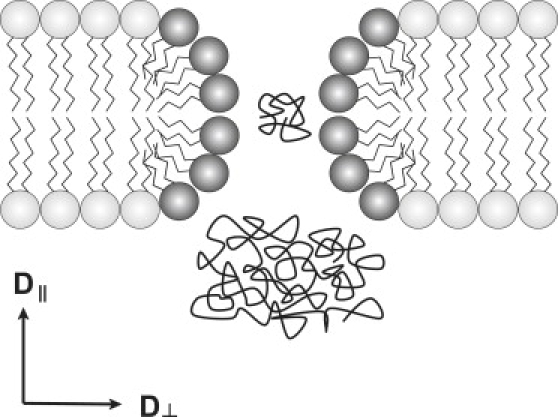
Schematic cross section through one defect in the smectic phase of DMPC/DHPC bicelles. Bicelles consist of DMPC-rich (light shaded) bilayer regions edged with DHPC-rich (dark shaded) curved regions. The defects correspond to either gaps between adjacent bicelle disks or toroidal perforations in bicellar lamellae. Diffusants smaller than the defect dimensions can diffuse freely whereas larger diffusants are hindered. The NMR diffusion experiment is arranged such that the component of the molecular diffusion tensor parallel to the direction of the transverse defect axis, D_‖, is measured exclusively.

Experimental

Materials

1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC), and 1,2-dimyristoyl-sn-glycero-3-phosphoglycerol (DMPG) were purchased from Avanti Polar Lipids (Alabaster, AL). Ytterbium chloride hexahydrate (YbCl₃(6H₂O)) and PEG of molecular weight 200, 600, 1000, 2000, 3400, and 4600 were purchased from Sigma-Aldrich (Oakville, ON, Canada), as were all other reagents employed.

PEG molecular weight and polydispersity

PEG molecular weights and molecular weight distributions were characterized by gel permeation chromatography (GPC) on a gel permeation chromatograph (Viscotek, Houston, TX) equipped with a VE3580 refractive index detector (Viscotek) and ViscoGEL G40000PWXL and G2500PWXL columns (Viscotek) maintained at 30°C. The eluent was aqueous 0.2 M KNO₃ containing 200 ppm NaN₃ at a flow rate of 1.0 mL/min achieved using a VE1122 solvent delivery system and VE7510 GPC degasser (Viscotek). Conventional calibration was performed using PEG molecular-weight standards obtained from Polysciences (Warrington, PA). Because the smaller size PEG eluted close to the solvent peak, their calibration was less reliable. Consequently, PEG 200, 600, and 1000 were also characterized by mass spectrometry on a Micromass ZQ mass spectrometer (Waters, Milford, MA). For PEG 1000, the GPC and mass spectrometry results agreed well, but for PEG 200 and 600, the latter method was judged more reliable.

Bicelle preparation

Bicelles composed of mixtures of DMPC+DMPG+DHPC were prepared to consist of 25 wt % lipid in 450 μL of buffered D₂O (10 mM Tris, pH 7.4, 150 mM NaCl) containing Yb³⁺ at a Yb³⁺/phospholipid ratio of 1:75. The ratio q, corresponding to moles (DMPC+DMPG)/DHPC, was set to either 3.5, 4.5, or 5.5. The DMPC/DMPG molar ratio was held constant at 20:1, i.e., 5 mol % DMPG relative to DMPC. A typical preparation involved dissolving the desired quantity of DMPC, DHPC, and DMPG in 350 μL of buffered D₂O, followed by a series of cycles of freezing, thawing, and gentle vortexing until a clear solution was obtained, to which the desired quantity of Yb³⁺ was added from a stock solution such that the final volume was 450 μL. The bicelle sample was stored at 4°C for up to 24 h before use. Where desired, PEG was added along with the Yb³⁺ solution, to achieve a final PEG concentration of 0.66 wt %.

The bicelle sample was transferred into a 5-mm NMR sample tube at 4°C and placed in the bore of an Infinity 500 MHz NMR spectrometer (Varian, Cary, NC). The sample temperature was then raised to 35°C. An annealing procedure was carried out involving repeated cycling of the temperature between 20 and 35°C with 10–15 min of equilibration at either extreme to encourage magnetic alignment, the quality of which was assessed via ³¹P NMR spectroscopy.

NMR spectroscopy

All NMR spectra were recorded on an Infinity 500 MHz NMR spectrometer (Varian) using a 5-mm double-resonance liquid probe (Varian) equipped with gradient coils along the z direction. The sample temperature was controlled to the desired value, between 25°C and 45°C, ±0.5°C, as calibrated separately using ethyleneglycol as an NMR thermometer (58).

³¹P NMR spectra were recorded at 202.31 MHz using acquisition and processing conditions described elsewhere (38). ¹H NMR diffusion measurements were performed at 499.78 MHz using the stimulated echo (STE) pulsed-field-gradient (PFG) procedure (59), with acquisition and processing conditions described previously (38), including details of phase cycling (60) and gradient strength calibration (61).

Results and Discussion

PEG degree of polymerization and polydispersity

Fig. 2 compares the size distributions for the six different PEGs investigated here expressed in terms of the degree of polymerization N. The lines of best fit assuming a Schulz distribution (62) for PEG 200, 600, 2000, and 3400 are shown, while Table 1 lists the relevant fitting parameters, average degrees of polymerization, and polydispersity indexes (PDI). Poorer fits were obtained with the other commonly-used log-normal or Tung distribution functions (62), except for the cases of PEG 1000 and 4600 where there was an obvious low molecular-weight tail in the distribution. In these two cases, the Tung distribution was clearly superior and is shown in the figure. In all cases, the PDI fell near or below 1.10, indicating reasonably monodisperse size distributions in these PEG samples, by polymer standards.

Figure 2.

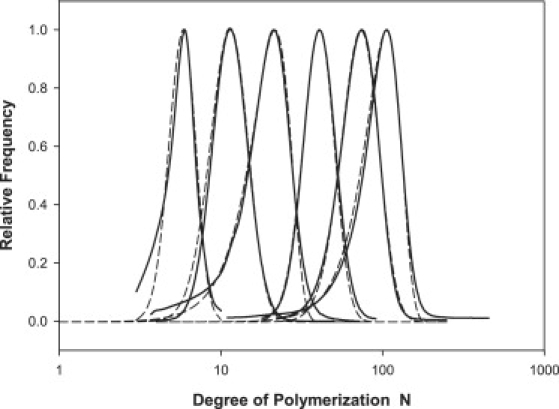
Gel permeation chromatography (solid lines) determination of PEG size and polydispersity for PEG 200, 600, 1000, 2000, 3400, and 4600, expressed as the degree of polymerization N. The number and weight average degrees of polymerization and corresponding polydispersity indexes are listed in Table 1. The dashed lines represent theoretical fits to the experimental size distributions assuming either a Schulz (PEG 200, 600, 2000, 3400) or a Tung (PEG 1000, 4600) distribution function, with fitting parameters detailed in Table 1.

Table 1.

PEG degree of polymerization and polydispersity

PEG	〈Nn〉	〈Nw〉	PDI
				Schulz distribution parameters∗
				b	a
200†	5.92	6.23	1.052	28	0.19
600†	12.53	13.34	1.065	15	0.49
2000‡	39.68	41.77	1.053	20	1.22
3400‡	67.5	72.91	1.08	14	4.8
				Tung distribution parameters∗
				y	m
1000‡	17.16	18.25	1.064	1.875 × 10−6	4.2
4600‡	86.16	96.66	1.122	6.0 × 10−10	4.5

^∗See Rogošić et al. (62) for details.

^†From mass spectrometry.

^‡From gel permeation chromatography.

³¹P NMR spectra

Fig. 3 shows ³¹P NMR spectra of Yb³⁺ doped, positively magnetically aligned bicelles at q values of 3.5, 4.5, and 5.5, at 35°C, all in the presence of 0.66 wt % PEG 2000. Two resonances are resolved: the broader resonance at roughly 22 ppm is assigned to DMPC, whereas the narrower resonance at roughly 10 ppm is assigned to DHPC. DMPG is not resolved from DMPC. The observed chemical shifts are consistent with bicelles preferentially oriented with their bilayer normal parallel to the magnetic field direction, as anticipated due to surface-bound Yb³⁺. The resonances of both DMPC and DHPC are significantly broadened by Yb³⁺. Assignments are based on the expected preference of DMPC for planar regions and of DHPC for highly curved regions of the bicelle, combined with the correlation between the relative integrated intensity of DHPC versus DMPC with differences in q.

Figure 3.

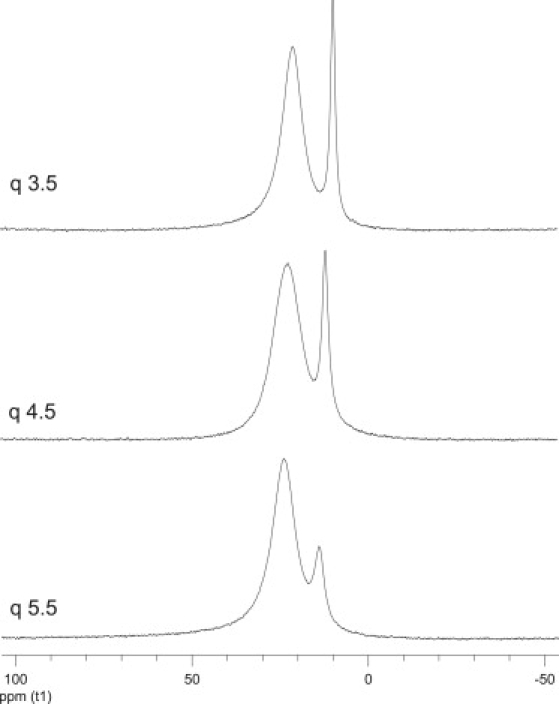
³¹P NMR spectra (35°C) of positively magnetically aligned bicelles composed of 100:5 (mol/mol) DMPC/DMPG plus DHPC in the molar ratio q = [DMPC+DMPG]/DHPC as indicated in the figure. All bicelle samples contained 25% w/w lipid/water and included ytterbium in the ratio Yb³⁺/P = 1:75, in addition to 0.66 wt % PEG 2000 for these particular spectra.

The observed chemical shifts of both DMPC and DHPC increase progressively with increasing q, a manifestation of the well-known inverse scaling of bicelle ordering with the content of the short chain amphiphile (1). The chemical shift of the DHPC resonance reflects, in addition, fast exchange between populations resident in planar regions versus regions of high curvature, as per the “mixed bicelle model” (28). The relative populations of amphiphiles in planar versus highly curved regions is then expressed in terms of the ratio q^∗,

$$q\ast =\left[\frac{q+{\omega }^{\ast }}{1-{\omega }^{\ast }}\right],$$ (1)

where q = (DMPC+DMPG)/DHPC, and ω^∗ = ω_DHPC/ω_DMPC, with ω_DHPC and ω_DMPC being the observed chemical shifts of DHPC and DMPC, respectively. The values of q^∗ listed in Table 2 indicate that a significant fraction of DHPC resides in planar regions of the bicelle, in accord with previous findings (22,38,38).

Table 2.

Selected properties of positively magnetically aligned bicelles

	q = (DMPC+DMPG)/DHPC
	3.5	4.5	5.5
q∗	6.3 (±1.0)	8.9 (±0.8)	15.1 (±1.2)
qv	10.8 (±1.0)	15.4 (±0.8)	33.7 (±1.2)
DW/D0	0.36	0.27	0.23
RpD-D	165	125	125
RdT	191	271	587
RintT	76	81	151
RpT	71	66	109

All radial dimensions are in Å. The superscript D-D refers to the Davidson and Deen model (76,77), whereas the superscript T refers to the Triba model (28,79).

STE PFG ¹H NMR spectra of positively magnetically aligned bicelles

Fig. 4 shows a series of ¹H NMR spectra of Yb³⁺-doped q = 4.5 bicelles containing PEG 2000 as a function of the gradient amplitude in the STE PFG NMR sequence. The intense resonance at 4.5 ppm is assigned to HDO. The free PEG 2000 produces the resonance at 3.3 ppm arising from the protons of the ethylene oxide units. The width-at-half-maximum-intensity for the resonance of the PEG ethylene oxide units is not significantly greater in the presence versus the absence of Yb³⁺, suggesting no significant interactions of PEG with the lanthanide.

Figure 4.

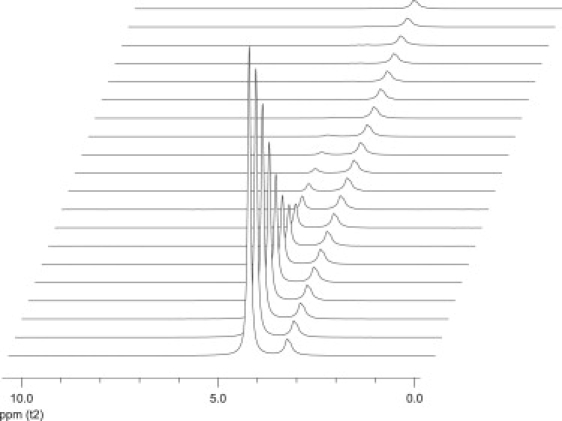
¹H NMR spectra (35°C) of positively magnetically aligned bicelles as a function of the field-gradient pulse amplitude in the STE PFG NMR sequence. Bicelle composition was as per Fig. 3q = 4.5. The stimulated echo delay in this case was 400 ms. The water resonance is at 4.5 ppm while the resonance at 3.3 ppm is due primarily to the free PEG 2000.

Most lipid proton resonances are either absent or exhibit quite low intensity due to their rapid transverse relaxation. However, the choline methyl resonances of DMPC and DHPC, which occur in the vicinity of the PEG proton resonances, are visible to a degree and are difficult to resolve in the spectra of positively magnetically aligned bicelles.

Water diffusion in positively magnetically aligned bicelles

In Fig. 4 the intensity of the water resonance decays rapidly with increasing gradient amplitude, as expected given water's small size and, hence, rapid diffusion. The echo amplitude depends on the experimental and sample variables as per Eq. 2,

$$I_{\text{k}}=I_0\text{exp}\left(\frac{-2{\tau }_2}{T_2}\right)\text{exp}\left(\frac{-{\tau }_1}{T_1}\right)\text{exp}\left[-kD\right],$$ (2)

where k = [(γgδ)² (Δ-δ/3)], δ (s) is the duration of the square gradient pulse of magnitude g (T m⁻¹), γ is the magnetogyric ratio, τ₁ and τ₂ are, respectively, the longitudinal and transverse delay times in the STE sequence, and Δ = τ₁ + τ₂ (s) is the experimental diffusion time, while T₁ and T₂ are the longitudinal and transverse relaxation times, respectively. The diffusion coefficient is obtained from the slope in a plot of Ln(I/I₀) versus k.

For the case of a diffusant confined between the lamellae of magnetically aligned bicelles, the diffusion coefficient is anisotropic with tensor elements as defined in Fig. 1 (63,64). Transforming to the laboratory frame defined by the applied pulsed-field gradients g_z yields Eq. 3, where θ is the polar angle between the bilayer normal and the applied field gradient,

$$D_{\text{zz}}=D_{\perp }{\text{sin}}^2\theta +D_{\Vert }{\text{cos}}^2\theta \text{.}$$ (3)

For positively magnetically aligned bicelles and pulsed-field gradients g_z, the experiment measures solely D_‖.

The diffusive decay of the water resonance was monoexponential, characterized by a single effective diffusion coefficient, as found previously (38). The quantity D^W/D₀, representing the ratio of the water diffusion coefficients in positively magnetically aligned bicelles versus bulk solution, decreased from 0.36 at q = 3.5, to 0.27 at q = 4.5, and further to 0.23 at q = 5.5, again as found previously (38). The principal determinant of water diffusion in the direction normal to the plane of the aligned bicelles is the fractional surface area of lamellar f(obs) = 1–D^W/D₀ versus defect regions f(defect) = D^W/D₀ in the plane occupied by the smectic array of bicelles.

PEG diffusion in positively magnetically aligned bicelles

For PEG free in bulk solution, the observed diffusive decays were monoexponential in all cases (data not shown), in accord with expectations for their low PDI values (65,66). The diffusion coefficients obeyed a scaling relationship D = 1.33 × 10⁻⁹ m² s⁻¹ 〈N〉^−0.535, where N is the degree of polymerization, with the scaling exponent 0.535 lying close to the theoretical prediction (67), in agreement with numerous studies of PEG diffusion (44,45,54,68–72). One may confirm that the polydispersities of these PEG yield apparently monoexponential STE PFG NMR diffusive decays using the simulation described by von Meerwall (65) (data not shown).

Fig. 5 shows the diffusive decays obtained for a range of diffusion times Δ with various size PEG confined between positively magnetically aligned bicelles having q = 4.5. There is little or no dependence on the particular diffusion time. Note that, because it can be difficult to resolve the PEG resonance from the DMPC or DHPC choline methyl resonances in a given spectrum, there can be some apparent curvature for the case of larger k values, since the choline resonances will not decay due to diffusion.

Figure 5.

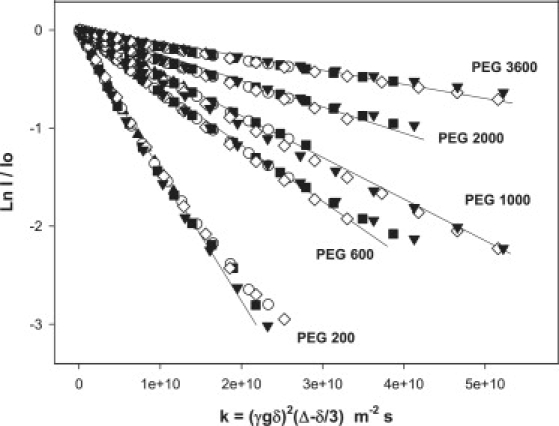
Normalized diffusive intensity decays from STE PFG ¹H NMR spectra (35°C) of various molecular-weight PEG (as indicated) confined within positively magnetically aligned q = 4.5 bicelles. Results for PEG 4600 are not shown, to avoid cluttering the figure. Symbols represent different diffusion times: 210 ms (solid triangles), 410 ms (open circles), 610 ms (solid squares), 810 ms (open diamonds), and 1010 ms (solid inverted triangles). The solid lines are fits using Eq. 2.

For PEG to diffuse in a direction parallel to the bilayer normal, it must pass through bicelle defects. Hence, the smectic array of bicelles can be regarded as a set of parallel, equally spaced, permeable barriers: a situation first dealt with by Tanner (73). A characteristic feature of such situations is that the apparent diffusion coefficient is diffusion-time-independent only in the asymptotic limit that the root-mean-square diffusion displacement has exceeded many multiples of the barrier spacing. The root-mean-square displacement 〈x²〉^1/2 = (6DΔ)^1/2, even for the slowest diffusing, largest molecular weight PEG 4600, where D ≤ 1 × 10⁻¹¹ m² s⁻¹, even at the shortest diffusion time employed here, is approximately several microns. The barrier spacing is estimated to equal 100 Å according to SANS studies of 25 wt % bicelles of composition similar to those employed here (17). Thus, even the largest PEG investigated here has diffused through hundreds of barriers and, therefore, Tanner's asymptotic limit applies. Hence, the effective diffusion coefficient may then be obtained simply by fitting with Eq. 2, as shown by the solid curves in Fig. 5.

Fig. 6 shows the reduced diffusion coefficient D/D₀ obtained by fitting intensity decays such as those shown in Fig. 5 for each of the various molecular-weight PEG at each q value as a function of the Stokes-Einstein radius R_s of the particular PEG. The latter was obtained from the Stokes-Einstein equation using the diffusion coefficient D₀ of the corresponding free PEG,

$$D_0=\frac{kT}{6\pi \eta R_{\text{S}}},$$ (4)

where k is the Boltzmann constant, T is the absolute temperature, and η is the viscosity (0.719 cP at 35°C). The data points for the smallest radius are D^W/D₀ at the three q values. The profound hindrance to PEG diffusion with increasing PEG molecular weight is evident from this comparison, as is the fact that the degree of hindrance increases with increasing q value.

Figure 6.

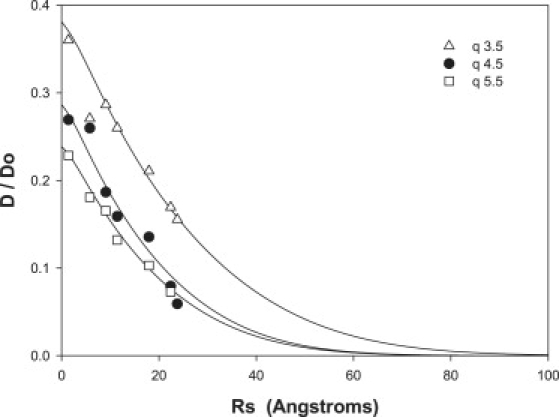
Reduced diffusion coefficients D/D₀ for various molecular weight PEG as a function of the corresponding Stokes-Einstein radius R_s. Data are shown for three q values: 3.5 (triangles), 4.5 (circles), and 5.5 (squares). Solid curves show the best-fit Davidson and Deen model (76,77) predictions for the mean pore radii 〈R_p〉 listed in Table 2.

Modeling bicelle hindrance of PEG diffusion

To extract an estimate of the size of the bicelles' lamellar defects from the hindrance to PEG diffusion, we employ a model for the diffusion of flexible polymers within cylindrical pores. Such models have a long developmental history, reviewed thoroughly by Deen (74). The various approaches each predict a reduced effective diffusion coefficient for a flexible polymer within a pore due to a combination of steric exclusion from the pore and increased hydrodynamic drag within the pore, such that

$$D/D_0\approx f\left(\text{defect}\right)\mathrm{\Phi }{K}^{-1},$$ (5)

where Φ is the partition coefficient, describing the energetic cost, largely entropic in origin, of a polymer entering such a pore. K⁻¹ accounts for the increased hydrodynamic drag on a polymer contained within such a pore.

A widely cited example is the scaling model of de Gennes (75), which predicts the scaling trends expected as a function of the relative size of the polymer and the pore. However, the de Gennes model is intended strictly for polymers of radial dimensions exceeding that of the pore, where hindrance far exceeds the degree evident in Fig. 6. Furthermore, it incorporates undetermined scaling coefficients, which render comparisons with experiment problematic.

The Davidson and Deen hydrodynamic model (76,77) describes successfully the hindered diffusion of a variety of flexible polymers of known size in pores of known size. The model expresses the increased hydrodynamic drag in terms of the solute-to-pore size ratio λ = R_s/R_p,

$$K^{-1}=1-2.848\lambda +3.269{\lambda }^2-1.361{\lambda }^3,$$ (6)

for situations 0 ≤ λ ≤ 0.87. For the partition coefficient, they used the expression of Casassa (78),

$$\mathrm{\Phi }=4\sum _{\text{i}=1}^{\mathrm{\infty }}(1/d_{\text{i}}^2)\text{exp}(-d_{\text{i}}^{\text{2}}{\lambda }_{\text{g}}^2),$$ (7)

where λ_g = R_g/R_p is the ratio of the polymer's radius of gyration to the pore radius and d_i values are the roots of J₀(d) = 0, J₀ representing the Bessel function of the first kind, of order zero. The value λ_g/λ is taken to equal 1.369 for PEG (77). For our purposes, we introduce, in addition, the quantity f(defect) = D^W/D₀ to account for the surface area of defects available for PEG to enter.

The solid curves in Fig. 6 show the lines of best fit of this modified Davidson and Deen model to the reduced PEG diffusion coefficients in bicelles at the three q values investigated, for the consensus values of R_p equal to 165 Å for the case q = 3.5 and 125 Å for both q = 4.5 and 5.5 (see also Table 2).

Comparison with bicelle disk and perforated lamellae models

The bicelle disk and perforated lamellae models of bicelle morphology provide quantitative predictions of, respectively, disk and toroidal pore radii as a function of q. Perhaps the most highly evolved of such models is that developed by Triba et al. (28,79) based on the relative volume fractions of DHPC occupying edge versus lamellar regions of the bicelle, the latter being derived from ³¹P NMR as per Eq. 1. The bicellar disk radius R_d equals

$$R_{\text{d}}=\frac{1}{4}{r}_{\perp }{q}_{\text{v}}\left[\pi +{\left({\pi }^2+\frac{32}{3q_{\text{v}}}\right)}^{1/2}\right],$$ (8)

where q_v is the ratio of the volumes occupied by amphiphiles in bilayer versus edge regions,

$$q_{\text{v}}=\frac{V_{\text{bilayer}}}{V_{\text{edge}}}=\frac{qr\prime +w^{\ast }}{1-w^{\ast }},$$ (9)

with q and ω^∗ as defined previously, whereas r′ = r_‖/r_⊥ = 20:11 corresponding to the ratio of the lengths of a fully extended DMPC versus DHPC molecule. Table 2 lists values of R_d calculated in this fashion for the three different q values employed here, and these agree closely with those reported by Triba et al. (28,79). A more pertinent dimension for PEG diffusion studies is the radius, R_int, of the largest circular cross section able to fit between any three adjacent disks, assuming a hexagonal array of bicelle disks arranged within a plane,

$$R_{\text{int}}=\frac{a}{\sqrt{3}}-(R_{\text{d}}+r_{\perp }),$$ (10)

where a is the center-to-center separation,

$$a={\left[\frac{2\pi }{\sqrt{3}}-\frac{(R_{\text{d}}+r_{\perp })}{(1-D^{\text{w}}/D_0)}\right]}^{1/2}\text{.}$$ (11)

Values of R_int obtained in this fashion are listed in Table 2 and predict a doubling of R_int as q increases from 3.5 to 5.5.

For the perforated lamellae model, Triba et al. (28,79) derived the following expression for the pore radius R_p,

$$R_{\text{p}}=\frac{1}{4}\frac{r_{\perp }}{f^{\ast }}{\left[\pi +\left({\pi }^2-\frac{32f^{\ast }}{3}\right)\right]}^{1/2},$$ (12)

where

$$f^{\ast }=\frac{1-D^{\text{W}}/D_0}{1+q_{\text{v}}{D}^{\text{W}}/D_0},$$ (13)

in which we again equate the surface density of pores to the reduced transverse diffusion of water. Values of R_p predicted in this fashion are listed in Table 2 and point to an increase in pore size with increasing q of ∼50%:

A comparison in Table 2 of the apparent bicellar defect dimensions derived from fitting of experimental PEG diffusion data to the Davidson and Deen model, with predictions obtained from the bicelle disk and perforated lamellae models, show rough agreement between experiment and prediction only at q = 5.5. At lower q values, experimental bicelle defect apparent dimensions are systematically larger than those predicted from geometric models.

A potential complication with the Davidson and Deen model is that any attractive potential between a particular macromolecule and the pore walls will alter the apparent diffusion in that model. When the attraction is modest, it primarily influences the partition coefficient Φ(λ_gi) and leads to enhanced diffusion. When the attraction exceeds some threshold potential, polymer adsorption to the pore wall follows, reducing the effective pore radius and decreasing diffusion. For the molecular-weight range of interest here, however, PEG is not attracted to phosphatidylcholine lipid bilayers (80,81).

PEG may bind cations such as Na⁺ (82), which in turn can alter PEG's conformation and diffusion. However, in aqueous solution, Na⁺ is one of the weakest PEG binding alkali metal ions and its binding constant decreases with increasing ion concentration (83). Binding of Yb³⁺ to PEG is also possible and would be expected to be far stronger than Na⁺ binding, other factors being equal. However, the affinity of Yb³⁺ for the phosphates of the phospholipids will exceed that for PEG by a considerable margin, particularly given that the lipid bilayer surface contains negatively charged DMPG.

A singular shortcoming of models such as that of Davidson and Deen (76,77) or Triba et al. (28,79) as applied to the diffusion measurements in bicelles is that the obstructions to diffusion are treated as static objects. Yet it is well known that mobile obstructions offer less hindrance to diffusion than do immobile obstructions (84). In addition, bicelles, whether disks or perforated lamellae, are far from immobile. Certainly, any in-plane diffusion of objects as large as the defects deduced here should be too slow relative to PEG to have a significant influence. However, bicelles experience rapid out-of-plane fluctuations about their average orientation, the degree of which is quantified by the so-called bicelle order parameter, which decreases progressively with increasing DHPC content (1). If such fluctuations enhance transverse diffusion, this might explain the disparity between the defect dimensions obtained by fitting the Davidson and Denn model to experimental PEG diffusion data and those predicted by the Triba models. Specifically, the Davidson and Deen model will overestimate the static pore dimensions required to yield a given apparent hindrance to diffusion due to real mobile obstructions. Conversely, the static defect dimensions predicted by the Triba models will overestimate the resultant hindrance to diffusion produced by real mobile obstructions of the same dimension. The fact that the agreement between the Davidson and Deen model and the Triba models is best at higher q values, where bicelle fluctuations are least, supports this interpretation.

Conclusions

The surface fraction of bicelle defects f(defect) = D^w/D₀ increases proportionately with the amount of DHPC available to form edge regions, from 0.23 at q = 5.5 to 0.36 at q = 3.5. The molecular-weight dependence of the reduced PEG diffusion through such bicelle defects reflects the defect dimensions. Fitting the reduced PEG diffusion coefficients to the Davidson and Deen model (76,77) for diffusion of a flexible polymer through immobile pores indicates a decrease in defect radius from 165 Å for q = 3.5 to 125 Å for both q = 4.5 and 5.5. Such a trend is not predicted by static geometric models of either bicelle disks or perforated lamellae morphologies. The agreement between experimental fitting models and predictive geometric models improves as the bicelle mobility decreases, suggesting that incorporating the possibility of mobile obstructions will be essential for extracting any deeper insights from such diffusion studies.