Diffusion in Cytoplasm: Effects of Excluded Volume Due to Internal Membranes and Cytoskeletal Structures

Abstract

The intricate geometry of cytoskeletal networks and internal membranes causes the space available for diffusion in cytoplasm to be convoluted, thereby affecting macromolecule diffusivity. We present a first systematic computational study of this effect by approximating intracellular structures as mixtures of random overlapping obstacles of various shapes. Effective diffusion coefficients are computed using a fast homogenization technique. It is found that a simple two-parameter power law provides a remarkably accurate description of effective diffusion over the entire range of volume fractions and for any given composition of structures. This universality allows for fast computation of diffusion coefficients, once the obstacle shapes and volume fractions are specified. We demonstrate that the excluded volume effect alone can account for a four-to-sixfold reduction in diffusive transport in cells, relative to diffusion in vitro. The study lays the foundation for an accurate coarse-grain formulation that would account for cytoplasm heterogeneity on a micron scale and binding of tracers to intracellular structures.

Introduction

Realistic models of macromolecular diffusion in cells have been recently of renewed interest (1,2) in the light of in vivo experiments that involve naturally fluorescent proteins (3–5). Tracer molecules in the cell diffuse in a crowded environment filled with other solutes and large intracellular structures, such as cytoskeletal meshwork and internal membranes (6). Even in the absence of intracellular structures, diffusion of a tracer in the cytosol is affected by macromolecular and hydrodynamic interactions and therefore constitutes a complicated many-body problem (7). Remarkably, its solution for repulsive interactions is formulated in terms of the self-diffusion of individual particles with a diffusion coefficient corrected for macromolecular crowding and hydrodynamic effects (2,8,9); we denote this coefficient, which describes diffusion in cytosol free of intracellular structures, by D₀. Note that D₀ is different from the diffusion coefficient in a dilute aqueous solution, D_{in vitro}.

Diffusion of a tracer is further hindered by cellular structures that are largely immobile, i.e., cytoskeleton, endoplasmic reticulum (ER), and other internal membranes (10). This is due to increased path lengths and potential binding interactions (diffusion may also slow down due to an increase in viscosity in the proximity of a structure). The increase in path length, sometimes termed the effect of excluded volume, is the focus of this article. Both in vitro studies (11) and experiments where inert particles were microinjected into living cells (12–15) indicate that the excluded volume effect can be significant. A possible role of intracellular structures as diffusion barriers in forming cAMP microdomains is discussed in Rich et al. (16).

Macromolecular diffusion in a convoluted space is notoriously difficult to describe; in fact, it is legitimate to ask whether Fick's law and the notion of an effective diffusion coefficient is applicable to diffusive fluxes in a disordered medium (17). The issue can be addressed by analyzing time dependence of the mean-squared displacement, 〈x²(t)〉, for a particle undergoing random walks in an occluded space (the angular brackets denote ensemble averaging). One such numerical experiment with randomly distributed spherical obstacles is described in Fig. 1 (see Methods for computation details). In agreement with earlier Monte Carlo studies of diffusion on lattices (18) and experiments with diffusion in gels (11), 〈x²(t)〉 is linear on a sufficiently large spatial scale: 〈x²〉 ∝ t (inset in Fig. 1 b). This is a signature of normal diffusion with an effective diffusion coefficient D_eff = lim_t→∞〈x²〉/(6t).

Figure 1.

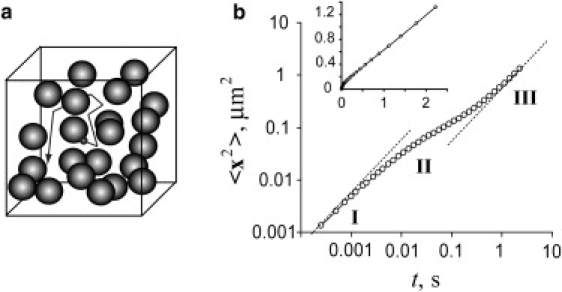
Monte Carlo simulations of particle tracking. (a) Schematic of diffusion of a tracer amid random spherical obstacles; (b) Three diffusive regimes demonstrated by a log-log plot of 〈x²(t)〉 of a tracer for high obstacle number density: I, unobstructed diffusion; II, intermediate (anomalous) behavior; and III, normal effective diffusion. Simulation parameters are described in Methods. (Inset) Same dependence in linear scales.

For inaccessible volume fractions in a biologically relevant range, ϕ = 0.1–0.5 (10), effective diffusion takes place on the length scale λ determined approximately by the average distance between obstacles and the tracer size: λ ≈ 0.1–0.5 μm (19–21) (see also Fig. 2, a and c, and below for detailed discussion of spatial scales). In the proximity of the percolation limit ϕ_c (a minimum inaccessible volume fraction at which the tracer is trapped by obstacles), λ diverges as (ϕ_c − ϕ)^−0.88 (22), and for ϕ ≥ ϕ_c, 〈x²〉 is no longer ∝ t (anomalous diffusion) (17). For large tracers, the inaccessible volume can be greater than the volume occupied by obstacles (Fig. 3): for example, for the tracer diffusing amid filaments, the inaccessible volume is approximately four times the volume of the filaments, if the diameters of the tracer and the filaments are equal. The increase in inaccessible volume can bring the system to a percolation limit. Indeed, anomalous diffusion of 0.3-μm granules has been observed in actin meshwork with a volume density of ∼1%, virtually impermeable for particles of this size (23,24).

Figure 2.

Actin filaments and ER, simulated and in vivo. (a) Electron micrograph of actin filaments in a keratocyte (adapted from (21)). (b) Representation of cytoskeletal filaments by long thin cylinders (aspect ratio χ = 100, excluded volume fraction ϕ = 0.0636). (c) Optical section of ER of the unfertilized sea urchin eggs, courtesy of Mark Terasaki (confocal depth is 2–3 μm; see (20) for experimental details). (d) Modeling of ER sheets by random three-dimensional disks (aspect ratio χ = 0.125, excluded volume fraction ϕ = 0.2926). As in confocal sectioning, the image was obtained by combining z sections from a 2.5 μm-thick slice. Note that the bright lines in the image are not short filaments, but rather cumulative projections of disks nearly orthogonal to the confocal plane.

Figure 3.

Diffusion of a tracer of finite size among obstacles of volume v modeled as diffusion of a point particle among effective obstacles of volume v′. The increase in obstacle size equals the tracer radius. Even if the real obstacles do not overlap, the effective ones may partially intersect.

In this article, we analyze how microgeometry of intracellular structures affects D_eff. Determining an effective property of a composite medium is a classical problem that dates back to Poisson, Faraday, Clausius and Mossotti, and Lorentz and Lorenz, who studied effective magnetic, dielectric, and optical properties of heterogeneous materials (25). The problem of computing D_eff for a medium with obstacles is mathematically equivalent to determining the effective conductivity, σ_eff, of a conductor with dielectric inclusions, where σ_eff is the analog of the transformed effective diffusion coefficient ${\tilde{D}}_{\text{eff}}=(1-\phi )D_{\text{eff}}$ (25,26). In 1873, Maxwell solved for the conductivity of a dilute suspension of spheres and found σ_eff = σ₀(1 − 1.5ϕ). This result was generalized to other shapes of inclusions (27): σ_eff = σ₀(1 − αϕ), where α differs from 1.5, depending on the shape and spatial positioning of inclusions (for example, α = 5/3 in the case of randomly oriented long cylinders). Numerical approaches to computing α for irregular shapes have been discussed in Douglas and Garboczi (28). The dilute solution approximation does not apply to ϕ in the range typical for intracellular structures (26). Extension to larger ϕ for spheres, derived with an effective-medium approximation (29), yields σ_eff = σ₀(1 − ϕ)^3/2. A general form of this power law, σ_eff = σ₀(1 − ϕ)^m, known as Archie's law (30), has been shown empirically to be a useful approximation for some natural composites. Still, this law breaks down when the shape of obstacles differ significantly from spherical. Overall, no general solution has been found for this classical problem (25,31).

This study presents the first systematic numerical approach to the problem in the context of effective diffusion in cells. The Monte Carlo method used to obtain the results of Figs. 1 and 4 is conceptually simple, but is prohibitively expensive for a comprehensive study. We have developed a fast algorithm based on the concept of homogenization (32). Details of the algorithm, along with representation of intracellular geometry, are described in the Model, below. We have found that for random overlapping obstacles, a simple two-parameter power law provides a remarkably accurate description of the excluded volume effect over the entire range of volume fractions and obstacle shapes (see Results). This universality allows for fast computation of effective diffusion coefficients, once the shapes of obstacles and their excluded volume fractions are specified. Estimates obtained for obstacles characteristic of intracellular structures demonstrate that the excluded volume effect is a major factor that accounts for most reduction in diffusivity in cells, relative to diffusion in vitro. In the Discussion, the results are compared with experimental data.

Figure 4.

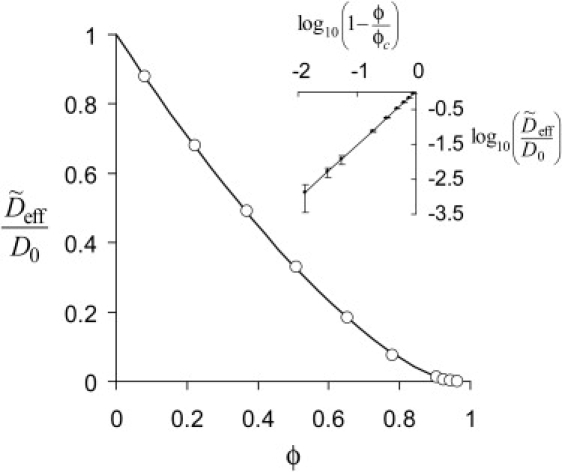
D_eff(ϕ)/D₀ for random spheres, from Monte Carlo simulations (solid dots with error bars) and by the homogenization method with different number of obstacles per unit cell. (Inset) D_eff(ϕ)/D₀ in the vicinity of ϕ_c = 0.955.

Model

Irregular geometry of intracellular structures is approximated by sets of randomly positioned, overlapping obstacles, the approach known as a Swiss-cheese model (33). Cytoskeletal filaments are mimicked by long thin cylinders (Fig. 2 b), whereas thin flat disks approximate sheetlike regions of internal membranes (Fig. 2 d). Disks and cylinders are the shapes with limiting values of the aspect ratio χ = h /2r, equal to 0 and ∞, respectively (r is radius of the cylinder and h is its height). In studying the effect of obstacle shape on D_eff, we also consider cylinders with intermediate aspect ratios, as well as spheres. By allowing the obstacles to intersect, deformable and branching structures are conveniently modeled by means of rigid objects of simple shapes (Fig. 2, b and d). In addition, when the finite size of a tracer is taken into account through a corresponding increase in the obstacle size, the resulting effective obstacles may intersect, at least partially (Fig. 3). Structural disorder, typical of the intracellular environment, is achieved by placing and orienting obstacles randomly in space.

In the Swiss-cheese model, with no restrictions on overlapping of obstacles, the fraction of inaccessible volume is ϕ = 1 − exp(−V), where V is the sum of volumes of individual obstacles per unit volume. The relation is derived in Supporting Material, along with an interpolation formula for the case where only partial intersection is allowed. For identical obstacles, V = nv₀, where v₀ is the volume of one obstacle and n is the obstacle number density. Inversely, V can be expressed in terms of ϕ: nv₀ = ln[(1 − ϕ)⁻¹]. For a cytoskeletal network, an estimate of an average distance between the obstacles is $\sim r/\sqrt{n{v}_0}$ (see derivation in Supporting Material) and yields ∼0.05 μm for r = 5 nm (10) and ϕ = 0.01 (34). For the disks, a similar estimate yields the distance ∼h/(nv₀) ≈ 0.2 μm for h = 0.1 μm and ϕ = 0.4 (10).

These estimates agree with experimental findings (Fig. 2, a and c) and give an idea about a length scale for which the concept of the effective diffusion coefficient is applicable. Indeed, the log-log plot of 〈x²(t)〉 for spherical obstacles (Fig. 1 b) exhibits three distinct diffusive regimes observed at different length- and timescales. The first is unobstructed diffusion in the space between neighboring obstacles. It is observed on a scale of less than the average distance between the obstacles, i.e., at submicron lengths. Once the tracer hits the obstacle, it enters an intermediate (anomalous) diffusive regime where 〈x²(t)〉 is no longer ∝ t. Yet on a larger length scale, the mean-squared displacement becomes again linear in time, signifying re-emergence of normal diffusion characterized by D_eff. Simulations for other shapes and on lattices (18) yield similar results, which also agree with the experimental data (11). An important observation that follows from the Monte Carlo studies is that when ϕ is not too close to the percolation threshold, normal diffusion resumes on lengths that are comparable to several average distances between the obstacles: at these lengths, the current and initial positions of the tracer are no longer correlated. From estimates of characteristic mesh sizes of intracellular structures, we conclude that the concept of an effective diffusion coefficient holds on a micron scale.

Existence of two distinctly different spatial scales allows one to compute D_eff based on the principle of homogenization (32,25). The method is an alternative to microscopic particle tracking mimicked by Monte Carlo simulations and is equivalent to determining effective diffusion coefficients from Fick's law: the steady-state diffusive flux is measured as a function of the concentration difference maintained between the opposite sides of a large rectangular box. Mathematically, homogenization is an asymptotic analysis that utilizes a small parameter, the ratio of micro- and macro-length scales, to obtain accurate effective characteristics of the medium (35). We used this approach to develop a numerical algorithm for computing D_eff more efficiently than from stochastic simulations. The algorithm, described in Methods, made it possible to perform extensive numerical studies of various factors that affect D_eff.

The homogenization technique was originally formulated for composites with periodic microstructures (36). Consider a periodic arrangement of identical obstacles in a large rectangular box Ω with the free space Ω₁ in it and φ = 1 − |Ω₁|/|Ω|. The spatial periods a₁, a₂, and a₃ in respective Cartesian directions are such that the ratio

$$\varepsilon =\sqrt{a_1^2+a_2^2+a_3^2}/\sqrt[3]{|\Omega |}$$

is small: ɛ ≪ 1. The diffusion coefficient,

$$D_{\varepsilon }\left(\mathbf{x}\right)=\{\begin{array}{c}{D}_0,\text{if}\mathbf{x}\in {\Omega }_1\\ 0,\text{otherwise}\end{array},$$

oscillates with the same periods.

Steady-state diffusive fluxes in Ω are determined by the tracer distribution u_ɛ(x), found by solving the equation

$$\mathit{div}(D_{\varepsilon }\left(\mathbf{x}\right)\nabla u_{\varepsilon })=0,$$ (1)

with the Dirichlet boundary conditions maintaining mismatch of the tracer concentrations at the opposite sides of Ω.

The idea behind homogenization is that when ɛ → 0, u_ɛ(x) converges to a homogenized distribution u₀(x) that satisfies a macroscopic diffusion equation similar to Eq. 1. Note that u₀(x) is defined only in free space (as is u_ɛ(x)), so that the macroscopic density is u′(x) = (1−ϕ) u₀(x) (26); also, the effective diffusion coefficient is generally a tensor because periodic structures of asymmetric obstacles are anisotropic. Therefore, the macroscopic diffusion equation is

$$div({\mathbf{D}}_{\text{eff}}\nabla u\prime )=div({\mathbf{D}}_{\text{eff}}(1-\phi )\nabla u_0)=div({\tilde{\mathbf{D}}}_{\text{eff}}\nabla u_0)=0\text{.}$$ (2)

The tensor ${\tilde{\mathbf{D}}}_{\text{eff}}=\left\{{\tilde{D}}_{\text{eff, ij}}\right\}$, (i,j = 1, 2, 3), is obtained by means of multiscale analysis (25) that takes advantage of the smallness of ɛ in Eq. 1 (see Supporting Material for details). The result is that ${\tilde{D}}_{\text{eff, ij}}$ are expressed in terms of auxiliary functions w_i(x) (i = 1, 2, 3) defined in the unit cell ω = (0, a₁)x(1, a₂)x(1, a₃) and determined by solving

$$div\left(D_{\varepsilon }\left(\mathbf{x}\right)(\nabla w_{\text{i}}\left(\mathbf{x}\right)+{\mathbf{e}}_{\text{i}})\right)=0,i=1,2,3$$ (3)

in ω with periodic boundary conditions; e_i, i = 1, 2, 3, are the orts co-linear with the edges of ω (and Ω). Then,

$${\tilde{D}}_{\text{eff, ij}}=\frac{D_0}{\left|\omega \right|}\underset{{\omega }_1}{\int }(\nabla w_{\text{i}}\left(\mathbf{x}\right)+{\mathbf{e}}_{\text{i}})(\nabla w_{\text{j}}\left(\mathbf{x}\right)+{\mathbf{e}}_{\text{j}})d\mathbf{x},$$ (4)

where ω₁ is the free space in ω (see Supporting Material for derivation). Then, for isotropic periodic structures, the actual effective diffusion coefficient D_eff (ϕ) is

$$D_{\text{eff}}=\frac{D_0}{(1-\phi )\left|\omega \right|}\underset{{\omega }_1}{\int }{(\nabla w_1\left(\mathbf{x}\right)+{\mathbf{e}}_1)}^{2}d\mathbf{x}\text{.}$$ (5)

The concept of homogenization can be extended to random structures where stochastic homogeneity is the analog of periodicity (25). This is done by approximating a disordered medium with a periodic one, where the unit cell ω includes N randomly placed obstacles; N should be sufficient to yield, for a given number density of obstacles n, a statistically stationary D_eff. In practical terms, the question is how many obstacles per unit cell, N = n |ω|, would yield a sufficiently accurate approximation of D_eff/D₀ (say, with an absolute error of 0.01). The value N might not be necessarily large for biologically relevant n, since the tracer achieves normal diffusion after bypassing only few obstacles. In the proximity of the percolation limit, however, N must be large, as the free space breaks into weakly connected large linear clusters.

To estimate an appropriate N, the homogenization method was applied to randomly placed spheres. The values of D_eff, N (ϕ), computed for N = 50, 100, 200, and 400 (Fig. 4), compare well with D_eff (ϕ) obtained from the Monte Carlo simulations (see Methods for simulation details). Even with N as small as 50, the homogenization method yields sufficiently accurate results. In this study, we used N ∼ 2500 to obtain D_eff with the absolute error <0.02.

Methods

Monte Carlo simulations

Stochastic trajectories of N tracers, x_i(t), i = 1,…, N, are generated in a sufficiently large box with randomly placed obstacles. The position of a tracer is advanced with a fixed time step Δt,

$${\mathbf{x}}_{\text{i}}(t+\Delta t)={\mathbf{x}}_{\text{i}}\left(t\right)+{\mathit{\xi }}_{\text{i}}\sqrt{6D\Delta t}(i=1,2,3),$$

where ξ_i are random vectors uniformly distributed in [−1,1]³ and D is the diffusion coefficient in free space. If the tracer collides with an obstacle, new trials are performed to find a position in the accessible space. Monte Carlo integration is used to evaluate ϕ. The mean-squared displacement is computed as

$$\langle {\mathbf{x}}^2\left(t\right)\rangle =(1/N){\sum }_{\text{i}=1}^{\text{N}}{({\mathbf{x}}_{\text{i}}\left(0\right)-{\mathbf{x}}_{\text{i}}\left(t\right))}^2\text{.}$$

Results were obtained for D = 1 μm²/s with Δt = 10⁻⁶–10⁻⁷ s and N > 10⁴. Accuracy of results is limited by computational cost: error bars in Fig. 4 reflect both the statistical error due to finite N and the truncation error due to finite t.

Homogenization algorithm

The algorithm, based on Eqs. 3–5, involves solving Eq. 3 and a subsequent evaluation of diagonal values of ${\tilde{\mathbf{D}}}_{\text{eff}}$ (Eq. 4). A Poisson solver for solving Eq. 3 with periodic boundary conditions has been implemented in VCell (37,38). A three-dimensional geometry, generated automatically from a set of obstacles by a custom-written code, was entered in VCell as a z stack of two-dimensional images. Because the structure of randomly arranged obstacles is expected to be isotropic, ${\tilde{D}}_{\text{eff}}$ was computed as ${\tilde{D}}_{\text{eff}}=(1/3)Tr\left({\tilde{\mathbf{D}}}_{\text{eff}}\right)=(1/3){\sum }_{\text{i}=1}^3{\tilde{D}}_{\text{ii}}$ with ${\tilde{D}}_{\text{ii}}$ evaluated according to Eq. 4. For details of the algorithm as well as its validation and error analysis, see Supporting Material.

Fitting of Eq. 6 to computed values of ${\tilde{D}}_{\text{eff}}$ was done by seeking, through variations of ϕ_c, an optimal linear fit of $\log \left({\tilde{D}}_{\text{eff}}\left(\phi \right)\right)$ as a function of log(1−φ/φ_c); the line slope then yields parameter μ. The least-squares fitting to a linear function was performed with the Excel optimization solver (Microsoft, Richmond, WA).

Computation time

All computations were done on an Altix 3700 (SGI, Fremont, CA) with a 1.6 GHz Itanium II CPU. The Monte Carlo method required an average of 100 hours per point in Fig. 4, whereas the homogenization method takes only half an hour for a datapoint of comparable accuracy.

Results

In this section, we show that the excluded volume effect of a mixture of random obstacles of varying shapes can be understood in terms of effective diffusion occluded by a system of overlapping spheres. This universality allows one to estimate the effective diffusion coefficient for a mixture of structures with shapes and composition characteristic of the intracellular environment.

The dependence ${\tilde{D}}_{\text{eff}}$ (φ) is described accurately by a two-parameter power law

The dependence D_eff (ϕ) in Fig. 4 is complicated. Linear at small volume fractions, it decreases more rapidly for ϕ > 0.5 before inflecting near the percolation threshold (inset in Fig. 4). However, when presented in terms of ${\tilde{D}}_{\text{eff}}\left(\phi \right)$, the function assumes a simpler form (Fig. 5) resembling a power function, ${\tilde{D}}_{\text{eff}}\left(\phi \right)\propto {({\phi }_{\text{c}}-\phi )}^{\mu }$. This function is predicted by percolation theory, but only near the percolation limit. Remarkably, our data for ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ are fitted well by the two-parameter power law,

$${\tilde{D}}_{\text{eff}}/D_0={(1-\phi /{\phi }_{\text{c}})}^{\mu },$$ (6)

over the entire range of volume fractions and for all shapes! (Interestingly, the same function approximates well the effective conductance of a variety of binary metal-insulator mixtures over a wide range of ϕ (39).)

Figure 5.

${\tilde{D}}_{\text{eff}}\left(\phi \right)/D_0$ for random spheres obtained with N = 2560 (symbols) and fitted by Eq. 6 (solid curve). (Inset) $\text{Log}({\tilde{D}}_{\text{eff}}/D_0)$ plotted as a function of log(1 − ϕ/ϕ_c); best linear fit is obtained with ϕ_c = 0.955.

For spheres, the best fit is with ϕ_c = 0.955 ± 0.025, μ = 1.47 ± 0.03 and the fitting error of ≈0.003 (the fitting error is the average difference between the power law of Eq. 6—shown by solid line in Fig. 5—and the datapoints). The results for ϕ_c and μ agree with the previously published data: ϕ_c = 0.9699 ± 0.0003 (40) (similar values were also reported in (41)) and μ = 1.6 ± 0.2 (42). For overlapping circles, another example with known parameter values, ϕ_c = 0.6763 (43) and μ = 1.3 ± 0.1 (33,44) (see also (45,46)), ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ from our numerical experiments is best approximated by Eq. 6 with ϕ_c = 0.672 ± 0.025 and μ = 1.35 ± 0.05; an average error of fit is 0.01 (Fig. S3). The insets in Fig. 5 and Fig. S3 demonstrate linearity of ${\log }_{10}({\tilde{D}}_{\text{eff}}/D_0)$ as a function of log₁₀(1 − ϕ/ϕ_c); this illustrates applicability of Eq. 6 over the entire range of ϕ.

Equation 6 describes ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ equally well for shapes other than spherical (Fig. 6 and Fig. 7 a). Overall, our numerical results indicate that Eq. 6 accurately describes ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ for the Swiss-cheese model, over a wide range of ϕ and for all obstacle shapes. When recalculated in terms of the actual effective diffusion coefficient D_eff, the equation takes the form

$$D_{\text{eff}}/D_0=\frac{{(1-\phi /{\phi }_{\text{c}})}^{\mu }}{1-\phi }\text{.}$$ (7)

From a technical viewpoint, describing ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ and D_eff (ϕ) by two-parameter functions greatly simplifies computations for arbitrary shapes. It follows from a dilute limit expansion that μ = α × ϕ_c, and the problem reduces to determining α and ϕ_c. The value of α can be accurately estimated by computing the transformed effective diffusion coefficient for some small volume fraction ϕ₁. For this, diagonal values of ${\tilde{\mathbf{D}}}_{\text{eff}}\left({\phi }_1\right)$ are computed based on Eqs. 3 and 4 for one obstacle placed at the center of a unit cube; then $\alpha ={\phi }_1^{-1}(1-Tr\left({\tilde{\mathbf{D}}}_{\text{eff}}\left({\phi }_1\right)\right)/3D_0)$. A few other values of ${\tilde{D}}_{\text{eff}}$ for different volume fractions ϕ are required to determine ϕ_c from fitting to Eq. 6 (see Methods for details).

Figure 6.

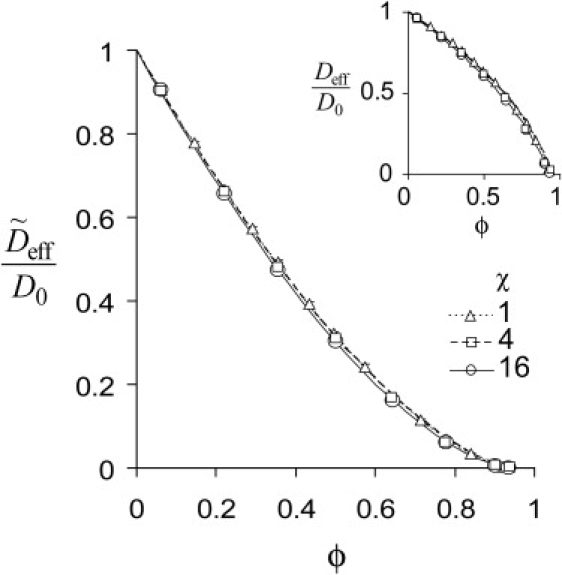
${\tilde{D}}_{\text{eff}}\left(\phi \right)/D_0$ for random cylinders (N = 2560) fitted by Eq. 6. (Inset) Corresponding D_eff(ϕ)/D₀ fitted by Eq. 7.

Figure 7.

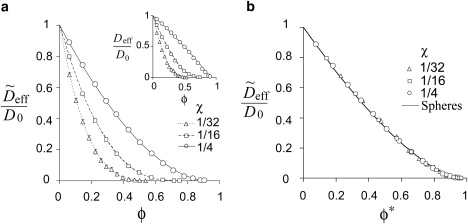
Randomly distributed disks. (a) ${\tilde{D}}_{\text{eff}}\left(\phi \right)/D_0$ for χ = 1/4, 1/16 (N = 2560) and χ = 1/32 (N = 320), fitted by Eq. 6. (Inset) Corresponding D_eff(ϕ)/D₀ fitted by Eq. 7; (b) collapse of ${\tilde{D}}_{\text{eff, disks}}\left(\phi \right)/D_0$ onto ${\tilde{D}}_{\text{eff, spheres}}(\phi \ast )/D_0$ with ϕ^∗ defined by Eq. 8 and for k(χ) from Table S1.

Effect of structure shape on D_eff

A spectrum of shapes, from prolate to oblate, has been studied with the use of cylinders of varying aspect ratios χ (see Model for definition). For all of them, the effective diffusion coefficients are accurately described by Eqs. 6 and 7; corresponding values of ϕ_c and μ are summarized in Table 1. The results for elongated cylinders, shown in Fig. 6, are essentially independent of the aspect ratio: the curves obtained for χ = 1, 4, and 16 are barely distinguishable. Moreover, ϕ_c and μ for long cylinders are close to those obtained for spheres. Therefore, diffusion of a tracer through a network of cytoskeletal filaments is fully determined by the fraction of inaccessible volume.

Table 1.

Parameters μ and ϕ_c for various shapes (aspect ratios χ)

Aspect ratio, χ	μ	ϕc
16	1.58	0.942
4	1.56	0.953
1	1.54	0.946
0.25	1.79	0.925
0.0625	2.66	0.74
0.03125	3.44	0.59
Sphere	1.47	0.955

The situation is qualitatively different for oblate obstacles, represented in our numerical experiments by disks with small aspect ratios. Here, the dependencies D_eff (ϕ) differ significantly for different values of χ (Fig. 7 a): thinner disks are more efficient, relative to the occupied volume, in impeding the tracer. In fact, for sufficiently small χ, the excluded volume fraction is no longer a meaningful parameter for describing effective diffusion, because both the volume fraction and the percolation threshold change synchronously with the aspect ratio. It is intuitively clear that the actual space shielded by the disk is essentially equidimensional, with a linear size of approximately the disk radius, r. Indeed, we have found that under the scaling transformation r^∗ = k(χ)r, the dependencies ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ for disks collapse onto the dependence ${\tilde{D}}_{\text{eff}}(\phi \ast )$ for spheres with the equivalent volume fraction ϕ^∗ calculated as

$$\phi \ast =1-{(1-\phi )}^{2k^3\left(\chi \right)/3\chi }$$ (8)

(see Supporting Material for derivation). The quality of collapse is illustrated in Fig. 7 b for χ = 1/4, 1/16, and, 1/32. The corresponding values of k(χ), along with k(1/250), are given in Table S1. This remarkable universality suggests a method for estimating D_eff (ϕ) for a mixture of shapes, with spheres effectively replacing objects of varying shapes. The method is used in subsequent sections.

Finally, we estimate D_eff of a subnanometer molecule diffusing 1), through a network of cytoskeletal filaments and 2), in the presence of the sheetlike ER. In this case, the inaccessible volume equals the volume of the structure (for larger particles, see Effect of Tracer Size). For cytoskeletal filaments, Eq. 7 with the long-cylinder parameters, μ = 1.58 and ϕ_c = 0.942, and ϕ ≈ 0.1 yields D_eff ≈ 0.93 D₀, indicating only a minor effect. One can also ask how dense the cytoskeletal network should be to slow a small molecule by 90%. To find the corresponding ϕ, we solve Eq. 7 with D_eff/D₀ = 0.1 and the μ and ϕ_c, as above. The result, ϕ ≈ 0.89, corresponds to extremely tight packing, with the cytosol occupying only 11% of volume.

The sheets of ER can be modeled as oblate objects. Disks with an aspect ratio of χ = 1/32 and a thickness of h = 100 nm have a diameter 2r =3.2 μm, not an unreasonable number (Fig. 2 c). The parameters of the power law for this aspect ratio are μ = 3.44 and ϕ_c = 0.59 (Table 1), and for ϕ = 0.1, as in the previous example, Eq. 7 yields D_eff ≈ 0.59 D₀. We conclude that the internal membranes have a major impact on the effective tracer diffusion.

Mixture of shapes

Membrane organelles and cytoskeleton can both be present in the same micron-scale volume unit. Therefore, it is necessary to be able to describe effective diffusion for a mixture of shapes. The question then arises whether Eq. 6 can describe ${\tilde{D}}_{\text{eff}}$ for a mixed structure and if so, how to express the mixture parameters μ and ϕ_c in terms of the parameters for individual forms.

Our numerical experiments show that Eq. 6 does hold for structures composed of different shapes. Fig. 8 a shows results of one such experiment, where ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ is computed for a mixture of cylinders (χ = 4) and disks (χ = 1/16) with equal individual volumes and number densities. In general, a mixture of obstacles of two different shapes and sizes is defined by the individual volumes, v₁ and v_2, and the number densities, n₁ and n₂ of the components. Numerical experiments, in which all of these parameters were varied independently, have shown that if the sizes are of the same order of magnitude, the effective diffusion coefficient of a tracer depends on the ratio V₁/V₂ ≡ n₁v₁/n₂v₂, rather than on individual parameters. In this case, diffusion in the mixture is fully characterized by phase fractions, f₁ = V₁/(V₁ + V₂) and f₂ = V₂/(V₁ + V₂), f₁ + f₂ = 1, and by parameters μ₁, ϕ_c,1 and μ₂, ϕ_c,2 for pure forms. We measured percolation thresholds for two-shape mixtures of varying composition and found that the dependence on individual fractions is essentially linear, φ_c ≈ φ_c,1f₁ +φ_c,2f₂. Fig. 8 b presents results for the mixtures of cylinders (shape 1) and disks (shape 2) with the aspect ratios of 4 and 1/16, respectively.

Figure 8.

Mixture of shapes. (a) ${\tilde{D}}_{\text{eff}}\left(\phi \right)/D_0$ for the mixture of cylinders (χ = 4) and disks (χ = 1/16) with phase fractions f₁ = f₂ = 0.5, fitted by Eq. 6 (solid line). (Inset) Corresponding D_eff(ϕ)/D₀ fitted by Eq. 7. (b) Percolation threshold ϕ_c for the cylinder-disk mixture as a function of disk fraction, f₂. Error bars reflect the difference between values obtained by fitting to Eq. 6 and determined directly from sampling an appropriate interval of ϕ with steps Δϕ ≈ 0.01–0.02.

To determine the exponent μ(f₂) for the mixture of a given composition (f₁, f₂), note that μ(f₂) = α(f₂) × ϕ_c(f₂), where α is the slope of ${\tilde{D}}_{\text{eff}}\left(\phi \right)/D_0$ in the dilute limit, and in which overlapping of obstacles is negligible. This then results in a linear superposition,

$$\alpha \left(f_2\right)\approx {\alpha }_1{f}_1+{\alpha }_2{f}_2=({\mu }_1/{\phi }_{\text{c,1}})f_1+({\mu }_2/{\phi }_{\text{c,2}})f_2,$$

and back-substitution yields

$$\mu \left(f_2\right)\approx (1+f_2({\phi }_{\text{c,2}}-{\phi }_{\text{c,1}})/{\phi }_{\text{c,1}}){\mu }_1{f}_1+(1+f_1({\phi }_{\text{c,1}}-{\phi }_{\text{c,2}})/{\phi }_{\text{c,2}}){\mu }_2{f}_2\text{.}$$

We can now estimate D_eff of a tracer for a mixture of structures with shapes and composition characteristic of the intracellular environment. From the data available for hepatocytes (10), ϕ ≈ 0.44. For small tracers, the effect of cytoskeleton can be ignored (see discussion of the effect of the cytoskeleton on large tracers below). Organelle shapes can be classified as oblate and spheroidlike, with the corresponding volumes being in proportion 3:5, respectively (10). We therefore model the excluded space as a mixture of overlapping disks (shape 1) and spheres (shape 2) with ϕ = 0.44 and V₁/ V₂ = 0.6 (f₁ = 0.375 and f₂ = 0.625). Assuming χ = 1/32 for the disks, the corresponding percolation threshold of the mixture is ϕ_c = 0.818 and the exponent is μ = 2.58. Then, from Eq. 7, D_eff ≈ 0.24 D₀. Thus, effective diffusion of a small tracer in the cytoplasm is predicted to be four times slower than that in the extracts free of intracellular organelles.

An alternative way of estimating D_eff in this case is to use the disk-to-sphere mapping, as described above. Accordingly, disks can be replaced with spheres, so that

$${\tilde{D}}_{\text{eff}}\left(\phi \right){|}_{\text{mixture}}={\tilde{D}}_{\text{eff}}(\phi \ast ){|}_{\text{spheres}}$$

with

$$\phi \ast =1-{(1-\phi )}^{f_2+\frac{2k^3\left(\chi \right)}{3\chi }{f}_1}$$

(see Supporting Material for derivation). For f₁ = 0.375, f₂ = 0.625, and ϕ = 0.44 as above, and k(1/32) = 0.578, ϕ^∗ ≈ 0.716. Then, using the sphere parameters, μ₂ = 0.955 and ϕ_c,2 =1.47, ${\tilde{D}}_{\text{eff}}\left(\phi \right)={(1-\phi \ast /{\phi }_{\text{c,2}})}^{{\mu }_2}\approx 0.13D_0$ and $D_{\text{eff}}\left(\phi \right)={\tilde{D}}_{\text{eff}}\left(\phi \right)/(1-\phi )=0.23D_0$. Thus, both methods yield similar estimates of the effective diffusion coefficient in the cytoplasm.

Effect of tracer size

The tracer size has little or no effect on diffusion in the presence of oblate objects with small aspect ratios (membrane sheets). Although thicker membranes occupy larger volume, D_eff in this case is essentially insensitive even to significant changes of the aspect ratio. Indeed, because ϕ ≪ 1, $D_{\text{eff}}\left(\phi \right)\approx {\tilde{D}}_{\text{eff}}\left(\phi \right)$, and ${\tilde{D}}_{\text{eff}}\left(\phi \right)$ can be estimated through mapping onto effective spheres,

$${\tilde{D}}_{\text{eff}}\left(\phi \right){|}_{\text{disks}}={\tilde{D}}_{\text{eff}}(\phi \ast ){|}_{\text{spheres}},$$

where ϕ^∗ is defined by Eq. 8,

$$\phi \ast \approx \frac{2k^3\left(\chi \right)}{3\chi }\phi$$

(again exploiting the smallness of ϕ). The overlap of disks is also small, so that φ ≈ nπr³χ (n is the number density), hence, φ^∗ ∼ k³(χ). Because k(χ) is a slow function of χ, the excluded volume fraction of effective spheres ϕ^∗ and therefore D_eff are not particularly sensitive to changes in χ. Thus, even for tracer sizes comparable to, or greater than, ER thickness (∼100 nm), the ratio D_eff/D₀ is virtually the same as for small molecules. This may explain why the size effect had not been detected in some experiments (15).

In contrast, diffusion through a network of filaments is sensitive to tracer sizes if they are comparable to, or greater than, the diameter of the filaments. The latter range between 2.5 and 10 nm. Let V be the total volume of individual filaments in a unit volume and R the tracer radius. Then the fraction of volume inaccessible to the tracer is V_eff ≈ V(1 + R/r)² (r is the radius of the filament). With overlapping,

$${\phi }_{\text{eff}}=1-\exp (-V{(1+R/r)}^2)=1-{(1-\phi )}^{{(1+R/r)}^2},$$ (9)

where ϕ is the volume fraction of overlapping filaments. Once ϕ_eff is computed, a simple and accurate way to estimate the effect of the tracer size on diffusion is to use a multiplication rule (47),

$$D_{\text{eff}}\approx D_{\text{eff}}^{\left(0\right)}{D}_{\text{eff}}^{\left(1\right)}\left({\phi }_{\text{eff}}\right)/D_0,$$

where $D_{\text{eff}}^{\left(0\right)}$ and $D_{\text{eff}}^{\left(1\right)}$ are, respectively, the effective diffusion coefficients for the structure that does not include the cytoskeleton and the one that includes filaments only. Approximating $D_{\text{eff}}^{\left(1\right)}$ by Eq. 7 with the parameters for long cylinders yields

$$D_{\text{eff}}(\phi ,R)/D_{\text{eff}}^{\left(0\right)}\approx \frac{{(1-{\phi }_{\text{eff}}/{\phi }_{\text{c,cyl}})}^{{\mu }_{\text{cyl}}}}{1-{\phi }_{\text{eff}}},$$ (10)

where ϕ_c,cyl = 0.942, μ_cyl = 1.58, and ϕ_eff is determined by Eq. 9.

Equation 10 can be compared directly to the experimental findings reported in Luby-Phelps et al. (12). In the experiments, fluorescently labeled inert particles of controlled sizes were injected into live cells. The effective diffusion coefficients were measured by fluorescence recovery after photobleaching and normalized to those in water. Satisfactory agreement between the experimental data and predictions from Eq. 10, shown in Fig. 9, was achieved with ϕ = 0.024, a reasonable estimate of the volume fraction of actin (34).

Figure 9.

Normalized D_eff as a function of tracer radius R. Experimental data (12) (dots with error bars) are compared with predictions from Eq. 10 with ϕ = 0.024 (solid line). The experimental values of D_eff are from Table 1 of Luby-Phelps et al. (12) after averaging over all particles in a sample.

We conclude with estimating D_eff for a tracer of a nanometer size, R = r =2.5 nm, in the cytoplasm. Because the particle is relatively large, the size effect needs to be included. Therefore, in addition to the intracellular structures, as above, we take now into account cytoskeletal filaments with ϕ = 0.04. From Eq. 9, ϕ_eff = 0.15 and Eq. 10 yields $D_{\text{eff}}\approx 0.79D_{\text{eff}}^{\left(0\right)}$, where $D_{\text{eff}}^{\left(0\right)}=0.24D_0$ (see previous section). Overall, D_eff ≈ 0.19D₀; this indicates that the effective diffusion of a relatively large tracer can be five times slower than it would be in the extract free of intracellular structures.

Discussion

Diffusion of molecules in cytoplasm is a complicated phenomenon involving many factors. In the course of diffusive transport, macromolecules can bind to and unbind from other molecules; they experience and exert hydrodynamic forces and move in a heterogeneous environment where space is occluded by internal membranes, cytoskeletal meshwork, and by other solutes. To be able to analyze such a complicated system, it is necessary to make simplifying assumptions that allow considering these factors independently. This article presents a systematic numerical study of the excluded volume effect due to intracellular structures, such as internal membranes and cytoskeleton. It shows that this effect is a major factor that accounts for most of the reduction in diffusive transport of the inert tracer, compared to in vitro diffusion.

A key step is to develop an adequate approximation of the intricate geometry of intracellular structures. In this study, the geometry is mimicked by random overlapping obstacles of appropriate shapes, an approximation known as a Swiss-cheese model. This approach permits modeling deformable and branching structures by means of rigid objects of simple shapes. In particular, cytoskeletal filaments are modeled as long thin cylinders whereas ER cysternae are represented by thin disks. For biologically relevant volume fractions ϕ, Monte Carlo simulations indicate onset of normal diffusion on a micron scale. The Monte Carlo method is impractical, however, for extensive studies of diffusion in a variety of conditions because of its prohibitive computational cost. Instead, we have implemented a more efficient method of computing D_eff based on the idea of homogenization (32,25), which enabled exhaustive studies of diffusion in space crowded by obstacles of different shapes and number densities.

Numerical experiments have uncovered unexpected similarities. First, D_eff (ϕ) is accurately described by a unique two-parameter function (Eqs. 6 and 7) that applies to the entire range of volume fractions and to all shapes and their mixtures. This universality simplifies computations: all that is needed for determining D_eff for all ϕ is to estimate two parameters for a given shape. Second, a scaling transformation has been identified under which dependencies for oblate objects collapse onto that for spheres. This simplifies estimation of D_eff for mixtures of obstacle shapes.

Shapes, characteristic of intracellular environment, have been shown to bring about a four-to-fivefold reduction in diffusive transport, compared to diffusion in cytosol free of intracellular structures. In the extract with a total macromolecular content of ∼100 mg/mL, the diffusion coefficient of a solute is D₀ ≈ 0.8 D_{in vitro} (2,7,9). Then the overall reduction is D_eff = 0.19–0.24 D₀ = 0.16–0.2 D_{in vitro}. These estimates agree with experimentally measured ranges for inert particles and globular proteins (6,15,48). For a 20–30 kDa protein of radius R = 1.5 nm, D_{in vitro}, estimated by the Stokes-Einstein equation, is D_{in vitro} = k_BT/6πη_waterR, where k_B is the Boltzmann constant, T is the absolute temperature, and η_water is the viscosity of water. With T = 300 K and η_water = 0.01 g/(cm·s), D_{in vitro} ≈ 150 μm²/s. Then a typical value of the in vivo diffusion coefficient for this protein would be ≈ 30 μm²/s, an estimate comparable to the experimental data for globular proteins with no significant binding interactions in cytoplasm (48).

The analysis also shows that cytoskeletal filaments are unlikely to constitute diffusion barriers sufficient for formation of a microdomain of small molecules: to reduce diffusivity of a small molecule 10-fold, the filaments would need to fill ∼90% of space, a very tight packing! In contrast, ER sheets appear to be much more efficient in slowing down diffusion. This may explain why diffusion of vesicle-sized beads remain slow even after all major cytoskeletal filaments are disassembled (6).

Perhaps most importantly, this study lays the foundation for an accurate coarse-grain formulation that would account for the mesoscale heterogeneity of cytoplasm and the binding of tracers to intracellular structures.

Supporting Material

Supplemental text, three figures and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01045-5.