Abstract
Force-field validation is essential for the identification of weaknesses in current models and the development of more accurate models of biomolecules. NMR coupling and relaxation methods have been used to effectively diagnose the strengths and weaknesses of many existing force fields. Studies using the ff99SB force field have shown excellent agreement between experimental and calculated order parameters and residual dipolar calculations. However, recent studies have suggested that ff99SB demonstrates poor agreement with J-coupling constants for short polyalanines. We performed extensive replica-exchange molecular-dynamics simulations on Ala3 and Ala5 in TIP3P and TIP4P-Ew solvent models. Our results suggest that the performance of ff99SB is among the best of currently available models. In addition, scalar coupling constants derived from simulations in the TIP4P-Ew model show a slight improvement over those obtained using the TIP3P model. Despite the overall excellent agreement, the data suggest areas for possible improvement.
A significant challenge in the use of computation to study complex biomolecular systems is force-field accuracy. Force fields are made up of a molecular-mechanics energy function with empirical parameters, which are typically obtained from fitting to experimental or high-level quantum mechanical (QM) data. These approximations may lead to inaccuracies in calculated kinetic and/or thermodynamic properties. One such force field is ff94 (1), which has a strong bias favoring helical content. Although it is not always apparent in short simulations, ff94 leads to overstabilization of helical systems and the adoption of stable helices for sequences that have nonhelical experimentally determined structures (2). Even in cases where the force field matches well to the QM data used in parameter development, errors can arise from inconsistencies in the model. For example, many nonpolarizable force fields employ partial charges that are intended to reproduce the enhanced dipoles found in aqueous solution, yet the dihedral potentials are fit to reproduce gas-phase QM energy profiles using these charges. These effects, combined with the relatively small size of the systems used for parameter development, indicate that validation against experimental data is vital.
ff99SB was developed to improve the secondary structure balance of the previous Amber protein force fields, as well as to improve the description of glycine residues (3). Although the parameters were fit with the use of QM data, the development relied on the validation of candidate parameters against experiment. Decoy sets of helical peptides, hairpins, and miniproteins demonstrated the correct energy minima. Calculated NMR order parameters for ubiquitin and lysozyme also showed better agreement with experiment than previous force fields. Showalter and Bruschweiler (4) demonstrated that ubiquitin dynamics as measured by residual dipolar couplings obtained from ff99SB simulation are “comparable to or better than the best static structural models and the NMR ensemble”. Other works have shown similarly good agreement between ff99SB simulations and NMR structural and relaxation data (5–8). Overall, these studies suggest that ff99SB is in at least reasonable agreement with experiment for a variety of proteins.
One disadvantage of performing such studies on complex systems is that it can be difficult to decompose inaccuracies into the specific force-field terms that need improvement. Short polyalanines have become useful, simple model systems for studying the conformational variability of unfolded states; however, in such states the structural preferences are weak and therefore the system is highly sensitive to small inaccuracies (9–12). A recent study of Alan (n = 3–7) by Graf et al. (13) showed that significant differences exist between the experimental and calculated J-coupling constants from unweighted simulation data. Building on this availability of extensive experimental data, Best et al. (14) performed a follow-up study on Ala5 using variations of the Amber (15), CHARMM (16), GROMOS (17), and OPLS (18) force fields using various sets of Karplus parameters to calculate the scalar coupling constants. They evaluated the force fields using a χ2 value that represented the sum of deviations of each calculated J-coupling constant compared with the experimental values, normalized by a factor related to the assumed systematic error in the coupling constant calculations. Of the parameter sets tested, ff99SB was ranked among the worst for this data set. Later, Best et al. (19) corrected key aspects of the data, with the result that ff99SB's ranking improved significantly. We present here a more detailed analysis of ff99SB's performance using two water models and peptides of different lengths.
We performed replica-exchange molecular-dynamics simulations (20,21) for 50 ns/replica of Ala3 and Ala5 in two explicit water models. Precision was quantified by means of fully independent simulations from different initial structures. Simulation details are included in the Supporting Material. In this study we address the performance of the ff99SB force field, compare the effects of using different water models, and suggest improvements to ff99SB that may improve agreement with experiment.
We calculated the scalar coupling constants for each polyalanine simulation using the same three Karplus parameter sets employed in the study by Best et al. (14) (Table 1). We also employed the same χ2 calculation as Best et al. to evaluate the deviation of the J-coupling constants from the experimental values. For Ala3, the χ2 values varied from 1.57 to 2.17 depending on the solvent model and the parameter set. The Ala5 J-coupling constants were also quite sensitive to these different variables, but even with the larger peptide size, the χ2 values remained < 2.0. Of importance, the χ2 values for Ala5 were at least as low as any of the other force fields evaluated by Best et al. (14).
Table 1.
Scalar coupling χ2 values for Ala3 and Ala5 using three different Karplus equation parameter sets
In addition to the protein force field, the water model may also be expected to have a significant effect on accuracy for these short, solvent-exposed peptides. To compare solvent effects, we generated simulations using the TIP3P (22) and TIP4P-Ew (23) solvent models. Simulations using TIP4P-Ew have shown better agreement between calculated and experimental NMR observables (6,24) due to more realistic diffusion and tumbling in this water model. However, TIP3P has been shown to be better than TIP4P-Ew at reproducing solvation free energies of small molecules (25). Our data for both polyalanines indicate that the deviations from experiment are modestly smaller (3–16% reduction in the χ2 value) when the TIP4P-Ew solvent model is used (Table 1). These data and those from the previous studies suggest that the combination of using the ff99SB force field with the TIP4P-Ew solvent model is one of the best combinations currently available, at least for short peptides.
To address the remaining issues with the force field, we compared the J-coupling constants across the sequence for the Ala peptides. We selected 3J(HN,Hα) and the 2J(N,Cα) constant because of their sensitivity to the ϕ and ψ angles of the backbone (Fig. 1). For the middle residues of Ala5, the calculated 3J(HN,Hα) values show deviations ranging from 1.2 to 1.7 Hz from the experimental observables and ranging from 6.8 to 7.4 Hz depending on the parameter set (compared with the experimental values of 5.6–6.0 Hz). These trends are observed in the other polyalanine simulations as well (see the Supporting Material); the coupling constants from the simulations are too large, indicating too much sampling of β-like local backbone conformations as compared with PPII, although the latter remains the dominant conformation. In contrast, the calculated 2J(N,Cα) constants are in excellent agreement with the experimental values, with the largest deviation in residue 2, which shifts to values that suggest slightly too much α-helical conformation (which are generally ∼6.50 Hz on the Karplus curve). Therefore, the most apparent issue for the local backbone conformations in these simulations is that the ensembles are shifted slightly away from favored PPII conformations.
Figure 1.
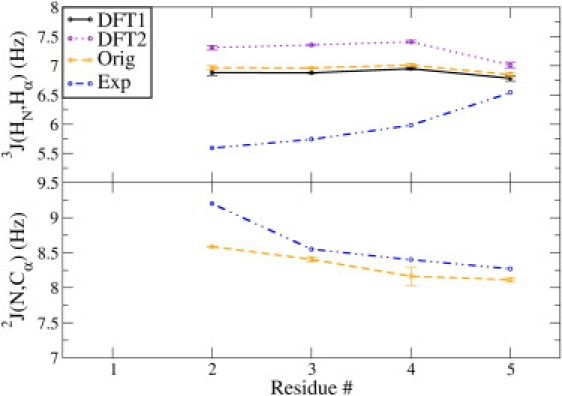
Average 3J(HN,Hα) and 2J(N,Cα) scalar constants for simulations of ALA5 in the TIP4P-Ew solvent model. These constants are calculated with the original DFT1 (black), DFT2 (purple), and original Karplus (orange) parameters, respectively. Experimental scalar values are plotted in each graph in blue. Error bars are calculated from the average difference between two simulations.
Our results show that scalar coupling calculations are sensitive to the implemented Karplus parameter sets (Table 1 and Fig. 1). Based on the calculated 3J(HN,Hα) values, the DFT2 (26) parameters should have the worst χ2 value; however, the Orig set (13) produces the worst results for Ala5 in the TIP4P-Ew model. In Fig. S2, the average J-coupling scalar constants are shown for the other scalar constants involved in the χ2 analysis. The parameter sets show similar trends for most of the scalar constants except for 3J(HN,Cβ), where the DFT2 set performs the best, compensating for the errors in the 3J(HN,Hα) and resulting in lower overall χ2. Thus the χ2 data should be interpreted with caution, and the influence of Karplus parameters on individual errors must be considered. Furthermore, the Orig parameters implicitly include the effects of motional averaging, and one would therefore expect worse agreement with experiment when scalar couplings are back-calculated from the full ensembles using empirical parameters fit to experimental data (27). Since this is not apparent, it appears that the effect of force-field inaccuracies on the simulated ensembles may exceed the effects of including dynamic fluctuations both implicitly in the Karplus parameters and explicitly in the molecular-dynamics ensembles.
Helical structural bias is a problem that has been associated with previous Amber force fields. We therefore focused on Ala5 since its sequence is long enough to permit an α-helical hydrogen bond. We calculated the percentage of α-helical conformations sampled by the central residue of Ala5 with the definition used by Best et al. (14) (Table S5). In the TIP3P and TIP4P-Ew solvent models, the α-basin populations are 20% and 15%, respectively, a significant improvement over the ff94 and ff99 force fields (90–95% of the ensembles sample an α-helical population depending on simulation conditions) (14). Nevertheless, one must use caution in interpreting these results in terms of helix formation. These calculations measure only the ϕ/ψ Ramachandran basin at the residue level; the structures may not sample an actual α-helical hydrogen bond. To test this, we repeated our calculations employing the dictionary for secondary structure prediction (DSSP) (28) definition for helicity, which resulted in populations of 0.4% and 0.0% of 310 and α-helix in both solvent models. Hence, the ff99SB ensemble does not suffer from the ailments of the previous force fields because it samples local α-helical conformations only in the random coil state, and no measurable amount of helical conformations.
In conclusion, comparisons of the Ala3 and Ala5 ensembles in both water models exhibit an excellent agreement between experimental and calculated scalar couplings. We also find that these calculations are somewhat solvent model-dependent, indicating that the TIP4P-Ew water model is the better choice for comparisons with NMR scalar coupling data. The deviations of the calculated and experimental 3J(HN,Hα) scalar constants with all of the parameter sets suggest that the deviations are largest in the ϕ-torsional potential, which could have effects on larger systems. Nevertheless, ff99SB does not present the helical bias issues of the previous force fields. In future work, we plan to use these experimental data as a reference to further improve our force-field parameters.
Supporting Material
Simulation and analysis details, error analysis, and tables, figures, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01031-5.
Supporting Material
Acknowledgments
We thank G. Hummer and R. Best for J-coupling scripts and feedback, and A. Roitberg for helpful discussions.
This work was supported by the National Institutes of Health (GM61678), National Center for Supercomputing Applications and National Institute for Computational Sciences (NPACI MCA02N028), and Department of Energy (DE-AC02-98CH10886).
Footnotes
Asim Okur's present address is Laboratory of Computational Biology, National Heart Lung and Blood Institute, National Institutes of Health, Bethesda, Maryland.
References
- 1.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 2.Okur A., Strockbine B., Hornak V., Simmerling C. Using PC clusters to evaluate the transferability of molecular mechanics force fields for proteins. J. Comput. Chem. 2003;24:21–31. doi: 10.1002/jcc.10184. [DOI] [PubMed] [Google Scholar]
- 3.Hornak V., Abel R., Okur A., Strockbine B., Roitberg A. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Showalter S.A., Bruschweiler R. Quantitative molecular ensemble interpretation of NMR dipolar couplings without restraints. J. Am. Chem. Soc. 2007;129:4158–4159. doi: 10.1021/ja070658d. [DOI] [PubMed] [Google Scholar]
- 5.Koller A.N., Schwalbe H., Gohlke H. Starting structure dependence of NMR order parameters derived from MD simulations: implications for judging force-field quality. Biophys. J. 2008;95:L4–L6. doi: 10.1529/biophysj.108.132811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fawzi N.L., Phillips A.H., Ruscio J.Z., Doucleff M., Wemmer D.E. Structure and dynamics of the AB(21–30) peptide from the interplay of NMR experiments and molecular simulations. J. Am. Chem. Soc. 2008;130:6145–6158. doi: 10.1021/ja710366c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wickstrom L., Okur A., Song K., Hornak V., Raleigh D.P. The unfolded state of the villin headpiece helical subdomain: computational studies of the role of locally stabilized structure. J. Mol. Biol. 2006;360:1094–1107. doi: 10.1016/j.jmb.2006.04.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Showalter S.A., Johnson E., Rance M., Bruschweiler R. Toward quantitative interpretation of methyl side-chain dynamics from NMR by molecular dynamics simulations. J. Am. Chem. Soc. 2007;129:14146–14147. doi: 10.1021/ja075976r. [DOI] [PubMed] [Google Scholar]
- 9.Shi Z.S., Chen K., Liu Z.G., Kallenbach N.R. Conformation of the backbone in unfolded proteins. Chem. Rev. 2006;106:1877–1897. doi: 10.1021/cr040433a. [DOI] [PubMed] [Google Scholar]
- 10.Zagrovic B., Lipfert J., Sorin E.J., Millettt I.S., van Gunsteren W.F. Unusual compactness of a polyproline type II structure. Proc. Natl. Acad. Sci. USA. 2005;102:11698–11703. doi: 10.1073/pnas.0409693102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Makowska J., Rodziewicz-Motowidlo S., Baginska K., Vila J.A., Liwo A. Polyproline II conformation is one of many local conformational states and is not an overall conformation of unfolded peptides and proteins. Proc. Natl. Acad. Sci. USA. 2006;103:1744–1749. doi: 10.1073/pnas.0510549103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mezei M., Fleming P.J., Srinivasan R., Rose G.D. Polyproline II helix is the preferred conformation for unfolded polyalanine in water. Proteins. 2004;55:502–507. doi: 10.1002/prot.20050. [DOI] [PubMed] [Google Scholar]
- 13.Graf J., Nguyen P.H., Stock G., Schwalbe H. Structure and dynamics of the homologous series of alanine peptides: a joint molecular dynamics/NMR study. J. Am. Chem. Soc. 2007;129:1179–1189. doi: 10.1021/ja0660406. [DOI] [PubMed] [Google Scholar]
- 14.Best R.B., Buchete N.V., Hummer G. Are current molecular dynamics force fields too helical? Biophys. J. 2008;95:L7–L9. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Case D.A., Cheatham T.E., Darden T., Gohlke H., Luo R. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brooks B.R., Bruccoleri R.E., Olafson B.D., States D.J., Swaminathan S. CHARMM—a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 17.van Gunsteren W.F., Billeter S.R., Eising A.A., Hünenberger P.H., Krüger P. Vdf Hochschulverlag, ETH Zurich; Switzerland: 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. [Google Scholar]
- 18.Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 19.Best R.B., Buchete N.V., Hummer G. Are current molecular dynamics force fields too helical? Erratum in. Biophys. J. 2008;95:4494. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hansmann U.H.E. Parallel tempering algorithm for conformational studies of biological molecules. Chem. Phys. Lett. 1997;281:140–150. [Google Scholar]
- 21.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 22.Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 23.Horn H.W., Swope W.C., Pitera J.W., Madura J.D., Dick T.J. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 24.Wong V., Case D.A. Evaluating rotational diffusion from protein MD simulations. J. Phys. Chem. B. 2008;112:6013–6024. doi: 10.1021/jp0761564. [DOI] [PubMed] [Google Scholar]
- 25.Shirts M.R., Pande V.S. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J. Chem. Phys. 2005;122:134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 26.Case D.A., Scheurer C., Bruschweiler R. Static and dynamic effects on vicinal scalar J couplings in proteins and peptides: a MD/DFT analysis. J. Am. Chem. Soc. 2000;122:10390–10397. [Google Scholar]
- 27.Bruschweiler R., Case D.A. Adding harmonic motion to the Karplus relation for spin-spin coupling. J. Am. Chem. Soc. 1994;116:11199–11200. [Google Scholar]
- 28.Kabsch W., Sander C. Dictionary of protein secondary structure—pattern-recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


