Determining the direction of vestibular-evoked balance responses using stochastic vestibular stimulation

Abstract

As a tool for investigating vestibulo-motor function, stochastic vestibular stimulation (SVS) has some advantages over galvanic vestibular stimulation. However, there is no technique currently available for extracting direction information from SVS-evoked motor responses. It is essential to be able to measure the direction of response if one wishes to investigate the operation of key spatial transformation processes in the brain. Here we describe and validate a technique for determining the direction of SVS-evoked balance responses based on the correlation between a random waveform of stimulating current and ground-reaction shear force.

To make effective use of vestibular information the brain must first transform the sensory signals from a head-fixed reference frame to a reference frame appropriate for the task at hand, e.g. a feet-fixed reference frame for standing balance. A pre-requisite for studying transformation processes is the ability to measure the direction of vestibular-evoked responses. Typically, galvanic vestibular stimulation (GVS) has been used: repeated square-wave currents are applied and the average body sway response indicates direction (reviewed in Fitzpatrick & Day, 2004). Stochastic vestibular stimulation (SVS) (Fitzpatrick et al. 1996; Pavlik et al. 1999; Dakin et al. 2007), in which quasi-random currents are applied whilst ongoing motor activity is recorded, provides an alternative method and offers some advantages over GVS: (1) it provides both time and frequency domain information in a single experiment; (2) there is an inherent absence of expectancy effects; (3) less time is required to obtain sufficient data; (4) it can be less destabilising. The last two points may be particularly relevant for studying disabled neurological patients. With SVS, however, there is no existing method for extracting precise direction of the evoked balance response. The time domain association between SVS and motor output (Dakin et al. 2007) introduces scope to achieve this. Dakin et al. (2007) mainly utilised EMG as their measure of motor output, but this does not contain sufficient spatial information. Ground reaction force (F; the force acting on the body) captures the net result of all the distributed muscles involved in the response in Cartesian space. Here we devise a method to determine the direction of the SVS-evoked balance response essentially involving identification of the direction along which F is maximally correlated with the stimulus. We test our technique using the well-established one-to-one relationship between head yaw angle and the direction of vestibular-evoked balance responses (Lund & Broberg, 1983; Pastor et al. 1993).

Methods

Ethical approval

The study received UCL Research Ethics Committee approval and conformed to the Declaration of Helsinki. All participants gave written, informed consent.

Procedure

Ten females and six males, aged 19–44, with no known history of neurological or vestibular problems were studied. Participants stood barefoot with their feet together, pointing forwards. Eye-height targets were placed at seven horizontal-plane angles (0, ±30, ±60, ±90 deg). Participants were instructed to orient their head to look at one of these targets (Fig. 1A). This could be accomplished using a combination of neck and trunk rotation, but we asked participants to keep eye-in-head position constant. Participants closed their eyes and SVS was applied for 30 s. An experiment consisted of 42 trials split into six blocks of seven trials. Within a block, one trial was performed at each head angle in a random order, and 45 s breaks were provided between trials. Three minutes of seated rest was provided between blocks.

Figure 1. Experimental set-up, and examples of raw signals and SVS–F cumulant densities.

A, experimental set-up showing subject's head oriented torward one (+30 deg) of seven targets and the convention for description of head yaw angle. B, example the SVS signal and raw F_LabX and F_LabY data collected with target head angle at +30 deg. C, single subject example of SVS–F_LabX CDF (left column) and SVS–F_LabY CDF (right column) for 0 deg (top row), +90 deg (middle row), and −90 deg (bottom row) target head angles. The dashed horizontal lines are the 95% confidence limits.

Stimulation and recording

A 1000 Hz, 180 s random signal was generated using the rand function in Matlab R13 (The Mathworks Inc., Natick, MA, USA). The random time-series was digitally low-pass filtered (20 Hz; 6th order Butterworth) and then amplified according to the desired stimulus intensity level. The signal was cut into six 30 s sections, each being used as the stimulus in one of the six blocks. The stochastic signal was sent via a digital-to-analog converter (Power 1401; Cambridge Electronic Design, Cambridge, UK) to a voltage-controlled variable current stimulator (in-house design). The stimulus had an RMS of 0.6 mA and peak amplitude of ±2 mA. Carbon rubber electrodes (10 cm²) coated with electrode gel were placed binaurally over the mastoid processes and fixed in place with adhesive tape and a headband. A positive value in the input signal generated an anode right, cathode left (ARCL) current and vice versa.

A CODA motion-capture system (Charnwood Dynamics, Rothley, UK) was used to record, at 1000 Hz, ground reaction 3D forces (Kislter 9286AA, Winterthur, Germany) and, at 200 Hz, the 3D positions of three non-collinear markers placed on a light, rigid plastic head-piece. A 3D local coordinate system was created using the head markers after removal of offsets during a 3 s static trial in which the subject fixated an eye-height target directly in front of the midline. The Cardan rotation of this head coordinate system about the laboratory coordinate system represented head-on-feet angle (Fig. 1A).

Association between SVS and F

The proposed method requires a time-domain measure of correlation between the SVS signal and F motor output. We use the cumulant density function (CDF), a time-domain measure equivalent to cross-correlation, obtained via the frequency-domain as the inverse Fourier transform of the cross-spectrum of two signals (Halliday et al. 1995). The frequency-based approach facilitates (1) generation of complimentary frequency-domain and time-domain measures of association, that can aid in the interpretation of vestibulo-motor responses (Dakin et al. 2007), and (2) construction of confidence intervals that play an important role (see Discussion). The CDF is an unbound measure of correlation, with magnitude dependent on input units. For uncorrelated signals, the CDF has an expected value of zero and statistically significant deviations from zero indicate a correlation between the two signals at a given time lag.

Details of the calculation of CDF are provided in online Supplemental Material. Briefly, DC offset was removed from raw F signals prior to analysis and spectral estimates were based on 42 (7 per trial) × 4.096 s segments of data (total data = 172.032 s; frequency resolution = 0.244 Hz). Less than 5% of signal power was below 0.244 Hz (Supplemental Material). Using different frequency resolutions for CDF calculation, or using cross-correlation instead of CDF, does not substantially alter the SVS-evoked response component of interest or its relationship with head angle (Supplemental Material).

Positive and negative values of CDF indicate an association between SVS and F signals of the same and opposite polarities respectively. For example, a positive SVS–F_LabX CDF is due to association between ARCL current and a rightward F component as well as association between ALCR current and leftward F component. For brevity, when referring to the direction of F associated with SVS we shall generally only refer to the direction associated with an ARCL current, the interpretation for ALCR current being antipodal.

Example of SVS–F CDF

Figure 1B provides an example of the SVS signal and raw F data over a 30 s time window. Figure 1C shows typical SVS–F CDF at three head positions (0, +90, and −90 deg). To validate the current method, our interest is in the medium-latency component (labelled ML_F in Figs. 1 & 2). The mean latency of the ML_F peak was 347 ms when averaged across subjects and head positions.

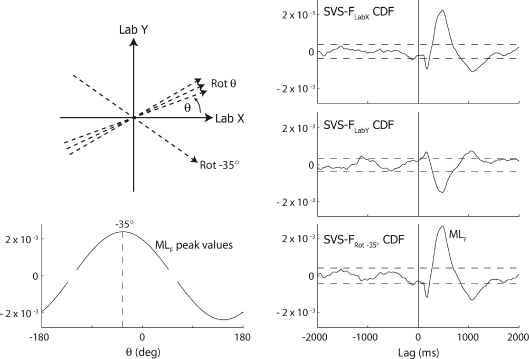
Figure 2. Approach for quantification of response direction.

Top left, partial schematic of incrementally rotating axis (dashed axes) along which the F time series is represented. Four out of the 360 axes are illustrated in addition to Lab X and Lab Y. The axis at minus 35 deg corresponds to the response angle determined from the example data in the rest of the figure. Bottom left, single subject example (−30 deg target head angle) of the SVS–F_Rotθ CDF ML_F peak plotted as a function of θ. In this example θ=−35 deg is identified as the response angle. The gaps in the curve represent axis rotations at which the detected SVS–F_Rotθ CDF ML_F peak is less than the confidence limits of the CDF. Right column, bottom row: SVS–F_Rotθ CDF for θ=−35 deg. Right column, top two rows: SVS–F_LabX CDF and SVS–F_LabY are shown for comparison.

With head forward (0 deg), there is clear association between SVS and F_LabX but not between SVS and F_LabY. The significant positive ML_F in the SVS–F_LabX CDF indicates that ARCL currents are associated with rightward F during the lag range 250–650 ms in this example. Smaller peaks indicating SVS–F_LabX association of opposite polarity are also seen at approximately 140 and 1000 ms. As the head is turned 90 deg left or right, the relationship shifts from the Lab X to Lab Y direction whilst maintaining the same shape, but with a polarity that is dependent on direction of head turn.

Quantification of F response direction to SVS

Figure 1 is suggestive of an ML_F response to SVS that is craniocentric with an approximately interaural response direction. To quantify this more precisely and in particular to establish direction when the response is not directed along the laboratory axes, the following method was adopted. An axis, Rotθ, with a starting direction equal to the Lab X, was rotated ±180 deg, in 1 deg increments (Fig. 2; top left). For each degree of rotation (θ), the time series representing the component of the F acting along the rotated axis (F_ROTθ), was calculated:

where s is sample, followed by determination of SVS–F_Rotθ CDF. The ML_F peak of the SVS–F_Rotθ CDF was determined for each θ (programmatically established as the largest absolute peak in the range 225–500 ms) and plotted as a function of θ (Fig. 2; bottom left). The θ resulting in the largest positive ML_F peak was deemed to represent the response angle. This response angle captures the orientation and direction of the axis along which there is greatest correlation between SVS and shear F at the time of the ML_F response.

Statistics

The relationship between head angle and response direction was analysed using linear regression analysis for the sample population (Reg_S) and for individuals (Reg_I). Student's t-statistic (2-tailed) was used to test whether the mean coefficients of Reg_I (single sample t-test) and the coefficients of Reg_S (t-test for regression coefficients) equalled the hypothesised values (Zar, 1999 pp. 91 and 336). Statistical significance was accepted at P < 0.05.

Results

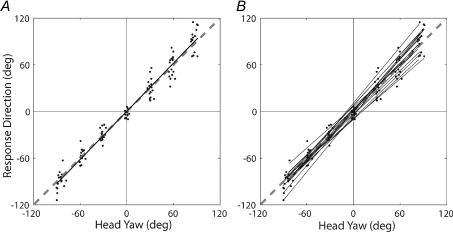
The relationship between measured head yaw angle (HA) and response direction (RD) is shown in Fig. 3. Regression analysis on the group as a whole (Fig. 3A) yielded a significant linear relationship: RD = 0.09 ± 1.04 HA, r²= 0.97 (P < 0.001). The y-intercept of this relationship was not significantly different from zero (t(110) = 0.09, n.s.) and the slope was not significantly different from one (t(110) = 1.95, n.s.). Regression analysis was also performed on the individual subjects’ HA–RD relationships (Fig. 3B). Single sample t-tests indicate the average y-intercept (0.07 ± 6.8; mean ±s.d.) and slope (1.03 ± 0.11) across subjects was not significantly different from zero (t(15) = 0.04, n.s.) and from one (t(15) = 1.21, n.s.) respectively. Average (across subjects) head roll and pitch angles relative to the offset trial were within the range −3 to 3 deg across conditions, and thus unlikely to impact on the HA–RD relationship.

Figure 3. Relationship between head yaw angle and response direction.

Continuous black lines are the regression lines for the entire sample (A) and for individual subjects (B). The dashed grey line in both plots is the line of identity, extended beyond the full data range to aid its visibility. A contributory factor to the increased vertical spread of data points for conditions either side of head forward, apparent in (A), is inter-subject variability in the slope of HA-RD relationships (B).

A single subject assessment of variability of RD measurement across nine test occasions (head forward position) revealed a trade-off between reliability and recording duration (Supplemental Material). Recording duration of 172 s gave an inter-test RD standard deviation of 3 deg.

Discussion

Our approach to determining the direction of the SVS-evoked balance response was to identify the axis along which the correlation between SVS and a component of F was largest. It should be noted that with this method, the motor responses to anodal stimulation and cathodal stimulation of the same side both contribute to the identified response axis. Thus, if there is an asymmetry such that the anodal response is not antipodal to the cathodal response, the representative axis will lie somewhere between the response to each polarity of stimulation.

We chose to study the medium-latency component of F (ML_F) because the GVS-evoked counterpart produces the principal body-sway response (Britton et al. 1993; Marsden et al. 2002), which is known to be directed toward the anodal ear over a range of head yaw angles (Lund & Broberg, 1983; Pastor et al. 1993). The direction of the SVS-evoked ML_F exhibited a one-to-one relationship with head yaw angle (regression slope = 1) and was directed toward the anodal ear (regression intercept = 0), thereby validating our method.

An alternative approach could have been to calculate a vector using the peak magnitudes of SVS–F_LabX and SVS–F_LabY as its orthogonal components. We saw two problems with this approach. First, the SVS–F_LabX and SVS–F_LabY CDF may have peaks at different times. This becomes particularly problematic when the peaks are small and not well defined. A solution could be to fix the latency at which orthogonal component measurements are made, but there was large inter-subject variability of peak latencies (range: 270–470 ms). Secondly, one of the orthogonal components may have a peak that is close to or less than the 95% confidence interval, suggesting absence of correlation (e.g. Fig. 1C). It is not clear whether one should then include that component in the vector calculation. The current approach avoids these problems and furthermore allows the use of the confidence intervals to objectively decide if a response is present at all. Thus, if there is no axis along which there is SVS–F_Rotθ CDF exceeding the 95% interval, the response may be considered absent. This was never the case in the current study, but may well be important if utilising lower stimulus intensities or when studying individuals who may have disordered vestibulo-motor processing.

Glossary

Abbreviations

ALCR

anode left cathode right

ARCL

anode right cathode left

CDF

cumulant density function

F

ground reaction force

GVS

galvanic vestibular stimulation

HA

head angle

ML

medium latency

SVS

stochastic vestibular stimulation

RD

response direction

Author contributions

Both authors conceived and designed the study, interpreted the data, and wrote the manuscript. O.S.M. collected and analysed the data. Experiments were conducted at the UCL Institute of Neurology.