Abstract
We have employed rate-equilibrium free energy relationship (REFER) analysis to characterize the dynamic events involved in the allosteric regulation of cystic fibrosis transmembrane conductance regulator (CFTR) function. A wide range of different hydrolysable and poorly hydrolysable nucleoside triphosphates were used to elucidate the role of ATP hydrolysis in CFTR function. The linearity of the REFER plots and Φ values near unity for all ligands tested implies that CFTR channel gating is a reversible thermally driven process with all structural reorganization in the binding site(s) completed prior to channel opening. This is consistent with the requirement for nucleotide binding for channel opening. However, the channel structural transition from the open to the closed state occurs independently of any events in the binding sites. Similar results were obtained on substitution of amino acids at coupling joints between both nucleotide binding domains (NBD) and cytoplasmic loops (CL) in opposite halves of the protein, indicating that any structural reorganization there also had occurred in the channel closed state. The fact that fractional Φ values were not observed in either of these distant sites suggests that there may not be a deterministic ‘lever-arm’ mechanism acting between nucleotide binding sites and the channel gate. These findings favour a stochastic coupling between binding and gating in which all structural transitions are thermally driven processes. We speculate that increase of channel open state probability is due to reduction of the number of the closed state configurations available after physical interaction between ligand bound NBDs and the channel.
CFTR is distinct both as an ABC ‘transporter’ that functions as an ion channel and as an ion channel that is gated by the hydrolysable cytoplasmic ligand ATP when maintained in the appropriate phosphorylation state. The mechanism of coupling the structural elements to ion channel gating is not well understood. The low resolution 3D structure of purified CFTR (Rosenberg et al. 2004) reveals only a general structural shape common for eukaryotic ABC transporters and cannot help to recognize the structural elements of the signal transduction pathway.
A recent homology molecular model of CFTR (Serohijos et al. 2008) has provided some insight into the coupling of nucleotide binding domains (NBDs) to cytoplasmic loops of membrane spanning domains that constitute the channel pore (Fig. 1). This structural model predicts that domain swapping as originally described by Dawson & Locher (2006) in the Sav1866 exporter also occurs in CFTR. Cysteine cross-linking confirmed that domain swapping occurs symmetrically between NBDs and cytoplasmic loops (CLs) in opposite halves of the CFTR molecule and revealed that single-channel gating, which persisted after the introduction of a Cys pair at each interface, was completely and reversibly inhibited by cross-linking (Serohijos et al. 2008; He et al. 2008). This finding indicates a requirement for dynamic contact at these interfaces and should be taken into account in the development of a functional model. Experimental techniques to measure protein structural dynamics require a large amount of pure protein in the native functional state which is an especially challenging task for a multi-domain membrane protein like CFTR. However, individual structural domains can be used for this purpose with some restrictions. NMR studies using isolated NBD1 and R-domain have revealed changes in the structural order of segments of the latter and in their interactions with the former on PKA phosphorylation (Baker et al. 2007). Motions of residues in transmembrane helices during the gating cycle have been deduced from changes in sensitivity to modifying reagents (Cheung & Akabas, 1996; Fatehi & Linsdell, 2008; Beck et al. 2008). Nevertheless, a microscopic mechanism of how the impact of ligand binding may be propagated to the channel pore has not been elaborated except at the level of analogy with the nucleotide sandwich model of other ABC proteins. In these models the closure of the interface between two NBDs upon ATP binding induces a conformational change of membrane spanning domains and the channel open state (Smith et al. 2002; Vergani et al. 2005). ATP hydrolysis is then envisaged to enable some degree of NBD separation and a subsequent return of the transmembrane elements to the channel closed state configuration. While such a deterministic power-stroke model is superficially consistent with some experimental data (Gadsby et al. 2006), it has not been rigorously proven. Moreover, this mechanistic power-stroke model does not seem to explain the observation that gating can occur even without ATP hydrolysis (Aleksandrov et al. 2000), and in fact, in the complete absence of NBD2, the only catalytic domain in CFTR (Cui et al. 2007; Wang et al. 2007). It has been proposed that under physiological conditions gating is driven by a different cycle requiring free energy input (Csanady et al. 2006). Indeed, difference in microscopic mechanism between hydrolytic and non-hydrolytic cycles could be significant as are the temperature dependences of their open probabilities (Po) that are oppositely directed (Aleksandrov et al. 2000). Nevertheless, the fulfilment of the condition Po=τo/(τo+τc) for wild-type CFTR under physiological conditions means that the time-average value of an observable is equivalent to an ensemble-average, and the Ergodic Hypothesis holds (Aleksandrov & Riordan, 1998). An ensemble meeting this requirement is traditionally called a microcanonical ensemble or a physically isolated system with conserved total energy. In such a system the free energy of ATP hydrolysis should be dissipated into heat and cannot be considered as a driving force for the gating process while an external device maintains the system at constant temperature. The absence of the free energy input in the gating cycle precludes the role of a power-stroke in the gating process but does not exclude a reversible deterministic model where the gating process is driven by ligand binding and dissociation. The key assumption of this model requires that any structural transformation giving rise to the change in channel functional state should be initiated in the binding site. The failure to fulfil this requirement means that stochastic models should be considered as alternatives. No strong correlation between coupled processes is required in stochastic models. The model of Monod–Wyman–Changeux (1965) is a classic but not the only example of this type. In general, all ligand gated channels can be qualitatively described by these types of models despite the serious quantitative differences and specific peculiarities for the each channel family (Colquhoun, 2006).
Figure 1. CFTR model.
CFTR structural elements are shown in scale according to a homology model (Serohijos et al. 2008). TMs, CLs and NBDs specify the areas occupied by transmembrane domains, cytoplasmic loops and nucleotide binding domains, respectively. The positions of the structural elements used for the REFER analysis are shown as a black spheres and labelled by the number of the amino acid in the sequence.
There are limited means to probe functional dynamics on the single molecule level. Rate equilibrium free energy (REFER) analysis is one that has been successfully applied to ligand gated channels (Grosman et al. 2000). In spite of some problems with interpretation, this strongly empirical approach is a powerful tool to probe structural dynamics of intra-molecular signal transduction at the single molecule level (Colquhoun, 2005; Auerbach, 2007). We have applied this approach to CFTR single channel function to examine the relationship between nucleotide binding and further test whether CFTR is a ligand-gated channel distinguished from other ligand-gated channels only by its ability to hydrolyse ligand in the binding site (Aleksandrov et al. 2007). In this paper we provide experimental evidence favouring a stochastic type of CFTR regulation typical for ligand gated channels over a deterministic lever-arm mechanism elaborated for ABC transporters.
Methods
Construction and expression of mutants
A stable CHO cell line expressing wild-type CFTR was selected and maintained using methotrexate as previously described (Chang et al. 1993). Point mutations were introduced into the wild-type CFTR construct in the pcDNA3 plasmid using the Stratagene Quick Exchange protocol. PCR generated DNA fragments were confirmed by automated DNA sequencing (UNC-CH Genome Analysis Facility).
Human embryonic kidney (HEK) 293 cells were transiently transfected using the Effectene transfection reagent (Qiagen, Valencia, CA, USA) according to the manufacturer's instructions. To promote maturation of CFTR variants, transfected HEK cells were incubated at 27°C for 48 h before harvesting cells for membrane preparation.
Membrane isolation
CHO cells expressing wild-type CFTR or HEK cells expressing CFTR variants were harvested by scraping, and homogenized on ice in 10 mm Hepes, pH7.2, 1 mm EDTA containing a protease inhibitor cocktail (benzamidine at 120 μg ml−1, E64 at 3.5 μg ml−1, aprotinin at 2 μg ml−1, leupeptin at 1 μg ml−1 and Pefabloc at 50 μg ml−1). Centrifugation at 600 g for 15 min removed nuclei and undisrupted cells. The supernatant was centrifuged at 100 000 g for 30 min to pellet membranes which were then resuspended in phosphorylation buffer (10 mm Hepes, pH 7.2 containing 0.5 mm EGTA, 2 mm MgCl2, and 250 mm sucrose). Brief (3 × 20 s) bath sonication was used to generate vesicles of uniform size for single channel measurements.
Membrane vesicles were phosphorylated by incubation with 50 nm PKA catalytic subunit (Promega Corp., Madison, WI, USA) and 2 mm Na2ATP (Sigma, St Louis, MO, USA) in phosphorylation buffer for 15 min at room temperature. The membranes were aliquoted and stored at −80°C until used.
Single channel recording
Single channel experiments were performed as described previously (Cui et al. 2006). The membrane vesicles containing CFTR variants were phosphorylated for 20 min at +4°C by 100 U ml−1 of PKA and 200 μm ATP in buffer containing 250 mm sucrose, 5 mm MgCl2, 10 mm Hepes, pH 7.3. To maintain uniform channel orientation, 5 mm of a nucleotide triphosphate and 10 μl membrane vesicles at 1 mg ml−1 total protein concentration were added to the 1.1 ml ‘cis’ compartment only. In addition, 100 U ml−1 of PKA catalytic subunit was added to the ‘cis’ compartment to maintain complete phosphorylation of CFTR variants during single channel recording. Ion channels were transferred into the preformed lipid bilayer by spontaneous fusion. All measurements were done at 30°C in symmetrical salt solution containing: 300 mm Tris/HCl pH 7.2, 3 mm MgCl2 and 1 mm EGTA. Heating and temperature control were established using a Temperature Control System TC2BIP (Cell MicroControls, Norfolk, VA, USA). Single channel currents were measured at −75 mV under voltage-clamp conditions using an Axopatch 200B amplifier (Axon Instruments/Molecular Devices, Sunnyvale, CA, USA). The output signal was filtered with an 8-pole Bessel low-pass filter LPBF-48DG (NPI Electronic, Tamm, Germany) with cut-off frequency of 50 Hz to eliminate all closures lasting less than 20 ms including intraburst closings with characteristic life-time < 5 ms (Aleksandrov & Riordan, 1998; Carson et al. 1994). A reduced two states kinetic model C ⇌ O can be used to fit these data. An example of data analysis is shown in Fig. 1 for the wild-type CFTR driven by different ATP analogues. All ATP analogues and CFTR variants were tested at 2 mm and 5 mm concentrations. No differences in the gating kinetics were found, confirming that the kinetic parameters were obtained at saturating ligand concentrations (Aleksandrov et al. 2002; Cui et al. 2006).
Origin 4.1 software (OriginLab Corp., Northampton, MA, USA) was used to fit all-points histograms (pCLAMP 9.2, Axon Instruments) by multi-peak Gaussians. Single-channel current was defined as the distance between peaks on the fitting curve and used for the calculation of the single-channel conductance. The probability of the single channel being open (Po) was calculated as a ratio of the area under the peak for the open state to the total area under both peaks on the fitting curve.
For kinetic analysis the signal was digitized (Digidata 1322; Axon Instruments) with a sampling rate of 500 Hz and analysed using pCLAMP 9.2 (Axon Instruments) software. Dwell-time histograms for the open and closed states were plotted in the logarithmic binning mode and fitted by a single exponential function (Levenberg–Marquard method with value of 2.5 × 10−7 for the convergence criterion). The validity of the reduced two states kinetic model is evident from the single exponential fit seen for both closed and open dwell time histograms.
REFER analysis
Formally, a rate equilibrium free energy relationship means that the following equation holds:
where k and K are rate and equilibrium constants for the reaction in which the structure of reagents are systematically varied. For a single step transition between two stable states, it means that the effect of small perturbation on the free energy of the transition state (TS) is a linear combination of their effects on the end states (Auerbach, 2003). The log–log plot of rate against equilibrium constants is linear with a slope Φ representing an index of the progress of a local reaction coordinate relative to the overall global transition between functional states (Fersht, 2004). Only limiting cases with Φ≈ 0 and Φ≈ 1 have clear physical meaning denoting perturbations in the sites that are not coupled with the formation of TS (Straub & Karplus, 1990; Fersht, 2004). Any structural rearrangements in these sites can affect the energy profile within the same functional state without any effects on the transition between functional states.
Numerical values used for REFER analysis of CFTR gating were calculated as log(kc) = log(1/τo), log(ko) = log(1/τc) where τo and τc are the mean open and closed times calculated from dwell time histograms while log(K) = log(Ao/Ac) where total open Ao and closed Ac times are the area under the peaks for open and closed states on the all-points histograms. Experimental data are shown as mean values ±s.e.m. for at least 3 experiments. The linear fit of experimental points was prepared by using Origin 4.1 software. The Φ values are the slopes of the linear fit ± standard error of the mean. The correlation coefficient R and probability P of no correlation are shown in the figure legends.
Results
REFER analysis of CFTR gating induced by different nucleotides
In general a linear three-state model with one open and two closed states is sufficient to describe the gating kinetics of completely phosphorylated wild-type CFTR ion channel gating driven by ATP where only long-lasting inter-burst intervals are ATP concentration dependent (Winter et al. 1994). A large difference between two populations of closed time constants makes a reduction to a two state process available after strong low pass filtration using a 50 Hz cut-off frequency. As a result only a single population of ATP-dependent closed states lasting longer than 20 ms remains (Fig. 2A). Hence mean open and mean closed times in our reduced two state kinetic scheme correspond to the burst durations and between burst intervals as they were defined in the three state kinetic scheme (Winter et al. 1994; Carson et al. 1994). The burst definition as a functional state initiated by ATP binding and terminated by ATP hydrolysis is not well defined for wild-type CFTR gating driven by poorly hydrolysable ATP analogues where gating and hydrolytic cycles do not coincide (Aleksandrov et al. 2002; Vergani et al. 2003). Thus the definition of burst should be extended to include a non-hydrolytic burst termination initiated by ligand dissociation. For some ligands both hydrolytic and non-hydrolytic closing pathways are available and may be indistinguishable by their gating kinetics (Aleksandrov et al. 2002).
Figure 2. REFER plots for the wild-type CFTR driven by different ATP analogues as ligands.
A, selective examples of single channel recordings of the wild-type CFTR driven by different ligands (second column). The top level of each trace is a channel closed state. Ligand type is shown above the traces. The values of the equilibrium constant, K, were calculated as a ratio of the areas under the peaks on the all-points histogram (left column) whereas the rate constants were calculated from the dwell-time histograms as ko= 1/τc and kc= 1/τo (two right columns). B, REFER plot for the wild-type CFTR ion channel openings induced by different nucleotides. The specific nucleotides are indicated opposite the experimental points. Each experimental point is a mean value ±s.e.m. of at least 3 in dependent experiments. Slope Φ is shown under the graph. The exact parameters of the best fit are: for the upper line slope is 0.965 ± 0.07 (R= 0.994, P < 0.0063). For the lower line slope is 0.974 ± 0.05 (R= 0.989, P < 0.0001). C, REFER plot for wild-type CFTR channel closing driving by the same set of different nucleotides. Each experimental point is a mean value ±s.e.m. of at least 3 in dependent experiments. Slope Φ is shown under the graph. The exact parameters of the best fit are: for the upper line slope is 0.021 ± 0.048 (R= 0.319, P= 0.681), for the lower line slope is 0.024 ± 0.058 (R= 0.226, P= 0.529).
The structural dynamics of channel closing should be pathway specific for the hydrolytic and non-hydrolytic closings if ATP hydrolysis provides additional free energy input that is not available for non-hydrolytic closings. In this case the hydrolytic gating cycle would be irreversible and the Φ value of the backward process would not be equal to the Φ value of the forward process minus 1 as expected for reversible processes. We chose a set of nucleotide ligands having different affinities and susceptibilities to hydrolysis to reveal any possible differences in structural dynamics between pathways which should appear as non-linearity of the REFER graph (Fersht et al. 1994). After low pass filtration the reduced two state kinetic model holds as a rough approximation for all nucleotides used. The set of selected single channel recordings together with the all-points histograms and dwell-time histograms are shown on Fig. 2A. The all-points histograms were used to calculate the numerical values of equilibrium constants K as a ratio of the areas under the peaks while dwell-time histograms were used to calculate rate constants for the REFER plots as ko= 1/τc and kc= 1/τo. The REFER plots for the channel gating driven by different ligands are shown on Fig. 2B. We note that no assumptions were made as to the reversibility of the gating process to calculate rate and equilibrium constants. Indeed, as is evident from Fig. 2B, the Φ value of the backward process is approximately equal to the Φ value of the forward process minus 1. This provides evidence that the process is indeed reversible.
The linearity of the REFER plot may be interpreted as a conservation of the original reaction mechanism regardless of small perturbations in the structure of reactants (Fersht et al. 1986). If so, all experimental points should demonstrate linear deviation from that of wild-type CFTR driven by MgATP. Different chemical modifications should reveal a trend, and any experimental point that deviates from the trend should be excluded from the analysis as a perturbation induced alternative reaction pathway (Fersht et al. 1986; Grosman et al. 2000). Based on this strategy only four (GTP, ATP, 2′N32′dATP and 3′dATP) of a total of 14 ligands tested appeared to be suitable for REFER analysis. We refer to this group of four, including MgATP, as readily hydrolysed ligands and assume the same reaction pathway for all of them. The rest of the ligands demonstrate non-linear deviation from MgATP in the REFER plot in Fig. 2B and should be considered as using a different reaction pathway. Surprisingly, all of them can be organized in their own group with linear deviation from dATP, which was found to be poorly hydrolysed by wild-type CFTR (Aleksandrov et al. 2002). We did not measure hydrolytic activity for each ligand tested and the only reason for the group names is the appearance of readily hydrolysed ATP in one group and poorly hydrolysed dATP in the other. As a result, all ligands tested fall on one of two lines grouping them as readily hydrolysed (open circles) and poorly hydrolysed (open triangles). Both groups exhibit linear relationships with slope Φ= 0.98. All of the poorly hydrolysed ligands are well fitted as a single data set independently of the real difference in their susceptibility to hydrolysis, which may vary considerably. This result indicates that transition between functional states is independent of the susceptibility of the ligand to hydrolysis.
The role of the NBD1–CL4 interface in channel gating
We next examined the effect of structural perturbations at the contact interfaces between NBDs and CLs on the ion channel gating kinetics induced by single amino acid substitutions. A 3D structure of CFTR derived by homology modelling and supported by direct cross-linking experiments reveals an important role for Phe508, the residue most commonly deleted in cystic fibrosis patients, in the interface between NBD1 and the most C-terminal cytoplasmic loop between membrane spanning helices (CL4) (Serohijos et al. 2008). Several additional disease associated mutations also occur at the NBD1–CL4 interface (Seibert et al. 1996; Cotten et al. 1996). The Phe508 aromatic side chain is believed to contribute to CFTR structural assembly (Lewis et al. 2005; Thibodeau et al. 2005; Du et al. 2005) and channel gating (Cui et al. 2006), but the relationship between these processes is unknown.
Based on the homology model we speculate that an aromatic pocket at the NBD1–CL4 interface consisting of Phe508, Phe1068, Tyr1073 and Phe1074 could be a structural element in the signal transduction pathway from NBD1 to the ion channel gating structure (Serohijos et al. 2008). Indeed, restriction of mobility at this interface by the cross-linking of residues on opposite sides was observed to arrest channel gating. REFER analysis has the capacity to reveal any possible correlation between structural dynamics in the aromatic pocket and channel gating.
Selective examples of the single channel recordings and the REFER plot for a series of amino acid substitutions at position 508 are shown on Fig. 3. All mutants have nearly the same mean open time of 220 ms while mean closed times varied from 230 ms for the wild-type CFTR to 7.8 s for F508A. The experimental points are well fitted by a linear function with slope Φ= 0.95 for the channel opening, which implies that physical interactions of Phe508 with its immediate surroundings at this interface do not provide free energy input for the transition between functional states. This suggests that any structural reorganization in the vicinity of Phe508 occur in the closed functional state.
Figure 3. REFER plots for mutants at residues 508 and 1068 driven by MgATP.
A, selective examples of single channel recordings of the CFTR mutants at 508 and 1068 positions are shown. The top level of each trace is the channel closed state. The values of the equilibrium constant, K, were calculated as ratios of the areas under the peaks on the all-points histogram (left) whereas the rate constants were calculated from the dwell-time histograms as ko= 1/τc and kc= 1/τo. The REFER plots for the processes of channel openings for CFTR mutants at position 508 (B) and 1068 (C) are shown. The type of amino acid is shown in one-letter code near each experimental point. Experimental points shown as mean values ±s.e.m. Slope Φ is shown under the graphs. The exact parameters of the best fit are: for the left graph slope is 0.953 ± 0.06 (R= 0.998, P < 0.0001), for the right line slope is 0.968 ± 0.05 (R= 0.989, P < 0.0001).
A comparison of Φ values for contact residues belonging to the different structural domains could reveal the relative motions on either side of the interface. We had found that Phe508 on the NBD1 surface contacts Phe1068 in CL4 (Serohijos et al. 2008). Selective examples of the single channel recordings and the REFER plot for amino acid substitutions at position 1068 are shown on Fig. 3. All mutants at position 1068 have mean open times narrowly distributed around 220 ms with mean closed times ranging widely from 100 ms for F1068M to 3.1 s for F1068W. The experimental points are well fitted by a linear function with slope Φ= 0.94 for channel opening. Thus Φ≈ 1 was found for the perturbations at both Phe508 and Phe1068. This agrees well with our previous hypothesis that structural reorganizations occurring in the vicinity of Phe508 affect the set of closed states only.
The role of the NBD2–CL2 interface in channel gating
CFTR has a pseudo-symmetrical structure since there are similar interactions between each NBD and cytoplasmic loops of MSDs in the opposite half of the molecule. The co-localization of Q1280 (NBD2) and C276 (CL2) has been predicted from the CFTR homology model and confirmed by direct cross-linking experiments (Serohijos et al. 2008). These covalent cross-links between cysteines on either side of this interface arrest channel gating, indicating a requirement for dynamic contact between these sites. However, the functional role of this contact is yet to be defined. Again we used Φ-analysis to probe the relationship between channel gating and structural dynamics at the NBD2–CL2 interface.
Several selective examples of the single channel recordings and REFER plots for point mutations at CFTR positions 276 and 1280 are shown on Fig. 4. The Φ values are close to 1 for channel opening in both cases. As at the NBD1–CL4 interface, this implies that structural reorganizations in the vicinity of the C276/Q1280 residue pair at the NBD2–CL2 joint are required but should be completed in the channel closed state.
Figure 4. REFER plots for mutants at residues 276 and 1280.
A, selective examples of single channel recordings of the CFTR mutants at 276 and 1280 positions are shown. The top level of each trace is the channel closed state. The values of the equilibrium constant, K, were calculated as a ratio of the areas under the peaks on the all-points histogram (left column) whereas the rate constants were calculated from the dwell-time histograms as ko= 1/τc and kc= 1/τo (two right columns). B, REFER plots for the processes of openings of CFTR mutants at position 276 (A) and position 1280 (B). The type of amino acid is shown in one-letter code near each experimental point. Experimental points shown as mean value ±s.e.m. Slope Φ is shown under the graphs. The exact parameters of the best fit are: for the left graph the slope is 0.938 ± 0.04 (R= 0.997, P= 0.0002), for the right the slope is 0.967 ± 0.09 (R= 0.985, P= 0.0002).
Discussion
REFER analysis
The interpretation of the REFER graph linearity and physical meaning of Φ values was originally applied in chemical kinetics and based on the concept of the transition state. The definition of the transition state for structural reorganization in proteins is different from the traditional one employed in organic chemistry. It may be defined as a set of structural states with a probability of 0.5 to evolve in any of two sets of terminal functional states (Du et al. 1998). A set of structural states means multiple paths between the stable states and the clear physical meaning of transition state used in chemical kinetics is lost. We do not consider a theoretical treatment of protein dynamics here but only the meaning of the extreme Φ values of 1 and 0 which are not related to the transition state formation.
Any structural unit in a protein has its own local Φ value between 0 and 1 that reflects the change in the local interactions in the process of transition state formation. Only limiting values of 0 and 1 have clear physical meaning and indicate that the perturbed residue does not change its local interactions in the process of transition state formation and that they are identical to those in the final (Φ= 1) or initial (Φ= 0) functional states (Fersht et al. 1986). Partial Φ values (0 < Φ < 1) are more complex to interpret within the framework of a microscopic model but clearly point to progressive changes in local interactions of a perturbed residue as the gating process proceeds from the initial to a final state (Zhou et al. 2005; Auerbach, 2007). This approach has made significant progress in recent years in understanding the AChR channel gating process (Grosman et al. 2000; Colquhoun, 2005; Auerbach, 2007). The idea that Φ values provide a measure of the temporal sequence of intermediate events in the gating process has utility at least for qualitative analysis despite the limitations in rigorous theoretical justification (Zhou et al. 2005; Auerbach, 2007).
Based on a local Φ value the role of each residue in a protein structural transition between functional states can be defined as non-participant (Φ= 0), direct participant (0 < Φ < 1) or supporter (Φ= 1). Even such a crude separation can help to understand the involvement of any structural segment of the protein in the dynamics of the gating process.
The parallel shift of the REFER graphs for readily and poorly hydrolysed nucleotides (Fig. 1) indicates that this type of analysis is sensitive to the change in the reaction mechanism. The ratio of the wild-type CFTR hydrolytic activities for ATP and dATP was estimated previously VmaxATP/VmaxdATP= 5.53 requiring a value of 1/5.53 = 0.18 for the ratio of hydrolytic cycle durations (Aleksandrov et al. 2002). At the same time the ratio of the gating cycle durations (τo+τc)ATP/(τo+τc)dATP= 0.73. This fourfold difference led us to conclude that the gating events induced by dATP binding could be terminated by two different pathways: hydrolytic and non-hydrolytic in a ratio 1: 4. Based on these data it was concluded that there is no strong mechanical coupling between gating and hydrolysis in CFTR function. (Aleksandrov et al. 2002). Indeed, enzymatic activity is not measured in CFTR single channel recordings. Nevertheless, based on a parallel shift of REFER plots along the X-axis we can estimate the input of non-hydrolytic events in CFTR gating induced by ATP, which is traditionally considered as strongly hydrolytic. With only a single hydrolytic site in CFTR the enzymatic events can be presented in the traditional form:
where E represents NBD2; S – ATP; P – products of ATP hydrolysis and only the ES* state correlating with the channel open state Po∼[ES*]/[Etotal]. In single channel recordings we can measure Po, ko and kc. At saturated ligand concentration and with the assumption that k2≈k6 the relations between measurable gating parameters and enzymatic rate constants is: kc= 1/τo=k4+k5 and 1/ko=τc= 1/k6+ 1/k3. Then a value of Δlog(K) ≈ 0.3 from the parallel shift of REFER graphs provides a rough estimate of k4≈ 0.5k5. This means that even at +30°C the input of non-hydrolytic events in the gating process should not be completely ignored, but detailed study is required to clarify their role.
The linearity of both graphs together with the validity of the complementary relationship for Φ values requires the reversibility of the gating process and excludes the possibility of the irreversible step of free energy input from nucleotide hydrolysis. REFER graphs for the set of ligands yielded slope Φ≈ 1 for the openings and Φ≈ 0 for the closings. This means that ligand interaction with the binding site including ATP hydrolysis may affect only the set of the closed state structural configurations without having any effect on the sets of open or transition states.
However, it is important to point out that neither the REFER graph linearity nor the value of the slope Φ can be considered as proof of any particular microscopic mechanism. On the contrary, any reasonable microscopic model should be tested for its ability to explain the results of REFER analysis, and those which are inconsistent with experimental data should be excluded from further consideration. This means that a whole class of microscopic mechanisms for CFTR gating based on irreversible free energy input from ATP hydrolysis is not applicable.
Furthermore, the fact that Φ≈ 1 for the perturbations in the positions 508, 1068, 276 and 1280 suggests that none of them is directly involved in the dynamics of transition state formation for the gating process (Figs 3 and 4). However, this does not imply the absence of any structural transformation at these positions during the gating cycle. On the contrary, a wide variation in the opening rates suggests strong restrictions on the structural dynamics in the closed state for the mutants. It implies that any residue with Φ= 1 should be in its final position to allow opening to occur. At the same time, none of the tested sites change their local interaction in the backward process of the channel closing (Φ= 0).
Thus far no contradictions between CFTR function and the basic principles of ligand gated channels have been found (Aleksandrov et al. 2007). Moreover, a recent paper on the interpretation of the action of partial agonists in the nicotinic receptor superfamily demonstrates the independence of open state on the type of agonist and argues that the major difference between agonists lies at an earlier stage of structural reorganization in the closed state induced by ligand binding (Lape et al. 2008). An intermediate ‘flipped’ state was proposed in addition to the resting state to explain this phenomenon as a preconditioning required for the opening process to occur. The introduction of such an intermediate state(s) formally means the absence of strong mechanical coupling between non-adjacent intermediate states. It is in a good agreement with our finding of Φ= 1 for ligand binding in CFTR.
A temporal interpretation of fractional Φ values found in the AChR channel gating process assumes the appearance of a ‘conformational wave’ initiated by ligand binding and propagated from the binding site to the channel pore (Grosman et al. 2000; Purohit et al. 2007). The principle of microscopic reversibility requires the ability of a backward process to occur. Formally it should be a ‘conformational wave’ initiated by channel closing, propagated from the channel pore to the ligand binding site and promoting ligand dissociation. This does not appear to be a reasonable scenario for CFTR. It requires that ATP hydrolysis should be available only as a result of channel structural transformation from the open to the closed state. This would contradict the experimental fact that ATP hydrolysis by CFTR is available without PKA phosphorylation whereas it is strongly required for the channel gating (Li et al. 1996). Another mechanism should be supposed for CFTR to explain the results of REFER analysis. The absence of the strong correlation between events in the binding sites and channel gating (Φ= 1) along with the thermally driven nature and reversibility of the gating process (Po=τo/(τo+τc)) influences us to favour a stochastic rather than a deterministic process as the most reasonable speculation.
Speculations
Following the basic del Castillo and Katz (1957) idea of separating the gating and binding processes (see also Colquhoun, 1998) and based on the results of our REFER analysis we speculate that CFTR transition between functional states is a thermally driven process with very low open probability in the non-liganded state of the NBDs. We suppose that ligand binding initiates formation of a structural element which in turn can be used to stabilize a favourable thermally driven fluctuation of the gating structure in the open state configuration. Formally this cannot be simple trapping of the open state as according to the experimental data the closing process is independent of the binding state. To fulfil this requirement we should simply restrict a set of closed state configurations and the probability of the open state will increase as a result of the shortened life-time in the closed states. The simplest version of this basic idea is shown on Fig. 5 as an energy profile for the channel gating process. In our speculation the structural states of the NBDs provide an external switch for the channel structural state. The channel responds to the ‘on’ and ‘off’ position of the switch and does not recognize how the switch attains or loses the ability to restrict the number of closed states. In turn, the pore structural transformations are thermally driven transitions between available structural states. Of course, a more detailed map of Φ values for multiple residues in the predicted crucial areas of CFTR domain–domain contacts along with more detailed structural data is needed to verify or disprove our speculation. The distinctive property of the mechanism suggested is the reduction in the number of the closed state configurations available rather than driving of an open state formation. In a mechanical analogy it is a brake instead of a transmission. This type of mechanism is well known as a Brownian ratchet and widely discussed in application to biological motors (Vale & Osawa, 1990; Astumian, 1997; Oster, 2002). The highly conserved structural elements at the interfaces of the NBDs and the cytoplasmic loops (Dawson & Locher, 2006; Zolnerciks et al. 2007) suggest that some of the insights into CFTR dynamics gained from REFER analysis may aid in interpretation of the dynamics of ABC transporters.
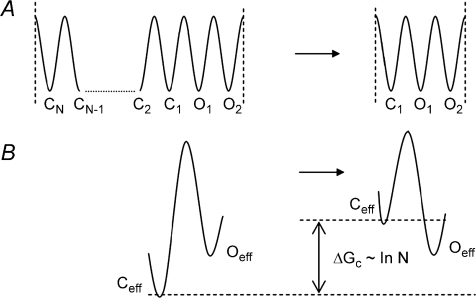
Figure 5. A simplified model of gating energy profile transformations leading to extreme Φ values.
The left energy profile in A represents ligand unbound states of the CFTR channel with N closed states and 2 open states available. It relates to the pore structure only and is assumed to be independent of the influence of unliganded NBDs. For simplicity all open (Oi) and closed (Ci) structural substates of the CFTR channel are shown as states of equal energies with identical energy barriers between them. This energy profile will result in equilibrium constant K=ko/kc=τo/τc= 2/N and ΔG∼ logK∼ log(2/N). The probability of the open state Po=K/(1 +K) = 2/(2 +N) could be very low for the unbound CFTR if N≫ 2. We assume that a set of N available closed state structural configurations could be dramatically reduced to not less than 1 as a result of interaction of ligand bound NBDs with the channel structure. All open states as well as the rest of available closed states remain invariant. For simplicity we left only a single closed state configuration available after interaction of ligand bound NBDs with the channel structure and the invariant set of 2 open state configurations. The energy profile in A with a single closed state and the same set of 2 open states is a result of such an interaction and will lead to ΔG∼ logK∼ log2. The overall ΔΔG for the gating process is proportional to log N and Po will increase. The arrest in the closed states is available after ligand dissociation only when the multiplicity of closed states resets and no additional coupling is required. Of course, the real energy profile is much more complex and we have used a simplified version to demonstrate the basic idea and distinctive properties of the mechanism suggested. The transitions to C1 are still available in the open state on the right side of Fig. 5A and could be recorded as a brief intraburst closing if the experimental set-up has sufficient time resolution. The effective two state energy diagram available from single channel recording after strong low pass filtration is shown in B. The Φ value for the process of closed states reduction is 1 and does not impose restrictions on the backward process.
Acknowledgments
This work was supported by the NIH (DK051619).
Glossary
Abbreviations
- CFTR
cystic fibrosis transmembrane conductance regulator
- CL
cytoplasmic loop
- NBD
nucleotide binding domain
- PKA
cAMP-dependent protein kinase, catalytic subunit
- REFER
rate equilibrium free energy relationship
Author contributions
A.A.A. designed and performed research, and wrote the draft. L.C. designed and constructed cDNA, and wrote the draft. J.R.R. designed research, and critically revised the drafting article. All authors read and approved the final version.
References
- Aleksandrov AA, Riordan JR. Regulation of CFTR ion channel gating by MgATP. FEBS Lett. 1998;431:97–101. doi: 10.1016/s0014-5793(98)00713-3. [DOI] [PubMed] [Google Scholar]
- Aleksandrov AA, Chang X-B, Aleksandrov L, Riordan JR. The non-hydrolytic pathway of cystic fibrosis transmembrane conductance regulator ion channel gating. J Physiol. 2000;528:259–265. doi: 10.1111/j.1469-7793.2000.00259.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aleksandrov AA, Aleksandrov L, Riordan JR. Nucleoside triphosphate pentose ring impact on CFTR gating and hydrolysis. FEBS Lett. 2002;518:183–188. doi: 10.1016/s0014-5793(02)02698-4. [DOI] [PubMed] [Google Scholar]
- Aleksandrov AA, Aleksandrov LA, Riordan JR. CFTR (ABCC7) is a hydrolyzable-ligand-gated channel. Pflugers Arch. 2007;453:693–702. doi: 10.1007/s00424-006-0140-z. [DOI] [PubMed] [Google Scholar]
- Astumian RD. Thermodynamics and kinetics of a Brownian motor. Science. 1997;276:917–922. doi: 10.1126/science.276.5314.917. [DOI] [PubMed] [Google Scholar]
- Auerbach A. Life at the top: the transition state of AChR gating. Sci STKE. 2003;188:re11. doi: 10.1126/stke.2003.188.re11. [DOI] [PubMed] [Google Scholar]
- Auerbach A. How to turn the reaction coordinate into time. J Gen Physiol. 2007;130:543–546. doi: 10.1085/jgp.200709898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker JMR, Hudson RP, Kanelis V, Choy WY, Thibodeau PH, Thomas PJ, Forman-Kay JD. CFTR regulatory region interacts with NBD1 predominantly via multiple transient helices. Nat Struc Mol Biol. 2007;14:738–745. doi: 10.1038/nsmb1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck EJ, Yang Y, Yaemsiri S, Raghuram V. Conformational changes in a pore-lining helix coupled to cystic fibrosis transmembrane conductance regulator channel gating. J Biol Chem. 2008;283:4957–4966. doi: 10.1074/jbc.M702235200. [DOI] [PubMed] [Google Scholar]
- Carson MR, Travis SM, Winter MC, Sheppard DN, Welsh MJ. Phosphate stimulates CFTR Cl− channels. Biophys J. 1994;67:1867–1875. doi: 10.1016/S0006-3495(94)80668-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang X-B, Tabcharani JA, Hou Y-X, Jensen TJ, Kartner N, Alon N, Hanrahan JW, Riordan JR. Protein kinase A (PKA) still activates CFTR chloride channel after mutagenesis of all 10 PKA consensus phosphorylation sites. J Biol Chem. 1993;268:11304–11311. [PubMed] [Google Scholar]
- Cheung M, Akabas MH. Identification of cystic fibrosis transmembrane conductance regulator channel-lining residues in and flanking the M6 membrane-spanning segment. Biophys J. 1996;70:2688–2695. doi: 10.1016/S0006-3495(96)79838-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D. Binding, gating, affinity and efficacy: The interpretation of structure-activity relationships for agonists and of the effects of mutating receptors. Br J Pharmacol. 1998;125:923–948. doi: 10.1038/sj.bjp.0702164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D. From shut to open: what can we learn from linear free energy relationships. Biophy J. 2005;89:3673–3675. doi: 10.1529/biophysj.105.071563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D. Agonist-activated ion channels. Br J Pharmacol. 2006;147:S17–S26. doi: 10.1038/sj.bjp.0706502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotten JF, Ostedgaard LS, Carson MR, Welsh MJ. Effect of cystic fibrosys-associated mutations in the fourth intracellular loop of cystic fibrosys transmembrane conductance regulator. J Biol Chem. 1996;271:21279–21284. doi: 10.1074/jbc.271.35.21279. [DOI] [PubMed] [Google Scholar]
- Csanady L, Nairn AC, Gadsby DN. Thermodynamics of CFTR channel gating: a spreading conformational change initiates an irreversible gating cycle. J Gen Physiol. 2006;128:523–533. doi: 10.1085/jgp.200609558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui L, Aleksandrov L, Chang X-B, Hou Y-X, He L, Hegedus T, Gentzsch M, Aleksandrov A, Balch WE, Riordan JR. Domain interdependence in the biosynthetic assembly of CFTR. J Mol Biol. 2007;365:981–994. doi: 10.1016/j.jmb.2006.10.086. [DOI] [PubMed] [Google Scholar]
- Cui L, Aleksandrov L, Hou Y-X, Gentzsch M, Chen J-H, Riordan JR, Aleksandrov AA. The role of cystic fibrosis transmembrane conductance regulator phenylalanine 508 side chain in ion channel gating. J Physiol. 2006;572:347–358. doi: 10.1113/jphysiol.2005.099457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson RJP, Locher KP. Structure of a bacterial multidrug ABC transporter. Nature. 2006;443:180–185. doi: 10.1038/nature05155. [DOI] [PubMed] [Google Scholar]
- Del Castillo J, Katz B. Interaction at end-plate receptors between different choline derivatives. Proc Roy Soc Lond B Biol Sci. 1957;146:369–381. doi: 10.1098/rspb.1957.0018. [DOI] [PubMed] [Google Scholar]
- Du R, Pande VS, Grosberg AY, Tanaka T, Shakhnovich ES. On the transition coordinate for protein folding. J Chem Phys. 1998;108:334–350. [Google Scholar]
- Du K, Sharma M, Lukacs GL. The F508 cystic fibrosis mutation impairs domain-domain interactions and arrests post-translational folding of CFTR. Nat Struc Mol Biol. 2005;12:17–25. doi: 10.1038/nsmb882. [DOI] [PubMed] [Google Scholar]
- Fatehi M, Linsdell P. State-dependent access of anions to the cystic fibrosis transmembrane conductance regulator chloride channel pore. J Biol Chem. 2008;283:6102–6109. doi: 10.1074/jbc.M707736200. [DOI] [PubMed] [Google Scholar]
- Fersht AR, Leatherbarrow RJ, Wells TNC. Quantitative analysis of structure-activity relationships in engineered proteins by linear free-energy relationships. Nature. 1986;322:284–286. doi: 10.1021/bi00393a013. [DOI] [PubMed] [Google Scholar]
- Fersht AR, Itzhaki LS, ElMasry NF, Matthews JM, Otzen DE. Single versus parallel pathways of protein folding and fractional formation of structure in the transition state. Proc Natl Acad Sci U S A. 1994;91:10426–10429. doi: 10.1073/pnas.91.22.10426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fersht AR. Relationship of Leffler (Bronsted) α values and protein folding Φ-values to position of transition-state structure on reaction coordinates. Proc Natl Acad Sci U S A. 2004;101:14338–14342. doi: 10.1073/pnas.0406091101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadsby DC, Vergani P, Csanády L. The ABC protein turned chloride channel whose failure causes cystic fibrosis. Nature. 2006;440:477–483. doi: 10.1038/nature04712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosman C, Zhou M, Auerbach A. Mapping the conformational wave of acetylcholine receptor channel gating. Nature. 2000;403:773–776. doi: 10.1038/35001586. [DOI] [PubMed] [Google Scholar]
- He L, Aleksandrov A, Serohijos AWR, Hegedus T, Aleksandrov LA, Cui L, Dokholyan NV, Riordan JR. Multiple membrane-cytoplasmic domain contacts in the cystic fibrosis transmembrane conductance regulator (CFTR) mediate regulation of channel gating. J Biol Chem. 2008;283:26383–26390. doi: 10.1074/jbc.M803894200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lape R, Colquhoun D, Sivilotti LG. On the nature of partial agonism in the nicotinic receptor superfamily. Nature. 2008;454:722–727. doi: 10.1038/nature07139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis HA, Zhao X, Wang C, Sauder JM, Rooney I, Noland BW, Lorimer D, Kearins MC, Conners K, Condon B, Maloney PC, Guggino WB, Hunt JF, Emtage S. Impact of the F508 mutation in first nucleotide-binding domain of human cystic fibrosis transmembrane conductance regulator on domain folding and structure. J Biol Chem. 2005;280:1346–1353. doi: 10.1074/jbc.M410968200. [DOI] [PubMed] [Google Scholar]
- Li C, Ramjeesingh M, Wang W, Garami E, Hewryk M, Lee D, Rommens JM, Galley K, Bear CE. ATPase activity of the cystic fibrosis transmembrane conductance regulator. J Biol Chem. 1996;271:28463–28468. doi: 10.1074/jbc.271.45.28463. [DOI] [PubMed] [Google Scholar]
- Monod J, Wyman J, Changeux J-P. On the nature of allosteric transitions: A plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- Oster G. Darwin's motor. Nature. 2002;417:25. doi: 10.1038/417025a. [DOI] [PubMed] [Google Scholar]
- Purohit P, Mitra A, Auerbach A. A stepwise mechanism for acetylcholine receptor channel gating. Nature. 2007;446:930–933. doi: 10.1038/nature05721. [DOI] [PubMed] [Google Scholar]
- Rosenberg MF, Kamis AB, Aleksandrov LA, Ford RC, Riordan JR. Purification and crystallization of the cystic fibrosis transmembrane conductance regulator (CFTR) J Biol Chem. 2004;279:39051–39057. doi: 10.1074/jbc.M407434200. [DOI] [PubMed] [Google Scholar]
- Serohijos AW, Hegedus T, Aleksandrov AA, He L, Cui L, Dokholyan NV, Riordan JR. Proc Natl Acad Sci U S A. 2008;105:3256–3261. doi: 10.1073/pnas.0800254105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seibert FS, Linsdell P, Loo TW, Hanrahan JW, Clarke DM, Riordan JR. Disease-associated mutations in the fourth cytoplasmic loop of cystic fibrosis transmembrane conductance regulator compromise biosynthetic processing and chloride channel activity. J Biol Chem. 1996;271:15139–15145. doi: 10.1074/jbc.271.25.15139. [DOI] [PubMed] [Google Scholar]
- Smith PC, Karpowich N, Millen L, Moody JE, Rosen J, Thomas PJ, Hunt JF. ATP binding to the motor domain from an ABC transporter drives formation of a nucleotide sandwich dimer. Mol Cell. 2002;10:139–149. doi: 10.1016/s1097-2765(02)00576-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straub JE, Karplus M. The interpretation of site-directed mutagenesis experiments by linear free energy relations. Protein Eng. 1990;3:673–675. doi: 10.1093/protein/3.8.673. [DOI] [PubMed] [Google Scholar]
- Thibodeau PH, Brautigam CA, Machius M, Thomas PJ. Side chain and backbone contributions of Phe508 to CFTR folding. Nat Struc Mol Biol. 2005;12:10–16. doi: 10.1038/nsmb881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vale RD, Oosawa F. Protein motors and Maxwell's demons: does mechanochemical transduction involve a thermal ratchet? Adv Biophys. 1990;26:97–134. doi: 10.1016/0065-227x(90)90009-i. [DOI] [PubMed] [Google Scholar]
- Vergani P, Nairn AC, Gadsby DC. On the mechanism of MgATP-dependent gating of CFTR Cl− channels. J Gen Physiol. 2003;121:17–36. doi: 10.1085/jgp.20028673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergani P, Lockless SW, Nairn AC, Gadsby DC. CFTR channel opening by ATP-driven tight dimerization of its nucleotide binding domains. Nature. 2005;433:876–880. doi: 10.1038/nature03313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Bernard K, Li G, Kirk KL. Curcumin opens cystic fibrosis transmembrane conductance regulator channels by a novel mechanism that requires neither ATP binding nor dimerization of the nucleotide-binding domains. J Biol Chem. 2007;282:4533–4544. doi: 10.1074/jbc.M609942200. [DOI] [PubMed] [Google Scholar]
- Winter MC, Sheppard DN, Carson MR, Welsh MJ. Effect of ATP concentration on CFTR Cl– channels: A kinetic analysis of channel regulation. Biophys J. 1994;66:1398–1403. doi: 10.1016/S0006-3495(94)80930-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Pearson JE, Auerbach A. Φ-value analysis of a linear, sequential reaction mechanism: theory and application to ion channel gating. Biophys J. 2005;89:3680–3685. doi: 10.1529/biophysj.105.067215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zolnerciks JK, Wooding C, Linton KJ. Evidence for a Sav1866-like architecture for the human multidrug transporter P-glycoprotein. FASEB J. 2007;21:3937–3948. doi: 10.1096/fj.07-8610com. [DOI] [PubMed] [Google Scholar]