Abstract
Human subjects can quickly adapt and maintain performance of arm reaching when experiencing novel physical environments such as robot-induced velocity-dependent force fields. Using anodal transcranial direct current stimulation (tDCS) this study showed that the primary motor cortex may play a role in motor adaptation of this sort. Subjects performed arm reaching movement trials in three phases: in a null force field (baseline), in a velocity-dependent force field (adaptation; 25 N s m−1) and once again in a null force field (de-adaptation). Active or sham tDCS was directed to the motor cortex representation of biceps brachii muscle during the adaptation phase of the motor learning protocol. During the adaptation phase, the global error in arm reaching (summed error from an ideal trajectory) was similar in both tDCS conditions. However, active tDCS induced a significantly greater global reaching (overshoot) error during the early stage of de-adaptation compared to the sham tDCS condition. The overshoot error may be representative of the development of a greater predictive movement to overcome the expected imposed force. An estimate of the predictive, initial movement trajectory (signed error in the first 150 ms of movement) was significantly augmented during the adaptation phase with active tDCS compared to sham tDCS. Furthermore, this increase was linearly related to the change of the overshoot summed error in the de-adaptation process. Together the results suggest that anodal tDCS augments the development of an internal model of the novel adapted movement and suggests that the primary motor cortex is involved in adaptation of reaching movements of healthy human subjects.
Humans and primates can rapidly adapt goal-directed arm reaching in novel dynamic environmental conditions such as robot-induced force fields. The development of a new internal model for controlling the position and velocity of the hand during reaching in these altered external forces involves the motor commands sent to the arm and copies thereof, proprioceptive information of arm position or a combination of the two types of information in order to anticipate the perturbing force (Shadmehr & Mussa-Ivaldi, 1994; Wolpert et al. 1995). Experimentally, the acquisition and subsequent longer term retention of a newly learned internal model is often manifest as an after-effect or ‘overshoot’ error in hand trajectory during initial reaching movements when the force field is taken away. It has been suggested that this after-effect is the result of newly formed predictive action, whereby a subject will push in the direction of the expected force and results in a trajectory error that is opposite in direction compared to that in early adaptation to a force field (Shadmehr & Mussa-Ivaldi, 1994; Thoroughman & Shadmehr, 1999).
Employing a new internal model to maintain overall reaching performance results in a refined interplay between muscle co-contraction, spinal and supraspinal reflex feedback and execution-related sensory/motor signal-dependent noise. These and other factors can be altered to optimize trial-by-trial performance during real behaviour or in computational models of motor adaptation (Shadmehr & Mussa-Ivaldi, 1994; Harris & Wolpert, 1998; Osu et al. 2002; Milner & Franklin, 2005; Darainy & Ostry, 2008; Guigon et al. 2008). For example, force field-induced motor adaptation occurs during healthy childhood and adolescent development, despite a higher level of trial-by-trial spatial and temporal variability in youngsters compared to adults (Takahashi et al. 2003) and the degree of adaptability may already be genetically determined by factors such as handedness (Schabowsky et al. 2007).
The neural correlates of motor adaptation to force fields include cortical regions such as primary motor cortex (PMC) and premotor cortex, as well as striatal and cerebellar regions at early (<2 h) and later (>6 h and up to months) stages of the adaptation process (Shadmehr & Holcomb, 1997; Krebs et al. 1998). With this cortical involvement in motor adaptation in mind, recent studies have used transcranial magnetic stimulation (TMS) to explore the role of PMC in motor adaptation and retention to altered force fields. When repetitive low frequency TMS (<1 Hz) was applied over the PMC after arm reaching with no force fields, but before adaptation of reaching with force fields, the acquisition of learned novel force field-induced dynamics during adaptation was not affected. However, movement errors were greater 24 h later when subjects performed reaching with no force perturbation once again (Richardson et al. 2006). On the other hand, low frequency TMS applied to PMC shortly after force field motor adaptation did not disrupt subsequent consolidation of the newly formed internal model (Baraduc et al. 2004). Lastly, TMS delivered immediately after each reaching trial during adaptation to visual rotation could reduce the retention of adapted motor control; that is the subject took fewer de-adaptation trials to return to baseline values for target errors (Hadipour-Niktarash et al. 2007). These results suggest a possible role of PMC in motor (de)adaptation, but did not directly test the hypothesis that formation of a new internal model during adaptation is modified by cortical stimulation.
Whilst the PMC has been implicated in a variety of motor learning tasks involving the hand/digits and cortical stimulation (e.g. Muellbacher et al. 2002; Nitsche et al. 2003b; Kuo et al. 2008), its role in reaching adaptation is not yet fully understood. Secondly, there are relatively few studies focused on enhancing PMC function by increasing cortical excitability during motor adaptation (e.g. Nitsche et al. 2003b; Reis et al. 2009) rather than disrupting PMC function by lowering motor cortical excitability (Baraduc et al. 2004; Richardson et al. 2006).
Therefore in the present study, we aimed to clarify the involvement of PMC in internal model formation and thus dynamic control of reaching movements by using anodal transcranial direct current stimulation (tDCS) to increase cortical excitability in the PMC during force field adaptation. Direct current stimulation is thought to modulate membrane polarization rather than evoking neuronal firing directly and evoke NMDA receptor-dependent motor excitability changes (Nitsche & Paulus, 2000, 2001; Nitsche et al. 2003a). The rationale for using anodal tDCS was based on our previous work demonstrating that it can increase motor cortical excitability in a predictable manner (Nitsche & Paulus, 2000) and this can improve performance when applied to PMC during an implicit motor learning task (Nitsche et al. 2003b). A recently developed technique for measuring trajectory errors within the initial stage of a reaching movement was also used as a more direct estimate of internal model formation during adaptation (Osu et al. 2003).
In this study, anodal tDCS was hypothesized to augment the development of a novel internal model of motor control when applied to PMC during force field-induced motor adaptation and that this would result in greater after-effect or overshoot errors during de-adaptation.
Methods
Reaching task
Fourteen healthy right-handed adults (22–31 years old; 7 male) gave written informed consent to participate following approval from the University of East London Ethics Committee. All experiments were conducted in accordance with the Declaration of Helsinki. Motor adaptation took place using a shoulder/arm robotic manipulandum (Interactive Motion Technologies, Cambridge, USA). Subjects sat in a customized chair and grasped the manipulandum with their right hand (70 deg shoulder flexion, 90 deg elbow flexion, and semi-pronated forearm). Centre-out-back planar reaching movements (15 cm path length) were made along the midline towards the chest from a central start position (1 cm diameter) to a peripheral target (1 cm diameter). The real-time hand position (sampled at 1000 Hz) was represented on a vertically oriented computer screen situated at eye level above the manipulandum. Subjects were instructed to make the most accurate straight line movement from the central start position to the peripheral target when it turned colour from grey to yellow. The guide period for moving was 1.0 s, indicated by the peripheral target turning from yellow to red. Over 98% of all trials from all subjects were within ±1 s.d. of average move time and ±0.1 s of the guide time. To reduce reaching predictability and maintain attention, subjects made reaching movements in response to ‘Go’ targets (i.e. towards the chest), but not towards ‘NoGo’ targets positioned away from the chest (i.e. 180 deg from ‘Go’ targets; Go/NoGo ratio was 50%).
Motor adaptation to the robot-induced force field
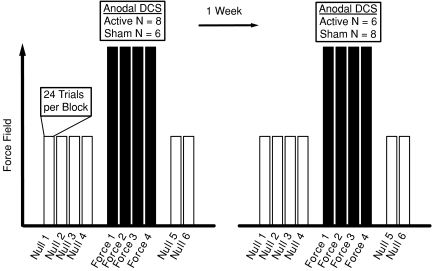
Performance measurements before, during and after motor adaptation were made whilst each subject performed 10 blocks of 24 reaching trials (240 trials in total per session) with each block separated by 1 min rest periods. The first 96 trials (4 blocks; N1–N4 in figures) were performed in a null force field and were preceded by approximately 60 familiarization reaches, during which no performance measures were made. The second 96 reaching trials (4 blocks; F1–F4) were performed in the velocity-dependent force field. In this study, the robotic device induced clockwise, velocity-dependent force fields (25 N s m−1) perpendicular to the path of the manipulandum. Finally, subjects performed 48 reaching trials (2 blocks; N5–N6) in the null field once again. All subjects completed a total of six blocks of washout trials as well as the familiarization movements between each session involving force fields. Previously, it has been shown that this extended repetition of null field trials performed after motor adaptation minimizes learning carryover between sessions (Caithness et al. 2004).
Transcranial direct current stimulation
Anodal stimulation (1 mA; total duration 17 min) was delivered using a battery-driven constant current stimulator with the current flow controlled by a voltmeter (Schneider Electronic, Gleichen, Germany). Two sponge-covered saline-soaked rubber electrodes (5 cm ×7 cm) were applied to the subject's head. The centre of the anodal electrode was positioned over the left motor cortical representation of the contracting right biceps brachii and that of the reference electrode over the right supraorbital area. The position of the anodal electrode was identified by applying TMS in 1 cm steps around the presumed upper limb area to determine the optimal position for biceps activation measured as a motor-evoked potential (MEP). The position was defined by the lowest stimulator intensity required to elicit 5 out of 10 MEPs of >50 μV at rest, using a figure-of-eight 70 mm diameter coil (Magstim 200, Magstim, UK; Rossini et al. 1994).
Experimental protocol
Each subject undertook motor adaptation during active and sham tDCS conditions. Stimulation was turned on in both conditions after null field blocks were complete (i.e. after Block N4). The current was increased in a 30 s ramp-like fashion out of view of the subject. In the sham condition, the stimulation was then turned off after 30 s, whilst stimulation remained on continuously for the duration of the force field blocks in the active tDCS condition. Active cortical stimulation was terminated before the subsequent first trial in a null force field during de-adaptation (i.e. before Block N5). The order of stimulation conditions was randomized for each subject and the two motor adaptation sessions were separated by at least 1 week (Fig. 1).
Figure 1. Study design.
Each subject undertook two sessions of motor adaptation involving target reaching in velocity-dependent force fields separated by 1 week. The order of active or sham tDCS during motor adaptation was randomized for each subject. The protocol included 96 trials of reaching with no force field (Null 1–4), then 96 trials of reaching with force fields (Force 1–4) followed by 48 trials of reaching with no force field (Null 5–6).
Measures of motor performance
Motor performance was quantified with two measures of trajectory error in each trial. Summed error is a global movement error calculated as the cumulative perpendicular distance between the hand position and the ideal trajectory (values are positive regardless of path directionality) for the duration of the reaching movement. All possible neural and biomechanical components of motor control contribute to this measure. Signed error represents the cumulative perpendicular distance between the hand position and the ideal trajectory in the first 150 ms of movement, whereby the reaching paths to the right and left of the ideal trajectory were given positive and negative values respectively (Osu et al. 2003). It has been suggested that a change in signed error represents formation of an internal model of a new motor task, for example as the subject predicatively pushes counter-clockwise in order to compensate for the expected clockwise force field resistance. By using this particular measure, the present study could therefore address how formation of an internal model during adaptation could be modulated by anodal tDCS. Other measures of movement performance included movement time (ms), reaction time (ms) and peak velocity (m s−1) in order to assess temporal control before, during and after motor adaptation. Trial-by-trial variability in summed and signed errors as well as movement time (i.e. indices of signal-dependent noise; Harris & Wolpert, 1998; Takahashi et al. 2003; Guigon et al. 2008) were calculated as the standard deviation (s.d.) of error values across the 24 trials in each block for each subject. s.d. values were then averaged across subjects for each block. Summed trajectory error and movement time were calculated from movement onset threshold, which was defined as the time that the hand exceeded a compound x–y velocity of 0.03 m s−1 to movement offset, which was defined as the time when velocity fell below 0.03 m s−1. Signed error was measured from movement onset and reaction time was calculated as the time from the Go signal to movement onset.
Data analysis and statistics
The effects of anodal tDCS during and after motor adaptation were analysed separately. Changes in motor performance during or after adaptation were compared using repeated measures ANOVA with corrections for sphericity.
An initial level of analysis of performance errors used Block and tDCS condition as main effect factors with an interaction factor of Block–tDCS condition for baseline (Block N4), early (Block F1) and late (Block F4) adaptation periods. Similar analysis was performed on data in Blocks N4, N5 (early de-adaptation) and N6 (later de-adaptation) to investigate after-effects of combined force field learning and cortical stimulation. The specific a priori null hypothesis was that active tDCS during motor adaptation would not change spatial and temporal errors during early, late or after motor adaptation. If significant ANOVA results existed for either main effect factor or the interaction term (P <0.05), then paired t tests were performed on block data (e.g. Fig. 3B).
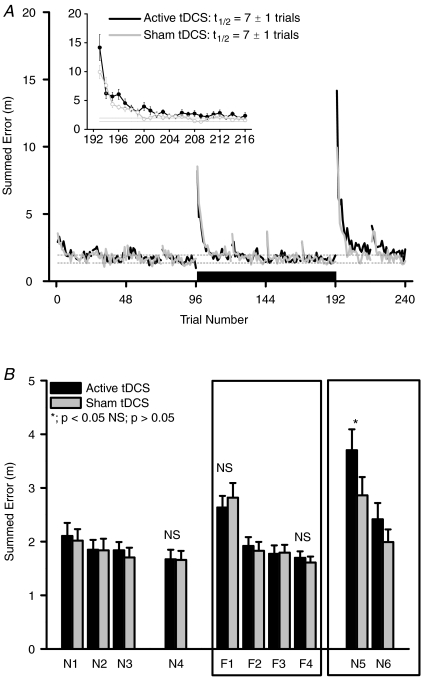
Figure 3.
A, effect of anodal tDCS on summed trajectory error during motor adaptation. Main panel: trial-by-trial error during pre-adaptation (trials 1–96; Blocks N1–N4), motor adaptation (trials 97–192; Blocks F1–F4) and after adaptation (trials 193–240; Blocks N5–N6) periods. Black bar represents period of tDCS application. Black line is continual active tDCS condition (1 mA; 17 min) and grey line is sham tDCS condition (1 mA; 30 s). Dotted lines are s.e.m. values of average data from pre-adaptation null field trials in the sham tDCS condition (trials 73–96; Block N4). Trial values are means only (s.e.m. not included for clarity; n= 14 for each tDCS condition). Inset: mean ±s.e.m. trial-by-trial data (n= 14) during early de-adaptation period (trials 193–216; Block N5) after combined tDCS and motor adaptation. Half-lives (t1/2; trials) were calculated using an exponential decay curve fit. B, differences in summed trajectory error before, during and after motor adaptation between active vs. sham tDCS. Summed error (values are mean ±s.e.m.; n= 14) was averaged from 24 trials in each block. Blocks N1–N4, pre-adaptation null force field. Blocks F1–F4, during motor adaptation to the velocity-dependent force field. Blocks N5–N6, null force fields after motor adaptation. Black columns are active tDCS and grey columns are sham tDCS conditions. NS, no significant difference between active and sham tDCS in that block. *Significant difference between active and sham tDCS conditions in that block (paired t test; P < 0.05). Main statistical analysis is restricted to Blocks N4, F1, F4 and N5 (see text for full results).
A second level analysis using paired t tests was performed on changes in performance errors in the early period after motor (de)adaptation (i.e. Block F1–N4 and N5–N4 differences; denoted by Δ in Figs 4 and 5), since most (de)adaptation occurs during the first 30 movement trials in/after a velocity-dependent force field (Schabowsky et al. 2007).
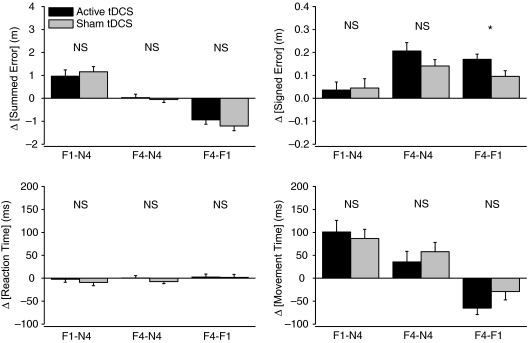
Figure 4. Comparisons of trajectory and movement errors during motor adaptation with anodal tDCS.
Effects were analysed during motor adaptation (Blocks F1 and F4) compared to baseline (Block N4). There were no significant differences in comparisons between active vs. sham tDCS during motor adaptation for summed error, movement time or reaction time. There was a significantly greater development of signed error during motor adaptation with active tDCS compared to sham tDCS (Block F4–Block F1). *Significant difference at P < 0.05 level.
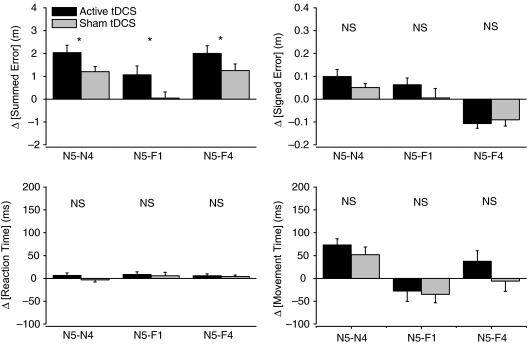
Figure 5. Comparisons of trajectory and movement errors after motor adaptation with anodal tDCS.
Effects were analysed after motor adaptation (Block N5) compared to baseline (Block N4). There was a significantly greater summed error after motor adaptation with active tDCS compared to sham tDCS (Block N5, all comparisons). *Significant difference at P < 0.05 level. There were no significant differences in comparisons between active vs. sham tDCS after motor adaptation for signed error, movement time or reaction time.
A third level of analysis used ANOVA and paired t tests to investigate the development of errors during adaptation (i.e. Δ Block F4–Block F1) because significant changes in PMC function during adaptation are correlated with motor adaptation and have been implicated by neuroimaging studies (e.g. Krebs et al. 1998). Lastly, associations between significant changes in errors during and after motor adaptation were investigated using linear regression correlations. Values are means ± s.e.m. with an overall 2-tailed significance set at P < 0.05.
Results
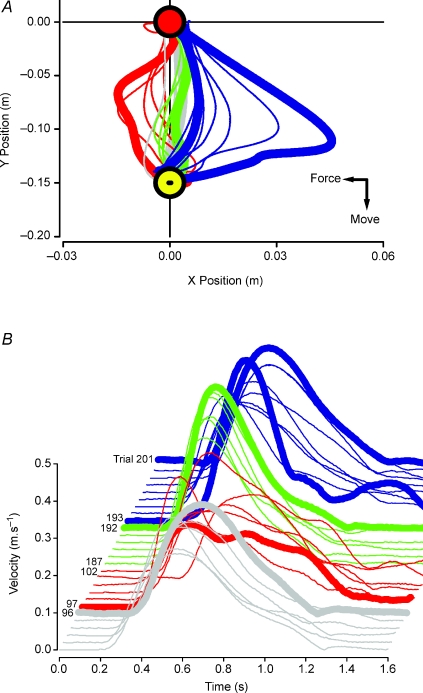
There were no reports of side effects of the stimulation during or after the experiments and no subjects reported any perceptual differences in stimulation between the active and sham stimulation conditions. The trial-by-trial adaptation in velocity and hand path trajectory before, during and after robot-induced force field application and anodal tDCS is illustrated in Fig. 2 for a typical subject.
Figure 2. Kinematics of arm reaching during motor adaptation to a velocity-dependent force field (clockwise force) with active tDCS.
A, hand path trajectory from the start position (0, 0 m) towards target (0, −0.15 m) position in a single subject. Reaching in pre-adaptation null field trials (thick grey line) is close to ideal. Reaching in a novel force field (first trial, thick red line) shows a perturbed trajectory, which is gradually reduced with reaching repetition (thin red lines). After practice, the hand trajectory (trials in late adaptation; thin green lines) approaches that of pre-adaptation null trials (last trial; thick green vs. thick grey lines). The first trial after adaptation (thick blue line) had a trajectory which was in the opposite direction and greater: i.e. the typical after-effect is augmented by active tDCS. The trajectories of the subsequent 8 trials approached control paths (thin blue lines and thick blue vs. thick grey lines). B, movement velocity curves of individual trials shown in A. Last pre-adaptation null trial (trial 96; thick grey line) illustrates a bell-shaped profile which becomes less smooth and has more peaks when the subject reaches in a velocity-dependent force field (trials 97–102; red lines). After practice in the force field, the velocity curves assume a bell-shaped profile once more (trials 187–192; green lines). Withdrawal of the force field causes a loss of smoothness in the velocity profile which is rapidly recovered (trials 193–201; blue lines).
Initially, the induced force field led to increased trajectory error in a clockwise direction which was reduced with further reaching trials. When the force field was withdrawn, an ‘overshoot’ error or after-effect (counter-clockwise) in hand trajectory was apparent. With relatively few trials in the null force field during de-adaptation, these errors return towards to pre-adaptation levels.
Pre-adaptation motor performance and effect of session order
There were no significant differences between active vs. sham tDCS conditions in pre-adaptation motor performance (i.e. Block N4) for summed error (+1.67 ± 0.18 vs.+1.66 ± 0.16 m; t= 0.05, P= 0.96), signed error (+0.10 ± 0.03 vs.+0.10 ± 0.04 m; t= 0.12, P= 0.90), movement time (654 ± 25 vs. 654 ± 27 ms; t= 0.02, P= 0.98), reaction time (320 ± 11 vs. 332 ± 10 ms; t= 1.60, P= 0.13) and peak velocity (0.39 ± 0.02 vs. 0.39 ± 0.02 m s−1; t= 0.06, P= 0.96). This indicated that the number of washout trials used (i.e. Blocks N1–N3 and N5–N6; 120 trials in a null field) was sufficient to minimize any carryover effects in de-adaptation between the two test sessions (Caithness et al. 2004) and that randomization reduced the possibility of an effect of session order on the de-adaptation processes. This was verified by testing for a session order main effect with a 3-way ANOVA using summed error data from Blocks N4, N5 and N6, whereby Order and tDCS condition main effect factors were not significant (ANOVA F= 3.50 and 1.66; P= 0.12 and 0.255 respectively), whereas the Block main effect was significant (ANOVA F= 74.9; P= 0.0001). The main effect of Block on summed error confirmed that subjects were establishing repeatable motor adaptation characteristics with the present experimental protocol. Trial-by-trial variability during Block N4 was similar between active vs. sham tDCS conditions for summed error (1.00 ± 0.10 vs. 1.00 ± 0.10 m; t= 0.07, P= 0.95), signed error (0.11 ± 0.01 vs. 0.11 ± 0.01 m; t= 0.25, P= 0.81) and movement time (76 ± 8 vs. 79 ± 3 ms; t= 0.43, P= 0.68).
Effects of tDCS on motor performance errors during force field adaptation
Summed error
Adaptation to the force field involved an immediate significant increase of approximately double in summed error in both tDCS conditions (e.g. Trial 97 in Fig. 3A). Analysis of mean block data revealed a significant main effect of Block (ANOVA F= 36.7; P= 0.0001; Blocks N4, F1 and F4; Fig. 3B), but there was no main effect of tDCS condition (ANOVA F= 0.2; P= 0.89) or interaction of Block–tDCS condition (ANOVA F= 0.57; P= 0.57). Summed error was significantly increased in Block F1 from Block N4 values, but to a similar degree in both tDCS conditions (Fig. 4; Block F1–N4 difference; +0.97 ± 0.28 vs.+1.16 ± 0.23 m; active tDCS vs. sham tDCS; t= 0.72, P= 0.49) and returned to pre-adaptation values in Block F4, again to a similar degree in both conditions (Block F4–N4 difference; +0.03 ± 0.15 vs.−0.05 ± 0.13 m; active tDCS vs. sham tDCS; t= 0.51, P= 0.62). The development of summed error during motor adaptation was similar in both conditions (Block F4–F1 difference; −0.94 ± 0.19 vs.−1.21 ± 0.20 m; active tDCS vs. sham tDCS; t= 1.21, P= 0.25; Fig. 4).
Signed error
Analysis revealed a significant main effect of Block (ANOVA F= 32.2, P= 0.0001; Blocks N4, F1 and F4), but not a main effect of tDCS condition (ANOVA F= 0.09; P= 0.77) or Block–tDCS interaction (ANOVA F= 1.6, P= 0.21). Signed error gradually increased during motor adaptation so that in late adaptation it was significantly greater than pre-adaptation values in both tDCS conditions (Fig. 4; Block F4–N4 difference; +0.21 ± 0.04 m in active tDCS; t= 5.54; P= 0.0001 and +0.14 ± 0.03 m in sham tDCS; t= 5.18, P= 0.0001). However, unlike summed error, the magnitude of development of signed error during adaptation was significantly greater during active tDCS compared to sham tDCS (Fig. 4; Block F4–F1 difference; +0.17 ± 0.02 vs.+0.10 ± 0.02 m; active tDCS vs. sham tDCS; t= 2.61, P= 0.02).
Movement and reaction times
Analysis of movement time revealed a significant main effect of Block (ANOVA F= 21.1; P= 0.0001; Blocks N4, F1 and F4), but not for tDCS condition main effect (ANOVA F= 0.01; P= 0.95) or a Block–tDCS interaction (ANOVA F= 0.8; P= 0.45). Early reaching movements (Block F1) in the force field were significantly prolonged in duration, but to a similar extent in both tDCS conditions compared to pre-adaptation (Fig. 4; Block F1–N4 difference; active tDCS, +100 ± 25 ms vs. sham tDCS, +87 ± 20 ms; t= 0.62, P= 0.55). Movement time shortened during force field adaptation towards pre-adaptation values in a similar fashion for tDCS conditions (Block F4–F1 difference; −65 ± 14 ms vs.−29 ± 18 ms; active tDCS vs. sham tDCS; t= 1.96, P= 0.07). Reaction time remained at pre-adaptation levels in both tDCS conditions throughout (Fig. 4, no more than ± 10 ms change across all block comparisons; main effect of Block, ANOVA F= 0.8; P= 0.44; main effect of tDCS condition, ANOVA F= 0.23; P= 0.83; interaction of Block–tDCS condition, ANOVA F= 0.48; P= 0.63).
Trial-by-trial variability
Trial-by-trial variability in summed error followed similar changes to absolute summed error values during motor adaptation. There was a significant main effect of Block (ANOVA F= 48.8; P= 0.0001), but not for tDCS condition (ANOVA F= 0.1; P= 0.92) or Block–tDCS condition interaction (ANOVA F= 0.8; P= 0.43). Summed error was greater during Block F1 compared to N4, but not Block F4 (see Table 1 for t test results). Signed error variability increased in Blocks F1 and F4 compared to Block N4 in both conditions (main effect of Block, ANOVA F= 31.3; P= 0.0001; main effect of tDCS condition, ANOVA F= 0.04; P= 0.85; interaction of Block–tDCS condition, ANOVA F= 0.03; P= 0.96). Movement time variability changed in a similar fashion to summed error (main effect of Block, ANOVA F= 17.3; P= 0.0001; main effect of tDCS condition, ANOVA F= 0.2; P= 0.65; interaction of Block–tDCS condition, ANOVA F= 0.1; P= 0.98). In summary, whilst trial-by-trial variability changed during or after motor adaptation for all performance errors there was not a specific effect of tDCS condition.
Table 1.
Trial-by-trial variability of movement dynamics during and after motor adaptation with tDCS
| Block N4 | Block F1 | Block F4 | Block N5 | ||
|---|---|---|---|---|---|
| Summed error (m) | Active | 1.0 ± 0.1 | 2.0 ± 0.2* | 1.0 ± 0.1 | 3.1 ± 0.4* |
| Sham | 1.0 ± 0.1 | 2.1 ± 0.2* | 0.9 ± 0.1 | 2.4 ± 0.3* | |
| Signed error (m) | Active | 0.11 ± 0.01 | 0.17 ± 0.02* | 0.13 ± 0.01* | 0.18 ± 0.02* |
| Sham | 0.11 ± 0.01 | 0.17 ± 0.01* | 0.14 ± 0.01* | 0.16 ± 0.01* | |
| Movement time (ms) | Active | 76 ± 8 | 108 ± 9* | 83 ± 8 | 113 ± 8* |
| Sham | 79 ± 4 | 112 ± 9* | 88 ± 8 | 107 ± 10* |
Values are mean s.d. values ±s.e.m. (n= 14) measured across 24 trials in each block and subject.
Significantly different from Block N4 (P < 0.05). There were no significant differences (P > 0.05) between active vs. sham tDCS for any variable in any block.
Effect of tDCS on motor performance errors after adaptation from force fields
Summed error
Reaching movements in a null field during early de-adaptation (i.e. Block N5) following sham tDCS had a summed error in hand trajectory that was opposite in direction (but of a similar magnitude) to that induced in early force field adaptation (see Figs 3B and 5; Block N5–N4 difference vs. F1–N4 difference; +1.16 ± 0.23 vs.+1.20 ± 0.23 m; t= 0.17, P= 0.87).
On the other hand, active tDCS induced a significantly greater summed error in reaching performance during early de-adaptation than sham tDCS. ANOVA analysis revealed a significant main effect of Block (ANOVA F= 59.1, P= 0.0001) and a significant Block–tDCS condition interaction (ANOVA F= 3.8, P= 0.049; Blocks N4, N5 and N6), but not a main effect of tDCS condition (ANOVA F= 1.4; P= 0.25). The increased summed error measured during early de-adaptation was short-lived in both conditions. Thus, whilst active tDCS induced a significantly greater change in summed error during initial trials of early de-adaptation (Block N5; +3.70 ± 0.39 vs.+2.86 ± 0.34 m; active tDCS vs. sham tDCS; t= 2.43, P= 0.03), summed errors during Block N6 were reduced towards Block N4 values and similar (Block N6; +2.41 ± 0.30 vs.+2.00 ± 0.24; active tDCS vs. sham tDCS; t= 1.54, P= 0.15; see Fig. 3B). The effect of active tDCS was significantly greater than sham tDCS during early de-adaptation, whether compared using pre-adaptation, early or late adaptation values (Fig. 5; Block N5 vs. N4, F1 or F4 respectively). The rate of error minimization across trials in Block N5 was similar between tDCS conditions (i.e. similar time constants of 7 ± 1 trials calculated using an exponential decay curve fit; Davidson & Wolpert, 2004; see Fig. 3A inset).
Signed error
There was a trend for an increase in signed error in initial reaching trials during early de-adaptation (Fig. 5), but this rapidly returned to pre-adaptation values for both tDCS conditions (main effect of Block, ANOVA F= 12.5, P= 0.0001; main effect of tDCS condition, ANOVA F= 0.1; P= 0.75; interaction of Block–tDCS condition, ANOVA F= 1.4; P= 0.25).
Movement and reaction times
Movement time significantly increased during early de-adaptation, but to similar values following both tDCS conditions (Block N5–N4 difference; active tDCS, +73 ± 14 ms; sham tDCS, +52 ± 17 ms; t= 5.4, P= 0.0001 and t= 3.1, P= 0.01) and returned towards pre-adaptation values (Fig. 5). Analysis revealed a significant main effect of Block (ANOVA F= 23.8, P= 0.0001), but not a main effect of tDCS condition (ANOVA F= 0.1; P= 0.80) or a Block–tDCS condition interaction (ANOVA F= 0.8, P= 0.45). Reaction times remained unaffected during early de-adaptation compared to pre-adaptation (main effect of Block, ANOVA F= 0.1; P= 0.90; main effect of tDCS condition, ANOVA F= 0.19; P= 0.66; interaction of Block–tDCS condition, ANOVA F= 1.0; P= 0.39).
In summary, the development of a signed error during motor adaptation (internal model; Osu et al. 2003) was augmented by active tDCS, whilst overall summed trajectory error remained unaffected. On the other hand, following motor adaptation, the main after-effect was manifest as an increase in summed error with active tDCS compared to sham tDCS. Changes in timing errors during and after motor adaptation were not specifically affected by active tDCS.
Relationship between development of signed error during and the overshoot in summed error after motor adaptation with tDCS
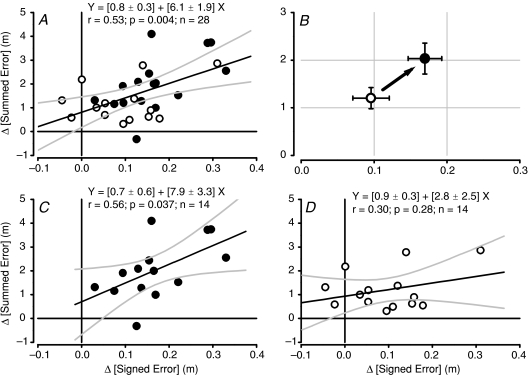
There was a significant positive linear correlation between the development of signed error during force field adaptation and the subsequent overshoot in summed error after force field adaptation across subjects and tDCS conditions (Fig. 6A; Y= (0.8 ± 0.3) + (6.1 ± 1.9)X; r= 0.53; ANOVA F= 9.9; P= 0.004). Active tDCS induced significantly greater values for both error measures (illustrated in Fig. 6B; see Figs 4 and 5 for separate error comparisons). The linear correlation across all subjects had a Y-intercept and slope which were both significantly greater than zero (t= 2.6; P= 0.015 and t= 3.15; P= 0.004, respectively). When analysed separately, the active tDCS condition subject group had a significant linear relationship between signed error development and summed error overshoot (Y= (0.7 ± 0.6) + (7.9 ± 3.4)X; r= 0.31; ANOVA F= 5.4; P= 0.031; n= 14), where the intercept was not significantly greater than zero (t= 1.1; P= 0.29), but the slope was greater than zero (t= 2.3; P= 0.04). On the other hand, the sham tDCS group did not have a significant linear relationship (Y= (0.9 ± 0.3) + (2.8 ± 2.5)X; r= 0.30; ANOVA F= 1.3; P= 0.28; n= 14; see Fig. 6C and D) and although the intercept was significantly greater than zero (t= 2.9; P= 0.01) the slope was not (t= 1.1; P= 0.28). This suggests there may be an underlying alteration in the relationship between internal model formation and subsequent overshoot errors induced by active tDCS of PMC.
Figure 6. Correlation between development of signed error during motor adaptation with anodal tDCS and summed trajectory error after motor adaptation.
A, correlation between signed and summed errors from both tDCS conditions using all data in regression analysis (n= 28 total; filled circles, active tDCS; open circles, sham tDCS). Thick dark line is mean with ± 95% confidence intervals for regression (grey lines). Values are mean ±s.e.m. for regression equation components. B, illustration of main effect of anodal tDCS on error relationships during and after motor adaptation. Mean values (±s.e.m.; n= 14) for signed error development during motor adaptation (X-axis) and global summed error after adaptation (Y-axis) for the two tDCS conditions. Open circle is sham tDCS and filled circle is active tDCS. C, correlation between signed and summed errors from active tDCS condition only (n= 14). Thick dark line is mean with ± 95% confidence intervals for regression (grey lines). D, correlation between signed and summed errors from sham tDCS condition only (n= 14). Thick dark line is mean with ± 95% confidence intervals for regression (grey lines). Values are mean ±s.e.m. for regression equation components in C and D.
Discussion
The two predominant effects of active tDCS delivered to PMC during force field adaptation were to increase the development of the signed movement error during motor adaptation and to increase the summed movement error after force field adaptation. When analysed in detail, there was a correlation between these two variables measured independently in time, suggesting that internal model formation during force field adaptation was modulated by anodal tDCS leading to an increase in overshoot errors once the force field was taken away. These findings provide new direct evidence to suggest that overshoot errors are a result of internal model formation and that anodal tDCS can modulate the relationship. These results were independent of active tDCS-induced modulation of changes in trial-by-trial variability or reaction and movement times during and after force field adaptation. The effect of active anodal tDCS was thus directed towards spatial trajectory errors rather than timing and signal-dependent noise during motor (de)adaptation.
Anodal tDCS-induced modulation of reaching performance in novel force fields
The absence of effect of anodal tDCS on summed error during adaptation is similar to that demonstrated in studies using 15 min of 1 Hz repetitive (r)TMS over the PMC prior to motor adaptation to novel force fields (Richardson et al. 2006) or single pulse TMS delivered at the end of each reaching movement (Hadipour-Niktarash et al. 2007). Perhaps this should not be surprising, since summed trajectory error is a global behavioural index measured across the whole reaching path. The ability to minimize this global error with relatively few practice trials (< 24; Figs 2 and 3) in novel force fields with or without artificial brain stimulation, indicates the effective formation of a new internal model for the new external conditions experienced regardless of additional influences on PMC function. In other words, humans can cope in behavioural terms with multiple ‘interfering’ factors during motor adaptation whether they are beneficial or not for internal model formation.
This study offers the first direct insight into how the formation of a new internal model may involve the PMC. Anodal tDCS applied to PMC augmented the development of a positive signed error during motor adaptation. The positive signed error is a parameter calculated during the initial segment of the reaching movement and it has been taken to represent a feedforward signal as part of a new internal model (Osu et al. 2003), which is not directly related to longer latency sensory feedback (e.g. Milner & Franklin, 2005). Thereby, the subject predicts the force field and pushes more energetically into the expected direction of the imposed force in order to minimize overall movement error (defined in detail in Osu et al. 2003).
The augmented signed error is not at the expense of either temporal errors or increased trial-by-trial variability in spatial or temporal components of reaching, in other words execution-related signal-dependent noise (cf. Takahashi et al. 2003; Guigon et al. 2008). However, the faster development of a feedforward internal model with anodal tDCS could have been accompanied by greater muscle co-contraction. Co-contraction is known to occur during force field motor adaptation and is thought to assist control of limb impedance (see examples in Thoroughman & Shadmehr, 1999; Franklin et al. 2003; Milner & Franklin, 2005; Darainy & Ostry, 2008). Further studies focusing on muscle co-contraction would be instructive in addressing this hypothesis.
Possible mode of action of anodal tDCS-induced modulation of PMC function during and after motor adaptation
Several studies have shown that the development of an internal model during motor adaptation is most commonly manifest as an ‘overshoot’ trajectory error or after-effect once the force field is taken away (Shadmehr & Mussa-Ivaldi, 1994). The significant augmentation in summed error during initial trials after motor adaptation with anodal tDCS in this study is different to the reduction in target errors after visuomotor rotation adaptation using single TMS (Hadipour-Niktarash et al. 2007). The new important finding in this study is that there was a significant correlation between tDCS-induced modulation of a behavioural component of internal model formation (increased signed error) during motor adaptation and the subsequent performance afterwards (increased summed error; Fig. 6) with no effect of session order on de-adaptation processes. Such relationships were not studied in the visuomotor rotation study, but it was hypothesized that single TMS immediately after each trial disrupted the retention of an acquired internal model rather than acquisition per se (Hadipour-Niktarash et al. 2007). Notwithstanding different adaptation protocols and techniques used, tDCS may have augmented retention of, as well as acquisition of, an internal model in the present study. However, the lack of significantly elevated signed error during the early de-adaptation period argues against this somewhat (Fig. 5).
The present study was designed to investigate the immediate effects of tDCS during adaptation and early de-adaptation. This is different to a recent study using low frequency rTMS prior to robot-induced force field adaptation where trajectory errors were measured 24 h later and presented evidence that longer term retention of a motor memory was disrupted (Richardson et al. 2006). Therefore, it is not possible to directly compare those findings to the present results. However, this study and those investigating longer term retention of internal models all suggest that the PMC is involved in motor adaptation, albeit possibly at different stages of motor memory development.
Intriguingly, lowering motor excitability with low frequency TMS led to an increased overshoot error 24 h later (Richardson et al. 2006), whilst in the present study, the initial increase in overshoot error was invoked by raising motor excitability with anodal tDCS. A possible explanation for why both raising and lowering motor cortex excitability leads to disruption of a global index of performance (summed error) at different stages of motor memory development, may be that different intracortical pathways could have been (de)activated depending on the frequency of TMS or current direction in tDCS. Thus, cortical stimulation may have differential effects on motor memory development at different time points. Certainly, both short term intracortical facilitatory and inhibitory circuits are active during robot-induced reaching (Turner et al. 2008). Further studies using cathodal tDCS which also lowers motor cortical excitability (Nitsche & Paulus, 2000) during robot-induced force field motor adaptation and memory formation may further enable comparisons across stimulation technologies and differentiate the role of different intracortical circuits in internal model formation at different stages of development.
The cellular mechanism underpinning the effect of anodal tDCS might be the augmented strengthening of adaptation-related synapses mediated via long-term potentiation-like mechanisms in PMC (Rioult-Depotti et al. 2000; Nitsche et al. 2003a). Acquisition of a new force field motor memory in humans, without tDCS, has been shown to depend in part on NMDA-mediated mechanisms (Donchin et al. 2002). However, in that pharmacological investigation it was not possible to ascertain the site (neuron sub-populations) of drug action.
Lastly, it is possible that the period of anodal tDCS during adaptation may have induced an increase in motor cortex excitability which outlasted stimulation (and also motor adaptation) and thus contributed to modulation of de-adaptation processes per se rather than, or in addition to, operating via changes in internal model formation (Nitsche & Paulus, 2001). It is not possible to exclusively rule this possibility out; however, in other studies when anodal tDCS is applied during the performance of a specific motor task, it does not affect subsequent performance of a different motor task (e.g. Nitsche et al. 2003b; Kuo et al. 2008). Secondly, in this study the rate of de-adaptation was similar in both tDCS conditions (Fig. 3A inset).
Could anodal tDCS of PMC also affect remote regions involved in motor adaptation?
Motor adaptation to robot-induced force fields has a robust neural correlate which involves a network of several cortical and subcortical brain areas including PMC and premotor cortex. Functional neuroimaging studies have shown that cortico-striatal circuits are active during the early stages of force field learning (e.g. Blocks F1 and F2 in this study) and that this pattern shifts to a cortico-cerebellar circuit in late learning when movement errors are similar to baseline values (Blocks F3 and F4 in this study; Krebs et al. 1998). Motor adaptation thus involves a dynamically changing network of cortical regions.
Whilst anodal tDCS was employed in this study to specifically modulate activity in PMC during motor adaptation, tDCS may also have altered excitability of, or connectivity between, PMC and remote cortical and subcortical regions (Lang et al. 2005). Further, anodal tDCS applied via electrodes of 35 cm2 in area, is relatively non-focal in terms of the current delivered to a specific target (for example compared to TMS) and thus an exclusive role of PMC in motor adaptation remains equivocal.
Despite this, the putative role for PMC in motor adaptation demonstrated in this study and other neuroimaging/brain stimulation studies is also supported by elegant electrophysiological recordings in primates. A series of studies have demonstrated that during learning novel movement dynamics, some neuron pools in the PMC are recruited (tuned-in), whilst other neurons are de-recruited (tuned-out; Gandolfo et al. 2000) corroborating our suggestion that anodal tDCS may induce a circuit-specific response in separate intracortical subpopulations of adaptation-related synapses in human subjects. Two subgroups of tuned-in neurons maintained a ‘memory trace’ firing pattern after adaptation to force fields, whereas as a whole population, the motor cortex was re-organized in a way sufficient to regain behavioural performance; that is, balance roles in both overall motor performance (summed errors) and learning (signed errors) during adaptation as we have demonstrated here (cf. Li et al. 2001). This flexibility may underpin the ability to minimize global trajectory errors rather quickly (Figs 2 and 3) and possibly offer the adaptation-related neuron level target for tDCS-mediated modulation of internal model formation in this study (Fig. 6).
Region-specific relationships between motor adaptation and temporal neural activity patterns also occur in supplementary motor, dorsal and ventral premotor and to a lesser degree in cingulate motor areas (Padoa-Schioppa et al. 2004; Xiao et al. 2006; Richardson et al. 2008) again highlighting the possibility that tDCS may also influence non-PMC regions implicated in motor adaptation either directly or indirectly.
Conclusion
This study was designed to assess the effects of single-session anodal tDCS applied to PMC on internal model formation during robot-mediated force field motor adaptation. The results from the present study suggest anodal tDCS may modulate formation of an internal model during one session of motor adaptation and this is manifest as a short-lived after-effect on trajectory errors during de-adaptation. Another recent study has considered repeated sessions (daily) of anodal tDCS application during motor skill learning and demonstrated an improvement in motor skills via a longer term consolidation process (Reis et al. 2009). The time span and number of adaptation sessions as well as the motor skills (upper arm reaching vs. finger/thumb pinch) of that and the present study are different. Nevertheless when considered together, the two studies demonstrated a consistent improvement in motor skill development invoked by anodal tDCS and suggest an effective clinical use for example during robot-assisted rehabilitation in brain-injured individuals.
Acknowledgments
T. Hunter was funded by a UEL scholarship.
Glossary
Abbreviations
- tDCS
transcranial direct current stimulation
- TMS
transcranial magnetic stimulation
Author contributions
All authors contributed equally to the work. All experiments were conducted at the University of East London, UK.
References
- Baraduc P, Lang N, Rothwell JC, Wolpert DM. Consolidation of dynamic motor learning is not disrupted by rTMS of primary motor cortex. Curr Biol. 2004;14:252–256. doi: 10.1016/j.cub.2004.01.033. [DOI] [PubMed] [Google Scholar]
- Caithness G, Osu R, Bays P, Chase H, Klassen J, Kawato M, Wolpert DM, Flanagan JR. Failure to consolidate the consolidation theory of learning for sensorimotor adaptation tasks. J Neurosci. 2004;24:8662–8671. doi: 10.1523/JNEUROSCI.2214-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darainy M, Ostry DJ. Muscle co-contraction following dynamics learning. Exp Brain Res. 2008;190:153–163. doi: 10.1007/s00221-008-1457-y. [DOI] [PubMed] [Google Scholar]
- Davidson PR, Wolpert DM. Scaling down motor memories: de-adaptation after motor learning. Neurosci Lett. 2004;370:102–107. doi: 10.1016/j.neulet.2004.08.003. [DOI] [PubMed] [Google Scholar]
- Donchin O, Sawaki L, Madupu G, Cohen LG, Shadmehr R. Mechanisms influencing acquisition and recall of motor memories. J Neurophysiol. 2002;88:2114–2123. doi: 10.1152/jn.2002.88.4.2114. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Osu R, Burdet E, Kawato M, Milner TE. Adaptation to stable and unstable dynamics achieved by combined impedance control and inverse dynamics model. J Neurophysiol. 2003;90:3270–3282. doi: 10.1152/jn.01112.2002. [DOI] [PubMed] [Google Scholar]
- Gandolfo F, Li C, Benda BJ, Schioppa CP, Bizzi E. Cortical correlates of learning in monkeys adapting to a new dynamical environment. Proc Natl Acad Sci U S A. 2000;97:2259–2263. doi: 10.1073/pnas.040567097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guigon E, Baraduc P, Desmurget M. Computational motor control: feedback and accuracy. Eur J Neurosci. 2008;27:1003–1016. doi: 10.1111/j.1460-9568.2008.06028.x. [DOI] [PubMed] [Google Scholar]
- Hadipour-Niktarash A, Lee CK, Desmond JE, Shadmehr R. Impairment of retention but not acquisition of a visuomotor skill through time-dependent disruption of primary motor cortex. J Neurosci. 2007;27:13413–13419. doi: 10.1523/JNEUROSCI.2570-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Krebs HI, Brashers-Krug T, Rauch SL, Savage CR, Hogan N, Rubin RH, Fischman AJ, Alpert NM. Robot-aided functional imaging: application to a motor learning study. Hum Brain Mapp. 1998;6:59–72. doi: 10.1002/(SICI)1097-0193(1998)6:1<59::AID-HBM5>3.0.CO;2-K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo MF, Unger M, Liebetanz D, Lang N, Tergau F, Paulus W, Nitsche MA. Limited impact of homeostatic plasticity on motor learning in humans. Neuropsychologia. 2008;46:2122–2128. doi: 10.1016/j.neuropsychologia.2008.02.023. [DOI] [PubMed] [Google Scholar]
- Lang N, Siebner HR, Ward NS, Lee L, Nitsche MA, Paulus W, Rothwell JC, Lemon RN, Frackowiak RS. How does transcranial DC stimulation of the primary motor cortex alter regional neuronal activity in the human brain? Eur J Neurosci. 2005;22:495–504. doi: 10.1111/j.1460-9568.2005.04233.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- Milner TE, Franklin DW. Impedance control and internal model use during the initial stage of adaptation to novel dynamics in humans. J Physiol. 2005;567:651–664. doi: 10.1113/jphysiol.2005.090449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muellbacher W, Ziemann U, Wissel J, Dang N, Kofler M, Facchini S, Boroojerdi B, Poewe W, Hallett M. Early consolidation in human primary motor cortex. Nature. 2002;415:640–646. doi: 10.1038/nature712. [DOI] [PubMed] [Google Scholar]
- Nitsche MA, Fricke K, Henschke U, Schlitterlau A, Liebetanz D, Lang N, Henning S, Tergau F, Paulus W. Pharmacological modulation of cortical excitability shifts induced by transcranial direct current stimulation in humans. J Physiol. 2003a;533:293–301. doi: 10.1113/jphysiol.2003.049916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitsche MA, Paulus W. Excitability changes induced in the human motor cortex by weak transcranial direct current stimulation. J Physiol. 2000;527:633–639. doi: 10.1111/j.1469-7793.2000.t01-1-00633.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitsche MA, Paulus W. Sustained excitability elevations induced by transcranial DC motor cortex stimulation in humans. Neurology. 2001;57:1899–1901. doi: 10.1212/wnl.57.10.1899. [DOI] [PubMed] [Google Scholar]
- Nitsche MA, Schauenburg A, Lang N, Liebetanz D, Exner C, Paulus W, Tergau F. Facilitation of implicit motor learning by weak transcranial direct current stimulation of the primary motor cortex in the human. J Cogn Neurosci. 2003b;15:619–626. doi: 10.1162/089892903321662994. [DOI] [PubMed] [Google Scholar]
- Osu R, Burdet E, Franklin DW, Milner TE, Mitsuo K. Different mechanisms involved in adaptation to stable and unstable dynamics. J Neurophysiol. 2003;90:3255–3269. doi: 10.1152/jn.00073.2003. [DOI] [PubMed] [Google Scholar]
- Osu R, Franklin DW, Kato H, Gomi H, Domen K, Yoshioka T, Kawato M. Short- and long-term changes in joint co-contraction associated with motor learning as revealed from surface EMG. J Neurophysiol. 2002;88:991–1004. doi: 10.1152/jn.2002.88.2.991. [DOI] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Li CS, Bizzi E. Neuronal activity in the supplementary motor area of monkeys adapting to a new dynamic environment. J Neurophysiol. 2004;91:449–473. doi: 10.1152/jn.00876.2002. [DOI] [PubMed] [Google Scholar]
- Reis J, Shambra HM, Cohen LG, Buch ER, Fritsch B, Zarahn E, Celnick PA, Krakauer JW. Noninvasive cortical stimulation enhances motor skill acquisition over multiple days through an effect on consolidation. Proc Natl Acad Sci U S A. 2009;106:1590–1595. doi: 10.1073/pnas.0805413106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson AG, Overduin SA, Valero-Cabre A, Padoa-Schioppa C, Pascual-Leone A, Bizzi E, Press DZ. Disruption of primary motor cortex before learning impairs memory of movement dynamics. J Neurosci. 2006;26:12466–12470. doi: 10.1523/JNEUROSCI.1139-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson AG, Lassi-Tucci G, Padoa-Schioppa C, Bizzi E. Neuronal activity in the cingulate motor areas during adaptation to a new dynamic environment. J Neurophysiol. 2008;99:1253–1266. doi: 10.1152/jn.01096.2007. [DOI] [PubMed] [Google Scholar]
- Rioult-Depotti MS, Friedman D, Donoghue JP. Learning-induced LTP in neocortex. Science. 2000;290:533–536. doi: 10.1126/science.290.5491.533. [DOI] [PubMed] [Google Scholar]
- Rossini PM, Barker AT, Berardelli A, Caramia MD, Caruso G, Cracco RQ, Dimitrijević MR, Hallett M, Katayama Y, Lücking CH. Non-invasive electrical and magnetic stimulation of the brain, spinal cord and roots: basic principles and procedures for routine clinical application. Report of an IFCN committee. Electroencephalogr Clin Neurophysiol. 1994;91:79–92. doi: 10.1016/0013-4694(94)90029-9. [DOI] [PubMed] [Google Scholar]
- Schabowsky CN, Hidler JM, Lum PS. Greater reliance on impedance control in the nondominant arm compared with the dominant arm when adapting to a novel dynamic environment. Exp Brain Res. 2007;182:567–577. doi: 10.1007/s00221-007-1017-x. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Holcomb HH. Neural correlates of motor memory consolidation. Science. 1997;277:821–825. doi: 10.1126/science.277.5327.821. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci. 1994;14:3208–3224. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi CD, Nemet D, Rose-Gottron CM, Larson JK, Cooper DM, Reinkensmeyer DJ. Neuromotor noise limits motor performance, but not motor adaptation, in children. J Neurophysiol. 2003;90:703–711. doi: 10.1152/jn.01173.2002. [DOI] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Electromyographic correlates of learning an internal model of reaching movements. J Neurosci. 1999;19:8573–8588. doi: 10.1523/JNEUROSCI.19-19-08573.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner DL, Hunter T, Sacco P. Intracortical inhibition and excitation preceding robot-mediated arm reaching. Brain Stimulat. 2008;1:248. [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science. 1995;269:1880–1882. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]
- Xiao J, Padoa-Schioppa C, Bizzi E. Neuronal correlates of movement dynamics in the dorsal and ventral premotor area in the monkey. Exp Brain Res. 2006;168:106–119. doi: 10.1007/s00221-005-0074-2. [DOI] [PubMed] [Google Scholar]