Segmentation of Fluorescence Microscopy Images for Quantitative Analysis of Cell Nuclear Architecture

Abstract

Considerable advances in microscopy, biophysics, and cell biology have provided a wealth of imaging data describing the functional organization of the cell nucleus. Until recently, cell nuclear architecture has largely been assessed by subjective visual inspection of fluorescently labeled components imaged by the optical microscope. This approach is inadequate to fully quantify spatial associations, especially when the patterns are indistinct, irregular, or highly punctate. Accurate image processing techniques as well as statistical and computational tools are thus necessary to interpret this data if meaningful spatial-function relationships are to be established. Here, we have developed a thresholding algorithm, stable count thresholding (SCT), to segment nuclear compartments in confocal laser scanning microscopy image stacks to facilitate objective and quantitative analysis of the three-dimensional organization of these objects using formal statistical methods. We validate the efficacy and performance of the SCT algorithm using real images of immunofluorescently stained nuclear compartments and fluorescent beads as well as simulated images. In all three cases, the SCT algorithm delivers a segmentation that is far better than standard thresholding methods, and more importantly, is comparable to manual thresholding results. By applying the SCT algorithm and statistical analysis, we quantify the spatial configuration of promyelocytic leukemia nuclear bodies with respect to irregular-shaped SC35 domains. We show that the compartments are closer than expected under a null model for their spatial point distribution, and furthermore that their spatial association varies according to cell state. The methods reported are general and can readily be applied to quantify the spatial interactions of other nuclear compartments.

Introduction

The mammalian cell nucleus is structurally and functionally complex and contains morphologically distinct chromatin domains and numerous protein subcompartments constrained within a defined nuclear volume. These include the nucleolus, SC35 domains (also known as splicing speckles or interchromatin granule clusters), Cajal bodies, and promyelocytic leukemia (PML) nuclear bodies (NBs). It is generally accepted that the spatial organization of these nuclear compartments is inherently connected to their role in gene expression and cell regulation. Confocal laser scanning microscopy (CLSM) of fluorescently labeled antibodies directed against specific antigens has proven to be an especially valuable tool in the study of the mammalian interphase nucleus. Such imaging not only provides the opportunity for visualizing nuclear compartments in situ but also facilitates quantitative approaches to investigate the spatial interactions of these compartments. To date many nuclear associations have been identified subjectively and there is now a growing need to establish quantitative methods that take into account statistical and probabilistic spatial associations of nuclear compartments, particularly given the complexity and dynamic nature of nuclear function. A major problem in analyzing CLSM images of interphase nuclei is an inability to objectively and accurately segment images, particularly if they contain irregular-shaped objects of multiple overlapping foci.

Currently, user-defined thresholding is the most common approach for segmenting CLSM images of the cell nucleus (e.g., (1–3)). Generally, the user selects a global threshold such that individual image pixels are labeled as object pixels if their intensity is greater than that threshold and as background pixels otherwise. The correct choice of threshold is crucial since further processing and analysis of the distinct compartments entirely depends on the quality of the segmentation; too low a threshold can result in background pixels being included in the analysis, while too high a threshold may lead to low-intensity signal being discarded (4). User-defined thresholding is generally considered the gold standard for segmentation of CLSM images since the human visual system outperforms most algorithms at qualitative tasks (5). While such thresholding may be accurate it is fundamentally subjective, and this generates a demand for automated methods that perform as well as manual thresholding. Furthermore, automated methods are becoming increasingly desirable to cope with high-throughput microscopy techniques since they eliminate the time-consuming labor associated with manual thresholding.

At present, most automated segmentation algorithms work in two dimensions (2D); these algorithms therefore segment three-dimensional (3D) CLSM image stacks slice by slice, losing valuable information about the 3D image set. Some thresholding algorithms have been designed for 2D and 3D microscopy images but their applications are limited and generally focus on the task of cell or nucleus segmentation (6–8). Here we present a novel automatic threshold method, based on attribute similarity ideas (9), that has been designed specifically for the task of segmenting nuclear compartments in 3D CLSM image stacks. The algorithm, named stable count thresholding (SCT), delivers an accurate 3D segmentation of nuclear compartments that is readily accessible to subsequent statistical spatial analysis of the thresholded objects. To demonstrate the effectiveness of the SCT algorithm, we apply it to real image stacks of cell nuclei immunofluorescently-labeled for PML protein (a constituent protein of PML NBs), nucleoli, SC35 domains and fluorescence in situ hybridization (FISH)-labeled telomeres, simulated image stacks (where the ground truth is known), and image stacks of fluorescent beads (where the size and shape of the bead is known). We also measure the size distribution of PML NBs in 350 SCT-segmented image stacks and show that the thresholded objects correlate well with the quoted size of PML NBs found by electron microscopy (10).

In addition to describing the SCT algorithm and measuring its performance, we have also employed formal statistical tests based on spatial point pattern (SPP) analysis (11) to explore the spatial interactions of SCT-segmented nuclear compartments. We have analyzed the difficult case of the spatial association between the punctate pattern of PML NBs with large and irregular-shaped SC35 domains. PML NBs are multiprotein aggregates (5–30 per cell; 0.1–1 μm diameter (10)) involved in a number of cellular processes including transcription, apoptosis, tumor suppression, and viral infection; for reviews see (12,13). Disruption or reorganization of PML NBs is correlated with profound cellular consequences (14,15). In patients with acute promyelocytic leukemia, PML NBs are disrupted into a microgranular appearance with numerous PML foci (14). Studies suggest that PML NBs are positionally stable over long periods during interphase and that their size and position may be dictated by their interactions with chromatin (16). SC35 domains are relatively large, irregularly shaped structures that are distributed within the interchromatin region of the nucleoplasm and are sites rich in pre-messenger RNA (mRNA) splicing factors, including snRNPs and spliceosomal subunits (17). SC35 itself is a non-snRNP splicing factor (18), and is involved in pre mRNA processing (19). As well as locating to splicing speckles, SC35 is also a diffuse component of the nucleoplasm (20) and flux of splicing factors between SC35 domain and nucleoplasm is controlled via phosphorylation events (17). Upon inhibition of transcription, SC35 domains have been shown to enlarge (21), hinting that splicing speckles themselves are not sites of pre-mRNA modification, but are instead the storage locations for the key components of this process (17).

PML NBs have previously been observed juxtaposed with SC35 domains (2,12,22–24); however, this association is putative and no quantitative description has been established. Both transcription foci and certain genomic regions and genes share spatial associations with SC35 domains and PML NBs. Nascent RNA transcripts show a tight association with the periphery of SC35 domains in Hep-2 cells (25), and they are also found to associate to the periphery of PML NBs (26), in an early G1 cell cycle phase-related manner (25). Specific gene clusters, such as the gene-rich major histocompatibility complex on chromosome 6, show a highly nonrandom association with PML NBs (2), as do certain transcriptionally active genomic regions (1), despite not being the sites of transcription for these genes. Active genes and gene-rich chromosomal R-bands have been demonstrated to contact SC35 domains (27). SC35 domains may therefore represent a focus for local-euchromatic neighborhoods as opposed to purely being splicing factor storage depots (27). The positioning of both SC35 domains and PML NBs together with transcriptionally active and genomic regions indicates that both compartments play important roles in transcriptional processes. Interestingly, PML NBs and SC35 domains have also jointly been implicated as sites for the transcription and replication of DNA viruses, such as human cytomegalovirus (HCMV) (22). HCMV genomes have been shown to deposit between PML NBs and SC35 domains and early RNA transcripts are produced (22).

We have examined the spatial interaction of PML NBs with SC35 domains in nuclei of both interphase and serum-starved MRC5 fibroblasts to quantify any association between the two compartments and measure whether the interaction changes according to the cell state. We find statistically significant but subtle differences in their association depending on cell state, demonstrating that statistical approaches can quantify and differentiate spatial relationships while avoiding visual cognitive bias. Furthermore, our thresholding algorithm and statistical methods reported are general and can be applied to deduce the quantitative spatial interactions of other nuclear compartments.

Theory

SCT algorithm

CLSM image stacks consist of a series of 2D digital images (xy axes) that span a given volume at sequential depths in the z axis. Elements of the 3D image stack are referred to as voxels. We propose a novel method, the SCT algorithm, to automatically determine threshold levels in CLSM image stacks. Thresholding segments an input image voxel to an output binary image voxel (S_{X, Y, Z}) as

$$S_{\text{X,Y,Z}}=1\text{for}{I}_{\text{X,Y,Z}}\ge \text{T,}$$

$$S_{\text{X,Y,Z}}=0\text{for}{I}_{\text{X,Y,Z}}\mathrm{<}\text{T,}$$

where I_{X, Y, Z} is the grayscale voxel intensity and T is the threshold. The SCT algorithm proceeds as follows.

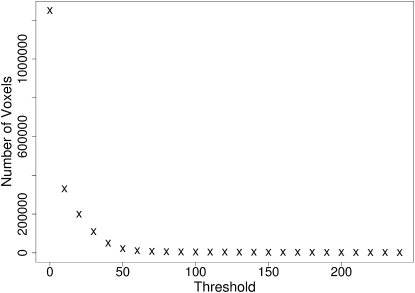
Let N denote the number of voxels in the image stack with an intensity greater than or equal to a threshold, T (see Fig. 1),

$$N_{\text{T}}=\sum _{X=1}^{X_{\text{max}}}\sum _{Y=1}^{Y_{\text{max}}}\sum _{Z=1}^{Z_{\text{max}}}{S}_{\text{X,Y,Z}}(T\in \{0,1,2,\dots ,T_{\text{max}}\}),$$

where X_max, Y_max, and Z_max are the lengths of the X, Y, and Z axes respectively, and T_max is the maximum intensity in the image stack.

Figure 1.

Plot of the number of voxels with an intensity greater than or equal to the given threshold in a typical image stack of an MRC5 cell nucleus with immunofluorescently tagged PML NBs.

The principle of the SCT algorithm is to establish when the voxel count becomes stable in T. At this intensity, we propose that the image objects become distinguished from the background. The SCT algorithm measures W,

$$W_{\text{T}}=\left|\frac{N_{\text{T}-\delta }-2\left(N_{\text{T}}\right)+N_{\text{T}+\delta }}{{\mathit{\delta }}^2}\right|(\mathit{\delta }\in \{1,2,3,\dots \})\text{.}$$

W is derived from the central difference formula for the numerical second derivative, based on three points (28)—N_T−δ, N_T, and N_T+δ. The SCT algorithm segments the image stack using the smallest threshold, satisfying W_T and W_T+δ < α. If no thresholds satisfy α, then the value of α is increased until one does.

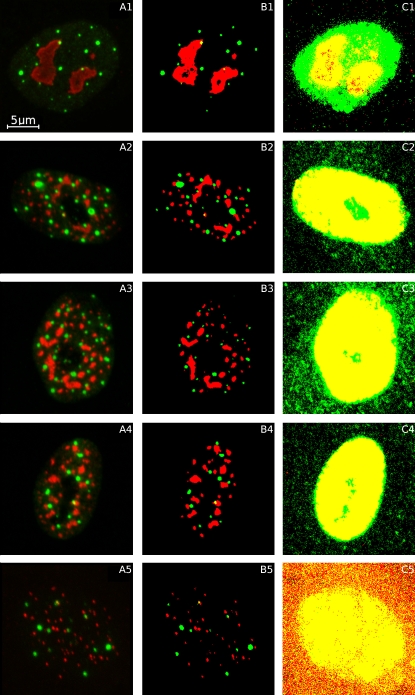
We have found that δ = 10 and $\alpha =\frac{N_{\text{T}}}{2000}$ return accurate segmentations for image stacks with typical signal/noise ratios. The segmentation that results from applying the SCT algorithm to each color channel of the image stacks shown in Fig. 2 A is illustrated in Fig. 2 B. The segmented images suggest that the green compartment (PML NBs) and the red compartments (nucleoli, SC35 domains, and telomeres) are thresholded accurately by the algorithm.

Figure 2.

(A) Z-projection images (consisting of all the flattened image slices superimposed at maximum transparency) of nuclei in MRC5 primary fibroblasts. Nucleoli (red, A1), SC35 domains (red, A2–A4), and PML NBs (green, B1–B5) were labeled using primary antibodies directed against nucleolar protein B23, the splicing factor SC35 and PML protein, respectively; and fluorescently tagged secondary antibodies were targeted to the primaries. Telomeres (red, A5) were imaged using FISH labeling with a Cy3-conjugated PNA probe. Each image slice captures 20.8 μm × 20.8 μm. (B) Projection images of the segmentations produced by applying the SCT algorithm to each color channel of the image stacks shown in panel A. Yellow regions represent voxels that have been segmented as both PML NB (green) and red object (nucleoli, SC35 domains, or telomeres). (C) Projection images of the segmentations produced by applying Otsu's algorithm to each color channel of the image stacks shown in panel A.

Methods

Antibodies and fluorescence in situ hybridization

Primary antibodies used were as follows: PML (15–1745 bps) was bacterially expressed (pET-15b expression system; Novagen, EMD Chemicals, Darmstadt, Germany), and used to raise a polyclonal antiserum (29), a monoclonal mouse IgG1 anti-nucleophosmin (B23) clone FC-61991 of 0.5 mg/mL, which reacts with the C terminus of B23 (cat. No. 32-5200; Zymed Laboratories, South San Francisco, CA); monoclonal mouse IgG1 anti-splicing factor SC-35 of 4.6 mg/mL, which recognizes a phospho-epitope of the non-snRNP (small nuclear ribonucleoprotein particle) factor SC-35 (cat. No. S4045; Sigma-Aldrich, St. Louis, MO); and affinity purified goat polyclonal IgG anti-Lamin B (M-20) of 0.2 mg/mL, which reacts with the C terminus of Lamin B (sc-6217; Santa Cruz Biotechnology, Santa Cruz, CA). Secondary antibodies used were as follows: fluorescein isothiocyanate (FITC) conjugated donkey anti-rabbit IgG (H+L) with an antibody concentration of 1.5 mg/mL, and a fluorophore/protein molar ratio of 3.3 (cat. No. 711-095-152; Jackson ImmunoResearch Laboratories, West Grove, PA), indocarbocyanine (Cy3) conjugated donkey anti-mouse IgG (H+L) with an antibody concentration of 1.4 mg/mL and a fluorophore/protein absorbance ratio (A652:A280) of 2.9 (cat. No. 715-165-151; Jackson ImmunoResearch Laboratories), and indodicarbocyanine (Cy5) conjugated donkey anti-goat IgG (H+L) with an antibody concentration of 1.5 mg/mL and an A652/A280 of 2.7 (cat. No. 705-175-147; Jackson ImmunoResearch Laboratories).

Fluorescence in situ hybridization of telomeres was performed using a Cy3-conjugated peptide nucleic acid (PNA) probe (cat. No. K5326, Dako UK, Cambridgeshire, UK).

Cell culture

MRC5 human primary fibroblast cells (CCL-171) were obtained from the American Type Culture Collection (Manassas, VA). Cells were cultured in Roswell Park Memorial Institute (RPMI) medium (Gibco, Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum, 2 mM L-glutamine, and pen-strep (50 IU/mL penicillin, 50 g/mL streptomycin) (Gibco, Invitrogen). MRC5 VA (SV-40 virus transformed MRC5) cells (obtained from Cancer Research UK, London, UK) were cultured in Dulbecco's Modified Eagle Medium (Invitrogen) supplemented with 10% fetal bovine serum, 2 mM L-glutamine, and pen-strep. Cells were incubated at 37°C in 5% CO₂.

Cells were plated onto glass coverslips of 22 × 22 mm and 0.17-mm thickness (part No. MNJ-400-030Yl; Menzel-Glaser, Braunschweig, Germany) in Corning Costar six-well cell culture clusters (Corning Costar, Corning, NY) and left for 48 h. For serum starvation, MRC5 cells were plated as above, but 24 h postplating, the medium was changed to RPMI supplemented with 0.1% fetal bovine serum and 2 mM L-glutamine only. Cells were then left for eight days.

Before fixing, cells were rinsed in phosphate-buffered saline (PBS), then fixed for 10 min in 4% w/v PF (1 part 16% paraformaldehyde w/v (cat. no. F017, TAAB Laboratories, U.K.) to three parts PBS) with shaking at room temperature. Cells were then washed in PBS, followed by permeabilization in 0.5% v/v Triton X-100 (Sigma-Aldrich St. Louis, MO) in PBS for 20 min, also with shaking at room temperature. They were then subjected to three sequential 5 min PBS washes, and stored in PBS at 4°C.

Cells were concurrently incubated with the three primary antibodies diluted in PBS as follows: rabbit anti-PML 1:200, mouse anti-nucleophosmin 1:50 or mouse anti-splicing factor SC-35 1:500, and goat anti-lamin B 1:100. The incubation time was 30 min at 37°C. Secondary antibodies were diluted in PBS as follows: donkey anti-rabbit FITC, donkey anti-mouse Cy3, and donkey anti-goat, all 1:100. The incubation time was 30 min at 37°C, and cells were also incubated with all three secondary antibodies concurrently. Controls omitting primary antibodies were performed.

For FISH of telomeres using a Cy3-conjugated PNA probe, cells were cultured, plated, and fixed and permeabilized as above. They were then washed in 0.1 M HCl for 10 min at room temperature, followed by simultaneous denaturation with the PNA probe at 80°C for 5 min. Hybridization of probe and telomeric DNA took place overnight in a humid chamber at 37°C. Cells were then subjected to three sequential 5 min 2× saline sodium citrate (SSC) buffer washes at 37°C, followed by a 30-min incubation of the primary antibodies in 4× SSCT (4× SSC, 0.1% Tween-20; Sigma-Aldrich) at 37°C. Subsequent washes and the secondary antibody incubation also took place in 4× SSCT at 37°C.

Fluorescent beads

Slides containing FluoSpheres sulfate microspheres of 4 μm diameter (Gibco, Invitrogen) with red fluorescent dye (580:605) were prepared and imaged according to the manufacturer's protocol.

Microscopy

In our experiments with real image stacks, MRC5 human primary fibroblast cells were captured using a Zeiss LSM 510 (Carl Zeiss, Hertfordshire, UK) confocal microscope with a Zeiss Plan Apochromat 63 × oil immersion objective with numerical aperture of 1.4. Z stacks were obtained by capturing slices taken at 0.4 μm intervals through each nucleus, and consisted of ∼20 slices collected sequentially. The pixel resolution was 0.283 μm/pixel, with a digital zoom of 3.4 × being used to achieve a resolution of 0.083 μm/pixel.

Excitation of dyes was achieved as follows. FITC was excited using the 488-nm line of an Argon laser, and Cy3 and Cy5 were excited by the 543-nm and 633-nm lines, respectively, of an HeNe laser. The emission fluorescence was first split using an NFT 635 VIS dichroic mirror. For FITC and Cy3 detection, the resulting fluorescence of wavelengths <635nm was split with a NFT 545, and then a 505–530 bandpass filter used to collect FITC, and a bandpass 585–615 filter used to collect Cy3, with detection by a photomultiplier tube (PMT). For Cy5 detection, the resulting fluorescence (>635 nm) was passed through a plate followed by a longpass 650 filter before collection by a PMT. PMT voltages were adjusted so that images showed no saturation.

Cell nuclei to be imaged were chosen at random by the operator. However, cells with nuclei that did not fit the field-of view (FOV), a region of interest covering an area of 250 × 250 pixels, were excluded. To ensure that both the upper and lower boundaries of the nucleus were not excluded from the imaging, the fluorescence-free regions directly above and below the nucleus were included in the Z stack. The region of interest was delineated, and the Z stack boundaries were defined, using the manufacturer's acquisition software. Image stacks were exported as 8-bit (gray values from 0 to 255) 250 × 250 tiff image sequences.

Simulated images

Our objective is to assess the performance of the SCT algorithm. Quantitative assessment requires access to ground truth, and as such, we appeal to simulation. Here, we describe methodology for generating artificial images consistent with real cell images obtained by the microscopy procedure described above. All the computational work, including image simulations, and automatic thresholding calculations, was performed using custom-written R (30) code running on a personal computer equipped with a dual 1.83 GHz processor and 2 GB of RAM.

Images were simulated to replicate the major noise contributions that are intrinsically present in real CLSM images of immunofluorescently labeled PML nuclear bodies, including Poisson noise (also known as shot or counting noise), nonspecific staining (NSS), background noise, and the point spread function (PSF).

Simulated images: nuclear volume and PML bodies

Real MRC5 fibroblast cell nuclei are shaped like a flattened ellipsoid spanning approximately half the slices in an image stack. Thus, nuclei were simulated as the middle section of an ellipsoid with the centroid in the center of the FOV, XC = 125, YC = 125, ZC = 10 and simulated semiaxis lengths, XR, YR, and ZR. The nuclear volume was then derived for Z ∈ {5, 6, …, 15} using

$$\frac{{(X-XC)}^2}{X{R}^2}+\frac{{(Y-YC)}^2}{Y{R}^2}+\frac{{(Z-ZC)}^2}{Z{R}^2}=1,$$

where XR ∼ N(85,10²), YR ∼ N(100,8²), and ZR = 60; N(a,b) denotes the normal distribution with mean, a and variance, b. These semiaxis lengths were derived from measurements of real MRC5 cell nuclei shapes. Next, the simulated nucleus was rotated in the XY plane to represent the random positioning of a real nucleus in the microscope's FOV.

As noted above, the nucleus usually contains roughly 5–30 PML NBs, ranging in diameter from 0.2 to 1 μm (equivalent to 2.4–12 pixels). The total number of PML NBs, N_P, and the diameter of each PML NB, V_i, were simulated accordingly,

$$N_{\text{P}}\sim \mathbf{U}(5,6,\dots ,30)$$

$$V_{\text{i}}\sim N(5,1.08),i\in \{1,2,\dots ,N_{\text{P}}\},$$

where U denotes the discrete uniform distribution. The latter values were selected such that P(2.4 < V_i < 12) ≈ 0.99. The location of the geometric center of each PML NB was simulated uniformly within the volume of the nucleus and the volume of the i^th PML NB was constructed by marking the V_i³ nearest voxels. The PML NB voxels were given an intensity, I_PML ∼ N(150,20²) to reflect a typical intensity range of fluorescent PML NBs in real image stacks. If I_PML > 255, I_PML was set to 255, representing intensity saturation. The next step in the simulation procedure was to degrade the ideal image stack generated above in a manner analogous to the corruption imposed by the real system.

Simulated images: NSS

One of the most prominent features of real image stacks is the accumulation of fluorescent signal in the nucleoplasm, which we define as NSS. The observed signal is most likely caused by immunofluorescent labeling of non-SUMO-modified PML protein in the nucleoplasm (31); we choose to define it as NSS since the signal is not specific to PML NBs. We assume that NSS occurs uniformly within the nuclear volume with an intensity proportional to the intensity of object voxels. In real image stacks, the intensity of NSS/Object was approximated as 0.07:1; NSS was negligible outside the nucleus. Thus, in the simulations NSS was generated within the nuclear volume with an intensity equal to I_PML × 0.07. The intensity of the image stack after modeling NSS is denoted as A_{X, Y, Z}.

Simulated images: PSF

Any image obtained from a microscope is actually the convolution (denoted ⊗) of the intensity in the specimen (A_{X, Y, Z}) with the PSF (F_{X, Y, Z}). The value F_{X, Y, Z} is reasonably approximated by a 3D Gaussian blur (8). To model the PSF, simulated image stacks were convolved with a 3D Gaussian smoothing kernel with a standard deviation of 1 and a radius of three voxels (voxels further away effectively have zero effect on the blurring). The intensity of the image stack after modeling the PSF is denoted as B_{X, Y, Z},

$$B_{\text{X,Y,Z}}=A_{\text{X,Y,Z}}\otimes F_{\text{X,Y,Z}}\text{.}$$

Simulated images: Poisson noise

Poisson noise affects the measurement of the intensity in each voxel independently and can produce small bright features in an image that are only one voxel large (32). Poisson noise is considered the most significant type of degradation in CLSM. Following the approach in Comeau et al. (33), we simulate the effects of Poisson noise with the noise matrix, U_{X, Y, Z}. The value U_{X, Y, Z} was generated and applied to each voxel in B_{X, Y, Z} as

$$U_{\text{X,Y,Z}}\sim N(0,1)$$

$$C_{\text{X,Y,Z}}=B_{\text{X,Y,Z}}+WF\sqrt{B_{\text{X,Y,Z}}}{U}_{\text{X,Y,Z}},$$

where C_{X, Y, Z} is the intensity of the voxel after adding Poisson noise and WF is a scaling coefficient known as the width factor. Varying WF allows us to explore how Poisson noise affects the performance of the SCT algorithm.

Simulated images: background noise

Finally, background noise was modeled using the approach in Comeau et al. (33). The noise matrix, H_{X, Y, Z}, was added to C_{X, Y, Z} to generate the simulated image stack, D_{X, Y, Z},

$$H_{\text{X,Y,Z}}\sim N(0,1)$$

$$D_{\text{X,Y,Z}}=C_{\text{X,Y,Z}}+H_{\text{X,Y,Z}}\text{.}$$

D_{X, Y, Z} models the overall result of capturing real CLSM image stacks of fluorescently tagged PML nuclear bodies in MRC5 fibroblast cell nuclei.

Quantitative analysis of nuclear architecture

As noted above, the spatial configuration of certain nuclear compartments can be represented as an SPP. Locations are referred to as events to differentiate them from other points in the region of space. Processes that generate SPPs can be categorized as producing locations that are: completely random (points lie uniformly and independently of each other), or aggregated (points are clustered together) or regular (points are arranged in a uniform fashion) (11). Statistical reasoning about these processes begins with reference to the null model of complete spatial randomness (CSR), which corresponds to an homogeneous spatial Poisson process (34). CSR states that events are distributed independently and are equally likely to occupy any part of the region, and represents the divide between regular and aggregated patterns (11).

One approach to the analysis of SPPs is based on nearest-neighbor distances (NNDs) (11). Distance is a fundamental concept in the analysis of SPPs; inter-event distances are often used to construct test statistics under the assumption of CSR. These distances can be used to test hypotheses about spatial relationships between different types of nuclear body (including irregularly shaped compartments). In comparing compartments of two different types, let u_ij denote the NND from the i^th Type 1 object to the j^th Type 2 object. One test for CSR, that also serves as a summary description for SPPs, uses Ĝ(u) (11), the empirical distribution function (EDF) of the u_ij.

As is usual in the study of SPPs, test functions are generally calibrated using Monte Carlo simulation. We have employed this approach to study the SPPs of PML NBs (Type 1 events) with respect to SC35 domains (Type 2 events). NNDs were measured from the geometric centers of the segmented PML NB objects to the nearest segmented voxel of SC35 domain. To implement Monte Carlo simulation it was necessary to delineate the nuclear volume. This was achieved using immunofluorescent staining directed against lamin B, a protein component of the filamentous lamina network that lies beneath the nuclear envelope. For the s^th Monte Carlo realization, PML NB locations were randomly positioned within the nuclear volume according to CSR and Ĝ(u) was recorded. Finally, the observed Ĝ(u) was compared with a large number, M of simulated Ĝ(u) realizations, s = 1, 2, …, M.

Results and Discussion

Simulation results

Five sets of 100 image stacks were simulated, each set with a different degree of Poisson noise. The expression C × noise indicates WF = C with the exception of 1 × noise, which is denoted as standard (STD) noise. The PSF, NSS and background noise were kept constant.

Simulated images were segmented using the SCT algorithm and, for comparison, Otsu's thresholding method (35,36), the Isodata thresholding algorithm (37,38), and mixture modeling thresholding (MMT) (39,40). These alternative thresholding methods are all implemented in the public domain image processing program, ImageJ (41). These popular thresholding procedures have been widely implemented in the segmentation of fluorescent microscopy images (7,8,42–45). The methods examine the image intensity histogram; for example, Otsu's method selects the threshold that minimizes the overlap between the two components in the histogram.

To quantify the results of the automated segmentation methods versus ground-truth, we assess performance using a number of measures, beginning with the probability of error (see Table 1), also known as the misclassification error (46). For an object-background image, this is defined as

$$P\left(error\right)=P\left(Obj\right)P\left(Backgn{d}_c\right|Obj)+P\left(Backgnd\right)P\left(Ob{j}_c\right|Backgnd),$$

where P(Backgnd_c|Obj) is the probability of classifying object as background, and P(Backgnd) is the a priori probability of class background. This measure is often used in the evaluation of thresholding techniques (47). In general, Table 1 shows that the misclassification error for the SCT algorithm increases as WF is increased; however, the probability of error for Otsu's method, the Isodata algorithm, and the MMT procedure are roughly three-orders-of-magnitude larger than the SCT algorithm.

Table 1.

TP and FP rates and P(error) of the SCT algorithm versus Otsu's method, the Isodata algorithm and MMT

Noise	Method	FP rate	TP rate	P(error)
STD	SCT	4.62 × 10−4 (5.44 × 10−4)	9.56 × 10−1 (7.09 × 10−2)	5.52 × 10−4 (4.89 × 10−4)
	Otsu	1.55 × 10−1 (5.64 × 10−2)	9.96 × 10−1 (1.88 × 10−3)	1.55 × 10−1 (5.64 × 10−2)
	MMT	4.99 × 10−1 (3.55 × 10−2)	1.00 (0.00)	4.98 × 10−1 (3.55 × 10−2)
	Isodata	2.43 × 10−1 (3.66 × 10−2)	9.99 × 10−1 (1.08 × 10−3)	2.43 × 10−1 (3.66 × 10−2)
2 ×	SCT	3.30 × 10−4 (2.51 × 10−4)	9.46 × 10−1 (1.71 × 10−1)	4.39 × 10−4 (4.41 × 10−4)
	Otsu	1.54 × 10−1 (4.72 × 10−2)	9.79 × 10−1 (1.00 × 10−2)	1.54 × 10−1 (4.72 × 10−2)
	MMT	4.63 × 10−1 (3.26 × 10−2)	1.00 (7.03 × 10−5)	4.62 × 10−1 (3.62 × 10−2)
	Isodata	1.73 × 10−1 (3.07 × 10−2)	9.94 × 10−1 (7.90 × 10−3)	1.73 × 10−1 (3.07 × 10−2)
3 ×	SCT	3.59 × 10−4 (2.33 × 10−4)	8.94 × 10−1 (2.15 × 10−1)	5.41 × 10−4 (3.96 × 10−4)
	Otsu	1.64 × 10−1 (3.83 × 10−2)	9.64 × 10−1 (2.52 × 10−2)	1.64 × 10−1 (3.83 × 10−2)
	MMT	4.20 × 10−1 (3.08 × 10−2)	1.00 (5.80 × 10−4)	4.20 × 10−1 (3.08 × 10−2)
	Isodata	1.51 × 10−1 (2.36 × 10−2)	9.88 × 10−1 (1.77 × 10−2)	1.50 × 10−1 (2.36 × 10−2)
5 ×	SCT	1.69 × 10−4 (1.44 × 10−4)	6.98 × 10−1 (1.79 × 10−1)	6.85 × 10−4 (4.09 × 10−4)
	Otsu	1.79 × 10−1 (1.78 × 10−2)	9.61 × 10−1 (1.97 × 10−2)	1.79 × 10−1 (1.77 × 10−2)
	MMT	3.89 × 10−1 (2.75 × 10−2)	9.82 × 10−1 (6.46 × 10−3)	3.88 × 10−1 (2.75 × 10−2)
	Isodata	1.41 × 10−1 (1.52 × 10−2)	9.58 × 10−1 (2.03 × 10−2)	1.40 × 10−1 (1.52 × 10−2)
10 ×	SCT	2.81 × 10−3 (6.54 × 10−3)	4.68 × 10−1 (1.40 × 10−1)	3.75 × 10−3 (6.39 × 10−3)
	Otsu	1.70 × 10−1 (1.25 × 10−2)	8.05 × 10−1 (2.53 × 10−2)	1.69 × 10−1 (1.25 × 10−2)
	MMT	3.55 × 10−1 (2.30 × 10−2)	8.57 × 10−1 (2.03 × 10−2)	3.55 × 10−1 (2.30 × 10−2)
	Isodata	1.32 × 10−1 (9.57 × 10−3)	7.92 × 10−1 (2.59 × 10−2)	1.32 × 10−1 (9.52 × 10−3)

The FP rate is defined as the proportion of voxels in the image stack erroneously labeled as PML NB voxels when they are in fact background voxels. The TP rate is defined as the fraction of actual PML NB voxels correctly labeled as object. Standard deviations are shown within parentheses.

The misclassification error does not capture all areas of performance so to further evaluate the segmentation methods, we have examined the false-positive (FP) and true-positive (TP) rates of the procedures. The FP rate is defined as P(Backgnd)P(Obj_c|Backgnd), which is the proportion of voxels in the image stack erroneously labeled as object (PML NB) voxels when they are in fact background voxels. The TP rate is defined as P(Obj)P(Obj_c|Obj), which is the proportion of actual object voxels correctly labeled as object. It is clear from Table 1 that the alternative segmentation methods have much higher FP rates than the SCT algorithm. With STD noise: Otsu's method drastically undersegments the simulated images, incorrectly thresholding over 15% of the image stack as object, the Isodata algorithm incorrectly assigns over 24% of the voxels as object, MMT erroneously segments almost 50% of the voxels as object. The high FP rate of these methods drives their high misclassification error.

Fig. 3 shows a typical image simulation with STD noise that has been segmented using Otsu's method and the SCT algorithm. Otsu's method is regarded as the best and most commonly employed global thresholding technique (48). Otsu's method considerably outperformed the Isodata algorithm and MMT with STD noise. The SCT algorithm segments all of the PML NB voxels in Fig. 3 but also segments a number of background voxels adjacent to object voxels. This is caused by the PSF, which blurs the image and as a result increases the intensity of background voxels that are close to object voxels. Deconvolution could be used to try to gain a more accurate segmentation; however, deconvolution is inadvisable when the purpose of the segmentation is to resolve object geometric centers (49). Otsu's method drastically undersegments the simulated image. A major reason for this is that Otsu's method (like the Isodata thresholding algorithm and MMT) thresholds each slice of the stack separately, and therefore it loses important information about the 3D image. Slices of the image stack that do not contain object voxels are assumed to have a bimodal intensity histogram and are thresholded at relatively very low intensity. In slices where object voxels do exist, Otsu's method appears to delineate the NSS. This result is also pertinent when Otsu's method is applied to real image stacks (see Fig. 2 C).

Figure 3.

Projection images of a simulated image stack (A) segmented using the SCT algorithm (B) and Otsu's method (C). The misclassification error for Otsu's method is roughly three-orders-of-magnitude larger than the SCT algorithm. This error is driven by the high false positive rate of Otsu's method.

User-defined thresholding

Currently, user-defined thresholding is considered the gold standard method for segmenting fluorescence microscopy images of nuclear compartments. However, manual thresholding is subjective and is prone to inter- and intraoperator variability (4). We have generated synthetic image stacks and so can directly compare the SCT algorithm with user-defined thresholding.

Ten image stacks with STD noise and 10 image stacks with 10× noise were segmented using the SCT algorithm, and manually thresholded by a trained expert. The FP and TP rates as well as the misclassification error for the two methods are summarized in Table 2. With STD noise, the SCT algorithm has a higher TP rate than user-defined thresholding although it also has a higher FP rate. Overall, the SCT algorithm performs as well as manual thresholding for image stacks with STD noise. Furthermore, manual thresholding of the simulated image stacks was very time-consuming, taking ∼5 min per image stack. The SCT algorithm, on the other hand, calculated a threshold in seconds. When there is very high noise, manual thresholding proved slightly better than the SCT algorithm for all measures. However, we would not expect to encounter real image stacks with such high levels of noise.

Table 2.

Evaluation of the SCT algorithm versus manual thresholding

Measure	Noise	SCT	Manual
Accuracy	STD	1.00 (3.91 × 10−4)	1.00 (2.54 × 10−4)
	10 ×	9.97 × 10−1 (6.45 × 10−3)	9.99 × 10−1 (5.87 × 10−4)
FP rate	STD	3.19 × 10−4 (4.22 × 10−4)	4.15 × 10−5 (7.14 × 10−5)
	10 ×	2.20 × 10−3 (6.63 × 10−3)	1.52 × 10−4 (5.21 × 10−5)
TP rate	STD	9.67 × 10−1 (6.18 × 10−2)	9.16 × 10−1 (1.40 × 10−1)
	10 ×	4.49 × 10−1 (1.38 × 10−1)	4.64 × 10−1 (5.96 × 10−2)
P(error)	STD	4.00 × 10−5 (3.90 × 10−4)	2.17 × 10−5 (2.54 × 10−4)
	10 ×	3.41 × 10−4 (6.43 × 10−3)	1.37 × 10−4 (5.87 × 10−4)

Ten image stacks were simulated for each noise level and the average accuracy, TP and FP rates, and P(error) of each thresholding technique across the simulations is summarized. Standard deviations are shown within parentheses.

Segmentation of fluorescent beads

An image stack of a 4 μm fluorescent bead (see Fig. 4) was captured to further assess the performance of the SCT algorithm. For comparison, the same image stack was segmented using Otsu's method. The SCT algorithm accurately delineates the bead. Otsu's method, however, greatly overestimates the size of the bead; giving further support to the argument that the method has a high FP rate. In particular, Otsu's method has a very high FP rate in slices where no bead is present.

Figure 4.

Projection images of a 4 μm fluorescent bead (A) segmented using the SCT algorithm (B) and Otsu's method (C). Since the object is known to be 4 μm in diameter and sphere-shaped, it is clear that the SCT algorithm selects a suitable threshold to delineate the bead. Otsu's method vastly undersegments the bead.

Segmentation of asymmetric nuclear compartments

The task of thresholding PML NBs may be eased because they are geometrically well-defined, roughly spherical objects. The efficacy of the SCT algorithm is more completely demonstrated when segmenting nucleoli, SC35 domains, and FISH-labeled telomeres (for examples, see Fig. 2 B). Unlike PML NBs, nucleoli and SC35 domains are relatively large structures that are irregularly shaped. SC35 domains are especially diffuse compartments (see Fig. 2, A2–A4). FISH-labeled telomeres are also imaged and segmented using the SCT algorithm, showing that this type of fluorescent labeling can also be handled by the algorithm (see Fig. 2, B5). For comparison, the image stacks are also segmented using Otsu's thresholding algorithm in Fig. 2 C. Otsu's method struggles to segment the objects of interest and instead roughly delineates the nucleoplasm in both color channels.

Specimen preparation and microscopy procedures for successful automated image analysis are stricter than for manual methods since computers are easily misled by artifacts, variability, confounding objects, and clutter (4). Thus, it is important to ensure that the objects of interest are delineated with a high degree of contrast against the background. We have successfully used the SCT algorithm to segment almost 1000 image stacks of nuclear compartments including SC35 domains, nucleoli, FISH-labeled telomeres, centromeres, RNA polymerase II sites, and PML NBs.

Size distribution of segmented PML NBs

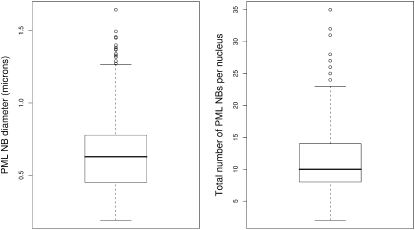
We have applied the SCT algorithm to real image stacks of PML NBs in populations of interphase, serum-starved, and SV40 virus-transformed MRC5 cells to investigate the size distribution of SCT-segmented PML NBs in these nuclei. Measuring the dimensions associated with each NB and scaling, and assuming PML NBs are spherical, provides the means to estimate NB diameter. Fig. 5 illustrates the diameters (in microns) and counts of 4039 PML NBs from 348 segmented image stacks. PML NB diameter ranges from 0.189 μm to 1.64 μm with a mean diameter of 0.623 μm. The number of PML NBs per nucleus ranges from 2 to 35 with a mean of 11.6. These size and count distributions correspond remarkably well with fluorescence and electron microscopy estimates, which suggest that the number of PML NBs in the mammalian cell nucleus typically varies between 5 and 30, ranging in diameter from 0.1 or 0.2–1 μm (10,50); >95% of SCT-segmented PML NBs fall in the range 0.189–1 μm.

Figure 5.

Boxplots describing the sizes (left) and counts (right) of >4000 PML NBs in 348 segmented image stacks. PML NB diameter ranges from 0.189 μm to 1.64 μm with a mean diameter of 0.623 μm. The number of PML NBs per nucleus ranges from 2 to 35 with a mean count of 11.6.

One clear problem with such analysis is that the output image from CLSM is not a perfect representation of the real objects. For instance, the efficiency of the primary and secondary fluorescent antibodies that label the nuclear compartments is affected by several factors such as avidity, suitability, and titer, which can greatly influence the fluorescence intensity profile and therefore the overall size of the nuclear compartment stained and later visualized (4). Compartments also tend to have indistinct borders, with the fluorescence intensity profile tailing off gradually (4). These problems as well as the PSF can cause significant downstream errors with the quantitative volumetric analysis of the image objects and can only be reduced with careful experimental procedures and accurate image analysis. Additionally, the typical lateral resolution of the CLSM is only 0.2 μm (32), which is roughly the size of the smallest PML NB that we record (0.189 μm). Our estimate of PML NB size, however, fits well with the quoted range of the compartment by electron microscopists (10), which suggests that the SCT algorithm delivers accurate segmentations of PML NB volume.

SPP analysis of PML NBs and SC35 domains

The SCT algorithm was developed to facilitate the analysis of SPPs within 3D images. Nuclear architecture has traditionally been studied via fluorescence microscopy and subsequent observational interpretation of the images, usually as 2D projections of 3D image stacks (4,51–53). Visual inspection is inadequate, however, to evaluate complex spatial point patterns within the nucleus, especially when the patterns are highly punctate. Statistical tools can help to quantitatively decode the complex spatial relationships that underlie nuclear architecture.

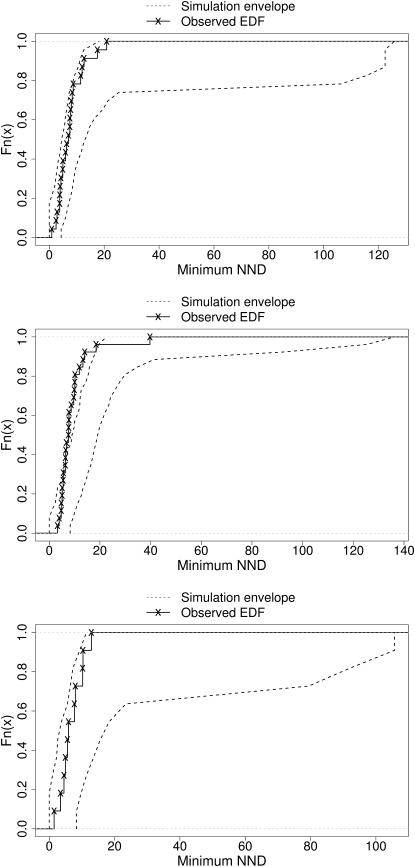
We have investigated the spatial relationship of PML NBs with SC35 domains (for examples, see Fig. 2, A2–A4). The NND from each PML NB centroid was measured to the nearest segmented SC35 domain voxel. To assess whether the observed PML NB SPP rejects the null hypothesis of CSR with relation to SC35 domains, we calibrated Ĝ(u), using M = 5000 simulated Ĝ(u) realizations to define upper and lower limits of a 99% simulation envelope (11). If the observed Ĝ(u) is not completely contained inside the simulation envelope, then we have evidence to reject the null hypothesis of CSR. Fig. 6 illustrates the results of applying this procedure to the segmented image stacks shown in Fig. 2, A2–A4. Putatively examining the projection images or image stacks in question may have compelled an unwary observer to infer that, in all three cell nuclei, PML NBs were closer to SC35 domains than a random distribution would suggest. However, at the 1% significance level, quantitative analysis provides no reason to doubt that the SPP of PML NBs is CSR with respect to SC35 domains in the nuclei shown in Fig. 2, A2 and A4, but we do have evidence to reject CSR for the nucleus shown in Fig. 2 A3. These results suggest that complex SPPs such as those displayed in Fig. 2 are extremely difficult to interpret visually.

Figure 6.

Plot of the empirical distribution function of the distances from each PML NB centroid to the nearest segmented SC35 domain voxel. The observed distribution of PML NB NNDs is shown by the solid line, while the simulation envelope (from Monte Carlo testing) is shown with the dotted lines. The top, middle, and bottom EDFs correspond to the nuclei in Fig. 2, A2, A3 and A4, respectively.

The analysis above was carried out on a total of 50 interphase MRC5 cells and 50 serum-starved MRC5 cells. In both populations, 42 out of 50 cells had evidence to reject CSR. Moreover, in these 84 cells, the observed Ĝ(u) EDFs penetrated the lower limit of the simulation envelope and therefore we infer that the observed PML NBs are situated closer to SC35 domains than one would expect under CSR. Thus, we have formal, quantitative evidence to suggest that PML NBs are associated with SC35 domains in both interphase and serum-starved MRC5 human primary fibroblast nuclei. To our knowledge this association has been observed, but never quantified until now. The functional consequences of this interaction are unclear. Both PML NBs and SC35 domains have been shown to associate closely with sites of nascent RNA transcription (25,26), and nascent transcripts are often found at the edges of either compartment, but not typically within. The HCMV viral genome is also found to locate between PML NBs and SC35 domains upon entry to the nucleus (22), and this bears relevance to its transcription. Certain genomic regions and genes are spatially associated with PML NBs and SC35 domains (1,2,27). Hence, both PML NBs and SC35 domains are implicated in transcription, albeit potentially in distinct processes (with PML NBs most likely to be involved in the events preceding and during production of nascent transcripts, whereas SC35 domains play a role in posttranscriptional pre-mRNA processing). Alternatively PML NBs may themselves also show involvement in pre-mRNA processing (54), which could account for their neighboring of SC35 domains. The juxtaposition of PML NBs and SC35 domains, facilitated by their sharing of the interchromatin space, may therefore allow their organization into a transcriptional processing hub that is able to respond to the requirements of the cell as appropriate. Thus, the significantly close configuration of PML NBs and SC35 domains is consistent with such a proposal.

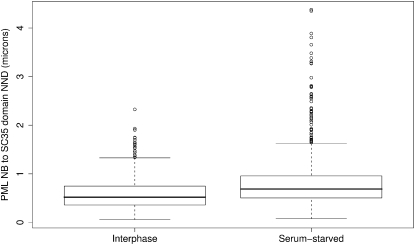
Furthermore, we have investigated the degree of the spatial interaction in both cell populations using the NND from each PML NB to SC35 domain voxel. Fig. 7 illustrates these distances (in microns) in the interphase and serum-starved MRC5 cell nuclei. The mean NND was 0.605 μm in the interphase nuclei and 0.811 μm in the serum-starved nuclei. Performing a Mann-Whitney-Wilcoxon test using all the NNDs from the two samples rejected the null hypothesis that the two samples were drawn from a single population (p < 10⁻¹⁵). Thus, we have evidence to suggest that the distance between the SC35 domain and PML NBs is significantly smaller in the interphase nuclei. The closer spatial interaction in these cells suggests that subtle changes in spatial positioning at the local compartment level, in response to changes in cellular requirements, are possible without large-scale disruption of nuclear organization. In the case of serum-starved cells, which show low levels of transcriptional activity compared to interphase cells, PML NBs and SC35 domains are found to be further apart than in interphase cell nuclei, suggesting that the degree of spatial association is indicative of cellular activity.

Figure 7.

Boxplots describing the inter-event distances from PML NB to SC35 domain voxel in 50 interphase MRC5 nuclei (left) and 50 serum-starved nuclei (right). Inter-event distance ranges from 0.057 μm to 2.33 μm with a mean distance of 0.604 μm in the interphase nuclei and from 0.076 μm to 4.38 μm with a mean distance of 0.811 μm in the serum-starved nuclei.

Conclusion

Here we present a novel method to segment CLSM image stacks of nuclear compartments. Image segmentation is a core problem in microscopy and the importance of threshold selection cannot be overemphasized since further processing and analysis of the segmented objects entirely depends on the quality of the segmentation. User-defined thresholding is a common approach for segmenting fluorescence microscopy images. Although such thresholding may be accurate, it is also subjective and time-consuming. Automated segmentation methods are objective and generally much faster than manual thresholding. The SCT algorithm is fully automated and yields an accurate 3D segmentation of nuclear compartments that may also be applicable to fluorescent microscopy techniques other than CLSM, such as wide-field fluorescence microscopy.

The SCT algorithm was evaluated by processing real image stacks of PML NBs, simulated image stacks and image stacks of fluorescent beads. In all three cases, the SCT algorithm was shown to replicate the accuracy of manual thresholding by an experienced operator, and to outperform the popular and well-established Otsu method, the Isodata thresholding algorithm, and MMT. Additionally, the SCT algorithm is deterministic, i.e., it will always choose the same threshold for any given image stack. This is an advantage over user-defined thresholding (with inter- and intraoperator variability), because any subsequent analysis of the segmented image stacks will give consistent conclusions. We have applied the SCT algorithm to almost 1000 real image stacks of nuclear compartments with great success. The algorithm is general and flexible, and can be applied to any similarly structured data. Moreover, it is not subject to user bias and arguably subsumes the human operator; at the very least, it serves as a powerful tool to assist segmentation of complex cell biology images.

The SCT algorithm directly lends itself to quantitative spatial analysis of the thresholded objects. Spatial relationships between nuclear compartments may give significant clues to the function of the compartments. However, to date many spatial associations have been defined as significant by subjective visual assessment. Such observations can be misleading. Currently we have high-resolution imaging technology to visualize the cell nucleus and a wide range of statistical approaches with which to study the derived data. The key question in attempting to understand spatial configurations is whether non-CSR SPPs are the cause or consequence of function. We show that PML NBs are significantly closer to SC35 domains than expected under CSR in both interphase and serum-starved MRC5 human primary fibroblast nuclei. Since both PML NBs and SC35 domains are implicated with transcriptional functions their juxtaposition may create a transcriptional processing hub set up to respond to the transcriptional requirements of the cell as appropriate. In serum-starved nuclei (where transcription levels are lower than in interphase cells), the NND between PML NBs and SC35 domains is significantly greater. This small-scale rearrangement may be a reflection of the change in cellular state. Furthermore, such a change in the spatial relationship would be extremely difficult to interpret by eye. Therefore, the statistical methods employed here are an extremely useful tool and an appropriate choice to reveal subtle but significant changes in spatial relationships.