Abstract
The neural cell adhesion molecule (NCAM) plays an important role in nervous system development. NCAM forms a complex between its terminal domains Ig1 and Ig2. When NCAM of cell A and of cell B connect to each other through complexes Ig12(A)/Ig12(B), the relative mobility of cells A and B and membrane tension exerts a force on the Ig12(A)/Ig12(B) complex. In this study, we investigated the response of the complex to force, using steered molecular dynamics. Starting from the structure of the complex from the Ig1-Ig2-Ig3 fragment, we first demonstrated that the complex, which differs in dimensions from a previous structure from the Ig1-Ig2 fragment in the crystal environment, assumes the same extension when equilibrated in solvent. We then showed that, when the Ig12(A)/Ig12(B) complex is pulled apart with forces 30–70 pN, it exhibits elastic behavior (with a spring constant of ∼0.03 N/m) because of the relative reorientation of domains Ig1 and Ig2. At higher forces, the complex ruptures; i.e., Ig12(A) and Ig12(B) separate. The interfacial interactions between Ig12(A) and Ig12(B), monitored throughout elastic extension and rupture, identify E16, F19, K98, and L175 as key side chains stabilizing the complex.
Introduction
Adhesion proteins, which bind cells to other cells or to the extracellular matrix, experience tension because of the mechanical coupling of the cell to its environment. The response of adhesion molecules (1), and of biomolecules in general (2), to force can affect not only the rates but also the mechanisms of cellular processes. To understand the effect of mechanical force on biomolecular function, it is important to identify the force transmitting elements in the structure (3). Interestingly, several proteins involved in force transmission between cells or between cells and the extracellular matrix have multimodular architectures (4). Whereas some proteins respond to force by unfolding (5,6), in many cases, so-called tertiary structure elasticity results from changes in the relative arrangement of different domains (7). Given the number of such modular adhesion proteins, the latter elasticity might be expected to be more pervasive.
Although simulations demonstrated the elastic behavior of individual multimodular proteins (8–11), the response of adhesive protein complexes to force is more relevant to their biological function. Several studies explored the relationship between the dimensions of adhesion proteins and the intercellular separation (12–14), but adhesion molecules are often under tension that could perturb the protein and/or complex dimensions. Under a range of physiologically relevant forces, the extracellular region of transmembrane adhesion proteins could therefore span greater intermembrane separations than those suggested by their crystallographic dimensions.
The wide range of physiologically relevant forces and loading depends on the type of adhesion molecule, its physiological location within the organism, and the cell motility or contractility (prestress). The forces may also vary with time during dynamic cell rearrangements. Evans and Calderwood (15) suggested that cell-adhesion complexes in tissues apparently under static stress can experience transient loading at rates as low as ∼1 pN/s. Under these conditions, individual bonds can rupture under forces of a few pN. In contrast, much higher loading rates of ∼104 pN/s are involved in the initial attachment of immunological cells in the vasculature. For example, during neutrophil rolling, a single complex between P-selectin and its glycoprotein ligand can experience forces of well over 100 pN (16), with only a modest increase in the corresponding off-rate. At intermediate loading rates of 100–500 pN/s (comparable to the contractile forces in the filopodia of those cells), Benoit et al. measured single-adhesion receptor unbinding forces centered around 23 pN (17). Even in stationary human fibroblasts, focal adhesions experienced forces of ∼5 nN/μm2 (18). This corresponds to a lower limit of pN forces/bond if the integrins are assumed to be close-packed in the focal adhesion complex. In motile fibroblasts, tensile forces on focal adhesions can exceed the rupture forces of the receptor-ligand bond.
Of the thousands of adhesion proteins identified, the neural cell adhesion molecule (NCAM) was one of the first cell adhesion molecules to be isolated, and it is a paradigmatic member of the Ig superfamily of cell adhesion molecules (IgSF cell adhesion molecules) (19). Involved in both cell-cell adhesion and signaling (20), it plays an important role in the development, maintenance, and regeneration of the nervous system (21–24). It has three major isoforms, which differ in their mode of attachment to the cell membrane. However, all isoforms share a common extracellular region. This consists of five Ig domains (Ig1–Ig5), followed by two fibronectin type III (Fn III) domains (Fig. 1 A). Several biochemical and biophysical studies have shown that homophilic NCAM adhesion (NCAM/NCAM) involves multiple Ig domains (25–33). Surface plasmon resonance measurements (28), bead binding assays, as well as surface force (29) and single-molecule atomic force microscope (AFM) measurements (30) demonstrated that both Ig12/Ig12 and Ig3/Ig3 bonds could form. Bead aggregation assays (31) and force measurements (29,30) with both full-length and domain deletion fragments have further shown that both domain interactions can bridge apposing surfaces to form an adhesive or trans-complex. Although it was also suggested (32) that Ig12 could form cis (lateral) binding, there is also the possibility that Ig12 domains could form both cis and trans bonds, although presumably not simultaneously.
Figure 1.
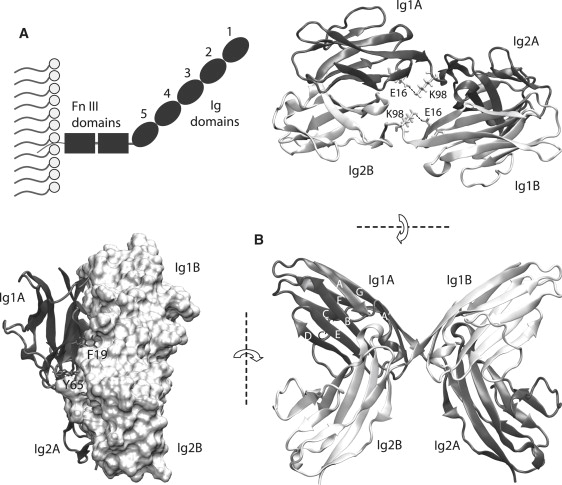
(A) Schematic of the extracellular part of NCAM showing the arrangement of its different domains. (B) Structure of the complex formed between Ig12 of molecule A (dark gray) and Ig12 of molecule B (light gray) in cartoon representation (bottom right). The view on the left shows the two main aromatic residues of Ig1(A) that bind to their pockets in Ig2(B) (surface representation). The view on the top right shows the interdomain, intramolecule bonds in the linker region between E16 (of Ig1) and K98 (of Ig2).
Whereas it is well established that NCAM forms homophilic complexes that bridge cells, how these complexes physically respond to tension or to variations in intermembrane spacing is currently unknown. Addressing this knowledge gap is important to understanding NCAM function, because NCAM and its posttranslationally modified form regulate tissue architecture and physiological function by modulating intercellular spacing (21). The posttranslationally modified form of NCAM abrogates cell adhesion (21), because of the steric and electrostatic effects of the attached polysialic acid (34). Expression of NCAM-polysialic acid disrupts cell adhesion complexes by “prying apart” cell membranes by virtue of increased repulsion. This repulsion is sufficient to overwhelm adhesion between apposed NCAM proteins. NCAM complexes also are likely to experience dynamic loading during morphogenesis, neurite extension, and axon pruning (35), all of which are dynamic processes. For example, filopodial retraction speeds measured at the leading edge of neuronal growth cones in vivo (where NCAM is localized (36,37)) were ∼0.02 μm/s (38). Depending on the elastic modulus (spring constant) of the complex, this could generate effective loading rates of several hundred pN/s. When single NCAM bonds were ruptured using the AFM (30) at comparable loading rates, the bonds sustained forces of tens of pN before rupture. The response of NCAM complexes to physiologically relevant forces and loading rates is important to understand how the protein structure defines its mechanical role in cell biology.
The force response of a protein complex depends on its structure. Crystal structures of both the Ig12 and the Ig123 fragments of NCAM were solved (28,32). In both crystals, the Ig12 region of one NCAM fragment bound to Ig12 of another (Fig. 1 B). The two Ig12 structures had essentially the same binding interface; however, the Ig12/Ig12 complex in the crystal of the Ig12 fragment had an end-to-end length of 49 Å, whereas the complex in the Ig123 crystal had an end-to-end length of 57 Å. Previous mutation studies (33) also showed that charged residues E11, E16, K98, and R177 were important for Ig12 dimerization. In the crystal structures, E11 and E16 formed salt bridges with R177 and K98, and all four residues were located close to the interdomain linker region. Whereas the E16-K98 pair formed intermolecule bonds in the Ig12 crystal structure, the same residues in the Ig123 crystal structure formed intramolecule bonds between adjacent domains (Fig. 1 B, top right). Additionally, although F19 is critical for the Ig1-to-Ig2 interaction (26), the crystal structures show that another aromatic residue, Y65, also forms multiple bonds connecting Ig1 and Ig2. The relative importance of these different interactions in a solvated complex and their contribution to complex stabilization under force has not been demonstrated.
Molecular dynamics (MD) simulations are increasingly important and powerful means of investigating biomolecular dynamics (39). In particular, steered molecular dynamics (SMD) simulations are complementary to, if not the sole means of, gaining molecular-level insight into the dynamics of biomolecules under force (7). Although the timescales of MD simulations are still faster than are those of experimental and in vivo dynamics, several predictions based on SMD simulations (8,40–42) were experimentally validated (9,43–45). In the case of complexes between adhesion molecules, MD simulations can be used to address at least three questions. First, do the crystal structures reflect the equilibrated structures in a fully solvated environment? Second, does the complex respond to physiologically relevant forces? Discounting unfolding studies, the complete stretching response of only ankyrin to weak constant forces of tens of pN has been simulated (8) and was later confirmed experimentally (9). Third, can one determine the molecular details of the side chain interactions during unbinding? As demonstrated by Bayas et al. (46), using force measurements, SMD simulations (47) identified the key load-bearing amino acids stabilizing an Ig-family adhesive complex under force. The response of protein complexes to a directionally biased loading force, as in the SMD simulations, is especially relevant for cell adhesion molecules, which evolved to resist force. Consequently, the results of such simulations can provide critical insight into functionally important interactions.
The study presented here used MD simulations to investigate several aspects of the Ig12/Ig12 complex of NCAM. The simulations showed that the complex undergoes significant relaxation when solvated. We showed how the complex responds to low constant forces (tens of pN), and we further determined how the complex fails under dynamic loading. First, our equilibration simulations (without external force) reconciled some of the apparent differences in overall topology and binding interactions between the structure of the Ig12/Ig12 complex in crystals of the Ig12 and Ig123 fragments. Second, we demonstrated that the NCAM Ig12/Ig12 complex responds elastically to low constant forces because of the reorientation of protein domains. This is referred to as “tertiary structure elasticity” (8,10,11). Third, at a loading rate low enough to unbind the complex without unfolding, we identified key residues stabilizing the complex under force.
Methods
MD simulations were performed using the program NAMD (48) and the CHARMM22 force field (49,50). The VMD (51) program was used for the system setup, data analysis, and molecular graphics. The structure of the Ig12/Ig12 complex was computationally isolated from the structure of the Ig123 NCAM fragment (PDB ID 1QZ1, residues 1–190 in each Ig12 fragment) and then solvated in a box (86 × 94 × 219 Å3) of explicit water (TIP3) that was large enough to keep the protein solvated even after complex dissociation. 108 Na+ and 100 Cl− ions were added. This corresponds to 100 mM NaCl, which is similar to the salt concentration in the extracellular environment. The ion numbers maintain system electroneutrality. Simulations of the resulting system comprising 168,000 atoms were performed with an integration time step of 1 fs. Electrostatics calculations were done using the particle mesh Ewald method, and other nonbonded interactions were cut off at 12 Å, with a switching distance of 10 Å. Simulations were carried out with periodic boundary conditions, with both temperature (298 K) and pressure (1 atm) controlled during equilibration. We used Langevin dynamics and Langevin piston pressure control as described in Phillips et al. (48).
The system was equilibrated as follows: The protein complex was fixed under a harmonic restraint, and the energy was minimized for 10,000 steps, followed by 100 ps of equilibration. Then, keeping the Cα atom of residue 190 in the Ig12(A) fixed and the corresponding atom in Ig12(B) harmonically restrained, 10,000 steps of minimization was followed by 3 ns of equilibration. At this time, the complex root mean-square deviation (RMSD) stabilized to 1.6 ± 0.1 Å relative to the initial crystal structure (Fig. 2). Finally, the restraint on the Cα atom of residue 190 in Ig12(B) was released, and the complex was allowed to equilibrate until both the end-to-end distance of the complex and its RMSD stabilized.
Figure 2.
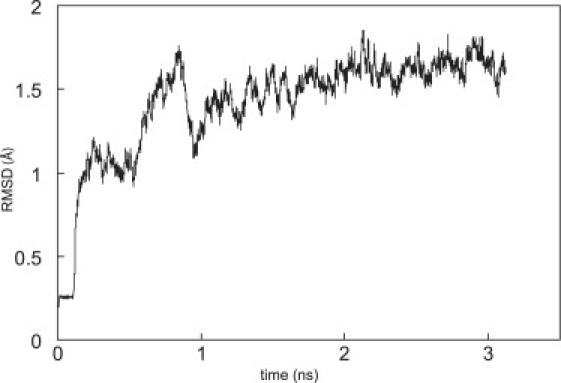
Time evolution of the RMSD of the complex during the minimization and equilibration steps before releasing the restraints on the SMD atom.
Steered MD simulations were performed with the Cα of residue 190 of Ig12(A) held fixed (fixed atom) while that of molecule B (SMD atom) was subjected to a force (F). The force had one of two functional forms: either (i), F = constant when the SMD atom was subjected to a constant force of either 30, 50, 60, or 70 pN; or (ii), F = k(vt − Δd) for constant velocity pulling, in which the SMD atom was attached to a virtual spring with force constant k, whose other end was pulled at a constant velocity v. Here Δd was the position of the SMD atom relative to its initial position along the pulling direction. The spring force constant was 70 pN/Å (1 kcal/mol Å2) and the pulling velocity was either 0.1 or 0.01 Å/ps.
Results
The following describes the results of simulations in which we (i), equilibrated the fully solvated Ig12/Ig12 complex, (ii), determined its response to constant forces in the tens of pN range, and (iii), followed the rupture of the protein-protein complex when pulled at constant velocity.
Equilibration of the fully solvated Ig12/Ig12 complex
The initial equilibration steps were carried out with the C-terminal Cα atom of Ig12(A) fixed and the corresponding atom in Ig12(B) (SMD atom) harmonically restrained, but free to move in a direction along the length of the complex. During these steps, all intermolecular interactions, as well as intramolecule, interdomain linker interactions, were maintained.
When the restraints on the SMD atom were released, the end-to-end distance of the complex (defined as the distance between the last Cα atoms of the C-termini of molecules A and B) increased to 57Å within 3 ns, with a concomitant increase in and stabilization of the complex RMSD (Fig. 3, inset). Of the intramolecule interdomain linker interactions (Fig. 4 A) in both molecules A and B, E11-R177 remained stable, whereas E16-K98 broke within 1 ns, in both molecules. Moreover, E16(A) formed a brief intermolecule H-bond with K98(B). In the equilibrated structure, E16 and K98 were positioned such that they could form either inter- or intramolecule bonds. Among the intermolecule A/B interactions, the H-bond between the backbone −NH of F19 and the carbonyl of G178, as well as the ionic bond between K18 and R177, and the nonpolar interactions with F19 were maintained. The H-bonds between Y65 and K133, E171 and R173 (Fig. 4 B), and T63 (with R173) either stayed bound (A/B) or broke intermittently but reformed. An H-bond also formed between the backbone carbonyl of S17 (A) and backbone HN− of I180 (B). This interaction was present in the Ig12 crystal structure, but not in the structure of Ig123. Outside the main binding interface, salt bridges formed intermittently between N46 and R137, an interaction that was not observed in the crystal structures. When equilibrated over 13 ns, the end-to-end distance varied from 55 to 64 Å, whereas the RMSD remained constant throughout.
Figure 3.
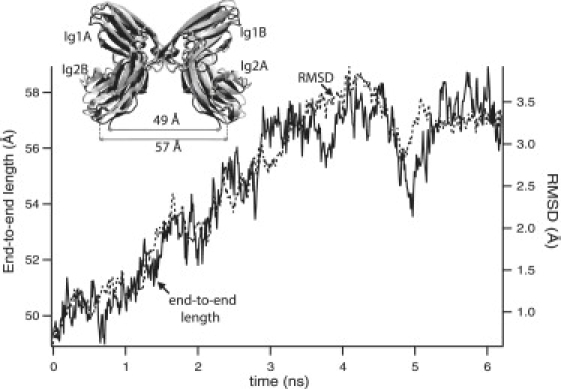
Variation of the end-to-end length and the RMSD of the complex (relative to that at time t = 0) with time, after releasing the restraints on the SMD atom. Inset: The conformations of the complex before (black) and after (gray) this final equilibration step, shown superimposed.
Figure 4.
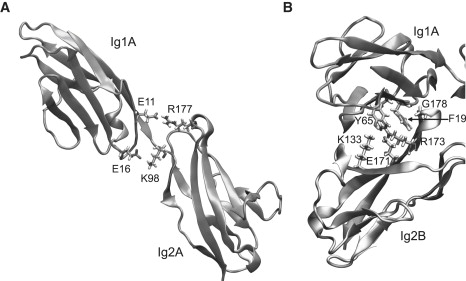
(A) Initial state of the intramolecule interdomain bonds in molecule A (similar in molecule B) before equilibration. (B) Hydrogen bonding partners of the aromatic residues Y65 (K133, E171, and R173) and F19 (G178) in the Ig1(A)/Ig2(B) interface.
Complex response to low constant forces
The significant increase in the complex end-to-end length during constant velocity pulling (see below) motivated us to explore the response of the complex to low, constant, physiologically relevant forces. The protein complex responded to tensile forces of tens of pN, with a substantial change in its end-to-end length. The extension arose from a change in the relative orientation of the domains. When subjected to a low force of 50 pN, the end-to-end distance increased and stabilized within nanoseconds to 77 Å (Fig. 5). Subjecting the complex to external forces of 60 and 70 pN led to proportionally greater extensions of the end-to-end length. The linear dependence of the end-to-end extension (or length) of the complex to this range of low forces (50–70 pN) corresponds to a spring constant of 0.02 N/m for the protein complex. This is within a factor 4–8 of the softest protein spring known, which is that of ankyrin (7). To determine the elasticity between 0 and 50 pN, we simulated the response of the complex to a 30 pN external force. The complex extended to an end-to-end length of 72 Å to 30 pN, which, together with the 0 and 50 pN data, yielded a spring constant of ∼0.04 N/m. Thus, the overall spring constant of the complex was ∼0.03 N/m when subjected to forces of tens of pN (<70 pN).
Figure 5.
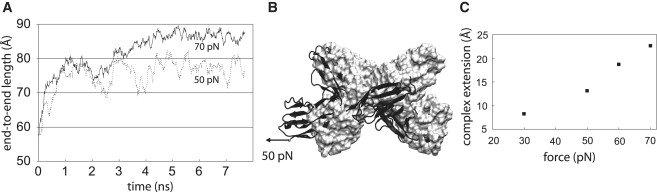
(A) Evolution of the end-to-end length of the complex with time, when subjected to constant forces of 50 and 70 pN. (B) The resting conformation (surface representation), shown in gray, and the conformation of the complex when subjected to 50 pN force shown in black (cartoon representation). (C) Plot showing the dependence of the increase in end-to-end length of the complex (relative to the unstrained complex) on the applied force.
In addition to domain-level rearrangements, the low forces also led to the rupture and formation of several bonds. Under a 50 pN external force, the intramolecule, interdomain E16-K98 H-bonds in the crystal (Fig. 1 B) that broke during the equilibration never reformed. Instead, E16 (of A or B) intermittently bonded with K98 of the other molecule (B or A). Also, all three H-bonds formed by Y65 broke within 1.3 ns. The H-bond formed by T63 also broke, but then reformed. Interestingly, alteration of the last H-bond between the G and C′ strands of domain 1 (V14-F96, −NH–O) in both molecules led to alternate breakage and reformation. This bond broke within 5 ns and did not reform when the complex was subjected to a force of 70 pN. Otherwise, the bonds were similarly affected in response to 30, 60, and 70 pN forces.
Identification of a loading rate for unbinding
At constant velocity pulling (Fig. 6), the initial force response of the complex was a stretching motion (similar to that demonstrated with low constant forces above), in which the end-to-end length of the complex increased. This was only because of a change in the orientation of the domains relative to each other and to the direction of the external force. The fully stretched end-to-end length was >95 Å. After this extension, the complex begins to unbind.
Figure 6.

Identification of a loading rate for unbinding: response of the Ig12/Ig12 complex to pulling at two computationally realizable loading rates. At the two loading rates, the complex initially stretches to almost twice its end-to-end length, after which its response depends on the loading rate. The complex unfolds as it unbinds at a loading rate of 7 pN/ps (v = 0.1 Å/ps), but unbinds without unfolding at 0.7 pN/ps (v = 0.01 Å/ps).
A pulling speed of 0.1 Å/ps (at a loading rate of 7 pN/ps) was not low enough to preserve the secondary structure integrity of the complex. Here, the rupture of the Ig1(A)/Ig2(B) interface before that of Ig1(B)/Ig2(A) initiated the unfolding of the G strand of Ig1B. This involved sequential breakage of the five H-bonds between the G and C′ strands and the ten H-bonds between the G and A′ strands.
In contrast, at a 10-fold lower pulling speed of 0.01 Å/ps (loading rate of 0.7 pN/ps), the complex ruptured without unfolding. There were no Ig1(A)/Ig1(B) interactions as the Ig12 molecules separated during the pull. The unbinding trajectory of the intact molecules is discussed below.
Unbinding trajectory
When subjected to constant velocity pulling with a 0.7 pN/ps loading rate, the complex ruptured within 5.5 ns, as shown in Fig. 7. The atomistic details of the unbinding trajectory, in combination with the time dependence of the force experienced by the molecule, give useful information about the different interactions stabilizing the complex under tension. Most of the rupture events in the Ig1(A)/Ig2(B) interface occurred almost simultaneously with those in the Ig2(A)/Ig1(B) interface, except where indicated. Hence, Fig. 7 focuses mainly on the Ig1(A)/Ig2(B) binding interface.
Figure 7.
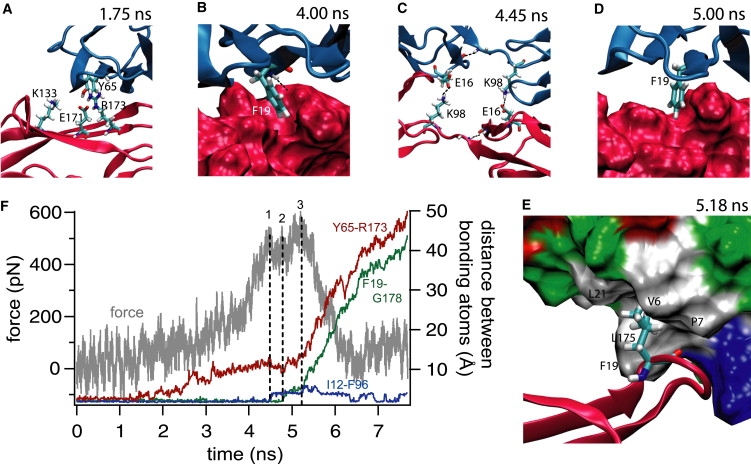
Unbinding trajectory of the complex during 0.01 Å/ps constant velocity pulling. All images show the binding interface between Ig1(A) and Ig2(B). (A) By 1.75 ns, Y65's H-bond with K133 is already broken, whereas its H-bonds with E171 and R173 are about to break. (B) Even at 4 ns, F19 remains bound to its complementary pocket in Ig2, as shown. The H-bond between the backbone −NH of F19 and G178 is also shown. (C) By 4.45 ns, E16 and K98, which are interdomain intramolecule H-bonds initially, have ruptured and formed intermolecule bonds instead. (D) By 5 ns, F19 is only loosely bound to its now half-open pocket in Ig2. (E) As F19 slips away from its initial binding pocket, L175 binds to a nonpolar pocket (white-colored region) of Ig1 (colored according to residue type in surface representation) formed by V6, P7, F19, and L21 as pictured at 5.18 ns. Its rupture 0.1 ns later forms the final rupture event (marked “3” in F). (F) Time evolution of the force experienced by the complex and the bond distance of the Y65(A)-R173(B), I12(A)-F96(A), and F19(A)-G178(B) H-bonds. The major force peaks are marked 1, 2, and 3. Ig1A is shown in blue and Ig2B in red in A–D. Residue structures in A–E are shown in licorice representation with the atom-based color-codes N-blue, C-cyan, O-red, and H-white.
The three H-bonds involving Y65 (A) broke within 1.8 ns, and the S17-I180 and T63-R173 H-bonds broke within 2 and 2.45 ns, respectively (Fig. 7 A). Whereas the V14-H96 H-bond between β strands G and C′ of domain 1 in both molecules broke (as expected from the constant low-force simulation results) at 3.4 ns, the adjacent I12-F96 (O–HN) H-bond between the same strands of both molecules also broke, albeit only at much higher forces, at 4.48 ns. This latter bond also reformed in molecule B after unbinding. Both of the intermolecule E16-K98 bonds formed within 4.35 ns. The rupture of the F19-G178 (A/B) H-bond at 4.78 ns caused the next force peak (marked “2” in Fig. 7 F), whereas the corresponding B/A bond broke at 4.85 ns. The A/B E16-K98 bond also broke at this time. The nearby K18-R177 bonded tightly only at 3.9 ns and ruptured at 4.9 ns. The B/A E16-K98 bond ruptured at 5.17 ns, and the largest force peak at 5.19 ns (“3” in Fig. 7 F) arose from the rupture of the nonpolar interaction of L175 of one molecule with V6, F19, and L21 of the other (Fig. 7 E). Thus, even as F19 slid out of its pocket, it is the transient interaction of L175 in Ig2 with a hydrophobic pocket in Ig1 of the other molecule that concluded the rupture.
Discussion
This study used molecular dynamics simulations to address three distinct aspects of NCAM Ig12/Ig12 homophilic binding. First, the equilibration simulations resolved several apparent differences between two related crystal structures of the Ig12/Ig12 complex. Second, constant low-force simulations showed that the complex responds to physiologically relevant forces within the multi-ns timescale. Third, the complex unbinding trajectory revealed key interactions that stabilize the complex.
The relative domain orientations and end-to-end lengths of cell-cell adhesion complexes are important parameters that help determine their place in the cellular context (e.g., cis versus trans binding). We considered the NCAM Ig12/Ig12 complex from the crystal structure of the Ig123 fragment, because it exhibits a slightly tighter binding compared to that from the Ig12 crystal, which exhibits a longer end-to-end length in the structure. However, the equilibration of the former complex structure led to a final end-to-end length that was comparable to that of the latter Ig12/Ig12 complex. This suggests that the Ig123 structure is under strain in the crystal. Also, one of the primary differences between these crystal structures was that, although E16-K98 was an intermolecule bond in the Ig12 NCAM crystal, it was an intramolecule bond in the Ig123 crystal. Our equilibration simulations showed that the intramolecule E16-K98 bonds break and the residues are poised to form intermolecule bonds in the relaxed and more extended complex. Thus, MD simulations of solvated molecules complement crystallographic data by testing and validating the interactions observed in the crystal structures.
The mechanical response of single proteins with long, multiple-repeat architectures has been explored previously both computationally (8,52–54) and experimentally (44,55). Here, we have shown that the Ig12/Ig12 complex responds to forces as low as tens of pN within several nanoseconds. As indicated in the introduction, combining in vivo filopodial retraction speeds of ∼0.02 μm/s with the spring constant of the complex estimated in this work of ∼0.04 N/m (in the 0–50 pN range) yields a loading rate of 800 pN/s. Of direct relevance to this work, AFM measurements showed that, at a loading rate of ∼700 pN/s, the rupture forces were centered around 40 pN. Thus, the NCAM complex can experience tens of pN forces in physiological circumstances. In our low constant-force simulations, we probed this range and showed that the force versus extension relationship is piecewise linear in the ranges 0–50 pN and 50–70 pN. Although this yields a useful estimate of the local spring constant of the protein complex, depending on the force, stretching can only occur up to ∼90 pN (when the complex stretches fully). Even thermal fluctuations can increase the end-to-end length of the equilibrated structure up to 64 Å. Accordingly, the overall response from a few pN to 90 pN is nonlinear and plateaus above 90 pN.
In AFM experiments, the forces inducing NCAM unbinding were tens of pN, and increased to well over 100 pN at the higher end of the loading rates used in the AFM study (30). But the protein immobilization chemistry in AFM measurements makes it hard to detect such small changes in end-to-end length of protein complexes: the linker attaching the protein to the AFM tip is itself elastic, and the complex's stretching response may get buried in the response of the linker. Although experiments have been useful in elucidating the elastic behavior of single, long proteins such as titin or even ankyrin, SMD simulations can provide a complementary means to address the mechanical properties of shorter protein complexes, as demonstrated here. It is instructive to note that the spring constant of 0.03 N/m that we computed here for the low-force extension of the NCAM Ig12/Ig12 complex is about one half the computed value for the extracellular region of a single cadherin with calcium. However, it is comparable to that of cadherin without calcium (11) and an order of magnitude less than that computed for a spectrin repeat unit (56). Thus, the NCAM Ig12/Ig12 complex acts as a relatively soft spring, whose stretching behavior is facilitated by flexible linker regions connecting the Ig domains. This behavior is schematically shown in Fig. 8. This elasticity should be taken into consideration in determining whether adhesion complexes can bridge a given intercellular spacing.
Figure 8.
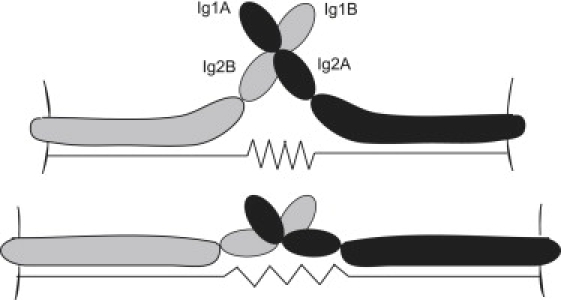
Schematic illustration of the nanomechanical spring-like behavior of NCAM when bound as an Ig12/Ig12 trans complex. Note that Ig domains 3–5, the putative hinge, and the two Fn III domains are lumped together in this schematic and that they also contribute to the effective spring constant.
Constant velocity pulling explored the response of the Ig12/Ig12 complex to a range of forces during a single pull, with the aim of characterizing the unbinding trajectory. Whereas the high forces attained can unbind the protein complex, the high velocities (and, therefore, high loading rates) employed in SMD simulations can also lead to unfolding of the complex. This can be explained on the basis of an effect of the time-varying force on the energy landscape of the complex (57). Although the pulling spring constant and pulling speed of 0.1 Å/ps were less than or similar to that of other recent SMD studies (58–60), we found that the Ig12/Ig12 complex unfolded as it unbound at this pulling rate. Even though this unfolding is an artifact of the high pulling speed, it is interesting to note that, at the same loading rate, the CD2-CD58 complex—another cell adhesion complex involving Ig domains—does not unfold. Instead, it requires an order of magnitude higher loading to unfold (47). Qualitatively, the different responses of the two complexes may be explained as follows: In the NCAM Ig12/Ig12 complex, Ig1 reorients to align perpendicular to the direction of force (Fig. 6). Thus, the G β strand unzips (sequential breakage of H-bonds) more readily. The CD2-CD58 complex investigated by Bayas et al. (47) had only a single domain in each molecule in the simulation, and hence the domains oriented more parallel to the force direction requiring larger shear forces to unfold their β strands.
Unbinding without unfolding at the lower loading rate of 0.01 Å/ps suggests that the domains unbind without unfolding both in vitro and in vivo where the loading rates are still lower. This agrees with force measurements of forced NCAM binding (29,30), in which there was no evidence of unfolding. Although the simulated loading rate is several orders of magnitude higher than the rate in experiments, the primary results extracted from the unbinding trajectory are likely valid for the following reasons: First, the breakage of interdomain intramolecule (E16-K98) bonds was observed even during equilibration. Their reformation as intermolecule bonds was also observed in the low-constant-force simulations, which involved forces similar to those in AFM. Second, Y65, one of the two primary aromatic residues inserted in hydrophobic pockets, ruptured even in the low-force simulations. Third, the hydrophobic contact involving F19 was essentially the only contact that sustained the load in the low force and in high loading rate simulations. Fourth, the final rupture event was the unbinding of L175 from a hydrophobic pocket involving F19, rather than vice versa. However, F19 and L175 have essentially the same position coordinate along the direction of pulling, and, hence, the effect of increased loading rate is expected to be minimal. Apart from the binding interactions of the complex, the V14-F96 backbone H-bond at the end of the G and A′ strands is inherently weak because of the unfavorable NH–O angle, and it broke in all low-force simulations. However, at 0.01Å/ps, the adjacent I12-F96 bond only breaks at high forces (Fig. 7 F). This I12-F96 bond rupture could be due to the high loading rates used, such that it could remain intact at lower loading rates (corresponding simulations would be computationally prohibitive).
We also compared the simulations with mutagenesis studies. Mutating either E11, E16, and K18 or R173, R177, and E179 to alanines entirely abolished the Ig12/Ig12 interaction as shown by gel filtration (33). Based on the most recent crystal structure of the Ig12 complex (32), this was attributed to the disruption of the E11-R177 and E16-K98 salt bridges, which helped orient Ig1 with respect to Ig2 of the same molecule. Also, the disruption of the K18-R177 H-bond was postulated to affect the interactions of nearby F19. Similarly, mutating F19 (27) abrogated Ig12 dimerization as shown by sedimentation equilibrium. In our simulations, the equilibrated structure and the molecular picture of unbinding helps us better understand these experimental results. First, the E16-K98 linkage does not remain an intramolecule interdomain bond, but it forms an intermolecule bond that resists substantial force. Thus, the loss of this salt bridge directly affects the intermolecular complex stability. Second, the E11-R177 salt bridge forms a stable interdomain bond that does not rupture in any of the simulations. This linkage is therefore likely to limit the range of relative orientations of Ig1 and Ig2 and hence stabilize reciprocal Ig1/Ig2 interactions. Third, Y65 interactions rupture early, even during low-force stretching. Conversely, it appears that F19 primarily stabilizes the complex. This observation accounts for the critical nature of this residue. Furthermore, in addition to providing insight into the structural basis of the mutagenesis results, simulations predict that mutating L175 would adversely affect the complex stability under force. In view of the aforementioned importance of the E16-K98 bond, the dynamic mechanism by which it is maintained is particularly interesting: As shown in Fig. 9, during the 0.01 Å/ps constant velocity pulling, the E16-K98 (A/B) bond forms at 1.2 ns and lasts until 4.85 ns. During this time, because of thermal fluctuations, either of the three hydrogens of lysine bond to either of the two oxygens of glutamate in a complementary fashion, leading to bond maintenance under varied conformational substates of either of the residues.
Figure 9.
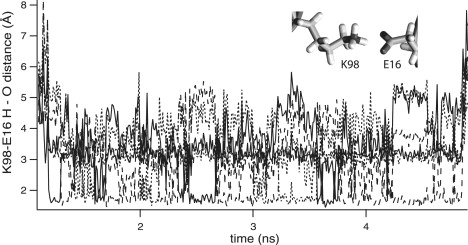
Complementary H-bond formation between E16(A) and K98(B) (inset). The distance between each of the 3 hydrogens of lysine's −NH3+ and the 2 oxygens of glutamate's −COO- show that when any one H-bond breaks, another one forms and that they do so in a mutually exclusive, but complementary, way between 1.2 and 4.85 ns.
In conclusion, these simulations demonstrated that (i), the equilibration of the solvated complex reconciles differences between the crystal structures of the complexes from the Ig12 and Ig123 fragments: namely, the end-to-end length and the role of the linker region bonds; (ii), NCAM Ig12/Ig12 reorientations under forces of tens of pN correspond to a tertiary structure elasticity of ∼0.03 N/m; and (iii), the unbinding trajectory demonstrates the importance of the salt bridges in the intermolecule linker region and the nonpolar residues L175 and F19 in resisting force. Our study also underscores the importance of dynamic interactions between interacting residues in adhesion complexes and the ability of steered molecular dynamics to elucidate their importance in adhesion.
Acknowledgments
We thank Marcos Sotomayor and the Theoretical and Computational Biophysics group for helpful discussions.
This work was supported by National Institutes of Health grants GM63536 and 2 R01 GM51338 (D.E.L), and P41-RR05969 and 1 R01 GM073655 (K.S). Computer time was provided through Large Resource Allocations Committee grant MCA93S028. V.M. was partially supported by a Drickamer Research Fellowship.
References
- 1.Leckband D. Nanomechanics of adhesion proteins. Curr. Opin. Struct. Biol. 2004;14:524–530. doi: 10.1016/j.sbi.2004.09.002. [DOI] [PubMed] [Google Scholar]
- 2.Bustamante C., Chemla Y.R., Forde N.R., Izhaky D. Mechanical processes in biochemistry. Annu. Rev. Biochem. 2004;73:705–748. doi: 10.1146/annurev.biochem.72.121801.161542. [DOI] [PubMed] [Google Scholar]
- 3.Johnson C.P., Tang H.Y., Carag C., Speicher D.W., Discher D.E. Forced unfolding of proteins within cells. Science. 2007;317:663–666. doi: 10.1126/science.1139857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vogel V. Mechanotransduction involving multimodular proteins: converting force into biochemical signals. Annu. Rev. Biophys. Biomol. Struct. 2006;35:459–488. doi: 10.1146/annurev.biophys.35.040405.102013. [DOI] [PubMed] [Google Scholar]
- 5.Rief M., Gautel M., Oesterhelt F., Fernandez J.M., Gaub H.E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276:1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 6.Erickson H.P. Reversible unfolding of fibronectin type III and immunoglobulin domains provides the structural basis for stretch and elasticity of titin and fibronectin. Proc. Natl. Acad. Sci. USA. 1994;91:10114–10118. doi: 10.1073/pnas.91.21.10114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sotomayor M., Schulten K. Single-molecule experiments in vitro and in silico. Science. 2007;316:1144–1148. doi: 10.1126/science.1137591. [DOI] [PubMed] [Google Scholar]
- 8.Sotomayor M., Corey D.P., Schulten K. In search of the hair-cell gating spring elastic properties of ankyrin and cadherin repeats. Structure. 2005;13:669–682. doi: 10.1016/j.str.2005.03.001. [DOI] [PubMed] [Google Scholar]
- 9.Lee G., Abdi K., Jiang Y., Michaely P., Bennett V. Nanospring behaviour of ankyrin repeats. Nature. 2006;440:246–249. doi: 10.1038/nature04437. [DOI] [PubMed] [Google Scholar]
- 10.Lee E.H., Hsin J., Mayans O., Schulten K. Secondary and tertiary structure elasticity of titin Z1Z2 and a titin chain model. Biophys. J. 2007;93:1719–1735. doi: 10.1529/biophysj.107.105528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sotomayor M., Schulten K. The allosteric role of the Ca++ switch in adhesion and elasticity of C cadherin. Biophys. J. 2008;94:4621–4633. doi: 10.1529/biophysj.107.125591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Choudhuri K., Wiseman D., Brown M.H., Gould K., van der Merwe P.A. T-cell receptor triggering is critically dependent on the dimensions of its peptide-MHC ligand. Nature. 2005;436:578–582. doi: 10.1038/nature03843. [DOI] [PubMed] [Google Scholar]
- 13.Aricescu A.R., Siebold C., Choudhuri K., Chang V.T., Lu W. Structure of a tyrosine phosphatase adhesive interaction reveals a spacer-clamp mechanism. Science. 2007;317:1217–1220. doi: 10.1126/science.1144646. [DOI] [PubMed] [Google Scholar]
- 14.Aricescu A.R., Jones E.Y. Immunoglobulin superfamily cell adhesion molecules: zippers and signals. Curr. Opin. Cell Biol. 2007;19:543–550. doi: 10.1016/j.ceb.2007.09.010. [DOI] [PubMed] [Google Scholar]
- 15.Evans E.A., Calderwood D.A. Forces and bond dynamics in cell adhesion. Science. 2007;316:1148–1153. doi: 10.1126/science.1137592. [DOI] [PubMed] [Google Scholar]
- 16.Alon R., Hammer D.A., Springer T.A. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 1995;374:539–542. doi: 10.1038/374539a0. [DOI] [PubMed] [Google Scholar]
- 17.Benoit M., Gabriel D., Gerisch G., Gaub H.E. Discrete interactions in cell adhesion measured by single-molecule force spectroscopy. Nat. Cell Biol. 2000;2:313–317. doi: 10.1038/35014000. [DOI] [PubMed] [Google Scholar]
- 18.Balaban N.Q., Schwarz U.S., Riveline D., Goichberg P., Tzur G. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 19.Cunningham B.A., Hemperly J.J., Murray B.A., Prediger E.A., Brackenbury R. Neural cell adhesion molecule: structure, immunoglobulin-like domains, cell surface modulation, and alternative RNA splicing. Science. 1987;236:799–806. doi: 10.1126/science.3576199. [DOI] [PubMed] [Google Scholar]
- 20.Ditlevsen D.K., Povlsen G.K., Berezin V., Bock E. NCAM-induced intracellular signaling revisited. J. Neurosci. Res. 2007;86:727–743. doi: 10.1002/jnr.21551. [DOI] [PubMed] [Google Scholar]
- 21.Rutishauser U., Acheson A., Hall A.K., Mann D.M., Sunshine J. The neural cell adhesion molecule (NCAM) as a regulator of cell-cell interactions. Science. 1988;240:53–57. doi: 10.1126/science.3281256. [DOI] [PubMed] [Google Scholar]
- 22.Walsh F.S., Doherty P. Neural cell adhesion molecules of the immunoglobulin superfamily: role in axon growth and guidance. Annu. Rev. Cell Dev. Biol. 1997;13:425–456. doi: 10.1146/annurev.cellbio.13.1.425. [DOI] [PubMed] [Google Scholar]
- 23.Maness P.F., Schachner M. Neural recognition molecules of the immunoglobulin superfamily: signaling transducers of axon guidance and neuronal migration. Nat. Neurosci. 2007;10:19–26. doi: 10.1038/nn1827. [DOI] [PubMed] [Google Scholar]
- 24.El Maarouf A., Rutishauser U. Use of PSA-NCAM in repair of the central nervous system. Neurochem. Res. 2008 doi: 10.1007/s11064-008-9635-7. [DOI] [PubMed] [Google Scholar]
- 25.Ranheim T.S., Edelman G.M., Cunningham B.A. Homophilic adhesion mediated by the neural cell adhesion molecule involves multiple immunoglobulin domains. Proc. Natl. Acad. Sci. USA. 1996;93:4071–4075. doi: 10.1073/pnas.93.9.4071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Atkins A.R., Osborne M.J., Lashuel H.A., Edelman G.M., Wright P.E. Association between the first two immunoglobulin-like domains of the neural cell adhesion molecule N-CAM. FEBS Lett. 1999;451:162–168. doi: 10.1016/s0014-5793(99)00554-2. [DOI] [PubMed] [Google Scholar]
- 27.Atkins A.R., Chung J., Deechongkit S., Little E.B., Edelman G.M. Solution structure of the third immunoglobulin domain of the neural cell adhesion molecule N-CAM: can solution studies define the mechanism of homophilic binding? J. Mol. Biol. 2001;311:161–172. doi: 10.1006/jmbi.2001.4861. [DOI] [PubMed] [Google Scholar]
- 28.Kiselyov V.V., Berezin V., Maar T.E., Soroka V., Edvardsen K. The first immunoglobulin-like neural cell adhesion molecule (NCAM) domain is involved in double-reciprocal interaction with the second immunoglobulin-like NCAM domain and in heparin binding. J. Biol. Chem. 1997;271:10125–10134. doi: 10.1074/jbc.272.15.10125. [DOI] [PubMed] [Google Scholar]
- 29.Johnson C.P., Fujimoto I., Perrin-Tricaud C., Rutishauser U., Leckband D. Mechanism of homophilic adhesion by the neural cell adhesion molecule: use of multiple domains and flexibility. Proc. Natl. Acad. Sci. USA. 2004;101:6963–6968. doi: 10.1073/pnas.0307567100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wieland J.A., Gewirth A.A., Leckband D.E. Single molecule adhesion measurements reveal two homophilic neural cell adhesion molecule bonds with mechanically distinct properties. J. Biol. Chem. 2005;280:41037–41046. doi: 10.1074/jbc.M503975200. [DOI] [PubMed] [Google Scholar]
- 31.Atkins A.R., Gallin W.J., Owens G.C., Edelman G.M., Cunningham B.A. N-CAM homophilic binding mediated by the two N-terminal Ig domains is influenced by intramolecular domain: domain interactions. J. Biol. Chem. 2004;279:49633–49643. doi: 10.1074/jbc.M409159200. [DOI] [PubMed] [Google Scholar]
- 32.Soroka V., Kolkova K., Kastrup J.S., Diederichs K., Breed J. Structure and interactions of NCAM Ig1-2-3 suggest a novel zipper mechanism for homophilic adhesion. Structure. 2003;11:1291–1301. doi: 10.1016/j.str.2003.09.006. [DOI] [PubMed] [Google Scholar]
- 33.Jensen P.H., Soroka V., Thomsen N.K., Ralets I., Berezin V. Structure and interactions of NCAM modules 1 and 2, basic elements in neural cell adhesion. Nat. Struct. Biol. 1999;6:486–493. doi: 10.1038/8292. [DOI] [PubMed] [Google Scholar]
- 34.Johnson C.P., Fujimoto I., Rutishauser U., Leckband D.E. Direct evidence that neural cell adhesion molecule (NCAM) polysialylation increases intermembrane repulsion and abrogates adhesion. J. Biol. Chem. 2005;280:137–145. doi: 10.1074/jbc.M410216200. [DOI] [PubMed] [Google Scholar]
- 35.Kiss J.Z., Muller D. Contribution of the neural cell adhesion molecule to neuronal and synaptic plasticity. Rev. Neurosci. 2001;12:297–310. doi: 10.1515/revneuro.2001.12.4.297. [DOI] [PubMed] [Google Scholar]
- 36.van den Pol A.N., di Porzio U., Rutishauser U. Growth cone localization of neural cell adhesion molecule on central nervous system neurons in vitro. J. Cell Biol. 1986;102:2281–2294. doi: 10.1083/jcb.102.6.2281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cremer H., Chazal G., Goridis C., Represa A. NCAM is essential for axonal growth and fasciculation in the hippocampus. Mol. Cell. Neurosci. 1997;8:323–335. doi: 10.1006/mcne.1996.0588. [DOI] [PubMed] [Google Scholar]
- 38.Baker M.W., Macagno E.R. In vivo imaging of growth cone and filopodial dynamics: evidence for contact-mediated retraction of filopodia leading to the tiling of sibling processes. J. Comp. Neurol. 2007;500:850–862. doi: 10.1002/cne.21228. [DOI] [PubMed] [Google Scholar]
- 39.Karplus M., McCammon J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 40.Lu H., Isralewitz B., Krammer A., Vogel V., Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 1998;75:662–671. doi: 10.1016/S0006-3495(98)77556-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Craig D., Gao M., Schulten K., Vogel V. Tuning the mechanical stability of fibronectin type III modules through sequence variations. Structure. 2004;12:21–30. doi: 10.1016/j.str.2003.11.024. [DOI] [PubMed] [Google Scholar]
- 42.Ortiz V., Nielsen S.O., Klein M.L., Discher D.E. Unfolding a linker between helical repeats. J. Mol. Biol. 2005;349:638–647. doi: 10.1016/j.jmb.2005.03.086. [DOI] [PubMed] [Google Scholar]
- 43.Marszalek P.E., Lu H., Li H., Carrion-Vazquez M., Oberhauser A.F. Mechanical unfolding intermediates in titin modules. Nature. 1999;402:100–103. doi: 10.1038/47083. [DOI] [PubMed] [Google Scholar]
- 44.Oberhauser A.F., Badilla-Fernandez C., Carrion-Vazquez M., Fernandez J.M. The mechanical hierarchies of fibronectin observed with single-molecule AFM. J. Mol. Biol. 2002;319:433–447. doi: 10.1016/S0022-2836(02)00306-6. [DOI] [PubMed] [Google Scholar]
- 45.Johnson C.P., Gaetani M., Ortiz V., Bhasin N., Harper S. Pathogenic proline mutation in the linker between spectrin repeats: disease caused by spectrin unfolding. Blood. 2007;109:3538–3543. doi: 10.1182/blood-2006-07-038588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bayas M.V., Kearney A., Avramovic A., van der Merwe P.A., Leckband D.E. Impact of salt bridges on the equilibrium binding and adhesion of human CD2 and CD58. J. Biol. Chem. 2007;282:5589–5596. doi: 10.1074/jbc.M607968200. [DOI] [PubMed] [Google Scholar]
- 47.Bayas M.V., Schulten K., Leckband D. Forced detachment of the CD2-CD58 complex. Biophys. J. 2003;84:2223–2233. doi: 10.1016/S0006-3495(03)75028-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.MacKerell A.D., Bashford D., Bellott M., Dunbrack R.L., Evanseck J.D. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 50.Buck M., Bouguet-Bonnet S., Pastor R.W., MacKerell A.D. Importance of the CMAP correction to the CHARMM22 protein force field: dynamics of hen lysozyme. Biophys. J. 2006;90:L36–L38. doi: 10.1529/biophysj.105.078154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 52.Gao M., Sotomayor M., Villa E., Lee E.H., Schulten K. Molecular mechanisms of cellular mechanics. Phys. Chem. Chem. Phys. 2006;8:3692–3706. doi: 10.1039/b606019f. [DOI] [PubMed] [Google Scholar]
- 53.Altmann S.M., Grunberg R.G., Lenne P.F., Ylanne J., Raae A. Pathways and intermediates in forced unfolding of spectrin repeats. Structure. 2002;10:1085–1096. doi: 10.1016/s0969-2126(02)00808-0. [DOI] [PubMed] [Google Scholar]
- 54.Lee E.H., Gao M., Pinotsis N., Wilmanns M., Schulten K. Mechanical strength of the titin Z1Z2-telethonin complex. Structure. 2006;14:497–509. doi: 10.1016/j.str.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 55.Schwaiger I., Sattler C., Hostetter D.R., Rief M. The myosin coiled-coil is a truly elastic protein structure. Nat. Mater. 2002;1:232–235. doi: 10.1038/nmat776. [DOI] [PubMed] [Google Scholar]
- 56.Paramore S., Ayton G.S., Mirijanian D.T., Voth G.A. Extending a spectrin repeat unit. I: linear force-extension response. Biophys. J. 2006;90:92–100. doi: 10.1529/biophysj.105.066969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Evans E. Probing the relation between force — lifetime — and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 58.Itsuo H., Tomoaki H., Satoyuki K. The antigen-antibody unbinding process through steered molecular dynamics of a complex of an Fv fragment and lysozyme. J. Phys. Condens. Matter. 2008;20 255238-1–255238-10. [Google Scholar]
- 59.Thompson A.J., Chau P.L., Chan S.L., Lummis S.C. Unbinding pathways of an agonist and an antagonist from the 5-HT3 receptor. Biophys. J. 2006;90:1979–1991. doi: 10.1529/biophysj.105.069385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kim T., Rhee A., Yip C.M. Force-induced insulin dimer dissociation: a molecular dynamics study. J. Am. Chem. Soc. 2006;128:5330–5331. doi: 10.1021/ja0607382. [DOI] [PubMed] [Google Scholar]


