Obstacles on the Microtubule Reduce the Processivity of Kinesin-1 in a Minimal In Vitro System and in Cell Extract

Abstract

Inside cells, a multitude of molecular motors and other microtubule-associated proteins are expected to compete for binding to a limited number of binding sites available on microtubules. Little is known about how competition for binding sites affects the processivity of molecular motors and, therefore, cargo transport, organelle positioning, and microtubule organization, processes that all depend on the activity of more or less processive motors. Very few studies have been performed in the past to address this question directly. Most studies reported only minor effects of crowding on the velocity of motors. However, a controversy appears to exist regarding the effect of crowding on motor processivity. Here, we use single-molecule imaging of mGFP-labeled minimal dimeric kinesin-1 constructs in vitro to study the effects of competition on kinesin's processivity. For competitors, we use kinesin rigor mutants as static roadblocks, minimal wild-type kinesins as motile obstacles, and a cell extract as a complex mixture of microtubule-associated proteins. We find that mGFP-labeled kinesin-1 detaches prematurely from microtubules when it encounters obstacles, leading to a strong reduction of its processivity, a behavior that is largely independent of the type of obstacle used here. Kinesin has a low probability to wait briefly when encountering roadblocks. Our data suggest, furthermore, that kinesin can occasionally pass obstacles on the protofilament track.

Introduction

The microtubule cytoskeleton serves as a system of tracks for transport of a broad variety of cargos to specific subcellular positions (1,2). A microtubule typically provides 13 protofilament tracks (3), each composed of a large, but limited, number of identical binding sites, that run roughly parallel to the long axis of the microtubule. Inside living cells, these tracks are shared by a multitude of nonmotile microtubule-associated proteins (MAPs) and molecular motors transporting different cargos (4–6). Therefore, the question arises how competition for binding sites might influence motor motility in the crowded environment of the cell. Little is known about the potential effects of crowding on transport efficiency, because to date only a small number of studies have addressed this question experimentally.

Kinesin-1, the founding member of the kinesin protein family (7), is one of the most important players in microtubule-based transport of vesicles, organelles, and nucleic acid/protein complexes (6,8–11). Native kinesin is a heterotetramer with two heavy chains and two regulatory light chains (12). Minimal kinesins generated from the truncated heavy chain containing the motor domain and a subsequent dimerization domain are often used for biophysical studies of kinesin motor transport (13,14). Both native kinesin bound to cargo via its C-terminus and truncated, minimal dimeric kinesins are highly processive enzymes that can take >100 consecutive steps along a microtubule without detaching (14–17). The two motor domains of a kinesin dimer operate in a hand-over-hand mechanism (18), and the step size is 8 nm (19), corresponding to the distance between adjacent binding sites on the microtubule (3).

Early studies addressing how crowding or competition on the microtubule affects kinesin motility investigated the effect of the neuronal MAP tau on motor-mediated vesicle movement in vivo (20), and later studies focused on the movement of purified green-fluorescent-protein (GFP)-tagged kinesin fragments in vitro (21). In both situations, the binding frequency of the vesicles or of the motors was found to be reduced, whereas the velocity of movement remained essentially unaltered. However, different results were obtained for the processivity, which was reported to decrease in vivo (20), but not (21) or only mildly (22) in vitro. The observation that a MAP like tau does not occupy the same binding site as kinesin on the microtubule (23) provided an explanation for the small effect tau has on the processivity of kinesin in vitro, but left the effect on the binding frequency of kinesin unanswered. Recently, it was shown in vitro that the travel distance of cargos transported by multiple kinesins can be reduced by the presence of tau on the microtubule (22). This was explained by the tau-dependent reduction in the probability that kinesin will rebind to the microtubule after dissociation, providing an explanation for the apparently different effects of tau on the processivity of vesicles in vivo and of individual kinesins in vitro. Differential regulation of vesicle traffic could therefore be achieved by modulation of motor-microtubule interactions by different MAPs or MAP isoforms (22,24,25).

More recently, single GFP-labeled kinesins were found to detach from microtubules in vitro when they encountered patches consisting of several tau proteins on the microtubule, causing a substantial decrease in processivity (25). This might indicate that larger obstacles that directly block the binding sites of kinesin cause it to detach from the microtubule. Direct blocking of the kinesin binding site was achieved in a defined manner in earlier stopped-flow in vitro experiments (26) where either purified motile wild-type kinesin or a nonmotile kinesin rigor mutant were used as crowding agents. In both cases, strongly accelerated unbinding of kinesin from the microtubule was observed, corresponding to a drastic reduction of the run length of kinesin (assuming that the stepping rate was largely unaffected). Seemingly contradictory results regarding kinesin's processivity were found later by imaging quantum-dot-labeled kinesins on crowded microtubules in vitro (27) and single kinesin molecules fused to GFP (28) or quantum dot (55) in cultured mammalian cells.

Models of molecular motor crowding based on an asymmetric simple exclusion process have predicted a decrease of the mean velocity with increasing crowding and local accumulation of motors, generating a phase separation between high- and low-motor-density areas (29–31). Such a model combined with chemomechanically driven stepping kinetics of motors can predict, in principle, either a decrease of run length with crowding or independence of run length on crowding, provided that certain kinetic transitions are predominant (32). Given the importance of understanding the competition between different microtubule binding proteins for our understanding of the collective behavior of motors and microtubules in the cell on the basis of quantitative models (29–32), we decided to reexamine crowding effects on the motility of kinesin-1 in the presence of three very different crowding agents in vitro. In particular, we wanted to clarify how obstacles occupying the binding site of kinesin affect its processivity, and we wanted to test directly whether, in a complex environment like a cell extract, kinesin competes with other MAPs or motors while performing its runs. We used single-molecule imaging of fluorescently labeled kinesins moving along immobilized microtubules. To mimic the crowded situation inside living cells, we added cell extract to the immobilized microtubules and compared the runs of fluorescently labeled kinesins with those of kinesins in the presence of defined concentrations of purified motile or nonmotile obstacles with known properties. Several improvements of our single-molecule imaging setup in combination with extensive automated data analysis of large populations of single molecules allowed us to overcome weaknesses of some of the earlier reports.

Materials and Methods

All chemicals are from Sigma (Taufkirchen, Germany) unless otherwise stated.

Protein biochemistry

The DNA sequence coding for the first 401 amino acids of conventional kinesin from Drosophila melanogaster (13) was amplified by polymerase chain reaction and cloned into a pETM-Z expression vector, generating His₆-z-Kin₄₀₁. For fluorescence imaging, we ligated the sequence of monomeric GFP (mGFP) (33,34) to the C-terminal end of the kinesin sequence, generating His₆-z-Kin₄₀₁mGFP (see also Bieling et al. (35)). Furthermore, we introduced a T99N substitution in the kinesin motor domain to obtain a nonmotile rigor mutant, which constitutively associates to the microtubule in a strongly bound state. This construct also contained sequence coding for a C-terminal monomeric Cherry (36) tag (His−₆z-Kin₄₀₁[T99N]mCherry) or a monomeric GFP tag (His₆-z-Kin₄₀₁[T99N]mGFP).

The recombinant fusion proteins were expressed in Escherichia coli (BL21(DE3) CodonPlus-RIL induced with 0.2 mM IPTG for 16 h at 18°C). Harvested cells were resuspended in ice-cold buffer A (50 mM NaPi with pH 7.2, 350 mM KCl, 1 mM MgCl₂, 0.2 mM MgATP (adenosine-5′-triphosphate supplemented with equimolar MgCl₂), and 1 mM β-mercaptoethanol) containing protease inhibitors (Roche, Basel, Switzerland) and were lysed using an Emulsiflex C-5 (Microfluidics, Lampertheim, Germany). Clarified lysates were loaded onto a Talon column (Clontech, Mountain View, CA), the column was washed with buffer A containing 7 mM imidazole, and proteins were eluted in buffer A containing 400 mM imidazole. The His₆-z-tag was cleaved off overnight by His-tagged TEV protease at 4°C (1 mg protease/50 mg substrate), generating the proteins Kin₄₀₁, Kin₄₀₁mGFP, and Kin₄₀₁[T99N]mCherry. The cleaved proteins were dialyzed into buffer A, then passed through a Talon column to remove the His₆-z-tag and the TEV protease. Kin₄₀₁[T99N]mCherry was further purified by gel filtration (Superdex 200, GE Healthcare, Piscataway, NJ) in buffer A. Kin₄₀₁ and Kin₄₀₁mGFP were further purified by cosedimentation with microtubules in the presence of 2 mM AMP-PNP followed by subsequent release in 5 mM ATP (37). Concentrations were determined by Bradford assay using bovine serum albumin as the standard and are expressed in monomer concentration. Proteins were frozen in liquid nitrogen after adding 20% (V/V) glycerol.

Purification of tubulin was performed as previously described (38). Labeling of tubulin with Alexa Fluor 647 carboxylic acid succinimidyl ester (Invitrogen, Karlsruhe, Germany) and with 6((biotinoyl)amino)hexanoic acid succinimidyl ester (Invitrogen) was performed as described previously (39). Tubulin (containing 5% Alexa-Fluor-647-labeled tubulin and 5% biotinilated tubulin) was allowed to polymerize in mictotubule (MT) buffer (80 mM K-PIPES, pH 6.8, 1 mM MgCl₂, and 1 mM EGTA) for 20 min. Polymerized microtubules were then stabilized with 20 μM taxol for 20 min, centrifuged, and resuspended.

Surface chemistry

Functionalized glass coverslips with biotin-polyethylene glycol (PEG), as well as PLL-PEG passivated glass slides, were prepared as described (40).

Preparation of cell extract

Insect cell extract was prepared from cultured Sf9 cells. Cells in medium were centrifuged at 1000 rpm for 5 min, the cell pellet was resuspended in 0.5-pellet volumes of buffer (12 mM K-PIPES at pH 6.8, 1 mM MgCl₂, and 1 mM EGTA), and 10 μg/ml cytochalasin D was added before lysing cells with a douncer. Centrifugation of the lysate at 80,000 rpm for 10 min at 4°C separated insoluble cell debris from the soluble, cytosolic cell extract. An additional 10 μg/ml cytochalasin D was added to the cell extract after centrifugation to prevent actin polymerization. The extract was then kept on ice for not more than 1 h until the start of the experiment.

Single-molecule assay

Flow chambers consisting of a biotin-PEG functionalized coverslip and a PLL-PEG passivated glass separated by double-sided tape (Tesa, Hamburg, Germany) were prepared at room temperature (chamber size 5 × 5 × 0.1 mm). The chamber was then equilibrated with MT buffer (80 mM K-PIPES at pH 6.8, 1 mM MgCl₂, and 1 mM EGTA) and potential residual unspecific binding sites were blocked by flowing in 1% Pluronic F-127 and 50 μg/ml κ-casein in MT buffer on ice. The chamber was then incubated with 50 μg/ml NeutrAvidin (Invitrogen) and 50 μg/ml κ-casein in MT buffer on ice for 5 min, washed with a minimum of 10 chamber volumes of MT buffer, and incubated with labeled and stabilized microtubules in MT buffer containing 5 μM taxol for 5 min at 25°C. Microtubules not being immobilized were removed by washing the flow chamber. For imaging kinesins in cell extract, oxygen scavengers (20 μg/ml catalase (∼13,200 U/mg), 160 μg/ml glucose oxidase (∼270 U/mg; SERVA, Heidelberg, Germany), and 20 mM glucose) were added to the extract 20 min before the experiment, and 2 mM MgATP and 2 nM Kin₄₀₁mGFP were added immediately before introducing the extract into the flow cell. For imaging kinesins in buffer, Kin₄₀₁mGFP and Kin₄₀₁ were diluted in assay buffer (12 mM K-PIPES at pH 6.8, 1 mM MgCl₂, and 1 mM EGTA, 10 mM b-mercaptoethanol, 5 μM taxol, 2 mM MgATP, and oxygen scavengers) and added to the flow chamber. The concentration of Kin₄₀₁mGFP in reference experiments with “noncrowded” (or undecorated) microtubules was 5–10 pM. In crowding experiments, the ratio of labeled to unlabeled kinesin was kept at ∼:250, respectively, in order to collect similar numbers of events at the different concentrations of crowding motor. For the crowding experiment with the mutant kinesin, the flow cell was incubated with 2 nM Kin₄₀₁[T99N]mCherry for 5 min in assay buffer and the unbound rigor mutant was then washed out of the flow chamber. Then, the final sample with Kin₄₀₁mGFP in assay buffer was introduced into the flow cell.

Total internal reflection fluorescence microscopy

Fluorescently labeled microtubules and kinesins were visualized at 25°C on an inverted microscope (IX71, Olympus, Hamburg, Germany) with a total internal reflection fluorescence (TIRF) condenser (IX2-REVA TIRF, Olympus), TIRF objective (PlanApo 100X 1.45 TIRFM, Olympus) and a cooled charge-coupled device camera (Cascade II, Photometrics, Tucson, AZ). Fluorescence excitation was accomplished by coupling three diode-pumped solid-state laser lines into the condenser via a fiberoptic light guide: 639 nm (iBeam-640, TOPTICA, Graefeling, Germany) for imaging Alexa Fluor 647 microtubules, 532 nm (Compass 215M, Coherent, Dieburg, Germany) for mCherry-tagged kinesin, and 488 nm (85-BCD-020, Melles Griot, Bensheim, Germany) for mGFP-tagged kinesin. The laser lines were controlled with shutters (UniBlitz, Bfi Optilas, Puchheim, Germany), and laser power was adjusted using an acousto-optical filter (AA Opto-Electronics, Orsay, France). Metamorph (Molecular Devices, Downingtown, PA) was used to control the shutters, acousto-optical filter, dichroic mirrors, and camera. Laser intensity was set to minimize bleaching and optimize temporal resolution and the signal/noise ratio. One still image of the microtubules was acquired, followed by continuously streamed image acquisition of the green channel with an exposure time of 100 ms (10-Hz frame rate). In the experiment with the rigor mutant of kinesin, a still image of the mCherry signal was acquired before continuous streaming of the mGFP signal.

Data analysis

The movement of single kinesin molecules on microtubules was analyzed by automated particle tracking implemented in a commercial software environment (Kalaimoscope, TransInsight, Dresden, Germany). The signal/noise-ratio-dependent accuracy of localization of the mGFP signal was ∼40 nm as determined by the mean-squared displacement (MSD) versus time relationship (41) of statically bound Kin₄₀₁mGFP in the presence of AMP-PNP. From the positions and times at the very beginning (landing of kinesin on the microtubule) and the very end of a track (dissociation from the microtubule), dwell time (total duration), run length (travel distance), and mean velocity were determined for those kinesins that traveled on the microtubule for at least three frames (300 ms, our temporal cutoff for track identification). From the distributions of the determined parameters, we calculated the mean parameters for each condition studied. Histograms of dwell times and run lengths were fitted with a single exponential function (Appendix A) by least-squares minimization. Histograms of velocities were Gaussian and the mean was calculated on the basis of maximum likelihood estimation. In addition, the mean velocity was also estimated by fitting a parabola to the MSD curve. To determine the rate of landing events of Kin₄₀₁mGFP, the number of runs on a microtubule was normalized by the concentration of labeled motor used in each experiment relative to that in the control experiment (no crowding agent) and divided by microtubule length and observation time. The number of observed landing events was corrected for the temporal cutoff, as described in Appendix A. Interruptions of continuous forward movement, i.e., “pause” events followed by continuation of the run, and “stop” events followed by detachment from the microtubule leading to the end of a run, were detected as described in Appendix B. Detected pauses and stops have a minimal duration of 300 ms (according to the definition of our temporal cutoff). Event probabilities (dissociation, pause, and stop) per 8-nm step were calculated according to Appendix C. Mean pause and stop times were determined from single-exponential fits to the histograms of pause and stop times. We note that mean pause, stop, or dwell times <300 ms can be obtained from exponential distributions despite our temporal cutoff of detection assuming that the distributions are monomodal (single-point process) and provided that a large number of data is collected (see Appendix A, and Materials and Methods in the Supporting Material). If not stated otherwise, the 95% confidence interval was chosen as the uncertainty parameter. Numerical calculations and fitting were performed with MATLAB (The MathWorks, Natick, MA).

Results

We studied the processive movement of single kinesin-1 dimers from Drosophila melanogaster in the presence and absence of obstacles by TIRF microscopy. In contrast to previous studies (21,25,27), we introduced several modifications in the experimental setup to increase the control of the system and the accuracy of the results. First, we chose to use minimal dimeric kinesin constructs, containing only the sequence strictly necessary for processive movement. Our constructs lacked most of the C-terminal part of kinesin, but contained the neck region of kinesin that is required and sufficient for homodimerization (13) (Fig. 1 A). Second, we chose to label our kinesin motors using monomeric fluorescent proteins (see Methods). By using minimal kinesin constructs and choosing monomeric fluorescent tags, we intended to avoid potential problems of nonspecific interactions or oligomerization. Third, we chemically functionalized the glass surfaces in our experimental setup with a dense layer of biotin-PEG, to which stabilized, biotinylated microtubules could be selectively attached via neutravidin links (Fig. 1 B). The PEG polymer brush on the surface reduces unspecific binding of proteins from solution and thereby ensures that protein concentrations in the experiments are not affected by potential depletion effects. Consequently, final protein concentrations were ∼10-fold smaller and more defined compared to experiments on plain glass using β-casein as the blocking agent (see Materials and Methods in the Supporting Material). We demonstrated in control experiments that the PEG polymer brush does not affect the behavior of kinesin on immobilized microtubules (Fig. S1 A) (35). Surface passivation by the PEG layer also allowed us to perform experiments in protein-rich environments such as cell extracts under controlled conditions (Fig. 1 C). Finally, we used automated detection of the processive runs of single fluorescent kinesins. Our spatial accuracy for the detection of the position of fluorescent kinesins was 40 nm and the lower temporal threshold for the detection of a processive run was set to 300 ms (see Materials and Methods). Extensive statistical analysis of the characteristics of the identified runs was based on at least 500 automatically identified runs per condition.

Figure 1.

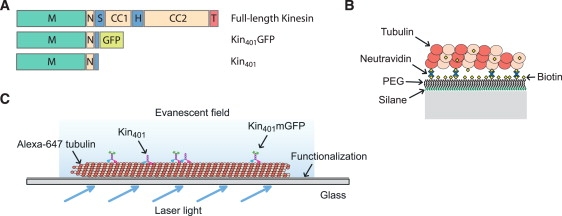
Kinesin constructs and experimental assay. (A) Comparison of the domains of the truncated and mGFP-labeled kinesin-1 construct, with the native full-length kinesin. M, motor domain; N, neck linker; S, swivel; CC, coiled coil; H, hinge; T, tail. (B) Detailed scheme of the surface components involved for immobilization of stabilized microtubules. PEG, polyethyleneglycol. (C) Overview of the assay, allowing single-molecule imaging in buffer and cell extract. An evanescent field emerging from totally reflected laser light at the functionalized side of the glass slide excites the fluorophores in close proximity to the surface.

Kinesin motility during molecular crowding in cell extract

In a reference experiment, we first established the basic motile characteristics of individual mGFP-labeled kinesin molecules (Kin₄₀₁mGFP) on “empty” microtubules in buffer, i.e., in the absence of competing proteins on the microtubule. In agreement with previous results obtained with other kinesin constructs labeled with enhanced GFP (14,15,42), the run-length distribution of Kin₄₀₁mGFP was monoexponential, with a mean run length of ∼1.2 μm (Fig. 2 A, gray). In a similar way, the distribution of its dwell time, the time spent on the microtubule between binding and dissociation, was also monoexponential, with an average dwell time of ∼1.8 s (Fig. 2 B, gray). The mean velocity distribution was Gaussian, with a mean of 0.66 μm/s and a standard deviation of 0.11 μm/s (Fig. 2 C, gray). The same average velocity was obtained by fitting the MSD versus time plot (41) with a parabola, MSD = v²t² (Fig. S2 A). The intensity of the tracked mGFP signals (Fig. S2 B) correlated neither with run length (Pearson product-moment correlation coefficient r = 0.23 (Fig. S2 C)) nor with dwell time (r = 0.22 (Fig. S2 D)), and exclusion of events with higher intensity did not significantly alter any of the motile characteristics, indicating that the large majority of observed events corresponds to individual kinesin dimers.

Figure 2.

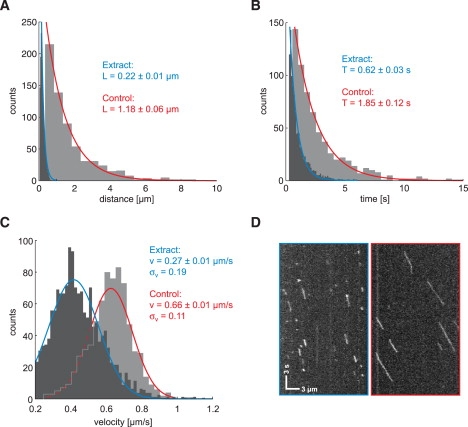
Motility of kinesin-1 in cell extract. The motile characteristics of Kin₄₀₁mGFP in insect cell extract (black) are compared with those in the assay buffer used as control (gray). The histograms were fitted with associated distribution functions, and fitting parameters and 95% confidence intervals are presented for extract (blue) and buffer (red). (A) The run lengths (i.e., travel distances) are exponentially distributed for both conditions, but the mean length is >80% smaller in extract compared to control. (B) In a similar way, the dwell (i.e., association) times of kinesin with the microtubule are exponentially distributed and generally reduced in extract. (C) The mean velocities show a Gaussian distribution. The center of the distribution is downshifted in extract, and the width (σ_v) is slightly increased, suggesting greater variability compared to the control. (D) Exemplary space-time plot (kymograph) of the mGFP signal along a microtubule in the extract (left) and in buffer (right), confirming the results seen in A–C of short and generally slower runs in extract. Scale bars apply for both images.

We then prepared lysate from cultured insect cells and incubated it with the same mGFP-labeled Drosophila kinesin construct (see Materials and Methods). Because most of the C-terminal part of kinesin was lacking in our truncated construct, it cannot interact with cargo or biochemical regulators present in the extract that are known to require kinesin's C-terminus for interaction (see, e.g., Verhey and co-workers (43,44)). Therefore, the motile properties of our construct can be influenced only by nonmotile MAPs and/or motors from the extract that we expected to bind to the microtubule and to act as roadblocks for our minimal kinesin probe. A comparison of the space-time plots (kymograph, Fig. 2 D) from raw data illustrates the marked reduction in both processivity and speed of Kin₄₀₁mGFP in cell extract as compared to the behavior of the same kinesin in buffer. Quantitative analysis of automatically detected processive runs revealed in detail how the motile properties of kinesin were altered by the presence of proteins in the cell extract: The run length was strongly reduced (Fig. 2 A, black) by 80% to an average run length of only ∼0.2 μm and the average dwell time was also strongly reduced by 75% to only ∼0.6 s compared to the control values in buffer. The average velocity was less affected and was reduced by 60%. The standard deviation of the Gaussian distribution of the velocity was almost twice that of the control value, indicating that the stepping process of kinesin in the extract was disturbed and, thus, not as uniform as in buffer. These results demonstrate that the behavior of our minimal kinesin probe is drastically altered in cell extract. The strong reduction of kinesin's processivity appears to be a consequence of encounters of kinesin on the microtubule with other MAPs or motors present in the extract, causing it to dissociate prematurely. To test this in a simpler and molecularly more defined situation, we decided to investigate whether crowding of the microtubule with purified kinesin molecules in buffer also generates premature detachment as a consequence of frequent encounters between kinesins.

Crowding with wild-type kinesin in buffer

Kinesins step stochastically (19), and as a consequence of the Poisson stepping process, they do not move smoothly with uniform velocity, but show variations in velocity. This raises the question of whether high densities of kinesins on a microtubule lead to frequent encounters, thereby interfering with each other's stepping. We therefore mixed large concentrations of unlabeled Kin₄₀₁ with low concentrations of Kin₄₀₁mGFP and measured how the single-molecule behavior of the labeled kinesins was affected by the presence of excess unlabeled motors. A representative kymograph with runs of Kin₄₀₁mGFP (added at 120 pM) in the presence of 30 nM Kin₄₀₁ is shown in Fig. 3 A (right inset) in comparison with a kymograph showing kinesin's motility on “noncrowded” microtubules in the absence of competing motors (left inset). Strikingly, the lengths of the individual runs were found to be drastically shortened. Furthermore, the runs contained occasional intermediate pauses or, in some cases, even extended stop periods before kinesin dissociated from the microtubule.

Figure 3.

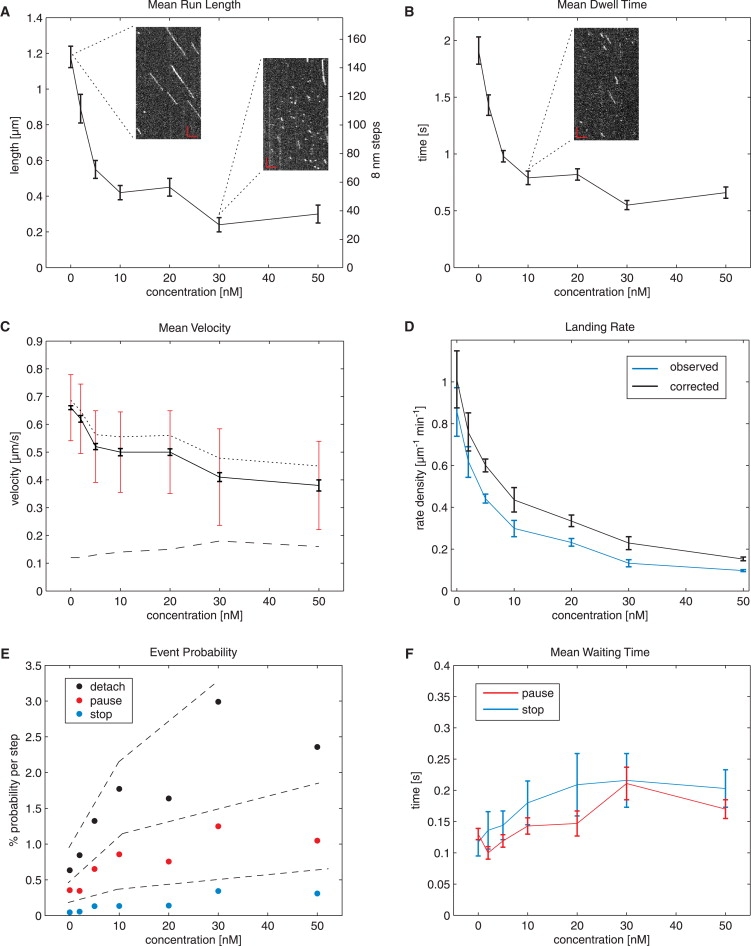
Changes in motility with increasing kinesin crowding on microtubules in buffer. Dependence of mean run length (A) and mean dwell time (B) of Kin₄₀₁mGFP on the total concentration of kinesin, as determined from distributions as presented in Fig. 2. All runs, with and without pauses and stops, were included in the analysis. Exemplary kymographs (insets) show typical runs in the presence of 0, 10, and 30 nM Kin₄₀₁. The largest effect is seen in the range 0–10 nM, whereas the curve flattens for higher concentrations. Scale bars, 3 μm (horizontal) and 3 s (vertical). (C) Shift and broadening of the velocity distribution with increase in crowding. Black error bars denote the 95% confidence interval of the peak value of the (Gaussian) distribution as shown in Fig. 2C, and red error bars denote the standard deviation (see also dashed line) of the distribution. The dotted curve represents the mean velocity analyzed from tracks without detectable pauses and stops. (D) Landing rate normalized to microtubule length as a function of kinesin concentration, as observed in the experiment (blue) and corrected (black) according to Appendix A. (E) Relationship between the concentration of kinesin and the probability per 8-nm step of the three events, “detach” (black), “pause” (red), and “stop” (blue), determined from the run length and frequency of detected pauses and stops. Detachment has the highest probability for all concentrations measured. Dashed lines emphasize the three regimes for these probabilities. (F) Mean pause (red) and stop (blue) durations both tend to increase (by a factor of ∼2) for the concentrations measured here. Note that no significant difference was seen between the two parameters. If not otherwise stated, error bars represent the 95% confidence interval.

To determine how exactly varying degrees of crowding on the microtubule influence the movement of labeled kinesins, we systematically varied the concentrations of the unlabeled motors up to 50 nM. We found that the most drastic decrease of the mean run length of the labeled kinesins was already occurring at very low concentrations of the unlabeled crowding motor, within a range of 0–10 nM, and was followed by only a minor decrease in the range of 10–50 nM of crowding motor (Fig. 3 A). Interestingly, only a minor decrease was observed for the mean velocity in the same concentration range of crowding motor, with the largest changes occurring again at the lower concentrations (Fig. 3 C). These results show that increasing numbers of stochastically stepping kinesins on the microtubule cause mutual interference, leading to a strong reduction of kinesin processivity, but not to a strong slowdown of movement.

The mean dwell time of Kin₄₀₁mGFP also decreased strongly within the concentration range of 0–10 nM of crowding motor and then leveled off toward higher concentrations (Fig. 3 B). Finally, as expected, a consequence of the competition for microtubule binding sites was that the rate of observed landing events of labeled kinesins on the microtubule strongly decreased with increasing concentrations of unlabeled motors. The largest changes were observed again in the lower concentration range (Fig. 3 D, blue line). Because motility events <300 ms were below the resolution limit of our automated analysis, we calculated also the rate of the total landing events (Fig. 3 D, black line), assuming that the exponential dwell time distribution can be extrapolated toward 0 ms for each condition (Appendix A). The rate of total landing events is a measure of the accessibility of binding sites on the microtubule at different kinesin concentrations and again decreased most drastically in the lower nanomolar range.

Taken together, the major effect of crowding the microtubule with motile kinesins was accelerated detachment from the microtubule. Dissociation was in most cases immediate within our time resolution. In some cases, however, brief stops were observed before detachment. In a similar way, brief pauses that did not lead to detachment but were followed by continuation of the run were also observed. The more frequent occurrence of these pausing events in the presence of obstacles was reflected not only by the minor but significant decrease of the mean velocity, but also by an increase of the standard deviation in the normal distribution of the velocity with increasing concentrations of crowding motor (Fig. 3 C, dashed line). This is additional evidence that the stepping behavior of kinesin becomes more heterogeneous on a crowded, compared to an undecorated, microtubule. Strikingly, the effects of crowding using excess motile kinesin in buffer were similar to the results from measurements in cell extract (Fig. 2 C).

To better understand the interfering interactions between kinesins on crowded microtubules, we automatically detected and quantified the occurrence of pauses during runs and stops at the end of runs by analyzing the frame-to-frame vector displacement of the signal spot relative to the main axis of movement along microtubules (Appendix B). Our algorithm detected pauses and stops of 300-ms duration or longer. We counted pausing events, stopping events, and also immediate detachment events relative to the observed run length, allowing us to calculate the respective event probabilities per 8-nm step (Appendix C). For pauses and stops, these are the probabilities that an 8-nm step will be followed by a pause or stop. Fig. 3 E demonstrates that these probabilities increase with the concentration of total kinesin. The probability for immediate detachment was always highest throughout the concentration range tested. However, the increase of the pause and stop probabilities with kinesin concentration indicates that encounters between kinesins on microtubule protofilaments can also cause kinesin to be in brief waiting periods. Both pause and stop time distributions were exponential (see Fig. S3, E and F). This allowed us to determine the mean duration of pause and stop times, which were found to increase slightly up to ∼200 ms within the concentration range studied (Fig. 3 F). Note that mean pause and stop times smaller than our temporal cutoff could be determined by monoexponential fitting of the distributions (Appendix A). With an average occurrence of pauses of ≤0.5 per run and a mean pause time of ≤200 ms under conditions of crowding, kinesin spends only a small fraction of its unperturbed dwell time (∼1.8 s) waiting in the presence of hindering kinesins. Instead of waiting for long periods, it rather dissociates prematurely as compared to noncrowded conditions.

The mGFP-labeled kinesin as the fluorescent probe and the unlabeled kinesins are conceptually interchangeable during an encounter, because both motors can, in principle, play the role of the obstacle, simply depending on their geometrical configuration during the encounter. Therefore, the question arises whether our kinesin probe really detaches from the microtubule when stepping onto an obstacle or if instead it is kicked off from the microtubule by another kinesin stepping onto it. In a similar way, one can ask, what is the molecular interpretation of a pause event? The transition from the pausing to the moving state of the fluorescent probe could, for example, be a consequence of an unlabeled obstacle leaving the binding site onto which the fluorescent kinesin attempts to step. To answer these questions, we decided to introduce static obstacles into the experiment that are irreversibly bound to the microtubule.

The effect of static roadblocks on kinesin's motility

To be able to test how irreversibly bound obstacles affect the motility of kinesins, we generated a minimal dimeric Drosophila kinesin-1 construct with a threonine 99-to-asparagine substitution, which corresponds to the previously described T93N rigor mutation in rat kinesin (26). This Drosophila construct was additionally fused to mCherry (36). We confirmed that this Kin₄₀₁[T99N]mCherry did not hydrolyze ATP in the presence of microtubules (Fig. S4 A), but cosedimented with microtubules in the presence of ATP (Fig. S4 B). We also established by single-molecule imaging that individual mutant kinesins (10 pM) did not dissociate from the microtubule in the presence of a moderately high concentration (2 nM) of unlabeled wild-type kinesins (Kin₄₀₁) (Fig. 4 A, left). Occasional stepwise fluorescence signal loss (Fig. 4 A, upper right) could be attributed to stepwise bleaching. The average rate of this fluorescence loss of an ensemble of microtubule-bound labeled mutant on the microtubule corresponded to our slow bleaching time of typically 30 s as determined from an ensemble of surface-immobilized mCherry-labeled mutant (Fig. 4 A, lower right). Hence, Kin₄₀₁[T99N]mCherry is a rigor mutant that strongly binds to microtubules, and wild-type kinesin is not able to kick this mutant off the microtubule.

Figure 4.

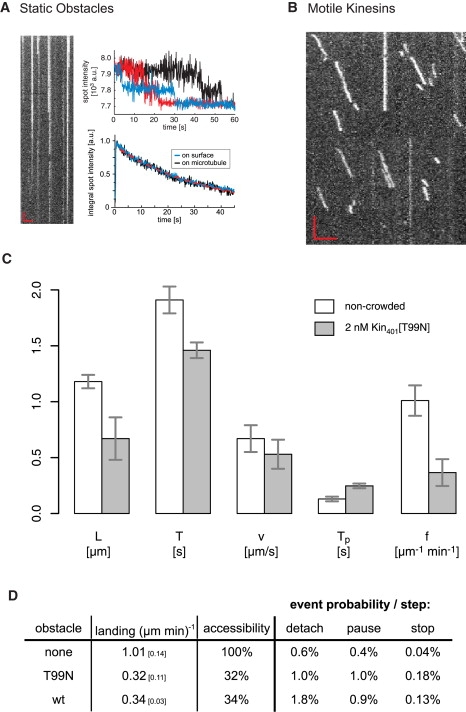
Crowding with a static obstacle. (A) Results of an experiment in which microtubules were incubated with 10 pM of labeled mutant (rigor) kinesin, which were then imaged in the presence of 2 nM unlabeled wild-type kinesin. The kymograph (left) shows that kinesins bound statically to microtubules, and signal spots typically disappear in a two-step fashion (upper right), indicating that these were indeed single dimers. Analysis of the integrated signal of a population (lower right) indicated that the disappearance of spots followed the same time constant as normal bleaching (typically ∼30 s from exponential fit, dashed red line) of kinesins nonspecifically attached to the surface, demonstrating that mutant kinesins did not dissociate because of high molecular crowding. (B) Sample kymograph of the signal from Kin₄₀₁mGFPs on a microtubule that were incubated with 2 nM mutant kinesin as roadblock. Red scale bars are as in Fig. 3A. (C) Mean values of run length (L), dwell time (T), velocity (v), pause time (T_p) and landing rate (f) of Kin₄₀₁mGFP with (gray) and without (white) prior incubation with mutant kinesin as roadblock. Changes are generally similar to those seen in the wild-type crowding experiment. Error bars represent the 95% confidence interval. (D) Comparison of the event probabilities per 8-nm step for detachment, pause, and stop at the end of a run in control conditions (no obstacles), with roadblocks (T99N) or with motile obstacles (wild-type kinesin). The conditions compared were those for which the concentration of obstacle gave similar landing (mean and 95% confidence) and thus indicated similar accessibility to the microtubule (32–34%). Both obstacles increased the pausing and stopping probability of Kin₄₀₁mGFP to the same degree, whereas the probability of detachment with motile kinesins was almost twice that with roadblocks.

We then partly decorated microtubules with this rigor mutant (see Materials and Methods) and then added motile, kinesin labeled with mGFP (Kin₄₀₁mGFP). As before, we measured the characteristics of the motility of wild-type Kin₄₀₁mGFP, but this time in the presence of irreversibly bound obstacles. A representative kymograph shows, in contrast to the situation on noncrowded microtubules, irregular runs of strongly reduced length, similar to the situation with motile obstacles (Fig. 4 B). Automated quantitative analysis of >500 runs revealed that the mean run length was reduced by 43% and the mean dwell time by 24% on decorated compared to undecorated microtubules (Fig. 4 C). The mean velocity decreased only by 19%. Therefore, the main effect of static obstacles as measured here is also a strong reduction of kinesin's processivity.

Again similar to wild-type crowding, we observed frequent stops at the ends of runs in the presence of static obstacles (Fig. 4 D). To our surprise, however, we observed also an increase in the occurrence of pauses in the presence of static obstacles. Stop and pause frequencies were in a range similar to those of crowding experiments with wild-type kinesin under conditions of comparable accessibility of the microtubule for kinesin landing (Fig. 4 D). The average pause time increased to ∼250 ms (Fig. 4 C), which is only slightly longer than in the situation of wild-type crowding. Although pausing in the case of wild-type crowding could be interpreted as labeled kinesins briefly waiting for the unlabeled obstacle to detach or move ahead before they continue their run, this interpretation is not possible in the case of irreversibly bound obstacles. Therefore, to better understand how the behavior of kinesin leads to pauses in this experiment, we decided to estimate the density of the rigor mutant on the microtubules. To this end, we measured the total fluorescence intensity per length on the microtubule and compared this value to the maximum intensity one obtains after adding Kin₄₀₁[T99N]mCherry to microtubules at saturating concentrations. We found that under conditions of our roadblock experiment ∼8% of the microtubule was decorated with the rigor mutant (Fig. S4 C). Consequently, the available stretches of unoccupied binding sites between obstacles are shorter than the runs of kinesins (Appendix E; see also Discussion). This implies that kinesin might be able to “pass” obstacles, suggesting that pauses indicate such events.

Discussion

Using single-molecule fluorescence imaging, we have measured how the runs of minimal dimeric kinesin-1 motors labeled with monomeric GFP are affected by the presence of other minimal kinesins that act as obstacles on the microtubule. Measurements with purified proteins under controlled conditions in buffer, with subsequent automated particle tracking and statistical analysis of several hundred runs per condition, demonstrated that different types of obstacles reduce strongly the processivity of the kinesin-1 motor, although they have only a mild effect on its average velocity.

Our finding of a marked reduction of kinesin's processivity on crowded microtubules agrees qualitatively with results from an earlier kinetic study (26). Stopped flow and flash photolysis in combination with dynamic light scattering was used in this study to measure the kinetics of dissociation of kinesin from microtubules saturated either with wild-type kinesin or with mixtures of wild-type and monomeric rigor kinesin. When the system relaxed back from an overcrowded situation where the microtubule was probably completely saturated with motors, very fast detachment of wild-type kinesins was observed, yielding an upper limit for the processivity of kinesin of only one or very few steps before detachment under these conditions (26). Here, we find by single-molecule imaging that at steady state also, i.e., under less drastic crowding conditions, the runs of minimal kinesin motors are considerably shorter than on noncrowded microtubules, even though the reduction of the processivity is less dramatic than in the previous study (26). The reduction of kinesin's processivity on crowded microtubules is also in good agreement with the earlier observation made in steady-state ATPase experiments that the enzymatic efficiency, k_cat/K_m, decreases with increasing motor/microtubule ratios (45). Crowding-stimulated dissociation of kinesin from the microtubule might also explain why the maximum density of wild-type kinesins on microtubules is at saturation significantly lower than that of rigor bound kinesin ((27) and this study, data not shown).

Our single-molecule imaging approach allowed us also to address the question whether premature termination of processive stepping of kinesins in the presence of obstacles was immediate or whether kinesin could be observed to wait for a certain period before detachment from the microtubule. We found that in most cases detachment was immediate within the resolution of our analysis. A minor fraction of runs, however, exhibited stops, i.e., detectable waiting periods before detachment from the microtubule. The frequency and duration of these stop periods increased with molecular crowding on the microtubule. Thus, kinesin waits with a certain probability when encountering an obstacle before being induced to detach prematurely. The mean waiting time before detachment was, however, found to be on average at most 200 ms and therefore one magnitude shorter than the mean dwell time under conditions of no crowding. This very short stop duration of kinesin before detachment in our experiment differs somewhat from the stop times measured in a recent single-molecule fluorescence imaging study of a minimal GFP-labeled rat kinesin construct (42). In that study, kinesin was observed to wait for roughly its unimpeded dwell time when it encountered streptavidin molecules irreversibly bound to biotinylated microtubules that served as obstacles for kinesin. Apparently, the details of the molecular setup of the experiment, such as the biochemical natures of the obstacle and the kinesin construct, can have an influence on exactly how kinesins interact with obstacles on the protofilament track.

Similar to the short stop periods terminating the runs of mGFP-labeled kinesin, we also observed short intermediate pauses whose frequency and duration increased similarly with the degree of crowding. The increased tendency to display short, detectable, and also even shorter unresolved, waiting periods during and at the end of runs with increased crowding on the microtubule explains the observed mild decrease of the mean velocity under crowding conditions (even for runs without detectable waiting periods, Fig. 3 C, dotted line). The mild effect of obstacles on kinesin's mean velocity is in agreement with most other single-molecule imaging studies that have addressed the effect of obstacles on the in vitro motility of GFP-labeled kinesin (21,25,42). However, our observation in this study that the processivity of mGFP-labeled kinesin is strongly reduced by obstacles differs strongly from the previous observation that the processivity of kinesins labeled with streptavidin-coated quantum dots is unaltered or even increased in the presence of motile obstacles (27).

To elucidate the origin of this difference, we tested the behavior of biotinylated kinesin linked to streptavidin-coated quantum dots that were used in the previous study (27) in the presence of the rigor mutant used as a static obstacle in this study (see Materials and Methods in the Supporting Material). We found that quantum-dot-labeled kinesins were indeed less prone to detachment and exhibited much longer pause and stop periods (Fig. S5) compared to Kin₄₀₁mGFP under the same crowding conditions (Fig. S1 B). This indicates that nonspecific interactions between microtubule-bound obstacles and the streptavidin-coated quantum dots can prevent detachment or promote immediate rebinding after detachment. Nonspecific interactions between motile obstacles on the microtubule and streptavidin-coated quantum dots could therefore also have led to accumulation of motile obstacles on quantum dots in the previous study (27). In agreement with this scenario, we observed in another experiment that streptavidin-coated quantum dots are occasionally transported in the presence of high concentrations of nonbiotinylated kinesins. This raises the possibility that due to accumulation of motors on a quantum dot transported on a microtubule crowded with motors, the obstacle-induced reduction of the processivity at the single motor level could have been (more than) compensated for by an increase of the overall processivity of the quantum dot due to interactions with multiple motors (22,32). Therefore, not only the nature of the obstacle, but also the characteristics of the fluorescent reporter used for imaging can affect the interaction between kinesin and competing molecules on the microtubule. In light of the results found in this study, quantum-dot-labeled motors appear to have a tendency to transform into multimotor objects on microtubules that are highly crowded with motors in vitro (27).

An interesting finding of this study relates to the molecular interpretation of pauses. Starting from the natural level of pauses expected for a stochastic stepper like kinesin (Appendix D), irreversibly bound rigor-type roadblocks surprisingly lead to a further increase of the pause frequency and average pause duration in addition to an increase of stops and immediate detachments. Is it possible that kinesin has the ability to change protofilament while it waits after having encountered a static obstacle? For randomly positioned obstacles, the interobstacle distance is exponentially (geometrically) distributed and is expected to be, on average, ∼0.1 μm (13 binding sites) in our experiment with the rigor mutant where we measured an average decoration of the microtubule binding sites of ∼8% (Fig. S4 C and Appendix E). This distance is considerably smaller than the measured average run length of the motile wild-type kinesins of ∼0.67 μm (84 steps) in the presence of the irreversibly bound mutant. Together with the 2.5-fold increase of the pause frequency in the presence of the rigor mutant, this suggests that kinesin is able to pass obstacles several times per run. An alternative explanation for longer-than-expected run lengths could be that obstacles are not distributed completely randomly. We regard this as unlikely, because we did not observe regions of the microtubule with distinctly increased landing rate or run length. Passing an obstacle could involve a side step to a neighboring protofilament (46,47) or detachment followed by immediate rebinding, potentially mediated by a weak interaction with the obstacle. Pauses of wild-type kinesins were also observed in previous studies where tau or streptavidin were used as obstacles (25,42). In contrast to those experiments, however, in our experiments the rigor mutant occupies exactly the binding site of kinesin, suggesting that kinesin most likely can bypass an obstacle by changing the protofilament.

Our experiments in buffer have characterized the behavior of the mGFP-labeled minimal dimeric kinesin in the presence of static and motile obstacles. Measuring the effects of crowding in a highly concentrated cell extract using the same method of analysis allows us to draw conclusions about the crowding conditions on microtubules under closer-to-physiological conditions. Because our kinesin probe is devoid of the C-terminal part of wild-type kinesin and of its light chains, autoinhibition mediated by kinesin's tail domain (48–50), and modulation by other regulatory factors targeting the C-terminal part, can be excluded (43,51–53). Moreover, any slowing of the motor molecule by viscous drag can be neglected (1,54), and increasing ionic strength plays only a minor role in the reduction of processivity (14,35). Therefore, our experiments in extract tested most likely the effect of microtubule-bound obstacles on kinesin's basic motile properties in the absence of biochemical regulation. Our finding of strongly reduced processivity of the minimal kinesin in an insect cell extract indicates that extract proteins indeed bind to the microtubules, hence acting as obstacles for our mGFP-labeled kinesin probe. These proteins could be nonmotile MAPs or other motor proteins.

Single-molecule imaging in living cells yielded apparently different results. C-terminally truncated kinesin constructs labeled either with a triple-citrine tag and expressed in mammalian cells (28) or with a streptavidin-coated quantum dot and internalized by pinocytosis (55), were reported to perform intracellular runs with a processivity very similar to that of minimal kinesins in buffer in the absence of obstacles. This result appears to indicate that either the level of crowding on the microtubules on which kinesin runs were observed in cells is extremely low or, alternatively, the truncated, labeled kinesins were able to interact with other MAPs or cargos that prolonged their runs (22,32), compensating for the decrease in processivity at the single-motor level. The observation that triple-citrine-labeled kinesin monomers were statically bound for a period of time to the microtubules in these cells (28) might indicate such cooperative interaction, because kinesin monomers are known to interact only briefly and nonprocessively with microtubules in buffer (14,35). Under our experimental conditions, we found that the basic kinetic properties of mGFP-labeled kinesin are strongly affected by the presence of cell extract (53) in a manner similar to how they are affected by obstacles in buffer. It will be important in future works to study other examples of kinesin movement in other cell extracts and cell types, visualized ideally using small fluorescent labels.

Premature detachment of processive motors under crowded conditions may be of physiological importance during transport of cargo by a team of motors. To ensure high velocity of collective transport under crowded conditions, it could be better to allow a reduction of the processivity at the single-motor level, which can be compensated for easily by an increase in the number of motors on the cargo (22,32) than to allow extended waiting periods for individual motors when they encounter obstacles. Knowledge of how, exactly, the kinetic parameters of cargo transporting motors respond to encounters with obstacles at an individual motor level is therefore essential for our quantitative understanding of the efficiency of transport at the ensemble level (32,56).

Conclusion

In this study, we provide experimental evidence that 1), minimal kinesins are more likely to detach than to wait when they encounter obstacles; 2), waiting periods (pauses and stops) last on average 200–250 ms, which is considerably less than the undisturbed dwell time of kinesin of 1.8 s; 3), the velocity of movement is comparably little affected by crowding; and 4), kinesins have a low, but finite, probability of passing obstacles, possibly by changing protofilaments.

Appendix A: Fitting exponential distributions with cutoff

Our automated track analysis detects only runs of kinesin with a minimal duration (dwell time) of three frames (300 ms). Shorter interactions of kinesin with microtubules are not detected, and the first bin in the histograms of the dwell time distribution is consequently underpopulated or even empty (Fig. 2 B). Hence, the number of all observed landing events is lower than the number of the total landing events that occurred. However, the mean dwell time and the total number can be estimated by assuming that dwell times are exponentially distributed and monomodal. The probability density function, P_e, of an exponentially distributed event X with mean T > 0 is

$$P_e\left(X=t\right)=\frac{1}{T}\text{exp}\left(-\frac{t}{T}\right),$$ (1)

and the number N of events with dwell times between t and t + Δt (e.g., a histogram bin) for a sample with a total of N_S events is

$$N\left(t;t+\Delta t\right)=N_S\underset{t}{\overset{t+\Delta t}{\int }}{P}_e\left(t\right)dt=N_S\text{exp}\left(-\frac{t}{T}\right)\times \left(1-\text{exp}\left(-\frac{\Delta t}{T}\right)\right)\approx \frac{N_S}{T}\Delta t\text{exp}\left(-\frac{t}{T}\right)\text{.}$$ (2)

However, when τ is the lower cutoff, the total number of events, N_S, is divided into observed and missing events according to

$$N_S=N_S\underset{0}{\overset{\mathrm{\infty }}{\int }}{P}_e\left(t\right)dt=N_S\left(\underset{0}{\overset{\tau }{\int }}{P}_e\left(t\right)dt+\underset{\tau }{\overset{\mathrm{\infty }}{\int }}{P}_e\left(t\right)dt\right)=N_{\text{mis}}+N_{\text{obs}}\text{.}$$ (3)

Integration and rearrangement of the second integral leads to the total number of events:

$$N_S=N_{\text{obs}}\text{exp}\left(\frac{\tau }{T}\right)\text{.}$$ (4)

This makes it possible to calculate the total number of events, N_S, provided that T can be estimated. This is possible if τ is known, because combining formulas 2 and 4 gives

$$N\left(t;t+\Delta t\right)\approx \frac{N_{\text{obs}}}{T}\Delta t\text{exp}\left(-\frac{t-\tau }{T}\right),$$ (5)

and the corresponding distribution can be fitted to obtain T.

We tested the feasibility and theoretical accuracy when fitting such exponential distributions that suffer from a lower cutoff time (see Materials and Methods in the Supporting Material). It can be shown that a mean T value can be determined even for τ > T at the expense of accuracy. The 95% confidence interval of the estimated T value increases exponentially with the cutoff time, τ. However, acquiring more data points can fully compensate for the loss in accuracy (Fig. S6).

Appendix B: Definition of pauses and stops

An interruption of forward movement is characterized by a temporarily steady position within the noise level present in the image data. Such interruptions can occur within the exposure time of one frame or can last over several frames. Our automatic analysis detects extended waiting periods, defined as at least three consecutive frame-to-frame intervals with no observed forward movement that is beyond our spatial noise level (40 nm per frame). The temporal detection limit of at least three frames allows a rather robust detection. However, waiting periods briefer than three frame intervals are not included in the population of detected waiting periods. If the waiting period occurs at the end of a run, it is called a “stop”; otherwise, it is called a “pause” (Fig. 5). The associated durations are called “stop time” and “pause time”, and were found to exhibit an exponential distribution with cutoff τ = 300 ms (Fig. S3, E and F). Because we have enough data points, we can estimate the expected pause time and stop time according to Appendix A, even though it is below the cutoff. For more details, see the Supporting Material.

Figure 5.

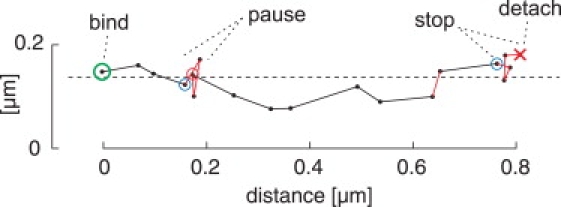
Pause and stop events. Sample plot of the automatically tracked position of Kin₄₀₁mGFP (dots) for consecutive frames, indicated by the interconnecting lines. The binding (landing) is highlighted with a green circle and the detachment with a red cross. A waiting period is considered a “stop” when it occurs at the end of the run; otherwise, it is considered a “pause”. The main axis of displacement is indicated by the dashed line and refers to the microtubule axis. Red and blue circles represent the beginning and end, respectively, of a detected waiting period.

Appendix C: Calculation of event probability

We first consider the case in which kinesins are not disturbed by obstacles. Assuming that the probability p for kinesin to dissociate in each step is constant and independent of preceding step processes, the probability of the kinesin dissociating after x consecutive steps is

$$P_g\left(X=x\right)=p{\left(1-p\right)}^{x}x=0,1,2,\dots ,$$ (6)

representing a geometric probability distribution. One can show that the expected value for X is

$$E\left[X\right]=\frac{1-p}{p}\text{.}$$ (7)

Thus, given the probability p of dissociating, kinesin is expected to make p⁻¹ – 1 steps, which is ∼p⁻¹ for p << 1. This geometric probability distribution is the discrete analogue of the exponential distribution of run lengths. Working in reverse order, we can calculate p from the observed mean (≈ expected) run length, expressed as the number of 8-nm steps (see also Fig 3 A, left versus right axis), of runs that do not show a pause or a waiting period at the end. In a similar way, the probability of a waiting event (pause or stop) occurring in an 8-nm step can be calculated by dividing the number of respective events by the number of 8-nm steps, assuming a constant probability after each step that kinesin will start a waiting period.

On a crowded microtubule, encountering an obstacle might alter the event probabilities instantaneously. For example, the probability for detachment may be the same as in control experiments until the motor encounters an obstacle on its path, causing this probability to be greater for that particular step. However, since encounters are not directly detected in our assay, we attribute changes of the frequency of detachment, pausing, and stopping to the steps a motor makes by assuming that encountering can happen any time with equal probability.

Appendix D: Natural occurrence of pauses exhibited by a Poisson stepper

Kinesin makes on average ∼80 steps/s. However, the stepping process is stochastic, leading to fluctuations of the stepping rate. Because we defined a pause as not more than 3 × 40 nm forward movement within 3 × 100 ms (see Appendix A), the question arises as to what is the natural probability that kinesin will be occasionally observed to make such a pause, even in the absence of obstacles. According to Poisson statistics, the probability that kinesin will make x steps within the interval Δt is

$$P_p\left(X=x\right)=\text{exp}\left(-\Delta t\lambda \right)\frac{{\left(\Delta t\lambda \right)}^x}{x!},$$ (8)

with λ = 80 s⁻¹ being the mean stepping rate. The maximal forward displacement within the minimal pause time allowed by our pause definition (3 × 40 nm within 3 × 100 ms) corresponds to ∼15 steps. According to formula 8, the probability of observing 15 or fewer steps in this interval is ∼3.4%, as calculated by the cumulative distribution function of P_p with Δt = 0.3 s. Hence, in 3.4% of all events within three frames, kinesin naturally moves for a distance that is so short that our algorithm detects a pause.

To calculate the (average) probability p per step that a pause will occur (regardless of the temporal stepping properties given by the Poisson process, see Appendix C), we use the cumulative distribution function F of P_g in formula 6 for x = 15, which expresses the probability of showing a pause after 15 or fewer steps. Hence,

$$F_X\left(x\right)=P_g\left(X\le x\right)=1-{\left(1-p\right)}^{x+1}\text{.}$$ (9)

Solving for p with F_X(15) = 3.4% (as explained above) gives p = 0.2%. It is interesting to note that this pause probability per step is comparable to what we find in the control experiment in the absence of obstacles (∼0.4%, Figs. 3 E and 4 D).

Appendix E: Distribution of obstacles and average interobstacle distance

We consider a microtubule as an arrangement of 13 independent protofilaments. Let a protofilament with N consecutive binding sites be uniformly decorated with n obstacles (n ≤ N), i.e., the probability that a binding site is occupied is $p_O=n/N$. Then, the number of nonoccupied binding sites between obstacles, D, is geometrically distributed, and the expected distance between obstacles is $E\left[D\right]=p_O^{-1}$ binding sites (same argument as in Appendix C). For example, for 10% decoration, the average distance is 80 nm (10 binding sites). In case the interobstacle distance is measured on a continuous scale, the corresponding distribution is exponential, $P_e\left(X=x\right)=\lambda \text{exp}\left(-\lambda x\right)$, with expected (≈ mean) length λ⁻¹.

Supporting Material

Materials and methods, references, and six figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00478-0.