Abstract
We examined the ionic mechanisms mediating depolarization-induced spike activity in pancreatic β-cells. We formulated a Hodgkin-Huxley-type ionic model for the action potential (AP) in these cells based on voltage- and current-clamp results together with measurements of Ca2+ dynamics in wild-type and Kv2.1 null mouse islets. The model contains an L-type Ca2+ current, a “rapid” delayed-rectifier K+ current, a small slowly-activated K+ current, a Ca2+-activated K+ current, an ATP-sensitive K+ current, a plasma membrane calcium-pump current and a Na+ background current. This model, coupled with an equation describing intracellular Ca2+ homeostasis, replicates β-cell AP and Ca2+ changes during one glucose-induced spontaneous spike, the effects of blocking K+ currents with different inhibitors, and specific complex spike in mouse islets lacking Kv2.1 channels. The currents with voltage-independent gating variables can also be responsible for burst behavior. Original features of this model include new equations for L-type Ca2+ current, assessment of the role of rapid delayed-rectifier K+ current, and Ca2+-activated K+ currents, demonstrating the important roles of the Ca2+-pump and background currents in the APs and bursts. This model provides acceptable fits to voltage-clamp, AP, and Ca2+ concentration data based on in silico analysis.
Introduction
Excitable cells express voltage-gated Ca2+ channels (VGCCs) along with K+ channels that precisely regulate action-potential (AP) firing, triggering a variety of biochemical events involved in the control of cell function. In general, the profile of the AP waveform and the gating properties of the VGCCs determine the peak and duration of the voltage-gated Ca2+ current (IVCa), which in turn dictates the pattern of Ca2+ influx. Changes in the AP profile can alter AP-driven Ca2+ signaling. This is of physiological relevance especially for pancreatic β-cells, in which Ca2+ dynamics are accompanied by changes in insulin secretion (1–3).
Over the physiological range of glucose concentrations, β-cell electrical activity often consists of depolarizing bursts in plasma membrane potential (Vm). These occur as depolarized plateaus, on which the bursts of APs occur separated by repolarized electrically silent intervals. Riding on these depolarized plateaus, the rapid voltage spikes (frequency, 1–5/s), which further depolarize the electrical syncitium of islet β-cells to ∼−20 mV. Bursts become continuous spikes at high glucose levels (4–8). Spike and burst behavior depend on multiple different channels, modified by inhibitors and activators as well as by posttranslational modification and changes in gene expression. The pattern of electrical activity likely involves complex interactions between many different ion channels (1,2). However, the mechanisms underlying spikes and burst behavior in pancreatic β-cells have been incompletely characterized.
In this study, we examined the ionic mechanisms mediating depolarization-induced spike activity using electrophysiological experiments, Ca2+ measurements with high temporal resolution, and a novel computational model based on the properties of individual β-cell currents. We simulated the experimental data obtained for mouse islets, because they have been the most thoroughly studied. Although several ionic models for β-cell spikes have been described (9–12), they include a limited subset of channels. Experimental data obtained with recently characterized channel modifiers and, in particular, data on the Kv2.1−/− mouse model indicate that a broader set of channels and pumps are involved in regulating insulin secretion. Here, we describe a more extensive model to consider an extended variety of ion channels and we show how this model can be used to investigate spontaneous Vm activity, initiation and termination of the bursts of spikes, and Ca2+ dynamics in pancreatic β-cells.
Methods and Theory
Vm recordings and calcium measurements
To test the role of K+ channels in glucose-stimulated APs, intact mouse islet β-cell membrane potentials were recorded using the perforated-patch current-clamp configuration. Ca2+ measurements were also made with high temporal resolution. Experimental methods were performed as previously described (13–15).
Formulation of the model
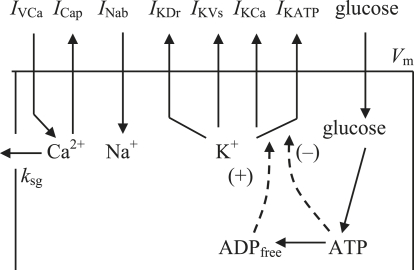
To provide a rigorous quantitative test of the experimental data, we developed a mathematical model in which specific ionic currents were included (Fig. 1). The differential equation describing time-dependent changes in the plasma membrane potential is the current balance equation:
| (1) |
where IKDr is the rapid delayed-rectifier current, IKVs is the slowly-activated K+ current, IKATP is the ATP-sensitive K+ channel current, IKCa is the Ca2+-activated K+ current, ICap is the plasma membrane Ca+-pump current, and INab is the Na+ background current. Cm is the whole-cell membrane capacitance. The currents are listed in Fig. 1.
Figure 1.
Schematic diagram of the ionic current and Ca2+ fluxes. Transmembrane currents are the IVCa, the ICap, the INab, the IKDr, the IKVs; the IKCa; and the IKATP. Calcium enters the β-cells primarily through voltage-activated Ca2+ channels by diffusion along an inwardly-directed electrochemical gradient. At the plasma membrane, two processes are involved in transporting Ca2+ out of the cell: a Ca2+ pump, and removal of Ca2+ sequestrated in insulin granules by exocytosis (coefficient ksq).
A conventional Hodgkin-Huxley-type model was used for time-dependent Ca2+ and K+ channels. Boltzman-type equations are assumed for steady-state activation and inactivation functions (Appendix). The gating variables were set equal to their steady-state values, if the time constants of the activation and/or inactivation of the gating variables are small in comparison with the time interval for one spike. Coefficients used in this model were either adopted from the model of Fridlyand et al. (16,17) or are described here. The parameters for which there are no specific experimental data were chosen to be consistent with experimental data presented here, as well as previously published data, to obtain the proper magnitude of the voltage and frequency of the spikes that were experimentally recorded in β-cells. However, all parameters and constants were fitted to be in their physiological ranges. A full set of current equations and parameter values are given in the Appendix and Tables 1 and 2.
Table 1.
Cell and membrane current parameters
| Parameter | Definition | Value | Reference |
|---|---|---|---|
| Cm | Membrane capacitance | 6158 pF | 16 |
| Vi | Cytosol volume | 0.764 pL | 16 |
| fi | Fraction of free Ca2+ in cytoplasm | 0.01 | 16 |
| F | Faraday constant | 96,487.0 C/mol | |
| ksg | Coefficient of the sequestration rate of [Ca2+]i. | 0.0001 ms−1 | 16 |
| gmVCa | Maximum conductance for IVCa | 1500 pS | f |
| gmKDr | Maximum conductance for IKDr | 45,000 pS | f |
| gmKVs | Maximum conductance for IKVs | 2200 pS | f |
| gmKCa | Maximum conductance for IKCa | 20 pS | f |
| gmNab | Maximum conductance for INab | 25 pS | f |
| gmKATP | Maximum conductance for IKATP | 30,000 pS | f |
| PmCap | Maximum ICap current | 4800 fA | f |
| KKCa | Half-maximum Ca2+ binding constant for IKCa | 0.1 μM | 16 |
| KCap | Half-maximum Ca2+ binding constant for ICap | 0.1 μM | 16 |
| ECa | Reversal potential for Ca2+ current | 100 mV | 9 |
| EK | Reversal potential for K+ current | −75 mV | 16 |
| ENa | Reversal potential for Na+ current | 70 mV | 26 |
| τdKDr | Time constant for dKDr | 25 ms | f |
| τdKs | Time constant for dKs | 300 ms | f |
f, adjusted to fit the experimental values.
Table 2.
Initial conditions for state variables at low glucose level
| Variable | Definition | Initial value |
|---|---|---|
| Vm | Membrane potential | −59.4 mV |
| dCa | IVCa activation gating variable | 0.00346 |
| f2Ca | IVCa slow-inactivation gating variable | 0.856 |
| dKDr | IKDr activation gating variable | 4.17 10−5 |
| dKs | IKVs slow-activation gating variable | 4.17 10−5 |
| [Ca2+]i | Intracellular Ca2+ concentration | 0.08 μM |
Unless otherwise noted, [ADP]i = 100 μM.
Voltage-gated Ca2+ current (IVCa)
The whole-cell Ca2+ current in mouse β-cells flows principally through VGCCs (2,18,19). In addition to having superior conductance properties, Ca2+ channels undergo rapid but incomplete inactivation during sustained depolarizing voltage pulses (20,21). β-cells also display a slow Ca2+-dependent inactivation (19,22–24). Modeling the inactivation behavior of Ca2+ channels involves both voltage and calcium dependence, and several models have been proposed to reproduce this behavior (25–27). In our case, we used the activating gating variable (dCa) (Eq. A2) and two inactivating gating variables: one rapid and voltage-sensitive (fVCa) and the other slow and Ca2+-dependent (f2Ca). Our introduction of these two inactivating gating variables for a Hodgkin-Huxley-type model of Ca2+ current is based on discussions by others (25,26).
The steady-state activation curve (dCa∞) (Eq. A3) can be described by a Boltzman-type equation (28,29). Ca2+ channels open rapidly upon membrane depolarization, with a time constant of ∼1 ms (24,27), and we obtained the equation for the activation time (τdCa) (Eq. A4) by fitting data from Fig. 4 B of Gopel et al. (24).
Figure 4.
Experiments with relative Ca2+ measurement (as F535/F535o (13–15)). (A) Glucose-induced bursts and spikes with simultaneous APs and Ca2+ measurement in control islets from wild-type mouse during treatment with 14 mM glucose. The lower record represents, at a faster timescale, part of the upper record. (B) TEA-induced bursts and Ca2+ spikes in control mouse islet at 14 mM glucose and 20 mM TEA.
We used the conventional equation for voltage-sensitive inactivating gating variables (fVCa) (Eq. A5). Ca2+ channels close rapidly after a depolarizing pulse (28), and we suggest that the time for fVCa inactivation is also very fast, e.g., fVCa = fVCa∞. The steady-state inactivation curve for fVCa∞ (Eq. A5) was adopted as a Boltzman-type equation.
We formulated a new equation for the slow Ca2+-dependent inactivating gating variable (f2Ca), because cytoplasmic Ca2+ changes during one spike apparently do not exceed 0.1 μM over the basal level in pancreatic β-cells, leading to only insignificant changes in f2Ca if we used the coefficients represented in other models (25,26) for cardiac muscle cells. The dynamics of Ca2+ channels seem similar to the predominant L-type channel, but they have not been investigated in sufficient detail in pancreatic β-cells to completely understand differences in the kinetics of inactivation. However, Shermann et al. (30) suggested that Ca2+-current-dependent inactivation of IVCa better reflects the inactivation process in β-cells over a simple Ca2+-concentration-dependent inactivation. Therefore, we have suggested that the rate of inactivation of f2Ca is proportional to a Ca2+ current through a unitary channel (the term IVCa/gmVCa in Eq. A6) rather than Ca2+ concentration as has been suggested in other models (25,26). The dynamic of f2Ca is determined by the relative rates of activation and inactivation (Eq. A6). Parameters (Table 1) were set so that the difference in the magnitude of IVCa was most pronounced at potentials from −45 to −10 mV, in the characteristic functional range of mouse β-cells (19,24,29).
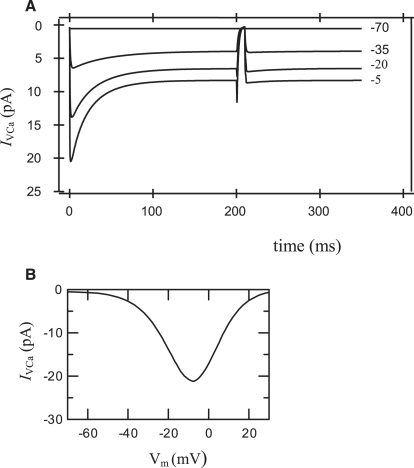
We simulated the double-pulse protocol for voltage-clamp measurements to compare the predictions of the model with specific experiments (Fig. 2 A). The f2Ca variable undergoes an IVCa-dependent inactivation. Time dependence of Ca2+ currents and an initial inactivation time (∼20 ms) are in good quantitative agreement with experimental data (19,22,24,29). Simulated voltage dependence of whole-cell peak calcium currents are shown in Fig. 2 B. The simulated peak I/V curve also compares well with experimental results (19,24,28,29).
Figure 2.
(A) Simulation of voltage-clamp experiments for a Ca2+ current (IVCa), using a double-pulse protocol. The membrane potential was stepped from the holding potential (−70 mV), where dCa = 0.00244 and f2Ca = 0.884, to the prepulse potential (pointed in figure) for 200 ms. Voltage was then stepped back to the holding potential (−70 mV) for 10 ms and finally stepped to test potential. Current record simulations were made for prepulses (−70, −35, −20, −5 mV). (B) Simulated voltage dependence of whole-cell peak calcium currents obtained as in the left part of Fig. 2 A. Current parameters and equations for IVCa are shown in Table 1 and the Appendix.
Rapid delayed-rectifier K+ current (IKDr)
Voltage-gated K+ channels (Kv) determine AP repolarization in the pancreatic β-cells. The principal voltage-gated K+ current in mouse β-cells, a relatively rapid delayed-rectifier K+ current (IKDr), is responsible for >80% of the current (2,13,24,31–33).
A Hodgkin-Huxley-type model for IKDr with activation (dKDr) and inactivation (fKDr) gating variables was used (see Appendix Eqs. A7 and A8). Inactivation of IKDr was negligible during a 200-ms depolarization (14,24,31). Therefore, we have suggested that fKDr = 1. The activation of the IKDr could be described by n2 kinetics (31). Activation time for dKDr (τdKDr) is in the range of 10–30 ms (14,24,28) and was approximated as a constant (Table 1), chosen to provide an acceptable frequency of glucose-induced spikes that corresponds to experimental data. The value of gmKDr (Eq. A7) was calculated as 45 nS for standard conditions (Table 1).
Slow-activated TEA-insensitive K+ current
A minor part of the KV current in insulin-secreting cells from mouse islets or β-cell lines is insensitive to tetraethylammonium ion (TEA), a nonspecific pharmacological blocker of voltage-gated K+ channels ((34–37), see also Discussion). Therefore, we now include a TEA-insensitive small-conductance slow-voltage-activated K+ current (IKVs) regulating the TEA-induced AP duration and frequency. For simplicity, we propose that maximum conductance of this current is 10% of the maximum conductance for IKDr (Table 1), in agreement with experimental evidence that this current is small. For simplification, we also set its voltage-gated characteristics similar to those of IKDr (Eqs. A10–A12), except that its activation time constant (τdKs) (300 ms for IKVs) is considerably longer than for IKDr.
Currents with time- and voltage-independent gating variables during one spike
To isolate the rhythmogenic potential of the currents considered above, we have also included several additional currents with gating variables that are time- and voltage-independent during one spike interval. They serve as background currents and can be modeled without using activation and inactivation voltage-dependent gating variables.
ATP-sensitive K+ current
KATP channels are the predominant inwardly rectifying potassium channel β-cells. They maintain the resting potential in quiescent β-cells at ∼−70 mV, slightly elevated from the electrochemical equilibrium potential for K+ (∼−75 mV). Free ATP inhibits KATP channels, whereas intracellular free ADP ([ADP]i) activates them. Glucose elevates the intracellular concentration ratio of ATP to ADP that causes KATP channel closure and membrane depolarization (1,17). The endogenous KATP current is reasonably linear over the physiological voltage range (38,39). This current can be simulated by a term relating dependence of K+ flux to resting potential, i.e., V – EK (10,11,40). We adopted a kinetic model (Eqs. A13–A15 in the Appendix) for the value of whole-cell KATP channel conductance from Fridyland et al. (17). Maximum conductance for IKATP is close to that employed previously (17) and falls in the range that was measured for the maximum KATP conductance for β-cells.
Ca2+-activated K+ currents with time- and voltage-independent gating variables
Different Ca2+-activated K+ (KCa) channels with time- and voltage-independent gating variables are expressed in β-cells. (Eqs. A16 and A17). These include both TEA-sensitive KCa channels (31,33,35) and channels that have lower sensitivity to TEA (33,41,42). We included a calcium-activated K+ current as the current termed IKCa from our model (16).
Plasmalemma Ca2+-pump current
Plasma membrane Ca2+ pumps are capable of establishing a membrane potential when operating with H+/Ca2+ = 1 (43). For this reason, Ca2+ pumps provide an outward current (ICap) and also contribute to Vm (Eq. A18). The equation, the maximum rate, and the half-maximum Ca2+-binding constant for ICap were adapted from Fridlyand et al. (16).
Na+ background current
A tetrodotoxin-insensitive Na+ inward current has been described in β-cells. It may be an Na+ current through nonselective cation channels with time- and voltage-independent gating variables (16,44–47). This current can be considerable, because there is a large difference in Na+ concentration between the cytoplasm and the surrounding medium. We have included this current (INab) in our model as a linear Na+ background current. We used the equation for INab (Eq. A19) according to the model of Luo and Rudy (26).
Currents not included in the model
Application of tetrodotoxin, a specific voltage-gated Na+ channel blocker, is known to have a negligible effect on APs in mouse β-cells (1,24). The picture in human cells is more complex for the inward current (33,48,49), but as we are focusing on the mouse, we did not include a Na+ voltage-dependent current in this model.
The Na+-K+ pump extrudes three Na+ ions from the cell in exchange for two K+ ions, generating a net outward current. Currents provided by Na+-Ca2+ exchangers also contribute to Vm. Both these currents were included in our recent β-cell ionic model (16,17). Other inward and outward currents have also been found in β-cells (1,2,16). The changes in their conductance do not appear to play a role in the short time interval during one spike, so we do not consider these currents in our model. We have included in our model the time- and voltage-gated independent outward (IKCa, ICap, and IKATP) as well as inward (INab) currents and suggest that a combination of these currents is sufficient to describe the effects of the background currents during one spike interval.
Ca2+ dynamics
Based on the considerations in our general model (16), and including only IVCa and ICap, the equations for free cytoplasmic Ca2+ ([Ca2+]i) dynamics can be written as
| (2) |
where fi is the fraction of free Ca2+ in cytoplasm, F is Faraday's constant, Vi is the effective volume of the cytosolic compartment, and ksg is a coefficient of the sequestration rate of [Ca2+]i.
Simulation methods
The complete system consists of six state variables: differential equations describing the time rate of change in membrane voltage (Vm) (Eq. 1), [Ca2+]i (Eq. 2) and voltage-dependent gating variables dCa (Eq. A2), f2Ca (Eq. A6), dKDr (Eq. A8), and dKs (Eq. A11).
Equations and parameter values (Table 1) and initial conditions (Table 2) contain all the information necessary to carry out the simulations presented in this article. The parameters (units) are time (ms), voltage (mV), concentration (μM), current (fA), conductance (pS), and capacitance (fF). Numerical integration of the Hodgkin-Huxley-type ionic model was carried out using standard numerical methods (16,17). This model is available for direct simulation on the website “Virtual Cell” (www.nrcam.uchc.edu) in “MathModel Database” on the “math workspace” in the library “Fridlyand” with name “MouseSpike”. Visualization and graphical analysis were performed using Igor Pro (WaveMetrics, Lake Oswego, OR).
Results
AP and Ca2+ measurements
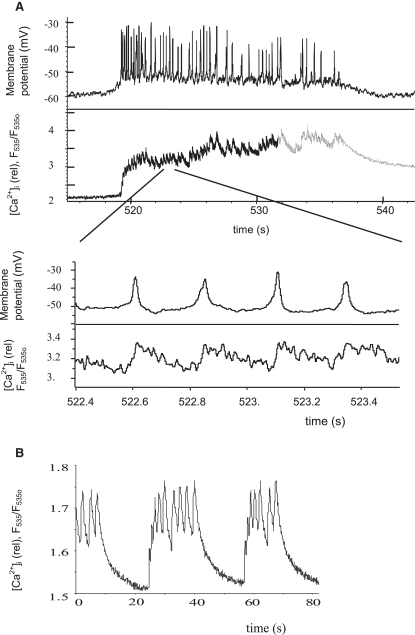
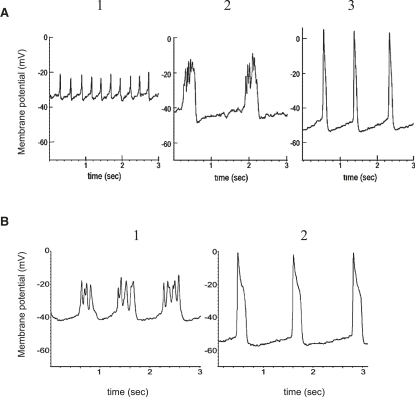
Fig. 3 A1 shows typical glucose-induced single-spike behaviors on depolarized plateaus of bursts for wild-type mouse islets. Our studies with wild-type mouse islets showed also that Kv2.1 inhibition with stromatoxin increases the amplitude of glucose-induced APs but decreases their frequency while increasing their width (14). A typically complex structure of one spike after stromatoxin action with several Vm oscillations is shown in Fig. 3 A2. Application of TEA in the mouse β-cell prolongs the AP duration and increases its amplitude (Fig. 3 A3). Loss of Kv2.1 in the Kv2.1 null mouse (Fig. 3 B) caused glucose-stimulated AP duration to increase, with an associated reduction in AP firing frequency and a new complex AP structure that resembled the effects of specific Kv2.1 inhibitors (compare Fig. 3, A2 and B1). On the other hand, TEA has effects in Kv2.1 null islets similar to those in control wild-type islets (compare Fig. 3, A3 and B2). Every glucose-induced AP is accompanied by a [Ca2+]i spike (Fig. 4 A, showing one burst). Measurements of relative Ca2+ changes after application of TEA during several bursts are shown in Fig. 4 B. In this case, relative [Ca2+]i changes during one spike were significantly higher after TEA application than during glucose-induced spikes in Fig. 4 A. Note that we performed only relative Ca2+ measurements. For this reason, we compared a relative change of Ca2+ level during one spike with the relative Ca2+ level during the repolarized electrically silent interval between bursts to make a valid comparison among different experiments. Relative Ca2+ changes during one glucose-induced spike in Kv2.1 knockout mouse islets that were measured by Jacobson et al. (14) also had greater relative amplitude compared with wild-type islets.
Figure 3.
(A) Control islets from wild-type mouse treated with stromatoxin and TEA. Control islet electrical activity was recorded during treatment of 14 mM glucose alone (1), or in combination with 100 nM stromatoxin ScTx-1 (2) or 15 mM TEA (3). Representative APs are shown. (B) Kv2.1−/− islet electrical activity in response to 14 mM glucose (1) or in combination with 15 mM TEA (2). Representative APs are shown.
Modeling of spikes and generation of bursts in pancreatic β-cells
Spontaneous glucose-induced spike activity in wild-type β-cells
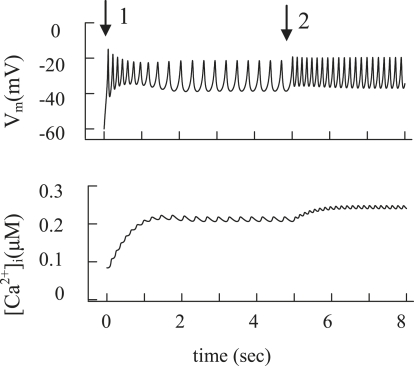
In our model, the membrane potential reaches the AP threshold through the depolarizing effect of decreased IKATP. Increased glucose was modeled by closure of KATP channels after a rise in [ATP]/[ADP] (6,17). The resting membrane potential was −59.4 mV at 100 μM free [ADP]i (Table 2). KATP channel closure was simulated by a decrease of [ADP]i from 100 μM to 15 μM, leading to depolarization and spontaneous spiking (Fig. 5 A, arrow 1). The result gives the continuous spike activity in this simulation, as in Fig. 6 A. The simulated closing of additional KATP channels after an initial glucose-induced depolarization was simulated by a reduction in free [ADP] (Fig. 5 A, arrow 2) that leads to decreased KATP channel conductance in our model (resulting Vm depolarization and [Ca2+]i changes are shown in Fig. 5). The simulated AP agrees with a large body of experimental data (Fig. 3 A1 and Fig. 4 A) (2,4,5,7,8,14,28,33).
Figure 5.
Modeling of spontaneous glucose-stimulated spikes and changes of the intracellular Ca2+ concentration. Glucose-induced spikes were simulated at a step decrease of the free [ADP]i at arrow 1 from a high to an intermediate value (from 100 μM to 15 μM) at t = 0 and at initial parameters as in Table 2; all other parameter settings are standard (Table 1). To simulate a glucose increase, the free [ADP]i was decreased from 15 μM to 8 μM at arrow 2. (B) Corresponding changes in [Ca2+]i were simulated using Eq. 2.
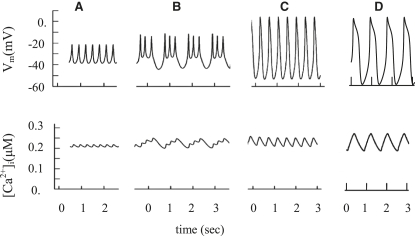
Figure 6.
Simulated glucose-induced spike behavior and [Ca2+]i. of glucose-induced spikes with the same initial simulation as in the beginning of Fig. 5 (A) and of Kv2.1 channel blocking (B). For simulation of Kv2.1 channel blocking, the maximal conductance (gmKDr) for the delayed rectifier K+ channels was decreased from 45,000 pS to 4500 pS, and τdKDr was decreased from 25 ms to 20 ms. (C and D) Simulation of TEA action. In both cases, the maximal conductance for TEA-dependent K+ channels was decreased: from 30,000 to 15,000 pS for KATP (gmATP), and from 45,000 pS to 45 pS for delayed-rectifier K+ channels (gmKDr). In addition, for the mechanism in C, the maximal conductance for KCa channels (gmKCa) was decreased from 20 pS to 0.1 pS. In the case of the mechanism in D, gmKCa was increased from 20 to 200 pS and KKCa was increased from 0.1 μM to 0.3 μM (Eq. A17). However, IKVs was eliminated (gmKs = 0).
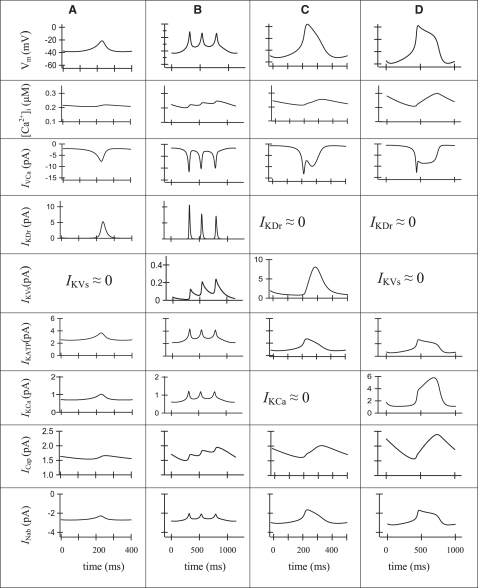
The possible mechanisms underlying the AP, [Ca2+]i changes, and roles of different currents can be better understood by considering the voltage-dependent currents during one spike (Fig. 7). Fig. 7 A shows Vm, [Ca2+]i, and the various currents during a simulation of one spike of a glucose-generated AP, as in Fig. 6 A. In agreement with the suggestion of Rorsman and Trube (28), the depolarizing phase of the action potential results from activation of voltage-gated Ca2+ channels. Activation of rapid delayed-rectifier K+ channels (current IKDr) is responsible for a repolarization of the AP. IKVs contributes insignificantly to depolarization, since this current is small in comparison with IKDr. Other currents are small and in this model have an insignificant influence on AP.
Figure 7.
Simulation of single spikes. Action potential (Vm), [Ca]i, IVCa, IKDr, IKVs, IKATP IKCa, ICap, and INab are represented for one characteristic spike. The units are shown in series, as labeled in the first column, if no units are represented on the axis. (A) The model solution is represented for the spike after simulation of glucose addition as in Fig. 5 or Fig. 6A. The IKVs and IKCa currents are minor contributors in this mode of oscillation. (B) A single characteristic spike after simulation of Kv2.1 blocker application, as in Fig. 6B. The ICap and IKVs currents are the major contributors in this repolarizing part of the AP. (C) A single characteristic spike after simulation of TEA action as in Fig. 6C. The proposal for full blocking of IKCa current was accepted (IKCa ≈ 0). The IKVs and ICap currents are the major contributors in this repolarizing part of the AP. (D) A single characteristic spike as in Fig. 6D after simulation of TEA action in a model that incorporates Ca2+-dependent TEA-independent K+ channels (current IKCa) instead of a slow-activated TEA-insensitive K+ current (IKVs = 0). In this case, gmKCa = 200 pS, KKCa = 0.3 μM (Eq. A17) and gmKs = 0. The IKCa and ICap currents are the major contributors in the repolarizing part of AP.
Specific blockers of voltage-gated K+ channels and Kv2.1 null mouse
To investigate the role of voltage-gated K+ channels, we simulated spikes with decreasing “rapid” delayed-rectifier K+ channel conductance (Figs. 6 B and 7 B), which corresponds in action to some specific blockers of voltage-gated K+ channels, or islets from the Kv2.1 null mouse.
According to Jacobson et al. (14) Kv2.1−/− β cells have a current amplitude that is only 17% that of control wild-type. Pharmacological inhibition of Kv2.1 caused a similar degree of reduction in control β cells. However, only 53% of the remaining Kv current was sensitive to block by TEA (14). Consequently, the TEA-sensitive remaining Kv current amounts to ∼9% of the total Kv current in control wild-type cells. In line with these data, the simulated decreased IKDr conductance was only 10% of the total IKDr conductivity used in the simulation of glucose-induced spikes for control wild-type in Figs. 6 A or 7 A. The overall shape of the simulated AP (Figs. 6 B or 7 B) resembles the experimental AP seen in AP studies after application of the Kv2.1 channel blocker stromatoxin (Fig. 3 A2) or in islets from the Kv2.1−/− mouse (Fig. 3 B1, and see Jacobson et al. (14)).
Fig. 7 B, shows Vm, [Ca2+]i, and the various currents during simulation of one spike, as in Fig. 6 B. The major depolarizing current for single spikes was again IVCa, as in Fig. 7 A. The remaining part of IKDr in the interaction with IVCa generated several fast Vm oscillations in the plateau phase of an AP by the same mechanisms as observed at glucose-generated AP in Fig. 6 A. However, it occurs at higher Vm levels, where IKDr has an increased value even at small conductance. During the single spike, the slow-activating TEA-insensitive K+ channels (IKVs) contribute increasingly in AP, because the time constant for their activation was evaluated in the range of several hundred milliseconds in our model. Increased IKVs leads to a repolarization. However, the simulated increase of IKCa, and specifically ICap, also makes a considerable contribution to an outward current, with an increase of [Ca2+]i during the spike and in the subsequent repolarization (Fig. 7 B).
Note that similar APs can be obtained even in the absence of IKVs if we substantially increase the current of IKCa. For example, a fitting with gKCa = 70 pS and KKCa = 0.3 μM for IKCa (at IKVs = 0) leads to results similar to those shown in Figs. 6 B or 7 B (not shown). In this case, a slow increase in the K+ outward current leading to a repolarization could be explained by an increase of IKCa and ICap after the [Ca2+]i increase during a single spike. Our model shows that if IVCa is the depolarized current, then the repolarizing small currents, such as the resting current from IKDr and some outward currents (IKVs and/or IKCa and ICap), which increase during a spike, can explain this complex oscillatory behavior.
Modeling the effects of TEA
Classical pharmacological blockers of voltage-gated K+ channels such as TEA are often employed in β-cell electrophysiological studies despite a limited selectivity between different K+ channels. The effects of TEA on K+ channels were studied in cultured insulin-secreting HIT cells using the patch-clamp technique (35). High TEA concentrations partially blocked the majority of islet K+ channels, but it was a more effective inhibitor of TEA-sensitive KCa channels (EC50 = 0.15 mM) than of KATP channels (EC50 = 15 mM) or “rapid” delayed rectifier K+ channels (EC50 = 3 mM) (35). However, the detailed mechanisms that lead to changes in spike behavior after TEA treatment remain unknown. We have modeled the action of TEA (15–20 mM of TEA is typically used in experiments) by decreasing the maximal conductance of K+ currents (Figs. 6, C and D, and 7, C and D). We considered two hypothetical mechanisms.
In the first mechanism, we suggest that IKDr and IKCa were decreased almost entirely after TEA application, and no resting IKDr current exists. Since IKATP is less sensitive to TEA, the initial conductance of IKATP was decreased by half (Figs. 6 C and 7 C). Fig. 7 C shows Vm, [Ca2+]i, and the various currents during simulation of one spike, as in Fig. 6 C. Activation of IVCa depolarizes the membrane. Subsequently, the activation of TEA-insensitive IKVs can contribute increasingly, leading to repolarization. This current has a small conductance in our model (5% of the whole-cell conductance of rapid delayed-rectifier K+ channels), and its influence is observed only when IKDr is inhibited and Vm increased. An increase in the ICap with [Ca2+]i increase during a spike also plays a considerable part in the repolarization of the AP.
In the second mechanism, we simulated persistent activity of TEA-insensitive Ca2+-dependent K+ channels after TEA treatment (Fig. 6 D, and see Fig. 7 D for a single spike). The experimental basis for this proposal is the existence of some TEA-insensitive Ca2+-dependent K+ channels (see above and Discussion). However, the conductance and characteristics of this channel have not been adequately explored. As in the first mechanism, IKDr was totally blocked. For simplicity, we also proposed that a slow voltage-activated K+ outward current is absent in this case (IKVs = 0). Thereafter, we attempted to determine the coefficients for the model that closely simulate AP behavior after TEA treatment. We found that when the conductance and half-maximal Ca2+ binding constant for IKCa from Eqs. fdA16 and A17 were increased (from gmKCa = 20 pS (Table 1) to gmKCa = 200 pS and KKCa from 0.1 μM (Table 1) to 0.3 μM), the simulation reproduced the characteristic AP after TEA application (Figs. 6 D and 7 D). The following mechanism is simulated in the model: when IKDr and IKVs were totally blocked, and conductivity of IKCa was increased, an increase of [Ca2+]i during a single spike leads to activation of IKCa and ICap, with subsequent repolarization. The inclusion of this IKCa conductance in our general model does not change the picture of simulated glucose-induced spikes represented in Fig. 5 or Fig. 7 A (not shown).
In both mechanisms, TEA simulation prolonged the AP and increased amplitude, but spike frequency was decreased (Fig. 6, C and D). This occurs because IKVs (or IKCa in the second mechanism) and ICap are smaller and activate more slowly compared with IKDr. This allows IVCa to progress to a point with higher Vm in the absence of IKDr (Figs. 6, C and D, and 7, C and D). Nevertheless, in both cases, IKATP makes also a contribution to outward K+ currents with an increase of Vm, because the driving force of K+ flux increases with a depolarization (Fig. 7, C and D, and see Eq. A13).
The two mechanisms generate spike patterns similar to what is seen in both Kv2.1−/− and control islets after TEA application (compare Fig. 6, C and D, with Figs. 3 A3 and 4 B2, and with Fig. 2 from Jacobson et al. (14)). Our simulations are also consistent with previous observations (4,5,51,52). Thus, we can simulate the behavior of APs after TEA applications by almost entirely blocking the voltage-gated rapid delayed-rectifier K+ channel conductance.
It is interesting to note that the TEA simulation at low (subthreshold) glucose ([ADP]i = 100 μM, see Table 2) does not lead to spike activity in our model. Vm was still lower (−43.25 mV) than the threshold level for spike generation (not shown). However, simulation of TEA effects diminishes the decrease in [ADP]i that is necessary for spike generation. In this case, spike generation takes place at [ADP]i = 50 μM instead of [ADP]i = 15 μM without a simulation of TEA action (not shown). This effect can be explained by blocking KATP channels with TEA that leads to decreased IKATP even at moderate [ADP]i levels. These results agree with experimental data showing that TEA usually does not generate spikes at low glucose levels, but decreases the glucose level required for spike generation (4,51).
Burst activity and fast Ca2+ oscillations
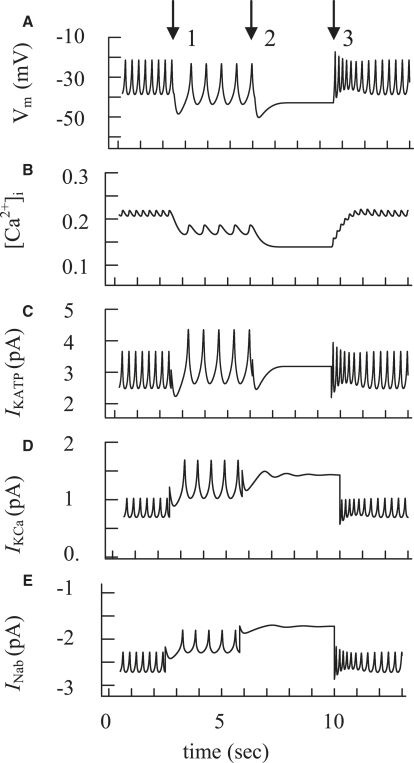
AP bursts likely reflect slow periodic changes of some currents. This kind of change in overall current can lead to periodic repolarizations of plasma membrane potential (with a duration greater than several seconds) with similar [Ca2+]i periodicity, usually described as [Ca2+]i oscillations (see, e.g., Fig. 4 A, where one burst is represented, and (6,7,11,40)). The depolarizing component predominates at the beginning of the burst, but the resultant influx of Ca2+ during the burst may lead to a progressive increase in K+ channel activity and/or a decrease in an inward Na+ current, leading to repolarization (6,10,16,44). The model allows us to demonstrate that, for example, the cyclic simulation of the channel conductivity for KATP channels, Ca2+-activated K+ channels, and an inward Na+ current can lead to a burst pattern in our model (Fig. 8, A–E) (for details, see Discussion). Note that in all cases only small changes in currents (in the range of 2 pA) were necessary to simulate burst behavior (see Fig. 8, C–E). Two or three of these current-activity changes may also act simultaneously during burst generation, requiring even smaller changes in the individual currents. The amplitude and frequency of APs progressively decrease during the burst, terminated by repolarization and an electrically silent interval (see Fig. 4 A, for example, and (6,7,40)). This behavior was also simulated with a gradual cell repolarization in our model (Fig. 8 A).
Figure 8.
Simulation of glucose-induced burst activity and [Ca2+]i with the initial simulation, as in Fig. 6A for glucose-induced spikes in wild-type mouse. (A–C) Action potential (A), [Ca2+]i (B), and IKATP change (C) as regulators of bursting. Slow electrical bursting and [Ca2+]i changes were simulated by a step increase and decrease of the KATP channel conductance by changes in [ADPf]i. At arrow 1, the [ADPf]i was increased from 15 μM to 20 μM, at arrow 2 from 20 μM to 25 μM, and at arrow 3 from 25 μM back to 15 μM. (D) IKCa change as a regulator of bursting. AP and [Ca2+]i oscillations were simulated at a step increase and decrease of the KCa channel conductance. At arrow 1, the gmKCa was increased from 20 pS to 35 pS, at arrow 2 from 35 pS to 50 pS, and at arrow 3 from 50 pS back to 20 pS. Only IKCa is shown. AP and [Ca2+]i changes were the same as in Fig. 8, A and B. (E) INab change as a regulator of bursting. AP and [Ca2+]i oscillations were simulated at a step decrease and increase of the Na+ background current (INab) conductance. At arrow 1, the gmNab was decreased from 25 pS to 20 pS, at arrow 2 from 20 pS to 15 pS, and at arrow 3 from 15 pS back to 25 pS. Only INab is shown. AP and [Ca2+]i changes were the same as in Fig. 8, A and B.
Discussion
We developed this model to gain further insights into coupling cation flux to [Ca2+] regulation in β-cells, a critical process for physiological insulin secretion that remains incompletely understood. We used the Hodgkin-Huxley formalism to describe the behavior of channels. This choice is consistent with our goal, to reconstruct the AP that results from ensemble currents through many individual channels. The key feature of the model is that it can be used to explore the putative mechanisms underlying AP spike activity. This semiquantitative model simulates the behavior of β-cell APs under a wide range of experimental conditions, including:
-
1.
Changes in the period and amplitude of AP oscillations in response to glucose challenge.
-
2.
Complex AP behavior due to K+ channel blockade with TEA.
-
3.
Increases in the duration of the plateau phase of AP spikes observed in response to specific KV2.1 blockers.
-
4.
Changes in islet electrical activity from the Kv2.1 null mouse compared with controls.
Chay and Keizer (9) described the first Hodgkin-Huxley-type ionic model based on electrophysiological data for β-cells, where generation of spikes was simulated as a result of an interaction between only two channels (voltage-gated Ca2+ and voltage-gated delayed-rectifier K+ channels). Keizer and Magnus (10) improved this model by including KATP channels, an approach also used in later models to describe spikes in pancreatic β-cells (11,16). The temporal interaction of IVCa and IKDr is sufficient to explain the repetitive spiking observed in glucose-induced β-cells, simulating a reasonably accurate glucose-induced spike pattern (9,11,13). The interaction focusing on IVCa and IKDr was also used for a simulation of glucose-induced spikes in the model presented here. However, the use of mathematical models of APs where only the interaction between IVCa and IKDr is included presents difficulties for a detailed recapitulation of more complex experimental conditions. In particular, the spikes obtained from islets of Kv2.1 knockout mouse and the similar spikes obtained after application of specific Kv2.1 inhibitors (Fig. 3, A2 and B1) had a specific complex shape that cannot readily be explained by existing models. These experimental results show that other channels must be included for an explanation of the regulation of spike activity in these circumstances. We found that implementing a small residual TEA-sensitive KV current (IKDr), TEA-insensitive slow-activated K+ channels (IKVs), or Ca2+-activated K+ current, as well as currents contributed by Ca2+ pumps, can help the model to more closely simulate the full range of spike behavior observed experimentally, particularly in the absence of Kv2.1, or induced by application of TEA.
As in previous models, IVCa is the major depolarizing current during spike generation. For the IKDr conductance, our simulations show that Kv2.1 is a likely candidate for the principal delayed-rectifier isoform expressed in mouse β-cells, in keeping with findings from several experimental studies (14,32). The absence of Kv2.1 channels results in an increased glucose-stimulated AP duration, a decreased firing frequency, and a complex AP behavior (Fig. 3, A2 and B1; see also Jacobson et al. (14)). These changes in AP can be explained by the existence of other Kv currents (IKCa, IKVs, and residual IKDr current, which remain intact after blockade of Kv2.1 channels) and ICap (see Figs. 6 B and 7 B). By reducing the IKDr conductance 10-fold in the model, the simulated complex spikes resembled the spike picture in experiments with Kv2.1−/− islets. However, in contrast to mouse, the Kv2.1 isoform appears to make only a small contribution in human β-cells, consistent with observations that Kv2.1 blockade had only modest effects on electrical activity (33).
Which channels can be responsible for these currents?
Residual IKDr current, which remains intact after blockade of Kv2.1 channels
According to our simulations to explain the complex behavior of APs obtained after elimination of Kv2.1 channels, the conductance IKDr should be reduced to ∼10% of the initial IKDr conductance to obtain a residual current that has detectable effect. Such a small residual TEA-dependent KV current is indeed detectable in the Kv2.1 null mouse islets (14). However, it remains incompletely characterized. There is limited data on molecular identification of all of the non-Kv2.1 channels involved in the TEA-sensitive part of the KV current. Some channels other than Kv2.1 channels expressed in β-cells are TEA-sensitive, for example, Kv3.1 and Kv3.2 (36,53) and could be responsible for the residual TEA-sensitive KV current.
Small TEA-insensitive voltage-dependent current (IKVs)
We set the conductance for this current to 5% of the total KV channel conductance (see Table 1) and found that this small value is enough to closely approximate experimental data. A small TEA-insensitive current really found in β-cells contributes to the outward K+ current, and its maximal conductance is within the range used in our model for IKVs (34–36,54). However, to accurately describe the experimental data, in particular the prolongation of AP duration with TEA, our model used a slow activation time (300 ms in Table 1) for this current.
Which TEA-insensitive channels can lead to repolarization during a spike after TEA application, and what other characteristics should it display? We can rule out residual TEA-sensitive Kv2.1 channels, because spike behavior after TEA application is similar in wild-type and KV2.1 knockout mouse islets (see Fig. 3, A3 and B2). TEA-insensitive Kv1.4 and/or Kv4.2 channels could contribute to an inactivating portion of MIN6 cell outward K+ current recorded after TEA application (54). Another candidate is the TEA-insensitive voltage-gated KCNQ1 channel that was detected in INS-1 cells and in mouse islets (55). The TEA-insensitive voltage-gated ether-a-go-go K+ channels (or human ERG channels) can also influence both insulin secretion and AP firing frequency in isolated human islets (56). ERG channels were found recently in β-cells from rat islets (57). Interestingly, ERG currents activate slowly (in several seconds) upon depolarization to potentials below 0 mV (58). This time-activated kinetics of the ERG current looks remarkably similar to the proposed IKVs current in our model.
We also found that the spike shape in β-cells after blockade of Kv channel by TEA resembles the AP in the cardiac sinoatrial node myocytes (see, e.g., Berecki et al. (59)). In these cells a fast Na+ current appears to be small or absent (60) and the AP activating mechanisms may be determined by Ca2+ and KV channels interacting, similar to the spike generating mechanism in β-cells. The slow- as well as fast-activating delayed-rectifier K+ channels were found in cardiac sinoatrial node myocytes. In these cells, the slow-activating K+ channels are activated at membrane potentials similar to those for fast-activating K+ channels but with different kinetics, and these slowly-activated currents determine the latter phase of repolarization (20). HERG and KCNQ1 K+ channels play a major role in action potential repolarization in these myocytes (59,60). Based on these investigations, we can suggest that TEA-insensitive voltage-dependent KCNQ1 and/or HERG channels could contribute to the slowly-activated voltage-gated K+ channels in β-cells. However, further studies are needed to better understand these channels in β-cells from different species.
Plasma membrane Ca2+-pump current (ICap) and Ca2+-activated K+ current (IKCa)
We investigated another possible explanation for spike generation in cases where APs are long and of high amplitude. The relative Ca2+ concentration increases moderately during each glucose-generated spike (Fig. 4 A) in comparison with Ca2+ changes during high amplitude with slow spikes after Kv2.1 channel blockade (see Fig. 4 in Jacobson et al. (14)) or TEA application (Fig. 4 B). Other studies using Ca2+-sensing fluorescent dyes to monitor temporal changes have also shown small but detectable changes in [Ca2+]i within tens of milliseconds during a single glucose-induced electrical spike followed by large-amplitude [Ca2+]i changes after TEA application (52).
As the [Ca2+]i oscillations are small, the changes in Ca2+-dependent currents (IKCa and ICap) are also small compared with the change of IKDr during the simulation of glucose-generated spikes in wild-type mouse islets (see Figs. 6 A and 7 A) and provide only background currents in our model. However, the larger [Ca2+]i increase during single TEA or Kv2.1 block-induced spikes can activate IKCa and ICap (Fig. 7, C and D). In this case, TEA-insensitive small-conductance voltage-independent, Ca2+-dependent K+ channels and ICap could contribute to repolarization of APs and, together with IVCa, could also be considered as candidate pacemakers for some long and high-amplitude spikes.
Spike repolarization induced by IKCa activation was originally suggested in earlier studies (12,61). However, a role for ICap was not considered. Surprisingly, the results of the simulations show that a plasma membrane Ca2+-pump current can also contribute to the AP mechanism when spikes have high amplitude and low frequency.
Which Ca2+-activated K+ channels can be responsible for repolarization during a spike after TEA application or after Kv2.1 channel blockade? Several Ca2+-activated K+ channels are expressed in β-cells. One of them is highly TEA-sensitive (Kd <1 mM), the maxi-KCa (BKCa, slo)-like channels (18,62). Another class of KCa channel genes expressed in β-cells is the small-conductance (SK) channels (18,41). Small-conductance KCa channels, in particular SK4, are only weakly sensitive to TEA (63). These channels could be responsible for a TEA-insensitive voltage-independent Ca2+-dependent current in our model.
Note that our model suggests that the mechanism for specific amplification of spike activity leads to increased [Ca2+]i, which correspondingly may enhance glucose-dependent insulin secretion, similar to the results with blockers of the β-cell KATP channels (Figs. 5 and 6). If useful tissue specificity could be engineered, such blockers might provide alternatives to currently available treatment for type 2 diabetes (3,32,64).
Bursts of APs and the Ca2+ oscillations
Mechanisms that generate and terminate spikes are responsible for the bursts of APs and Ca2+ oscillations. Changes in voltage-gated Ca2+ and K+ currents and/or voltage-independent gating variable currents can take part in burst generation. For example, the spikes and the burst itself can be terminated during a single burst, if some parameters in the equations for voltage-gated currents (for example, IVCa, IKDr, and IKVs in our model) that we accepted as constants can instead change slowly in comparison with a single spike period. This would require drift in a direction leading to Vm repolarization and spike and burst cancellation. Such a mechanism may require modeling of time-dependent changes of coefficients in the equations for voltage-gated currents. However, at this time, there is no experimental evidence for this kind of mechanism. Another hypothesis concerning the mechanisms of spike generation and cancellation during the bursts employs slow cyclic changes in conductance of the voltage-independent gating variable currents. For example:
-
1.
A [Ca2+]i increase during a burst can lead to a decrease in ATP/ADP ratio, leading to opening of KATP channels and plasma membrane depolarization (8,10,16). We found that repolarization followed by a silent interval with a [Ca2+]i decrease can be simulated by a gradual increase of KATP channel conductance after an increase in free [ADP] to 5 μM and 10 μM, correspondingly. Decreasing ADP concentration to initial levels restored spike activity and generated the burst (Fig. 8, A–C).
-
2.
An increase in K+ channel activity can occur via an effect on slowly-activating and deactivated specific Ca2+-activated K+ channels (6,37). This channel was not directly modeled here. However, we were able to reproduce the reversible conductivity changes in Ca2+-activated K+ channels in general. Fig. 8 D shows the burst behavior that can be simulated by an increase and a decrease of IKCa conductance. (Note that in the second and third cases, the behavior of APs and [Ca2+]i was the same as for the first mechanism, and we do not show them separately.)
-
3.
Increased [Ca2+]i can lead to increased [Ca2+] in endoplasmic reticulum. This decreases an inward Na+ or Ca2+ current through nonselective cation channels (16,44,45). We simulated this mechanism by gradually decreasing INab conductance, with a subsequent increase (Fig. 8 E). It also leads to a simulation of the burst and the corresponding Ca2+ changes.
Our simulations in Fig. 8 show clearly that after the large depolarizing effect of closing KATP channels, the subsequent generation and termination of the bursts can be determined by small cyclic changes, in the range of 2 pA, of the background voltage-independent gating variable currents. Several suggestions have been made as to the mechanism that underlies the cyclic changes in the conductivity of some background currents (further discussion can be found in (11,16,17,65)).
Conclusion
Our experiments on Kv2.1−/− mouse islet cells, using specific Kv2.1 channel inhibitors and TEA application with model simulations, demonstrate the importance of Kv2.1 channels and also implicate other KV channels in AP regulation. This suggests that other voltage-gated K+ channels, along with Kv2.1 channels, not only take part in regulating normal spike activity but are able to control spikes in the membrane potential in the absence of Kv2.1 channels. It was possible to achieve a reasonable fit between our experimental results and a general mathematical model by employing a voltage-gated calcium current, a delayed-rectifier K+ current, a small slowly-activating K+ current, and several voltage-gated independent K+ and Na+ background currents. The results of the computer simulations using this adaptable model of islet AP spikes provide insight into the mechanism by which each channel contributes to APs under a variety of experimental conditions.
Appendix: Model Equations and Parameters
Ca2+ current (IVCa)
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
Delayed rectifier K+ current (IKDr)
| (A7) |
| (A8) |
| (A9) |
Slow-activated TEA-insensitive K+ current (IKVs)
| (A10) |
| (A11) |
| (A12) |
ATP-sensitive K+ channel current (IKATP)
| (A13) |
where
| (A14) |
| (A15) |
where OKATP is the fraction of open KATP channels, MgADPf is free Mg-bound ADP, [ADPf]i is free ADP concentration in cytoplasm.
Ca2+-activated K+ current (IKCa)
| (A16) |
where
| (A17) |
Plasma membrane Ca2+ pump current (ICap)
| (A18) |
Na+ background current (INab)
| (A19) |
Acknowledgments
We thank N. Tamarina for helpful discussions. This work was supported by National Institutes of Health grant DK48494 (L.H.P.) and University of Chicago grants DRTC P60 and DK20595.
References
- 1.Ashcroft F.M., Rorsman P. Electrophysiology of the pancreatic β-cell. Prog. Biophys. Mol. Biol. 1989;54:87–143. doi: 10.1016/0079-6107(89)90013-8. [DOI] [PubMed] [Google Scholar]
- 2.Houamed K., Fu J., Roe M.W., Philipson L.H. Electrophysiology of the pancreatic β cell. In: LeRoith D., Taylor S.I., Olefsky J.O., editors. Diabetes Mellitus: A Fundamental and Clinical Text. 3rd ed. Lippincott, Williams and Wilkins; Philadelphia: 2004. pp. 51–68. [Google Scholar]
- 3.Jacobson D.A., Philipson L.H. Action potentials and insulin secretion: new insights into the role of Kv channels. Diabetes Obes. Metab. 2007;9(Suppl 2):89–98. doi: 10.1111/j.1463-1326.2007.00784.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Atwater I., Ribalet B., Rojas E. Mouse pancreatic β-cells: tetrathylammonium blockage of the potassium permeability increase induced by depolarization. J. Physiol. 1979;288:561–574. [PMC free article] [PubMed] [Google Scholar]
- 5.Lebrun P., Atwater I. Effects of the calcium channel agonist, BAY K 8644, on electrical activity in mouse pancreatic β-cells. Biophys. J. 1985;48:919–930. doi: 10.1016/S0006-3495(85)83855-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Göpel S.O., Kanno T., Barg S., Eliasson L., Galvanovskis J. Activation of Ca2+-dependent K+ channels contributes to rhythmic firing of action potentials in mouse pancreatic β-cells. J. Gen. Physiol. 1999;114:759–770. doi: 10.1085/jgp.114.6.759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Antunes C.M., Salgado A.P., Rosario L.M., Santos R.M. Differential patterns of glucose-induced electrical activity and intracellular calcium responses in single mouse and rat pancreatic islets. Diabetes. 2000;49:2028–2038. doi: 10.2337/diabetes.49.12.2028. [DOI] [PubMed] [Google Scholar]
- 8.Kanno T., Rorsman P., Gopel S.O. Glucose-dependent regulation of rhythmic action potential firing in pancreatic β-cells by KATP-channel modulation. J. Physiol. 2002;545:501–507. doi: 10.1113/jphysiol.2002.031344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chay T.R., Keizer J. Minimal model for membrane oscillations in the pancreatic β-cell. Biophys. J. 1983;42:181–190. doi: 10.1016/S0006-3495(83)84384-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Keizer J., Magnus G. ATP-sensitive potassium channel and bursting in the pancreatic beta cell. A theoretical study. Biophys. J. 1989;56:229–242. doi: 10.1016/S0006-3495(89)82669-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sherman A. Contributions of modeling to understanding stimulus-secretion coupling in pancreatic β-cells. Am. J. Physiol. Endocrinol. Metab. 1996;271:E362–E372. doi: 10.1152/ajpendo.1996.271.2.E362. [DOI] [PubMed] [Google Scholar]
- 12.Chay T.R. Effects of extracellular calcium on electrical bursting and intracellular and luminal calcium oscillations in insulin secreting pancreatic β-cells. Biophys. J. 1997;73:1673–1688. doi: 10.1016/S0006-3495(97)78199-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tamarina N.A., Kuznetsov A., Fridlyand L.E., Philipson L.H. Delayed-rectifier (KV2.1) regulation of pancreatic β-cell calcium responses to glucose: inhibitor specificity and modeling. Am. J. Physiol. Endocrinol. Metab. 2005;289:E578–E585. doi: 10.1152/ajpendo.00054.2005. [DOI] [PubMed] [Google Scholar]
- 14.Jacobson D.A., Kuznetsov A., Lopez J.P., Kash S., Ämmälä C.E. Kv2.1 Ablation alters glucose induced islet electrical activity. Enhancing insulin secretion. Cell Metab. 2007;6:229–235. doi: 10.1016/j.cmet.2007.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bao S., Jacobson D.A., Wohltmann M., Bohrer A., Jin W. Glucose homeostasis, insulin secretion, and islet phospholipids in mice that overexpress iPLA2β in pancreatic. β-cells and in iPLA2β-null mice. Am. J. Physiol. Endocrinol. Metab. 2008;294:E217–E229. doi: 10.1152/ajpendo.00474.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fridlyand L.E., Tamarina N., Philipson L.H. Modeling of Ca2+ flux in pancreatic β-cells: role of the plasma membrane and intracellular stores. Am. J. Physiol. Endocrinol. Metab. 2003;285:E138–E154. doi: 10.1152/ajpendo.00194.2002. [DOI] [PubMed] [Google Scholar]
- 17.Fridlyand L.E., Ma L., Philipson L.H. Adenine nucleotide regulation in pancreatic β-cells: modeling of ATP/ADP-Ca2+ interactions. Am. J. Physiol. Endocrinol. Metab. 2005;289:E839–E848. doi: 10.1152/ajpendo.00595.2004. [DOI] [PubMed] [Google Scholar]
- 18.Yang S.N., Berggren P.O. β-cell CaV channel regulation in physiology and pathophysiology. Am. J. Physiol. Endocrinol. Metab. 2005;288:E16–E28. doi: 10.1152/ajpendo.00042.2004. [DOI] [PubMed] [Google Scholar]
- 19.Mears D., Rojas E. Properties of voltage-gated Ca2+ currents measured from mouse pancreatic β-cells in situ. Biol. Res. 2006;39:505–520. doi: 10.4067/s0716-97602006000300012. [DOI] [PubMed] [Google Scholar]
- 20.Nerbonne J.M., Kass R.S. Molecular physiology of cardiac repolarization. Physiol. Rev. 2005;85:1205–1253. doi: 10.1152/physrev.00002.2005. [DOI] [PubMed] [Google Scholar]
- 21.Cens T., Rousset M., Leyris J.P., Fesquet P., Charnet P. Voltage- and calcium-dependent inactivation in high voltage-gated Ca2+ channels. Prog. Biophys. Mol. Biol. 2006;90:104–117. doi: 10.1016/j.pbiomolbio.2005.05.013. [DOI] [PubMed] [Google Scholar]
- 22.Plant T.D. Properties and calcium-dependent inactivation of calcium currents in cultured mouse pancreatic β-cells. J. Physiol. 1988;404:731–747. doi: 10.1113/jphysiol.1988.sp017316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Satin L.S., Cook D.L. Calcium current inactivation in insulin-secreting cells is mediated by calcium influx and membrane depolarization. Pflugers Arch. 1989;414:1–10. doi: 10.1007/BF00585619. [DOI] [PubMed] [Google Scholar]
- 24.Göpel S.O., Kanno T., Barg S., Eliasson L., Galvanovskis J. Voltage-gated and resting membrane currents recorded from β-cells in intact mouse pancreatic islets. J. Physiol. 1999;21:717–728. doi: 10.1111/j.1469-7793.1999.00717.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.DiFrancesco D., Noble D. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1985;307:353–398. doi: 10.1098/rstb.1985.0001. [DOI] [PubMed] [Google Scholar]
- 26.Luo C.H., Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 1994;74:1071–1096. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- 27.Bondarenko V.E., Bett G.C., Rasmusson R.L. A model of graded calcium release and L-type Ca2+ channel inactivation in cardiac muscle. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H1154–H1169. doi: 10.1152/ajpheart.00168.2003. [DOI] [PubMed] [Google Scholar]
- 28.Rorsman P., Trube G. Calcium and delayed potassium currents in mouse pancreatic β-cells under voltage-clamp conditions. J. Physiol. 1986;374:531–550. doi: 10.1113/jphysiol.1986.sp016096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bokvist K., Ammala C., Berggren P.O., Rorsman P., Wahlander K. α2-adrenoreceptor stimulation does not inhibit L-type calcium channels in mouse pancreatic β-cells. Biosci. Rep. 1991;11:147–157. doi: 10.1007/BF01182483. [DOI] [PubMed] [Google Scholar]
- 30.Sherman A., Keizer J., Rinzel J. Domain model for Ca2+-inactivation of Ca2+ channels at low channel density. Biophys. J. 1990;58:985–995. doi: 10.1016/S0006-3495(90)82443-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Smith P.A., Bokvist K., Arkhammar P., Berggren P.-O., Rorsman P. Delayed rectifying and calcium-activated K+ channels and their significance for action potential repolarization in mouse pancreatic Biophys. J -cells. J. Gen. Physiol. 1990;95:1041–1059. doi: 10.1085/jgp.95.6.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacDonald P.E., Ha X.F., Wang J., Smukler S.R., Sun A.M. Members of the Kv1 and Kv2 voltage-dependent K+ channel families regulate insulin secretion. Mol. Endocrinol. 2002;15:1423–1435. doi: 10.1210/mend.15.8.0685. [DOI] [PubMed] [Google Scholar]
- 33.Braun M., Ramracheya R., Bengtsson M., Zhang Q., Karanauskaite J. Voltage-gated ion channels in human pancreatic β-cells. Electrophysiological characterization and role in insulin secretion. Diabetes. 2008;57:1618–1628. doi: 10.2337/db07-0991. [DOI] [PubMed] [Google Scholar]
- 34.Bokvist K., Rorsman P., Smith P.A. Effects of external tetraethylammonium ions and quinine on delayed rectifying K+ channels in mouse pancreatic β-cells. J. Physiol. 1990;423:311–325. doi: 10.1113/jphysiol.1990.sp018024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fatherazi S., Cook D.L. Specificity of tetraethylammonium and quinine for three K+ channels in insulin-secreting cells. J. Membr. Biol. 1991;120:105–114. doi: 10.1007/BF01872393. [DOI] [PubMed] [Google Scholar]
- 36.Su J., Yu H., Lenka N., Hescheler J., Ullrich S. The expression and regulation of depolarization-activated K+ channels in the insulin-secreting cell line INS-1. Pflugers Arch. 2001;442:49–56. doi: 10.1007/s004240000508. [DOI] [PubMed] [Google Scholar]
- 37.Zhang M., Houamed K., Kupershmidt S., Roden D., Satin L.S. Pharmacological properties and functional role of Kslow current in mouse pancreatic β-cells: SK channels contribute to Kslow tail current and modulate insulin secretion. J. Gen. Physiol. 2005;126:353–363. doi: 10.1085/jgp.200509312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rorsman P., Trube G. Glucose dependent K+-channels in pancreatic β-cells are regulated by intracellular ATP. Pflugers Arch. 1985;405:305–309. doi: 10.1007/BF00595682. [DOI] [PubMed] [Google Scholar]
- 39.Misler S., Gee W.M., Gillis K.D., Scharp D.W., Falke L.C. Metabolite-regulated ATP-sensitive K+ channel in human pancreatic islet cells. Diabetes. 1989;38:422–427. doi: 10.2337/diab.38.4.422. [DOI] [PubMed] [Google Scholar]
- 40.Kinard T.A., de Vries G., Sherman A., Satin L.S. Modulation of the bursting properties of single mouse pancreatic β-cells by artificial conductances. Biophys. J. 1999;76:1423–1435. doi: 10.1016/S0006-3495(99)77303-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tamarina N.A., Wang Y., Mariotto L., Kuznetsov A., Bond C. Small-conductance calcium-activated K+ channels are expressed in pancreatic islets and regulate glucose responses. Diabetes. 2003;52:2000–2006. doi: 10.2337/diabetes.52.8.2000. [DOI] [PubMed] [Google Scholar]
- 42.Kozak J.A., Misler S., Logothetis D.E. Characterization of a Ca2+-activated K+ current in insulin-secreting murine βTC-3 cells. J. Physiol. 1998;509:355–370. doi: 10.1111/j.1469-7793.1998.355bn.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hao L., Rigaud J.-L., Inesi G. Ca2+/H+ countertransport and electrogenicity in proteoliposomes containing erythrocyte plasma membrane Ca-ATPase and exogenous lipids. J. Biol. Chem. 1994;269:14268–14275. [PubMed] [Google Scholar]
- 44.Bertram R., Smolen P., Sherman A., Mears D., Atwater I. A role for calcium release-activated current (CRAC) in cholinergic modulation of electrical activity in pancreatic β-cells. Biophys. J. 1995;68:2323–2332. doi: 10.1016/S0006-3495(95)80414-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Roe M.W., Worley J.F., Qian F., Tamarina N., Mittal A.A. Characterization of a Ca2+ release-activated nonselective cation current regulating membrane potential and Ca2+ oscillations in transgenically derived β-cells. J. Biol. Chem. 1998;273:10402–10410. doi: 10.1074/jbc.273.17.10402. [DOI] [PubMed] [Google Scholar]
- 46.Leech C.A., Habener J.F. A role for Ca2+ sensitive nonselective cation channels in regulating the membrane potential of pancreatic β-cells. Diabetes. 1998;47:1066–1073. doi: 10.2337/diabetes.47.7.1066. [DOI] [PubMed] [Google Scholar]
- 47.Jacobson D.A., Philipson L.H. TRP channels of the pancreatic β cell. Handb. Exp. Pharmacol. 2007;179:409–424. doi: 10.1007/978-3-540-34891-7_24. [DOI] [PubMed] [Google Scholar]
- 48.Kelly R.P., Sutton R., Ashcroft F.M. Voltage-activated calcium and potassium currents in human pancreatic β-cells. J. Physiol. 1991;443:175–192. doi: 10.1113/jphysiol.1991.sp018829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pressel D.M., Misler S. Sodium channels contribute to action potential generation in canine and human pancreatic islet β-cells. J. Membr. Biol. 1990;116:273–280. doi: 10.1007/BF01868466. [DOI] [PubMed] [Google Scholar]
- 50.Reference deleted in proof.
- 51.Henquin J.C. Role of voltage- and Ca2+ dependent K+ channels in the control of glucose-induced electrical activity in pancreatic β-cells. Pflugers Arch. 1990;416:568–572. doi: 10.1007/BF00382691. [DOI] [PubMed] [Google Scholar]
- 52.Santos R.M., Rosario L.M., Nadal A., Garcia-Sancho J., Soria B. Widespread synchronous Ca2+ oscillations due to bursting electrical activity in single pancreatic islets. Eur. J. Phys. 1991;418:417–422. doi: 10.1007/BF00550880. [DOI] [PubMed] [Google Scholar]
- 53.Dukes I.D., Philipson L.H. K+ channels: generating excitement in pancreatic β-cells. Diabetes. 1996;45:845–853. doi: 10.2337/diab.45.7.845. [DOI] [PubMed] [Google Scholar]
- 54.MacDonald P.E., Sewing S., Wang J., Joseph J.W., Smukler S.R. Inhibition of Kv2.1 voltage-dependent K+ channels in pancreatic β-cells enhances glucose-dependent insulin secretion. J. Biol. Chem. 2002;22:44938–44945. doi: 10.1074/jbc.M205532200. [DOI] [PubMed] [Google Scholar]
- 55.Ullrich S., Su J., Ranta F., Wittekindt O.H., Ris F. Effects of I(Ks) channel inhibitors in insulin-secreting INS-1 cells. Pflugers Arch. 2005;451:428–436. doi: 10.1007/s00424-005-1479-2. [DOI] [PubMed] [Google Scholar]
- 56.Rosati B., Marchetti P., Crociani O., Lecchi M., Lupi R. Glucose- and arginine-induced insulin secretion by human pancreatic β-cells: the role of HERG K+ channels in firing and release. FASEB J. 2000;14:2601–2610. doi: 10.1096/fj.00-0077com. [DOI] [PubMed] [Google Scholar]
- 57.Mühlbauer E., Bazwinsky I., Wolgast S., Klemenz A., Peschke E. Circadian changes of ether-a-go-go-related-gene (Erg) potassium channel transcripts in the rat pancreas and β-cell. Cell. Mol. Life Sci. 2007;64:768–780. doi: 10.1007/s00018-007-6478-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Schwarz J.R., Bauer C.K. Functions of erg K+ channels in excitable cells. J. Cell. Mol. Med. 2004;8:22–30. doi: 10.1111/j.1582-4934.2004.tb00256.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Berecki G., Zegers J.G., Verkerk A.O., Bhuiyan Z.A., de Jonge B. HERG channel (dys)function revealed by dynamic action potential clamp technique. Biophys. J. 2005;88:566–578. doi: 10.1529/biophysj.104.047290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rudy Y., Silva J.R. Computational biology in the study of cardiac ion channels and cell electrophysiology. Q. Rev. Biophys. 2006;39:57–116. doi: 10.1017/S0033583506004227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Velasco J.M., Petersen O.H. Voltage-activation of high-conductance K+ channel in the insulin-secreting cell line RINm5F is dependent on local extracellular Ca2+ concentration. Biochim. Biophys. Acta. 1987;896:305–310. doi: 10.1016/0005-2736(87)90191-x. [DOI] [PubMed] [Google Scholar]
- 62.Tabcharani J.A., Misler S. Ca2+-activated K+ channel in rat pancreatic islet β cells: permeation, gating and blockade by cations. Biochim. Biophys. Acta. 1989;982:62–72. doi: 10.1016/0005-2736(89)90174-0. [DOI] [PubMed] [Google Scholar]
- 63.Joiner W.J., Wang L.Y., Tang M.D., Kaczmarek L.K. hSK4, a member of a novel subfamily of calcium-activated potassium channels. Proc. Natl. Acad. Sci. USA. 1997;94:11013–11018. doi: 10.1073/pnas.94.20.11013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Herrington J., Zhou Y.-P., Bugianesi R.M., Dulski P.M., Feng Y. Blockers of the delayed-rectifier potassium current in pancreatic β-cells enhance glucose-dependent insulin secretion. Diabetes. 2006;55:1034–1042. doi: 10.2337/diabetes.55.04.06.db05-0788. [DOI] [PubMed] [Google Scholar]
- 65.Bertram R., Sherman A., Satin L.S. Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am. J. Physiol. Endocrinol. Metab. 2007;293:E890–E900. doi: 10.1152/ajpendo.00359.2007. [DOI] [PubMed] [Google Scholar]