Abstract
Uptake of low density lipoprotein (LDL) by the arterial wall is likely to play a key role in atherogenesis. A particular process that may cause vascular scale heterogeneity in the rate of transendothelial LDL transport is the formation of a flow-dependent LDL concentration polarization layer on the luminal surface of the arterial endothelium. In this study, the effect of a spatially heterogeneous transmural water flux (that traverses the endothelium only via interendothelial cell clefts) on such concentration polarization is investigated numerically. Unlike in previous investigations, realistic intercellular cleft dimensions are used here and several values of LDL diffusivity are considered. Particular attention is paid to the spatially averaged LDL concentration adjacent to different regions of the endothelial surface, as such measures may be relevant to the rate of transendothelial LDL transport. It is demonstrated in principle that a heterogeneous transmural water flux can act to enhance such measures, and cause them to develop a shear dependence (in addition to that caused by vascular scale flow features, affecting the overall degree of LDL concentration polarization). However, it is shown that this enhancement and additional shear dependence are likely to be negligible for a physiologically realistic transmural flux velocity of 0.0439 μm s−1 and an LDL diffusivity (in blood plasma) of 28.67 μm2 s−1. Hence, the results imply that vascular scale studies of LDL concentration polarization are justified in ignoring the effect of a spatially heterogeneous transmural water flux.
Introduction
Atherosclerosis is a prevalent cardiovascular disease, characterized by the formation of lipid-rich lesions (or plaques) within the walls of arteries. Such lesions are known to occur in a spatially heterogeneous fashion, developing preferentially in regions of arterial branching and high curvature. Since these particular regions are associated with complex blood flow patterns it has been postulated that blood flow, which is also spatially heterogeneous at the vascular scale, may play an important role in modulating atherogenesis.
Several mechanisms that could lead to a flow dependence of atherogenesis have been suggested (1,2). One particular mechanism involves the formation of a low density lipoprotein (LDL)-rich layer adjacent to the luminal surface of the arterial endothelium (3,4), postulated to form as a result of a phenomenon called concentration polarization. Concentration polarization can occur when fluid containing a dissolved solute is forced to pass through a membrane. If the membrane offers a higher resistance to the solute than the fluid, then solute will be rejected by the membrane and accumulate on its upstream surface. It is this process of solute accumulation that is referred to as “concentration polarization”. The layer of rejected solute is often referred to as a “concentration polarization layer”.
LDL concentration polarization is postulated to occur in arteries due to the transmural water flux that flows radially outwards (from the lumen) through the arterial walls. There is an imbalance between the measured velocity of this water flux (∼4 × 10−2 μm s−1 (5)) and the permeability of the endothelium to LDL (∼2 × 10−4 μm s−1 (6)). Due to this imbalance, LDL convection toward the luminal surface of the endothelium is likely to be far greater that the rate of transendothelial LDL transport, resulting in the formation of an LDL-rich (concentration polarization) layer adjacent to the endothelial surface.
The dominant route by which LDL crosses the endothelium and enters the arterial wall is unknown. It is observed, however, that increasing plasma LDL concentration (and hence endothelial exposure to LDL) increases the rate of transendothelial LDL transport (7). Such a finding implies that the amount of LDL concentration polarization, which determines LDL concentration adjacent to the endothelium, could act to modulate the rate of LDL transport into the intima, and thus the likelihood of atherosclerosis occurring. If the local degree of LDL concentration polarization is dependent on vascular scale flow features, then the above mechanism provides a viable explanation for the observed flow dependence of atherogenesis.
Experiments suggest that a flow-dependent LDL concentration polarization layer does form within the vasculature (8,9). These experimental results are supported by vascular scale theoretical studies (10,11), which also quantify how the degree of concentration polarization might depend on vascular scale flow features. Due to their vascular scale nature, however, such theoretical studies overlook several features of the endothelial surface. In particular they do not account for the fact that the transmural water flux is likely to be spatially heterogeneous at the subcellular scale. Such heterogeneity arises because water traverses the endothelium predominantly via intercellular clefts between neighboring endothelial cells, rather than through the cells themselves (12). Also, within intercellular clefts there exists a complex structure of connections referred to as tight junction strands (13). These are thought to form a disjointed barrier around almost the entire cell periphery, with the passage of water occurring preferentially at locations where the junction strands are broken. Such structures within the depth of each cleft may result in further spatial localization of the transendothelial water flux.
Previous review articles (2,14) have stated that a heterogeneous transmural water flux is likely to affect LDL concentration polarization within the vasculature. However, the precise nature of such an effect and its influence on the flow-dependent entry of LDL into the arterial wall have not been established, and are not intuitively obvious. The problem has been addressed by one earlier numerical study (15). This previous study, however, did not use realistic intercellular cleft dimensions, nor did it fully investigate a realistic range of LDL diffusivities. The present study aims to assess the effect of a heterogeneous water flux on LDL concentration polarization using an idealized model with realistic parameter values. Particular attention is paid to measures of the concentration polarization layer that may quantify its effect on the rate of transendothelial LDL transport.
Overview of Idealized Model
The model is developed within a cellular-scale domain adjacent to the luminal surface of the arterial endothelium. The following general assumptions are made:
Only transport of water and LDL are considered; all other constituents of the blood are ignored.
It is assumed that LDL has no effect on the motion of the water.
It has been observed that an endothelial glycocalyx layer (EGL) covers the luminal surface of the endothelium (16). Previous studies have predicted that flow parallel to the endothelium is significantly retarded within the EGL, and that spatial heterogeneity in the transmural water flux is likely to be retained even at the luminal surface of the EGL (17). Based on these results, the EGL will be ignored in this simple model. This approach is in line with that adopted in previous studies of mass transport above the endothelium (18).
In reality, blood flow is pulsatile. Here, however, all dynamics within the domain are considered to be at steady state. This assumption reduces the size of the relevant parameter space and hence simplifies the analysis. The implications of making this assumption are discussed when the results are presented.
Idealized Model of Water Flow
Heterogeneous transmural flux
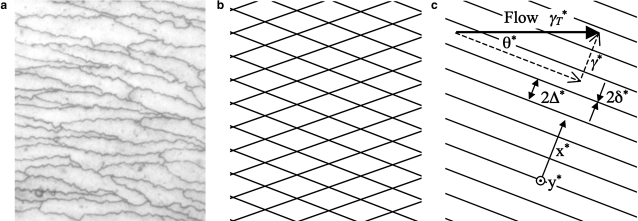
It is assumed that water traverses the endothelium only via intercellular clefts. Fig. 1 a depicts an en face view of the endothelium illustrating a typical pattern of interendothelial cell cleft entrances. As a first approximation, it is reasonable to represent the intercellular clefts by a repeating diamond pattern (Fig. 1 b). Here, however, a further simplification is made and the clefts are modeled as an infinite series of parallel outflow slits of width 2δ∗ and interslit spacing 2Δ∗ (Fig. 1 c). The domain is considered sufficiently small that the curvature of the arterial wall can be ignored. Hence, the infinitely long parallel outflow slits in Fig. 1 c are assumed to reside in a flat plane.
Figure 1.
Mouse endothelial cells shown in a (personal communication from A. R. Bond, Bristol Royal Infirmary, UK, 2007) appear approximately diamond-shaped (cleft entrances are stained dark using silver nitrate). Based on this observation, the cleft entrance structure can be approximated as a repeating diamond pattern (b), or even further simplified to an infinitely repeating array of infinitely long parallel outflow slits as shown in c. The simplified geometry (c) is characterized by only three parameters, namely the cleft half-width δ∗, the cleft half-spacing Δ∗, and the angle θ∗ between the clefts and the applied flow. (Reused with permission from P. E. Vincent et al., Physics of Fluids, 20, 063106 (2008). Copyright 2008, American Institute of Physics.)
A transmural water flux with an average velocity is drawn toward the endothelium via the application of a parabolic outflow velocity profile (with peak magnitude ) across the width of each cleft entrance. This profile is maintained uniformly along the length of each cleft. Applying such an entrance velocity profile is an approximation for two reasons. Firstly, it assumes the widthwise flow profile develops instantaneously to become parabolic, and secondly it neglects any further localization of the flow caused by tight junction strands (13) blocking portions of the clefts. The former of these two approximations is unlikely to have a significant effect on the results. However, the implications of the latter approximation are less clear, and will be discussed when the results are presented. Both of the approximations could be avoided by adding an idealization of the clefts internal structure to the model.
The formulation described above allows the direct enforcement of a measured transmural flux magnitude; it is not necessary to apply a pressure drop to drive the flow. Such an approach simplifies calculations, as it avoids having to couple equations governing the water velocity with those governing species concentration (which would be necessary to account for the effects of osmotic pressure).
Applied shear
It is assumed that the domain of interest resides within the momentum boundary layer. This is a layer of slow flow adjacent to the arterial wall within which viscous forces dominate. It is further assumed that this boundary layer is laminar (i.e., the flow is not turbulent). The outflow slits, which represent the intercellular clefts, are aligned at an angle θ∗ to the boundary layer flow, which applies a constant shear rate γT∗ to the endothelium (Fig. 1 c). Such alignment results in a shear rate of γ∗ = γT∗ sin θ∗ being applied perpendicular to the lengthwise extent of the clefts (in the x∗ direction). The shear rate applied to the domain is considered spatially constant, as the cellular scale domain is assumed to be small compared to the scale of spatial variations in the momentum boundary layer.
Domain
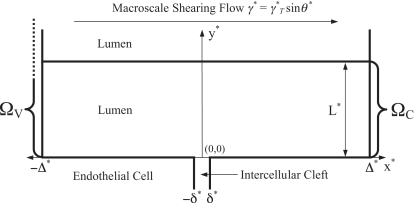
As a result of the simplifications outlined above, the problem becomes two-dimensional in nature. The periodically repeating semiinfinite two-dimensional domain of interest ΩV within which water motion is considered is illustrated in Fig. 2.
Figure 2.
Idealized periodically repeating domains ΩV and ΩC. ΩV is semiinfinite. However ΩC ⊂ ΩV is of finite extent in the y∗ direction, bounded between y∗ = 0 and y∗ = L∗. The depth of the intercellular cleft is not included in either domain.
Governing equations
The continuum approximation for water holds even at the scale of the intercellular clefts (19). Therefore, water is modeled as a free fluid within ΩV. For any flowing fluid a Reynolds number (Re) can be defined (thought of as the ratio between inertial and viscous forces within the flow). For water flow within ΩV Re ≪ 1, and hence, flow is dominated by viscous forces. Therefore the water velocity field v∗ within ΩV is a solution of the continuity equation
| (1) |
and Stokes equation
| (2) |
where μ∗ is the dynamic viscosity of water and p∗ is the hydrodynamic pressure in ΩV.
Nondimensionalization
Defining
| (3) |
where and are unit vectors in the x and y directions, respectively, and substituting Eq. 3 into Eqs. 1 and 2, one obtains the nondimensional governing equations
| (4) |
| (5) |
Consistent with these conventions, a nondimensional cleft half-width δ and nondimensional applied shear rate γ can be defined as
| (6) |
It should be noted that the conventions used to nondimensionalize Eqs. 1 and 2 are different to those used in our previous study of flow above the endothelium (17). The definition of γ is therefore also different to that used by Vincent et al. (17).
Nondimensional boundary conditions
To motivate development of the domain illustrated in Fig. 2, several boundary conditions have already been discussed. For clarity, all nondimensional conditions applied to Eqs. 4 and 5 are defined below.
Periodicity in x
Because the domain is periodic in x, it is required on physical grounds that the velocity fields at x = ±1 and the stress traction vectors acting on the interdomain interfaces at x = ±1 are continuous. Defining σ as the nondimensional stress tensor within ΩV, these interface conditions can be written as
| (7) |
and
| (8) |
where the negative sign on the right-hand side of Eq. 8 accounts for the fact that the traction vectors are obtained from normals of opposite sense.
Conditions at y = 0
A no-slip boundary condition is applied at y = 0, hence
| (9) |
In addition, a parabolic outflow velocity profile with peak (nondimensional) magnitude 3/(2δ) is applied at the entrance to the cleft, hence
| (10) |
Large y behavior
As y → ∞, the x component of the velocity should tend to γy, hence
| (11) |
Idealized Model of LDL Transport
Domain and governing equation
Fig. 2 illustrates the domain ΩC ⊂ ΩV within which the LDL distribution C∗ is obtained. ΩC is periodic in x∗. However, unlike ΩV, it is finite in y∗, being bounded between y∗ = 0 and y∗ = L∗. The choice of a suitable value for the height of the domain will be discussed shortly. Within ΩC it is assumed that C∗ is a solution of the steady-state advection diffusion equation
| (12) |
where D∗L is the diffusivity of LDL in the lumen.
Interface with vascular scale simulations
Definition of macroscale concentration polarization layer
The cellular scale nature of ΩC precludes the model developed in this study from describing the effect of vascular scale flow features on LDL concentration polarization adjacent to the arterial wall. Such a task can only be accomplished by a vascular scale simulation of blood flow and LDL transport.
Consider modeling the formation of an LDL concentration polarization layer within an artery at the vascular scale. Further, consider that the vascular scale model assumes LDL is rejected from the endothelial surface, and that the transmural water flux is spatially homogeneous with a velocity (the same average velocity as the heterogeneous transmural flux considered in this study). The concentration polarization layer predicted to form under the above assumptions will henceforth be referred to as the “macroscale LDL concentration polarization layer”. It will be assumed here that the macroscale concentration polarization layer is spatially constant at the cellular scale, and can be represented within the cellular scale vicinity of ΩC as a stagnant film (20). Such assumptions imply that the macroscale concentration polarization layer has a thickness ζ∗ within the vicinity of ΩC, given by
| (13) |
and a concentration profile within the layer, defined in terms of the y∗ coordinate illustrated in Fig. 2 as
| (14) |
where C∗E is the LDL concentration adjacent to the endothelium within the cellular scale locality of ΩC and CB∗ is the bulk LDL concentration in the lumen.
It should be noted that the actual profile of the macroscale concentration polarization layer will deviate slightly from within the locality of ΩC. Such deviation occurs because the stagnant film model does not explicitly account for LDL convection parallel to the endothelium, which is responsible for limiting the growth of the macroscale concentration polarization layer into the lumen. Instead, the stagnant film model requires a priori prescription of the macroscale concentration polarization layer thickness ζ∗ (or equivalently the parameters that define ζ∗ via Eq. 13).
Thickness of macroscale concentration polarization layer
Consider the diffusional transport of a species within a fluid. An associated Schmidt number (Sc) can be defined as the ratio of the dynamic viscosity of the fluid (the momentum diffusivity) to the diffusivity of the species within the fluid. For LDL in blood Sc ≫ 1, implying that the rate of diffusional momentum transport is far greater than the rate of diffusional LDL transport. Based on this imbalance in transport rates, it can be assumed that ζ∗ is substantially less than the thickness of the momentum boundary layer within the vicinity of ΩC.
Objective
The objective of the model developed here is to determine modifications (caused by a heterogeneous transmural water flux) to the macroscale concentration polarization layer within the cellular scale domain ΩC (when the domain is located at an arbitrary point on the arterial wall).
Nondimensionalization
Since CE∗ (the LDL concentration predicted to occur adjacent to the arterial wall within the cellular scale locality of ΩC due to a homogeneous transmural flux) is assumed to be spatially constant within ΩC, a nondimensional concentration distribution C can be defined as
| (15) |
Using Eq. 15 and relevant relations from Eq. 3, Eq. 12 can be nondimensionalized to give
| (16) |
where
| (17) |
is a Peclet number associated with the spatially heterogeneous convection toward the intercellular clefts. Consistent with the above conventions, a nondimensional domain height L and a nondimensional macroscale concentration polarization layer thickness ζ can be defined as
| (18) |
In addition, a nondimensional concentration profile within the macroscale concentration polarization layer can be defined as
| (19) |
Nondimensional boundary conditions
Periodicity in x
The domain is periodic in x, hence
| (20) |
| (21) |
Condition at y = 0
LDL can cross the vascular endothelium via both paracellular (21) and transcellular (22–24) routes. The dominant route for transendothelial LDL transport in vivo is still, however, a point of contention (25).
Paracellular transport of LDL through “normal” intercellular clefts is considered unlikely, given that they contain tight junctional strands. A small fraction of clefts, however, are thought to be leaky. Such leaky clefts provide a viable route for the paracellular transport of LDL (26). The periodicity of ΩC implies that all intercellular clefts considered here must be identical, i.e., either all normal or all leaky. In this study it is assumed that all the clefts are normal, and therefore that LDL is rejected from the cleft entrances. This is a reasonable assumption since the large majority of clefts are normal. However, it obviously precludes this study from investigating the effect of leaky clefts on LDL concentration polarization, and also precludes this study from assessing the effect of LDL concentration polarization on paracellular LDL transport.
Transcellular transport of LDL is thought to occur via vesicular pathways (transcytosis) or transcellular pores. Macroscale measurements of endothelial permeability to LDL (6) indicate that the rate of transcellular LDL transport is negligible compared to the bulk rate at which LDL is convected toward the endothelium by the transmural water flux (5). The effect of transcellular LDL transport can therefore be ignored when investigating LDL concentration polarization adjacent to the endothelium. In this study, it will be assumed that the rate of transcellular LDL transport is zero (i.e., that LDL is completely rejected from the surface of the endothelial cells). Note that although this assumption precludes transcellular LDL transport from having an effect on LDL concentration polarization, it does not preclude the degree of concentration polarization from having an effect on the rate of transcellular LDL transport; the latter can still be estimated by postprocessing the obtained concentration polarization results.
In summary, it is assumed that LDL is completely rejected from the endothelial surface. Convection must therefore balance diffusion at y = 0, and hence
| (22) |
Condition at y = L
The following three a priori assumptions are made regarding the nature of modifications (caused by a heterogeneous transmural water flux) to the macroscale concentration polarization layer:
Modifications do not affect the overall thickness ζ of the macroscale concentration polarization layer. This is equivalent to stating that ζ is determined only by vascular scale flow features.
- Beyond a nondimensional distance y = κ from the endothelium, the nondimensional concentration field solutions C obtained within ΩC are approximately one-dimensional and given by
where the constant Z will depend on the boundary condition applied at y = L. Such behavior is to be expected for two reasons. Firstly, two-dimensional perturbations to the velocity field decay with y, causing the problem to become one-dimensional in nature as y increases, and secondly, it is assumed that LDL is completely rejected from the endothelium at y = 0.(23) The macroscale concentration polarization layer is not completely destroyed by modifications arising from a heterogeneous water flux. i.e., ζ > κ. The validity of this assumption and any restrictions that it places on the results are assessed in Appendix A.
The first assumption can be enforced by requiring that for y > κ the solution C within ΩC tends toward the macroscale solution . Via the second and third assumptions this trivially implies that Z = 1, which can be enforced by applying
| (24) |
where L can be chosen arbitrarily but must satisfy L > κ.
Implementation
Water velocity field
The water velocity field v within ΩV can be obtained analytically. Consider defining a stream function ψ such that
| (25) |
where u and v are the x and y components of v, respectively. The nondimensional governing equations (Eqs. 4 and 5) can be reformulated in terms of ψ as
| (26) |
A suitable trial solution to Eq. 25 that is able to satisfy all relevant boundary conditions can be written as
| (27) |
where, to ensure periodicity in x,
| (28) |
An and Bn (which can depend on n) and G and J are all constants to be determined via the application of the boundary conditions defined by Eqs. 9–11. Applying these conditions results in
| (29) |
| (30) |
| (31) |
and
| (32) |
Expressions for u and v can therefore be written as
| (33) |
| (34) |
Note that v depends on only two parameters, δ and γ.
LDL concentration field
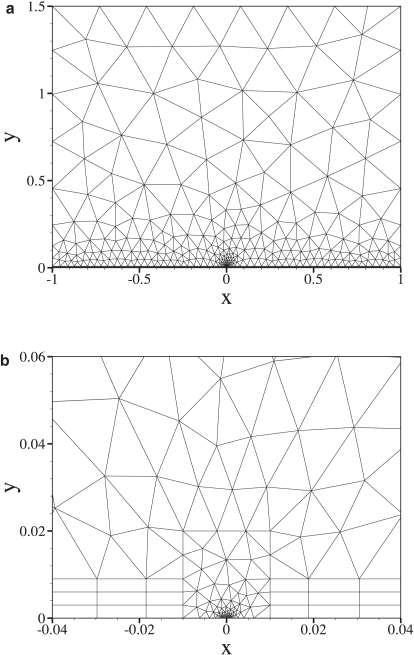
Solutions to Eq. 16 are obtained numerically using the spectral/hp element galerkin approximation (27). The domain ΩC is meshed in an unstructured fashion with triangular and quadrangular elements. Within each element the solution is represented using two-dimensional modal basis functions, which are generated from tensor products of one-dimensional polynomial bases of 9th order. An example mesh is shown in Fig. 3 a. Smaller elements are used in the region near the intercellular cleft as shown in Fig. 3 b. Convergence of the numerical solutions is assessed in Appendix B.
Figure 3.
An example computational mesh of the entire domain ΩC (a). Smaller elements are concentrated near the intercellular cleft (b).
Note that concentration field solutions C depend on v, and hence on δ and γ, as well as on the Peclet number Pec.
Parameter values
Value for the nondimensional cleft half-width δ
Values of Δ∗ = 10 μm and δ∗ = 0.01 μm are considered to be physiologically realistic, resulting in a fixed value of δ = 0.001.
Values for the nondimensional applied shear rate γ
Shear rates in the range γ∗ = 0–1000 s−1 are considered, along with transmural flux velocities in the range = 0.02–0.08 μm s−1. The transmural flux velocity of 0.0439 μm s−1 obtained by Tedgui and Lever (5) sits within this range. Based on these values (and using Δ∗ = 10 μm), a range of γ = 0–5 × 105 is used here. For the physiologically realistic value of = 0.0439 μm s−1 (and using Δ∗ = 10 μm), only the limited range of γ = 0–2.28 × 105 is relevant.
Values for the Peclet number Pec
The choice of a suitable value for LDL diffusivity within the lumen D∗L is contentious. In several vascular scale studies, a value of D∗L = 5 μm2 s−1 has been used (11,28). However, it has been suggested (2) that this value is unrealistically low and may therefore artificially enhance any LDL concentration polarization. Cellular scale studies have also used a value of D∗L = 5 μm2 s−1 (15), where the value has been obtained via the Stokes Einstein equation using the viscosity of whole blood. Such an approach is, however, unjustified since at the cellular scale red blood cells should be regarded as discreet objects, and thus LDL should be considered as residing and diffusing within the blood plasma. A range of D∗L = 1–100 μm2 s−1 is considered in the following analysis. This range spans an order of magnitude either side of D∗L = 28.67 μm2 s−1, the measured diffusivity of LDL in blood plasma (29). Based on this range for D∗L, and the value for Δ∗ and the range for given above, a range of Pec = 0.002 – 0.8 is considered here. When using values of Δ∗ = 10 μm, = 0.0439 μm s−1, and D∗L = 28.67 μm2 s−1 (suggested here to be physiologically realistic), a value of Pec = 0.015 is obtained. When using values of Δ∗ = 10 μm, = 0.04 μm s−1, and D∗L = 5 μm2 s−1 (the transmural flux velocity and LDL diffusivity often used in previous studies (10,11,15)), an increased value of Pec = 0.08 is obtained.
It should be noted that certain combinations of γ and Pec are unattainable within the limits of the dimensional parameter ranges given above. Specifically, for the dimensional parameter ranges used here, if Pec > 0.2 then it is required that γ < (1 × 105/Pec). Such a limitation should be taken into account when the nondimensional parameters γ and Pec are varied.
Value for the nondimensional height L of ΩC
For all cases, a value of L = 1.5 is used. This value is large enough that L > κ is always satisfied.
Results and Analysis
Water velocity field
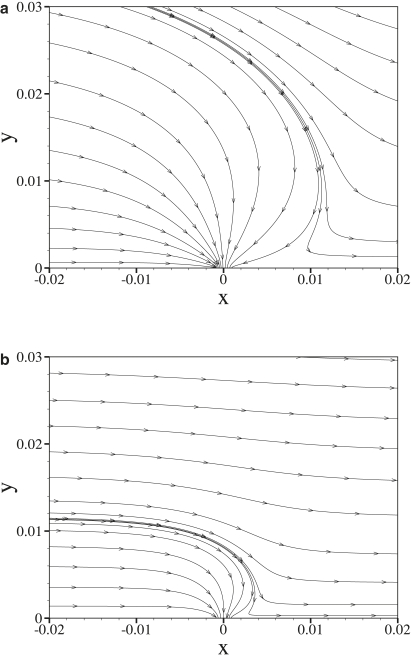
Fig. 4 shows streamlines of the water velocity field in the vicinity of an intercellular cleft for two values of the nondimensional shear rate γ, with fixed δ = 0.001. As γ is increased, perturbations to the velocity field caused by flow into the intercellular clefts protrude less far into the lumen.
Figure 4.
Velocity streamlines in the vicinity of an intercellular cleft obtained using γ = 3 × 103 (a) and γ = 3 × 104 (b) with fixed δ = 0.001.
LDL concentration field
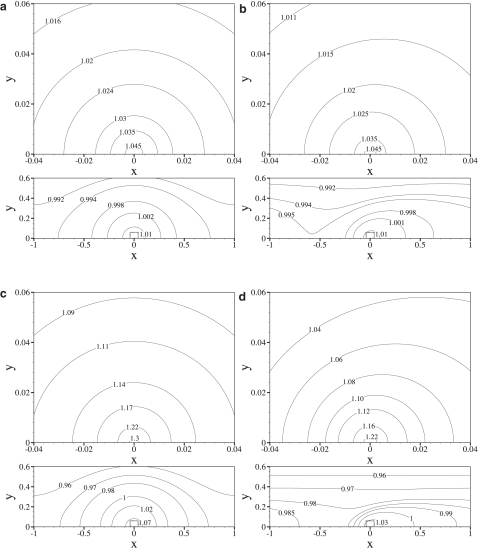
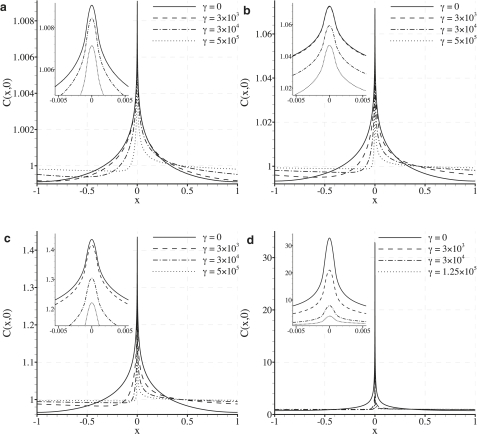
Fig. 5 shows contour plots of the nondimensionalized LDL concentration field C for various values of γ and Pec, with fixed δ = 0.001. Fig. 6 shows plots of the nondimensional LDL concentration adjacent to the endothelium (at y = 0). Again, various values of γ and Pec are considered, with fixed δ = 0.001. Note that the scale of the C(x, 0) axis in Fig. 6 changes between plots.
Figure 5.
Contour plots of C obtained using values of γ = 0 and Pec = 0.015 (a), γ = 3 × 103 and Pec = 0.015 (b), γ = 0 and Pec = 0.08 (c), and γ = 3 × 103 and Pec = 0.08 (d), all with fixed δ = 0.001. Within each subfigure, the upper plot is an enlargement of the region in the dotted box marked on the lower plot. Note that a spatially homogeneous transmural water flux (with the same average velocity as the heterogeneous flux used here) would result in a constant nondimensional concentration of unity adjacent to the endothelium.
Figure 6.
Plots illustrating how the LDL distribution adjacent to the endothelium varies with γ for Pec = 0.002 (a), Pec = 0.015 (b), Pec = 0.08 (c), and Pec = 0.8 (d) with fixed δ = 0.001. Intercellular clefts are centered at x = 0. Note that a spatially homogeneous transmural water flux (with the same average velocity as the heterogeneous flux used here) would result in a constant nondimensional concentration of unity adjacent to the endothelium.
Shear-dependent subcellular scale heterogeneity in the LDL concentration polarization layer is observed for all values of Pec, with peaks in LDL concentration localized above intercellular clefts (at x = 0). Such localization is expected, since LDL is convected directly toward the clefts by the heterogeneous transmural water flux, but cannot pass through them. As γ is raised, the peaks in LDL concentration become increasingly skewed (swept downstream), spreading the LDL distribution more evenly over the endothelial surface and reducing the peak LDL concentration above the clefts.
For the case of Pec = 0.015 (considered here to be the most physiologically realistic), the degree of heterogeneity in the LDL concentration polarization layer is relatively small. Specifically, peaks in the LDL concentration profile adjacent to the endothelium are only 7.2% (2 s.f.) greater than the average LDL concentration adjacent to the endothelium predicted by a vascular scale simulation using a homogeneous transmural water flux. This relatively small degree of heterogeneity is due to the fact that Pec ≪ 1 in this realistic case, and hence diffusional transport of LDL dominates over convective transport toward the clefts. For the case of Pec = 0.08 (obtained using values for the transmural water velocity and LDL diffusivity suggested in previous studies (10,11,15)), a more significant degree of heterogeneity is observed. Specifically, peaks in the LDL concentration profile adjacent to the endothelium are 43% (2 s.f.) greater than the average LDL concentration adjacent to the endothelium predicted by a vascular scale simulation using a homogeneous transmural water flux. For the case of Pec = 0.8, convective transport of LDL by the heterogeneous transmural flux becomes important, and the LDL concentration polarization develops very significant spatial heterogeneity. Specifically, peaks in LDL concentration adjacent to the endothelium are 3300% (2 s.f.) greater than the average LDL concentration adjacent to the endothelium predicted by a vascular scale simulation using a homogeneous transmural water flux. It should be noted, however, that a value of Pec = 0.8 is unlikely to occur physiologically.
Rate of transendothelial LDL transport
Definitions
Leaky junctions are not represented in this model. Therefore, the implications of the results for the rate of paracellular LDL transport cannot be assessed. It is still possible, however, to consider measures of the concentration polarization layer that may be relevant to the rate of transcellular LDL transport across the endothelium. Two such measures are considered. The first is simply the average nondimensional LDL concentration adjacent to the entire endothelium. This is denoted CU and defined as
| (35) |
CU is a reasonable measure to use if the endothelium is considered uniformly permeable to LDL at the cellular scale. The second measure is the average nondimensional LDL concentration adjacent to the endothelium within a (nondimensional) distance of 1/10 from each cleft center. This is denoted CN and defined as
| (36) |
CN may be more relevant to the rate of transcellular LDL transport than CU, since evidence suggests that caveolae, which can facilitate LDL transcytosis, are localized near cell borders (30, 31). Further, endothelial cells are thinner at their edges and have a nucleus near their center. These structural features may also increase the relative ease of transcellular LDL transport near the borders of endothelial cells.
It should be noted that both CU and CN are obtained from LDL concentration fields that have been nondimensionalized by CE∗. Therefore, the measures are independent of vascular scale flow features (which affect the macroscale LDL concentration polarization layer). The measures only reflect additional (possibly flow-dependent) modifications to the LDL concentration polarization layer caused by the heterogeneous transmural water flux.
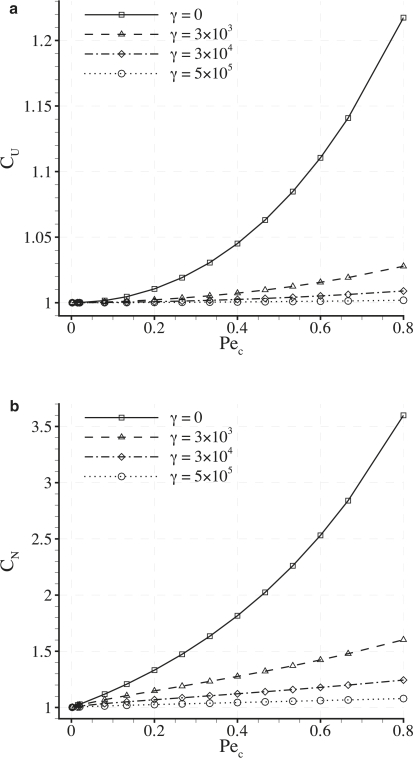
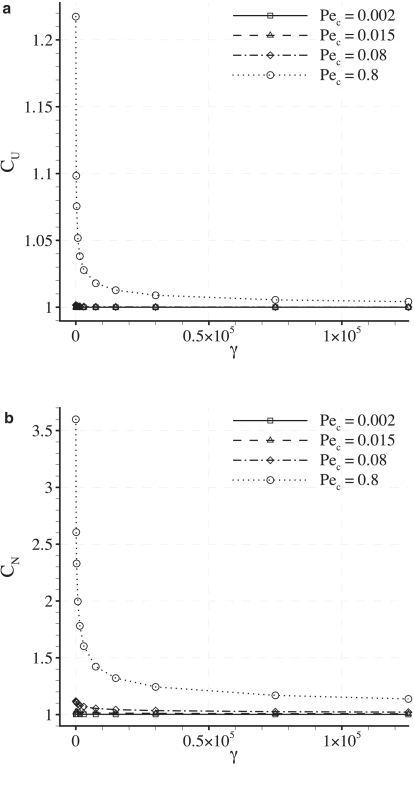
Dependence of CU and CN on Pec
Fig. 7 shows plots of CU and CN against Pec for various values of γ with fixed δ = 0.001. It can be seen that both CU and CN increase as Pec is increased (up to a value of Pec = 0.8). It can also be seen that values of CU and CN are greater than unity in all cases. Finally, it can be observed that values of CN are always greater than values of CU obtained using the same parameters, reflecting the fact that LDL is convected toward the intercellular clefts. These results indicate that the heterogeneous transmural flux acts to enhance the measures CU and CN to values greater than those resulting from a homogeneous transmural flux with the same average velocity (which are unity by definition). However, for cases where Pec = 0.015 (considered here to be physiologically realistic), both CU and CN exceed unity by only a negligible amount.
Figure 7.
Plots of CU (a) and CN (b) against Pec for various values of γ with fixed δ = 0.001.
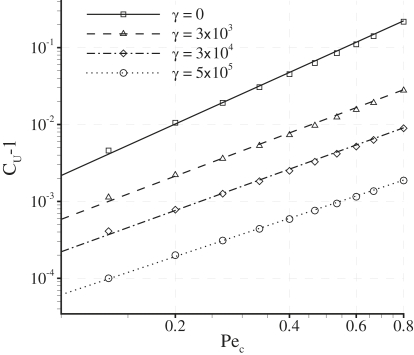
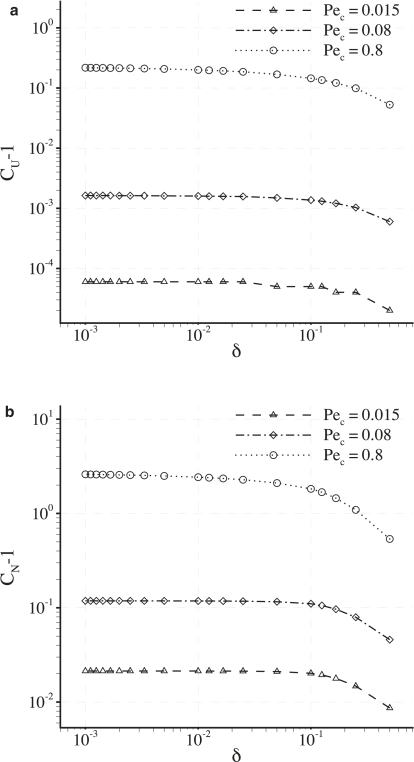
Fig. 8 shows a log-log plot of (CU − 1) against Pec. The straight lines indicate that, for a given value of γ (and when Pec < 0.8), a relationship exists between CU and Pec of the form
| (37) |
where both α and β depend on the value of γ considered.
Figure 8.
Plots of (CU − 1) against Pec for various values of γ with fixed δ = 0.001. The plots are on a log-log scale and hence the straight lines indicate a power law relationship between (CU − 1) and Pec.
Dependence of CU and CN on γ
Fig. 9 shows plots of CU and CN against γ for various values of Pec with fixed δ = 0.001. For the case of Pec = 0.015 (considered here to be physiologically realistic), both CU and CN vary negligibly with γ. For the case of Pec = 0.08 (obtained using values for the transmural water velocity and LDL diffusivity suggested in previous studies (10,11,15)), CU varies negligibly with γ, but CN decreases by 11% (2 s.f.) as γ varies between 0 and 5 × 105. For the case of Pec = 0.8, both CU and CN deviate significantly from unity and exhibit a pronounced shear dependence.
Figure 9.
Plots of CU (a) and CN (b) against γ for various values of Pec with fixed δ = 0.001.
It has been shown in previous studies (10,11) that vascular scale flow features may affect the overall degree of LDL concentration polarization adjacent to the endothelium, potentially resulting in a flow-dependent rate of transendothelial LDL transport. The results in Fig. 9 indicate that, in principle, a spatially heterogeneous transmural water flux can cause an additional shear (and hence flow) dependence of transendothelial LDL transport if Pec ∼ 1. However, this additional shear dependence is observed to be insignificant for the physiological value of Pec = 0.015.
Extending the parameter space
The behavior of solutions within an extended parameter space is briefly investigated. Such behavior is unlikely to have physiological relevance. However, it does put the physiological solutions into context.
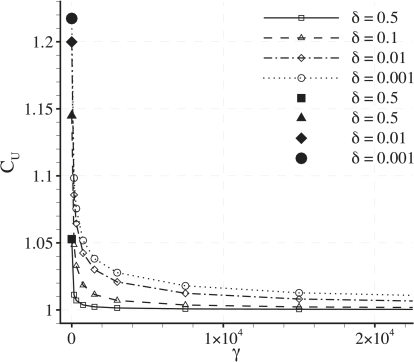
The previous results were obtained using a fixed (physiologically reasonable) value of δ = 0.001. Fig. 10 illustrates the effect of varying δ on CU and CN for various values of Pec with fixed γ = 0. It can be seen that both CU and CN asymptote toward a constant value as δ decreases. Specifically, for the physiological value of Pec = 0.015, CU and CN become independent of δ when δ < 0.01. Therefore, CU and CN are likely to be independent of δ for all physiologically reasonable parameter values.
Figure 10.
Plots of (CU − 1) (a) and (CN − 1) (b) against δ for various values of Pec with fixed γ = 0. The plots are on a log-log scale.
It has been shown in Fig. 9 a that CU becomes shear-dependent if Pec ∼1. Specifically, results for the case of Pec = 0.8 were presented. Fig. 11 shows further plots of CU against γ with fixed Pec = 0.8 for various values of δ. The shear dependence of CU decreases significantly as δ is increased. This observation supports the assertion that a heterogeneous transmural water flux facilitates the shear dependence of CU.
Figure 11.
Plots of CU against γ for various values of δ with fixed Pec = 0.8. The larger solid symbols at γ = 0 help to indicate where each line begins.
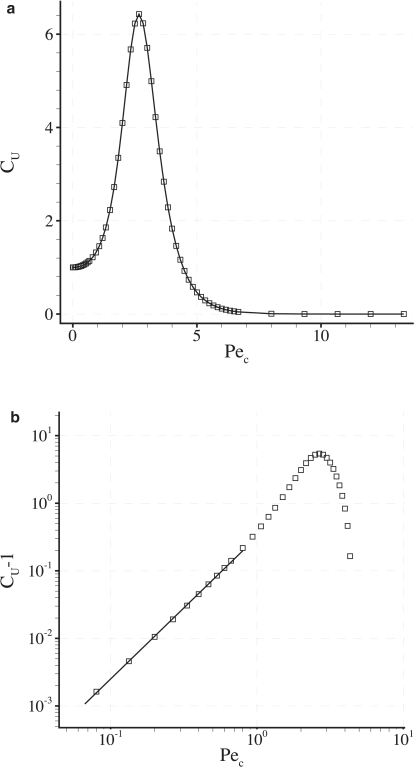
Fig. 12 a shows a plot of CU against Pec for fixed γ = 0 and δ = 0.001. An extended range of Pec = 0.002–13.3 is considered. It can be seen that a value of Pec exists that maximizes CU. Also, as Pec becomes large, CU → 0. Fig. 12 b shows a log-log plot of (CU − 1) against Pec for fixed δ = 0.001 and γ = 0. Beyond Pec ∼1, the power-law relationship between (CU − 1) and Pec observed in Fig. 8 breaks down, indicating that the relationship is not valid when transport is dominated by convection.
Figure 12.
Plots of CU against Pec (a) and (CU-1) against Pec (b) for fixed γ = 0 and δ = 0.001. The plot in b is on a log-log scale. The solid straight line in b highlights the power law relationship between (CU-1) and Pec previously observed in Fig. 8. This power-law relationship is seen to break down when Pec > 1.
Implications of neglecting tight junction strands
The effect of tight junction strands on the cleft entrance velocity profile has been ignored in this simple model. In reality, such strands (which form within the depth of the intercellular clefts) are likely to block water flow through certain portions of the cleft, further localizing flow to a subarea of each cleft entrance. The results obtained in this study indicate that CU and CN depend strongly on the Peclet number Pec (which can be thought of as the total water flux toward each cleft), but very weakly on the nondimensional cleft half-width δ (which determines how localized this total flux becomes at each cleft entrance). Increased localization of flow at the cleft entrances due to the presence of tight junction strands is therefore unlikely to have a significant impact on the results. It should be noted, however, that such an assertion can only be confirmed by developing a model that explicitly includes tight junction strands (or at least their effect on the cleft entrance velocity profile).
Implications of neglecting pulsatile blood flow
Since blood flow is pulsatile, the shear rate applied to ΩV should vary with time. Time-dependent studies (the details of which are omitted for brevity) indicate that the LDL concentration field within ΩC is not completely quasisteady when exposed to pulsatile flow, i.e., additional time-dependent dynamics do exist. It is found, however, that when a physiologically realistic value of Pec = 0.015 is considered, time-averaged values of CU and CN remain almost exactly unity and independent of the applied flow form. The main findings of the steady-state analysis presented in this study are therefore not affected by the application of a time-dependent shear rate to ΩV.
Conclusions
The results indicate that a spatially heterogeneous transmural water flux will cause spatially heterogeneous and shear-dependent modifications to any LDL concentration polarization layer that develops adjacent to the endothelium. Measures of the concentration polarization layer that may be relevant to the rate of transendothelial LDL transport have been defined and calculated. It has been demonstrated, in principle, that a spatially heterogeneous transmural water flux can act to enhance such measures, and cause them to develop a flow dependence (in addition to any flow dependence of LDL uptake caused by vascular scale flow features affecting the overall degree of LDL concentration polarization). However, it has been shown that this enhancement and additional flow dependence are unlikely to be significant for physiological values of the Peclet number Pec. The results imply that for physiologically realistic parameter values, vascular scale studies of LDL concentration polarization are justified in ignoring the effect of a spatially heterogeneous transmural water flux.
Appendix A: Applicability
It has been assumed a priori that ζ > κ. Such an assumption puts a limit on the applicability of the model. Consider defining
| (38) |
as a measure of the y dependent deviation of the nondimensional concentration field C from the macroscale concentration polarization layer produced by a homogeneous transmural flux. For a given result C, κ can be quantitatively defined as the value of y such that
| (39) |
where ε is a tolerance taken to be ε = 0.005. The value of κ obtained for a given result C is equal to the nondimensional thickness ζ of the thinnest macroscale concentration polarization layer to which the model can be applied. Employing Eq. 13, one can define a minimum LDL concentration adjacent to the endothelium, C∗Em, associated with this minimum layer thickness as
| (40) |
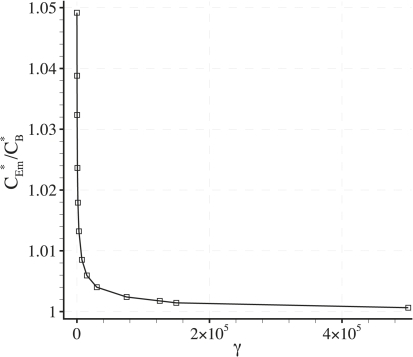
The value of κ and hence C∗Em will vary with δ, γ, and Pec. Fig. 13 shows plots of C∗Em/CB∗ against γ for values of δ = 0.001 and Pec = 0.08. This particular value of Pec allows comparisons to be made with plots of CE∗/CB∗ against γ produced by Wada et al. (11) for an artery with multiple bends.
Figure 13.
Plot of C∗Em/CB∗ against γ with fixed δ = 0.001 and Pec = 0.08.
Comparison of Fig. 13 with the results of Wada and Karino (11) shows that C∗Em/CB∗ < CE∗/CB∗, for the majority of points adjacent to the luminal surface the arterial wall. This result indicates that the applicability of the model is not significantly limited by the a priori assumption that κ < ζ (i.e., the assumption that the macroscale concentration polarization layer is not completely destroyed by heterogeneous modifications).
Appendix B: Convergence of the Concentration Field Solutions
Consider representing C within each element of the domain using two-dimensional modal basis functions generated from tensor products of one-dimensional bases of Mth order. Based on the relevant measure of interest CN, an M-dependent measure of error E(M) in the solution C can be defined as
| (41) |
where CN(M) is the value of CN obtained from a simulation using a two-dimensional basis within each element generated from Mth order one-dimensional bases, and CN(14) is the value of CN obtained from a simulation using a two-dimensional basis within each element generated from 14th order one-dimensional bases (viewed as a definitive solution).
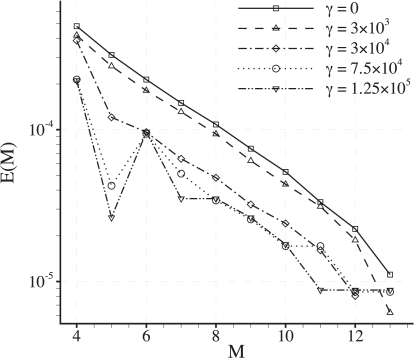
Convergence of E(M) with increasing M (for a given mesh) is assessed for cases where Pec = 0.8. Within the range Pec = 0.002–0.8 such cases can be viewed as the most demanding from a convergence standpoint, because they produce the most spatially heterogeneous solutions. Fig. 14 shows plots of E(M) against M for various values of γ with fixed δ = 0.001 and Pec = 0.8. Note that when using Pec = 0.8 the maximum value of γ attainable given the dimensional parameter ranges is 1.25 × 105. For all values of γ the errors E(M) are seen to converge approximately exponentially with M. For the value of M = 9 used here the relative error E(9) < 1 × 10−4 for all values of γ.
Figure 14.
Plots of E(M) against M for various values of γ with fixed δ = 0.001 and Pec = 0.8.
Acknowledgments
The authors thank Profs. Kim Parker, Charles Michel, Sheldon Weinbaum, David Rumschitzki, and John Tarbell for useful discussions.
This work was funded by the Engineering and Physical Sciences Research Council.
References
- 1.White C.R., Frangos J.A. The shear stress of it all: the cell membrane and mechanochemical transduction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2007;362:1459–1467. doi: 10.1098/rstb.2007.2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ethier C.R. Computational modeling of mass transfer and links to atherosclerosis. Ann. Biomed. Eng. 2002;30:461–471. doi: 10.1114/1.1468890. [DOI] [PubMed] [Google Scholar]
- 3.Colton C.K., Friedman S., Wilson D.E., Lees R.S. Ultrafiltration of lipoproteins through a synthetic membrane. Implications for the filtration theory of atherogenesis. J. Clin. Invest. 1972;51:2472–2481. doi: 10.1172/JCI107061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Keller K.H. The influence of shear dependent diffusion in blood on atherogenesis and thrombogenesis. In: Nerem R.M., editor. Fluid Dynamics Aspects of Arterial Disease. Ohio State University; Columbus, OH: 1974. [Google Scholar]
- 5.Tedgui A., Lever M.J. Filtration through damaged and undamaged rabbit thoracic aorta. Am. J. Physiol. 1984;247:H784–H791. doi: 10.1152/ajpheart.1984.247.5.H784. [DOI] [PubMed] [Google Scholar]
- 6.Bratzler R.L., Chisolm G.M., Colton C.K., Smith K.A., Lees R.S. The distribution of labeled low-density lipoproteins across the rabbit thoracic aorta in vivo. Atherosclerosis. 1977;28:289–307. doi: 10.1016/0021-9150(77)90177-0. [DOI] [PubMed] [Google Scholar]
- 7.Nielsen L.B. Transfer of low density lipoprotein into the arterial wall and risk of atherosclerosis. Atherosclerosis. 1996;123:1–15. doi: 10.1016/0021-9150(96)05802-9. [DOI] [PubMed] [Google Scholar]
- 8.Deng X., Marois Y., How T., Merhi Y., King M. Luminal surface concentration of lipoprotein (LDL) and its effect on the wall uptake of cholesterol by canine carotid arteries. J. Vasc. Surg. 1995;21:135–145. doi: 10.1016/s0741-5214(95)70252-0. [DOI] [PubMed] [Google Scholar]
- 9.Wang G., Deng X., Guidoin R. Concentration polarization of macromolecules in canine carotid arteries and its implication for the localization of atherogenesis. J. Biomech. 2003;36:45–51. doi: 10.1016/s0021-9290(02)00277-4. [DOI] [PubMed] [Google Scholar]
- 10.Wada S., Koujiya M., Karino T. Theoretical study of the effect of local flow disturbances on the concentration of low-density lipoproteins at the luminal surface of end-to-end anastomosed vessels. Med. Biol. Eng. Comput. 2002;40:576–587. doi: 10.1007/BF02345458. [DOI] [PubMed] [Google Scholar]
- 11.Wada S., Karino T. Theoretical prediction of low-density lipoproteins concentration at the luminal surface of an artery with a multiple bend. Ann. Biomed. Eng. 2002;30:778–791. doi: 10.1114/1.1495868. [DOI] [PubMed] [Google Scholar]
- 12.Clough G., Michel C.C. Quantitative comparisons of hydraulic permeability and endothelial intercellular cleft dimensions in single frog capillaries. J. Physiol. 1988;405:563–576. doi: 10.1113/jphysiol.1988.sp017348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Adamson R.H., Michel C.C. Pathways through the intercellular clefts of frog mesenteric capillaries. J. Physiol. 1993;466:303–327. [PMC free article] [PubMed] [Google Scholar]
- 14.Tarbell J.M. Mass transport in arteries and the localization of atherosclerosis. Annu. Rev. Biomed. Eng. 2003;5:79–118. doi: 10.1146/annurev.bioeng.5.040202.121529. [DOI] [PubMed] [Google Scholar]
- 15.Wada S., Karino T. Prediction of LDL concentration at the luminal surface of a vascular endothelium. Biorheology. 2002;39:331–336. [PubMed] [Google Scholar]
- 16.Weinbaum S., Tarbell J.M., Damiano E.R. The structure and function of the endothelial glycocalyx layer. Annu. Rev. Biomed. Eng. 2007;9:121–167. doi: 10.1146/annurev.bioeng.9.060906.151959. [DOI] [PubMed] [Google Scholar]
- 17.Vincent P.E., Sherwin S.J., Weinberg P.D. Viscous flow over outflow slits covered by an anisotropic Brinkman medium: a model of flow above interendothelial cell clefts. Phys. Fluids. 2008;20:063106–063111. [Google Scholar]
- 18.Hodgson L., Tarbell J.M. Solute transport to the endothelial intercellular cleft: the effect of wall shear stress. Ann. Biomed. Eng. 2002;30:936–945. doi: 10.1114/1.1507846. [DOI] [PubMed] [Google Scholar]
- 19.Squires T.M., Quake S.R. Microfluidics: fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005;77:977–1018. [Google Scholar]
- 20.Zeman L.J., Zydney A.L. CRC Press; Boca Raton, FL: 1996. Microfiltration and Ultrafiltration: Principles and Applications. [Google Scholar]
- 21.Cancel L.M., Fitting A., Tarbell J.M. In vitro study of LDL transport under pressurized (convective) conditions. Am. J. Physiol. Heart Circ. Physiol. 2007;293:H126–H132. doi: 10.1152/ajpheart.01188.2006. [DOI] [PubMed] [Google Scholar]
- 22.Vasile E., Simionescu M., Simionescu N. Visualization of the binding, endocytosis, and transcytosis of low-density lipoprotein in the arterial endothelium in situ. J. Cell Biol. 1983;96:1677–1689. doi: 10.1083/jcb.96.6.1677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Simionescu M., Gafencu A., Antohe F. Transcytosis of plasma macromolecules in endothelial cells: a cell biological survey. Microsc. Res. Tech. 2002;57:269–288. doi: 10.1002/jemt.10086. [DOI] [PubMed] [Google Scholar]
- 24.Tuma P.L., Hubbard A.L. Transcytosis: crossing cellular barriers. Physiol. Rev. 2003;83:871–932. doi: 10.1152/physrev.00001.2003. [DOI] [PubMed] [Google Scholar]
- 25.Kao C.H., Chen J.K., Kuo J.S., Yang V.C. Visualization of the transport pathways of low density lipoproteins across the endothelial cells in the branched regions of rat arteries. Atherosclerosis. 1995;116:27–41. doi: 10.1016/0021-9150(95)05519-3. [DOI] [PubMed] [Google Scholar]
- 26.Lin S.J., Jan K.M., Weinbaum S., Chien S. Transendothelial transport of low density lipoprotein in association with cell mitosis in rat aorta. Arteriosclerosis. 1989;9:230–236. doi: 10.1161/01.atv.9.2.230. [DOI] [PubMed] [Google Scholar]
- 27.Karniadakis G.E., Sherwin S.J. Oxford Scientific Publications; Oxford, UK: 2005. Spectral/HP Element Methods for Computational Fluid Dynamics. [Google Scholar]
- 28.Stangeby D.K., Ethier C.R. Computational analysis of coupled blood-wall arterial LDL transport. J. Biomech. Eng. 2002;124:1–8. doi: 10.1115/1.1427041. [DOI] [PubMed] [Google Scholar]
- 29.Karner G., Perktold H.P., Zehentner K. Computational modeling of macromolecule transport in the arterial wall. Comput. Methods Biomech. Biomed. Eng. 2001;4:491–504. [Google Scholar]
- 30.Millan J., Hewlett L., Glyn M., Toomre D., Clark P. Lymphocyte transcellular migration occurs through recruitment of endothelial ICAM-1 to caveola- and F-actin-rich domains. Nat. Cell Biol. 2006;8:113–123. doi: 10.1038/ncb1356. [DOI] [PubMed] [Google Scholar]
- 31.Sprenger R.R., Fontijn R.D., van Marle J., Pannekoek H., Horrevoets A.J.G. Spatial segregation of transport and signaling functions between human endothelial caveolae and lipid raft proteomes. Biochem. J. 2006;400:401–410. doi: 10.1042/BJ20060355. [DOI] [PMC free article] [PubMed] [Google Scholar]