Transitions between Closed and Open Conformations of TolC: The Effects of Ions in Simulations

Abstract

Bacteria, such as Escherichia coli, use multidrug efflux pumps to export toxic substrates through their cell membranes. Upon formation of an efflux pump, the aperture of its outer membrane protein TolC opens and thereby enables the extrusion of substrate molecules. The specialty of TolC is its ability to dock to different transporters, making it a highly versatile export protein. Within this study, the transition between two conformations of TolC that are both available as crystal structures was investigated using all-atom molecular dynamics simulations. To create a partially open conformation from a closed one, the stability of the periplasmic aperture was weakened by a double point mutation at the constricting ring, which removes some salt bridges and hydrogen bonds. These mutants, which showed partial opening in previous experiments, did not spontaneously open during a 20-ns equilibration at physiological values of the KCl solution. Detailed analysis of the constricting ring revealed that the cations of the solvent were able to constitute ionic bonds in place of the removed salt bridges, which inhibited the opening of the aperture in simulations. To remove the ions from these binding positions within the available simulation time, an extra force was applied onto the ions. To keep the effect of this additional force rather flexible, it was applied in form of an artificial external electric field perpendicular to the membrane. Depending on the field direction and the ion concentration, these simulations led to a partial opening. In experiments, this energy barrier for the ions can be overcome by thermal fluctuations on a longer timescale.

Introduction

During the last few decades, the problem of antibiotic resistance rose to a serious problem within the field of antibacterial treatment (1). One reason is the evolutionary overexpression of multidrug efflux pumps within the bacteria's cell envelope (2,3). In Gram-negative bacteria, e.g., Escherichia coli (E. coli) or Pseudomonas aeruginosa (P. aeruginosa), the cell envelope consists of two lipid bilayers, so-called membranes, with the periplasm in between. A large number of proteins have been found to be embedded in both the inner and the outer membrane of E. coli (4–6). There are also systems of proteins that span over the whole cell envelope, creating a pathway from the cytoplasm or the inner membrane's outer leaflet to the extracellular space (7). One important transport class therein is the multidrug efflux pumps. These efflux systems are employed to export antibacterial drugs such as antibiotics as well as protein toxins out of the cell. This mechanism can diminish the effect of certain classes of antibiotics. Hence, new antibiotics have to be found which are able to overcome this mechanism (8–10).

Embedded within the outer membrane, proteins belonging to the outer membrane factor family (11), like the channel-tunnel protein TolC (12), act as exit ducts for different efflux pumps. It is believed that TolC is closed (13) as long as it is not connected to any compatible inner-membrane transporter (14), e.g., HlyB (15) or AcrB (16–18) of E. coli. These examples describe the versatility, because in contrast to AcrB which is a RND transporter driven by proton-motive forces, HlyB is an ABC transporter which uses ATP to export its substrates. The closed structure of TolC shall ensure that no substrate is able to flow from the extracellular space into the periplasm. Furthermore, a membrane fusion protein (19) is required to stabilize the fusion of transporter and tunnel; in the two cases above, these are HlyD and AcrA (20), respectively. The number of membrane fusion proteins needed to form a functioning efflux pump of, e.g., AcrB and TolC, is so far not well known, but in Zgurskaya and Nikaido (21), AcrA was proposed to be a trimer. While connecting to a transporter, the periplasmic aperture of TolC shall open iris-like (22), but the final aperture radius might depend on the corresponding transporter. Additionally, it was shown that, under certain circumstances, the antibiotic vancomycin is able to use the TolC-HlyB complex as entrance into the periplasm (23,24).

To understand the mechanism of TolC docking to a transporter, it has to be investigated in which way the TolC aperture opens upon docking. Furthermore, it has to be examined which residues are responsible for keeping the protein closed and how the residues belonging to the aperture move into an open conformation. By understanding this transition and the final state, it is possible to study the transport of ions and translocation of antibiotics through TolC in its open state. Finally, one can get a better insight into how TolC docks to transporters like AcrB or HlyB.

The crystal structure of TolC has been published in 2000 (13) and shows a mono-barrel homotrimer (see Fig. 1 B). The 100 Å long, periplasmic tunnel of coiled coils consists of 12 α-helices with two pairs from each monomer (Fig. 1 A). One pair of each monomer is turned toward the center of the tunnel forming the aperture at the lower periplasmic end. In the middle of this periplasmic part, the equatorial domain is situated around the helices, which contains both short α-helices and short β-strands and probably functions as a hinge for the opening motions of the other helices. The other part of TolC, which is, in vivo, embedded in the outer membrane, consists of 12 β-sheets that form a 40 Å long β-barrellike a channel through the membrane. The diameter of this channel is roughly 35 Å.

Figure 1.

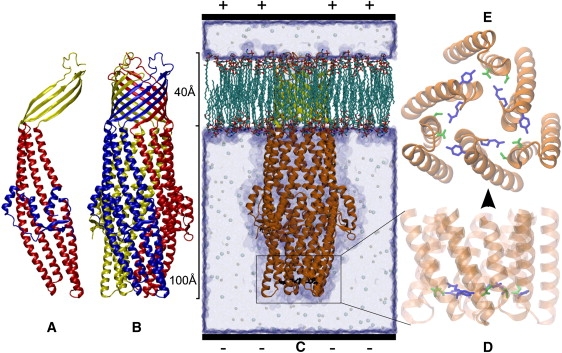
TolC protein structure in cartoon representation of the secondary structure (50) with (A) the β-barrel above and α-helical coiled coils below. (B) The monomers in different colors. (C) The protein in a simulation box with the orientation of the positive applied voltage (see Simulation Setup). (D) Zoom to the aperture with the constricting ring in licorice representation of the side chains (dark shaded, T152 and D153; light shaded, Y362 and R367). (E) Side view of panel D looking from the periplasm toward the membrane part (figures created with VMD (40)).

Most previous ideas and hypotheses that describe the open state and/or the opening mechanism when getting into contact with its counterparts to form an efflux pump were based on rigid body assumptions (22,25–27). In one very recent study (28), all-atom and coarse-grained molecular dynamics (MD) have been employed to investigate dynamical properties of wild-type (Wt) and one mutated TolC. These simulations as well as this one greatly differ from the rigid-body studies, because the flexibility of the protein structure is taken into account, enabling us to observe uncoiling of the periplasmic-coiled coils. Basically, springs and structural angle constraints are used to describe the quantum-mechanical nature of the chemical bonds that ensure the stability of the protein. In Vaccaro et al. (28), only equilibrium simulations have been performed and analyzed, whereas in this article, external forces are applied in most of the simulations.

Motivated by a recent crystal structure (29) of a TolC double mutant showing a partially open conformation, we simulated two comparable double mutants and the Wt structure to investigate the dynamic differences that lead to the opening. As in the experiment, the point mutations have been symmetrically applied to two residues of all three monomers in the constricting ring (Fig. 1 E, blue), which in vivo, keeps the aperture closed via salt bridges and H-bonds. This allows us to compare the Wt to two double mutants, derived from the Wt, as well as to the open crystal structure. Additionally, we also simulated the corresponding single mutants to one double mutant, which helped us to examine the importance of each point mutation for the effects to be observed in the double mutant.

Since our mutants are derived from the Wt crystal structure, they are in a closed conformation that allows us to dynamically observe how TolC might open due to the removal of the bonds in the constricting ring. In this article, the following questions will be addressed, among other topics:

• Is it possible to observe opening of the TolC aperture during ≈10-ns-long MD simulations?

• Will both double mutants (or any single mutant) relax into conformations that are similar to the open crystal structure?

• Is it possible to speed up the simulations by applying an electric (steering) field in such a way that the closed TolC structure transits into a partially open structure?

As will be shown below, applying an electric steering field for speeding up the simulations can be very important in obtaining the opening dynamics in the short simulation time available. The steering field enables us to overcome certain energy barriers that typically require much more time to be passed by thermal fluctuations. On the one hand, studying the effect of electric fields was motivated by recent investigations in MD simulations of membranes and membrane proteins (30–35) where their properties, including stability of the lipid bilayer and the protein structure, were investigated. (Using this information, we could ensure that no artificial effects due to the electric field occurred.) On the other hand, the electric steering field was motivated by the so-called grid-steered MD (36), which has been developed to steer molecules through membrane pores. In this study as well as in our investigations, the artificially applied electric field is used to speed up the MD simulations and is not meant to be applied in experiments. Additionally, several experimental studies have been performed on TolC (37–39), which helped us to focus on the important segments of the protein, i.e., basically the aperture region with a ring of residues that stabilize the constriction.

Simulation Setup

As stated above, the crystal structure of the wild-type (PDB code 1EK9) is simulated and compared to mutated versions of the same structure as well as a partially opened crystal structure. In contrast to the mutations in the literature (37–39) and to the mutation in the recent MD study (28), the mutations for the partially open crystal structure by Bavro et al. (29), Y362F and R367E, have been applied (i.e., tyrosine 362 is replaced by phenylalanine and arginine 367 by glutamate). For this mutant, two crystal structures with the symmetry variants C2 and P2₁2₁2₁, PDB codes 2VDD and 2VDE, respectively, were obtained. The two symmetry variants are due to variations in the crystallization setup. The simulations denoted “MCryst” below were started from the PDB 2VDE and compared to simulations starting from the closed crystal structure derived from Wt, but with the mutations equal to MCryst denoted “MGlu.” Thus, the sequence of the residues in the mutated crystal structure MCryst and our similar computer-generated mutant MGlu are identical. To investigate whether the effects on the mutant are due to the change in charge and/or length of the side chain, we also applied a double mutation Y362F and R367D, i.e., residue 367 is mutated into an aspartate which has a shorter side chain than the mutated residue above. This mutant is denoted “MAsp” in the simulations according to the amino acid into which the second residue is mutated (see Table 1).

Table 1.

Simulations

Mutation	Index	KCl Conc. [M]	Natoms	Voltage [V]	Time [ns]
Wild-type	Wt1a	0.1	203,907	+1.0	20
	Wt1b			−1.0	20
	Wt2a	1	200,547	+1.0	20
Y362F+R367D	MAsp1a	0.1	203,868	+1.0	20
	MAsp1b			−1.0	20
	MAsp2a	1	200,508	+1.0	30
Y362F+R367E	MGlu0a	0	204,067	+1.0	20
	MGlu0b			−1.0	20
	MGlu1a	0.1	203,877	+1.0	30
	MGlu1b			−1.0	20
	MGlu2a	1	200,517	+1.0	20
Y362F+R367E Crystallized	MCryst1a	0.1	198,139	+1.0	20
	MCryst1b			−1.0	10

Details of the different simulations: The index carries a character 0 at the end for a neutralized system with just the required number of counterions (24 potassium), a 1 for a 0.1 M concentration, and a 2 for a 1 M concentration. Furthermore, the voltage can be read from the last letter of the index: a for +1 V, b for −1 V.

Using VMD (40), the crystal structure of TolC was aligned to the z axis with the periplasmic helices pointing in positive z direction, placed into a preequilibrated POPE lipid bilayer in the x-y plane and solvated in TIP3P water (41). At the end of the buildup phase, all lipid and water atoms that overlapped with the protein have been removed. Furthermore, KCl ions have been added at random positions in the water to neutralize the charge of the protein and to generate specific salt concentrations (0.1 M and 1 M). This setup leads to a periodic box size of ≈(107 × 107 × 173) ų after the equilibration of the Wt, with slight deviations for the mutants shown in Table 1. These mutants have been obtained using the Mutator plug-in of VMD.

For the MD simulations, the MD program NAMD (42) was employed together with the CHARMM27 force field (43) and periodic boundary conditions. The particle-mesh Ewald method was used with a grid spacing of maximal 1 Å per grid point in each dimension. After minimizing the system for up to 50,000 steps, the atom velocities were randomly chosen to resemble a Maxwell distribution. The temperature was kept at 310 K by applying Langevin forces to all heavy atoms with the Langevin damping constant set to 5 ps⁻¹. The integration time step was chosen to be 1 fs, to ensure the accuracy of the simulations under applied voltages. During the equilibrations, the pressure was kept at 1.01325 bar for 10 ns in the NpT ensemble using the Nosé-Hoover Langevin piston pressure control. The van der Waals energies were calculated using a smooth cutoff (switching radius 10 Å, cutoff radius 12 Å). All subsequent simulations with an external electric voltage were carried out in the NVT ensemble with the direction of the field parallel to the z axis (see Fig. 1 C).

Although the simulations with electric steering fields have been run for at least 20 ns, only the later 10 ns have been used for deep analysis (see Table 1). During the simulations with applied voltage, the β-barrel of TolC has been constrained to the central position of the simulation box. The constraints were imposed by harmonic forces with the force constants set to 1 kcal/M Ų. We want to emphasize once more that the external electric field is used as steering force to speed up the MD simulations similar to the grid-steered MD (36). For example, within a simulation with an applied electric voltage of 1 V, the additional force experienced by monovalent charges is of magnitude of F ≈ 9 pN parallel to the z axis, which would correspond to an energy W ≈ 1 k_BT if an monovalent ion is moved 5 Å against the field direction. This sample calculation is based on the field strength, an approximation for the electrostatic force and corresponding work. The proposed ion movement, which will be discussed below, would also take place by thermal motion on a timescale larger than milliseconds. This is far beyond the timescales accessible by MD simulations.

Results

In the following, we analyze the simulations described in Table 1. Before going into the details of the individual simulations, we show in Fig. 2 that the simulation results of the Wt structure and the MAsp as well as MGlu mutants are qualitatively different when applying an external steering voltage. As can be clearly seen, the Wt structure remains in its closed conformation while the mutated versions open partially. Furthermore, Fig. 2 visualizes that the mutant MAsp opens asymmetrically, which appears to be qualitatively similar to the asymmetric C2 crystal structure reported in Bavro et al. (29). This asymmetry makes it inappropriate to use circular area calculations for the opening area. To quantify the effects of opening, we calculated the distances between representative aperture residues for which we chose G365 (Fig. 2). Again, the asymmetric opening of the MAsp mutant becomes apparent. Additionally, the last row shall visualize the paths of the aperture tips (C_α atoms of G365), which also indicates that they do not move equally.

Figure 2.

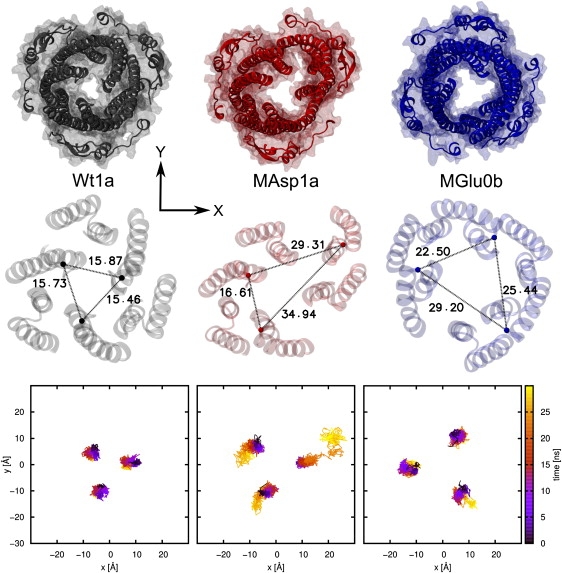
Results of simulations with applied voltage: In the first row, snapshots of the protein with backbone (cartoon) and all-atom (transparent surface) representation of the last frame are drawn using the same perspective as in Fig. 1E. In the second line, the distances (in Å) between the C_α atoms (van der Waals representation) of G365 are displayed with the protein backbone in transparent cartoon representation. In the third line, the traces of the residue G365 C_α atoms are shown with time-dependent coloring, starting from the equilibration.

To be able to compare the degrees of opening using one number, we calculated the triangular area between the C_α atoms of the residues G365 to get an average over the three monomers. This is certainly not the only way to calculate the area of the aperture that is actually overestimated, but it is easy to perform, and works in asymmetric structures for which other measures might not. Using methods to calculate the area of the channel more accurately at the position of residue G365 lead to certain problems, because the protein structure can no longer be described by a closed surface as one approaches conformations that are more open. The residue G365 was chosen in accordance with Bavro et al. (29), and shall indicate the motion of the helix pairs, but not the change of the internal area at the constriction, which is difficult to calculate because of the asymmetry. For comparison, the real internal area at the constriction of the Wt crystal structure can be estimated with A ≈ 16.7 Ų (or radius r = 2.3 Å) using the program CAVER (44). As mentioned above, this program calculates only a circular area.

An alternative approach to visualize and quantify the motion of the residues belonging to the aperture is called the porcupine plot, used before, e.g., in Barrett et al. (45) and Tömroth-Horsefield et al. (46). It is employed in Fig. 3 to represent the direction and magnitude of the deviation per residue below the equatorial domain. Here, the deviation for the final structure of MGlu0b with respect to the partially open crystal structure (2VDE) is shown using a color scale indicating the magnitude and the maximum deviation (values <2 Å are not shown). As can be seen easily, two monomers moved further away from the reference while the third one remained close to it. Looking at the trajectory of MGlu0b, the aperture is approximately passing through the state of the partially open crystal structure. We want to note in passing that the aperture is not moving closer to the membrane, indicated by the upper image. This can be also verified during the whole trajectory (data not shown).

Figure 3.

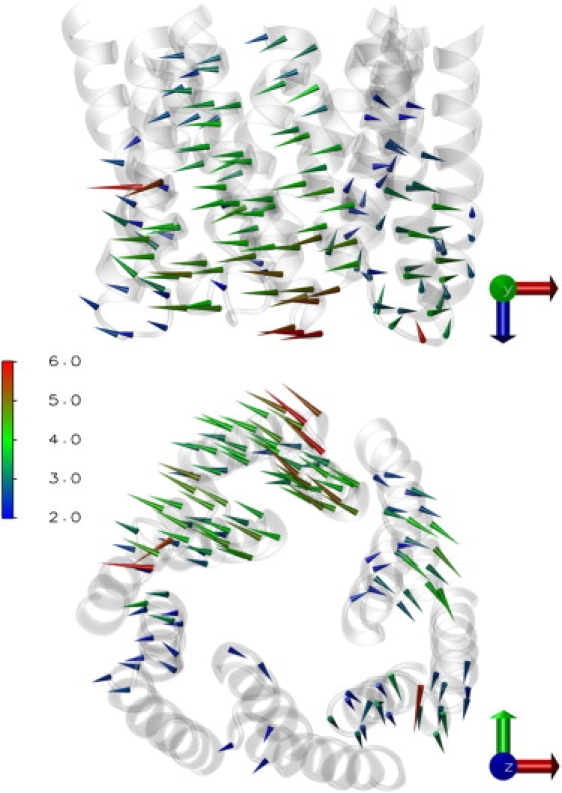
Porcupine plot pointing from open crystal structure (2VDE) to MGlu0b final structure with arrows per residue C_α atom lengthened and colored due to deviation value (values <2 Å omitted). (Top) Direction of view: perpendicular to the membrane; (bottom): toward the membrane (see Fig. 1).

Concerning the stability of the system, the standard analysis including RMSD calculations has been performed. There are no apparent distortions of the structure, but the obtained data is not expressive since the direction of the motion is not taken into consideration. Most important, all protein parts below the equatorial domain (see Fig. 1 D) are moving. The closer the residues are to the aperture, the more they tend to move (see upper image in Fig. 3). This indicates that the equatorial domain functions as a hinge.

Figs. 4 and 5 show the triangular area for the simulations with an applied voltage of +1 V and −1 V, respectively. As mentioned above, previous to all simulations there is a 10-ns equilibration phase without a steering field. The triangular area did not change much in these equilibration runs (data not shown), except for MGlu0. In the latter case, the protein already begins to open during the equilibration. Starting at the equilibrated crystal structures, Wt and MCryst, and applying a steering field, the areas also remain rather constant for the two simulations as can be seen in Figs. 4 and 5. This is not a surprise, because the voltage is not strong enough to significantly influence the protein itself. For the computer-generated mutants, the situation is different. For positive applied voltage, the mutant MGlu remains closed in the presence of a 100 mM KCl solution. Additionally, MGlu0a tends to close again toward an aperture size similar to MGlu1a, which indicates that the presence/absence of ions is of some importance. However, the simulations of MAsp do start to open and the triangular areas rise to values that are slightly larger than for MCryst. This is true for all investigated concentrations. When prolonging the trajectory for the MAsp2a case to 30 ns (data not shown), the area declines again slightly to approximately the value found for MCryst. Additional simulations with +0.5 V (data not shown) showed similar results, which indicates that the actual field strength is not of high importance, but instead, the presence of the field is. The reasons for this will be discussed below.

Figure 4.

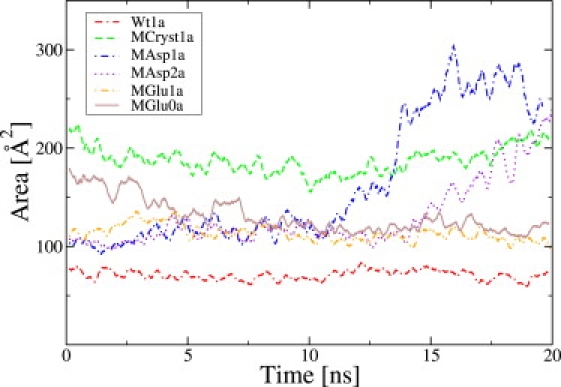
Comparison of the triangular area. The shown results are for an external voltage of +1 V. A running average has been calculated for each 250 ps.

Figure 5.

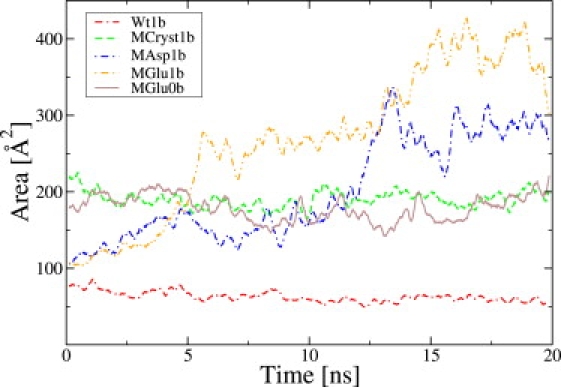
The same as in Fig. 4, but for a voltage of −1 V.

In the case of a negative applied voltage, MGlu and MAsp both show an opening of the protein. In contrast, prolonging the field-free equilibration runs of the mutants to 20 ns (data not shown) does not lead to a partially open conformation. The data for MGlu2 is not shown in Figs. 4 and 5, because the results are similar to those of MGlu1. For a voltage of −1 V, slightly more time is needed until the aperture begins to open. For the wild-type, there are no qualitative differences between Wt1 and Wt2. Comparing the values of MAsp1a and MGlu1b, the latter one reaches greater values in the triangular area than the former one, due to a higher asymmetry of the aperture region which does not significantly increase the area values. Furthermore, the helices in MAsp1a (see Fig. 2, second column), which are rather close to the initial conformation, move slightly inward. This can be interpreted as natural constraints of the coiled-coils versus breaking apart of the structure, especially the α-helical barrel.

Concluding, the electric steering voltage has an influence on the opening or at least on the speed of opening for some of the described setups, but not for all of them. The side-chain length of the mutated residue 367, which is the difference between the mutants MGlu and MAsp, seems to have some influence on the strength of the constricting ring. Of course, our findings are always restricted to the simulated time spans that were up to 40 ns in total (10 ns field-free equilibration plus 30 ns including external field).

To analyze the findings, we determined the electrostatic potential maps, which show the global distribution of all charges over the whole trajectory (30). Some of these maps are shown in Fig. 6 as slices through the middle of the protein (y = 0) which are averaged over all frames of the trajectory from 10 ns to 20 ns with applied voltage (30,31). Within this figure, the protein oriented along the z axis, and the lipid bilayer with the highest potential values along the x axis, are well distinguishable from the solution. Using this method, one can see the open aperture for both MAsp1a and MAsp1b (Fig. 6, C and D). In contrast to this mutant, MGlu does open in MGlu1b (similar to Fig. 6 D), but not in MGlu1a (Fig. 6 B). This cannot be understood readily just by looking at the secondary structure and global motions.

Figure 6.

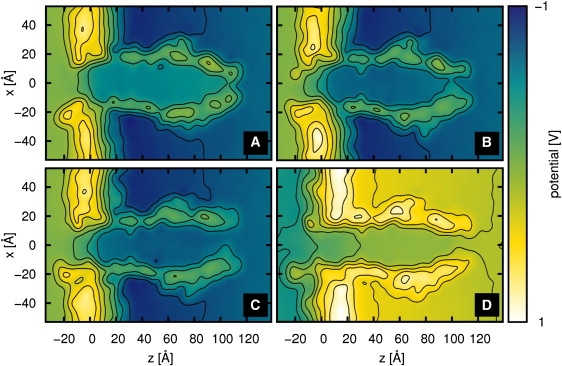
Slices through the potential map for different simulations: (A) Wt1a, (B) MGlu1a, (C) MAsp1a, and (D) MAsp1b.

Because this more global analysis of the charge distribution does not lead to a clear explanation of the electric field effects on the opening of the tunnel, a more local analysis was performed to understand why the aperture remains closed, e.g., in the simulation MGlu1a. To this end, we investigated the region close to the mutated residues (Fig. 1 E) considering the amino-acid conformations and charge locations. As described earlier (29), mutating R367 inhibits the salt bridge toward D153. At the same time, though, this mutation leads to a cation (affinity) pocket formed by the negatively charged residues D153 and D367/E367 as well as the polar T152, which can be occupied by potassium ions in this case. A similar residue configuration was described in Blaustein et al. (47), where Ca²⁺-binding domains of a Na/Ca exchanger protein have been investigated.

While analyzing the pathways of the ions, especially of the potassium ions, through the aperture and close to the three cation pockets between the monomers (Fig. 7), one can easily observe the attraction of potassium ions toward these pockets, which leads to new formations of ionic bonds mediated by these potassium ions. Especially, one can easily distinguish between simulations with positive and negative voltages applied. In the positive case, the cations flow through the channel and therefore pass closely by the cations' pockets. In the negative case, the cations instead accumulate in the region beside the protein and therefore comparatively seldom come close to the cation pockets. Particularly for the case of MGlu0b, i.e., a simulation with negative applied voltage and minimal ion concentration, there are basically no cations close to the cation pockets (see also discussion below).

Figure 7.

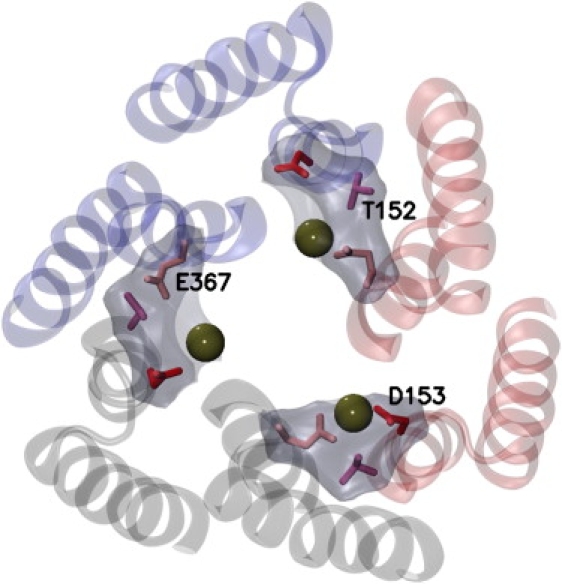
The MGlu aperture (cartoon representation) with the residue side chains (licorice representation colored by amino-acid type) of the cation pockets (transparent surface representation) occupied with potassium ions (van der Waals representation). Same perspective as in Fig. 1E. Each cation pocket consists of the residues T152, D153, and E367.

The occupation of the cation pockets over time during the last 10 ns of some of the applied voltage simulations is shown in Fig. 8. In these occupation numbers, a clear difference between the simulation MGlu1a (which does not show opening) and MAsp1a (which does show opening) can be seen. Fig. 8 indicates that as long as at least two cation pockets are occupied frequently, no opening of the channel occurs. This can be understood directly, since each monomer is connected to two of the pockets and both have to be empty to allow opening motions of this particular monomer.

Figure 8.

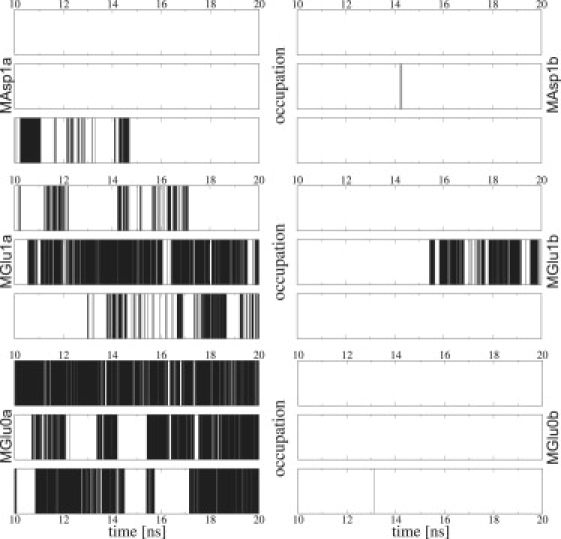
Occupation for each of the three cation pockets with ion selection range of 3 Å. A black line represents that the respective pocket is occupied.

Furthermore, the average occupation frequency was calculated over a time span of 10 ns for all three pockets in the different simulations and stages of the simulation, i.e., the equilibration; the first 10 ns; and the subsequent 10 ns with applied steering field (Fig. 9). Additionally, some simulations have been run with a voltage of +0.5 V using the state after the first 10 ns of the +1 V simulations. This was found to be applicable, because the structure did not change much within the first 10 ns. Despite the decreased voltage, the results are similar with a slightly higher occupation frequency of the cation pockets.

Figure 9.

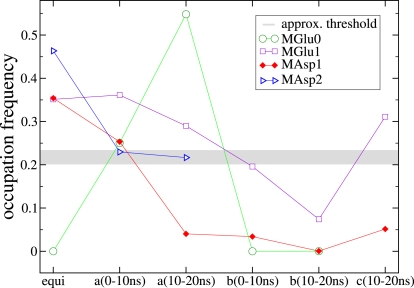
Average occupation frequency of the cation pockets. The label “equi” denotes the field-free equilibration runs, and the letters a, b, and c stand for +1 V, −1 V, and +0.5 V, respectively.

Comparing these occupation frequencies with the conformations of the aperture, the correlation is quite striking. If the occupation frequency is <∼0.2, the protein definitely opens. For values between 0.2 and 0.24, the opening depends on the concentration and the observed stage, e.g., both values for MAsp2a are similar although only the latter state is opened, which describes the transition into the partially open conformation. Hence, the correlation between occupation frequency and final conformation could be confirmed for all simulations performed with the double mutants that built up cation pockets. It has to be stated clearly that this observation is within the timescale currently accessible by MD simulations.

In addition, simulations with the single mutants from Y362F as well as R367D have been performed (data not shown) to examine the contribution of each residue to the strength of the constricting ring. Regarding the triangular area values (as in Fig. 4), it can be seen that the values remain lower than the values of MGlu for both single mutants. For R367D, the occupation of the cation pockets has been investigated, which resulted in an occupation frequency <0.2, although the protein did not open during the simulation. This verifies that, although the cation pockets are relatively empty, the protein is not able to open—which means that the occupation frequency threshold is only applicable for the double mutants. In general, it can be stated that both mutations have to be applied to enable the opening of the aperture without external stimuli.

Conclusion

The aim of this study was to investigate the dynamic effects of two point mutations, Y362F and R367E, on the aperture stability of TolC within MD simulations. In recent experiments (29), double mutations of this kind lead to a partially open structure. Interestingly enough, using equilibration runs at physiological salt concentrations did not lead to a major change in the conformation on a 10–20 ns timescale. This is also seen in Vaccaro et al. (28), with the mutations Y362F and R367S. By minimizing the salt concentration toward a solely neutralized system MGlu0, the protein opened slightly during the equilibration, which could finally be explained by the corresponding low ion-pocket occupation frequency (Fig. 9). In this simulation, the helices rotate iris-like toward an open conformation (Figs. 2 and 3), as also indicated in Bavro et al. (29). This leads to the suggestion that it might be favorable to use a minimal ion concentration when equilibrating mutants. Otherwise, ions might establish temporary ionic bonds that could increase the stiffness of the protein; see also Laine et al. (48). Furthermore, it was checked that it is not enough to simply mutate residues Y362 or R367 separately; a double mutation is needed to induce an opening of TolC.

The simulations showed that applying an electric steering field is an alternative approach to speed up simulations and to investigate the aperture stability of TolC. But in contrast to the crystal structure from Bavro et al. (29), the mutated protein does not open symmetrically under physiological conditions within the simulated time. Furthermore, the opening depends on the side-chain length and the charge/polarity of the residues within the constricting ring. One reason is that the ions are able to influence the opening by formation of ionic bonds in place of the wild-type salt bridges that have been deleted by the mutations. Although only potassium has been investigated here, it seems unlikely that the observed effects of the ions are restricted to this ion type. Because of two negative side chains in the pocket, other cations like Na⁺ or Ca²⁺ should have similar or stronger effects due to the charge, which is indicated in Blaustein et al. (47). Furthermore, the method employed for the initial ion placement might be a critical point. In this study the ions were distributed randomly in the water layer. If a Poisson-Boltzmann solver would be used to determine the positions for the ions at the electrostatic extrema, the cations might be placed directly into the cation pockets—which would be rather unfavorable for this and similar investigations.

In this study, the effect of bond reformation is likely to be only a problem of the timescale within MD simulations. In addition to the results specific to TolC, this investigation also shows how the ions of the solution can affect large domain motions. This is especially the case for spontaneous motions, and might be applicable to entirely different systems as well. For example, in Laine et al. (48), it was revealed that the structural flexibility of calmodulin depends on the number of bound calcium ions. Another example is given in Sotormayor and Schulten (49), where calcium ions protect cadherin from unfolding.

The obtained data can be used to investigate the electric conductance of the open state of the protein, which can be compared to experiments similar to studies of OmpF (35). In that study, the temperature dependent ion conductance of OmpF has been investigated. Therefore, it has to be examined how stable the opened structures are and which influence the mutations have on the measurements. Moreover, the rather symmetrically opened structure from MGlu0b can be used to analyze the docking of TolC with in vivo partners like AcrB and AcrA. In several hypothetical studies (26,27,29), it has been investigated how TolC might connect to AcrA. While opening the aperture of TolC, the α-helices turn to open a groove that is favorable to dock with the α-helical domain of AcrA. In Bavro et al. (29), it was pointed out that the connection to AcrB is required before the groove is accessible. Furthermore, it was stated that the bonds between the residues of the constricting ring are substituted by new bonds toward the TolC docking domain of AcrB. As can be seen from these simulations, the influence of the electrostatics and possible bound ions on the opening of TolC is rather important. In future studies, one could try to put charges such as those from AcrB close to the TolC Wt structure and analyze possible opening motions. As a starting point one could use the results of docking studies between the partially open crystal structure of TolC and AcrB (29). The obtained information from these next steps can be used to understand the mechanism of efflux pumps and antibiotic resistance in more detail, which is important for designing new antibiotics.