The Fip35 WW Domain Folds with Structural and Mechanistic Heterogeneity in Molecular Dynamics Simulations

Abstract

We describe molecular dynamics simulations resulting in the folding the Fip35 Hpin1 WW domain. The simulations were run on a distributed set of graphics processors, which are capable of providing up to two orders of magnitude faster computation than conventional processors. Using the Folding@home distributed computing system, we generated thousands of independent trajectories in an implicit solvent model, totaling over 2.73 ms of simulations. A small number of these trajectories folded; the folding proceeded along several distinct routes and the system folded into two distinct three-stranded β-sheet conformations, showing that the folding mechanism of this system is distinctly heterogeneous.

Main Text

Because β-sheets are a ubiquitous protein structural motif, understanding how they fold is imperative in solving the protein folding problem. Liu et al. (1) recently made a heroic set of measurements of the folding kinetics of 35 three-stranded β-sheet sequences derived from the Hpin1 WW domain. The results were notable because a model with both single exponential and stretched exponential components was found to be more appropriate than a single exponential below the melting temperature T_m for five of the sequences. However, the stretched exponential is difficult to interpret without atomic-level detail of WW domain folding. A detailed molecular dynamics (MD) simulation, which explicitly (at least for the protein) models all atoms and interatomic forces could provide powerful insights into the stretched exponential component.

Recently there has been much interest in developing new computational technology for running single, long protein folding trajectories (2), (3). These approaches seem to have the goal of generating one trajectory which results in one folding event. However, basic statistics denies the utility of any single observation of an event for reaching significant conclusions, especially for stochastic processes such as protein folding.

In this letter, we test whether a homogeneous folding mechanism is plausible in one of the proteins studied by Liu et al. (1), the Fip35 WW domain, by observing and comparing multiple folding events in molecular dynamics simulations. Freddolino et al. (4) recently generated a 10-μs MD trajectory from an extended conformation of Fip35. Experimentally, Fip35 folds with a timescale of ∼13 μs at 337 K making it an exceptionally appropriate target for MD simulations of folding. However, folding to a three-stranded β-sheet structure was not observed in this simulation, possibly due to inaccuracies in the force field. In our MD simulations, dozens of folding trajectories were generated by running thousands of long, independent trajectories on the distributed computing environment, Folding@home (5). For these calculations, we utilized graphics processing units (ATI Technologies; Sunnyvale, CA), deployed by the Folding@home contributors. Using optimized code, individual graphics processing units (GPUs) of the type employed for this study are capable of 80–200 ns/day for Fip35 (6). This distributed computing approach generated 13,195 independent simulations with an average length of 207 ns; 60 trajectories are longer than 3 μs and 143 are longer than 2 μs. The AMBER96 force field (ff96) was employed to represent the protein in these simulations. Solvent was modeled through the Onufriev-Bashford-Case (Type II) generalized Born implicit solvent model (7). A leap-frog Langevin integrator (8) was used at temperatures of 300 K and 330 K and using two conditions of simulated solvent friction: one at waterlike viscosity at 300 K, γ = 91 ps ⁻¹, and the other at γ = 1 ps ⁻¹ to accelerate sampling (9). For brevity, we will describe each of the four solvent conditions used in this study in the following way: the set of trajectories run at 300 K and γ = 91 ps ⁻¹ will be abbreviated T300-γ91, at 300 K and γ = 1 ps ⁻¹ as T300-γ1, etc.

Starting structures were kindly provided by Prof. K. Schulten (University of Illinois at Urbana-Champaign) including a model of the folded structure and two unfolded structures, one fully extended structure subjected to a short equilibration (unfolded structure 1) and a fully extended structure (unfolded structure 2, Fig. S1 in the Supporting Material). The model of the folded structure was used as a reference structure for calculations such as Cα root mean-square deviations (RMSD).

We observe the folding of Fip35 to three-stranded β- sheet conformations under all four solvent conditions. However, only one simulation (from T300-γ1) reached <3 Å Cα RMSD from the reference structure, because Fip35 is flexible in ff96 under these solvent conditions as indicated by the large average Cα RMSD of 3.8 Å in trajectories starting from the folded structure (Fig. S2 a) and under the mildest solvent conditions (T300-γ91). On the other hand, the β-sheet itself is stable under normal conditions, judged by the Cα RMSD of those residues (6–11, 16–21, and 25–28) of ∼1 Å at 300 and 330 K at waterlike viscosity, γ = 91 ps ⁻¹ and not much more in the T300-γ1 data (Fig. S2 b). Additionally, DSSP (10) shows that residues 6–10, 17–20, and 26–27 retain a β-sheet conformation (DSSP symbol “E”) in at least 90% of the trajectory snapshots of simulations started in the folded structure for T300-γ91. These residues have β-sheet conformations to a significant extent in the other solvent conditions as well (Fig. S2 c). For this reason, we employ combined criteria to judge a structure to be “folded”; first, the Cα RMSD of residues 6–11, 16–21, and 25–28 must be <3 Å, and second, residues 6–10, 17–20, and 26–27 listed above must have β-sheet conformation according to DSSP. Some folded structures from the trajectories started unfolded are shown in Fig. 1. Our criteria for being folded are adequate to capture the essential secondary structure of the Hpin1 domain: an antiparallel three-stranded β-sheet.

Figure 1.

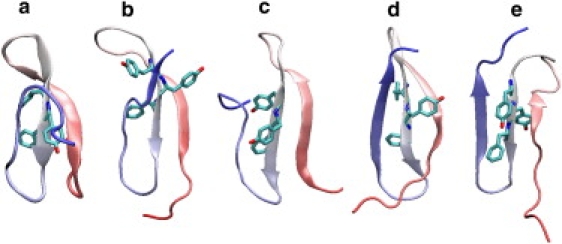
Five folded structures from the four trajectories started in unfolded configurations and one inverted structure. In the following, two Cα RMSD values are listed: one for all α-carbons and one for the β sheet residues. (a) T300-γ1, 3.832 Å, 0.491 Å, (b) T300-γ1, 6.300 Å, 2.639 Å, (c) T330-γ1, 7.444 Å, 1.722 Å, (d) T330-γ1, 6.492 Å, 2.004 Å, and (e) T300-γ1, 6.866 Å, 2.370 Å. The structures shown were those from each solvent condition with the lowest Cα RMSD for the β sheet. Structure e is misthreaded.

In all, 33 trajectories folded. The T300-γ91 and T330-γ91 solvent conditions each generated two folding trajectories. The low-viscosity simulations generated more folding trajectories, seven for T300-γ1 (from unfolded structures 2 and 3) and 22 for T330-γ1. Intriguingly, 10 of the 33 folding trajectories folded with the chain twisting the opposite direction of the presumptive native structure. This occurs in one of the T330-γ91 folding trajectories, and in one from T300-γ1; the other eight were produced in the T330-γ1 solvent condition. In these inverted structures, if Tyr-17 and Phe-19 are “behind” the β-sheet in the properly threaded structures (Fig. 1, a–d), they lie “in front” of the β-sheet in the misthreaded structure (Fig. 1 e), relative to structures with the N- and C termini in the same positions. The existence of both this inverted structure and the noninverted native structure in the folding simulations indicates that the folding of Fip35 is structurally heterogeneous.

To estimate the mean first passage time to the folded state, we use a simple Bayesian modification of a maximum likelihood formulation (11). This method uses information from both folding and unfolding trajectories. We use a single-exponential likelihood function for this calculation, which should still represent an overall forward rate in each solvent condition, even though a stretched exponential is observed experimentally. (Here, we pool data from the two unfolded starting structures to estimate the folding rate; in principle these structures could have slightly different folding rates.)

With this method, we computed a probability distribution of the rate; the mean barrier crossing time and its standard deviation were derived from this distribution. In the T300-γ91 solvent condition, Fip35 folds in 131 μs (standard deviation σ = 75 μs). However, in the solvent condition closest to experimental conditions, T330-γ91, Fip35 folds in a similar time as at the lower temperature, at 138 μs (σ = 80 μs). In the low-viscosity solvent conditions, folding is faster, taking 65 μs (σ = 23 μs) at 300 K and in 21 μs (σ = 4 μs) at 330 K. The smaller relative standard deviations for the low-viscosity simulation are due to the observation of many folding trajectories. The computed rates for the full viscosity conditions values are only one order of magnitude greater than the experimental value, suggesting agreement of the free energy of activation to within a factor of ∼2, reasonable for a force field of this type. This implies that these simulations present relevant evidence for mechanistic and structural relevance to experiments.

To show kinetic heterogeneity explicitly, we show four folding trajectories in Fig. 2. In Fig. 2 a (from T300-γ91), the first hairpin forms early, so that strands 1 and 2 β-sheet conformations (DSSP string “E”) before the Cα atoms of the β-sheet residues coalesce into a nativelike conformation; finally, strand 3 residues attain β-sheet conformations resulting in a folded protein. In Fig. 2 b, (from T300-γ1), we see a quick initial collapse (expected in a low-viscosity simulation), followed by rearrangements among collapsed conformations leading eventually to the β-sheet Cα RMSD and DSSP criteria being met essentially simultaneously. In Fig. 2 c (from T330-γ1), again there is a fast initial collapse, in such a way that the Cα RMSD criterion is satisfied early; from this near-native structure, the three strands find β-sheet conformations simultaneously. In Fig. 2 d (from T330-γ1) stably folding trajectory (Fig. 2 d), the second hairpin forms first, with the fast initial collapse, allowing strands 2 and 3 to reach β-sheet conformations early; soon after, the Cα RMSD criterion is met, followed later by strand 1 residues attaining a β-sheet conformation.

Figure 2.

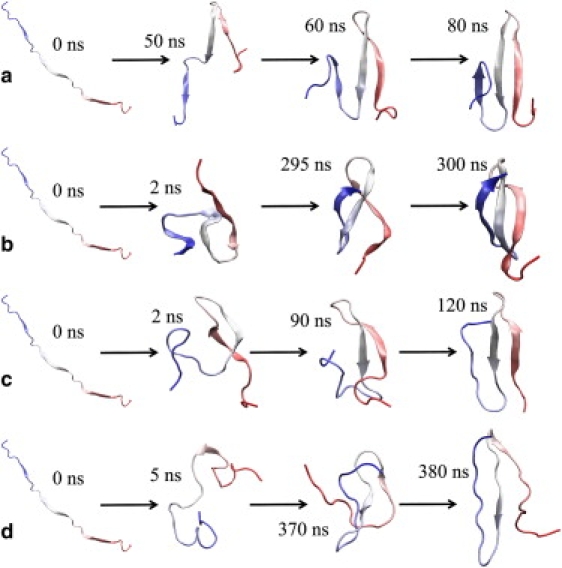
Four folding trajectories from (a) T300-γ91, (b) T300-γ1, (c), and (d) T330-γ1. Each proceeds by a distinct mechanism.

One of the misthreaded structures (from T330-γ91) folded to an intermediate degree of stability, retaining a low Cα RMSD and β-sheet conformations in strands 2 and 3 for at least 20 ns after first folding. This suggests that the improperly threaded structure is metastable with respect to the native state. Interestingly, this trajectory reached the misthreaded state with the same order of events as the second T330-γ1 trajectory: β-sheet conformations of strands 2 and 3 were attained first, followed by reaching a low Cα RMSD, finally relaxing into a β-sheet formation for strand 1. This shows that there is nothing special about this mechanism; following this pathway, Fip35 might fold into the correct structure or a misthreaded one.

Clearly, these protein folding trajectories show significant structural and mechanistic heterogeneity. We stress that this heterogeneity could not have been revealed by any single molecular dynamics trajectory, but rather must be investigated through an approach using an ensemble of many trajectories. Moreover, we feel that protein folding in larger systems is likely to be at least as complicated as shown here. Therefore, all simulation approaches to studying protein folding should involve observation of many folding events by running many trajectories.

One of the major questions facing the protein folding community is the degree of the heterogeneity of the folding mechanism. Indeed, the Fip35 system is of interest in part due to its unusual (stretched + exponential) kinetics (1), which could be evidence against a single relaxation pathway. Our ensemble of protein folding trajectories shows significant structural and mechanistic heterogeneity. We stress that the issue of heterogeneity cannot be revealed by any single molecular dynamics trajectory.

In conclusion, the combination of distributed computing with new GPU technology has allowed us to simulate many long folding trajectories. In addition to demonstrating that our model is sufficiently accurate to reach the folded state on a timescale comparable to experiment, we found a heterogeneous set of mechanisms. Due to the ubiquity of GPUs and the possibility of large GPU clusters, we suggest that this method may be of general use in studying protein folding, especially to address the key issue of the heterogeneity of folding pathways.

This study's raw trajectory data are available online at https://simtk.org/home/fip35gpu. The MD code for GPUs is also available at https://simtk.org/home/OpenMM.

Supporting Material

Two figures and a reference are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)004950.