Selecting anti-HIV therapies based on a variety of genomic and clinical factors

Abstract

Motivation: Optimizing HIV therapies is crucial since the virus rapidly develops mutations to evade drug pressure. Recent studies have shown that genotypic information might not be sufficient for the design of therapies and that other clinical and demographical factors may play a role in therapy failure. This study is designed to assess the improvement in prediction achieved when such information is taken into account. We use these factors to generate a prediction engine using a variety of machine learning methods and to determine which clinical conditions are most misleading in terms of predicting the outcome of a therapy.

Results: Three different machine learning techniques were used: generative–discriminative method, regression with derived evolutionary features, and regression with a mixture of effects. All three methods had similar performances with an area under the receiver operating characteristic curve (AUC) of 0.77. A set of three similar engines limited to genotypic information only achieved an AUC of 0.75. A straightforward combination of the three engines consistently improves the prediction, with significantly better prediction when the full set of features is employed. The combined engine improves on predictions obtained from an online state-of-the-art resistance interpretation system. Moreover, engines tend to disagree more on the outcome of failure therapies than regarding successful ones. Careful analysis of the differences between the engines revealed those mutations and drugs most closely associated with uncertainty of the therapy outcome.

Availability: The combined prediction engine will be available from July 2008, see http://engine.euresist.org

Contact: rosen@il.ibm.com

1 INTRODUCTION

1.1 Treating HIV patients

Most of the antiretroviral compounds used to treat HIV patients belong to one of three classes: protease inhibitors (PI), nucleotide reverse transcriptase inhibitors (NRTI) and non-nucleotide reverse transcriptase inhibitors (NNRTI). Mutations in the target protein confer resistance to the drug targeting that protein. Although various HIV subtypes exist, our study focuses on subtype B, which is prevalent in Europe. Today, highly active antiretroviral therapy, known as HAART, is commonly used for treating HIV patients. A typical HAART comprises three to four carefully selected drugs from at least two different drug classes. This approach is designed to minimize the probability that the virus will develop escape mutations.

1.2 The EuResist dataset

The EuResist integrated database (IDB) combines the ARCA database (Italy),¹ AREVIR database (Germany; Roomp et al., 2006) data coming from the Karolinska Infectious Diseases and Clinical Virology Department (Sweden), and a smaller dataset from Luxembourg. The EuResist database comprises records of 18K different patients and 65 K different therapies, of which 3K therapies contain genotype information. The information for the 18K different patients includes demographic data records such as gender, race and age, with the anonymization of patients data carried out before the data is stored in the IDB. Clinical measures of the disease state, such as viral load (VL) and CD4+ cell counts, are collected for each patient and for some of the therapies around a treatment switch. Sequence information of HIV protease (PRO) and reverse transcriptase (RT) obtained from genotypic resistance tests are also provided. A standard datum (SD) format was designed to define the characteristics of successful and failing therapies, respectively (minimal treatment length, handling of overlapping therapies, etc.). The SD format is also used to define which genotype and VL tests serve as baseline measures and are therefore associated with a therapy switch, and which follow-up VL is associated with a therapy outcome (8 weeks from the start of a therapy). Each therapy with a baseline and a follow-up VL is labeled a success if there is a drop of 2 log in VL or a drop below detection level (500 copies per milliliter); otherwise, the therapy is labeled as a failure. This process of generating a standard datum was motivated by the need to develop an online engine that performs as a decision support system and can recommend a drug combination for a patient. To this end, a minimal requirement for a prediction engine is defined containing the genotypic sequence for the two viral target proteins; the remaining information is treated as optional or maximal set of features.

1.3 Mutations

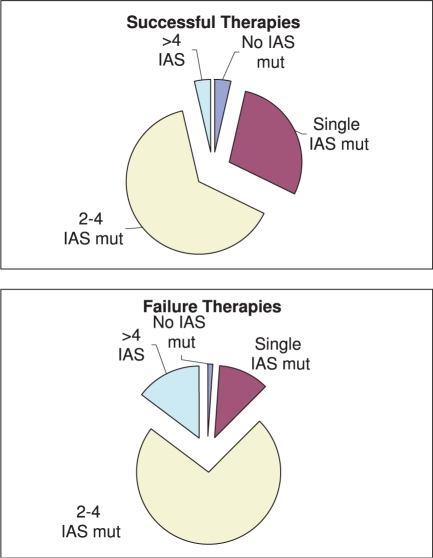
The HIV virus has a high mutation rate. In principle, all (about 10 000) positions in the viral genome are candidates for mutations. In particular, the related 99 amino acid positions of the PRO and the 440 amino acid positions of the RT have high mutation rates. This leads to an exceedingly high dimension. A prediction engine taking the whole relevant protein sequence into account is likely to suffer from the curse of dimensionality. One possibility of circumventing this problem is to make use of a predefined list of mutations expected to have the most significant effect on the therapy's outcome. The International Aids Society (IAS) maintains a constantly updated reference mutation list, known as IAS mutations, of the mutations of PRO and RT sequence (and additional new viral target proteins) that are known to play a role in drug resistance (Johnson et al., 2007). Indeed, if we count the number of such mutations in our data, separating failure therapies from successful ones, the baseline genotype of failing therapies has on the average 3.1±1.4 IAS mutations, while successful therapies have 2.2±1.2 (Fig. 1). Finally, we find a highly significant correlation between the number of IAS mutations and successful therapies (using an indicator variable with 1 for successful therapy and 0 for failure), correlation of −0.32 (with P-value < 10⁻⁵⁰). In our prediction engines described below, the list of IAS mutation was a natural candidate feature and in some of the engines this is the set of features picked for representing the protein sequences.

Fig. 1.

Number of IAS mutations in HIV genotypes submitted to drug therapies.

1.4 Related work

As soon as resistance to antiretroviral drugs was discovered, the need for tools to detect drug resistance arose. The majority of available Interpretation Systems (IS) work with hand-crafted tables (such as the IAS list) for every drug compiled by experts. These tables are used to classify the virus as susceptible or resistant to a single drug. These rules are built using expert knowledge from clinical experience and recently they incorporate experimentally generated–genotype–phenotype information. Some IS are completely data-driven rather than based on expert knowledge. For example, geno2pheno (Beerenwinkel et al., 2003) and VirtualPhenotype (Vermeiren et al., 2007) apply machine learning methods to predict in vitro drug resistance from the viral genotype. Recently published (data-driven) tools are able to predict in vivo response to a combination of antiretroviral drugs rather than single compounds. In Larder et al., (2007), committees of Artificial Neural Networks are used to predict the change in VL after treatment start, apart from information about the viral sequences and the intended regimen, CD4 + counts, baseline VL and four treatment history indicators that are used as input features. This approach was trained and validated on 1150 and 100 treatment change episodes, respectively. Geno2pheno–THEO by Altmann et al., (2007), another online tool, predicts the success probability of a putative treatment based on sequence information and the estimated genetic barrier of the viral variant to resistance against every drug in the combination therapy. However, geno2Pheno–THEO does not make use of information about the patient or other available clinical markers. In comparison to these two systems, our approach is able to predict the success probability of a regimen as well as the change in VL. Most important, our prediction system makes use of the fact that it employs three different highly optimized individual systems to provide a more robust prediction, i.e. one with a smaller variance in prediction accuracy and AUC scores, allowing us to gain further insight in the treatment–outcome relationship as this study demonstrates.

2 MATERIALS AND METHODS

We trained three separate engines. Each can be viewed as being composed of two layers, with a layer of feature generation and selection embedded within a discriminative method such as logistic regression, support vector machines (SVMs) or random forests. As logistic regression, compared with the other methods, requires much less parameter tuning efforts and performs similarly to the other two in the tests we carried out, we use logistic regression for the top layer and the engines differ in the type of features derived. We use the following three approaches:

1. Evolutionary models

2. Generative models

3. Mixture of effects

Given a core set of features selected by one of the methods above, we devoted extensive studies to figure out what other features, and in what format, should be added to the core set of extracted features to achieve a separate good performing engine. The result is a set of three engines—evolutionary engine (EV), a generative discriminative (GD) engine and a mixture of effects engine (ME).

Each of the engines is trained twice, once with the restriction that only drugs in the regimen and genotype information about the two viral targets are available (minimal feature set) and once with no such restriction (maximal feature set). In addition to these six engines aimed at binary classification, the prediction of the label of a therapy (success/failure), we train three engines with a target of predicting the drop in VL, i.e. regression (the minimal feature set is less adequate for this target of predicting change of VL as it requires not employing baseline VL). Each of these three additional engines uses the same set of derived features as those used for classification, obtains the baseline VL and predicts the drop of the VL. To simplify the discussion hereafter we focus on the classification case. Models and methods are very similar in the regression case. We provide results for all cases.

Each labeled therapy in the IDB contains information about antiretroviral drugs administered to the patient in the past, the drugs of the current therapy and past and current genotypic data. The additional demographic and clinical data types provided are listed in Table 1. There are 3023 such therapies of which 10% are set aside for testing purposes and 2722 are used for training. The test set is composed of a random selection of 10% of the failing therapies and 10% of the successful therapies and is neither used for feature selection nor for model selection. In addition, there are 17K labeled therapies that do not have a related genotype. In this article they are referred to as the incomplete labeled set. The engines generate predictions of a label to a therapy and provide the probability of therapy success. Later they are combined together to provide a single prediction.

Table 1.

IDB data fields

Field	[min max]	Corr (training data)	Corr (full labeled set)
NUMBER OF PAST TREATMENT LINES	[0 28]	–0.26 (8.0 × 10−42, 1.1 × 10−27)	–0.15 (0, 0)
RISKID	[1 6]a	–0.04 (–, 4.3 × 10−4)	–0.03 (1.3 × 10−3, 0)
GENDERID	[1 4]a	–0.02 (–, –)	0.00 (–, –)
AGE	[1 102]	0.01 (–, –)	0.04 (1.0 × 10−7, 5.6 × 10−15)
BASELINE VL	[34 7656900]	0.01 (–, 6.8 × 10−11)	0.01 (–, 0)
BASELINE CD4	[0 4411]	0.06 (–, –)	0.15 (0, 0)
BASELINE CD4 PERCENT	[0 70]	0.06 (–, 9.0 × 10−3)	0.17 (0, 0)
ALL TREATMENTS RECORDED	[0 1]a	0.10 (9.3 × 10−4, 5.4 × 10−3)	0.12 (7.2 × 10−43, 0)
DATABASEID	[1 4]a	0.12 (7.4 × 10−9, 1.5 × 10−10)	0.17 (0, 0)

P-values are provided in parenthesis only if they are below 0.05, − stands for higher values.

^aCategorical data, the χ²-test, second in parenthesis, is more informative.

2.1 Raw features in the IDB

All features defined in the SD, except for current and past drugs and genotype, are shown in Table 1. The table shows the minimal and maximal values for each of the features, the correlation with the therapy label, and the related P-value. We also apply the Kolmogorov–Smirnov (KS) test to check which features are distributed differently in the failure therapies and in the successful ones (second P-value in the parenthesis). In cases where the feature is categorical we use the χ²-test instead. All P-values are adjusted with Bonferroni correction. The three measures—correlation, its related P-values and a P-value for rejecting the null hypothesis that there is no association between the values of the feature and success/failure—are derived for all therapies in the training set/incomplete labeled set (third/fourth column, respectively). The features are sorted by correlation in ascending order. The first item is the number of past treatment lines; the more therapy switches in the patient's history, the more likely the current therapy will fail. The second, ‘RISKID’ stands for the infection risk group; this seems to be an indicator of whether a therapy will succeed or not. Although medically there is no reason that the manner of infection will impact response to treatment per se, it is known that intravenous drug abusers can experience less effective therapy due to lower adherence to the regimen or interplay with drug they abuse. Gender IDs stand for mail/female/undifferentiated/unknown; it does not seem to be directly related to the success/failure of a therapy.

Note that the two bottom rows in the table with the highest correlation are not defined as optional features in the SD. One row stands for the DATABASEID. The databases have different ratios of success/failure. This most likely occurs because some of the databases collect records of patients who visit clinic centers known to be specialized in HIV treatments and represent harsher cases as compared to ‘regular’ hospitals. This results in a high correlation between the DATABASEID and the success/failure. In order to be able to generalize for any patient, this feature was never exposed to the engines. Similarly, the field ALL TREATMENTS RECORDED is ignored. Value ‘1’ in this field stands for the event that the patient's record is complete with regards to past treatments, ‘0’ stands for incomplete. The correlation in the table means that not knowing the patient's history records is an indication that the therapy is more likely to fail. This presumably mirrors scenarios in which patients change from a local clinic to a specialized clinic due to acute disease condition (and hence having partial records in the new clinic).

The standard datum drugs are listed in Table 2. The number of therapies in which each of the antiretroviral drugs is administered is provided in the ‘Occ’ column. The number in the brackets stands for the number of therapies from the incomplete labeled set in which the drug occurs. We derive the success rate as obtained from the training set (and as obtained from the incomplete labeled set) for cases where that drug is administered (‘SR with’, second column) and for cases where the therapy does not contain the specific drug (‘SR without’, third column). The consistent lower success rate of the training set comparing with the incomplete labeled set is due to the bias by which the training set is selected—therapies that present a greater challenge than ususal and hence genotypic sequence is tested. We also provide P-values of χ²-tests of whether the success/failure rate of a therapy is similar when the drug is part of the HAART and when it is missing. P-values lower than 0.05 are provided after adjustment of Bonferroni correction.

Table 2.

Drugs and the associated success rate

Drug	Class	Occ	SR with	SR without	χ2-test
DDC	NRTI	28 (343)	0.36 (0.43)	0.67 (0.69)	– (0)
APV	PI	77 (344)	0.36 (0.40)	0.68 (0.69)	2.8 × 10−6 (0)
SQV	PI	195 (1560)	0.50 (0.49)	0.68 (0.70)	4.4 × 10−5 (0)
RTV	PI	130 (1035)	0.56 (0.57)	0.67 (0.69)	– (1.1 × 10−12)
D4T	NRTI	715 (5949)	0.57 (0.60)	0.70 (0.72)	4.6 × 10−9 (0)
NFV	PI	235 (2329)	0.57 (0.65)	0.68 (0.69)	– (–)
IDV	PI	193 (2322)	0.58 (0.67)	0.68 (0.69)	– (–)
DDI	NRTI	864 (4943)	0.59 (0.60)	0.70 (0.71)	1.2 × 10−5 (0)
NVP	NNRTI	308 (2221)	0.63 (0.68)	0.67 (0.69)	– (–)
ABC	NRTI	484 (3755)	0.67 (0.75)	0.67 (0.67)	– (0)
TDF	NRTI	1053 (4711)	0.70 (0.73)	0.65 (0.67)	– (9.8 × 10−10)
TC3	NRTI	1676 (13168)	0.70 (0.71)	0.63 (0.64)	2.8 × 10−3 (0)
RTVB	PI	1600 (6868)	0.72 (0.74)	0.61 (0.66)	6.6 × 10−7 (0)
LPV	PI	1108 (4156)	0.73 (0.73)	0.64 (0.67)	1.3 × 10−4 (2.9 × 10−10)
ATV	PI	271 (1643)	0.73 (0.81)	0.66 (0.68)	– (0)
EFV	NNRTI	526 (3524)	0.73 (0.78)	0.66 (0.67)	– (0)
FPV	PI	118 (449)	0.74 (0.73)	0.67 (0.69)	– (–)
AZT	NRTI	970 (7536)	0.76 (0.74)	0.63 (0.65)	1.0 × 10−11 (0)
FTC	NRTI	242 (1194)	0.80 (0.88)	0.66 (0.67)	1.6 × 10−3 (0)

– stands for P-value higher than 0.05, 0 stands for P-value lower than 10⁻²⁰ and SR stands for the success rate with and without the drug.

2.2 Evolutionary engine

This engine focuses on the development and use of evolutionary features. As stated before, one major obstacle in HIV-1 treatment is the virus's escape from drug therapy by developing resistance mutations. In order to accurately predict the outcome of an antiretroviral therapy information about viral evolution has to be presented to the underlying statistical learning method. Our representation of the viral evolution is based on mutagenetic trees. Briefly, the mutagenetic tree is reconstructed from all pairwise probabilities of defined events. Here, these events are occurrences of drug resistance mutations in the viral genome. Hence, a mixture of reconstructed mutagenetic trees represents possible resistance pathways along with probabilities for the development of the participating mutations. Using these trees we can compute the so-called genetic barrier to drug resistance by calculating the probability of the virus not to develop further mutations leading to a complete phenotypic resistance to that drug. A complete resistance pattern is observed if on average viruses with that mutational pattern exceed a certain level of phenotypic drug resistance. Here the cut-offs used by geno2pheno (Beerenwinkel et al., 2003) were applied. In previous work Altmann et al., (2007) could show that using the genetic barrier significantly improves the prediction of therapy response. Thus, the genetic barrier to drug resistance is computed for every single drug in the putative regimen given the viral sequences, and is together with other features, like indicators for single drugs in the treatment, the viral genotype as represented by indicators for IAS mutations, the treatment history, second order interactions between these features and the baseline VL input to a logistic regression (linear regression for the regression task). To select the features used in the final engine, a simple feature selection approach based on SVMs was applied. The approach works in three steps: first, the cost parameter of a linear SVM is optimized by maximizing the AUC (correlation for regression) in a 10-fold cross validation setting; second, 25 different linear SVMs are generated by five repetitions of 5-fold cross-validation using the optimized cost parameter; third, all features having a mean z-score larger than two were kept for use in the final model.

2.3 GD engine

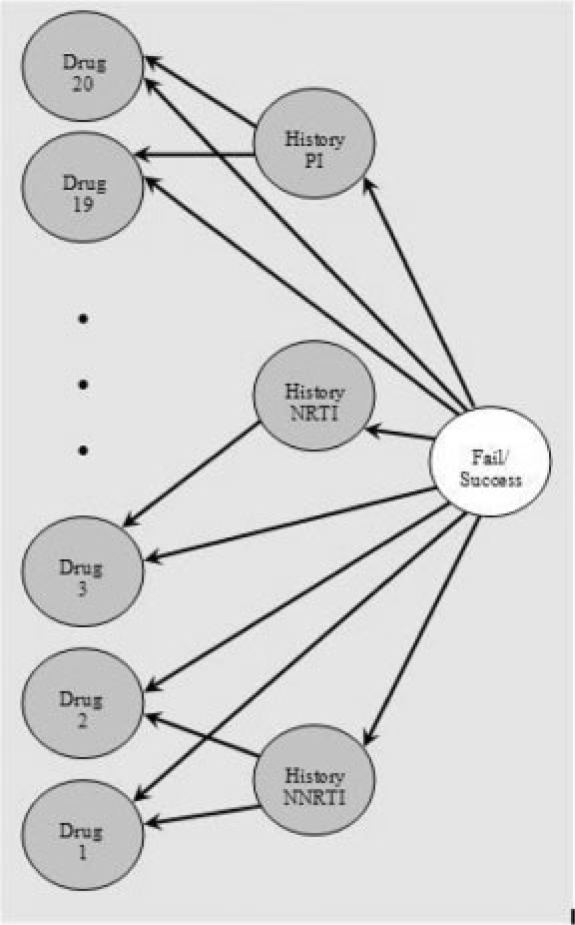
This engine develops and applies generative models of the interactions between current and history antiretroviral drugs. It is well known that subsequent use of previously employed and closely related drugs may be inefficient (see e.g. Piliero, 2003; Siliciano, 2001). Generative models are powerful when some expert knowledge for guidance of the design of the network is available (Pearl, 1988). In this case we have 20 drugs naturally divided into three classes, PI, NRTI and NNRTI. A number of candidate networks containing nodes representing the drugs individually and/or the drug classes are tested using 10-fold cross-validation with 20 divisions on a large training set. The data available for training is the incomplete labeled set along with the training dataset, a total of about 20 000 therapies. The network selected is shown in Figure 2. Root node and all leaves are binary nodes standing for success/failure, existence/not existence of a drug in current therapy, respectively. The three nodes in the middle are discrete nodes that stand for the count of number of history drugs adhered by the patient, a separate count per drug class. Each of these three nodes is a parent to the drugs from the related class. This Bayesian network, with no other features like genotype, yields an AUC of 0.716±0.001, it outperforms a Naive Bayes network trained with six leaves—count for history and current drugs (AUC of 0.698±0.002) and many other alternative networks.

Fig. 2.

Bayesian network used in the GD engine.

This core generative engine generates a prediction of success/failure, a number in the range [0 1] that is used as a trained feature. On top of it a second layer of discriminative engine is trained. The second layer engine uses logistic regression, and all candidate features from the data are tested for their contribution to this second layer. The features selected to stand for the genotype mutations are mutations with high correlation with success/failure, 20/25 mutations of PRO/RT in the baseline genotype and five mutations appearing in history genotype, see the Appendix for more details. The final list of features used in the generative discriminative engine contains, in addition to the above features, the 20 compounds, baseline VL and number of past treatment lines.

In a similar process a generative discriminative engine is developed for the case of the minimal feature set. The best performing Bayesian network is similar to the one in Figure 2, except that the middle layer with history drugs is replaced by an indicator that is 0/1 if the drug belongs/does not belong to a drug class. This Bayesian network alone results with AUC of 0.672±0.001, it outperforms a naive Bayes network trained with 20 leaves that stand for the drugs (AUC of 0.654±0.001) and a logistic regression engine trained on the same features (AUC of 0.662±0.001). The top layer of logistic regression engine trained on clinical genomic data with the 20 drugs, 20/25 mutations selected based on correlation with VL drop of PRO/RT results in AUC of 0.744±0.003. This performance improves when to that the single Bayesian network trained feature is added—AUC of 0.749±0.003.

2.4 Mixture of effects engine

This engine takes second- and third-order variable interactions into account.

The mixed-effects engine explores logistic regression for classification of virological success and multiple linear regression for regression of actual VL change.

Second- and third-order variable interactions were set up taking into account the following mixed effects:

1. drug × mutations

2. mutations × mutations

3. drug × drug

4. drug × drug × mutations

5. drug × drug × drug

The following are additional features included in the engine: information of past treatments, using either a continuous exponentially decreasing function or a binary indicator for each drug class; epidemiological information (such as risk factor, country of infection, age, sex, …); clinical markers (viral RNA load and CD4+ cell counts) and viral subtypes [assessed through BLAST (Altschul et al., 1990) scores on a reference data base of viral subtypes].

The engine was fed with the clinical, epidemiological and all genomic data (more than 500 mutations), with the mixed effects added (thousands of interaction variables). The modeling required a strong effort in feature selection, since the input attribute space ranged from hundreds to thousands of variables. The feature selection techniques used were: (i) filters, using univariable analysis (χ²-rank-sum tests) and correlation-based feature selection (CFS; Hall, 1998); (ii) embedded methods, using AIC selection (Akaike, 1974) and ridge shrinkage (Hoerl, 1962; Le Cessie et al., 1992).

For both classification and regression, 10-fold cross-validation was executed multiple times, in order to obtain a Gaussian distribution that could be compared with a t-statistic (adjusted for sample overlap and multiple testing), useful in model comparison or model selection (Nadeau et al., 2000). The models were tested using different feature spaces and different loss functions (accuracy, AUC).

2.5 Results

Prediction results of the regression engines are provided in Table 3. Averaged correlation between actual and predicted change in log(VL) as obtained from the 10-fold cross-validation test (and SD) are provided for the training and the test datasets (first two columns); the same partition of 10-folds is used with each of the engines. Means squared error of the predictions are also provided.

Table 3.

Log VL prediction results

Model	Correlation		Mean squared error
	Train	Test	Train	Test
GD	0.658 (0.023)	0.657	0.586	2.519
EV	0.679 (0.020)	0.678	0.602	2.745
ME	0.664 (0.023)	0.642	0.863	1.723

Prediction results of the six classification engines are provided in Table 4. AUC and accuracy, i.e. 1-misclassification error, on the training dataset are derived from 10-fold cross-validation tests, SD is provided in parentheses. Results on simple combinations of engines are also provided. Note the consistent decrease in SD when AUC and accuracy measures of combinations of engines are derived, this means that an engine that is a resultant of a combination of the three engines provides a more robust prediction. In Figure 3 we compare the failures and successes of the three engines (training and test data altogether) separately for the case where the therapy failed and for the case where the therapy succeeded. When a single engine is referred as correct (wrong) in the figure it means that the other two are wrong (correct). We find two interesting effects: (a) all engines tend to provide the same wrong answer on failure therapies more than on successful ones and (b) inconsistency among engines on failure therapies is much larger than the cases of successful therapies. We discuss these observations in the next section.

Table 4.

Binary prediction results

Model	AUC		Accuracy
	Train	Test	Train	Test
Minimal feature set
GD	0.747 (0.027)	0.744	0.745 (0.024)	0.724
EV	0.766 (0.030)	0.768	0.754 (0.031)	0.748
ME	0.758 (0.019)	0.745	0.748 (0.031)	0.757
Combined minimal
Min	0.771 (0.020)	0.765	0.746 (0.027)	0.761
Max	0.760 (0.023)	0.765	0.742 (0.030)	0.731
Median	0.773 (0.020)	0.766	0.759 (0.027)	0.766
Mean	0.777 (0.020)	0.772	0.760 (0.024)	0.744
Majority	0.683 (0.023)	0.660	0.759 (0.027)	0.738
Product	0.776 (0.020)	0.772	0.759 (0.025)	0.744
Oracle*	0.914 (0.015)	0.911	0.842 (0.025)	0.844
Maximal feature set
GD	0.768 (0.025)	0.760	0.752 (0.028)	0.757
EV	0.789 (0.023)	0.804	0.780 (0.032)	0.751
ME	0.762 (0.021)	0.742	0.754 (0.030)	0.757
Combined maximal
Min	0.792 (0.021)	0.793	0.760 (0.030)	0.764
Max	0.779 (0.021)	0.779	0.757 (0.030)	0.741
Median	0.789 (0.029)	0.786	0.768 (0.029)	0.761
Mean	0.794 (0.019)	0.793	0.780 (0.028)	0.781
Majority	0.697 (0.027)	0.683	0.768 (0.029)	0.761
Product	0.794 (0.019)	0.795	0.780 (0.027)	0.771
Oracle*	0.917 (0.013)	0.920	0.850 (0.022)	0.860

^*Assuming that miraculously the combined engine knows to pick the engine with best result.

Fig. 3.

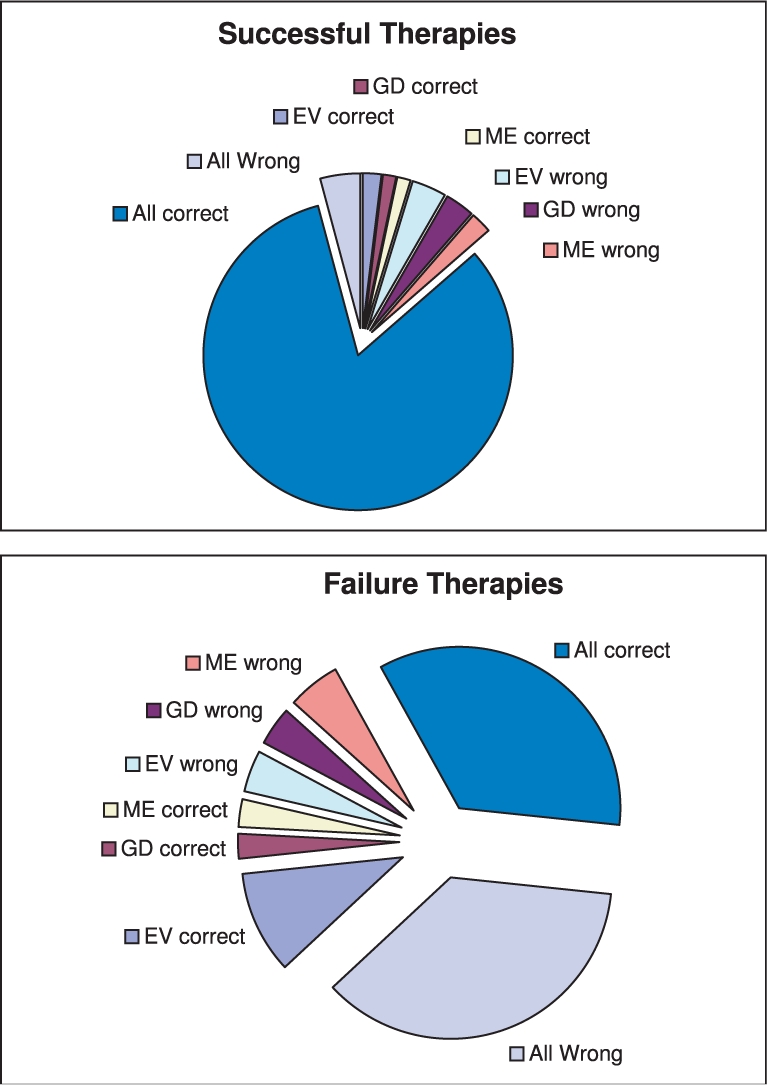
Comparison of success/failure of the three engines.

A combined engine is derived by taking the average probability of successful therapy obtained from each of the engines. It seems to have the best performance as measured by accuracy and AUC (Table 4). The accuracy of this combined engine when a maximal feature set used is significantly higher than when a minimal set feature set is used. A paired t-test results in a P-value of 0.00013/0.048 on training/test dataset, respectively. The P-value on the test set is reduced because fewer samples are available.

Furthermore, we compare the performance of the three engines and the combined engine with Stanford's online available (http://hivdb.stanford.edu) Interpretation System (IS) version 4.3.2 (De Luca et al., 2006).This system is widely used to classify a virus to be resistant against single drugs. Unlike in other expert algorithms individual scores are assigned to mutations in the genotype. The scores are derived from publications and from genotype–phenotype data. In this way the stanford system can be seen as an expert-derived linear regression model for resistance against single drugs. Comparison to a system that predicts therapy response to a combination of drugs was not possible, since the system by Larder et al. (2007), is not freely available. We extracted the nucleotide sequences for the test data from our Integrated Database and computed drug resistance with Stanford system. For 299 of the 301 sequences a classification with respect to drug resistance for both RT and PRO targeting drugs could be computed and were therefore used in the analysis. Four of the 299 considered treatments included the NRTI ddC which is not rated by the IS, and were thus excluded from the analysis. For the remaining 295 treatments the classifications ‘Susceptible’, ‘Potential Low-Level’, ‘Low-level’, ‘Intermediate’ and ‘Resistant’ given by the IS for every single drug were mapped to 1,1,0.5,0.5 and 0, respectively. This mapping refers ‘fully active’, ‘intermediate active’, and ‘not active’. The grouping was performed as suggested on the website of the online tool. The treatment score is then defined as the sum of the scores for drugs used in the treatment. This approach is frequently applied and termed Genotypic Susceptibility Score (GSS; Rhee et al., 2003)

In Figure 4 the AUC curves of engines trained with a minimal and maximal set of features are provided. It shows that the combined engine slightly outperforms the performance of Stanford system when trained on minimal features and significantly outperforms the system when engines are trained with full set of features.

Fig. 4.

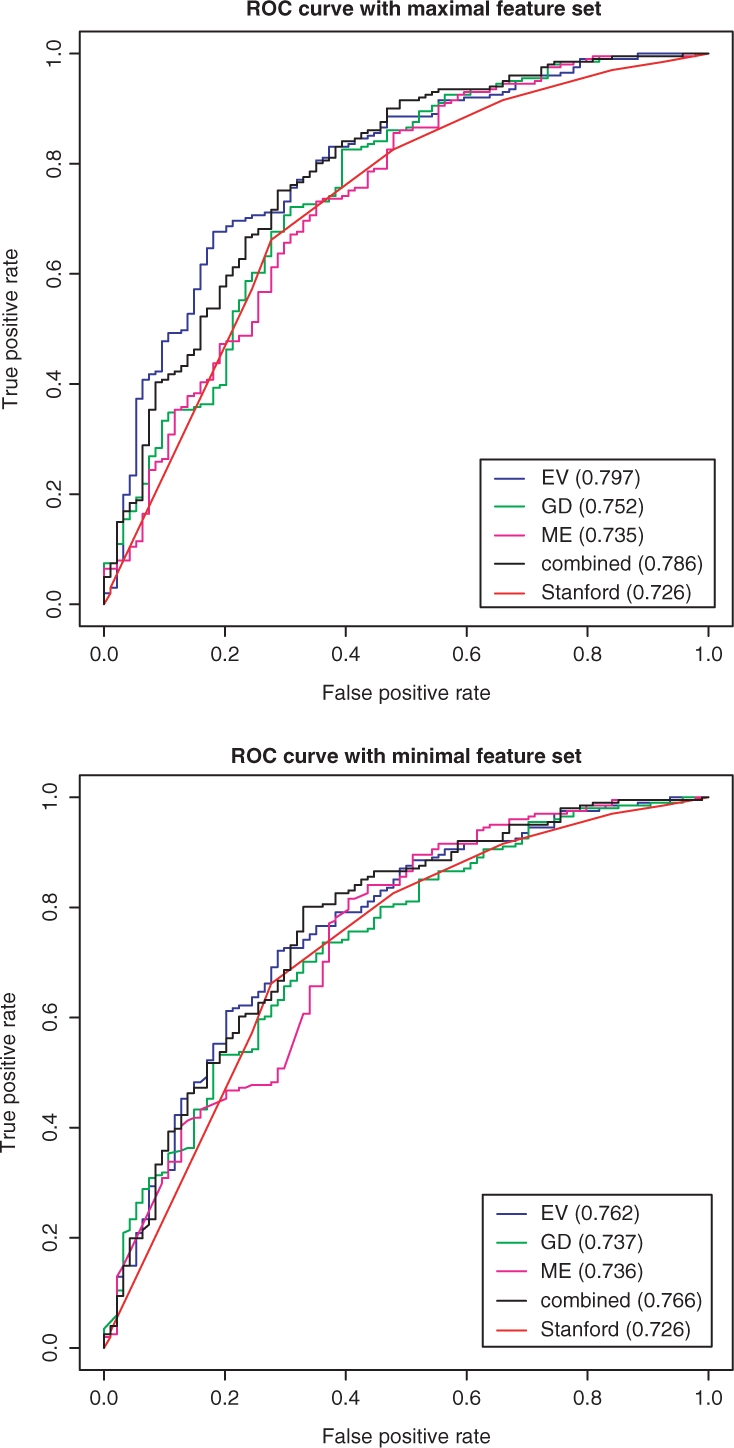
ROC curves for prediction engines on test data.

3 DISCUSSION

The comparison between the engines performance has lead to the two observations mentioned above.

Regarding the first observation, it should be noted that noisy examples are probably more prevalent in the failure cases than in the successful therapies. To assess this, we carried out the following test. Recall that a label is defined by the SD via a follow-up VL measure. In particular if multiple VL tests are provided, the one closest to 8 weeks from the therapy switch determines the label of the therapy where the test needs to be in the time window 4–12 weeks in order to be considered as a follow-up VL. In the training (test) set 350 (35) failing therapies are predicted to be successful by all three engines. Once during the course of therapy 145 (16) of these achieve a VL measure below 500 copies per mililiter Of the remaining 550 (64) failing cases in the training (test) set 100 (13) have a VL measure below 500 copies per mililiter once during the course of the therapy. A Fisher's exact test results in a P-value of 4.8 × 10⁻¹⁴ (0.011) on the training (test) set. Hence, the difference is highly significant. Our suspicion is that this behaviour is related to low adherence; it is known that law adherence disrupts the effectivity of HAART treatments, (see, e.g. Conway, 2007).

Regarding the second observation, we were interested in finding what are the features most related to disagreement between engines. Thus, we divide the 3K train/test therapies into the 592 cases where the engines provide different answers for the prediction and the 2431 cases where the engines provide identical prediction. We tested the correlation between individual drugs and individual mutations to an indicator of agreement/disagreement of the three engines. This is carried out to identify drugs and mutations that are most confusing, i.e. influence engines in different ways. We also use the χ²-test to check which features are distributed in the identical prediction case differently than in the different prediction case. In Table 5 we provide results with the lowest P-value after adjustment with Bonferroni correction, values higher than 0.05 are not provided (indicated by–). For completeness we also provide correlation, P-value and χ²-test tested against indicator of failure/success of the therapy. Note that the four drugs, D4T, DDI, SQV and NFV, found as most correlated with disagreement among engines, are those drugs whose success rate is unbiased. In other words, their success rate in the training data is around 0.5, Table 2. Interestingly, all mutations found are from the list of IAS mutations. Moreover, the three PRO mutations appearing in the table are among those most involved in cross-resistance within the PI class and the RT mutations listed in the same table comprise the thymidine analog mutations well known to mediate cross-resistance to all the NRTIs, (see, e.g. Gallant et al., 2003). These mutations seem to be related to therapies for which selecting antiretroviral compounds is most challenging.

Table 5.

Drugs and mutations most related to inconsistency among engines

Feature	Agreement/disagreement	Success/failure
D4T	–0.14 (3 × 10−9, 4 × 10−8)	–0.12 (9 × 10−7, 1 × 10−2)
DDI	–0.13 (1 × 10−7, 1 × 10−6)	–0.10 (3 × 10−3, –)
SQV	–0.12 (2 × 10−6, 2 × 10−5)	–0.10 (1 × 10−2, –)
NFV	–0.11 (6 × 10−4, 5 × 10−3)	–0.06 (– , –)
# IAS mutations	–0.24 (0, 0)	–0.32 (0, 0)
PRO L90M	–0.13 (4 × 10−7, –)	–0.22 (0, 3 × 10−12)
PRO L10I	–0.09 (2 × 102, –)	–0.21 (0, 3 × 10−13)
PRO M46I	–0.08 (–, –)	–0.19 (0,3 × 10−3)
RT T215Y	–0.18 (0,3.4 × 10−11)	–0.23 (0, 0)
RT M41L	–0.15 (5 × 10−11, 1 × 10−6)	–0.20 (0,0)
RT M184V	–0.14 (2 × 10−10, 7 × 10−8)	–0.13 (3 × 10−7, 4 × 10−5)
RT D67N	–0.14 (2 × 10−9,6 × 10−4)	–0.16 (7 × 10−14, 8 × 10−7)
RT K219Q	–0.12 (2 × 10−6, –)	–0.08 (–, –)
RT K70R	–0.11 (6 × 10−5, –)	–0.08 (–, –)
RT L210W	–0.10 (1 × 10−3, –)	–0.20 (–0, 9.4 × 10−11)
RT T215F	–0.10 (2 × 10−3, –)	–0.10 (3 × 10−3, –)
RT V118I	–0.09 (4 × 10−2, –)	–0.17 (2 × 10−15, 4 × 10−4)

4 CONCLUSION

The combination of three engines with different core technologies results in a robust predictor that outperforms the most widely used system available online. This novel combined engine is designed to provide a recommendation for a HAART therapy, given the genotype. The recommendation is expected to improve as more features are provided. The system scans through known combinations and provides the most promising therapies based on the likelihood of success as derived by the combined engine. Toxicity issues and interactions with other drugs consumed by the patient are not within the scope of the system. The system is designed to provide decision support when expert knowledge is required for using the system recommendation. The system is planned to be deployed and available online by the end of June 2008.

APPENDIX: MUTATIONS SELECTION BASED ON CORRELATIONS

The original feature space of the mutations is the product of the number of positions times the 20 amino acids. Each of these components is an indicator, 1 if mutation occurs, 0 otherwise. We tested for each of these components its correlation with the therapy outcome. If multiple mutations are found at the same position (due to subpopulations of the virus), components for all mutations, (and maybe also for the wild-type) are 1.

The 20 PRO mutations with highest (absolute value of) correlations, sorted from the highest correlation (0.29) to lowest correlation (0.11): I54V, V82A, L90M, L10I, I84V, A71V, M46I, L33F, G73S, Q58E, L63P, I54I, L10F, K20R, G73T, V82T, I54M, K43T, V82F, I47V.

The 25 RT mutations with highest (absolute value of) correlations, sorted from the highest correlation (0.22) to lowest correlation (0.07): T215Y, M41L, L210W, V118I, D67N, H208Y, M184V, E44D, T69D, T215F, T39A, K101Q, M184M, V75M, K219Q, K70R, K103N, L74I, L228H, S162D, T215N, Y181C, V75V, F77L, F116Y.

Top five mutations appearing in history genotype, followed by the value of correlation with therapy outcome: RT M41L, (0.19) PRO L10I, (0.19) PRO; L90M, (0.19) PRO; I54V, (0.18) PRO; L63P, (0.17).