Classification and feature selection algorithms for multi-class CGH data

Abstract

Recurrent chromosomal alterations provide cytological and molecular positions for the diagnosis and prognosis of cancer. Comparative genomic hybridization (CGH) has been useful in understanding these alterations in cancerous cells. CGH datasets consist of samples that are represented by large dimensional arrays of intervals. Each sample consists of long runs of intervals with losses and gains.

In this article, we develop novel SVM-based methods for classification and feature selection of CGH data. For classification, we developed a novel similarity kernel that is shown to be more effective than the standard linear kernel used in SVM. For feature selection, we propose a novel method based on the new kernel that iteratively selects features that provides the maximum benefit for classification. We compared our methods against the best wrapper-based and filter-based approaches that have been used for feature selection of large dimensional biological data. Our results on datasets generated from the Progenetix database, suggests that our methods are considerably superior to existing methods.

Availability: All software developed in this article can be downloaded from http://plaza.ufl.edu/junliu/feature.tar.gz

Contact: juliu@cise.ufl.edu

1 INTRODUCTION

Numerical and structural chromosomal imbalances are one of the most prominent and pathogenetically relevant features of neoplastic cells (Mitelman et al., 1972). One method for measuring genomic aberrations is comparative genomic hybridization (CGH) (Kallioniemi et al., 1992). CGH is a molecular-cytogenetic analysis method for detecting regions with genomic imbalances (gains or losses of DNA segments). Applying microarray technology to CGH measures thousands of copy number information distributed throughout the genome simultaneously (Pinkel and Albertson, 2005). Raw data from array CGH experiments is expressed as the ratio of normalized fluorescence of tumor and reference DNA. Normalized CGH ratio data surpassing predefined thresholds is considered indicative for genomic gains or losses, respectively. Chromosomal and array CGH data has been an important resource for cancer cytogenetics (Bentz et al., 1996; Desper et al., 1999; Gray et al., 1994; Hoglund et al., 2005; Joos et al., 2002; Jo Vandesompele et al., 2005; Mattfeldt et al., 2001).

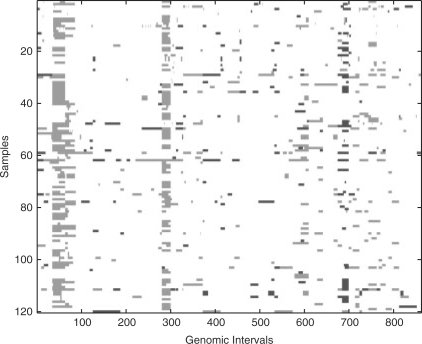
In contrast to the array CGH, the chromosomal CGH results (on which this article is based) are annotated in a reverse in situ karyotype format (Mitelman, 1995) describing imbalanced genomic regions with reference to their chromosomal location. CGH data of an individual tumor can be considered as an ordered list of status values, where each value corresponds to a genomic interval (e.g. a single chromosomal band). The terms feature and dimension are also used for genomic interval. The status can be expressed as a real number (positive, negative or zero for gain, loss or no aberration, respectively). We use this strategy and represent gain, loss and no change with +1, −1 and 0, respectively. Figure 1 shows a plot of 120 CGH cases belonging to Retinoblastoma, NOS (ICD-O 9510/3).

Fig. 1.

Plot of 120 CGH cases belonging to Retinoblastoma, NOS (ICD-O 9510/3). The X-axis and Y-axis denote the genomic intervals and the samples, respectively. We plot the gain, loss and no-change status in green (light gray), red (dark gray) and white, respectively.

An important task in cancer research is to separate healthy patients from cancer patients and to distinguish patients of different cancer subtypes, based on their cytogenetic profiles. This is also known as the classification problem. These tasks help successful cancer diagnosis and treatment. Cancer is currently responsible for about 25% of all deaths (Jemal et al., 2005). Early identification of the cancer is often vital for the survival of the patients. For example, colon cancer is 90% curable when it is identified at the early age. Over 500 000 people die each year from colon cancer in the world (El-Deiry, 2006).

Support vector machine (SVM) is one of the state-of-art kernel based machine learning techniques and has been widely used for the classification of microarray data (Li et al., 2004). Choosing or developing an appropriate kernel function greatly improves the performance of SVM (Tan, 2005). The frequently used linear kernel function does not exploit the following properties of CGH data and can lead to sub par performance for classification:

• Features in CGH data represent ordered genomic intervals on chromosomes and their values are categorical.

• Neighboring features are often highly correlated as a point-like genomic aberration can expand to the neighboring intervals This results in a contiguous run of gain or loss status in CGH data (Liu et al., 2006) (Fig. 1).

It is essential to develop a kernel that takes these properties into consideration.

Another related task is feature selection that selects a small subset of discriminative features. Feature selection has several advantages for CGH data. First, it reduces the risk of over fitting by removing noisy features thereby improving the predictive accuracy. Second, the important features found can potentially reveal that specific chromosomal regions are consistently aberrant for particular cancers. There is biological support that a few key genetic alterations correspond to the malignant transformation of a cell (Renan, 1993). Determination of these regions from CGH datasets can allow for high-resolution global gene expression analysis to genes in these regions and thereby can help in focusing investigative efforts for understanding cancer on them.

Existing feature selection methods broadly fall into two categories, wrapper and filter methods. Wrapper methods use the predictive accuracy of predetermined classification algorithms, such as SVM, as the criteria to determine the goodness of a subset of features (Duan et al., 2005; Guyon et al., 2002; Zhang et al., 2006). Wrapper methods based on SVM mostly use the linear kernel that is not suitable for CGH data. Also, they select features in a backward elimination scheme, which is inefficient in determining highly discriminative features and leads to poor predictive performance when a small feature set is selected. Filter methods select features based on discriminant criteria that rely on the characteristics of data, independent of any classification algorithm (Ding and Peng, 2005; Yu and Liu, 2004). Filter methods are limited in scoring the predictive power of combined features, and thus have shown to be less powerful in predictive accuracy as compared to wrapper methods (Chai and Domeniconi, 2004).

The classification problem of multiple classes is generally more difficult as compared to the classification of binary classes (Ding and Peng, 2005; Li et al., 2004). It also gives a more realistic assessment of the proposed feature selection method (Ding and Peng, 2005). In this article, we consider the problem of classification and feature selection for CGH data with multiple cancer types. We address the above-mentioned problems and develop SVM-based methods. This article has two important contributions:

1. We develop a novel kernel function called Raw for CGH data. This measure counts the number of common aberrations between any two samples. We show that this kernel measure is significantly better for CGH data than the standard linear kernel used in SVM-based methods.

2. We develop an SVM-based feature selection method for CGH data called Maximum Influence Feature Selection (MIFS). It uses an iterative procedure to progressively select features. In each iteration, an SVM-based model on selected features is trained. This model is used to select one of the remaining features that provides the maximum benefit for classification. This process is repeated until the desired number of features is reached. We extend the MIFS feature selection method described above for multiclass CGH data. In each iteration, a one-versus-all strategy is used to train multiple SVMs with each SVM corresponding to the classification of one class from the others. A radix sort-based approach is used to combine the rankings of remaining features from each SVM into a global ranking. The best feature based on this ranking is added to the selected set.

Our experimental results show that the Raw kernel improves the classification accuracy by 7.3% on average over twelve datasets. These datasets are systematically derived from the Progenetix database based on predefined similarity levels and sizes. These datasets will serve as benchmarks for future research on data mining methods for CGH data. We compared our MIFS method to well-known feature selection methods MRMR (Ding and Peng, 2005) (filter) and SVM-RFE (Guyon et al., 2002) (wrapper) on twelve datasets. The results show that MIFS outperforms both MRMR and SVM-RFE in terms of classification accuracy. The results also show that our methods only need 5% of all features to provide a comparable classification accuracy as compared to all the features. Further, our methods can improve the accuracy by 3.1% using only 10% of the features as compared to using all features.

The rest of this article is organized as follows. Section 2 presents background. Section 3 discusses the classification problem using SVM and introduces our new kernel function called Raw. Section 4 proposes our MIFS method based on Raw kernel for multi-class CGH data. Section 5 discusses our dataset resampling scheme for benchmarking purpose. Section 6 presents the experimental results and related discussions. We conclude our work in Section 7.

2 BACKGROUND

Classification aims to build an efficient and effective model for predicting class labels of unknown data. The model is built on the training data, which consists of data points chosen from input data space and their class labels. Classification techniques has been widely used in microarray analysis to predict sample phenotypes based on gene expression patterns. Li et al. have performed a comparative study of multiclass classification methods for tissue classification based on gene expression (Li et al., 2004). They have conducted comprehensive experiments using various classification methods including SVM (Vapnik, 1998) with different multiclass decomposition techniques, Naive Bayes, K-nearest neighbor and decision tree (Tan, 2005). They found SVM to be the best classifier for tissue classification based on gene expression.

The problem of feature selection was first proposed in machine learning. A good review can be found at Guyon and Elisseeff (2003). Recently, feature selection methods have been widely studied in gene selection of microarray data. These methods can be decomposed into two broad classes

1. Filter Methods: These methods select features based on discriminating criteria that are relatively independent of classification. Several methods use simple correlation coefficients similar to Fisher's discriminant criterion (Golub et al., 1999; Pavlidis et al., 2001). Others adopt mutual information (Ding and Peng, 2005) or statistical tests (t-test, F-test) (Ding, 2002; Model et al., 2001). Earlier filter-based methods evaluated features in isolation and did not consider correlation between features. Recently, methods have been proposed to select features with minimum redundancy (Ding and Peng, 2005; Yu and Liu, 2004). The methods proposed by Ding and Peng, (2005), uses a minimum redundancy—maximum relevance (MRMR) feature selection framework. They supplement the maximum relevance criteria along with minimum redundancy criteria to choose additional features that are maximally dissimilar to already identified ones. By doing this, MRMR expands the representative power of the feature set and improves their generalization properties.

2. Wrapper Methods: Wrapper methods utilize the classifier as a black box to score the subsets of features based on their predictive power. Wrapper methods based on SVM have been widely studied in machine-learning community (Guyon and Elisseeff, 2003; Rakotomamonjy, 2003; Weston,J. et al., 2000). SVM-RFE (Support Vector Machine Recursive Feature Elimination) (Guyon et al., 2002), a wrapper method applied to cancer research is called, uses a backward feature elimination scheme to recursively remove insignificant features from subsets of features. In each recursive step, it ranks the features based on the amount of reduction in the objective function. It then eliminates the bottom ranked feature from the results. A number of variants also use the same backward feature elimination scheme and linear kernel.

The methods aimed for binary class data use a recursive support vector machine (R-SVM) algorithm to analyze noisy high-throughput proteomics and microarray data (Zhang et al., 2006) and a method that computes the feature ranking score from statistical analysis of weight vectors of multiple linear SVMs trained on subsamples of the original training data (Duan et al., 2005).

For feature selection of multiclass data, Ramaswamy et al. used an one-versus-all strategy to convert the multiclass problem into a series of binary class problems and applied SVM-RFE to each binary class problem separately (Ramaswamy et al., 2001. Fu and Fu-Liu (2005) also proposed a method based on the one-versus-all strategy. For each binary class problem, they wrapped the feature selection into a 10-fold cross validation (CV) and selected features using SVM-RFE in each fold. They also developed a probabilistic model to select significant features from the 10-fold results.

Filter methods are generally less-computationally intensive than wrapped methods. However, they tend to miss complementary features that individually do not separate the data well. A recent comparison of feature selection methods for multiclass microarray data classification (Chai and Domeniconi, 2004) shows that wrapper methods such as SVM-RFE lead to better classification accuracy for large number of features, but often gives lower accuracy than filter methods when the number of selected features is very small.

3 CLASSIFICATION WITH SVM

Support vector machine is a state-of-art technique for classification (Vapnik, 1998). It has been shown to have better accuracy and computational advantages over their contenders (Guyon et al., 2002). It has been successfully applied for many biological classification problems. The technique works as follows. Consider a set of points that are presented in a high-dimensional space such that each point belongs to one of two classes. An SVM computes a hyperplane that maximizes the margin separating the two classes of samples. The optimal hyperplane is called decision boundary. Formally, let x₁,x₂,…,x_n and y₁,y₂,…,y_n denote n training samples and their corresponding class labels respectively. Let y_i∈{−1, 1} denote labels of two classes. The decision boundary of a linear classifier can be written as w·x+b=0 where w and b are parameters of the model. By rescaling the parameters w and b, the margin d can be written as d=2/‖w‖² (Tan, 2005). The learning task in SVM can be formalized as the following constrained optimization problem:

subject to y_i(w·x_i+b)≥1,i=1,2,…,n.

The dual version of the above problem corresponds to finding a solution to the following quadratic program:

Maximize J over α_i:

subject to 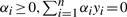, where α_i is a real number.

The decision boundary can then be constructed from the solutions α_i to the quadratic program. The resulting decision function of a new sample z is

with w=∑_iα_iy_ix_i and b=<y_i−w·x_i>. Usually many of the α_i are zero. The training samples x_i with non-zero α_i are called support vectors. The weight vector w is a linear combination of support vectors. The bias value b is an average over support vectors. The class label of z is obtained by considering the sign of D(z).

Standard SVM methods find a linear decision boundary based on the training examples. They compute the similarity between sample x_i and x_j using the inner product 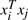. However, the simple inner product does not always measure the similarity effectively for all applications. For some applications, a non-linear decision boundary is more effective for classification. The basic SVM method can then be extended by transforming samples to a higher dimensional space via a mapping function Φ. By doing this, a linear decision boundary can be found in the transformed space if a proper function Φ is used. However, the mapping function Φ is often hard to construct. The computation in the transformed space can be expensive because of its high dimensionality. A kernel function can be used to overcome this limitation. A kernel function is defined as K(x_i,x_j)=Φ(x_i)^TΦ(x_j), where x_i and x_j denote the i-th and j-th sample respectively. It really computes the similarity between x_i and x_j. With the help of kernel function, an explicit form of the mapping function Φ is not required.

In our preliminary work, we have introduced a new measure called Raw that captures the underlying categorical information in CGH data (Liu et al., 2006). We will discuss how to incorporate it into the basic SVM method. CGH data consists of sparse categorical values (gain, loss and no change). Conceptually, the similarity between CGH samples depends on the number of aberrations (gains or losses) they both share. Raw calculates the number of common aberrations between a pair of samples. Given a pair of samples a=a₁,a₂,…,a_m and b=b₁,b₂,…,b_m. The similarity between a and b is computed as 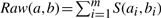. Here S(a_i,b_i)=1 if a_i=b_i and a_i≠0. Otherwise S(a_i,b_i)=0.

The main difference between Raw(a,b) and a^T·b is the way they deal with different aberrations in the same interval. For example, if two samples a and b have different aberrations at the i-th interval, i.e. a_i=1,b_i=−1 or a_i=−1,b_i=1, the inner product calculates this pair as a_i×b_i=−1 while Raw calculates S(a_i,b_i)=0. The similarity value between a and b computed by Raw is always greater than or equal to the inner product of a and b. We propose to use Raw function as the kernel function for the training as well as prediction.

Using SVM with the Raw kernel amounts to solving the following quadratic program:

Maximize J over α_i:

subject to .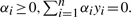

Accordingly, the resulting decision function of a new sample z is

The main requirement for the kernel function used in non-linear SVM is that there exists a transformation function Φ() such that the kernel function computed for a pair of samples is equivalent to the inner product between the samples in the transformed space (Tan, 2005). In other words, Raw(x_i,x_j)=Φ(x_i)^TΦ(x_j). This requires that the underlying kernel matrix is ‘semi-positive definite’. For given data points 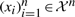, the kernel matrix can be defined as . If for all n, all sets of data points and all vectors v∈Rⁿ the inequality v^TMv≥0 holds, then M is called semi-positive definite. We now prove that our Raw kernel satisfies this requirement.

The function Φ(): a∈{1,0,−1}^m→b∈{1,0}^2m, is defined as follows;

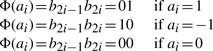For example, given a=[1,1,0,−1], Φ(a) is computed as Φ(a)=[0,1,0,1,0,0,1,0]. With this transformation, it is easy to see that the Raw kernel can be written as the inner product of Φ(x) and Φ(y), i.e. Raw(x,y)=Φ(x)^T·Φ(y). This is because Raw only counts the number of common aberrations in computing the similarity between two samples (if both the values are 0, they are not counted).

We define a 2m by n matrix u whose j-th column vector corresponds to Φ(x_j), i.e. u≔[Φ(x₁) Φ(x₂) ···]. The Raw kernel matrix can be written as

Now we have v^TMv=v^T(u^Tu)v=(uv)^Tuv=‖uv‖²≥0,∀v∈Rⁿ. Therefore, the Raw kernel is semi-positive definite.

4 MAXIMUM INFLUENCE FEATURE SELECTION

An important characteristic of CGH data is that neighboring features are strongly correlated (Fig. 1). Selecting these highly correlated features incurs ‘redundancy’ in the feature set. When the number of selected features is small, this ‘redundancy’ can lead to sub par performance for classification. For example, assume that we want to select two features for classification. If the ith feature is ranked high for well separating samples of different classes, the (i+1)-th or (i−1)-th feature are likely ranked high too. However, selecting both i-th and (i+1)-th (or (i−1)-th feature does not improve the classification accuracy significantly because they are redundant in discriminative power. On the other hand, if the j-th feature improves the classification accuracy when combined with the i-th feature but has a low ranking, the i-th and j-th feature should be selected instead.

Wrapper methods based on backward feature elimination, such as SVM-RFE (Guyon et al., 2002), are limited in choosing a small set of highly discriminative features. This is because they try to remove features that do not perform well with the remaining set of features. However, this does not imply that the eliminated feature would not work well for the final chosen set of features. Filter methods iteratively add features with the most discriminative power into an existing set. This easily causes redundancy in the selected features. The MRMR method (Ding and Peng, 2005) tries to address this limitation by adding features with maximum relevance and minimum redundancy. However, due to the difficulty in selecting complementary features, it often produces lower predictive accuracy as compared to wrapper method.

We propose a novel non-linear SVM-based method called MIFS for the classification of multiclass CGH data that addresses the limitations of existing wrapper methods.

A simple approach to feature selection is to perform an exhaustive search. Clearly, this is not computationally feasible but for a very small number of features. We use a greedy search strategy to iteratively add features to a feature subset in a similar vein as used by (Guyon et al., 2002). The basic approach is to compute the change in the objective function caused by removing or adding a given feature. In our case, we select the feature that maximizes the variation on the objective function. The added feature is the one that has the most influence or gain on the objective function.

The feature that has the most influence on the objective function is determined as follows. Let S denote the feature set selected at a given algorithm step and J(S) denote the value of the objective function of the trained SVM using feature set S. Let k denote a feature that is not contained in S. The change in the objective function after adding a candidate feature is written as DJ(k)=|J(S∪{k})−J(S)|. In the case of SVM, the objective function that needs to be maximized (under the constraint 0≤α_i and ∑_iα_iy_i=0) is:

For each feature k not in S, the new objective function J(S∪ k) has to be computed. One option is to compute this gain or influence for each remaining feature k, by retraining the SVM. However, the computational requirements can be significantly reduced by assuming that the value of α's do not change significantly after the feature k is added. Thus, the new objective function with feature k added can be defined as:

where x_i(+k) means training sample i with feature k added.

Therefore, the estimated (this is because we are not retraining the classifier with the additional feature) change of objective function is:

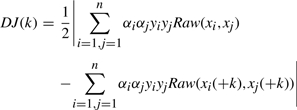We add the feature that has the largest difference DJ(k) to the feature set.

The above method requires S to be non-empty. To jump start the method, the first feature has to be derived. One approach is to compute J({k}) for every feature k by training a separate SVM for each feature k. One can, then, select the feature with the largest value as the starting feature. However, this can be computationally very expensive.

Another approach is to use the most discriminating feature (such as done by standard filter-based methods that rank features according to their individual predictive power). The mutual information I of two variables r and s is defined as

where p(r,s) is their joint probabilities; p(r) and p(s) are the respective marginal probabilities. Assuming that the k-th feature is a random variable, the mutual information I(k,y) between class labels y={y₁,y₂,…,y_n} and the feature variable k can be used to quantify the relevance of kth feature for the classification task. The feature k with the maximum I(k,y) is chosen as the starting feature. We have found that using such methods is satisfactory. Our preliminary experimental results showed that MIFS is not sensitive to the initial feature chosen.

The feature selection method proposed above only works for two-class problems. We derive the multiclass version using a one-versus-all approach as follows.

• First step. Let C≥3 denote the number of classes. For each i, 1≤i≤C, a binary SVM that separates the i-th class from the rest is trained based on the selected feature set S.

• Second step. For each binary SVM, DJ(k) is computed for every feature k not in S. All the candidate features are ranked based on the value of DJ. The larger value the value of DJ(k), the smaller is its rank of k (smaller is better). As a result, C ranked lists of features are obtained. Each ranked list corresponds to one of the C SVMs. Equivalently, each candidate feature corresponds to a ranking vector containing its rankings in these C ranked lists. For example, a feature can be ranked as the first in the first list; third in the second list; 20th in the third list, 15th in the fourth list. The vector that is used for ranking this feature is [1, 3, 20, 15].

• Third step. A feature that ranks low in one list may rank high in another. Our goal is to determine features that are most informative in discriminating one class from the rest even if they are quite uninformative in other classifications. This is achieved as follows. The ranking vector of each candidate feature is sorted in an ascending order. If one regards each element of the ranking vector as a digit, each ranking vector could represent a C digit number. The smallest ranking (the first element) represents the most significant digit. A least significant digit radix sort algorithm can then be used to sort all the ranking vectors and, accordingly, a global ranking of features can be derived. For example, assume we have three features, k₁, k₂ and k₃ whose rankings in four binary SVMs are [1, 3, 20, 15], [8, 4, 7, 6] and [5, 1, 30, 4], respectively. The vectors show that k₁ ranks top in separating class one from others and ranks third in separating class two from others etc. Each ranking vector is sorted in an ascending order. The resulting vectors are [1, 3, 15, 20], [4, 6, 7, 8] and [1, 4, 5, 30], respectively. Next, a radix sort algorithm is applied over the three vectors. The resulting order of vectors changes to [1, 3, 15, 20], [1, 4, 5, 30], [4, 6, 7, 8], which corresponds to the order of features: k₁, k₃, k₂. This provides a global ranking of the three features.

The lowest ranked feature is added into S. The above three step process is used iteratively to determine the next feature. This process stops when a predetermined number of features are selected or S contains all the features. Also, with the set S, the features are ranked based on the order of addition into this set. The iterative procedure for MIFS is formally defined as follows:

Input: Training samples {x₁,x₂,…,x_n} and class labels {y₁,y₂,…,y_n}, 1≤y_i≤C, initial feature set S, predetermined number of features r

1. Initialize: Ranked feature list RL=S, candidate feature set L=D−S (D is the set of all features)

2. While |S|<r

   1. For i=1 to C

      1. Construct new class labels {y₁′,y₂′,…,y_n′}, y_j′=1 if y_j=i, otherwise y_j′=−1;
      2. Train an SVM using training samples with features in RL;
      3. Compute the change of objective function DJ(k) for each candidate feature k∈L
      4. Sort the sequence of DJ(k),k∈L in descending order; create a corresponding ranked list of candidate features;
   2. Compute the ranking vectors for all the features in L from C ranked lists ;
   3. Sort the elements of each ranking vector in an ascending order;
   4. Perform a radix sort over all ranking vectors to produce a global ranking of features in L;
   5. Find the top ranked feature e and update RL=[RL,e] and L=L−{e}

3. Return: Ranked feature list RL

This algorithm can be generalized to add more than one feature in Step 2.e to speed up computations when the number of features r is large.

Time Complexity The training time complexity for SVM is dominated by the time for solving the underlying quadratic program. The conventional approach for solving the quadratic program takes time cubic in the number of samples and linear in the number of features (Chapelle, 2007). (Some approximate solutions make the empirical complexity to be O(n^1.7) (Joachims, 1999)). Based on this, the time complexity for this algorithm is O(n³r²C) in the worst case.

5 DATASETS

The Progenetix database (Michael Baudis and Michael, 2001) (http://www.progenetix.net) consists of more than 12 000 cases (Baudis, 2006). We use a dataset consisting of 5020 CGH samples (i.e. cytogenetic imbalance profiles of tumor samples) taken from Progenetix. These samples belong to 19 different histopathological cancer types that have been coded according to the ICD-O-3 system (Fritz et al., 2000). The subset with the smallest number of samples, consists of 110 non-neoplastic cases, while the one with largest number of samples, Adenocarcinoma, NOS (ICD-O 8140/3), contains 1057 cases. Each CGH sample consists of 862 ordered genomic intervals extracted from 24 chromosomes.

Testing the performance (predictive accuracy and run time) of the proposed methods, requires evaluating them over datasets with different properties such as (1) number of samples contained in the dataset, (2) number of cancer types contained in the dataset, and (3) the similarity level between samples from different cancer types, which indicating the difficulty of classification. Currently, there are no standard benchmarks for normalized CGH data that take the three properties into account. We propose a method to select subsets from the Progenetix database in a principled manner to create datasets with desired properties. The dataset sampler accepts the following three parameters as input: (1) Approximate number of samples (denoted as N) (2) Number of cancer types (denoted as C) (3) Similarity range (denoted as [δ_min,δ_max]) between samples belonging to different cancer types. An outline of the proposed dataset sampler is as follows:

1. For each cancer type, partition all the samples belonging to this cancer type into several disjoint groups using clustering. Each cluster corresponds to the different aberration patterns for a given cancer type.

2. Compute the pairwise similarity between pairs of groups obtained in the first step.

3. Construct a complete weighted graph where each vertex denotes a group of samples and the weight of an edge equals to the similarity between two groups that are connected by this edge.

One can use this graph to find a set of samples of a given size N (by choosing a subset of groups that sum to N), given number of cancer types, and based on level of similarity between groups (by only considering groups that have a similarity within the range of [δ_min, δ_max]). The advantage of the above dataset sampler is that a large number of datasets can be created with variable number of samples and cancer types as well as variable level of similarities between the chosen cancer types. This allows for testing the accuracy and performance of a new method across a variety of potential scenarios.

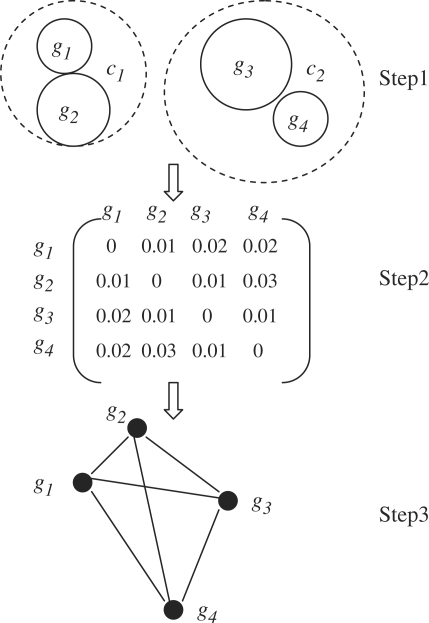
Figure 2 shows an example of how such a dataset sampler works. Consider a dataset containing 1000 CGH samples—400 samples belonging to cancer type c₁ and the other 600 samples belonging to cancer type c₂. Assume that each cancer type is clustered into 2 clusters. This results in 4 groups of CGH samples, which are denoted as g_i,1≤i≤4. Let the size of g₁, g₂, g₃ and g₄ be 150, 250, 450 and 150, respectively. The pairwise similarity between any two groups is shown in Figure 2. Using this, one can construct a weighted graph where each vertex denotes a group and the weight of each edge equals to the similarity between two groups that are connected by this edge. Suppose that a dataset needs to be sampled with N=400, C=2, δ_min=0.025 and δ_max=0.035. The graph can be parsed to find out that g₂ and g₄ satisfy the three conditions and a new dataset can be sampled by combining the samples in g₂ and g₄.

Fig. 2.

A working example of dataset sampler. c_i and g_j denote the ith cancer type and the jth group of samples, respectively. In the first step, the samples are partitioned in each cancer type into two disjoint groups. In the second step, pairwise similarity metrics are computed. In the third step, a complete weighted graph is generated.

The advantage of the above dataset sampler is that a large number of datasets can be created with variable number of samples and cancer types as well as variable level of similarities between the chosen cancer types. This allows for testing the accuracy and performance of a new method across a variety of potential scenarios.

We used our dataset resampling scheme to select datasets at four different similarity levels from the Progenetix dataset. We denote the similarity levels as Best, Good, Fair and Poor. The samples in Best has the highest similarity and those in Poor have the lowest similarity. For each similarity level, we created three datasets with four, six and eight cancer types respectively. Thus, in total, we have 12 datasets. For convenience, we use the similarity level followed by the number of cancer types to denote a dataset. For example, best6 denotes the dataset with similarity level Best (i.e. homogeneous samples) and contains six cancer types. The number of samples in each dataset is around 1000. Note that there is no topological relations between different datasets because we generate all datasets in separate runs. For example, any sample in best4 is not necessarily contained in best6 or best8. Details of each dataset are listed in Table 1 and Table 2.

Table 1.

Details of the cancers contained in the Progenetix dataset

Code	#cases	Code translation
A	310	Infiltrating duct mixed with carcinoma
B	323	Diffuse large B-cell lymphoma, NOS
C	346	B-cell chronic/small lymphocytic leukemia
D	1057	Adenocarcinoma, NOS
E	657	Squamous cell carcinoma, NOS
F	209	Adenoma, NOS
G	110	non-neoplastic or benign
H	286	Hepatocellular carcinoma, NOS
I	120	Retinoblastoma, NOS
J	171	Mantle cell lymphoma
K	180	Carcinoma, NOS
L	190	Multiple myeloma
M	141	Precursor B-cell lymphoblastic leukemia
N	133	Osteosarcoma, NOS
O	144	Adenocarcinoma, intestinal type
P	118	Leiomyosarcoma, NOS
Q	126	Ependymoma, NOS
R	271	Neuroblastoma, NOS

Term ‘#cases’ denote the number of cases in a cancer.

Table 2.

The comparison of classification accuracy for three feature selection methods, MIFS, MRMR and SVM-RFE (denoted as RFE), on 12 datasets

Dataset	Cancer code	N	Method	Number of Features
				4	8	16	40	60	80	100	150	250	500	862
			MIFS	0.696	0.765	0.811	0.819	0.814	0.819	0.821	0.824	0.814	0.815
poor4	A,B,C,D	803	MRMR	0.734	0.772	0.778	0.794	0.791	0.799	0.814	0.814	0.819	0.802	0.809
			RFE	0.567	0.644	0.681	0.706	0.746	0.771	0.794	0.814	0.821	0.821
			MIFS	0.527	0.59	0.615	0.622	0.64	0.654	0.659	0.645	0.649	0.633
poor6	A,B,C,D,E,F	815	MRMR	0.542	0.576	0.588	0.589	0.581	0.596	0.61	0.596	0.610	0.635	0.633
			RFE	0.337	0.37	0.431	0.531	0.551	0.564	0.578	0.593	0.608	0.635
			MIFS	0.338	0.394	0.433	0.469	0.470	0.488	0.496	0.513	0.53	0.486
poor8	A,B,C,D,E,F,G,H	764	MRMR	0.335	0.408	0.454	0.467	0.469	0.482	0.47	0.474	0.489	0.465	0.472
			RFE	0.259	0.274	0.303	0.39	0.423	0.435	0.457	0.456	0.456	0.475
			MIFS	0.621	0.687	0.755	0.784	0.802	0.816	0.816	0.809	0.808	0.806
fair4	B,D,I,J	812	MRMR	0.598	0.685	0.728	0.777	0.796	0.789	0.784	0.777	0.783	0.786	0.798
			RFE	0.466	0.527	0.608	0.693	0.753	0.753	0.771	0.786	0.787	0.806
			MIFS	0.587	0.698	0.754	0.814	0.822	0.825	0.827	0.82	0.82	0.807
fair6	B,C,D,E,F,I	880	MRMR	0.593	0.698	0.767	0.772	0.786	0.807	0.802	0.807	0.801	0.804	0.792
			RFE	0.504	0.64	0.696	0.761	0.775	0.78	0.781	0.78	0.797	0.816
			MIFS	0.536	0.641	0.684	0.7	0.736	0.733	0.727	0.735	0.732	0.713
fair8	B,C,D,E,H,I,K,L	767	MRMR	0.54	0.653	0.681	0.721	0.707	0.712	0.715	0.704	0.698	0.695	0.72
			RFE	0.398	0.528	0.616	0.677	0.687	0.688	0.702	0.70	0.701	0.709
			MIFS	0.586	0.673	0.763	0.773	0.782	0.78	0.783	0.774	0.778	0.767
good4	B,D,H,M	794	MRMR	0.609	0.681	0.755	0.761	0.779	0.78	0.78	0.77	0.772	0.761	0.755
			RFE	0.543	0.61	0.656	0.711	0.718	0.74	0.732	0.735	0.767	0.749
			MIFS	0.455	0.551	0.593	0.645	0.709	0.716	0.724	0.697	0.7	0.694
good6	D,J,K,L,N,O	867	MRMR	0.427	0.532	0.621	0.667	0.68	0.69	0.677	0.687	0.675	0.664	0.696
			RFE	0.339	0.437	0.517	0.597	0.638	0.653	0.66	0.682	0.674	0.698
			MIFS	0.373	0.477	0.567	0.659	0.674	0.676	0.665	0.673	0.666	0.655
good8	D,E,H,J,K,N,P,Q	827	MRMR	0.336	0.461	0.527	0.615	0.634	0.647	0.644	0.646	0.649	0.661	0.652
			RFE	0.258	0.346	0.424	0.508	0.53	0.581	0.605	0.624	0.632	0.654
			MIFS	0.650	0.754	0.763	0.817	0.829	0.832	0.829	0.821	0.838	0.82
best4	A,D,E,R	1158	MRMR	0.667	0.757	0.775	0.785	0.789	0.793	0.798	0.791	0.784	0.802	0.803
			RFE	0.596	0.659	0.708	0.753	0.766	0.789	0.776	0.791	0.803	0.817
			MIFS	0.497	0.568	0.699	0.731	0.767	0.765	0.763	0.77	0.75	0.755
best6	A,D,E,H,O,R	1095	MRMR	0.497	0.568	0.688	0.73	0.731	0.725	0.746	0.739	0.748	0.74	0.75
			RFE	0.449	0.499	0.587	0.667	0.71	0.712	0.727	0.729	0.736	0.749
			MIFS	0.427	0.543	0.635	0.726	0.737	0.733	0.735	0.732	0.735	0.727
best8	A,D,E,F,H,K,L,R	1016	MRMR	0.434	0.563	0.652	0.704	0.7	0.714	0.712	0.7	0.693	0.704	0.707
			RFE	0.342	0.429	0.532	0.641	0.648	0.687	0.694	0.723	0.719	0.724
			MIFS	0.524	0.612	0.673	0.713	0.732	0.736	0.737	0.734	0.735	0.723
Avg	N/A	N/A	MRMR	0.518	0.606	0.664	0.696	0.702	0.709	0.71	0.707	0.707	0.706	0.716
			RFE	0.422	0.497	0.563	0.636	0.662	0.679	0.69	0.7	0.708	0.721

The best accuracy obtained for each dataset is highlighted in bold. Term N denotes the number of cases. The cancer codes are explained in Table 1.

6 EXPERIMENTAL RESULTS

In this section, we describe the experimental comparison of our methods with SVM-RFE and MRMR. We developed our code using MATLAB and ran our experiment on a system with dual 2.59 GHz AMD Opteron Processors, 8 gigabytes of RAM, and a Linux operating system.

6.1 Comparison of linear and raw kernel

In this section, we compare the Raw kernel to linear kernel for the classification of CGH data. We perform the experiments over the twelve datasets using a 5-fold cross validation (CV). For each dataset, we randomly divided the data set into five disjoint subsets about equal size. For each fold, we keep one subset as the test data set and the other four sets as the training examples. We train two SVMs over the training examples using linear and Raw kernel respectively. We then use each SVM to predict the class labels of the set aside examples respectively. We compute the predictive accuracy of each SVM as the ratio of number of correctly classified samples to the number of test dataset examples. Next, we choose another subset as set aside examples and the rest as training examples. We repeat this procedure until each subset has been chosen as set aside examples. As a result, we have five values of predictive accuracy corresponding to each kernel respectively. We compute the average of the five values as the average predictive accuracy for each kernel in 5-fold CV.

We use the DAGSVM (Directed Acyclic Graph SVM) provided by MATLAB SVM Toolbox (Cawley, 2000) for the classification of multiclass data. All other parameters of SVM are set to the standard values that are part of the software package and existing literature.

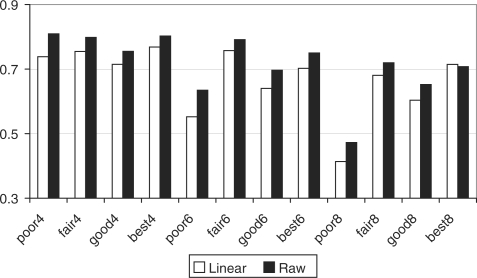
The results are presented in Figure 3. X-axis lists the 12 different datasets. Y-axis denotes the value of average predictive accuracy in 5-fold CV. For the 12 datasets, Raw kernel outperforms linear kernel in eleven datasets (except best8). On average, Raw kernel improves the predictive accuracy by 7.3% over 12 datasets compared to linear kernel. For the best8 dataset, the difference between Raw and Linear is less than 1%. These results demonstrate that SVM based on Raw kernel works better for the classification of CGH data as compared to linear SVM.

Fig. 3.

Comparison of predictive accuracies of SVM with linear and Raw kernels respectively. X-axis denotes different datasets. Y-axis denotes the predictive accuracy based on 5-fold CV.

The remaining set of experimental results in this section are limited to the Raw kernel (unless stated explicitly).

6.2 Comparison of MIFS with other methods

In this section, our method, MIFS, is compared against MRMR (a filter based approach) and SVM-RFE (a wrapper-based approach). MRMR is shown to be more effective than most filter methods, such as methods based on standard mutual information, F-statistic or t-statistic (Ding and Peng, 2005). The MIQ scheme of MRMR, i.e. the divisive combination of relevance and redundancy, is used because it outperforms MID scheme consistently. SVM-RFE is a popular wrapper method for gene selection and cancer classification. It is shown to be better than filter methods such as those based on ranking coefficients similar to Fisher's discriminant criterion. SVM-RFE is also shown to be more effective than wrapper methods using RFE and other multivariate linear discriminant functions, such as linear discriminant analysis and mean-squared error (Pseudo-inverse) (Guyon et al., 2002).

For each method, a 5-fold cross validation is used. In each fold, the feature selection method is applied over the training examples. Multiple sets of features with different sizes (4, 8, 16 features etc) are selected. For each set of features, a classifier is trained on the training examples with only the selected features. The predictive accuracy of this classifier is determined using the test (set aside) examples with the same set of features. These steps are repeated for each of the 5-folds to compute the average predictive accuracy.

In the experiments, we use the DAGSVM with Raw kernel as the classifier for testing the predictive accuracy of features selected by different methods. Since the SVM-RFE presented in the literature only works for two-class data, we extended it to multiclass data using the same ‘ranking scheme’ that we use to extend MIFS (as described in Section 4). The originally proposed SVM-RFE uses linear kernel for feature selection purpose. We stick to the same implementation of SVM-RFE in our experiments. We also implement a variant of SVM-RFE using Raw kernel. Based on our experimental results, the classification accuracy of Raw kernel-based SVM-RFE is roughly midway between the linear kernel based SVM-RFE and MIFS. Detailed results of Raw kernel-based SVM-RFE are not presented here due to space limitations.

The experimental results are shown in Table 2. In Table 2, the predictive accuracy of features selected by three methods, MIFS, MRMR and SVM-RFE, over twelve datasets are compared. For each feature selection method, the results for 4, 8, 16, 40, 60, 80, 100, 150, 250 and 500 features over each dataset are presented. The results are averaged over the 5-folds and reported in columns 5 to 14. In the 15th column, the average predictive accuracies of SVM built upon 862 features, i.e. no feature selection, are reported. The average predictive accuracies of the 12 datasets are reported in the last three rows. The key findings are described as follows.

Comparison between MIFS and MRMR The results show that, when the number of features is ≤16, there is no clear winner between MIFS and MRMR. Although, MIFS is slightly better than MRMR based on the average results of the 12 datasets, neither of the two methods are predominantly better than other. However, when the number of features is >16, MIFS outperforms MRMR in almost all cases. We believe that using SVM-based approach provides combination of features that have significantly better predictive power than MRMR for CGH datasets. Also, it is worth noting that if we compare the best predictive accuracy obtained for a given dataset (given in bold) by using MIFS to that of MRMR, we observe that MIFS always gives a better value.

Comparison between MIFS and SVM-RFE The results in Table 2 show that MIFS outperforms SVM-RFE in almost all cases. Clearly, as the number of features increases, the gap between MIFS and SVM-RFE drops. They become comparable in terms of predictive accuracy only when the number of features reaches more than a few hundred (we do not report these results due to the space limitations). We believe that a forward scheme is better because it first adds the highest discriminating features followed by features that individually may not be discriminating, but improve the classification accuracy when used in combination with the discriminating features. A backward elimination scheme fails to achieve this.

Using MIFS for feature selection The results in Table 2 shows that using only 40 features results in classification accuracy that is comparable to using all the features. Also, using 80 features derived from MIFS scheme results in comparable or better classification accuracy as compared to all the features. This is significant as beyond data reduction, the proposed scheme can lead to better classification. To support this hypothesis, we generated four new datasets using our dataset resampler. The resulting four datasets (newds1 to newds4) contain 4, 5, 6 and 8 classes, respectively. The number of samples in the four datasets are 508, 1021, 815 and 649. We applied the MIFS method over these datasets. We compare the classification accuracies obtained by using all 862 features to those using only 40 and 80 selected features. The results are shown in Table 3. These results substantiate our hypothesis that using around 40 features (roughly 5% of all features) can generate comparable accuracy to using all the features. Also, using around 80 features (roughly 10% of all the features) can result in comparable or better prediction than all the 862 features.

Table 3.

The comparison of classification accuracy using different number of features

Dataset	Number of features
	40	80	862
newds1	0.801	0.792	0.799
newds2	0.803	0.819	0.8
newds3	0.629	0.67	0.637
newds4	0.706	0.748	0.719
Average	0.735	0.757	0.739

It is worth noting that the other two methods, typically have lower or comparable accuracy when the number of features used is less than all the features.

7 CONCLUSIONS

Comparative Genomic Hybridization (CGH) is one of the important mapping techniques for cancerous cells. In this article, we develop novel SVM-based methods for classification and feature selection of CGH data. For SVM-based classification, we show that the kernel used by us is substantially better then the standard kernel for SVM. Our approach of greedily selecting features with the maximum influence on an objective function results in significantly better classification and feature selection. We compared our methods against SVM-RFE (wrapper) and MRMR (filter) approaches that have been used for classification and feature selection of large dimensional biological data. Our results on twelve datasets generated from the Progenetix database, suggests that our methods are considerably superior to existing methods. Further, unlike other methods proposed in the literature, our methods can improve the overall classification error by using a small fraction (around 10%) of all the features.