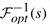Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2008 Jul 1;24(13):i132–i138. doi: 10.1093/bioinformatics/btn150

The multiple gene duplication problem revisited

Mukul S Bansal 1, Oliver Eulenstein 1,*
PMCID: PMC2718628  PMID: 18586705

Abstract

Motivation: Deciphering the location of gene duplications and multiple gene duplication episodes on the Tree of Life is fundamental to understanding the way gene families and genomes evolve. The multiple gene duplication problem provides a framework for placing gene duplication events onto nodes of a given species tree, and detecting episodes of multiple gene duplication. One version of the multiple gene duplication problem was defined by Guigó et al. in 1996. Several heuristic solutions have since been proposed for this problem, but no exact algorithms were known.

Results: In this article we solve this longstanding open problem by providing the first exact and efficient solution. We also demonstrate the improvement offered by our algorithm over the best heuristic approaches, by applying it to several simulated as well as empirical datasets.

Contact: oeulenst@cs.iastate.edu

1 INTRODUCTION

Gene duplication is known to have played a major role in the evolution of almost all life on Earth. For example, analyses of genomic data from numerous plants such as grasses (Guyot and Keller, 2004; Paterson et al., 2004; Schlueter et al., 2004; Wang et al., 2005; Yu et al., 2005), Arabidopsis or other Brassicaceae (Blanc et al., 2003; Bowers et al., 2003; Cannon et al., 2006; Schlueter et al., 2004; Schranz and Mitchell-Olds, 2006; Simillion et al., 2002; Vision et al., 2000; poplar (Sterck et al., 2005), cotton (Blanc and Wolfe, 2004; Rong et al., 2004) and Physcomitrella (Rensing et al., 2007), among others, have revealed evidence of ancient gene duplications. Complex evolutionary processes such as gene duplication and loss, recombination and horizontal gene transfer generate gene trees that differ from species trees. One approach to infer gene duplications is to reconcile the conflicting gene trees with respect to a trusted species tree (Bonizzoni et al., 2005; Chen et al., 2000; Goodman et al., 1979; Górecki and Tiuryn 2004; Guigó et al., 1996; Mirkin et al., 1995; Page, 1994; Zhang 1997). Existing techniques that reconcile gene trees to species trees can identify gene duplications but cannot, in general, accurately locate them on the species tree. Other approaches make use of sequence similarity to reconstruct the underlying evolutionary history of genes (see, for example, Wapinski et al., 2007a,b). Probabilistic models for gene/species tree reconciliation as well as gene sequence evolution have also been developed (Arvestad et al., 2003, 2004).

There is evidence that many gene duplications are part of larger multiple gene duplication episodes, during which a large portion of an organism's genome is duplicated. In fact, it is known that the entire genomes of numerous species (many eukaryotes for example) have been entirely duplicated one or more times. However, the rapid gene loss and gene rearrangements that follow a multiple gene duplication episode can make them difficult or even impossible to detect; and there is often no clear consensus on the number of ancient multiple gene duplication episodes or their precise location in evolutionary history.

Deciphering the location of gene duplications and multiple gene duplication episodes on the Tree of Life is a fundamental problem in understanding the way gene families and genomes evolve. The multiple gene duplication problem provides a framework for (i) mapping gene duplication events onto a given species tree and (ii) inferring and locating multiple gene duplication episodes. Informally, the multiple gene duplication problem is to assign duplication events to nodes in a species trees in such a way that the total number of multiple gene duplication episodes (or simply episodes in short) is minimized. This allows for a ‘parsimonious’ reconciliation of the gene trees with respect to a trusted species tree, which helps to locate gene duplications, as well as to detect multiple gene duplication episodes, more accurately.

Guigó et al. (1996) were the first to address a comprehensive phylogenetic problem that maps duplication events from a collection of rooted, binary gene trees onto a larger rooted binary species tree. They presented a heuristic that could be used to trace back the identified gene duplications to a few multiple gene duplication episodes. Later on, this heuristic approach was refined and restated in more formal terms, and used to study multiple gene duplication episodes in vertebrates by Page and Cotton (2002). Essentially, this heuristic approach sought to solve the multiple gene duplication problem of Guigó et al. by solving instead a similar problem which we refer to as the ‘episode clustering’ problem. An alternative version of the multiple gene duplication problem was introduced by Fellows et al. (1998b) which they proved to be intrinsically difficult. Hence, we direct our focus to the work of Guigó et al. and Page and Cotton. The episode clustering problem determines duplication events using the Gene Duplication (GD) model from Goodman et al. (1979). Each duplication can be placed on any species on a path between the two (not necessarily distinct) most recent species that could have contained the duplication and its parent, respectively. In case the parent does not exist, the path runs between the most recent species for the duplication and the root of the species tree. An example is depicted in Figure 1. The duplications in gene tree G are represented by the three bold vertices. Associated with each bold vertex is its path represented by an interval. For example, the interval [5,3] represents the path 〈5,4,3〉 in the species trees S. Let g denote the node corresponding to the interval [5,3]. Species 5 is the most recent species that could have contained g and the parent of species 3, i.e. 2, is the most recent species that could have contained the parent of g. The Episode Clustering (EC) problem is, given a collection of gene trees and a species tree, find a minimum number of locations in the species tree where all duplications in the gene trees can be placed. For example, all three duplications in Figure 1 can be placed on species nodes 2 and 3

Fig. 1.

Fig. 1.

Open in a new tab

A gene tree G and a comparable species tree S is depicted. The bold vertices in G are duplications and their intervals represent their allowed locations in the species tree S.

The EC problem itself has a long and interesting history. Guigó et al. (1996) presented a heuristic approach to solve this problem. This heuristic was somewhat imprecise, and there were hints, but no formal algorithm, on how to deal with certain optimization steps. Page and Cotton (2002) observed that the EC problem can be efficiently and cleanly reduced to the Set Cover problem. They approach the EC problem using a heuristic for the intrinsically difficult set-cover problem. Recently, Burleigh et al. (2008) gave an efficient and exact solution for the EC problem. However, the EC problem itself suffers from a major limitation: it minimizes the number of locations in the species tree at which gene duplications occur, but it need not minimize the total number of episodes of multiple gene duplication. In fact, it is easy to find examples where minimizing the number of locations, does not minimize the number of episodes. Indeed, the desired goal in the papers of both Guigó et al. (1996) and Page and Cotton (2002) is to minimize the number of episodes, and the EC problem was used only as a heuristic approach for this problem. We refer to this problem of minimizing the number of episodes as the Minimum Episodes (ME) problem. In essence, the ME problem is the multiple gene duplication problem as defined by Guigó et al. (1996).

Thus, all previous attempts at solving the ME problem have made use of heuristics approaches based on the EC problem. In this article we finally solve a longstanding open problem by providing the first exact and efficient solution to the ME problem (see Section 3). Our algorithm is surprisingly simple and extremely efficient. We have also implemented our algorithm and demonstrated the improvement it offers over the best heuristic approaches experimentally by applying it to several simulated as well as empirical datasets (see Section 4).

2 BASIC DEFINITIONS, NOTATION AND PRELIMINARIES

In this section we first introduce basic definitions and notation that we shall use and then define the preliminaries required for this work.

2.1 Basic definitions and notation

A tree T is a connected graph with no cycles, consisting of a node set V(T) and an edge set E(T). T is rooted if it has exactly one distinguished node called the root which we denote by ℛℴ(T). Let T be a rooted tree. We define ≤T to be the partial order on V(T) where x≤T y if y is a node on the path between ℛℴ(T) and x. The set of minima under ≤T is denoted by ℒℯ(T) and its elements are called leaves. If {x,y}∈E(T) and x≤T y then we call y the parent of x denoted by 𝒫𝒶T(x) and we call x a child of y. The set of all children of y is denoted by 𝒞𝒽T(y). If two nodes in T have the same parent, they are called siblings. The least common ancestor of a non-empty subset L⊆V(T), denoted as lca(L), is the unique smallest upper bound of L under ≤T. A subtree of T rooted at node y∈V(T), denoted by Ty, is the tree induced by {x∈V(T) :x≤y}. T is (fully) binary if every node has either zero or two children. Throughout this article, the term tree refers to a rooted fully binary tree.

Given a≤T b we define the interval [a,b]={x∈V(T)∣a≤T x≤T b}. The height of T, denoted by h(T) is the number of nodes on a maximal length path from ℛℴ(T) to a leaf node of T. Thus, a rooted binary tree with three leaves has height three.

2.2 The ME problem

In this section we formally define the ME problem. The ME problem seeks to assign duplication events to nodes in a species tree, where each duplication event is associated with an interval in the species tree describing the locations where that duplication can be placed. The definition of duplication is based on the (GD) model introduced by Goodman et al. (1979). Guigó et al. (1996) extended this model and defined the associated intervals for each gene duplication. Here we only provide definitions necessary to state the ME problem.

The GD model is based on a gene and species tree from which gene duplications can be derived. A species tree is a tree that depicts the evolutionary relationships of a set of species. Given a gene family for a set of species, a gene tree is a tree that depicts the evolutionary relationships among the sequences encoding only that gene family in the given species. Thus the vertices in a gene tree represent genes. In order to compare a gene tree G with a species tree S a mapping from each gene g∈V(G) to the most recent species in S that could have contained g is required.

DEFINITION 2.1 —

[LCA Mapping] A leaf-mapping ℒG,S : ℒℯ(G)→ℒℯ(S) specifies, for each gene g, the species from which it was sampled. The extension ℳG,S : V(G)→V(S) of ℒG,S is the LCA mapping defined by ℳG,S(g)=lca(ℒG,S(ℒℯ(Gg)).

DEFINITION 2.2 —

[Comparability] The trees G and S are comparable if there exists a leaf-mapping ℒG,S.1 A set of gene trees 𝒢 and S are comparable if each gene tree in 𝒢 is comparable with S.

Throughout the remainder of this article, 𝒢 denotes a collection of input gene trees, S a comparable species tree, and G denotes an arbitrary gene tree in 𝒢.

DEFINITION 2.3 —

[Duplication] A node v∈V(G) is a (gene) duplication if ℳG,S(v)=ℳG,S(u) for some u∈𝒞𝒽(v) and we define 𝒟𝓊𝓅(G,S)={g∈V(G) ∣g is a duplication }.

DEFINITION 2.4 —

[Interval I(g)] For every g∈𝒟𝓊𝓅(G,S), the interval I(g) is defined to be:

  • [ℳG,S(g),ℛℴ(S)], if g=ℛℴ(G),

  • [ℳG,S(g),ℳG,S(g)], if ℳG,S(g)=ℳG,S(𝒫𝒶(g)) and

  • [ℳG,S(g),ℳG,S(𝒫𝒶(g))]−{ℳG,S(𝒫𝒶(g))}, otherwise.

DEFINITION 2.5 —

[Valid Mapping] A mapping ℱG,S :V(G)→V(S) is called valid if for each g∈G,

graphic file with name btn150um1.jpg

Note: (i) ℱ is used to denote the mapping ∪G∈𝒢ℱG,S, and we say ℱ is valid if ℱG,S is valid for each G∈𝒢, (ii) given a mapping ℱ, and a node s∈V(S), we write ℱ−1(s) to denote the set {g: ℱ(g)=s} and (iii) in the remainder of this article, we denote by ℱℳ the valid mapping ∪G∈𝒢ℳG,S.

DEFINITION 2.6 —

[H(ℱ,s)] Given 𝒢 and S, a valid mapping ℱ, and a node s∈V(S), we define H(ℱ,s) to be the sub-graph of 𝒢2 induced by the node set ℱ−1(s).

Note that H(ℱ,s) must be a forest.

Throughout this article we abbreviate the term ‘multiple gene duplication episode’ simply to ‘episode’. Given any valid mapping ℱ, the following definition defines (i) the number of episodes, Δ(ℱ,s), at each node s∈V(S) and (ii) the total number of episodes Δ(ℱ). For the actual definition of an episode itself, we refer the reader to Guigó et al. (1996).

DEFINITION 2.7 —

[Δ(ℱ,s) and Δ(ℱ)] Given a valid mapping ℱ and a node s∈V(S), we denote by Δ(ℱ,s) the number of episodes at s caused by the mapping ℱ. Then, Δ(ℱ,s)=max{h(T) : T∈H(ℱ,s)}, and, Δ(ℱ)=∑s∈V(S)Δ(ℱ,s).

DEFINITION 2.8 —

[Δopt] Δopt =min{Δ(ℱ) :ℱ is any valid mapping}.

𝒢 and S form the input for the ME problem. The output is a valid mapping ℱopt :∪G∈𝒢V(G)→V(S), such that Δ(ℱopt) is minimized. More formally,

PROBLEM 1. —

Instance: A collection of gene trees 𝒢 and a comparable species tree S.

Find: A valid mapping ℱopt such that Δ(ℱopt)=Δopt.

3 THE ME PROBLEM

It is not hard to see that the number of distinct valid mappings can be extremely large (exponential in the size of the input). It is therefore infeasible to solve the ME problem by considering all possible valid mappings and then picking the one that causes the fewest episodes. In this section we give a simple and extremely efficient algorithm to solve the ME problem. The main idea of the algorithm is to traverse the species tree S in post-order, and perform greedy optimization steps at each node. As we shall prove, this leads us to a globally optimal mapping.

In order to state the algorithm, we must first define a few terms.

DEFINITION 3.1 —

[Leading node] Let ℱ be a valid mapping and let s∈V(S). Then, we say a node g∈ℱ−1(s) is a leading node if and only if g=ℛℴ(T) where T ∈H(ℱ,s) and h(T)=Δ(ℱ,s).

DEFINITION 3.2 —

[Free node] Given a valid mapping ℱ, and a node s∈V(S) such that s≠ℛℴ(S), a node g∈ℱ−1(s) is called free if and only if 𝒫𝒶(s)∈I(g).

For convenience, we refer to each node s∈V(S) for which ℱ−1(s)≠∅, as a relevant node. Also recall that ℱℳ denotes the mapping ∪G∈𝒢ℳG,S.

We begin by stating the intuitive idea behind our algorithm. Consider any valid mapping ℱ :∪G∈𝒢V(G)→V(S). Given any node s∈V(S), let ℱ′ be a new mapping constructed from ℱ by moving the mapping of all the free nodes in ℱ−1(s) to 𝒫𝒶(s). Clearly, ℱ′ must be a valid mapping. Now, if all the leading nodes in ℱ−1(s) are free, then we can show that Δ(ℱ′)≤Δ(ℱ). On the other hand, if not all the leading nodes in ℱ−1(s) are free, then we must have Δ(ℱ′)≥Δ(ℱ). This simple observation forms the basis of our greedy algorithm. If these greedy optimizations are carried out in a particular order, then it can be shown that the resulting mapping will be an optimal one.

We are now ready to state our algorithm. The algorithm starts with the LCA mapping from the gene trees to the species tree, and progressively modifies it so that when the algorithm terminates, we have an optimal valid mapping. First, a valid mapping ℱ :∪G∈𝒢V(G)→V(S) is initialized such that ℱ =ℱℳ. Next, we traverse S in post-order, and at each node, say s, we check if it is relevant and if all the leading nodes in ℱ−1(s) are free. If they are, then we modify the mapping ℱ by changing the mapping of all the leading nodes in ℱ−1(s) to 𝒫𝒶(s). It can be shown that when the post-order traversal is finished, the mapping ℱ must be a solution to the ME problem (see Theorem 3.1). This algorithm is described more formally in Algorithm 1.

graphic file with name btn150i24.jpg
Open in a new tab

We denote the final mapping output by Algorithm 1 by ℱopt. In the remainder of this section we first show that ℱopt is a valid mapping and Δ(ℱopt)=Δopt, and then study the complexity of Algorithm 1.

LEMMA 3.1. —

ℱopt is a valid mapping.

PROOF. —

Algorithm 1 starts with the mapping ℱ =ℱℳ which is valid by definition. During each iteration of the loop, the mapping ℱ may be modified according to Equation (1). However, Equation (1) only modifies the mapping of those nodes that are free, and hence produces a valid mapping. Therefore, each mapping produced by the algorithm, including the mapping ℱopt, is valid. ▪

LEMMA 3.2. —

Let ℱ: ∪G∈𝒢V(G)→V(S) be any valid mapping. Then we have the following:

  1. If s∈V(S) is a relevant node under mapping ℱℳ, then Δ(ℱℳ,s)−1≤Δ(ℱ,s)≤Δ(ℱℳ,s).

  2. If s∈V(S) is not a relevant node under mapping ℱℳ, then 0≤Δ(ℱ,s)≤1.

PROOF. —

Part 1: Here s is a relevant node i.e. Inline graphic. Let A denote the set of nodes that are present in Inline graphic but not in ℱ−1(s) and B denote the set of nodes that are present in ℱ−1(s) but not in Inline graphic. Observe that all the nodes in A must be leading nodes in Inline graphic. Relocating all the leading nodes in Inline graphic reduces Δ(ℱℳ,s) by exactly 1. Therefore, relocating the nodes in A reduces Δ(ℱℳ,s) by at most 1. This proves that Δ(ℱℳ,s)−1≤Δ(ℱ,s).

Consider now the set B. Let a and b be two gene duplication nodes from some gene tree in 𝒢 such that one is an ancestor of the other, and ℱℳ(a)≠ℱℳ(b). Then, Definition 2.4 implies that ℱ(a)≠ℱ(b). Therefore, none of the nodes in set B is an ancestor of another, and hence none of them is a leading node in ℱ−1(s). This proves that Δ(ℱ,s)≤Δ(ℱℳ,s).

Part 2: In this case Inline graphic, and therefore B=ℱ−1(s). Following the argument from the previous paragraph, we can conclude that none of the nodes in set B is an ancestor of another. This implies that Δ(ℱ,s)≤1. ▪

The following three lemmas are required for the proof of Theorem 3.1.

LEMMA 3.3. —

Let ℱ: ∪G∈𝒢V(G)→V(S) be a valid mapping and s∈V(S) be a node such that Δ(ℱopt,s)>Δ(ℱ,s). Then, Δ(ℱopt,s)=1.

PROOF. —

There are two possible cases: (i) s is not a relevant node under ℱℳ or (ii) s is a relevant node under ℱℳ. We analyze these cases separately.

Case (i): In this case, by Part 2 of Lemma 3.2, we must have Δ(ℱ,s)=0 and Δ(ℱopt,s)=1.

Case (ii): If Δ(ℱℳ,s)<2, then by Part 1 of Lemma 3.2 the result follows immediately; therefore, let us assume that Δ(ℱℳ,s)≥2. Part 1 of Lemma 3.2 implies that we must have Δ(ℱ,s)=Δ(ℱℳ,s)−1 and Δ(ℱopt,s)=Δ(ℱℳ,s).

Let A denote the set of nodes that are present in Inline graphic but not in ℱ−1(s), and B denote the set of nodes that are present in Inline graphic but not in Inline graphic. All the nodes in A must be leading nodes in Inline graphic, and since these nodes are not present in ℱ−1(s), all the nodes in A must be free as well. Also, none of the nodes in B can be a leading node in Inline graphic (see the proof of Part 1 of Lemma 3.2). Therefore, all of the leading nodes in Inline graphic must be present in A, which implies that all the leading nodes in Inline graphic are free. Thus, during the execution of Algorithm 1, the mapping for these nodes would have been changed. This is a contradiction, and hence we cannot have Δ(ℱℳ,s)≥2. ▪

LEMMA 3.4. —

Let node a be such that ℱℳ(a)<S ℱopt(a). If ℱ: ∪G∈𝒢V(G)→V(S) is a valid mapping such that ℱ(a) = ℱℳ(a), then Δ(ℱopt, ℱℳ(a))<Δ(ℱ,ℱℳ(a)).

PROOF. —

Since ℱ(a)<S ℱopt(a), a must be a leading node in Inline graphic. This implies that Δ(ℱ,ℱℳ(a))≮Δ(ℱℳ, ℱℳ(a)). Moreover, since ℱopt(a)≠ℱℳ(a), we have Δ(ℱopt,ℱℳ(a))=Δ(ℱℳ,ℱℳ(a))−1 (see Algorithm 1). The lemma follows. ▪

LEMMA 3.5. —

Let node a be such that ℱℳ(a)<S ℱopt(a). If Γ = {x : ℱℳ(a)<S x<S ℱopt(a)}, then ℱopt(x)=0 for all x∈Γ.

PROOF. —

Consider any node x∈Γ. There must exist some valid mapping ℱ, realized during the execution of Algorithm 1, for which ℱ(a)=x. However, as the execution of Algorithm 1 progresses, the mapping of a changes. This implies that a must be a leading node in ℱ−1(a). Observe that a could be a leading node in ℱ−1(a) only if Δ(ℱ,x)=1. Furthermore, for the mapping of a to be changed, all the nodes in ℱ−1(a) must be free, and would therefore not map to node x when the algorithm terminates. Thus, ℱopt(x)=0. ▪

THEOREM 3.1. —

Algorithm 1 solves the ME problem.

PROOF. —

In Lemma 3.1 we have already established that ℱopt is a valid mapping. Therefore, to establish the correctness of our algorithm, it is sufficient to show that Δ(ℱopt)=Δopt. Let us assume, for the sake of contradiction, that there exists some valid mapping ℱ for which Δ(ℱopt)>Δ(ℱ). This implies that there must be at least one node s∈V(S) for which Δ(ℱopt,s)>Δ(ℱ,s). We may assume, without any loss of generality, that s has the following property: there does not exist any other node t∈V(Ss) for which Δ(ℱopt,t)>Δ(ℱ,t).

By Lemma 3.3 we know that node s must be such that Δ(ℱopt,s) = 1. This implies that Δ(ℱ,s) = 0, i.e. ℱ−1(s) = ∅. We will now show that there exists at least one node t ∈V(Ss)∖{s} for which Δ(ℱopt,t)<Δ(ℱ,t). This would imply that Inline graphic.

Let Inline graphic; clearly A≠∅. We now have two possible scenarios, exactly one of which must be true: (i) ℱ(g)>S s for each g∈A or (ii) there exists some g∈A for which ℱ(g)<S s. If case (i) were possible, it would imply that all nodes in A are leading and free, and therefore Algorithm 1 would have already moved their mappings to nodes that are proper ancestors of s. Hence, case (ii) is the only possible scenario.

So far we have shown that if there exists some valid mapping ℱ for which Δ(ℱopt)>Δ(ℱ), then there must exist some node, say a, where a∈A and ℱ(a)<S s. Clearly, ℱℳ(a)≤S ℱ(a)<S s. This leads us to two possible cases, exactly one of which must be true: (i) ℱℳ(a)=ℱ(a) or (ii) ℱℳ(a)<S ℱ(a). If case (i) were true, then by Lemma 3.4 we must have Δ(ℱ,ℱ(a))>Δ(ℱopt,ℱ(a)). If case (ii) were true, then Lemma 3.5 implies that Δ(ℱopt,ℱ(a))=0, but Δ(ℱ,ℱ(a))≠0. Thus, in either case, there exists some t∈V(Ss)∖{s}, for which Δ(ℱopt,t)<Δ(ℱ,t). And hence, Inline graphic

Now, let Inline graphic and Inline graphic. Suppose there exists a node x such that ℱopt(x)∈V(S)∖V(Ss), and ℱ(x)∈V(Ss). Then, there are two possibilities: (i) ℱ(x)∈V(Ss)∖{s} or (ii) ℱ(x)=s. In case (i), Lemma 3.5 implies that Inline graphic must be empty, which is clearly a contradiction. Similarly, case (ii) leads to a clear contradiction as well since ℱ−1(s)=∅. Therefore, such a node x cannot exist. And hence Q⊆P.

All together, this implies that in the subtree Ss, the mapping ℱ induces at least as many episodes as the mapping ℱopt, even though Inline graphic. Let us now construct a new valid mapping ℱ′: ∪G∈𝒢V(G)→V(S) as follows:

graphic file with name btn150um2.jpg

In light of the observation made in the previous paragraph, we must have Δ(ℱ′)≤Δ(ℱ). Moreover, ℱ′ has fewer nodes s for which Δ(ℱopt,s)>Δ(ℱ′,s). Therefore, we can now set ℱ to be ℱ′ and a straightforward induction argument completes our proof. ▪

We now study the complexity of Algorithm 1. In order to simplify our analysis we assume that all G∈𝒢 have approximately the same size. The input for the ME problem is the set of gene trees 𝒢, and species tree S. Let n=|ℒℯ(S)|, k=|𝒢| and m=|ℒℯ(G)| for some G∈𝒢.

THEOREM 3.2. —

The time complexity of Algorithm 1 is O(kmn).

PROOF. —

Computing the LCA mapping for all the gene trees takes O(kmn) time (Zhang 1997). With-in this time, the inverse LCA mapping is also easily computed. All the intervals I(g) can be computed in O(km) time. Now, at each node, s, in the species tree, we must (i) find all the leading nodes in ℱ−1(s), (ii) check if these leading nodes are free and (iii) update the mapping ℱ. Let x=|ℱ−1(s)|, then, each of the Steps (i), (ii) and (iii) above can be completed in O(x) time. Hence, since x=O(km) and there are O(n) nodes in the species tree, we obtain a total time complexity of O(kmn) for Algorithm 1. ▪

4 EXPERIMENTAL RESULTS

We evaluated the efficacy and efficiency of our novel algorithm for the ME problem through comparative studies on simulated and empirical datasets. For this evaluation we implemented our algorithm in the program EXACTMGD. We compared our program against the program APPROXMGD of Burleigh et al. (2008) that implements the currently best known approach to solve the ME problem.

Recall that the objective of the ME problem is to produce a mapping which defines the fewest number of episodes. The smaller the number of episodes, the more accurate the mapping. Therefore, for each dataset we compared the programs by measuring three values: (i) The number of episodes defined by the initial LCA mapping (i.e. the unoptimized value), (ii) the number of episodes defined by the mapping produced by APPROXMGD and (iii) the number of episodes defined by the mapping produced by EXACTMGD. All analyses were performed on a 3 Ghz Intel Pentium 4 CPU based PC with Windows XP operating system. A run of EXACTMGD on each of these datasets terminated in less than 1s!

4.1 Simulated datasets

Our simulated datasets consist of 50 randomly generated gene trees, all with the same set of taxa, along with a randomly generated species tree.3 We generated four such datasets, each with a different number of taxa (50, 100, 200 and 400) in the input trees. EXACTMGD shows a significant reduction in the number of episodes as compared to APPROXMGD for each of the four datasets (Table 1).

Table 1.

Performance of EXACTMGD on simulated datasets

Dataset Unoptimized ApproxMGD ExactMGD
50 taxa 30 28 25
100 taxa 47 38 35
200 taxa 64 54 49
400 taxa 65 45 40
Open in a new tab

4.2 Empirical datasets

For the empirical study we evaluated two datasets from the literature. The first dataset consists of 53 gene trees, each representing the evolutionary history of different gene families from a set of 16 eukaryotes. This set was assembled and evaluated for episodes by Guigó et al. (1996). Subsequently, this dataset was reused and its evaluation refined by Page and Cotton (2002). The second dataset, assembled and evaluated for episodes by Burleigh et al. (2008), consists of 85 gene trees from the Phytome comparative plant genome database and contains genes from 136 plant taxa.

For brevity we refrain from performing biological analyses of our results; and only demonstrate the exceptional level of improvement offered by our algorithm over the best current methods. The results depicted in Table 2 show that the mappings produced by our algorithm are significantly more optimal compared to the mappings produced by the best current approaches. This leads to more accurate inference of the location of gene and genome duplications on the Tree of Life.

Table 2.

Performance of EXACTMGD on empirical datasets

Dataset Unoptimized ApproxMGD ExactMGD
Guigó et al. (1996) 9 7 5
Burleigh et al. (2008) 1180 1152 1042
Open in a new tab

5 OUTLOOK AND CONCLUSION

In this article we have provided the first exact and efficient algorithm for a longstanding open problem. Traditionally, the multiple episodes problem has been used to infer the location of episodes of multiple gene duplication on a given species tree. Our new algorithm allows this to be done far more accurately. But another interesting and important fallout of our algorithm is that it may also allow us to infer the ‘correct’ species trees. Consider the problem of constructing a species tree from conflicting gene trees based on the gene duplication optimality criteria. The gene duplication problem is to find for a given set of gene trees a corresponding species tree with the minimum reconciliation cost (Fellows et al., 1998a; Hallett and Lagergren, 2000; Ma et al., 2000; Stege, 1999). However, since these gene duplication events are usually a part of larger multiple gene duplication episodes, it might be more helpful if we can infer species trees directly based on the multiple gene duplication optimality criteria (see also Fellows et al. 1998b). Our algorithm offers the first practical and effective means to do so. The idea is to use a local search based hill climbing heuristic to traverse through the search space of possible species tree. Our algorithm can be used to compute the number of episodes induced by each candidate species tree during the local search steps. The lower the number of episodes, the better the species tree.

In addition, it would be interesting to extend the multiple GD model of Guigó et al. (1996) by relaxing the constraints on the possible locations of gene duplications on the species tree.

ACKNOWLEDGEMENTS

The authors wish to thank the anonymous referees for their invaluable comments.

Funding: This work was supported in part by National Science Foundation AToL grant EF-0334832.

Conflict of Interest: none declared.

Footnotes

1Note that mathematically speaking such a leaf-mapping always exists. However, in the current context, we are only concerned with biologically relevant leaf-mappings.

2When 𝒢 is viewed as a forest.

3Our randomly generated trees have a random (binary) topology and a random assignment of leaf labels.

REFERENCES

  1. Arvestad L, et al. Brisbane, Australia: 2003. Bayesian gene/species tree reconciliation and orthology analysis using mcmc. In; pp. 7–15. Proceedings of the Eleventh International Conference on Intelligent Systems for Molecular Biology (ISMB) [DOI] [PubMed] [Google Scholar]
  2. Arvestad L, et al. Gene tree reconstruction and orthology analysis based on an integrated model for duplications and sequence evolution. In. In: Bourne PE, Gusfield D, editors. California, USA: ACM, San Diego; 2004. pp. 326–335. Proceedings of the Eighth Annual International Conference on Computational Molecular Biology (RECOMB) [Google Scholar]
  3. Blanc G, Wolfe KH. Widespread paleopolyploidy in model plant species inferred from age distributions of duplicate genes. Plant Cell. 2004;16:1093–1101. doi: 10.1105/tpc.021345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Blanc G, et al. A recent polyploidy superimposed on older large-scale duplications in theArabidopsis genome. Genome Res. 2003;13:137–144. doi: 10.1101/gr.751803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bonizzoni P, et al. Reconciling a gene tree to a species tree under the duplication cost model. Theor. Comput. Sci. 2005;347:36–53. [Google Scholar]
  6. Bowers J, et al. Unravelling angiosperm genome evolution by phylogenetic analysis of chromosomal duplication events. Nature. 2003;422:433–438. doi: 10.1038/nature01521. [DOI] [PubMed] [Google Scholar]
  7. Burleigh JG, et al. Locating multiple gene duplications through reconciled trees. Vol. 4955 in. In: Vingron M, Wong L, editors. Lecture Notes in Computer Science. Singapore: Springer; 2008. pp. 273–284. [Google Scholar]
  8. Cannon S, et al. Legume genome evolution viewed through the Medicago truncatula and Lotus japonicus genomes. Proc. Natl Acad. Sci. 2006;103:14959–14964. doi: 10.1073/pnas.0603228103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chen K, et al. Notung: a program for dating gene duplications and optimizing gene family trees. J. Comput. Biol. 2000;7:429–447. doi: 10.1089/106652700750050871. [DOI] [PubMed] [Google Scholar]
  10. Fellows M, et al. Analogs & duals of the MAST problem for sequences & trees. Vol. 1533 in. In: Chwa K-Y, Ibarra OH, editors. Lecture Notes in Computer Science. Taejon, Korea: Springer; 1998a. pp. 103–114. [Google Scholar]
  11. Fellows M, et al. Korea: Springer, Taejon; 1998b. On the multiple gene duplication problem. In; pp. 347–356. 9th International Symposium on Algorithms and Computation (ISAAC'98), LNCS 1533. [Google Scholar]
  12. Goodman M, et al. Fitting the gene lineage into its species lineage. a parsimony strategy illustrated by cladograms constructed from globin sequences. Syst. Zool. 1979;28:132–163. [Google Scholar]
  13. Górecki P, Tiuryn J. On the structure of reconciliations. In. In: Lagergren J, editor. Recomb Comparative Genomics Workshop 2004. Vol. 3388. Bertinoro, Italy: Springer; 2004. [Google Scholar]
  14. Guigó R, et al. Reconstruction of ancient molecular phylogeny. Mol. Phylogenet. Evol. 1996;6:189–213. doi: 10.1006/mpev.1996.0071. [DOI] [PubMed] [Google Scholar]
  15. Guyot R, Keller B. Ancestral genome duplication in rice. Genome. 2004;47:610–614. doi: 10.1139/g04-016. [DOI] [PubMed] [Google Scholar]
  16. Hallett MT, Lagergren J. New algorithms for the duplication-loss model. In. In: Shamir R, et al., editors. Tokyo, Japan: ACM; 2000. pp. 138–146. Proceedings of the Fourth Annual International Conference on Computational Molecular Biology (RECOMB 2000) [Google Scholar]
  17. Ma B, et al. From gene trees to species trees. SIAM J. Comput. 2000;30:729–752. [Google Scholar]
  18. Mirkin B, et al. A biologically consistent model for comparing molecular phylogenies. J. Comput. Biol. 1995;2:493–507. doi: 10.1089/cmb.1995.2.493. [DOI] [PubMed] [Google Scholar]
  19. Page RDM. Maps between trees and cladistic analysis of historical associations among genes, organisms and areas. Syst. Biol. 1994;43:58–77. [Google Scholar]
  20. Page RDM, Cotton JA. Vertebrate phylogenomics: reconciled trees and gene duplications. In. In: Altman RB, et al., editors. Hawaii, USA: Lihue; 2002. pp. 536–547. Proceedings of the 7th Pacific Symposium on Biocomputing (PSB'02) [DOI] [PubMed] [Google Scholar]
  21. Paterson AH, et al. Ancient polyploidization predating divergence of the cereals, and its consequences for comparative genomics. Proc. Natl. Acad. Sci. 2004;101:9903–9908. doi: 10.1073/pnas.0307901101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Rensing S, et al. An ancient genome duplication contributed to the abundance of metabolic genes in the moss physcomitrella patens. BMC Evol. Biol. 2007;7:130. doi: 10.1186/1471-2148-7-130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Rong J, et al. A 3347-locus genetic recombination map of sequence-tagged sites reveals features of genome organization, transmission and evolution of cotton (Gossypium) Genetics. 2004;166:389–417. doi: 10.1534/genetics.166.1.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schlueter J, et al. Mining EST databases to resolve evolutionary events in major crop species. Genome. 2004;47:868–876. doi: 10.1139/g04-047. [DOI] [PubMed] [Google Scholar]
  25. Schranz M, Mitchell-Olds T. Independent ancient polyploidy events in sister families Brassicaceae and Cleomaceae. Plant Cell. 2006;18:1152–1165. doi: 10.1105/tpc.106.041111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Simillion C, et al. The hidden duplication past of Arabidopsis thaliana. Proc. Natl. Acad. Sci. 2002;99:13627–1632. doi: 10.1073/pnas.212522399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Stege U. Vancouver, Canada: Springer; 1999. Gene trees and species trees: the gene-duplication problem is fixed-parameter tractable. In. Proceedings of the 6th International Workshop on Algorithms and Data Structures, LNCS 1663. [Google Scholar]
  28. Sterck L, et al. EST data suggest that poplar is an ancient polyploidy. New Phytol. 2005;167:165–170. doi: 10.1111/j.1469-8137.2005.01378.x. [DOI] [PubMed] [Google Scholar]
  29. Vandepoele K, et al. Evidence that rice and other cereals are ancient aneuploids. Plant Cell. 2003;15:2192–2202. doi: 10.1105/tpc.014019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Vision T, et al. The origins of genome duplications in Arabidopsis. Science. 2000;290:2114–2117. doi: 10.1126/science.290.5499.2114. [DOI] [PubMed] [Google Scholar]
  31. Wang X, et al. Duplication and DNA segmental loss in the rice genome: implications for diploidization. New Phytol. 2005;165:937–946. doi: 10.1111/j.1469-8137.2004.01293.x. [DOI] [PubMed] [Google Scholar]
  32. Wapinski I, et al. Austria: Vienna; 2007a. Automatic genome-wide reconstruction of phylogenetic gene trees. In; pp. 549–558. Proceedings of 15th International Conference on Intelligent Systems for Molecular Biology (ISMB) & 6th European Conference on Computational Biology (ECCB), ISMB/ECCB (Supplement of Bioinformatics) [DOI] [PubMed] [Google Scholar]
  33. Wapinski I, et al. Natural history and evolutionary principles of gene duplication in fungi. Nature. 2007b;449:54–61. doi: 10.1038/nature06107. [DOI] [PubMed] [Google Scholar]
  34. Yu J, et al. The genomes of Oryza sativa: a history of duplication. PLoS Biol. 2005;3:266–281. doi: 10.1371/journal.pbio.0030038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Zhang L. On a Mirkin-Muchnik-Smith conjecture for comparing molecular phylogenies. J. Comput. Biol. 1997;4:177–187. doi: 10.1089/cmb.1997.4.177. [DOI] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES