Time Sequence Diffeomorphic Metric Mapping and Parallel Transport Track Time-Dependent Shape Changes

Abstract

Serial MRI human brain scans have facilitated the detection of brain development and of the earliest signs of neuropsychiatric and neurodegenerative diseases, monitoring disease progression, and resolving drug effects in clinical trials for preventing or slowing the rate of brain degeneration. To track anatomical shape changes in serial images, we introduce new point-based time sequence large deformation diffeomorphic metric mapping (TS-LDDMM) to infer the time flow of within-subject geometric shape changes that carry known observations through a period. Its Euler-Lagrange equation is generalized for anatomies whose shapes are characterized by point sets, such as landmarks, curves, and surfaces. The time-dependent momentum obtained from the TS-LDDMM encodes within-subject shape changes. For the purpose of across-subject shape comparison, we then propose a diffeomorphic analysis framework to translate within-subject deformation in a global template without incorporating across-subject anatomical variations via parallel transport technique. The analysis involves the retraction of the within-subject timedependent momentum along the TS-LDDMM trajectory from each time to the baseline, the translation of the momentum in a global template, and the reconstruction of the TS-LDDMM trajectory starting from the global template.

1 Introduction

Spatial-temporal images have been widely used in the field of medical image to record function and anatomy of human organs. Serial MRI human brain scans have facilitated the detection of brain development and of the earliest signs of neuropsychiatric and neurodegenerative diseases, monitoring disease progression, and resolving drug effects in clinical trials for preventing or slowing the rate of brain degeneration (Thompson et al., 2000; Chung et al., 2001; Wang et al., 2003; Apostolova et al., 2006b; Qiu et al., 2008; Xue et al., 2007). For instance, researchers have identified progressive hippocampal volume loss to be one of the hallmarks of Alzheimer’s disease (AD). Using brain warping techniques, neuroimaging studies previously found that patterns of hippocampal shape change distinguished early AD from healthy aging (Wang et al., 2003; Apostolova et al., 2006b; Qiu et al., 2008). Compared to volumetric assessments, rates of anatomical shape changes provide much richer information for disease discrimination (e.g. (Thompson et al., 1996; Christensen, Joshi, and Miller, 1997; Bookstein, 1997; Chung, 2001; Terriberry, Joshi, and Gerig, 2005; Ashburner and Friston, 2005; Apostolova et al., 2006a; Csernansky et al., 2004; Gilmore et al., 2007; Yu et al., 2007; Qiu et al., 2008)). Sensitive and accurate computational techniques are needed to track within-subject shape changes in brain structures based on serial MRI scans and then compare them across clinical populations.

To assess the location and process of atrophy or growth in a brain structure requires studying within-subject time-dependent deformation through the transformation. It characterizes the changes of anatomical coordinates from the baseline to other time points. The earliest mapping of biological coordinates via landmarks was in the early 1980s and continued by Bookstein (Bookstein, 1978; Bookstein, 1991; Bookstein, 1996; Bookstein, 1997) and via dense image by Bajcsy, Gee, Ashburner, and others (Bajcsy, Lieberson, and Reivich, 1983; Bajcsy and Kovacic, 1989; Dann et al., 1989; Collins et al., 1994; Friston et al., 1995; Davatzikos, 1996; Feldmar, Ayache, and Betting, 1997; Thirion, 1998; Gee and Haynor, 1999; Gee, 1999; Ashburner et al., 2003; Avants and Gee, 2004; Avants, Schoenemann, and Gee, 2006; Ashburner, 2007; Rao et al., 2004). As the brain mapping based on dense image is being carried on by many of groups; the mapping restricted to the cortical manifolds, including curves and surfaces, are being studied as well (Thompson, Schwartz, and Toga, 1996; Fischl, Sereno, and Dale, 1999; van Essen, 2004; Vaillant and Glaunèes, 2005; Yu et al., 2007; Chung, Dalton, and Davidson, 2008; Mangin et al., 2004; Collins, Goualher, and Evans, 1998; Hellier and Barillot, 2003; Cachier et al., 2001). Among these template-based brain mapping techniques, Large Deformation Diffeomorphic Metric Matching (LDDMM) algorithms have recently received a great attention. They provide a range of diffeomorphic matching methods for landmarks, curves, surfaces, images, vectors, as well as tensors (Joshi and Miller, 2000; Beg et al., 2005; Vaillant and Glaunès, 2005; Cao et al., 2005b; Cao et al., 2005a; Glaunès et al., 2008; Qiu and Miller, 2007). All of these mapping algorithms provide diffeomorphic maps — one-to-one, reversible smooth transformations that preserve topology. The use of LDDMM for studying the shapes of objects implies the placement of shapes in a metric space, provides a diffeomorphic transformation, and defines a metric distance that can be used to quantify the similarity between two shapes. Moreover, LDDMM provides a mechanism that allows for the reconstitution of the variations by encoding precise variations of anatomies relative to the template. The resultant template-based representation can be interpreted as a change of coordinates, representing anatomies in a local chart centered at the template. They have been successfully applied to a variety of functional and structural MRI studies (Miller et al., 2005; ?; Qiu et al., 2007; Qiu, Younes, and Miller, 2008; Kirwan et al., 2007; Qiu and Miller, 2008; Bakker et al., 2008).

Within-subject anatomical variation in multiple time points is naturally represented by the deformation needed to pass from the anatomy at the baseline through the anatomies at the remaining time points. When comparing two or more subjects, the absence of a common coordinate system across subjects can undermine hypothesis testing related to time-dependent within-subject deformation. One approach commonly used in the previous studies is to map subjects’ structures at different time points to a global template via brain warping techniques (Wang et al., 2003). The difficulty with this approach is that the transformations used to assess longitudinal changes in the structure included the variation of the transformation between different time points within and across subjects together. The weakness of this approach for detecting within-subject changes is that the variation across subjects is generally larger than the variation within subjects. The other commonly used approach is to map the anatomy at the baseline to the other time point and then translate the Jacobian determinant of the within-subject deformation to the global template by modulating the Jacobian determinant of the deformation between the subject and the global template (Kipps et al., 2005; Brambati et al., 2007). Again, across-subject deformation is involved in the group comparison. Recently, we have introduced a new technique in the LDDMM framework that decides how change in the anatomy of one subject can be translated into the similar deformation occurring in another subject without incorporating across-subject deformation in terms of remained deformation covariance structure (Younes, 2007; Younes et al., 2008; Qiu et al., 2008). The metric structure on anatomies provided by LDDMM offers a consistent approach for the translation of this information. This operation, parallel translation taken from Riemannian geometry, displaces vectors along a curve without changing properties such as the norms of the vectors or their dot products. In the Euclidean space, this operation is the standard translation of vectors; i.e., the infinitesimal displacement of subject 1 is applied to subject 2 without change. In curved spaces, however, parallel translation is nonlinear. We computed by solving a differential equation. This approach with the LDDMM-surface mapping (Vaillant and Glaunès, 2005; Vaillant et al., 2007) has been used to assess the hippocampal atrophy between the baseline and followup in normal healthy controls, converters and patients with AD (Qiu et al., 2008).

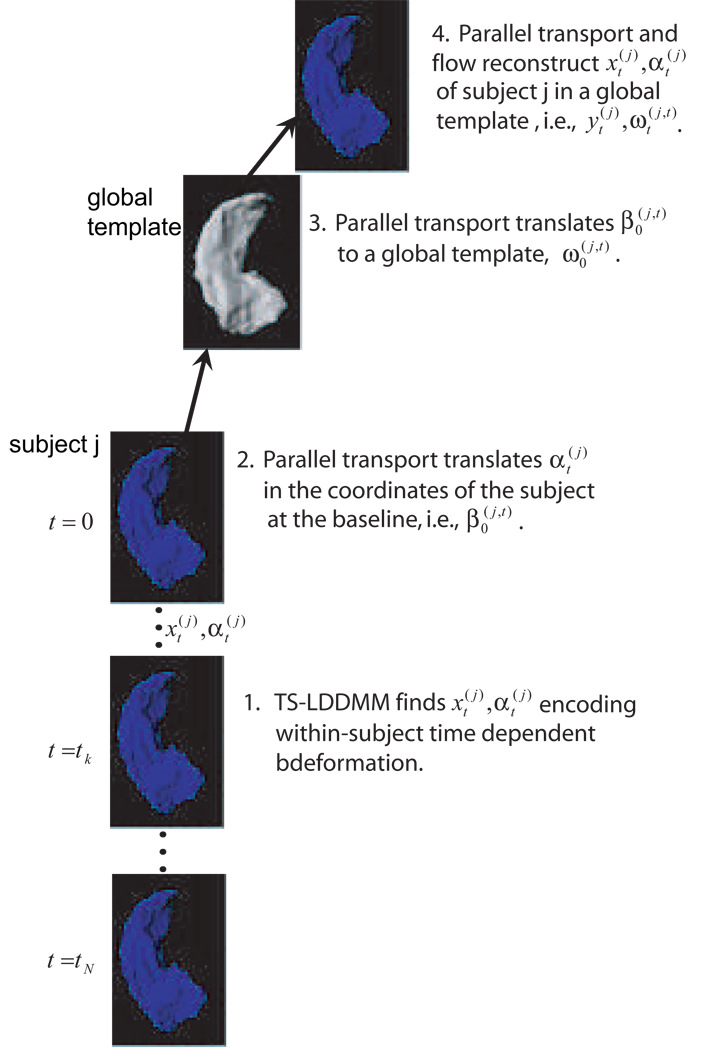
In this paper, we extend our previous longitudinal shape analysis (Qiu et al., 2008) for tracking shape changes between two time points to multiple time points as illustrated in Figure 1. We will first adapt the LDDMM mapping technique and develop a new algorithm, time sequence large deformation diffeomorphic metric mapping (TS-LDDMM) for constructing a trajectory connecting multiple observation of one subject in a shape space. This algorithm, which has been suggested in (Miller, Trouvé, and Younes, 2002) for the image matching case, seeks the optimal time flow of geometric changes that carry the known observations through a period time. We here generalize TS-LDDMM to anatomies represented by a set of points, such as unlabeled landmarks, or curves, or surfaces. We then adapt our parallel transport strategy to time series with an analysis along the following three steps, which are applied to each subject:

• -Retraction: Parallel transport of the deformation signature along the TS-LDDMM trajectory from each time t to the baseline t = 0.

• -Translation: Parallel transport the collected information from the subject baseline to a template, along a geodesic connecting the two shapes.

• -Extension: reconstruct a trajectory starting from the template based on the transported information, inverting the first step.

FIG. 1.

A schematic for studying time dependent shape changes.

We organize this paper by first reviewing static point-based LDDMM algorithms in Section 2. We then extend them to the dynamic case (Section 3). The technique of parallel transport is described in Section 4.

2 Static Point-based Large Deformation Diffeomorphic Metric Mapping

In the setting of diffeomorphic metric mapping, the set of anatomical shapes are placed into a metric shape space. This is modeled by assuming that the shape is generated one from the other via a flow of diffeomorphisms, solutions of ordinary differential equations ϕ̇_t = v_t (ϕ_t), t ∈ [0,1] starting from the identity map ϕ₀ = id, and associated velocity vector fields v_t, t∈[0,1]. We define a metric distance between target shape I_targ and template shape I_temp as the length of the geodesic curves ϕ_t. I_temp,t ∈ [0,1] through the shape space such that ϕ₁·I_temp = I_targ at time t = 1. For instance, in the landmark case, $I_{temp}={(x_i)}_{i=1}^n$ and the group action is taken as ${\varphi }_1\cdot I_{temp}={\varphi }_1{(x_i)}_{i=1}^n$. These geodesics ϕ_t · I_temp, t ∈ [0,1] are generalizations of simple finite dimensional curves. The metric between two shapes I_temp,I_targ is determined by the integrated norm ∥v_t∥_V of the vector field generating the transformation, where v_t ∈ V, a smooth Hilbert space with kernel k_V and norm ∥·∥_V. To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields (Trouvé, 1995; Dupuis, Grenander, and Miller, 1998). Equivalently, the metric distance can be computed through m_t, termed the momentum, a linear transformation of v_t defined by the kernel, $k_V:v_t\to m_t=k_V^{-1}{v}_t$ according to

$$\begin{array}{cc}\rho {(I_{temp,}{I}_{targ})}^2\hfill & =\underset{v_t:{\dot{\varphi }}_t=v_t({\varphi }_t),{\varphi }_0=\text{id}}{\text{inf}}{\displaystyle {\int }_0^1{\Vert v_t\Vert }_V^{2}dt\text{\hspace{1em}such}\text{that}{\varphi }_1\cdot I_{temp}=I_{targ}}\hfill \\ \hfill & =\underset{m_t:{\dot{\varphi }}_t=k_V{m}_t({\varphi }_t),{\varphi }_0=\text{id}}{\text{inf}}{\displaystyle {\int }_0^1<m_t,k_V{m}_t{>}_{2}dt\text{\hspace{1em}such}\text{that}{\varphi }_1\cdot I_{temp}=I_{targ}.}\hfill \end{array}$$ (1)

The Euler equation associated to Eq. (1) indicates that the momentum m_t along the geodesic ϕ_t is conserved (Miller, Trouvé, and Younes, 2002; Miller, Trouvé, and Younes, 2006) (it is constant when expressed in a fixed coordinate system). This implies that the initial momentum m₀ encodes the geodesic connecting I_temp and I_targ, the conservation equation being

$$\frac{d{m}_t}{dt}+D{v}_t{m}_t+m_t\nabla \cdot v_t+D{m}_t^T{v}_t=0$$ (2)

where D is the Jacobian matrix and (∇·) is the divergence operator. Although we wrote the equation in classical form, it must be noted that it may have singular solutions, and that this happens in particular with point-set LDDMM (the form taken by this equation for singular momenta is given below). This reduces the problem of studying shapes of a population in a nonlinear diffeomorphic metric space to a problem of studying the initial momenta in a linear space. This has been applied to landmarks and surfaces in (Vaillant et al., 2004; Qiu and Miller, 2008).

In the point-based LDDMM mapping, let $I_{temp}=\mathbf{x}={(x_i)}_{i=1}^n$ and $I_{targ}=\mathbf{y}={(y_i)}_{i=1}^m$ be the point sets on the objects of I_temp and I_targ, and define the trajectories $x_i(t)\doteq {\varphi }_t(x_i)$ for i = 1,…,n. The momentum, m_t, takes the singular form

$$m_t={\displaystyle \sum _{i=1}^n{\alpha }_i(t)\otimes {\delta }_{x_i(t)},}$$ (3)

where α_i(t) is the momentum vector of the i^th point at time t. The momentum here is not a function but a discrete vector measure, the notation being interpreted by the fact that, for any smooth vector-valued function u

$${\displaystyle \int u(x)\cdot d{m}_t(x)={\displaystyle \sum _{i=1}^N{\alpha }_i(t)\cdot u(x_i(t))}}.$$

Let ${\mathit{\alpha }}_{\mathit{t}}={({\alpha }_i(t))}_{i=1}^n$. We can rewrite Eq. (1) as

$$\rho {(\mathbf{x},\mathbf{y})}^2=\underset{{\mathit{\alpha }}_{\mathit{t}}:{\dot{\varphi }}_t=k_V{\mathit{\alpha }}_{\mathit{t}},{\varphi }_0=\text{id}}{\text{inf}}{\displaystyle {\int }_0^1{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left[k_V(x_i(t),x_j(t)){\alpha }_i(t)\right]}\cdot {\alpha }_j(t)dt\text{\hspace{1em}such}\text{that}{\varphi }_1\cdot \mathbf{x}=\mathbf{y}}}.$$ (4)

In practice, we often introduce a matching functional, E(ϕ₁ · x, y), and define an inexact matching problem: find a diffeomorphism ϕ_t between two objects x and y as a minimizer of

$$J({\mathit{\alpha }}_{\mathit{t}})=\underset{{\mathit{\alpha }}_{\mathit{t}}}{\text{argmin}}{\displaystyle {\int }_0^1{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left[k_V(x_i(t),x_j(t)){\alpha }_j(t)\right]}\cdot {\alpha }_i(t)dt+E({\varphi }_1\cdot \mathbf{\text{x, y}})}}.$$ (5)

. The matching functional, E, depends only on the positions of the finite number of points ${({\varphi }_1(x_i))}_{i=1}^n$. Here, we particularly review E when objects x and y are unlabeled points, including unlabeled landmarks, curves, and surfaces. They will be represented as discrete measures, in the form (using the same notation as above) (Glaunès, Trouvé, and Younes, 2004; Vaillant and Glaunès, 2005; Glaunès et al., 2008)

$${\mu }_{\mathbf{x}}={\displaystyle \sum _i{w}_{x_i}\otimes {\delta }_{x_i}}.$$ (6)

The action of ϕ₁ on the discrete measure μ_x is given in the form of

$${\varphi }_1\cdot {\mu }_{\mathbf{x}}={\displaystyle \sum _i{w}_{{\varphi }_1(x_i)}}\otimes {\delta }_{{\varphi }_1(x_i)}.$$

For unlabeled landmarks, the weights, w_xi are scalars; for 3D curves and surfaces, they are 3D vectors.

We use a kernel norm to compare ϕ₁.μ_x and μ_y. Let k_W be a kernel and μ be a measure. We define

$${\Vert \mu \Vert }_{k_W}^2\doteq {\displaystyle \int k_w(x,y)d\mu (x)\cdot d\mu (y)}.$$

The W in the notation comes from the fact that k_W can be interpreted as the reproducing kernel of a vector space (W) of smooth vector-valued functions and ∥.∥_kW is then the dual norm (Glaunès, Trouvé, and Younes, 2004; Vaillant and Glaunès, 2005; Glaunès et al., 2008; Durrleman et al., 2007).

We will let

$$E({\varphi }_1\cdot \mathbf{\text{x, y}})={\Vert {\varphi }_1\cdot {\mu }_{\mathbf{x}}-{\mu }_{\mathbf{y}}\Vert }_{k_W}^2.$$ (7)

With ${\mu }_{\mathbf{x}}={\displaystyle {\sum }_{i=1}^n{w}_{x_i}\otimes {\delta }_{x_i}}$ and ${\mu }_{\mathbf{y}}={\displaystyle {\sum }_{j=1}^m{\tilde{w}}_{y_j}\otimes {\delta }_{y_j}}$, this is equal to

$$\begin{array}{cc}E({\varphi }_1\cdot \mathbf{\text{x, y}})=\hfill & {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{{\varphi }_1(x_i)}}\cdot w_{{\varphi }_1(x_j)}{k}_W({\varphi }_1(x_i),{\varphi }_1(x_j))-2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{w}_{{\varphi }_1(x_i)}}\cdot {\tilde{w}}_{y_j}{k}_W({\varphi }_1(x_i),y_j)}}\hfill \\ \hfill & +{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^m{\tilde{w}}_{y_i}\cdot {\tilde{w}}_{y_i}{k}_W(y_i,y_j)}}.\hfill \end{array}$$ (8)

We now describe how this representation is implemented with unlabeled landmarks, curves and surfaces.

Unlabeled Landmarks

If x and y above represent unstructured unlabeled landmarks, the weight $w_{x_i}\text{and}{\tilde{w}}_{y_j}$ are scalars. They can be chosen in function of the application, the simplest choices being either $w_{x_i}\equiv 1\text{or}{w}_{x_i}\equiv 1/n$ and similarly for ${\tilde{w}}_{y_j}$.

Curves

When each curve is represented by a sequence of points, still denoted as $\mathbf{x}={(x_i)}_{i=1}^n$ and $\mathbf{y}={(y_j)}_{j=1}^m$ However, a curve cannot be uniquely reconstructed based on the locations of a set of points. We assume a curve embedded in ℛ³ is a one-dimensional manifold in the sense that the local region of every point on the curve is equivalent to a line which can be uniquely defined by this point and the tangent vector at this location. We use the representation (Glauneès et al., 2008; Qiu and Miller, 2007)

$${\mu }_{\mathbf{x}}={\displaystyle \sum _{i=1}^{n-1}{w}_{c_i}\otimes {\delta }_{c_i}}$$

with c_i = (x_i+1 + x_i)/2 and $w_{c_i}=x_{i+1}-x_i$ and similarly for y. The action of ϕ₁ on c_i is approximated as ϕ₁(c_i) = (ϕ₁(x_i+1) + ϕ₁(x_i))/2, and its corresponding $w_{{\varphi }_1(c_i)}$ is approximated by (ϕ₁(x_i+1) − ϕ₁(x_i). This representation in terms of vector measure accounts for the geometry of the curve (while the scalar measure used above would treat the sequence as an unordered list of points).

Surfaces

Now, let I_temp and I_targ be triangulated meshes with vertices $\mathbf{x}={(x_i)}_{i=1}^n$ and $\mathbf{y}={(y_j)}_{j=1}^m$, respectively. We assume the cortical surfaces embedded in ℛ³ to be a two-dimensional manifold in the sense that the neighborhood of every point on the surface is equivalent to a two-dimensional plane in Euclidean space. Such a plane can be uniquely defined by a point and a vector originated at this point and normal to the plane. We thus let (Vaillant and Glaunès, 2005; Vaillant et al., 2007)

$${\mu }_{\mathbf{x}}={\displaystyle \sum _{f\in {ℱ}_{\mathbf{x}}}{w}_{c_f}\otimes {\delta }_{c_f}},$$

where ℱ_x is the set of faces in the triangulation, and, for a positively ordered face $f=(x_{f_1},x_{f_2},x_{f_3}),w_{c_f}=\frac{1}{2}(x_{f_1}-x_{f_2})\times (x_{f_3}-x_{f_1})$ and $c_f=\frac{1}{3}(x_{f_1}+x_{f_2}+x_{f_3})$; μ_y is defined similarly. ϕ₁(c_f) and $w_{{\varphi }_1(c_f)}$ are respectively approximated as ${\varphi }_1(c_f)=\frac{1}{3}({\varphi }_1(x_{f_1})+{\varphi }_1(x_{f_2})+{\varphi }_1(x_{f_3}))$ and $w_{{\varphi }_1(c_f)}=\frac{1}{2}({\varphi }_1(x_{f_1})-{\varphi }_1(x_{f_2}))\times ({\varphi }_1(x_{f_3})-{\varphi }_1(x_{f_1}))$. Here again, the representation makes a direct use of the geometry of the point set as a triangulated surface. Note that the definitions of μ_x in the curve and surface cases come from discretizations of mathematical objects called currents, as described in (Vaillant and Glaunès, 2005).

Lemma 1 (Static Variational Solution)

The point-based LDDMM algorithm minimizes the energy Eq. (5), with variables ${\mathbf{x}}_t={(x_i(t))}_{i=1}^n$ and ${\mathit{\alpha }}_{\mathit{t}}={({\alpha }_i(t))}_{i=1}^n$ that are related via the dynamical equations

$$\frac{d{x}_i(t)}{dt}={\displaystyle \sum _{j=1}^n{k}_V(x_i(t),x_j(t)){\alpha }_j(t),i=1,2,\dots ,n}$$ (9)

with initial condition x₀ = x. The Euler-Lagrange optimality conditions for this variational problem imply

$$\frac{d{\alpha }_i(t)}{dt}=-{\displaystyle \sum _{j=1}^n{\alpha }_i(t)\cdot {\alpha }_j(t){\nabla }_1{k}_V(x_i(t),x_j(t))}$$ (10)

where ∇₁ denotes taking derivative of k_v(x_i(t),x_j(t)) with respect to its first variable.

This was proven previously (Vaillant et al., 2004). Eq. (9) and (10) indicate that the evolution from one object to the other is uniquely determined by α₀. Since α₀ carries the same information as $\frac{d\mathbf{x}(t)}{dt}$ at t = 0 and therefore corresponds to an infinitesimal variation of x₀, we shall term α₀ as “deformation signature” in the static point-based LDDMM. In fact, Eq. (10) is the form taken by the conservation of momentum equation (2) in the singular case of point momenta.

3 Time Sequence Large Deformation Diffeomorphic Metric Mapping for Landmarks, Curves, and Surfaces (TS-LDDMM)

In the time sequence large deformation diffeomorphic metric mapping (TS-LDDMM), time sequence observations are given and the goal is to infer the time flow of geometric change that carries the known observation through the period t ∈ [0,1]. Here flows of point sets are diffeomorphic, with t corresponding to actual real-time, and the comparison is examined by the similarity of the observables I_t, t ∈ [0,1] and the observable, I₀ at t = 0. I₀ plays the role of the so-called template. In the static point-based LDDMM algorithm discussed in the previous section, the time in Eq. (5) is a dummy time only used for algorithmic purposes with the single target observable at t = 1, and is not relevant to the time at which the data is collected. In the TS-LDDMM model, the observables, I_t, are generated from I₀ under space-time flows, ϕ_t such that ϕ_t. I₀ = I_t at all time t. We define an inexact point-based TS-LDDMM matching: find a time-dependent diffeomorphism ϕ_t connecting a point set $\mathbf{x}=I_0={(x_i)}_{i=1}^n$ and time-dependent point sets ${\mathbf{y}}_t=I_t={(y_j(t))}_{j=1}^m$ as a minimizer of

$$J({\mathit{\alpha }}_{\mathit{t}})=\underset{{\mathit{\alpha }}_{\mathit{t}}}{\text{argmin}}{\displaystyle {\int }_0^1{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left[k_V(x_i(t),x_j(t)){\alpha }_i(t)\right]}\cdot {\alpha }_j(t)dt+{\displaystyle {\int }_0^1{E}_t({\varphi }_t\cdot {\mathbf{\text{x, y}}}_t)dt}}},$$ (11)

where the matching functional, E_t, quantifies the closeness between the deformed template, ϕ_t · x, and observation, y_t at time t. In our applications, we choose E_t dependent of time and given by Eq. (7) adapted to the unlabeled landmarks, curve, and surface cases.

We can rewrite J into a matrix form

$$J({\mathit{\alpha }}_{\mathit{t}})={\displaystyle {\int }_0^1{\mathit{\alpha }}_{\mathit{t}}\cdot \left[k_V({\mathbf{x}}_{\mathbf{t}},{\mathbf{x}}_{\mathbf{t}}){\mathit{\alpha }}_{\mathit{t}}\right]dt+{\displaystyle {\int }_0^1{E}_t({\mathbf{x}}_t,{\mathbf{y}}_t)dt}},$$ (12)

where ${\mathit{\alpha }}_{\mathit{t}}={({\alpha }_i(t))}_{i=1}^n,{\mathbf{x}}_{\mathbf{t}}={\varphi }_t\cdot \mathbf{x}$, and ${\mathbf{y}}_t={(y_i(t))}_{i=1}^n$ are vectors of momentum and coordinates of x_t and y_t at time t.

Lemma 2 (Time-Sequence Variational Solution)

The Euler-Lagrange equation associated with the variational problem in Eq. (12) is given by (∇J)_t = 2α_t+η_t = 0, where vector ${\eta }_t={\displaystyle {\int }_t^1{\nabla }_{{\mathbf{x}}_s}}{E}_{s}ds+{\displaystyle {\int }_t^1{({\partial }_{{\mathbf{x}}_s}\left[k_V({\mathbf{x}}_s,{\mathbf{x}}_s){\mathbf{\alpha }}_s\right])}^{\ast }({\eta }_s+{\mathit{\alpha }}_s)dsand{\nabla }_{{\mathbf{x}}_s}{E}_s}$ is the derivative of E_s with respect to x_s.

The Euler-Lagrange optimality conditions for the point-based TS-LDDMM in Eq. (12) imply

$$\frac{d{\alpha }_i(t)}{dt}=-{\displaystyle \sum _{j=1}^n{\alpha }_i(t)\cdot {\alpha }_j(t){\nabla }_1{k}_V(x_i(t),x_j(t))+\frac{1}{2}{\nabla }_{x_i(t)}{E}_t},$$ (13)

where ∇₁ denotes taking derivative of k_v (k_i(t,x_j(t)) with respect to its first variable and ${\nabla }_{x_i(t)}{E}_t$ is the derivative of E_t with respect to x_t(t).

We give the proof of this lemma in Appendix.

Unlike the static point-based LDDMM with shape variations encoded in the initial momentum based on Eq. (9) and (10), the dynamic shape motion in the point-based TS-LDDMM also depends on the serial observations. Thus, the time-dependent momentum is needed to characterize the dynamic shape motion (not only the initial momentum). In the point-based TS-LDDMM we term this time-dependent momentum as “deformation signature” that carries the dynamic motion of the serial observations.

3.1 The Sampled TS-LDDMM

The usual problem in Computational Anatomy involves sample observables in time of the observed data $I_{t_k}={\mathbf{y}}_{t_k},k=1,\dots ,N$ with t₀ = 0, t_N = 1. Then the variational problem and its solution becomes a mixture of the static and dynamic solutions, interpolating between time points. Between sample points the geodesic satisfies the Euler-equation and conservation of momentum, with the observables entering at the boundary points t₁t,₂t,_N.

Lemma 3

The optimizing flow connecting the observables ${\mathbf{y}}_{t_k},k=1,\dots ,N$ given by

$$J({\mathit{\alpha }}_{\mathit{t}})=\underset{{\mathit{\alpha }}_{\mathit{t}}}{\text{arg}\text{min}}{\displaystyle {\int }_0^1{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left[k_V(x_i(t),x_j(t)){\alpha }_j(t)\right]}\cdot {\alpha }_i(t)dt+{\displaystyle \sum _{k=1}^{N}E({\varphi }_{t_k}\cdot {\mathbf{\text{x, y}}}_{t_k})}}}$$ (14)

has Euler-Lagrange optimality conditions for the point-based TS-LDDMM in Eq. (12) given by

$$\frac{d{\alpha }_i(t)}{dt}=-{\displaystyle \sum _{j=1}^n{\alpha }_i(t)\cdot {\alpha }_j(t){\nabla }_1{k}_V(x_i(t),x_j(t)),t\in (t_{i-1},t_i),i=1,\dots ,N}$$ (15)

with jumps at observation times defined as follows: ${\mathit{\alpha }}_1={\nabla }_{{\mathbf{x}}_1}{E}_1/2$, and ${\mathit{\alpha }}_{t_k^{+}}-{\mathit{\alpha }}_{t_k^{-}}={\nabla }_{{\mathbf{x}}_k}{E}_k/2$.

We give the proof of this lemma in Appendix (with the expression of the gradient of J with respect to α. This situation is intermediate between the static LDDMM and TS-LDDMM. It is easy to check that the whole trajectory α_t is characterized by the momenta at time 0, α₀ and at time $t_k^{+}$, for t_k < 1.

3.2 Implementation

We use a conjugate gradient routine to perform the minimization of functional J in (11) with respect to variables α_i(t). Of course any other optimization scheme could be considered at this point. The different steps required to compute the functional and its gradient for each iteration are the following:

1. from momentum vectors α_i(t), compute trajectories x_i(t) by integrating the system of ordinary differential equations (ODE) using Eq. (9).

2. evaluate J from Eq. (11)

3. compute vectors η_i(t) by integrating the system of ODE in Eq. (21)

4. compute gradient (∇J)_i(t) = 2α_i(t)+n_i(t)

All time-dependant variables are evaluated on a uniform grid t₁ = 0,…,t_T = 1 and a predictor/corrector centered Euler scheme was used to solve the systems of ODE in Eq. (9) and (21). The complexity of each iteration is of order dTN² where N = max(n, m). To speed up computations when N is large, all convolutions by kernels kv and k_W are accelerated with fast Gaussian transform (Yang et al., 2003), which reduces the complexity to dTN log (N).

3.3 Heart and Brain Applications

TS-LDDMM of MR Heart Image

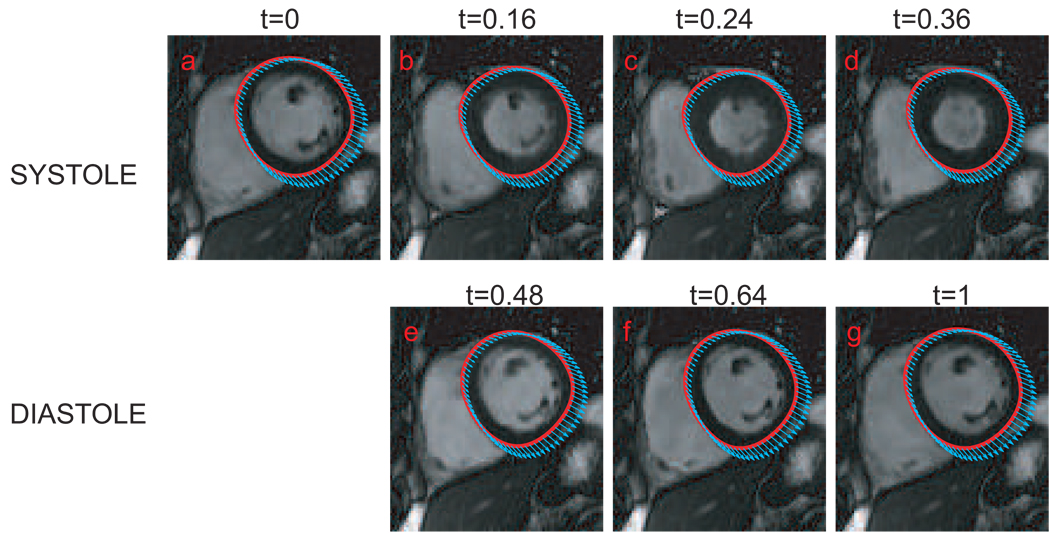
We illustrate an application of the TS-LDDMM for encoding heart motion in cardiac cycles. Total 25 image volumes were acquired per cardiac cycle. For the sake of simplicity, one cardiac cycle from the end-diastole (ED) to the next ED was normalized from t = 0 to t = 1 and sampled into 25 time points. Figure 2 illustrates a coronal section of the left ventricle selected from the systole phase (panels (a–d)) and the diastole phase (panels (e–g)). We applied the automatic segmentation algorithm (Jolly, 2006) for contouring the endocardium and epicardium in every phase, which are marked in green curves on each panel. The endocardium and epicardium curves in panel (a) served as template curves in the TS-LDDMM algorithm that map it to the curves at the rest of the cardiac cycle. Red curves in Figure 2 illustrate the deformed templates in each phase of the cardiac cycle, which are well overlapped with the segmented contours. The momentum, α_t, of the epicardium curves shown in Figure 3, encodes the trajectory of the heart motion through the flow equation (9).

FIG. 2.

A coronal section of the left ventricle was selected from the systole phase (panels (a–d)) and the diastole phase (panels (e–g)) during one cardiac cycle. Green curves on each panel ar the automatically segmented contours of endocardium and epicardium. Red curves on each panel are the deformed template at each phase. Red and green contours are overlapped very well, which indicates the accuracy of the TS-LDDMM algorithm. The time normalized into the range between 0 and 1 is indicated on the top of each panel.

FIG. 3.

Momentum vectors, αt, of the epicardium curves computed from the TS-LDDMM algorithm are shown in the template coordinates.

TS-LDDMM of Hippocampal Surface Shapes

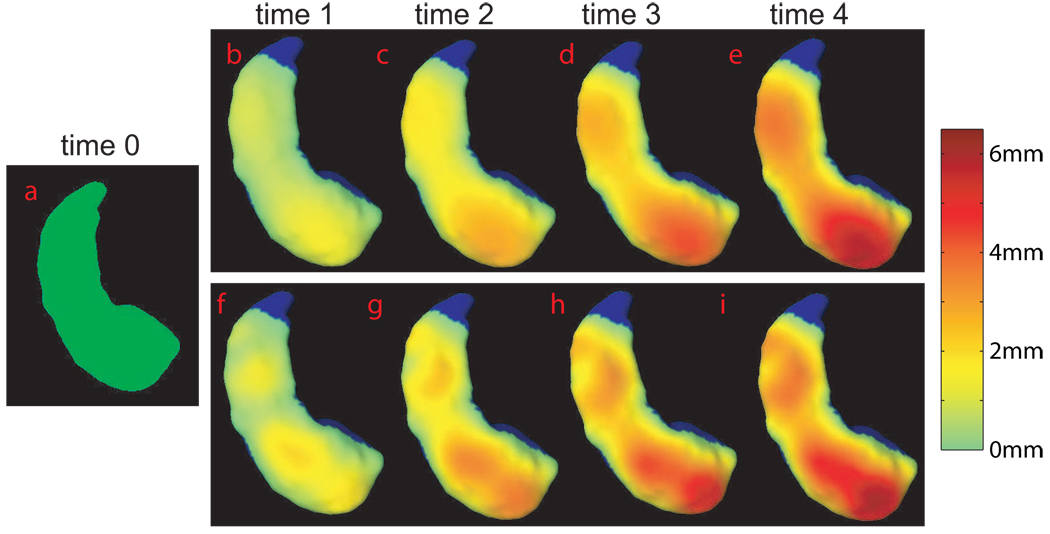
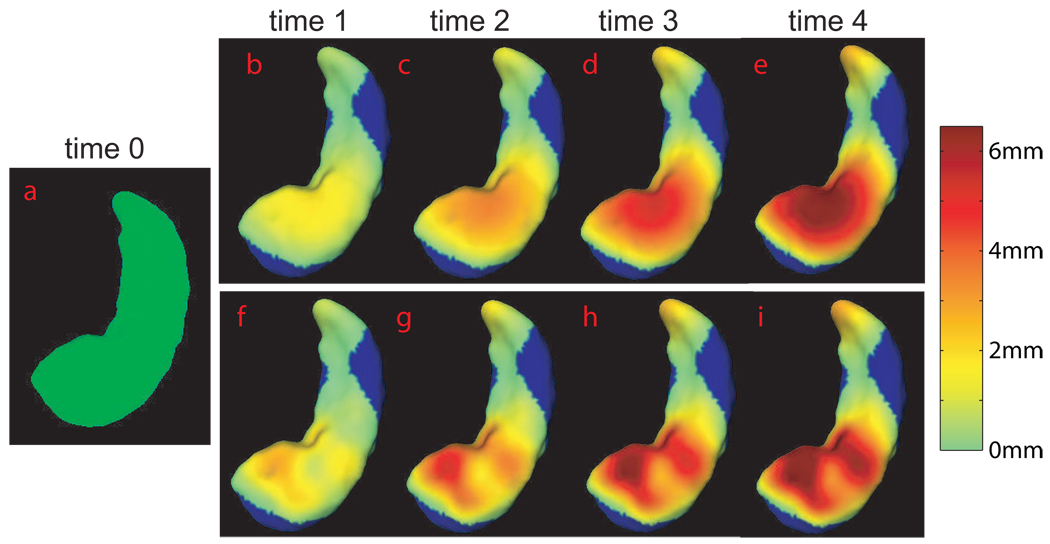
Subfield-specific shape changes of the hippocampus have been identified in mild cognitive impairment (MCI) and Alzheimer’s disease (AD). We demonstrate an application of the TS-LDDMM algorithms for tracking subfield-specific shape changes of the hippocampus in multiple time points in simulated datasets. To do so, we generated two sets of hippocampal surface shapes at five time points: one set with the surface-inward deformation only in the subiculum subfield (Figure 4); the other with the surface-inward deformation only in the subfields of CA1,2,3 (Figure 5). In each set, the hippocampal surfaces at time points 1–4 (panels (b–e)) were generated from the one at time 0 (panel (a)). Between any two subsequent time points, the reduction in the hippocampal volume is about 10%. Each surface in panels (b–e) is colored by its distance to the surface at time 0 to show the strength of the hippocampal atrophy. In the TS-LDDMM algorithm, each surface was represented by 3223 vertices and 6442 triangles. The hippocampal surface at time 0 was considered as within-subject template and the surfaces at the other time points were considered as time-dependent targets. 20 time steps were chosen between each time interval. The TS-LDDMM mapping for these examples took seven or eight minutes when using a 64-bit computer with a 2.4GHz CPU. Figure 4 and Figure 5(f–i) show the deformed template computed from the TS-LDDMM algorithm at each time point colored with its distance map to the template at time 0. Visually, the TS-LDDMM algorithm can well map the template to the time-dependent targets through trajectory, ϕ_t.

FIG. 4.

Panel (a) shows the hippocampal surface at time 0 in the inferior view. Panels (b–e) illustrate the hippocampal surfaces with surface-inward deformation in the subiculum subfield at times 1–4. The strength of the deformation is denoted by its distance to the hippocampal surface at time 0. Panels (f–i) show the deformed template computed from the TS-LDDMM algorithm at each time point . They are colored by their distances to the surface on panel (a). The region with no deformation is colored in blue.

FIG. 5.

Panel (a) shows the hippocampal surface at time 0 in the superior view. Panels (b–e) illustrate the hippocampal surfaces with surface-inward deformation in the subfields of CA1,2,3 at times 1–4. The strength of the deformation is denoted by its distance to the hippocampal surface at time 0. Panels (f–i) show the deformed template computed from the TS-LDDMM algorithm at each time point . They are colored by their distances to the surface on panel (a). The region with no deformation is colored in blue.

Making between-subject shape comparison possible requires to translate the deformation signature encoding the within-subject dynamic shape changes (e.g. vectors in Figures 3) to a global reference frame. In the subsequent section, we describe how the deformation signature obtained from the TS-LDDMM is transported first to the within-subject baseline, then to the global template along the curve connecting the within-subject template with the global template.

4 Parallel Transport in Diffeomorphisms

Via relation (9) the deformation signature ${\mathit{\alpha }}_{\mathit{t}}^{(j)}$ at time t is attached to the current position ${\mathbf{x}}_t^{(j)}$ of the evolving point set for subject j. In this section, we describe how this subject-dependent signature can be normalized to provide a new time series evolving from a fixed (subject independent) baseline, which will be used for between-subject comparison.

The basic operation for this purpose will be parallel transport in deformable point sets. It is performed along a curve traced on a Riemannian manifold, which allows to translate a tangent vector at one end of the curve to the other end of curve without change according to the intrinsic geometry of the manifold. This has been described in the diffeomorphic matching framework in (Qiu et al., 2008; Younes, 2007; Younes et al., 2008). In the context of this paper, parallel transport takes in input a trajectory, s ⟼ z_s, and a deformation signature ω_t at some time t (attached to z_t). The output is a transported signature, ω_s, at each time s of the trajectory. They satisfy the following dynamical system

$$\begin{array}{c}{\displaystyle \sum _{j=1}^n{k}_V(z_i(t),z_j(t))(\frac{d{\omega }_j(t)}{dt}+{\displaystyle \sum _{l=1}^n{\nabla }_1{k}_V(z_j(t),z_l(t))({\beta }_j(t)\cdot }{\omega }_l(t)+{\omega }_j(t)\cdot {\beta }_l(t)))}\\ ={\displaystyle \sum _{j=1}^n{\nabla }_1{k}_V(z_i(t),z_j(t))\cdot \left(({\displaystyle \sum _{l=1}^n{k}_V(z_i(t),z_l(t)){\omega }_l(t)-{\displaystyle \sum _{l=1}^n{k}_V(z_j(t),z_l(t)){\omega }_l(t)){\beta }_j(t)-({\displaystyle \sum _{l=1}^n{k}_V(z_i(t),z_l(t)){\beta }_l(t)-{\displaystyle \sum _{l=1}^n{k}_V(z_j(t),z_l(t)){\beta }_l(t)){\omega }_j(t)}}}}\right)}\end{array}$$ (16)

where β_t is defined by

$$\frac{d{z}_i(t)}{dt}={\displaystyle \sum _{j=1}^n{k}_V(z_i(t),z_j(t)){\beta }_j(t),i=1,2,\dots ,n}.$$ (17)

Since this is a first order linear dynamical system, knowing ω at time t uniquely specifies its value at all times.

The following notation will be convenient. Define $PT(\mathbf{z},t,\tilde{\mathit{\omega }},s)$ the solution at time s of System (16), for the curve s ⟼ z_s and ${\mathit{\omega }}_t=\tilde{\mathit{\omega }}$ at time t (i.e., the parallel translation of$\tilde{\omega }$ along z from time t to time s). Then, as illustrated in Figure 1, our normalization procedure for TS-LDDMM deformation signatures is defined as follows. We assume that a global template ${\mathbf{x}}_0^{\left(0\right)}$ has been chosen, as an examplar of the subject baselines, ${\mathbf{x}}_0^{(j)}$.

• - Retraction: for each subject j and each time t, parallel translate ${\mathit{\alpha }}_t^{(j)}$ from time t to time 0 along $s\mapsto {\mathbf{x}}_s^{(j)}$, yielding a vector denoted ${\mathbf{\beta }}_0^{(j,t)}$. With our notation, this is

  $${\beta }_0^{(j,t)}=PT({\mathbf{x}}^{(j)},t,{\mathit{\alpha }}_t^{(j)},0).$$
• - Translation: For each j, compute a geodesic z(^j) between ${\mathbf{x}}_0^{(j)}$ and the template ${\mathbf{x}}_0^{(0)}$ by solving the LDDMM problem in Eq. (5). Then, translate ${\mathit{\beta }}_0^{(j,t)}$ along this trajectory, yielding ${\mathit{\omega }}_0^{(j,t)}$. Thus,

  $${\mathit{\omega }}_0^{(j,t)}=PT({\mathbf{z}}^{(j)},0,{\mathit{\beta }}_0^{(j,t)},1).$$
• - Extension: This is the inverse of the retraction operation. For each j and each t, reconstruct a new trajectory ${\mathbf{y}}_t^{(j)}$ starting from the global template ${(\mathbf{y}}_0^{(j)}={\mathbf{x}}_0^{\left(0\right)})$, solving the system

  $$\frac{d{\mathbf{y}}_t^{(j)}}{dt}=k_v({\mathbf{y}}_t,{\mathbf{y}}_t){\mathit{\omega }}_t^{(j,t)}$$

  with ${\mathit{\omega }}_t^{(j,t)}=PT({\mathbf{y}}^{(j)},0,{\mathit{\omega }}_0^{(j,t)},t)$.

The result of this algorithm is a subject-indexed family of trajectories $(y_t^{(j)})$ which are all deformations of the same template, and therefore can be compared in a meaningful way. The extension step requires a double integration in its implementation: at each time t, parallel translation (System (16)) must be solved from 0 to t in order to update the trajectory ${\mathbf{y}}_t^{(j)}$.

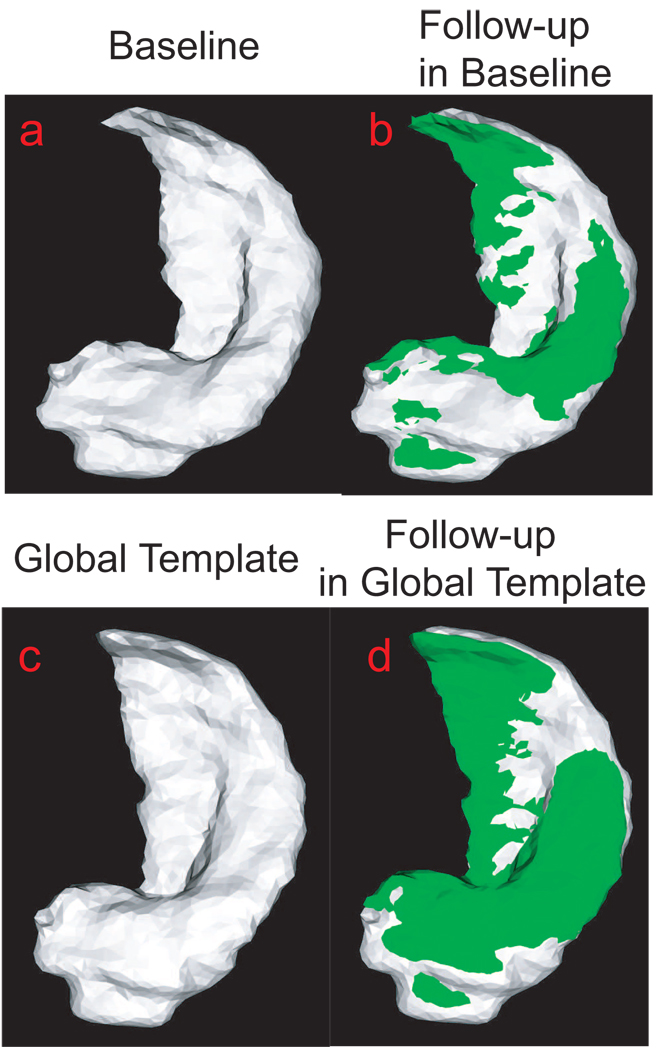
Figure 6 intuitively illustrates one example using parallel transport to represent within-subject deformation in the global template coordinates. Panel (a) shows the hippocampal surface of a subject at the baseline while Panel (b) shows the hippocampal surface of the same subject at the follow-up (green) superimposed with one at the baseline (gray). Panel (c) depicts the global hippocampal template. Panel (d) shows the hippocampal surface of this subject at the follow-up (green) represented in the global template coordinates (gray). The deformation of the hippocampal surface between baseline and follow-up represented by interlacing green and gray in panel (b) has a similar pattern as in panel (d). This indicates that the technique of parallel transport in diffeomorphism is a reasonable approach allowing us to study longitudinal shape variation within subjects in a global template coordinate system.

FIG. 6.

Panel (a) shows the hippocampus of a subject at the baseline. The hippocampus surface of this subject at the follow-up (green) is superimposed with one at the baseline in panel (b). Panel (c) shows the global hippocampus template. Panel (d) shows the hippocampus of this subject at the follow-up (green) represented in the global template coordinates (gray).

5 TS-LDDMM and Parallel Transport for Hippocampal Atrophy

We applied the TS-LDDMM and parallel transport algorithms for assessing differences in the hippocampal shape changes between 19 healthy elders (age: 74.6 ± 6.5) and 19 patients with Alzheimer’s disease (AD) (age: 74.0 ± 6.8). Each subject was scanned every three months so there were four MRI volumes per subject in a nine-month interval.

In structural delineation process, the hippocampus of each subject at the baseline was semiautomatically segmented using the method described in (Haller et al., 1997) and was then propagated to the rest time points using the LDDMM-image mapping (Beg et al., 2005). We represented the hippocampal shape using triangulated meshes. In the mapping process, the TS-LDDMM algorithm was applied to find an optimal trajectory that passes through the four observations of each subject in a metric shape space. This trajectory and its corresponding momenta encode the within-subject time-dependent shape changes. Then, following the illustration in Figure 1, the parallel transport operation first translated the within-subject time dependent momenta to the subject’s baseline coordinate system, and then to a global template. The within-subject shape trajectory was reconstructed in the global template coordinates via the flow and parallel transport. Finally, we computed the Jacobian matrix of the within-subject deformation in the global template x⁽⁰⁾, through the flow equation in Eq. (9) when α_t = ω_t^(j,t). The Jacobian determinant shows regions with expansion (Jacobian> 1) or compression (Jacobian< 1). Let F^(j)(p), p ∈ x⁽⁰⁾ denote the Jacobian determinant in the logarithmic scale for subject j.

To illustrate our results, we performed the statistical testing on the log Jacobian determinant that characterizes the shape changes in nine months. Assume F^(j)(p) arises from random processes. Its distribution models as random field in the global template that can be represented by a linear combination of orthonormal bases as follows:

$$F^{(j)}(p)={\displaystyle \sum _{i=1}^{10}{F}_i^{(j)}{\psi }_i(p),\mathrm{\hspace{1em}x}\in {\mathbf{x}}^{\left(0\right)}},$$ (18)

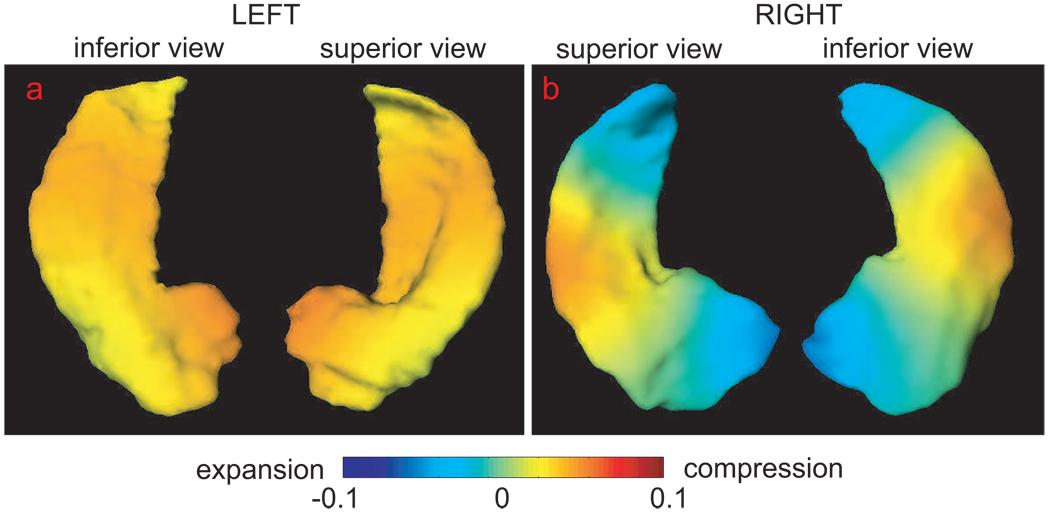
where ψ_i(x) is chosen as the ith basis of the Laplace-Beltrami (LB) operator on x⁽⁰⁾ (Qiu, Bitouk, and Miller, 2006). $F_i^{(j)}$ is the coefficient associated with ψ_i. In our study, 10 LB bases take 90% of total variation of F(^j). We hypothesized that the $F_i^{(j)}$’s are equal in the groups of healthy elders and patients with AD against that the $F_i^{(j)}$’s are not equal in both groups. To examine it, we performed two-sided Student t-tests on each individual $F_i^{(j)}$. At a significance level of 0.02, the shape differences between the two groups occur in the 1st (p=0.0171) and the 4th (p=0.0159) LB bases of the left hippocampus and the 3rd (p=0.0032) and the 10th p = 0.0156 LB bases of the right hippocampus. For the visualization purpose, we back projected these LB bases to the global template coordinates, which is shown in both superior and inferior views of the hippocampus in Figure 7. Compared with the healthy controls, regions in warm color has greater atrophy in patients with AD, while regions in cool color has less atrophy. This result suggests that the greater atrophy occurs in the left hippocampus, particularly in the posterior segment, and the lateral middle body of the right hippocampus.

FIG. 7.

Panel (a) shows the shape differences of the left hippocampus between the healthy elders and patients with AD in boths superior and inferior views. Panel (b) illustrates the shape differences of the right hippocampus. Compared with the healthy elders, regions with greater atrophy in the AD group are in warm color and regions with less atrophy in the AD group are in cool color.

6 Discussion

This paper presents shape analysis algorithms for tracking longitudinal shape changes for pointbased objects, including unlabeled landmarks, curves, and surfaces, under the diffeomorphic mapping framework. It incorporates two major diffeomorphic techniques: TS-LDDMM and parallel transport. The dynamic motion or shape change is encoded via time-dependent momentum obtained from TS-LDDMM. The parallel transport operation taken from Riemannian geometry in a diffeomorphic shape space translates these momentum vectors (tangent vectors) in the shape space to within-subject baseline coordinates and then to the global template without incorporating across-subject deformation. It preserves the metric or covariance of the momentum from a subject coordinate system to the global template coordinate system. The benefit from it is to directly make statistical inference for detecting across-subject shape differences.

The TS-LDDMM algorithms introduced in this paper are the extension of the static pointbased LDDMM algorithms (Glaunès et al., 2008; Glaunès, Trouvè, and Younes, 2004; Vaillant and Glaunès, 2005; Vaillant et al., 2007; Qiu and Miller, 2007). We consider point-based shapes, such as unlabeled landmarks, curves, and surfaces, as measure. The structure of a Hilbert space is imposed on the measure in the way its norm can be used to quantify the geometric similarity between two objects (Glaunès et al., 2008; Vaillant and Glaunès, 2005). We generalized the gradient derivation of the energy in the TS-LDDMM variational problem with respect to the momentum along the deformation trajectory for the point-based shapes, including unlabeled points, curves, and surfaces. Unlike the static LDDMM encoding the shape variation in the initial momentum, the TS-LDDMM Euler-Lagrange optimality conditions indicate that time-dependent shape changes are characterized by the time-dependent momentum, which do not satisfy the geometric evolution of Eq. (9) and (10). The TS-LDDMM algorithm provides a way to fit subject’s time-dependent observations by a smooth trajectory in the metric space.

The demonstrate of the use of the TS-LDDMM and parallel transport is given through an example of detecting time-dependent hippocampal atrophy patten in AD. A variety of other applications using the proposed analysis framework can be found in medical image analysis and computer vision (e.g. studying heart motion abnormalities in cardiac diseases).

Appendix A Gradient of a Point-Based Matching Functional in the TS-LDDMM setting

Lemma 4

The Euler-Lagrange equation associated with the variational problem in Eq. (12) is given by (∇J)_t = 2α_t + η _t = 0, where vector ${\eta }_t={\displaystyle {\int }_t^1{\nabla }_{{\mathbf{x}}_s}{E}_{s}ds+{\displaystyle {\int }_t^1{({\partial }_{{\mathbf{x}}_s}\left[k_V({\mathbf{x}}_s,{\mathbf{x}}_s){\mathit{\alpha }}_s\right])}^{\ast }({\eta }_s+{\mathit{\alpha }}_s)ds}}$ and ${\nabla }_{{\mathbf{x}}_s}{E}_s$ is the derivation of E_s with respect to x_s.

Proof

We consider a variation ${\mathit{\alpha }}_{\mathit{t}}^{ϵ}={\mathit{\alpha }}_{\mathit{t}}+ϵ{\tilde{\alpha }}_t$. Our goal is to express the derivative f′(0) of $f(ϵ)\doteq J({\mathit{\alpha }}_{\mathit{t}}^{ϵ})$ in function of α̃_t. Since

$$\frac{d{\mathbf{x}}_t}{dt}=K({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_{\mathit{t}}$$

The variation in α implies a first order variation in x, that we denote x˜ with

$$\frac{d{\tilde{\mathbf{x}}}_t}{dt}={\partial }_{\mathbf{x}}(K({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t){\tilde{\mathbf{x}}}_t+K({\mathbf{x}}_t,{\mathbf{x}}_t){\tilde{\alpha }}_t$$

From

$$J(\mathit{\alpha })={\displaystyle {\int }_0^1{\mathit{\alpha }}_t\cdot (K({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t)dt+{\displaystyle {\int }_0^{1}E({\mathbf{x}}_t,{\mathbf{y}}_t)dt}}$$

we get

$$\begin{array}{cc}f\prime (0)=\hfill & 2{\displaystyle {\int }_0^1{\tilde{\mathit{\alpha }}}_t\cdot (k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t)dt}\hfill \\ \hfill & +{\displaystyle {\int }_0^1({\nabla }_{{\mathbf{x}}_t}({\mathit{\alpha }}_t\cdot k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t)+{\nabla }_{\mathbf{x}}E({\mathbf{x}}_t))\cdot {\tilde{\mathbf{x}}}_{t}dt}.\hfill \end{array}$$ (19)

Introduce the matrix R_st defined by R_ss = identity and

$$\frac{d{R}_{st}}{dt}={\partial }_{{\mathbf{x}}_t}\left[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t\right]R_{st}.$$

Then we have

$${\tilde{\mathbf{x}}}_t={\displaystyle {\int }_0^t{R}_{st}{k}_V({\mathbf{x}}_s,{\mathbf{x}}_s){\tilde{\mathit{\alpha }}}_{s}ds},$$

as can be easily checked. Also, R_stR_ts = identity which implies

$$\frac{d{R}_{st}^{\ast }}{ds}=-{\partial }_{{\mathbf{x}}_t}{\left[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t\right]}^{\ast }{R}_{st}^{\ast }.$$

Introducing

$${\eta }_t={\displaystyle {\int }_t^1{R}_{ts}^{\ast }({\nabla }_{{\mathbf{x}}_s}({\alpha }_s\cdot k_V({\mathbf{x}}_s,{\mathbf{x}}_s){\mathit{\alpha }}_s)+{\nabla }_{\mathbf{x}}E({\mathbf{x}}_s))ds}$$

, we can rewrite (19) as

$$f\prime (0)=2{\displaystyle {\int }_0^1{\tilde{\mathit{\alpha }}}_t\cdot (K({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t)dt+{\displaystyle {\int }_0^1{\eta }_t\cdot (K({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t)dt}}$$ (20)

with η₁ = 0 and

$$\frac{d{\eta }_t}{dt}=-{\nabla }_{{\mathbf{x}}_t}E({\mathbf{x}}_t)-{\partial }_{{\mathbf{x}}_t}{\left[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t\right]}^{\ast }({\mathit{\alpha }}_t+{\eta }_t)$$ (21)

where we have used the fact that

$${\nabla }_{{\mathbf{x}}_t}({\mathit{\alpha }}_t\cdot k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t={\partial }_{{\mathbf{x}}_t}[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t{]}^{*}{\mathit{\alpha }}_t.$$

This provides the Euler Lagrange equations stated in the lemma. Moreover, from 2α_t = –η_t we get

$$\frac{d{\mathit{\alpha }}_t}{dt}=\frac{1}{2}{\nabla }_{{\mathbf{x}}_t}E({\mathbf{x}}_t)-\frac{1}{2}{\partial }_{{\mathbf{x}}_t}{\left[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t\right]}^{\ast }({\mathit{\alpha }}_t)$$

which coincide with the expression given in Lemma 2. This result was detailed in (Glaunès, Trouvé, and Younes, 2004) for unlabeled landmarks, (Glaunès et al., 2008) for curves, and (Vaillant and Glaunès, 2005) for surfaces.

The proof of Lemma 3 is very similar. We leave the details of the computation to the reader. One finds that the gradient of J is given by 2α_t + η_t

$${\eta }_t={\displaystyle {\int }_t^1{R}_{ts}^{\ast }}({\partial }_{{\mathbf{x}}_s}(k_V({\mathbf{x}}_s,{\mathbf{x}}_s){\mathit{\alpha }}_s))ds+{\displaystyle \sum _k{R}_{t{t}_k}^{\ast }{\nabla }_{{\mathbf{x}}_{t_k}}{E}_{t_k}{\mathbf{1}}_{\left[t_k,1\right]}(t)},$$

Computing the derivative as above, one finds that at all t ≠ t_k, η_t satisfies

$$\frac{d{\eta }_t}{dt}=-{\partial }_{{\mathbf{x}}_t}{\left[k_V({\mathbf{x}}_t,{\mathbf{x}}_t){\mathit{\alpha }}_t\right]}^{\ast }({\mathit{\alpha }}_t+{\eta }_t);$$

η_t is discontinuous at observation times with ${\eta }_1={\nabla }_{{\mathbf{x}}_1}{E}_1$, and the jump ${\eta }_{t_k^{-}}-{\eta }_{t_k^{+}}={\nabla }_{{\mathbf{x}}_k}{E}_k$. This translate directly into the conditions given in Lemma 3.

We have implicitly defined the gradient of J relatively to the metric given by k_V(x_t,x_t) with twofold advantages of being closer to the metric inducing the space of velocity field v and simplifying the formula for the gradient.