Investigation of microflow reversal by ac electrokinetics in orthogonal electrodes for micropump design

Abstract

Orthogonal electrodes have been reported to produce high velocity microflows when excited by ac signals, showing potential for micropumping applications. This paper investigates the microflow reversal phenomena in such orthogonal electrode micropumps. Three types of microflow fields were observed by changing the applied electric signals. Three ac electrokinetic processes, capacitive electrode polarization, Faradaic polarization, and the ac electrothermal effect, are proposed to explain the different flow patterns, respectively. The hypotheses were corroborated by impedance analysis, numerical simulations, and velocity measurements. The investigation of microflow reversal can improve the understanding of ac electrokinetics and hence effectively manipulate fluids.

INTRODUCTION

ac electrokinetics (ACEK) has been developing rapidly in recent years, and various types of microflows can be generated by applying only several volts ac signals. Easy to implement and compatible with microchip fabrication, ACEK is becoming an enabling technology for lab-on-a-chip devices, and ACEK has already been applied to develop micropumps and other devices.

Unlike dc electrokinetic devices, ACEK exerts local control of fluids and particles, so ACEK devices typically consist of microelectrodes covering microchambers. As a result, low voltage operation can be realized and electrochemical reactions can be avoided. Because ac electric fields are oscillatory, i.e., not directional, ACEK devices exhibit reflective symmetry, i.e., counter-rotating vortices are generated over a pair of electrodes. In order to use ACEK for pumping, it is essential to break the symmetry of electric fields within an electrode pair to produce a unidirectional flow. This can be achieved by polarization asymmetry or by spatial asymmetry in electrode design. Polarization asymmetry for directional flow motion has been reported using biased ac electroosmosis (ACEO).^{1, 2} Designs with spatial asymmetry to induce a net flow include asymmetric “side by side” electrodes by ACEO (Refs. ^{3, 4, 5}) and the ac electrothermal effect (ACET),⁶ orthogonal electrodes,⁷ and the three-dimensional (3D) step ACEO pump.^{8, 9} Because the local velocity of the electrokinetic flow is a function of electric field strength with asymmetric electrode designs, two electrodes in a pair will experience different electrode field strengths; hence, there are unequal flow velocities leading to directional net flows.

Among the many designs mentioned above, the design of an orthogonal electrode pair,⁷ as shown in Fig. 1a, accentuates the nonuniformity in the electric field, and, as a result, produces stronger net flows at lower voltages. In Ref. 7, when applying a voltage beyond 14 V_rms (150−500 μm electrode spacing) and below 1 MHz, a net flow velocity exceeding 1 mm∕s was obtained. The flow direction was from the vertical electrode tip toward the horizontal bar as shown in Fig. 1a. Because the direction is opposite to what is predicted by ACEO, its mechanism intrigues many research groups.

Figure 1.

(a) Arrays of orthogonal electrode pairs used for micropump design. The arrow indicates the net pumping direction. (b) A micromanipulator probe is used with a Pt wire (partially shown) to form an orthogonal electrode pair. The spacing between electrodes is measured to be 140 μm. Inset: Orthogonal electrodes fitted in the slip cover chamber on a glass slide.

Flow reversal in ACEK is not a rare occurrence and has been observed by several groups^{3, 8, 10} In Ref. 3, Studer et al. reported the reversal of the pumping direction at high frequencies (50–100 kHz) and relative high voltage (1−6 V_rms at 4.2 μm in-pair electrode spacing) compared with typical ACEO conditions (1 kHz, below 1 V_rms) in their microfluidic loop comprised of arrays of asymmetric planar electrodes. Wu et al. reported ACEO flow reversal by Faradaic charging (i.e., by electrochemical reactions) that induces co-ions instead of counterions at the electrodes. Flow reversal has also been observed for the 3D step ACEO micropump by Urbanski et al.⁸ They reported that the flow reversal threshold voltage increases as the operating frequency increases. Various hypotheses and explanations have been offered for flow reversal. For the orthogonal electrode micropump, Faradaic charging of electrodes has been suggested. However, the operating frequency is higher than the frequency range for Faradaic charging to dominate.

In this paper, we present our study of and the insight into the flow fields by the orthogonal electrode, i.e., how they change with the applied electric signals with respect to the frequency and potential. In our experiments, three distinct flow patterns were observed with fluid conductivity σ=20 mS∕m, applying to low frequency (<50 kHz) low voltage (<15 V_{peak to peak} or V_pp, at 140 μm electrode spacing), low frequency (<50 kHz) high voltage (>15 V_pp), and the high frequency range (>100 kHz), respectively. We suggest that ACEO by capacitive charging, ACEO by Faradaic charging, and the ACET effect are, respectively, the mechanisms behind the three different flow patterns. Impedance measurements, numerical simulations, and fluid velocity data are presented to support this hypothesis, which also agrees with the theoretical predictions. Hopefully, our work will improve the understanding of the ACEK manipulation of fluids.

EXPERIMENTAL OBSERVATIONS ON FLOW REVERSAL

Device construction

The device consists of the pair of electrodes that is oriented perpendicular to each other on a glass slide, forming a “T” configuration, as shown in Fig. 1b. The distance between the electrodes is measured to be 140 μm. A slip silicone cover (SA8R-0.5, Grace Bio-Laboratories, USA) is sealed on the glass slide to form the chamber. The chamber has a diameter of 9 mm and 0.5 mm in height. In order to maintain the uniformity of the electrode shape and tip curvature, a micromanipulator probe (Micromanipulator, USA) is used as the vertical electrode.

Fluorescent polystyrene particles (Invitrogen, USA) are used as tracers to follow the fluid flow and to extract the fluid velocity. Water at conductivity σ=20 mS∕m was used. The images and videos are taken by an Eclipse LV100 microscope (Nikon, Japan) at 20× magnification. In the experiments, traces of the fluorescent polystyrene particles (500 nm or 1 μm in diameter) were recorded by a charge-coupled device (CCD) video camera (Photometrics CoolSnap ES, USA), then the successive video frames (100 frames at 0.1 s interval) were superimposed using the Image-Pro 3DS software suite to obtain a single plot of particle traces. The velocity of the particles can be calculated by the built-in particle image velocimetry (PIV) analysis. The area used to calculate the velocity is located in the gap between the two electrodes, and 15 μm away from the electrode tip.

Observed microflow fields

Three types of flow fields were observed at various ac frequencies and potentials. At frequencies below 5 kHz and potentials below 15 V_pp, the fluid is observed to flow from the gap toward the sharp electrode tip, moving along the vertical electrode, and then extends into the fluid bulk, forming two vortices. Figure 2 and its linked online video clip show the flow field at 1 kHz and 10 V_pp. This flow pattern is consistent with ACEO flows induced by capacitive charging, i.e., fluid moving away from the electrode gap.

Figure 2.

Download video file ^{(4.8MB, mpg)}

Microflow traces at 1 kHz and 10 V_pp (σ=20 mS∕m) by superimposing 100 successive video frames. Fluorescent particles move from the electrode gap toward the electrode tip and form vortices in the bulk. Microflow induced by orthogonal electrode at 1 kHz and 10 V_pp (σ=20 mS∕m) (enhanced online).

If we keep the signal frequency below 1 kHz and gradually increase the voltage, a change in flow pattern is observed when the voltage exceeds 15 V_pp. Figure 3 shows the flow traces obtained at 200 Hz and 20 V_pp, which is extracted from the linked online video clip. The flow diverges at the tip of the vertical electrode. Within 20 μm from the tip, some flows reverse their directions, shooting from the tip toward the gap between the electrodes while the rest maintain their directions, moving along the electrode away from the tip. Obviously, this flow pattern is caused by mechanisms other than capacitive charging ACEO. As it is well known that a higher electric field at low frequency could lead to electrochemical reactions, Faradaic charging is proposed to be the responsible mechanism. At even higher voltages, corrosion of electrode tips was observed, confirming this hypothesis.

Figure 3.

Download video file ^{(5.1MB, mpg)}

Flow field at 200 Hz and 20 V_pp (σ=20 mS∕m). Flow diverges at the vertical electrode tip. Faradaic polarization causes the fluid to shoot from the tip into the gap. Microflow induced by orthogonal electrode at 200 Hz and 20 V_pp (σ=20 mS∕m) (enhanced online).

When the frequency is between 50 kHz and 1 MHz, a different type of microflow reversal occurs. The flow moves along the vertical electrode toward the gap as indicated in Fig. 4. The linked online video clip illustrates the fluid motion. The flow direction is opposite to that induced by capacitive charging ACEO at low frequencies and low voltages. The transition frequency between the two reversed flows is identified at around 30 kHz. Measurements of impedance and velocity data as a function of frequency suggest that the ac electrothermal effect is responsible for microflows at such conditions.

Figure 4.

Download video file ^{(4.7MB, mpg)}

Flow field at 500 kHz and 15 V_pp (σ=20 mS∕m). The fluid flows along the vertical electrode toward the gap of the electrodes. The flow pattern is reversed as compared with ACEO flow pattern in Fig. 2. Microflow induced by orthogonal electrode at 500 kHz and 15 V_pp (σ=20 mS∕m) (enhanced online).

DISCUSSION

ac electrokinetic mechanisms

Two major ACEK mechanisms, ac electroosmosis (ACEO) and the ac electrothermal effect (ACET), can induce microfluidic motion. ACEO generates fluid motion by inducing mobile charges in the double layers. When a small ac signal is applied over an electrode pair, the electrode surfaces become capacitively charged, i.e., forming a counterion accumulation. The counterions migrate with or against an electric field that is tangential to the electrode surface, which in turn produces fluid motion due to fluid viscosity.

ACEO typically happens at low frequency and low voltage strength when the interfacial process dominates. At low electric conductivity, the double layer will exhibit a high electric impedance (from a small capacitance), which may lead to a large portion of voltage drop across the double layer. As a result, ACEO flow predominates. Based on classical electrokinetic equations,¹¹ ACEO slip velocity is expected to have a quadratic relationship with the applied electric fields, u_ACEO∝−(ε_m∕η)QE_t, where ε_m and η are the permittivity and viscosity of the medium, E_t is the electric field parallel to the solid surface, and Q is the induced charge density. Q is proportional to the voltage drop over the charged double layer Δξ under the assumptions of low voltages and a dilute solution; however, it becomes nonlinear at large voltages.

When the electric field strength exceeds a certain threshold value, electrochemical reactions take place and the surface charge polarities are inverted. Instead of the counterions that are induced by capacitive changing, co-ions are produced at the tip of the vertical electrode. As a result, the electric fields tangential to the electrode drive the fluid toward the opposite direction. However, too high a voltage would degrade the electrodes and cause bubble generation, especially for high conductivity fluids. In the experiments, Faradaic polarization is observed to be strong at the electrode tip where the electric field is the highest. At some distance away from the electrode tip, the field strength reduces and the counterions dominate, hence the ACEO by capacitive charging occurs. So the divergence of the microflows at some distance away from the electrode tip (20 μm in the experiment) is due to the competition between the two polarization processes.

At higher frequencies, less voltage drops across the electrode∕electrolyte interface to induce ions in the double layer, and more voltage drops across the fluid bulk, which causes Joule heating. As a result, the ACET effect starts to dominate. The ACET effect induces fluid motions from the gradients in conductivity and permittivity of the fluid. When an electric field E_rms is applied over a fluid body, energy is dissipated as $⟨P⟩=\sigma E_{\mathrm{rms}}^2$. (σ is the electrolyte conductivity.) A nonuniform electric field will lead to a nonuniform temperature rise, i.e., temperature gradient ∇T, which will produce gradients in conductivity and permittivity as ∇ε=(∂ε∕∂T)∇T, ∇σ=(∂σ∕∂T)∇T. In turn, ∇σ and ∇ε generate mobile space charges ρ in the fluid bulk as

$$\mathbf{\rho }=\frac{\sigma \partial \epsilon ∕\partial T-\epsilon \partial \sigma ∕\partial T}{\sigma +i\omega \epsilon }\nabla T\cdot \mathbf{E}.$$

The electric field will impose on the induced space charges a force F_et=ρ^eE−1∕2∣E∣²∇ε. The polarities of the induced charges change with the electric field E, so flow direction can be sustained. Without any external heat sources, ACET velocity exhibits a quartic function (u∼V⁴) with respect to the applied voltage. With an external heat source, such as strong illumination of incident light, the velocity has a quadratic relationship (u∼V²), as reported by Castellanos et al.¹²

Operating frequencies of ACEK mechanisms

Low operating frequencies (below the charge relaxation frequency ω=σ∕ε, typically lower than 50 kHz) will favor ACEO as the interface impedance dominates. At higher frequencies, the ions at the surface do not have sufficient time to charge and discharge the double layer, and the ACEO velocity diminishes. From the prospective of an equivalent circuit, there is not sufficient voltage drop across the double layer capacitance at high frequency. The ACET effect occurs owing to the resistive property of the fluid, so its flow velocity has little dependency on frequency when it is well below a crossover frequency 3(σ∕ε).¹² However, because the actual voltage drop across the resistive bulk changes with frequency, the ACET flow may exhibit frequency dependence, i.e., weaker at low frequencies.

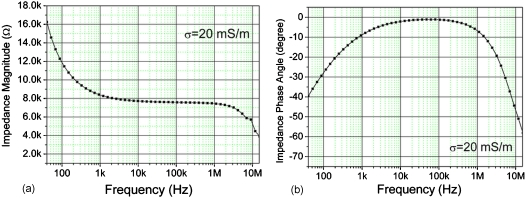
By studying the impedance spectra of the microfluidic system, some insights have been obtained with respect to which ACEK processes are responsible for the microflow patterns, respectively. Figure 5 shows the impedance magnitude and phase angle of the orthogonal electrodes described in Fig. 1. At low frequency, especially below 1 kHz, impedance shows a strong capacitive property, which favors the ACEO flow. It can also be seen that above 50 kHz the fluidic cell is almost resistive, so most of the electric potential drops in the bulk fluid, generating the thermal gradient and contributing to the ACET effect. Hence, it can be deduced that strong ACEO flow occurs at low frequency and the ACET effect dominates above 100 kHz. It should be noted that the impedance of the electrode cell can by changed by modifying the microchamber size and the electrode surface roughness. So the frequency range exhibiting resistive impedance could possibly be expanded into rather low frequencies if the electrodes have a porous surface.

Figure 5.

Impedance magnitude (a) and phase angle (b) of the orthogonal electrodes shown in Fig. 1 (with σ=20 mS∕m and 140 μm spacing between electrodes).

Simulation results

In this paper numerical simulation further corroborates that the change of flow patterns from that of Fig. 2 to Fig. 4 can be explained as the transition from ACEO flows to ACET flows. Numerical simulations are done using the finite element analysis (FEA) software Comsol Multiphysics. The dimensions are exactly the same as of the experiments. So a comparison can be made between simulations and experiments.

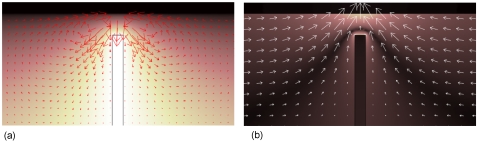
For the ACEO simulation, the Conductive Media DC model is first used to solve for the electric field distribution. The resulting electric field is used to calculate the boundary conditions for the incompressible Navier-Stokes module, which solves for a flow field. As Fig. 6a shows, the ACEO flow moves downward along the pin and two vortices are formed in the bulk fluid, which is consistent with experimental observation at low frequencies.

Figure 6.

Numerical simulations of (a) the ACEO flow field (arrows) and electric potential distribution and (b) the ACET flow field (arrows) and thermal gradients. (Light color indicates higher magnitude of electric potential and thermal gradients.)

The ACET simulation used the Conductive Media DC model for solving electric field, the convection and conduction model for solving thermal gradient from electric field, and the incompressible Navier-Stokes models for solving fluid velocity. For the thermal boundary conditions, the electrodes are set at a fixed temperature at the boundaries of the microchamber. Thermal continuity was assumed for the electrode sections within the fluid chamber. So the highest thermal gradient (also the highest charge density) happens at the space between the two electrodes, where the electric field is also the strongest, and this produces a different flow pattern than the ACEO. The flow pattern in Fig. 6b is similar to experimental results shown in Fig. 4.

Flow velocity dependence on voltage

ACEO and ACET velocities have different dependencies on the applied electric fields. By extracting the dependence of fluid velocity on voltage, the dominant ACEK mechanism might be identified. Here, two groups of velocity data were presented that are representative of low frequencies (500 Hz) and high frequencies (500 kHz), respectively.

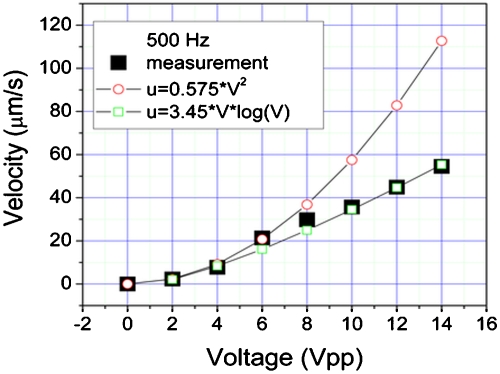
One group of velocities is obtained at 500 Hz with applied voltage varying from 2 V_pp to 14 V_pp with 2 V intervals, as shown in Fig. 7. Beyond 15 V_pp, electrochemical reactions, i.e., Faradaic charging, corrosion of the electrode, and bubble generation, prevent the accurate measurements of the fluid velocity. At 500 Hz below 15 V_pp, capacitive charging ACEO is expected to be the dominant mechanism acting on the fluid, and the theory predicts that ACEO flow velocity is a quadratic function of the applied voltage. The experimental data are fitted to two curves, which are also shown in Fig. 7. As the curve-fit shows, the quadratic relationship fits up to the 6 V_pp then the measured velocity becomes lower than the quadratic curve. From 8 V_pp and higher, the data seem to follow a V×log(V) relationship as Olesen et al. described in Ref. 13. Theoretically, the velocity scaling with the quadratic voltage function is only valid for low driving voltages comparable to thermal voltage (∼25 mV). When a higher voltage is applied, fluid velocity would deviate from the quadratic dependency on voltage because of the nonlinearity of the electric double layer capacitance. Instead of a quadratic relationship, fluid velocity scales more linearly³ or even saturates at high voltages.

Figure 7.

Velocity data at 500 Hz with the curve-fits (using 0.5 μm tracer particles).

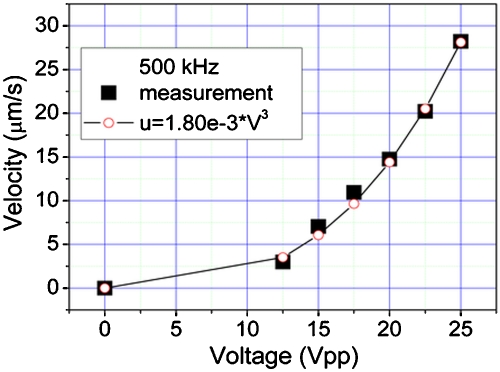
Another set of data is taken at 500 kHz, where the flow direction is reversed as compared with the condition at 500 Hz. The velocity data are plotted as shown in Fig. 8. Voltage ranges from 12.5 V_pp to 25 V_pp. ACET velocity scales with the conductivity of the fluid. For a conductivity of 20 mS∕m (tap water) used in our experiments, which is considered as low for the ACET effect, ACET flows are not prominent until a large voltage is used. The measured velocity for 12.5 V_pp is 3 μm∕s, and the flows are barely observable when the voltage is below 10 V_pp. As can be seen from Fig. 8, the measured data fits to the third power of voltage (u∼V³). ACEO velocity scales with a quadratic relation of the applied voltage, while theoretically ACET velocity scales with the voltage as V²∼V⁴,¹² depending on the heat transfer boundary conditions. So this indicates that microflows at 500 kHz should be attributed to the ACET effect, not the ACEO effect, as the main driving force.

Figure 8.

Velocity data at 500 kHz with the curve-fits (using 1 μm tracer particles).

CONCLUSION

This paper investigates microflow reversal by ac electrokinetics for orthogonal electrode configuration. Three flow patterns at different signal frequencies and voltages are observed. Three distinct ACEK processes are suggested as the responsible mechanisms, namely, ac electroosmotic flow for low frequency and low voltage, ac Faradaic polarization for low frequency and high voltage, and ac electrothermal effect for high frequency regions. Experimental observations are supported by the numerical simulation, and the hypotheses agree with the impedance analysis and flow velocity measurement.

The knowledge gained from this work helps us to determine the proper mechanism to manipulate fluid by selecting an appropriate signal frequency and strength. ACEO will provide stronger microflows for low ionic strength fluids, while ACET flows are preferred for high conductive biosolutions.