Crystallographic dependence of loss in domain engineered relaxor-PT single crystals

Abstract

Domain engineered ⟨001⟩ oriented relaxor-PbTiO₃ ferroelectric crystals exhibit high electromechanical properties and low mechanical Q values, analogous to “soft” piezoelectric ceramics. However, their characteristic low dielectric loss (≤0.5%) and strain-electric field hysteresis are reflective of “hard” piezoelectric materials. In this work, the electromechanical behavior of relaxor-PT crystals was investigated as a function of crystallographic orientations. It was found that the electrical and mechanical losses in crystals depends on the specific engineered domain configuration, with high Q observed for the ⟨110⟩ orientation. The high Q, together with high electromechanical coupling (∼0.9) for ⟨110⟩ oriented relaxor-PT crystals, make them promising candidates for resonant based high power transducer applications.

Relaxor-PT based ferroelectric single crystals, such as Pb(Zn_1/3Nb_2/3)O₃–PbTiO₃ (PZNT) and Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ (PMNT), have been reported to possess excellent properties in the ⟨001⟩ poled domain engineered state, with high piezoelectric coefficients d₃₃>2000 pC∕N and large electromechanical coupling factors k₃₃>0.90. In addition to the high electromechanical properties, the crystals exhibit low mechanical quality factors Q≤120, analogous to soft piezoelectric ceramics, such as PZT5H (DOD Type VI). The combination of high piezoelectric properties and lowQ make single crystals excellent components for nonresonant actuators and high frequency medical ultrasound transducers.^{1, 2, 3, 4, 5, 6, 7} In contrast, however, relaxor-PT single crystals exhibit low dielectric loss (tan δ<0.5%) and low strain-electric field hysteresis (<3%), characteristic of “hard” piezoelectric materials, such as PZT4 and PZT8 (DOD Types I and III) polycrystalline ceramics.^{8, 9, 10} In this paper, the electromechanical properties, the electrical and mechanical loss behavior for relaxor-PT single crystals were investigated as a function of crystallographic orientation, and discussed in relation to their specific domain engineered configuration.

Bridgman grown single crystals used in this work were obtained from TRS Technologies (State College, PA), with PMNT being the representative of other relaxor-PT based crystals. Two compositions were selected, PMNT30 being in proximity of the morphotropic phase boundary (MPB) and PMNT26, correspondingly far from MPB with a higher T_R-T. The crystals were oriented along crystallographic directions ⟨001⟩, ⟨110⟩, and ⟨111⟩ using real-time Laue X-ray. The oriented samples were cut to obtain longitudinal rods, with aspect ratios following IEEE piezoelectric standards.^{11, 12} Vacuum sputtered gold was applied as the electrodes. All samples were poled by applying a dc electric field of 10 kV∕cm at room temperature. High field polarization measurements were performed on plate samples at room temperature, using a modified Sawyer–Tower circuit. Dielectric, piezoelectric, electromechanical properties and the mechanical loss (inverse of Q) were determined from the longitudinal mode according to IEEE standards, using an HP4194A impedance-phase gain analyzer. In order to minimize stress (loading) effects on the samples during measurement, thin (0.06 mm diameter) silver wires were attached to the electrodes using a small amount of conductive silver.

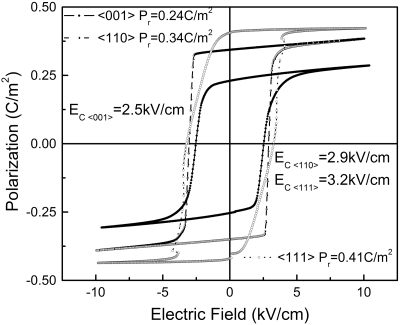
Figure 1 shows the measured electric field induced polarization hysteresis loops for ⟨001⟩, ⟨110⟩, and ⟨111⟩ oriented PMNT30 crystals. The remnant polarization P_r and coercive field E_C were found to be dependent on the orientation. From the symmetric loops, the P_r was found to be on the order of 0.24, 0.34, and 0.41 C∕m² for ⟨001⟩, ⟨110⟩, and ⟨111⟩ orientations, while the coercive field E_C was on the order of 2.5, 2.9, and 3.2 kV∕cm, respectively. Unlike acceptor modified PZT ceramics and/or relaxor-PT crystals,¹³ no internal bias field was observed for any of the orientations.

Figure 1.

Polarization hysteresis for PMNT30 crystals along crystallographic orientations ⟨001⟩, ⟨110⟩, and ⟨111⟩.

It is known that there are eight possible polarization orientations along the pseudocubic ⟨111⟩ direction for rhombohedral relaxor-PT single crystals (3 m symmetry). Upon applying an electric field, the dipoles reorientate as close as possible to the applied electric field direction. For ⟨001⟩ poled crystals, there are four equivalent polar vectors along the ⟨111⟩ direction, with an inclined angle of −54.7° from the poling field. The four ⟨111⟩ domains are equivalent with a domain engineered configuration resulting in a macrosymmetry 4mm labeled as “4R.” For ⟨110⟩ poled crystals, there are two equivalent polar vectors along the ⟨111⟩ direction, which will rotate 35.5° toward the applied field direction of ⟨110⟩ with a designated domain engineered configuration “2R.” For this case, the macroscopic symmetry is mm2. In contrast, there is only one polar vector along the ⟨111⟩ direction for ⟨111⟩ poled ferroelectric crystals, thus it will form a monodomain state, designated “1R,” exhibiting symmetry 3m. According to the domain engineered configurations, the polarization level derived from the hysteresis loops should correspond, in theory, to the intrinsic value along the polar axis of the monodomain crystal P_s, following $P_{r⟨001⟩}=P_{r⟨110⟩}∕\sqrt{2}=P_{r⟨111⟩}∕\sqrt{3}$.^{1, 14, 15, 16, 17, 18} As expected, the P_r values for the different orientations obtained from Fig. 1 corresponded well to the predicted values.

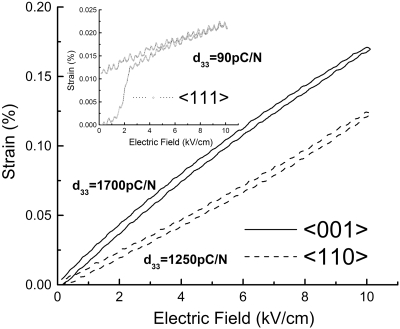
Figure 2 shows the unipolar strain behavior as a function of electric field for ⟨001⟩ and ⟨110⟩ oriented crystals. The strain behavior for the ⟨111⟩ direction is shown in the small inset in Fig. 2. The strain hysteresis (related to the piezoelectric loss by the non-180° domain reorientation under an electric field) was calculated from the ratio of the strain difference at half maximum electric field over the peak strain.⁵ The strain hysteresis was found to be on the order of <3% for both domain engineered ⟨001⟩ and ⟨110⟩ poled crystals. The nonhysteretic strain results from an absence of domain wall motion due to the inherent stability of the domain engineered configuration. For clarifications, when a sufficiently strong electric field is applied along the ⟨001⟩ orientation, the four degenerate domain variants are stabilized, with polar vectors along the ⟨111⟩, $⟨1\overline{1}1⟩$, $⟨\overline{1}11⟩$, and $⟨\overline{1}\overline{1}1⟩$ directions. Application of an electric field simply allows the polar vectors in each reversible domain variant to rotate continuously toward the direction of applied field. From the strain curves, the piezoelectric coefficients were found to be ∼1700 and ∼1250 pm∕V, for ⟨001⟩ and ⟨110⟩ oriented crystals, respectively. The piezoelectric coefficients obtained according to IEEE standards (Table 1) were comparable to the values derived from Fig. 2, reflecting the extrinsic contribution (domain wall motion) was less than ∼10%.¹⁹ In contrast, as shown in the small inset of Fig. 2, the strain field response of ⟨111⟩ oriented crystals was characteristically hysteretic due to non-180° domain switching, while at higher fields, the linear strain behavior was observed, corresponding to the pseudomonodomain state 1R, with a piezoelectric coefficient on the order of 90 pm∕V, again similar to the value obtained from the resonance method. It should be noted that the strain behavior for a relatively thick ⟨111⟩ oriented samples (>5 mm) exhibited a linear behavior, demonstrating that a stable single domain could be obtained.

Figure 2.

Typical strain-field (S-E) loop for ⟨001⟩, ⟨110⟩, and ⟨111⟩ oriented PMNT30 crystals.

Table 1.

Longitudinal properties for PMNT crystals with different orientations and compositions.

Material		Domain engineered structure14	εr	Loss (%)	k33	d33 (pC/N)	$s_{33}^E$ (pm2/N)	Q33
PMNT30	⟨001⟩	4R	5200	0.4	0.90	1500	60.0	120
	⟨110⟩	2R	4400	0.2	0.90	1050	35.9	600
	⟨111⟩	1R	810	0.2	0.42	90	6.5	1130
PMNT26	⟨001⟩	4R	4400	0.4	0.88	1200	47.8	150
	⟨110⟩	2R	3320	0.2	0.88	810	29.3	850
	⟨111⟩	1R	730	0.2	0.37	76	6.4	2200

Table 1 lists the longitudinal properties for pure PMNT30 (in proximity of the MPB) and PMNT26 (far away from MPB) crystals along their primary crystallographic directions ⟨001⟩, ⟨110⟩, and ⟨111⟩. It was found that the dielectric permittivity ε_r, dielectric loss (tan δ=1/Q_electric), piezoelectric coefficient d₃₃ and elastic compliance $s_{33}^E$ reached the highest values for the ⟨001⟩ domain engineering configuration (4R) and exhibited minimum values for the ⟨111⟩ monodomain crystal (1R), with values for ⟨110⟩ poled samples (2R) lying in between. In contrast, the mechanical quality factor Q was maximum for the ⟨111⟩ oriented samples, being on the order of ∼1100, with values being less than ∼120 for ⟨001⟩ oriented crystals. Of particular significance from Table 1 was the high mechanical Q, on the order of ∼600 for the ⟨110⟩ engineered domain configuration, with an electromechanical coupling factor k₃₃ on the order of ∼0.90.

To delineate the anisotropic loss behavior, we must consider the role of domains in the relaxor-PT single crystals. As stated, there are two types of domains in rhombohedral relaxor-PT ferroelectric crystals, the 180° ferroelectric domains and non-180° ferroelastic-ferroelectric domains (71° and 109° domains).^{20, 21, 22, 23, 24} The 180° domains refer to domain walls with antiparallel polarizations, but with strain tensors that are necessarily equivalent. Such domain walls will generally be moved by the application of an electric field,²⁰ which only contributes to the polarization (dielectric loss). The non-180° domain walls refer to walls between variants which differ in both polarization vector and strain tensor. Both 180° and non-180° domain walls generally form to decrease the effects of depolarization fields, whereas only non-180° domain walls may minimize the elastic energy. Thus, the dielectric and mechanical losses are originated from 180° and non-180° domain wall motion, respectively. For ⟨111⟩ poled single crystals, the domain engineered structure is pseudomonodomain, thus, both low dielectric loss and high mechanical Q values are expected. Indeed, the dielectric loss was found to be only 0.2%, with a mechanical Q on the order of ∼1100. As stated above, the 180° domain walls in ferroelectric crystals can be moved by the application of electric field and stabilized domain engineered configurations can be formed. This accounted for the low dielectric loss in the relaxor-PT single crystals. For the high Q, ⟨110⟩ case, with engineered domain configuration 2R, it was reported that the elastic energy for different spontaneous strains in domains could be compensated more efficiently for the domain set generated by ⟨110⟩ than by ⟨001⟩ oriented poling field. The local repoling experiments performed by applying electric field cycling at a scanning force microscope tip, demonstrated that the domain structure in poled ⟨110⟩ oriented single crystals was more stable than for ⟨001⟩ oriented crystals,²⁴ which may be due to the 109° domains parallel to the (110) face. This may explain why the mechanical Q value was found to be only ∼120 for ⟨001⟩ poled crystals, while much higher mechanical Q values, on the order of ∼600, are observed for ⟨110⟩ poled polydomain relaxor-PT crystals.

It was observed from Table 1 that the electromechanical and loss properties were not only dependent on the crystallographic direction, but also on the composition or proximity of the MPB (or relation to the value of T_R-T) of the crystals. For lower PT content crystals, being relatively far away from the MPB, lower dielectric and piezoelectric properties were observed but with higher mechanical Q values. The high Q for the domain engineered configuration 2R is due to the overall reduced domain wall mobility.

In summary, the electromechanical and loss behavior of relaxor-PT single crystals were found to be dependent on the crystallographic direction and/or domain engineered configuration. High electromechanical and low dielectric loss were observed for ⟨001⟩ and ⟨110⟩ oriented domain engineered configurations. However, the mechanical quality factor for crystals with the ⟨110⟩ domain engineered structure 2R was found to be >500, much higher than the typical value for 4R engineered domain, due to an overall reduced ferroelastic-ferroelectric domain wall motion. Unlike the acceptor doped ferroelectric crystals, no internal bias field was observed in the pure crystals, however, the crystals exhibited low dielectric loss and minimum strain hysteresis, due to the engineered domain configurations. Meanwhile, relaxor-PT crystals with lower PT content, being relatively far away from MPB, were found to possess higher mechanical Q. Of particular significance, the high mechanical Q, together with its high electromechanical coupling factor k₃₃ (∼0.9), make the ⟨110⟩ oriented relaxor-PT ferroelectric single crystals promising for resonant based high power applications.