Gait dynamics in Parkinson’s disease: Common and distinct behavior among stride length, gait variability, and fractal-like scaling

Abstract

Parkinson’s disease (PD) is a common, debilitating neurodegenerative disease. Gait disturbances are a frequent cause of disability and impairment for patients with PD. This article provides a brief introduction to PD and describes the gait changes typically seen in patients with this disease. A major focus of this report is an update on the study of the fractal properties of gait in PD, the relationship between this feature of gait and stride length and gait variability, and the effects of different experimental conditions on these three gait properties. Implications of these findings are also briefly described. This update highlights the idea that while stride length, gait variability, and fractal scaling of gait are all impaired in PD, distinct mechanisms likely contribute to and are responsible for the regulation of these disparate gait properties.

Parkinson’s disease (PD) is a common, debilitating neurodegenerative disease. Gait disturbances are a frequent cause of disability and impairment for patients with PD. This article provides a brief introduction to PD and describes the gait changes typically seen in PD. A major focus of this report is an update on the study of the fractal-like, long-range correlation properties of gait in PD and the relationship between this feature of gait and other walking properties. We examine the effects of several experimental conditions on these gait properties in order to probe common and feature-specific responses and the neural mechanisms that contribute to these different gait properties. Implications of these findings are also briefly described. This update highlights the idea that stride length, gait variability, and fractal scaling of gait are all impaired in PD. Nonetheless, the dissimilar responses to different stimuli demonstrate that overlapping but distinct mechanisms likely contribute to and are responsible for the regulation of these disparate gait properties. A challenge to future studies is to better map these properties and their changes in response to the progression of the disease and to various probes to the multiple networks and systems that are impaired in PD.

INTRODUCTION

PD is one of the most common neurodegenerative disorders. PD occurs in about 1% of the population over the age of 60 and its prevalence increases with age. About 20% of people over the age of 80 have Parkinsonism associated gait disturbances. The major motor disturbances in PD are bradykinesia (i.e., slowed movement), hypokinesia (small amplitude movements), resting tremor, rigidity, and postural instability. These major motor features of PD are associated with and are largely a result of the loss of dopaminergic innervation of the basal ganglia. Although a genetic predisposition has been identified in a subset of patients with PD and several other risk factors for PD have been identified,^{1, 2, 3} the cause and etiology of PD are largely unknown.^{1, 2, 3, 4, 5}

In addition to multiple other effects, the impaired basal ganglia function in PD leads to alterations in gait and balance. These motor changes in PD often restrict functional independence and are a major cause of morbidity and mortality among these patients.^{6, 7, 8, 9} In this review article, the changes in gait that are typically seen in patients with PD are briefly described and more specifically, studies that applied an approach based on nonlinear dynamics to the evaluation and understanding of Parkinsonian gait are summarized. In addition, we include new findings which expand the understanding of the “fractal” properties of gait, in general, and in PD, in particular. While the results of these studies may seem esoteric and without practical implications, we conclude with some suggestions for treatment and restoration of gait in patients with PD that stem from this review. (Portions of this general review on gait in PD are adapted from Hausdorffet al.¹⁰)

BACKGROUND

Gait disturbances in PD: Classification and clinical ramifications

The gait disturbances in PD may be divided into two types:¹ (1) continuous and (2) episodic.^{11, 12} The episodic gait disturbances occur occasionally and intermittently, surfacing in an apparently random, inexplicable manner. The episodic gait disturbances include festination, start hesitation, and freezing of gait.^{7, 13, 14} The latter is a debilitating phenomenon that is most commonly experienced by patients with advanced PD.^{7, 15, 16, 17} Conversely, the continuous changes refer to alterations in the walking pattern that appear, at least at first glance, to be more or less consistent from one step to the next, i.e., they persist and are apparent all the time. While both types of gait disturbances are a result of basal ganglia dysfunction and certain episodic symptoms are associated with other continuous symptoms (e.g., patients with freezing of gait have increased gait variability),^{18, 19, 20, 21} the specific mechanisms responsible for the episodic and continuous gait disturbances are likely somewhat independent. Here we focus on the continuous gait disturbances, in part, because they are more prone to an analysis that examines the ongoing dynamics. Nonetheless, it is important to note that this type of approach may also be beneficial in studying the episodic gait disturbances in PD, perhaps with some modifications.²² Also, it is important to keep in mind that both types of gait disturbances contribute to and exacerbate the risk of falls in PD.⁷

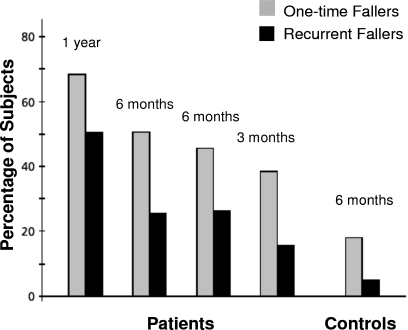
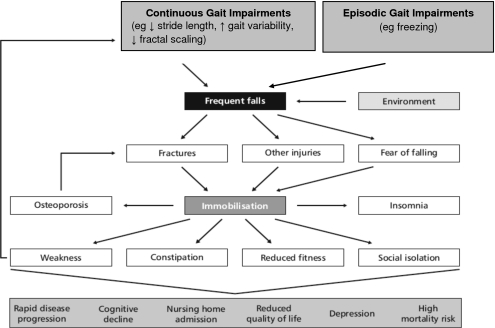
Falls are one of the most significant consequences of a disturbed gait in PD.^{7, 13, 23, 24, 25, 26, 27, 28, 29} As the disease progresses, gait impairment and falls become increasingly important and develop into one of the chief complaints among PD patients and their caregivers. Eventually most patients will sustain recurrent falls. Similar to the findings of Ashburn et al.,²³ in our study of 230 patients with PD, 43% reported falling at least once in 12 months.⁸ Other prospective surveys have documented the high incidence of falls and their consequences in PD.^{9, 13, 14, 24, 28, 29} Some of the observed fall rates were quite substantial, with several investigations reporting that almost 70% of patients fell during a one-year follow-up. This percentage is more than double that is typically seen in healthy older adults (see Fig. 1). Furthermore, it has been reported that recurrent falls occurred in about 50% of patients during one year. Compared to healthy subjects, the relative risk of sustaining recurrent falls during a six-month period was 9.0 for PD patients.¹³ Fall rates were even higher in studies that also included “near falls” (i.e., missteps and loss of balance without a full fledged fall).^{14, 30} Falls in general and in PD in particular may lead to injuries, hip fractures, fear of falling, and restriction of activities that in turn contribute to institutionalization, loss of independence, and increased mortality (see Fig. 2).^{13, 14, 26, 31, 32, 33}

Figure 1.

Fall rates in PD, as observed in four prospective studies, compared to age-matched controls. Despite the differences in duration of follow-up (3–12 months), a fairly consistent pattern emerges. Falling incidence increases with longer follow-up and are much larger than those observed in controls [From B. R. Bloem, J. M. Hausdorff, J. E. Visser, and N. Giladi, “Falls and freezing of gait in Parkinson’s disease: A review of two interconnected, episodic phenomena,” Mov Disord. 19, 871 (2004). Copyright ©2004 by Movement Disorder Society. Reprinted by permission of John Wiley & Sons, Inc.].

Figure 2.

Clinical impact of instability and falls in patients with PD. Note the vicious cycle that arises as a result of gait instability and impairment [From B. R. Bloem, J. M. Hausdorff, J. E. Visser, and N. Giladi, “Falls and freezing of gait in Parkinson’s disease: A review of two interconnected, episodic phenomena,” Mov Disord. 19, 871 (2004). Copyright ©2004 by Movement Disorder Society. Reprinted by permission of John Wiley & Sons, Inc.].

Continuous gait disturbances: The traditional approach

Classic studies of Parkinsonian gait have focused on the continuous gait disturbances, especially those that can be readily seen using visual observation. These include slowed ambulation (in part a manifestation of bradykinesia) with decreased or absent arm swing, longer double limb support (i.e., more time with both feet spent on the ground),^{6, 34, 35, 36} and impaired postural control.^{37, 38, 39, 40} One of the keys to these gait problems is the inability of patients with PD to generate sufficient stride length^{6, 36, 41} (a problem that has been related to impaired scaling of amplitude). In fact, the reduced and shortened stride length may explain many of the continuous gait disturbances in PD including the reduced gait speed and the increased time with the feet on the ground.

Increased gait variability in patients with PD

Gait disturbances in PD also include features that are not always easily quantifiable in routine clinical observation but become apparent when gait is evaluated quantitatively with gait analysis systems. Such changes include increased left-right gait asymmetry and diminished left-right bilateral coordination.^{20, 21, 42, 43, 44, 45} A loss of consistency in the ability to produce a steady gait rhythm, resulting in higher stride-to-stride variability, is also a characteristic feature of gait in PD.^{37, 46, 47, 48}

Increased gait variability can be seen throughout the disease, even in patients who were only recently diagnosed with PD have very mild disease and have not yet started to take anti-Parkinsonian medications.⁴⁶ The magnitude of the variability also tends to increase with disease severity. This gait feature is of interest for a number of reasons. First, unlike features such as gait speed, swing time, or double support time, which are based on average values or the first moment of a gait time series, variability measures reflect the second moment, and are, to a large degree, independent of stride length, both theoretically and experimentally (see further below). Gait variability (also referred to as unsteadiness or inconsistency and arrhythmicity of stepping) has also been found to be one aspect of walking closely associated with risk of falls in the elderly, even more so than measures based on the average value of a given gait parameter.^{38, 49, 50, 51, 52, 53, 54, 55, 56} Impairment in the ability to maintain a steady gait, with minimal stride-to-stride variations, is not only closely related to postural instability and fall risk; it is largely independent of gait speed and healthy-aging effects. Picture the drunken sailor (or perhaps a random walker) as he swaggers back and forth, unable to maintain a steady gait. He walks with high stride-to-stride variability, with his center of gravity frequently moving away from the base of support in an uncontrolled fashion. A small perturbation can further challenge the dynamic control of balance and send him to the floor. In this sense, gait variability may be used as a marker of unsteadiness, instability, and fall risk. Of course, this analogy is somewhat simplistic and not all variability is a mark of poor locomotor control. As in heart rate variability, some variability may reflect adaptability and be beneficial (see Li et al. and related discussions^{57, 58, 59, 60, 61}). Still, it appears that in the short term, relatively increased stride-to-stride variability of gait is generally a sign of diminished control and poor locomotor health. As shown further below, e.g., see Table 2, PD generally increases variability while therapeutic interventions generally decrease short-term variability. Nonetheless, at longer-time scales, some variability is a sign of health; in healthy subjects, variability tends to increase with the time scale. This relates to the scaling of the stride-to-stride fluctuations as discussed further below with reference to the fractal properties of gait.

Table 2.

Effects of various manipulations and interventions on gait dynamics in patients with PD. RAS: rhythmic auditory stimulation. Yes and No refer to statistically significant changes (p<0.05) compared to a control group (first two rows) or baseline state (other entries).

	Average stride length (gait speed)	Gait variability	DFA fractal scaling index
Altered in early, naïve PDa	Yes	Yes	No
Altered in more advanced PDb c, c	Yes	Yes	Yes
Improves in response to RAS set to usual stepping rated	Yes	No	No
Improves in response to RAS at 10% higher than usual stepping rated	Yes	Yes	No (became more random)
Improves while walking on treadmill set to usual-walking gait speede	No (since gait speed matched)	Yes	No
Improves while walking with a walkere	Yes	No	No
Improves in response to MPHf (i.e., Ritalin)	Yes	Yes	Yes
Further altered in response to easy dual task (phoneme monitoring and serial 3 subtractions)g	Yes	Yes	No
Further altered in response to difficult dual task (serial 7 subtractions)g	Yes	Yes	Yes

^aReference ⁴⁶.

^bReference ⁶².

^cAs reported in Hausdorff et al. (Ref. ⁶²) and confirmed on the analysis of data pooled from several studies (Refs. ⁴⁰, ⁴⁷, ⁶³, ⁶⁴). See also http:∕∕www.physionet.org∕physiobank∕database∕gaitpdb.

^dReference ⁶³.

^eReference ⁴⁷.

^fReference ⁶⁵.

^gReference ⁴⁰.

For further details regarding the protocol and study populations, see the references that are cited. Note that in most of these studies, the focus was different and the fractal behavior was not previously reported. It is also important to keep in mind that in these studies, gait was generally examined for only a minute or two, restricting the scaling range that can be examined and robust estimates of the long-range correlations.

As described above, gait variability apparently predicts falls in older adults with “idiopathic falls” and in other patients groups.^{38, 50, 51, 54, 56, 66} To better understand the effects of PD on walking, especially gait instability, and the factors that contribute to gait variability and fall risk in PD, we studied 32 subjects (23 men) with idiopathic PD in order to evaluate (1) the relationship between gait variability, fall history, and other Parkinsonian features and (2) the effect of levodopa on gait variability, fall frequency, and these relationships in subjects with PD. 41% of the subjects reported a history of falls. In the “off” state (i.e., more than 12 h after the last intake of anti-Parkinsonian medication when the drug effect is minimal), stride time variability was significantly (p<0.009) larger among fallers compared to nonfallers (see Table 1). Stride time variability significantly improved in response to levodopa—the mainstay of anti-Parkinsonian medications, both in fallers and nonfallers. Nonetheless, in the “on” state (after taking anti-Parkinsonian medication when symptoms are minimal), stride time variability remained significantly increased in fallers compared to nonfallers (Table 1). This difference in the on stride time variability between fallers and nonfallers remained statistically significant. This was true both when comparing subjects reporting on falls to subjects reporting no on falls or subjects reporting off falls compared to subjects reporting no off falls (p<0.005). At the same time, the average stride time was similar in fallers and nonfallers.

Table 1.

Gait variability in PD fallers and nonfallers. Off refers to off anti-Parkinsonian medications [Schaafsma et al. (Ref. ³⁹)].

Gait Measure	Fallers	Nonfallers	p-value
Off stride time variability (CV %)	8.8±7.9	4.2±1.3	0.009
On stride time variability (CV %)	5.0±1.9	3.3±1.6	0.013
Off average stride time (msec)	970±191	996±131	0.520
On average stride time (msec)	992±195	1035±82	0.293

These findings are consistent with other reports of increased stride-to-stride variability among patients with PD.^{37, 48, 67} They also extend the understanding of variability in PD in a number of key ways. It appears that the locomotor control system’s ability to regulate the stride-to-stride variations in gait timing is especially impaired among PD subjects with a history of falls. Further, fall frequency and stride-to-stride variability are not strongly related to other Parkinsonian features such as tremor, rigidity, or bradykinesia, in the off state, the untreated condition when the underlying pathology can be seen. Perhaps this explains, in part, why traditional measures of motor function have not been successful at evaluating fall risk in PD. In addition, these results demonstrate that levodopa has a positive, beneficial effect on stride-to-stride variability and suggest that dopamine networks contribute to the control gait variability. Nonetheless, even in the on state, in the treated condition when motor performance is optimal, the ability to regulate stride-to-stride variability is apparently further increased among PD subjects who fall. This finding suggests the possibility of damaged and exaggerated impairment of “internal clock” function in PD fallers.

Beyond the first and second moments: Fractal analysis of PD gait

Above, we described the changes in gait in PD that are related to the mean stride length or measures of gait variability, typically quantified as the standard deviation (SD) or the coefficient of variation (CV) of the stride time (SD normalized with respect to the first moment, the mean value). While these gait features are important and describe much of the observable changes in PD, they fail to account for and explain a more subtle alteration in the gait of PD. In particular, they do not examine the dynamics of gait, i.e., how gait changes over time, from one stride to the next within a given walk. Two time series can have identical means and variance but with very different ordering or dynamics (e.g., see http:∕∕www.physionet.org∕tutorials∕ndc∕). There are many ways to capture and quantify such properties;^{38, 42, 46, 53, 68, 69, 70, 71, 72, 73, 74, 75, 76} however, in this review, we focus on the fractal property of gait.

In healthy adults, gait appears to be relatively unvarying. That is, during steady-state walking, each stride looks like an identical copy of the one before. To a large degree, this is correct. However, closer examination reveals small and subtle stride-to-stride changes in the gait pattern, even in healthy young adults. For example, the stride time, i.e., the gait cycle duration or the stride interval, fluctuates about its mean (see Fig. 3); for healthy adults, the CV in the stride time is about 2% (the exact number depends on specifics of the protocol and signal processing methods). For a long time, it was thought these small fluctuations are essentially white noise. It was further assumed that there is no physiological meaning in these small stride-to-stride changes, other than those related to the size of the fluctuations, i.e., gait variability, as discussed above. However, a number of studies over the last decade have consistently demonstrated that there is information in the dynamics of these stride-to-stride fluctuations. In fact, not only is the value of the stride time related to neighboring stride times (i.e., short-range scaling), it turns out that a given stride time is related—at least on a statistical basis—to stride times ten and hundreds of strides later. In other words, stride-to-stride fluctuations are not simply random changes about the mean. Instead, they reflect “long-term” memory or long-range correlations in the stride time and suggest that the control of the stride time is regulated, to some degree, over hundreds of strides.

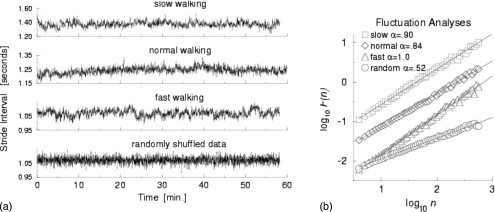
Figure 3.

(a) Example of time series of stride time during 1 h of walking in a healthy young adult at slow, normal, and fast walking rates, and below, after the fast data set is randomly shuffled. (b) While there are subtle effects of gait speed, DFA shows that there is fractal scaling at all three gait speeds. When the data are randomly reordered (shuffled), the slope becomes 0.5, reflecting white noise and an absence of fractal scaling [From J. M. Hausdorff, P. L. Purdon, C. K. Peng, Z. Ladin, J. Y. Wei, and A. L. Goldberger, “Fractal dynamics of human gait: stability of long-range correlations in stride interval fluctuations,” J. Appl. Physiol. 80, 1448 (1996). Copyright ©1996 by American Physiological Society. Reprinted by permission of American Physiological Society]. Data can be downloaded from www.physionet.org. Strictly speaking, Figs. 345 should be plotted as discrete points rather than points joined with lines. The points are joined together as a continuous line, however, since this makes it somewhat easier to visualize the dynamics.

This unexpected fractal-like property of gait can be quantified using a number of different techniques. One popular method is a modified random walk analysis, termed as detrended fluctuation analysis (DFA).^{77, 78, 79} In this case, we calculate a scaling or fractal exponent α that measures how the fluctuation size F(n) scales depending on the time scale or the window of observation (n). If the fractal scaling exponent is >0.5 and less than or equal to 1.0, the time series is said to be self-similar with long-range correlations. An α of 0.5, on the other hand, reflects white noise and an absence of scaling and the fractal behavior. Figure 3 shows an example of the fractal scaling of the stride time in a healthy young adult. Similar results have been observed among groups of healthy young adults. Stride interval fluctuations at one time scale were statistically similar to those at multiple other time scales. Subsequent studies using a variety of different techniques have confirmed the presence of long-range correlations and fractal-like scaling in the gait of healthy young adults (see below), even during slow walking and during running.^{80, 81, 82, 83, 84, 85, 86, 87}

From a neurophysiological control viewpoint, this behavior is of interest because it signifies the presence of long-term, non-trivial “dependence” or “memory” in the locomotor control system. This scale-invariance property has been associated with the survivability of the system in several physical and physiological systems.^{73, 77, 88, 89, 90, 91} One explanation is that this scaling reduces the risk that perturbations lead to “mode locking” or resonance. For example, trees do not possess a characteristic branch size but rather have a distribution of branch sizes, a property that makes them more resistant to storms. Bridges, on the other hand, may have a characteristic length and are therefore more vulnerable if the frequency of the storm matches the natural frequency of the bridge. Similarly, a healthy heart fluctuates at multiple time scales in a fractal-like manner, while alterations in the fractal scaling of the heart beat have been linked to cardiovascular disease, morbidity, and mortality.^{88, 90, 92, 93, 94} So too, a fractal-like gait may be more flexible and adaptable.

In a follow-up work, it was shown that the stride interval exhibited long-range correlations with power-law decay for up to thousands of strides at slow, usual, and fast walking rates in healthy young adults and apparently even during treadmill walking and blindfolded walking.^{47, 79, 95} Long-range correlations also exist during running.^{82, 84} In contrast, during metronomically paced walking, fluctuations in the stride interval are altered.^{79, 86} Thus, the fractal dynamics of the stride interval are normally quite robust, largely independent of speed, and intrinsic to the locomotor system.^{77, 78, 79} Studies have also shown that the fractal-like behavior may not be completely mature even in healthy 7 yr old children whose gait appears perfectly adultlike, that different aspects of stride dynamics mature at different ages,⁹⁶ that the fractal scaling index is significantly lower in the healthy older adults compared to young adults,⁹⁷ and that among older adults with a “higher level gait disturbance,”⁹⁸ the fractal scaling may distinguish fallers from nonfallers. Here, we describe how PD affects gait dynamics and the relationships between stride length, gait variability, and fractal-scaling.

METHODS

Protocols

The results described below are based on the analysis of data reported in several studies. More details regarding the specific methods used in each of these investigations can be seen in the cited references. In general, patients with idiopathic PD, as confirmed by an experienced neurologist, were recruited from outpatient movement disorders clinics and aged-matched, healthy controls were recruited from the community. PD subjects were excluded if they had other disease likely to impact their gait. Similarly, control subjects were included only if they reported normal walking function, had no obvious clinical impairment, did not have significant cognitive impairment, and were free of any neurological disorder or significant clinical history likely to affect their gait (e.g., stroke, Alzheimer’s disease). All subjects provided informed written consent. Subjects walked on level ground for 2–6 min (depending on the specific protocol) at their normal pace in an isolated hallway under usual lighting conditions. Subjects were told to turn around and continue walking when they reached the end of the hallway. Study subjects were not aware of the specific questions of the investigations.

Assessment of gait dynamics

Methods for quantifying gait variability and evaluating gait dynamics have been detailed elsewhere.^{38, 50, 97} Briefly, to measure the gait rhythm and the timing of the gait cycle, force sensitive insoles were placed in or under the subject’s shoe. The sensors produce a measure of the force applied to the ground during ambulation. Typically, a small, lightweight (5.5×2×9 cm³; 0.1 kg.) recorder was worn on the ankle (or lower back). An onboard analog-digital converter sampled the output of the footswitches (e.g., at 300 Hz) and stored the digitized force record. Subsequently, the digitized data were transferred to a computer workstation for analysis using software that extracts the initial and end contact time of each stride.⁹⁹ From the force signal, the stride time or duration of the gait cycle (time from initial contact of one foot to subsequent contact of the same foot) and swing time (time when one foot is in the air) were determined for each stride during the walk by applying a previously validated algorithm that locates initial contact times (and hence the stride time) and end contact time (for swing time) by finding large increases and changes in the slope of the force.⁹⁹

As an aside, we note that historically more research has focused on the dynamics of temporal parameters of gait, e.g., the stride and swing time, in part because they can readily be quantified accurately and reliably as described above or by using other “wearable” sensors (e.g., accelerometers). Although there have been some efforts aimed at measuring stride length on a stride-by-stride basis in ambulatory settings (see, for example, the work by Terrier et al.⁸⁷ and Terrier and Schutz¹⁰⁰), accurate and reliable long-term recordings of stride length remain a technological challenge.

To focus on the assessment of the dynamics of continuous, “normal” walking and each subject’s “intrinsic” dynamics and to ensure that the analysis was not influenced by atypical strides (e.g., the turning at the end of the hallway), a median filter was applied to each subject’s time series to remove data points that were three SDs greater than or less than the median value.^{38, 50} Subsequently, stride time variability, the magnitude of the stride-to-stride fluctuations in the gait cycle duration, and swing time variability were calculated by determining the CV of each subject’s stride time and swing time, respectively.^{38, 50} As mentioned above, stride-to-stride variability reflects gait unsteadiness and arrhythmicity and has been shown to prospectively predict falls.^{38, 50, 51, 54, 101, 102}

The CV and related measures quantify the magnitude of the stride-to-stride variability but are not sensitive to changes in the ordering of the stride times or the dynamics. Randomly reordering a time series will not affect the magnitude of the variability but may dramatically alter the dynamic properties. To quantify how the dynamics fluctuate over time during the walk, we applied DFA to each subject’s sequence of stride times.^{77, 78, 97, 103, 104} As discussed above, DFA was designed for evaluating the fractal scaling exponents and the degree of randomness in highly nonstationary physiological data. If the data are “well behaved” (e.g., the effects of trends are small), the DFA scaling index is linearly related to other fractal scaling indices such as the Hurst exponent and scaling indices derived from the autocorrelation function or Fourier analysis (i.e., 1∕f scaling).^{100, 103, 105, 106} However, DFA eliminates trends in the time series and therefore can avoid the spurious detection of correlations that are artifacts of nonstationarities. DFA is a modified random-walk analysis that makes use of the fact that a long-range (power-law) correlated time series can be mapped to a self-similar process by simple integration. Methodological details have been provided above and elsewhere.^{77, 78, 97, 103, 104} Very generally, healthy physiologic systems have fractal scaling indices of around 0.8–1.0 (depending on the specifics) and values closer to 0.5 reflect a deviation from the healthy state and more random, less ordered dynamics.^{77, 78, 97, 103, 104} Previous work has shown that the fractal scaling index provides a measure of subtle changes in underlying gait dynamics; this measure separates healthy young from healthy older adults, even when the magnitude of the stride-to-stride variability is unchanged.⁹⁷

A number of previous studies have examined the properties of the DFA, in general,^{103, 105, 107, 108} and its application to gait, more specifically.^{77, 78, 97, 104} It is helpful to note that DFA is relatively unchanged if a small number of points are deleted;¹⁰⁷ thus, the automated removal of the turns and stitching together of the time series generally do not have a large effect on DFA derived scaling indices. Similarly, DFA scaling of the stride time is relatively independent of the data collection method. Ivanov et al.⁷⁴ recently reported that DFA derived scaling indices of gait obtained using an accelerometer when healthy adults walk on a very long straight path are similar to those of healthy subjects who walked on an oval track while wearing footswitches.⁷⁹ Similar scaling values were found by West and Griffin¹⁰⁹ even though another experimental method was used (i.e., timing based on knee angles), the walking track was a large square path, and the analytical approach used was different. Others have also confirmed the existence of long-range scaling in gait using different analytical techniques.^{86, 110, 111} Appropriate filtering and preprocessing need to be applied. For a further discussion of the effects of turns on gait, for example, see the article by Jindrich and Qiao¹¹² in this volume and related studies by Huxham et al.^{113, 114} and Strike and Taylor.¹¹⁵

RESULTS

Changes in fractal properties of gait in PD

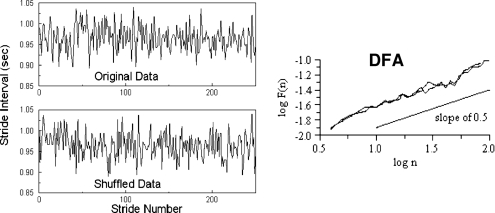
What happens to the long-range correlations of gait in patients with PD? Perhaps not too surprisingly, among patients with PD, the memory in gait “breaks down” and the stride-to-stride fluctuations in gait now become very similar to white noise or random fluctuations. Figure 4 shows an example of the times series of the stride time of a patient with PD, before and after the time series is randomly shuffled, artificially removing any memory and correlations. Visually, there is no difference between the original time series and the randomly shuffled time series. The DFA scaling exponent becomes close to 0.5 (the value for white noise; an absence of long-range correlations). Similar results were observed for a group of patients with PD⁶² demonstrating that the long-range scaling and fractal-like behavior are reduced and the stride-to-stride fluctuations become more random.

Figure 4.

Gait rhythm dynamics in a patient with PD. On the left, time series are shown before (original) and after random reordering of the data. Note that the temporal structure of the time series looks similar before and after reordering. This impression is confirmed using DFA (right). The slopes for the original data and the reordered data set are both close to white noise (0.5).

This breakdown of the long-range correlations could be interpreted in several different ways. One simple explanation for this finding is that among patients with PD, gait looses its automaticity and fluidity. To some degree, each stride starts a new process, unlinked and unrelated to the previous stride. Hence, the memory of the locomotor control system is not long term and fractal-like, but instead it becomes close to zero. In support of this idea, statistical models of the long-range correlations of gait and their breakdown have shown that many of the observed changes can be explained by the strength of the coupling among neighboring neural networks and a loss of neurons.^{69, 86, 116}

To better understand the relationship between average stride length, gait variability, and the fractal-like property of gait in PD, here we briefly examine the effects of different conditions and interventions on these gait features to see how each reacts to the different states. Table 2summarizes these findings. As further detailed, this summary underscores the idea that these three aspects of gait do not always respond in parallel.

Early, mild PD

The gait changes in advanced PD have been relatively well studied; however, much less is known about the alterations in gait in the initial stages of the disease. Only a few quantitative investigations of patients with PD included patients who were not yet treated with anti-Parkinsonian medications (de novo PD).¹¹⁷ To better understand the pathophysiological mechanisms that influence gait in PD, it is helpful to identify the early alterations, prior to and without the influence of any modification by anti-Parkinsonian treatments. To this end, we examined the gait of 35 patients with idiopathic PD (mean age: 60 yr) who were in the early stages of the disease (Hoehn and Yahr stage: 1.8±0.5) and were not yet treated with any anti-Parkinsonian medications and 22 age and sex-matched healthy controls.⁴⁶ The patients walked more slowly and with reduced swing times while also exhibiting increased left∕right swing asymmetry and marked inconsistencies in the timing of gait, i.e., increased variability compared to controls. In contrast, the fractal scaling exponent was apparently not significantly different from that seen in the controls. These findings indicate that in de novo PD, an altered gait pattern is already present, even though dramatic changes in the gait pattern may not yet be apparent visually (e.g., fairly intact gait speed). These alterations are not just the side effects of treatments or the result of changes in nondopaminergic pathways. Rather, there is evidence for motor programming deficits in gait, as revealed by reduced stride length and increased gait variability and asymmetry in timing. PD apparently impinges on the generation and regulation of a consistent gait rhythm, even early in the course of the disease, when observed alterations are not the result of any pharmacologic treatment and are largely confined to dopamine depletion in the nigro-striatal pathway. However, in this early stage, the self-similar behavior of the stride-to-stride fluctuations is largely intact, suggesting that this feature only becomes impaired later in the disease process. It remains to be seen if compensatory mechanisms help to retain this gait property early in the disease process or if the basal ganglia damage in the early stages is not yet sufficient to impact on the fractal-like scaling.

Effects of rhythmic auditory stimulation

Rhythmic auditory stimulation (RAS) is a promising means of improving gait in PD. By providing an external clock that helps to set the pace and comes in place of the impaired internal rhythmicity in PD, RAS can apparently improve, at least in the short term, many of the spatiotemporal features of gait in patients with PD.^{118, 119, 120, 121} When using RAS, administered in the form of a metronome, gait speed and stride length generally increase (become more normal) in PD patients, both in the on and off states.¹²² When RAS is administered at a rate either equal to the patients’ baseline step rate (cadence) or 10% higher, double support time is reduced and stride length increases.¹²³ Similarly, when RAS is set higher than the usual step rate, gait speed typically increases.^{124, 125} The effects of RAS may also carry over to none-RAS walking suggesting long-term retention effects. For example, after administration of RAS to PD patients for 3 weeks, an increase in gait speed and stride length has been observed, even when walking without stimulation.¹²⁶

Recently, we examined the effects of RAS on gait variability in patients with PD and age-matched healthy controls.⁶³ When RAS was set to the subject’s usual-walking rate, stride length and gait speed increased in PD patients. However, variability, which was relatively higher in the patients with PD compared to controls, did not improve significantly in response to RAS at this rate. When the RAS was set 10% higher than usual-walking pace, stride length and gait speed increased, compared to none-RAS walking. In addition, variability significantly decreased. Interestingly, an intriguing carryover effect was observed: 15 min after walking with RAS at 10% higher than the usual-walking cadence, stride length and variability were still significantly better than the baseline values. Surprisingly, however, the (short-range) fractal scaling index was relatively unresponsive to RAS. It was not different from baseline values in all other conditions, except that it became lower and more random 15 min later, despite improvement in stride length and the reduction in variability in this condition. Among the healthy control subjects, RAS had no significant effects on stride length, variability, or the DFA scaling exponent.

Effects of treadmill walking

Recent work also highlights the potential of using a treadmill to improve Parkinsonian gait.^{127, 128} The rationale is similar to that of RAS. Perhaps the treadmill can be used as an external cue to help restore, retrain, and∕or augment the impaired “pacemaker.” We examined the influence of treadmill walking on gait variability and dynamics in 36 patients with PD (Hoehn and Yahr stage 2–2.5) and 30 age-matched controls.⁴⁷ Subjects walked three times for 2 min each: (1) walking on level ground (unassisted), (2) walking on level ground while using a walker, and (3) walking on a treadmill. Consistent with previous findings, on level ground, stride length and gait speed were smaller among the patients with PD compared to the controls, stride time variability and swing time variability were significantly increased in the patients compared to the controls, and the fractal scaling index was smaller (i.e., more random fluctuations) in the patients compared to the controls. In both groups, the use of a walking aid did not significantly affect stride time variability or swing time variability, but the treadmill—which was set to each subject’s walking speed on the ground—reduced stride time variability and swing time variability in the patients (p<0.0001) and in the controls (p<0.02). Despite these improvements in variability, the fractal scaling index did not change when walking on the treadmill in patients with PD. It is also noteworthy that when walking with a walking aid on level ground, gait speed improved in the patients, compared to walking without the aid, but there was no effect on the fractal scaling or variability. These results indicate that during treadmill walking, PD subjects are able to walk with a less variable and more stable gait, i.e., in support of the idea that a treadmill can be used as a pacemaker. However, the fixed gait speed does not positively affect the fractal scaling, further demonstrating the independent nature of gait speed, variability, and the self-similar correlations in gait.

Dual tasking effects

The performance of another task while walking, i.e., dual tasking, may alter different aspects of the gait pattern. When asked to walk and perform a dual task, healthy young adults usually reduce their gait speed, while other aspects of gait are generally not affected.^{129, 130} Healthy older adults reduce both their gait speed and the duration of swing, increasing support time (stance), but gait variability is not dramatically affected.^{129, 131} In response to dual tasking, PD patients walk more slowly and with a reduced swing time.^{131, 132} In addition, gait variability⁴⁰ and asymmetry⁴⁵ increase and bilateral coordination of gait decreases, much more than seen in age-matched controls.¹³³ We examined 30 patients with idiopathic PD (mean age: 70.9 yr) with moderate disease severity (Hoehn and Yahr 2–3) and 28 age and gender-matched healthy controls⁴⁰ to assess the effects of dual tasking on gait dynamics in PD. Gait variability was measured under single and dual tasking conditions (with different levels of cognitive loading). Compared to the controls, gait variability was significantly increased in the PD group under all conditions (p<0.01). Further, as the degree of cognitive loading increased, so did gait variability, compared to usual walking, but only in PD patients (e.g., see Fig. 5). Thus, the gap between the gait variability of the healthy elderly controls and the patients grew as the cognitive loading level increased. In contrast, gait speed responded similarly in both groups; as “cognitive loading” increased, gait speed decreased. The effects of the fractal scaling index were apparently dose dependent in the patients. The fractal scaling index did not change significantly in response to the two relatively simple dual tasks (e.g., phoneme monitoring and serial 3 subtractions); however, during serial 7 subtractions, the scaling index became significantly reduced (more random, less like controls). Among the healthy controls, the DFA scaling index was not significantly different under any of the conditions. These findings indicate that dual tasking has different effects on gait speed, variability, and the fractal scaling index in healthy controls and in patients with PD.

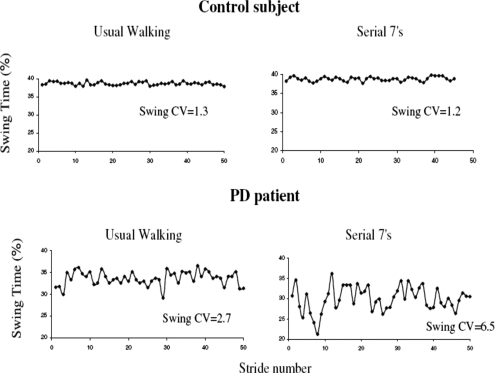
Figure 5.

Example of swing time series from a patient with PD and a control under usual walking conditions and when performing serial 7 subtractions. Under usual walking conditions, variability is larger in patient with PD (CV=2.7%) compared to the control (CV=1.3%). Variability increases during dual tasking in the subject with PD (CV=6.5%) but not in the control (CV=1.2%) [From G. Yogev, N. Giladi, C. Peretz, S. Springer, E. S. Simon, and J. M. Hausdorff, “Dual tasking, gait rhythmicity, and Parkinson’s disease: Which aspects of gait are attention demanding?,” Eur. J. Neurosci. 22, 1248 (2005). Copyright ©2005 Federation of European Neuroscience Societies. Reprinted by permission of Blackwell Publishing].

Effects of methylphenidate

As a final example of the effects of an intervention on gait dynamics in PD, we extend our analysis of the effects of methylphenidate (MPH) (commonly known as Ritalin) on patients with PD. MPH is a central nervous system stimulant derived from amphetamine that works as a potent inhibitor of catecholamine reuptake.¹³⁴ It is widely used to treat attention deficits in children and adults with attention deficit hyperactivity disorder. Because dopamine reuptake plays an important role in the regulation of dopamine in the synapse and the hypodopaminergic state is at the basis of much of the Parkinsonian syndrome, it has been suggested that MPH can improve motor function in PD.^{135, 136, 137} Given the decline in attention abilities in PD and the putative reliance of a steady gait on this cognitive domain (recall the profound dual tasking effects), we hypothesized that MPH may also improve gait and reduce fall risk in patients with PD.⁶⁵ Twenty-one patients with PD were studied before and 2 h after administration of a single dose of 20 mg MPH. In response to MPH, cognitive function, in particular, attention and executive function, significantly improved, while memory and visual-spatial performance were unchanged. Gait speed, stride time variability, and timed up and go times (demonstrated measures of fall risk) also significantly improved. In addition, the fractal scaling index also became larger (i.e., more “healthy”) in response to MPH. One interpretation of these findings is that an intervention that enhances attention (a cognitive domain) positively impacts gait speed, gait variability, and the fractal nature of the stride-to-stride fluctuations in patients with PD. Of course, it is possible that other mechanisms are responsible for the observed changes in response to MPH.

Associations among the different gait features

One question that has often piqued the interest investigators of gait dynamics is the role of stride length (and∕or the very closely related gait speed).^{52, 53} To paraphrase, if stride length is a fundamental property of gait, perhaps other features depend, to a large degree, on this characteristic. Table 3 summarizes the associations between different gait features among 118 patients with varying degrees of PD (subjects taken from previous reports^{40, 46, 47, 63}). A strong correlation between gait speed and stride length is seen, as expected. Measures of gait variability are moderately associated with gait speed and stride length, i.e., subjects who had a higher gait speed tended to have lower stride-to-stride variability; however, less than 25% of the variance in variability could be explained by stride length. Further, the fractal scaling index was not significantly correlated with variability, gait speed, or stride length. We also confirmed that compared to age-matched healthy controls (n=90), all of these measures were significantly altered in the patients with PD (p<0.005).

Table 3.

Correlations among different gait measures in 118 patients with PD. Data available at www.physionet.org∕physiobank∕database∕gaitpdb.

		Stride length	Gait speed	Stride time variability	Swing time variability	DFA fractal scaling exponent
Stride length (average)	Pearson correlation	1.000	0.899a	−0.262a	−0.409a	0.129
	P-value		0.001	0.004	0.001	0.164
Gait speed (average)	Pearson correlation	0.899a	1.001	−0.436a	−0.474a	0.109
	P-value	0.001		0.001	0.001	0.239
Stride time variability (CV)	Pearson correlation	−0.262a	−0.436a	1.001	0.677a	0.128
	P-value	0.004	0.001		0.001	0.167
Swing time variability (CV)	Pearson correlation	−0.409a	−0.474a	0.677a	1.001	−0.042
	P-value	0.001	0.001	0.001		0.649
DFA fractal scaling exponent	Pearson correlation	0.129	0.109	0.128	−0.042	1.001
	P-value	0.164	0.239	0.167	0.649

^aCorrelation is significant at the 0.01 level (two tailed).

DISCUSSION

This review highlights some of the issues that are related to gait dynamics in PD to spark an interest and motivate future investigations. The interested reader is referred to other papers for additional details about fractal analyses and the application of this type of approach to physiology, pathophysiology, and gait, as well as other reports that describe changes in gait among PD patients and in other populations.^{6, 36, 48, 62, 73, 77, 78, 79, 91, 138, 139} The review was intended to underscore the point that the continuous gait changes observed in patients with PD should be viewed on multiple levels. The reduced (average) stride length seen in patients with PD is one critical aspect. Increased stride-to-stride variability is a second. Therapeutic interventions that improve these gait properties will likely have a profound, positive impact on Parkinsonian gait, fall risk, and the health-related quality of life of these patients. Nonetheless, if we strive for a full understanding of the gait changes in PD and optimal interventions, we should also consider the changes in a third gait feature: the fractal properties of gait.

The changes in the fractal-like scaling in patients with PD, with respect to healthy adults, and the effects of the different interventions on the stride dynamics (recall Table 2) can be interpreted in several different ways. First, it is important to keep in mind that the existence of power-law scaling and long-range correlations places a number of restrictions on the types of models that can be used to explain the observed gait dynamics, and thus its changes with PD.^{69, 81, 109, 116} In turn, these restrictions have important implications for understanding the underlying neurophysiology and the effects of neurodegeneration. Second, many different explanations have been put forth to account for the long-range correlation scaling in various physiologic signals and systems.^{73, 77, 91, 140, 141} For example, Goldberger et al.^{77, 142} argue that the complex variability associated with long-range (fractal) correlations in physiologic systems reflects nonlinear complexity and adaptability while alterations with aging and∕or disease reduce the adaptability and the capacity to respond to unpredictable stimuli and stresses. This idea is related in part to studies of physical systems near a critical point.^{91, 103} The fractal-behavior promotes adaptability. Long-range correlations serve as a (self)-organizing mechanism for highly complex processes that generate fluctuations across a wide range of time scales, and the absence of a characteristic scale inhibits the emergence of highly periodic behaviors, which would greatly narrow functional responsiveness.⁷⁷ Thus, loss of scaling in the gait of patients with PD, as reported here, may reflect, in part, less flexible neurobiologic underpinnings. Similarly, West¹⁴³ suggests that allometric properties such as scaling in physiologic signals confer robustness. Conversely, some have suggested that correlation properties are merely a by-product of the fact that feedback occurs on multiple levels or that simple biomechanical properties cause the observed scaling in gait.¹⁴⁴ These theories are not consistent with the observed results and the effects of various “stresses” on long-range correlation properties; the stresses do not directly change biomechanics, yet fractal scaling may be altered (e.g., Table 2).¹⁴⁵

More specifically with regard to gait dynamics, several explanations have been put forth. Vaillancourt and Newell¹⁴⁶ suggest a limit cycle attractor-type process accounts for stride-to-stride changes in walking. This notion is, however, not fully consistent with the observed data.¹⁴² Based on the findings of long-range correlations in gait, our group proposed a reconsideration of classic central pattern generator oscillatory models underlying the control of locomotion and proposed a stochastic model of gait dynamics which consists of a random walk on a correlated chain, where each node of the chain is assumed to be a neural center and where correlations reflect, in part, connections among neural pathways.^{69, 116, 142} This random walk generates a fractal process and many of the changes that have been observed with aging and disease. West and co-workers^{80, 81, 106, 147} modified this model further and developed a supercentral pattern generator (SCPG) that reproduces both fractal and multifractal properties of the gait dynamics. In the present volume, Scafetta et al.¹⁰⁶ provide a comprehensive review of this model and its application to gait. They suggest that the model output changes with “stress condition” (e.g., natural and∕or psychophysical) and as a function of the evolution of the system (e.g., aging, maturation, disease). Based on findings in Table 2, one could speculate that advanced PD causes sufficient changes to the neural control system to reduce the scaling of gait dynamics, perhaps by altering the correlations between the neuron centers of the stochastic CPG, and that MPH, for example, alleviates stress or enhances the ability to cope with or compensate for underlying changes, thereby strengthening the healthy correlations. Additional modeling work and simulations based on Table 2 and SCPG-like models, perhaps combined with working models of the basal ganglia and its changes with PD, may help generate a more complete, detailed description of the mechanisms that influence gait dynamics and their changes with this common neurodegenerative disease.

More generally, the present analyses support the results of previous studies which suggested that the long-range correlations in gait are related to central nervous system mechanisms.^{79, 148} For example, Gates and Dingwell¹⁴⁸ observed that scaling indexes were unchanged in patients with peripheral disease. Similarly, here we find that methylphenidate, a pharmacologic agent that primarily enhances higher-level central nervous system function, improves the correlation behavior in patients with PD. Further, a difficult dual task, i.e., significant cognitive loading, diminishes scaling. All of the findings summarized in Table 2 are consistent with the idea that fractal-like scaling has higher-level origins.

Over the last decade there has been growing awareness that PD is not a simple disease of motor control. Rather it is becoming increasingly apparent that this is a complex neurodegenerative process that affects multiple systems, deteriorating at different rates, and controlled by distinct neural pathways.^{149, 150, 151} A challenge to future studies will be to map the alterations in stride length, gait variability, and fractal scaling, and their changes as the disease progresses to different stages and pathways that cause PD symptoms. One clear message already emerges from this review about the origins of gait disturbances in PD: the neural networks and other pathologic mechanisms responsible for these alterations overlap, but at the same time, they are also quite distinct. Stride length, gait variability, and fractal scaling are all altered in PD. However, their behavior is not identical and they do not reflect the same properties, underlying neural control mechanisms or pathology. For example, as seen in Table 2, it is likely that stride length and variability are disturbed relatively early in the disease process, while fractal scaling remains intact. There are many ways to interpret the details of Tables 2, 3. Perhaps the tuning of different models of gait dynamics can be used to help explain the observed findings.^{69, 80, 81, 86, 116} As discussed above, we leave the challenge of unraveling the exact mechanisms behind the different responses to therapeutic interventions and the interrelationships among the distinct gait features to the reader and future work.

For the sake of brevity and to maintain a focused presentation, the present report examined only a small subset of the potentially relevant gait parameters and a few dynamical measures. Many different aspects of gait could be examined with a dynamical approach using the techniques described as well as a long list of other analysis methods.^{38, 53, 74, 152} Hopefully, the present review and update will motivate additional studies and analyses of gait in PD. The results of this update demonstrate that models that attempt to simulate and mimic the changes in gait in PD should also consider the changes in the fractal scaling and the effects of different interventions on multiple gait characteristics. Similarly, a therapy that is able to address and restore all three aspects of gait may prove to be the most optimal. Along these lines, we note anecdotally, recent preliminary results which suggest that auditory stimulation which includes small fluctuations about the mean, and not a simple constant pacing, may have more beneficial effects on the gait of patients with PD, compared to purely RAS.¹⁵³ Similarly, while the constant pacing of a treadmill has been shown to improve certain aspects of gait automaticity in PD,^{47, 127, 128} one can speculate that the ideal rehabilitation therapy should include widely varying treadmill speeds and gait cadences in order to make the control system more flexible and restore some of the “adaptability” and complexity to the system. Perhaps in the future, optimal treatments of gait in PD will make use of this idea in order to maximize the restoration of gait. A similar concept was suggested with regard to the control of heart rate with pacemakers more than a decade ago;¹⁵⁴ however, treatment of movement disorders has not yet adapted this concept.