Abstract
A simulation formalism for the nonlinear response of vibrational excitons is presented and applied to the OH stretching vibrations of neat liquid H2O. The method employs numerical integration of the Schrödinger equation and allows explicit treatment of fluctuating transition frequencies, vibrational couplings, dipole moments, and the anharmonicities of all these quantities, as well as nonadiabatic effects. The split operator technique greatly increases computational feasibility and performance. The electrostatic map for the OH stretching vibrations in liquid water employed in our previous study [A. Paarmann et al., J. Chem. Phys. 128, 191103 (2008)] is presented. The two-dimensional spectra are in close agreement with experiment. The fast 100 fs dynamics are primarily attributed to intramolecular mixing between states in the two-dimensional OH stretching potential. Small intermolecular couplings are sufficient to reproduce the experimental energy transfer time scales. Interference effects between Liouville pathways in excitonic systems and their impact on the analysis of the nonlinear response are discussed.
INTRODUCTION
Coherent multidimensional spectroscopies1, 2, 3 have most recently become a valuable tool for the study of dynamics in complex systems. As the optical equivalent of two-dimensional (2D) nuclear magnetic resonance,4 both electronic and vibrational 2D coherent spectroscopies allow investigations of structural dynamics, coupling, dephasing, and relaxation mechanisms. So far, only a few 2D electronic spectroscopy studies have been reported.5, 6, 7, 8 Vibrational 2D spectroscopy, on the other hand, usually referred to as 2D infrared (2DIR) spectroscopy, has been successfully used to study a wide range of systems, such as peptides,9, 10, 11, 12, 13, 14, 15, 16, 17 proteins,18, 19, 20, 21 DNA,22, 23, 24 and neat liquids.25, 26, 27, 28
In general, the analysis of 2D spectra is complicated by the large linewidth of the transitions. The resulting overlap and interference between different peaks in the spectra often greatly distort the peak shapes, preventing simple extraction of the dynamic parameters of interest. The 2D spectra become even more convoluted in systems with pronounced intermode couplings which lead to delocalized excitations or formation of excitons. Some experimental approaches have been developed to amplify features of interest and reduce complexity of the spectra.29, 30 Still, high level theoretical modeling is required in order to reliably extract physical and chemical information from these data.
Initially, most 2D modeling approaches relied on the assumption of Gaussian statistics for transition frequency fluctuations of spatially localized vibrational or electronic modes. Then, the cumulant expansion can be truncated at second order31 and all nonlinear spectroscopic observables are characterized by the frequency correlation function (FCF) C(t)=⟨δω(t)δω(0)⟩. The FCF is usually obtained from molecular dynamics (MD) with various strategies for mapping the MD observables, e.g., electric fields, onto the transition frequencies.16, 32, 33, 34 This method was extended to include bath modulation of the transition dipole moments (non-Condon effects).35 In some special cases, approximate descriptions can be found to describe non-Gaussian statistics of the transition frequency fluctuations.17
Several methods have been developed to treat intermode coupling leading to energy transfer,16 chemical exchange,36 and formation of excitons.24, 37, 38 As long as the charge densities of the coupled states do not overlap, the delocalized states can be described as Frenkel excitons.39 When the site frequency fluctuations are small compared to the intermode couplings, one can describe the system in a fixed exciton basis, with perturbative description of the energy transfer between exciton states.34, 39 If the fluctuations and couplings are comparable, exciton transport is a nonadiabatic process and multiple state crossing prevents the use of that basis.15
Numerical integration of the Schrödinger equation16, 28, 36 (NISE) is well suited to describe such complex dynamics. The major drawback of the method has so far been the high computational cost since it required diagonalizing the two-particle Hamiltonian. For that reason, the method was limited to either linear response calculations or small systems. In Sec. 2, we show that by introducing the split operator technique28, 40 the computational cost of NISE can be dramatically reduced enabling this method to be applied to a wide range of molecular systems.
The first application of this approach was made to model the 2DIR spectrum of the OH stretching vibration in neat liquid H2O.28 Our recent experimental studies26 demonstrated that the OH stretching vibration shows extremely fast dynamics with no clear separation of time scales between the dephasing, energy transfer, and relaxation dynamics. Even more interesting, it was observed that the OH vibrational modes have a pronounced excitonic character at temperatures near freezing. In Sec. 3, we report on the simulations of the 2DIR response of liquid water. We present an ab initio electrostatic map of the OH stretching vibrations in water, as well as nonlinear response calculations that are in good agreement with experiment.
In the last section (Sec. 4) we discuss interference effects between the different Liouville pathways as they appear in simulations of the nonlinear response of excitons. These prevent simple interpretation and analysis of the individual pathways.
NONLINEAR RESPONSE OF VIBRATIONAL EXCITONS
In the following we present our NISE model which employs the split operator technique to calculate the third order optical response of vibrational excitons. This method can also be adapted straight forwardly to model electronic excitations.
The fluctuating Hamiltonian and dipole operator
We consider a system of M coupled vibrational oscillators described by the Hamiltonian
| (1) |
where describes the vibrational system and contains the interaction with the optical fields. The vibrational system is described by the effective Hamiltonian (we set ℏ=1 throughout this paper):
| (2) |
All bath interactions are incorporated into the Hamiltonian parameters. The first two terms describe the free harmonic system, where ωm(τ) is the fundamental transition frequency of mode m, is the Boson creation (annihilation) operator for mode m, . The second term contains the intermode coupling Jm,m′. The last term describes quartic anharmonicities V. Most commonly, only diagonal anharmonicities of local overtones Vmm,mm are considered. These give the anharmonicity shift between the 0→1 and 1→2 transitions. However, the above Hamiltonian allows for a description of combination band frequency shifts Vmn,mn and coupling anharmonicities (off-diagonal elements of V) as well.
The dipole operator is given by
| (3) |
Here, μm is the fundamental 0→1 transition dipole moment of mode m, and Δμ represents the dipole moment anharmonicities. In the Condon approximation, the time averaged amplitudes ⟨∣μ∣⟩τ are used, neglecting fluctuations and anharmonicities of the transition dipole moments. Non-Condon effects can be included35 by explicitly treating the bath influence and time dependence of μm. The second term in Eq. 3 allows for treatment of anharmonicities of the local 1→2 transition dipole moments Δμmmm, as well as anharmonicities of dipole moments involving intermode combination bands (other elements of Δμ).
The third order vibrational response
The third order contribution to the system’s polarization induced by the laser fields can be written as31, 38
| (4) |
where S(τ3,τ2,τ1,τ0) is the third order response function.
| (5) |
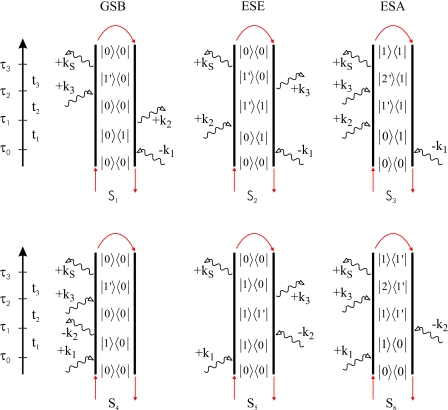
Sorting out the possible time orderings and invoking the rotating wave approximation, S can be written in terms of Liouville pathways for the different signal directions. We shall focus on kI=−k1+k2+k3 and kII=k1−k2+k3, also referred to as rephasing and nonrephasing pathways, respectively, represented by the double sided Feynman diagrams given in Fig. 1. The respective Green’s function expressions for the kI pathways (S1,S2,S3) and the kII pathways (S4,S5,S6) are given in Eq. 6. These diagrams are often referred to as ground state bleach (GSB) (S1 and S4), excited state emission (ESE) (S2 and S5), and excited state absorption (ESA) (S3 and S6).
| (6) |
Figure 1.
Double sided Feynman diagrams for the kI(S1−S3) and kII(S4−S6) phase matching conditions, see text. The red arrows indicate the closed time path loops used to calculate the contributions from these diagrams.
The Green’s functions propagate the ground, the singly excited, and the doubly excited state, respectively, from τa to τb. The dipole excitation and de-excitation operators and are derived from Eq. 3 and are given by
| (7) |
The third order response functions for the two techniques are given by the sum of the respective diagrams:
| (8) |
Harmonic systems [V≡0 in Eq. 2 and Δμ≡0 in Eq. 3] are linear; these contributions then cancel exactly and the signals vanish. The finite nonlinear response is induced by the anharmonicities V and Δμ.
The response functions in Eq. 6 are evaluated by a series of dipole operations and propagations of the many body system as indicated by the closed time path loops in Fig. 1. The challenging tasks in these operations are the propagations, in particular, for doubly excited states in diagrams S3 and S6.
Direct numerical propagation of vibrational excitons
All propagators are calculated using NISE:15, 28, 41
| (9) |
We calculate infinitesimal propagators , and propagate step wise. Setting the ground state energy to zero, the ground state propagator is simply unity. We can now express in the local basis for the singly (U(1)) and doubly (U(2)) excited states as given in Eq. 10,
| (10) |
where and . For not too large systems, U(1) can be calculated exactly by diagonalizing the single particle Hamiltonian , where the third term in Eq. 2 does not contribute.
However, propagation of doubly excited states ∣m,n⟩ is more challenging due to the large size of the symmetrized two-particle basis being M(M+1)∕2. For M≳40, direct diagonalization and data storage is computationally too expensive. Instead, we use the split operator method28, 40 for calculating these matrix exponentials. We split the Hamiltonian into the harmonic part [first two terms in Eq. 2] and anharmonic part (third term) and calculate the matrix exponential as given in Eq. 11.
| (11) |
The harmonic exponential can be calculated exactly from the single particle propagators, see Appendix A. The anharmonic part is usually small enough to allow first order Taylor expansion. The split operator technique gives good accuracy provided the time steps Δτ are small enough.
We note that in Eq. 11 one can avoid computationally expensive matrix multiplications. Consecutive propagation of the doubly excited states with the two infinitesimal propagators and is significantly faster.
Nonlinear signal calculation
If the optical pulses are short compared to the system dynamics, the nonlinear polarization can be described in the impulsive limit. Then, the third order signal along the kI direction is given by Eq. 12.
| (12) |
The 2DIR correlation spectra are obtained by double Fourier transformation with respect to t1 and t3, with ti=τi−τi−1:
| (13) |
Similarly, the pump probe (PP) signal in the impulsive limit is given by Eq. 14 with t1=0. Then, the rephasing and nonrephasing contributions are identical. The spectrally resolved PP response is given by Eq. 15.
| (14) |
| (15) |
In the impulsive limit, the PP signal is also known as heterodyne transient grating.
The polarization anisotropy (PA) SPA(t2) is calculated from the PP signal with parallel (∥) and crossed (⊥) polarization of the pump and probe pulses. This is done using the respective projections of the transition dipole moment vectors in Eq. 3 in the laboratory frame when calculating the nonlinear response functions. Orientational averaging is done numerically.
| (16) |
Equation 16 can be evaluated for either spectrally resolved or spectrally integrated PP, using the respective PP signals as input.
Similarly, the magic angle (MA) pump probe signal can be obtained spectrally resolved or spectrally integrated.
| (17) |
If the optical pulses are not short compared to the dynamics of the system, the finite length of pulses must be considered. Then, the nonlinear polarization has to be evaluated using Eqs. 4, 8 by convolving the nonlinear response function with the optical pulse temporal shape. The impulsive limit has a great advantage, since it only requires propagation along two time variables (t1 and t3 for selected values of t2 for the 2D spectra; t2 and t3 for PP), thus significantly reducing the computational cost compared to finite pulse length calculations. Approximate expressions for well separated pulses with finite bandwidth were derived recently.42, 43
Computational benchmarks
We now present a numerical approach for calculations of the third order vibrational response. The most expensive part of the calculations is the propagation of doubly excited states. Diagonalizing the two-particle Hamiltonian scales ∼M6 and will only be feasible for M≲40. With our split operator method, the propagation still scales ∼M4, whereas all other operations scale either ∼M2 (singly excited state propagation, doubly excited dipole interactions) or ∼M3 (matrix multiplications in the singly excited basis). On the other hand, the signal calculation of a single trajectory already contains an ensemble average (∼M), which results in a total scaling of our method as ∼M3.
In our simulations of H2O presented in Sec. 3 with M=128, the doubly excited state propagation consumes ≈99% of the calculation time. We found a good signal-to-noise ratio when averaging ≈100 trajectories per dipole orientation for pump and probe pulses. With 100 time steps in each time direction, a single trajectory calculation takes ≈2 h on an AMD Athlon© class processor, resulting in ≈1800 h single processor computation time to gain a 2D spectrum in the impulsive limit.
APPLICATION TO OH STRETCHING VIBRATIONS IN LIQUID WATER
The modeling approach described in Sec. 2 is well suited to simulate the nonlinear vibrational response of liquid water. This is due its capabilities, at least in principle, to reproduce the key features of the nonlinear response observed in the experiment:26 frequency dependent spectral diffusion dynamics, frequency dependent anharmonicities, likely nonadiabatic and partially coherent energy transfer dynamics, i.e., exchange between fluctuating disordered vibrational excitons. In the following we show how we obtain the vibrational Hamiltonian for liquid water and that, indeed, our model does reproduce these key features convincingly.
The effective vibrational Hamiltonian
The vibrational Hamiltonian was constructed according to Sec. 2A. We assumed two fundamental modes per molecular site (symmetric and antisymmetric stretch), as shown in Eq. 18. Here, and ωm,ν denote the creation operator and the fundamental transition frequency, respectively, for mode ν (ν=2,3, symmetric, antisymmetric) at the molecular site m. The intermolecular couplings Jmν,m′ν′ are calculated using dipole-dipole coupling as given in Eq. 19, where μm,1ν are the fundamental transition dipole moments at molecular site m, Rmm′ is the distance between sites m and m′, and . Since the electrostatic map provides instantaneous local eigenstates, we set all intramolecular couplings to 0.
| (18) |
| (19) |
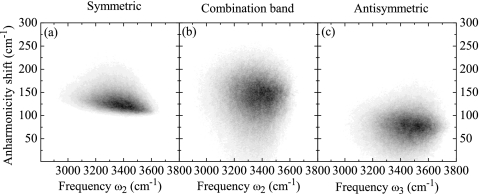
The intramolecular anharmonicities V with m=m′=n=n′ are calculated as the difference between the overtone frequencies provided by the electrostatic map and the respective harmonic values. For example, the anharmonicity shift of the antisymmetric overtone on molecule m=1 is V1313,1313=ω1,5−2ω1,3. The distributions of the intramolecular anharmonicities are shown in Fig. 2. We also treat intermolecular anharmonicities, or coupling anharmonicities, that arise from anharmonic transition dipole moments [see below, Eq. 20], affecting the dipole-dipole coupling between local overtones and intermolecular combination bands. Still, the anharmonicity matrix V is rather sparse, greatly reducing the computational effort.
Figure 2.
Diagonal frequency anharmonicities. (a) Symmetric overtone ω4, (b) antisymmetric overtone ω5, and (c) intramolecular combination band ω6, plotted as histograms vs their respective fundamental frequencies.
In a similar way, the transition dipole operator is constructed using Eq. 3 modified to account for the two fundamental modes per molecule, as shown in Eq. 20.
| (20) |
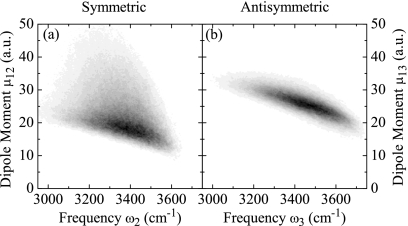
Here, μm,1ν are the fundamental transition dipole moments for mode m (transition from ground state into symmetric∕antisymmetric fundamental mode ν=2,3) at molecular site m. The distributions of amplitudes for fundamental transition dipole moments are shown in Fig. 3 as a function of the respective fundamental transition frequencies.
Figure 3.
Histograms of the fundamental transition dipole moment amplitudes as function of the respective transition frequencies. (a) Symmetric mode ν=2. (b) Antisymmetric mode ν=3.
In Eq. 20, we neglected intermolecular anharmonicities of the transition dipole moments. The intramolecular anharmonicities are calculated as the differences between the transition dipole moments involving overtones (μm,νν′,ν=2,3,ν′=4,5,6) and their harmonic counterparts. This is particularly important for harmonically forbidden transitions μm,25 and μm,34, which are now enabled due to the anharmonicities.
Ab initio electrostatic map
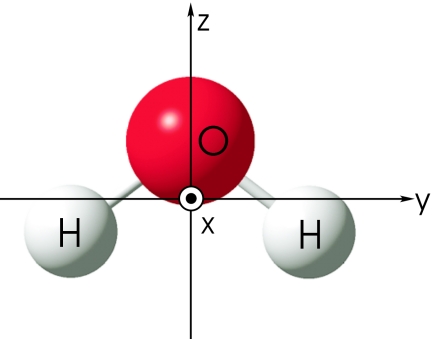
The electrostatic potential in the vicinity of a single H2O molecule generated by the surrounding molecules is expanded to second order in Cartesian coordinates (Fig. 4)
| (21) |
Apart from the overall shift U0, Eq. 21 has nine independent multipole coefficient parameters (note that Eαβ=Eβα). They were arranged in a vector
| (22) |
C was calculated analytically at the origin of the molecular frame coordinate system from the surrounding water partial charges of MD configurations.
Figure 4.
Coordinate system fixed on H2O.
The anharmonic gas phase vibrational potential surface of H2O in presence of the multipole field C is expanded in the three normal coordinates Qi to sixth order
| (23) |
where are the anharmonic force constants, which are calculated by the quantum chemical calculations at the MP2∕6-31+G(d,p) level using our modified GAUSSIAN 03 code.32 The Hamiltonian was expanded in a harmonic basis set and was recast into a normal ordered form.44 The vibrational eigenstates are calculated by diagonalizing a Hamiltonian using the implicit restarted Arnoldi method.44, 45, 46 High energy basis states where the total number of excitations nT≡n1+n2+n3 are larger than 14 are neglected.
Molecular vibrational frequencies of the six eigenstates (ground state, symmetric O–H stretch, antisymmetric O–H stretch, and their overtones and combinations) and the transition dipole moments between these states were parametrized with the multipole coefficients C.
The calculated gas phase frequencies of these six eigenstates are tabulated and compared to the reference high level calculation47 in Table 1. The calculated frequencies are 0.6% to 1.2% higher than the reference calculations which employed higher computational level with larger basis sets. The anharmonicities of symmetric and antisymmetric O–H stretches have good agreement with the reference calculations (103 versus 113 cm−1 and 71 versus 113 cm−1).
Table 1.
Calculated anharmonic frequencies in the gas phase (is in cm−1).
| State | Frequency | Reference calc.a | Description |
|---|---|---|---|
| 1 | 0.0 | 0.0 | Ground state |
| 2 | 3688.2 | 3657.0 | s-δ(O–H) |
| 3 | 3803.2 | 3779.5 | a-δ(O–H) |
| 4 | 7273.9 | 7201.6 | s-δ(O–H)v=2 |
| 5 | 7535.1 | 7445.1 | a-δ(O–H)v=2 |
| 6 | 7339.0 | s-δ(O–H)+a-δ(O–H) |
Reference 47.
The vibrational transition frequency from the ground state to state ν and the transition dipole moments between states ν and ν′ were parametrized using the multipole coefficient vector C.
| (24) |
Here α and β denote the nine independent Cartesian coefficients α,β=x,y,z,xx,yy,zz,xy,xz,yz of the multipole vector in the molecular frame coordinate system.
The expansion coefficients are calculated by using the central difference formulas.44 The calculated map is given in Table 2. Due to the molecular symmetry, the first derivatives with respect to the components Ex, Ey, Exy, Exz are 0. The electric field in parallel to the molecular axis (Ez) blueshifts both symmetric and antisymmetric O–H stretch frequencies since the negative charged oxygen moves toward the center of the hydrogens resulting in shorter O–H distances. The calculated map of the transition dipole moments is given in Table 3.
Table 2.
Electrostatic ab initio map of the frequencies of the six states. The state (n,m) represent the n and m quanta on symmetric O–H stretch and antisymmetric O–H stretch modes. Unit is in cm−1 for Ωgas and cm−1 a.u.−1 for .
| (1,0) | (0,1) | (2,0) | (0,2) | (1,1) | |
|---|---|---|---|---|---|
| Ωgas | 3 688.2 | 3 803.3 | 7 274.0 | 7 535.1 | 7 339.1 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 13.6 | −10.0 | 113.2 | −17.7 | −70.3 | |
| 718.4 | 2 468.7 | 1 621.9 | 4 410.5 | 2 983.1 | |
| 3 357.7 | 3 209.3 | 6 661.2 | 6 512.3 | 6 530.4 | |
| −2 327.6 | −346.0 | −4 618.7 | −893.1 | −3 197.5 | |
| −898.8 | −3 025.0 | −2 110.4 | −5 706.7 | −3 746.5 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| −36.8 | 40.3 | −241.0 | 116.2 | 123.1 | |
| −8 713 | −10 288 | −15 388 | −16 391 | −16 668 | |
| 35 | −1 025 | −1 495 | −952 | −5 528 | |
| 85 | −707 | 1 124 | −3 033 | −122 | |
| −1 458 | −1 139 | −4 708 | −1 936 | −4 474 | |
| −391 | −329 | −1 534 | −2 080 | −1 508 | |
| −146 732 | −18 760 | −433 759 | −122 156 | 57 031 | |
| −19 598 | 18 453 | −66 921 | −1 397 | 64 275 | |
| −5 335 | 3 976 | −13 762 | 1 491 | 4 906 | |
| −4 236 | 1 661 | −16 319 | −4 243 | 4 158 | |
| 730 072 | −238 293 | 2 166 068 | 206 542 | −874 097 | |
| −51 748 | −54 710 | −113 723 | −107 120 | −109 830 | |
| 36 402 | 28 076 | 68 327 | 63 670 | 70 467 | |
| 35 784 | 44 947 | 81 728 | 84 202 | 80 643 | |
| −43 643 | 41 195 | 1 784 127 | −6 716 | 62 014 | |
| −6 302 | −5 669 | −12 190 | −15 493 | −11 616 | |
| −46 859 | −54 927 | −96 941 | −110 177 | −101 532 | |
| 17 928 | 30 437 | 36 236 | 59 553 | 41 087 | |
| −4 856 | 7 162 | −11 763 | 11 318 | 13 978 | |
| −15 942 | −20 310 | −33 379 | −39 360 | −33 977 | |
| −14 357 | 15 009 | 1 667 989 | 4 962 | 26 631 | |
| −30 756 | −26 260 | −63 808 | −52 785 | −59 364 | |
| −23 895 | −19 764 | −46 442 | −38 728 | −44 292 | |
| −134 452 4 | 952 919 | −4 603 900 | 273 512 | 3 100 575 |
Table 3.
Electrostatic ab initio map of the allowed transition dipole moments of the six states (linear part). The state (n1,n2)→(m1,m2) represents the transition between the state (n1,n2) and (m1,m2). The x components of the transition dipole moments are always zero and y and z components are shown. Unit is in a.u. for Mgas and .
| (0,0)→(1,0) | (0,0)→(0,1) | (1,0)→(2,0) | (1,0)→(1,1) | (0,1)→(0,2) | (0,1)→(1,1) | |
|---|---|---|---|---|---|---|
| Mgas | (0.03, 4.11) | (10.66, −0.01) | (0.21, 5.60) | (10.72, −0.10) | (−14.30, 0.02) | (−0.03, 4.24) |
| (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | |
| (−447.6, −0.4) | (1.3, −127.1) | (−840.6, −0.4) | (9.8, −12.7) | (0.8, 246.4) | (−80.8, 0.2) | |
| (−1.1, −172.2) | (−154.9, 0.8) | (−10.8, −224.7) | (−155.4, 8.6) | (188.6, −0.7) | (5.9, −176.1) | |
| (0.1, −9.9) | (−35.2, −0.1) | (0.7, −14.1) | (−35.2, −0.4) | (−25.9, 0.2) | (−0.4, −10.2) | |
| (0.6, 170.1) | (297.9, −0.4) | (2.6, 234.2) | (298.9, −3.0) | (−416.9, 0.9) | (1.9, 171.0) | |
| (0.7, 64.7) | (6.3, −0.5) | (8.1, 80.7) | (6.7, −5.6) | (12.5, 0.2) | (−5.2, 67.7) | |
| (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | |
| (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | (0.0, 0.0) | |
| (1000.8, −0.1) | (−1.7, −49.7) | (1872.9, −1.1) | (−5.1, −285.0) | (1.8, −216.9) | (−121.6, 1.0) |
In order to construct the vibrational Hamiltonian, we performed a MD simulation of a small (M=64 molecules) simple point charge extended water system at room temperature and constant volume using the GROMACS-3.3.1 program.48 The electric fields generated by the solvent environment were calculated analytically32 at every molecular site and time step. The electrostatic map was applied to calculate the transition frequencies and dipole moments for each molecule and time step.
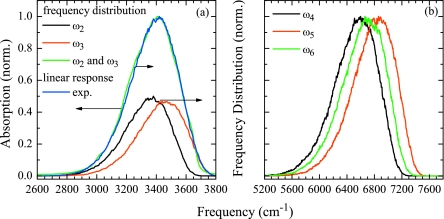
Comparing the resulting distributions of the fundamental transition frequencies ω2 and ω3 to the experimental absorption spectrum, we found the solvent shifts generated by the electrostatic map insufficient. We compensated for this effect by scaling all electric fields with a factor of 2.2 to match the maximum of the fundamental frequency distribution to the maximum of the linear spectrum of H2O, as shown in Fig. 5a. In Fig. 5b we show the resulting overtone frequency distributions.
Figure 5.
(a) Fundamental frequency distribution of the symmetric ω2 (black), antisymmetric ω3 (red) OH stretching vibration, and combined symmetric and antisymmetric frequency distribution (green), blue: experimental linear spectrum (Ref. 56). (b) Overtone frequency distributions, symmetric overtone ω4 (black), antisymmetric overtone ω5 (red), and combination band ω6 (green).
Nonlinear infrared response
Our recent study of liquid water28 focused on the effect of intermolecular coupling on the dynamics and the 2DIR correlation spectra of the OH stretching vibrations. We used the dielectric constant ϵ in the resonant dipole-dipole coupling Eq. 19 as a scaling factor to reproduce the PA decay regime of ≈80 fs observed experimentally,25, 26, 49 evident for the fully resonant coupling regime in liquid H2O. Good agreement with experiment was found for an average next neighbor coupling κ=12 cm−1.28 We will describe these results and discuss the effects observed in the context of the simulation method.
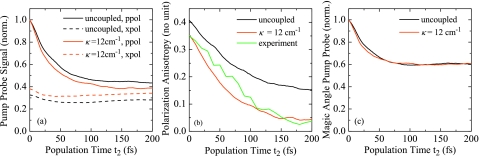
In Fig. 6a, we show the spectrally integrated PP signal for parallel and crossed polarization of pump and probe pulses for two coupling regimes. Figures 6b, 6c show SPA and SMA calculated from these signals, respectively. Also shown in Fig. 6b is the experimentally observed PA in H2O.26
Figure 6.
Spectrally integrated signals. (a) PP transients for parallel (ppol) and crossed (xpol) polarization of pump and probe pulses for two coupling regimes. (b) SPA calculated from (a), green: experimental PA (Ref. 26). (c) SMA calculated from (a).
For the uncoupled system, all dynamics observed in Fig. 6 are caused by modulations of the transition dipole moments, since all energy transfer pathways are blocked and all populations remain constant. The PA reflects orientational modulations of the transition dipole moments which are caused by two major effects—(i) fluctuations of the transition dipole moments and (ii) librational motion and rotational diffusion. The former is found to be very strong in H2O, accounting for ≈1∕2 of the signal decay. On the other hand, the SMA signal shows a fast initial decay that is entirely due to amplitude fluctuations of the transition dipole moments. This effect has not been addressed before, and we note that it should be considered when population relaxation dynamics are extracted from MA data.
When adding the intermolecular coupling, the anisotropy decay Fig. 6b speeds up with increasing coupling strength and the long-lived components vanish. This effect can be clearly assigned to intermolecular energy transfer. We expect that the transfer process is at least partially coherent, and has to be understood as randomized energy transport between the disordered excitons. Since the total exciton population remains unchanged, the SMA signal is unaffected by these processes, as can be seen in Fig. 6c.
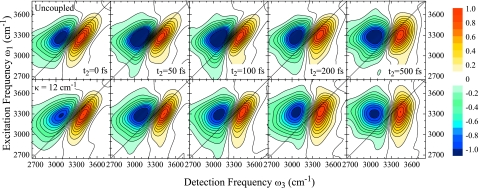
In Fig. 7, we show a series the 2DIR correlation spectra for two coupling regimes, uncoupled and κ=12 cm−1, for different population times t2. All spectra exhibit two peaks. The positive peak on the diagonal corresponds to the fundamental 0→1 transition. The negative peak originating from 1→2 ESA is red shifted due to anharmonicities. Strong interference between these two peaks results in significant signal cancellation and distortion of the peak shapes in the overlap region. Despite these distortions, we observe a clear V-shape of the ESA peak that, in part, is caused by the distributions of diagonal anharmonicities as shown in Fig. 2.
Figure 7.
2DIR correlation spectra of the OH stretching vibration in H2O for population times t2=0, 50, 100, 200, and 500 fs. Top panel: uncoupled system, bottom panel: κ=12 cm−1. Each spectrum is normalized to its maximum.
In both coupling regimes, the fundamental peak is stretched along the diagonal at population time t2=0 fs, indicative of initial inhomogeneity in the sample. This inhomogeneity is lost as with t2 on very similar time scales for both systems. However, no single time scale for loss of correlations can be extracted from these spectra. We instead observe these dynamics to vary across the spectrum. For both regimes, the red side loses correlations faster than the blue side. For the uncoupled system, we observe mainly two spectral components showing different dynamics which we attribute to the symmetric stretch on the red side and the antisymmetric OH stretch on the blue side. Extraction of the respective time scales is, however, difficult due to the spectral overlap of the two modes. For κ=12 cm−1, no such separation is observed. The excitonic energy transfer instead smoothes out the dynamics across the spectrum. This is most obvious from the bending of the fundamental peak shape and the nodal line between the peaks in the t2=100 and 200 fs spectra.
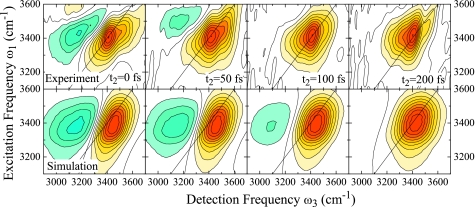
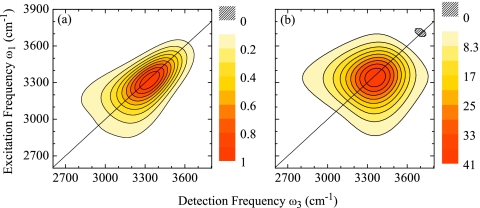
For direct comparison with experiment, we corrected our simulation results for κ=12 cm−1 to match the experimental conditions by multiplication of the frequency domain response with the experimental excitation pulse spectra along ω1 and ω3. Additionally, we included population relaxation effects using ad hoc description of the population relaxation with a population lifetime of T1=200 fs.25 We also model the persisting GSB observed in the experiment.26 The extraction of the GSB contribution to the total nonlinear response is, however, difficult for excitonic systems. This is discussed in Sec. 4. We instead use an approximate description for the GSB contribution as described in Appendix B. With these assumptions, we find close agreement between our simulations and experiment as is shown in Fig. 8.
Figure 8.
2DIR correlation spectra of the OH stretching vibration in H2O for population times t2=0, 50, 100, and 200 fs. Top panel: experimental data (Ref. 26), bottom panel: κ=12 cm−1 corrected for experimental pulse spectrum and ad hoc population relaxation, see text. Each spectrum is normalized to its maximum. Figure adapted from Ref. 28.
Discussion of the nonlinear vibrational response of H2O
The features and dynamics observed in the nonlinear vibrational response of neat H2O can be assigned to two major contributions—local intramolecular effects and excitonic effects. The former are caused by the local 2D OH stretching potential. Fluctuations in the local environment lead to modulations of the mixing between the states resulting in strong fluctuations of the fundamental dipole moments as well as the overtone frequencies and dipole moments. This can to some extent be interpreted as intramolecular energy transfer. Also, the strong local anharmonicities lead to breakdown of harmonic selection rules, enabling additional pathways contributing to the nonlinear response. Additionally, we observe faster fluctuations for the symmetric stretch mode on the red side of the spectrum, see Fig. 7, compared to the antisymmetric mode on the blue side. Very similar effects have been observed for water in acetonitrile,50 where this is attributed to non-Gaussian dynamics caused by local mode couplings. Similarly, modulations of the Fermi resonance of the symmetric mode with the OH bending mode overtone is likely to impact the fast fluctuation time scales observed. This is included in our model through the quantum chemical calculations leading to the electrostatic map.
Apart from all those dynamical effects, the distributions of transition frequencies and dipole moments and their anharmonicities also have significant impact on the peak shapes observed in the 2DIR correlation spectra. The dipole moment distributions as shown in Fig. 3 lead to amplitude distortion. The distributions of local frequency anharmonicities (see Fig. 2) create a distinct ESA peak shape and also lead to significant cancellation in the peak overlap region, see Fig. 10. The combination of all these effects makes it quite clear why a simple analysis of the spectra,51, 52 e.g., nodal line slope or dynamic line width analysis is likely to fail for H2O, even for the uncoupled system.
The intermolecular coupling on the other hand, mainly affects the PA dynamics. Here, the fast transfer time scales observed experimentally are reproduced for an average next neighbor coupling as small as 12 cm−1. We find that the large number of acceptor modes, as well as anharmonicities and fluctuations in the system open up many intermolecular transfer pathways, leading to a full decay of the PA on these fast time scales, even for these small couplings. It is not possible to estimate the coherence contributions to the energy transfer process from our simulations. No clear physical model of energy transfer and dynamic delocalization for such fluctuating disordered excitons has been developed to date.
Excitonic effects on the 2DIR correlation spectra are rather subtle. The overall dynamics are almost unaffected by the excitonic coupling. Rather than speeding up dynamics as one might expect, the excitonic interactions smooth out the fluctuations across the spectrum leading to a continuous distribution of spectral diffusion time scales from ≈100 fs on the red side to >200 fs on the blue side of the spectrum. These time scales are in close agreement with the experimental results.26
We show here that indeed a very high level of theory is necessary to satisfactorily model the nonlinear vibrational response of the OH stretching vibration of liquid H2O. Non-Gaussian distributions and dynamics, non-Condon effects, distributions of anharmonicities, and excitonic interactions all significantly affect the signal, and therefore must be accounted for. The NISE approach combined with our split operator technique provides all this functionality at manageable computational cost, and in its generality is highly adaptable to any excitonic system.
INTERFERENCE BETWEEN LIOUVILLE PATHWAYS IN EXCITONIC SYSTEMS
In this section, we will address interference effects as they appear in simulations of the nonlinear response of excitonic systems, and how they affect the interpretation of the signal. We note that these interferences are a purely theoretical phenomenon but may affect the total signal through numerical accuracy. This can be avoided by building in the interferences from the outset using a quasiparticle representation and the nonlinear exciton equation.54
The third order response of a three band exciton model has three Liouville pathways—GSB, ESE, and ESA—contributing to the total response along a given phase matching direction as shown in Fig. 1. For localized excitations these pathways can be analyzed and interpreted separately, i.e., the GSB pathway can be written such that it reproduces the dynamics and spectral features of a bleached vibrational ground state. For excitons this is not generally possible due to subtle interferences between the different pathways. Only the total signal as the sum of all pathways can be obtained. We will describe and discuss this phenomenon below.
Let us consider a collection of N vibrational chromophores, where the dipole moments are localized on each chromophore. The Green’s function expressions Eq. 6 are written in this local basis. For simplicity, we here apply the Condon approximation (μm(τ)≡μ) and will only look at the rephasing GSB diagram S1:
| (25) |
In the absence of vibrational coupling between these chromophores, i.e., localized excitations, G(1) is a diagonal matrix, and Eq. 25 simplifies even more.
| (26) |
Equation 26 can be interpreted as follows: if we think of the third order response as the correlation of coherences at different times, the two terms describe the coherences on modes k and i during t1 and t3, respectively. However, in Eq. 26 we not only sum over coherences of the same mode (i=k) but also over coherences between different modes (i≠k). For illustration, we recast Eq. 26:
| (27) |
The first term resembles what is usually discussed as GSB. It locally measures the correlations between coherences during t1 and t3 and then performs an ensemble average (∑i). Double Fourier transforming this first term alone produces a 2D spectrum with one peak on the diagonal and a peak shape according to the spectral diffusion dynamics of the system, as illustrated in Fig. 9a.
Figure 9.
Double Fourier transform of the first (a) and second (b) terms of Eq. 27. As an example, we used the t2=0 fs, κ=12 cm−1 water data shown in Fig. 7.
The second term of Eq. 27 on the other hand, measures correlations between coherences of different modes i and k. Even in the extreme case of a purely inhomogeneously broadened system, the 2D spectrum of this contribution alone would show a round shape (no stretching along the diagonal). An example is shown in Fig. 9b.
However, for localized excitations this second term does not produce nonlinear signal. It can be shown straight forwardly that it is cancelled exactly with equivalent terms in S2 and S3. Thus, by only considering these diagonal contributions to the response the usual picture and interpretation of the GSB, ESE, and ESA can be recovered.
For excitons, it is hard to extract the individual contributions to the total response. We can write down and interpret the response similarly to Eq. 27, but taking into account the vibrational couplings, resulting in nonzero off-diagonal elements of the Green’s functions:
| (28) |
The first term of Eq. 28 still resembles a GSB-like peak shape. The second term, however, does not cancel out exactly with the other diagrams S2 and S3 as soon as V≠0 or μ≠0, i.e., in the case of any anharmonicity in the system. This effect occurs due to energy transfer in the S3 diagram that essentially leads to redistribution of anharmonic effects. The nonlinear signal contribution emerging from these off-diagonal terms is neither GSB, ESE, nor ESA. It only emerges as a subtle interference and incomplete cancellation between the diagrams.
In general, these off-diagonal contributions scale as N4 since each dipole can act on a different chromophore. However, nonlinear signal is generated only when all four interactions occur within the coherence size of the exciton. Otherwise the contributions cancel due to destructive interference between all pathways. This partial destructive interference prevents a simple interpretation of the signal in terms of the individual pathways.53
We note that, in general, the total signal will be significantly weaker than the individual diagrams depending on the ratio between the total system size and the coherence size of the excitons. This interference reflects the fact that individual pathways scale as N4 whereas the overall response only scales as N2. It should be done carefully since it may affect the numerical accuracy of simulations. The quasiparticle representation and the nonlinear exciton equations build this interference from the outset and avoid this difficulty.38, 54
CONCLUSIONS
We presented a simulation formalism for calculations of the nonlinear optical response of excitons based on numerical integration of the Schrödinger equation. This protocol is highly versatile, enabling explicit treatment of nonadiabatic exciton transport, fluctuations of the transition frequencies, transition dipole moments, intermode couplings and the diagonal, and off-diagonal anharmonicities of all these quantities. The split operator technique greatly reduces computational cost, opening up a wide range of excitonic systems to be treated. Even though we here fully developed the model for vibrational excitons, it can be straight forwardly adapted to treat electronic excitations, as well.
We used the method to simulate the third order response of the OH stretching vibration in neat liquid water. An ab initio electrostatic map for the OH stretching vibrations in water is presented. The simulation results are in good agreement with the experimental data. It is found that intramolecular effects owing to the sensitivity of the two-dimensional OH stretching potential are the major cause of the dynamics observed. The experimental energy transfer times are reproduced for surprisingly small intermolecular couplings.
ACKNOWLEDGMENTS
This research was supported by the Canadian Institute of Photonics Innovation, Photonics Research Ontario, and the Natural Sciences and Engineering Research Council of Canada. S.M. gratefully acknowledges the support of the NIH (Grant No. GM59230) and the NSF (Grant No. CHE-0745891). A.P. thanks Thomas la Cour Jansen for many helpful discussions.
APPENDIX A: FACTORIZATION OF THE HARMONIC TWO-PARTICLE PROPAGATOR
In the following, we will consider the harmonic part of the effective Hamiltonian denoted as , i.e., the first two terms of Eq. 2:
| (A1) |
The infinitesimal propagators for singly excited states used in Eq. 9 are now denoted as written in the singly excited local basis :
| (A2) |
The doubly excited infinitesimal propagator can be calculated by factorization of . In the following, we omit the explicit τ dependence for clarity.
| (A3) |
where . This rather complicated structure of the two-particle propagator arises from the properties of the symmetrized two-particle basis. It can be shown straight forwardly that any basis transformation matrix in a symmetrized two-particle basis has the given structure.
APPENDIX B: AD HOC POPULATION RELAXATION FOR VIBRATIONAL EXCITONS
The phenomenon described in Sec. 4 has a direct impact on ad hoc description of population relaxation for vibrational excitons. Population relaxation is included by adding relaxation factors Γ to Eq. 8.
| (B1) |
It is often assumed that the different levels of excitation have different decay times,15, 55 i.e., T1 for ground and excited state populations ∣0⟩⟨0∣ and ∣1⟩⟨1∣, T1∕2 for ∣0⟩⟨1∣ coherences, and 3T1∕2 for ∣1⟩⟨2∣ coherences, as shown in Eq. B2.
| (B2) |
No such procedure is possible when treating vibrational excitons. If different ad hoc factors as shown in Eq. B2 are applied to the different diagrams, the proper cancellation between the diagrams is prevented and the resulting nonlinear signal is physically wrong. Consequently, for excitons one can only use one relaxation factor for all the diagrams, e.g.,
| (B3) |
This effect poses serious difficulties when trying to describe a persisting GSB as observed experimentally in the case of H2O discussed in Sec. 3C. Using a different T1 time for the GSB diagrams S1 and S4 is not possible since this would prevent proper cancellation of the off-diagonal elements of the response [second term in Eq. 28], and thus lead to wrong results.
We instead propose an approximate description for the GSB, that is the first term in Eq. 28 only. This can be expressed by rewriting the rephasing nonlinear response SI as follows. We now again include intermolecular couplings and fluctuations of the transition dipole moments.
| (B4) |
where we choose as
| (B5) |
The nonrephasing response SII is done equivalently. Here, T1,GSB is the lifetime of the GSB and T1 is the excited state population lifetime. Using Eqs. B4, B5, we can now choose different times T1,GSB and T1 without preventing the proper cancellation of the off-diagonal elements of the response, i.e., we can describe a ground state bleach that persists beyond the excited state population time T1, by using a, respectively, larger value T1,GSB. For the data shown in Fig. 8 we chose T1=200 fs and T1,GSB=∞.
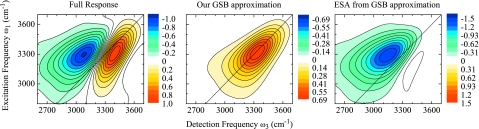
For illustration, we show the different contributions for the t2=0 fs, κ=12 cm−1 H2O data in Fig. 10. The GSB contribution as discussed above is shown in (b). At t2=0 fs, the ESE is identical to the GSB. It is therefore possible at this population time only, to fully dissect the response into the different contributions. In Fig. 10c we show the resulting ESA contribution. From the amplitudes of the signals we see that about 50% of the total amplitude is lost in the full response due to cancellation between the peaks. Similarly, the antidiagonal width of the peaks is significantly narrower in the full response compared to the individual contributions, greatly distorting simple analysis of the dynamics.
Figure 10.
2DIR correlation spectra of H2O at t2=0 fs for κ=12 cm−1. (a) Full response, (b) GSB only, and (c) ESA extracted from (a) and (b). All spectra are normalized to the full response amplitude. Note the scales for each spectrum.
References
- Mukamel S., Annu. Rev. Phys. Chem. 51, 691 (2000). 10.1146/annurev.physchem.51.1.691 [DOI] [PubMed] [Google Scholar]
- Jonas D. M., Annu. Rev. Phys. Chem. 54, 425 (2003). 10.1146/annurev.physchem.54.011002.103907 [DOI] [PubMed] [Google Scholar]
- Cho M., Chem. Rev. (Washington, D.C.) 108, 1331 (2008). 10.1021/cr078377b [DOI] [PubMed] [Google Scholar]
- Ernst R. R., Bodenhausen G., and Wokaun A., Nuclear Magnetic Resonance in One and Two Dimensions (Oxford University Press, Oxford, 1987). [Google Scholar]
- Brixner T., Stenger J., Vaswani H. M., Minhaeng C., Blankenship R. E., and Fleming G. R., Nature (London) 434, 625 (2005). 10.1038/nature03429 [DOI] [PubMed] [Google Scholar]
- Zigmantas D., Read E. L., Mancal T., Brixner T., Gardiner A. T., Cogdell R. J., and Fleming G. R., Proc. Natl. Acad. Sci. U.S.A. 103, 12672 (2006). 10.1073/pnas.0602961103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X., Zhang T., Borca C. N., and Cundiff S. T., Phys. Rev. Lett. 96, 057406 (2006). 10.1103/PhysRevLett.96.057406 [DOI] [PubMed] [Google Scholar]
- Collini E. and Scholes G. D., Science 323, 369 (2009). 10.1126/science.1164016 [DOI] [PubMed] [Google Scholar]
- Hamm P., Helbing J., and Bredenbeck J., Annu. Rev. Phys. Chem. 59, 291 (2008). 10.1146/annurev.physchem.59.032607.093757 [DOI] [PubMed] [Google Scholar]
- Hamm P., Lim M., and Hochstrasser R. M., J. Phys. Chem. B 102, 6123 (1998). 10.1021/jp9813286 [DOI] [Google Scholar]
- DeCamp M. F., DeFlores L., McCracken J. M., Tokmakoff A., Kwac K., and Cho M., J. Phys. Chem. B 109, 11016 (2005). 10.1021/jp050257p [DOI] [PubMed] [Google Scholar]
- Rubtsov I. V., Wang J., and Hochstrasser R. M., Proc. Natl. Acad. Sci. U.S.A. 100, 5601 (2003). 10.1073/pnas.0931292100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolano C., Helbing J., Kozinski M., Sander W., and Hamm P., Nature (London) 444, 469 (2006). 10.1038/nature05352 [DOI] [PubMed] [Google Scholar]
- Bloem R., Dijkstra A. G., Jansen T. l. C., and Knoester J., J. Chem. Phys. 129, 055101 (2008). 10.1063/1.2961020 [DOI] [PubMed] [Google Scholar]
- Jansen T. l. C. and Knoester J., J. Phys. Chem. B 110, 22910 (2006). 10.1021/jp064795t [DOI] [PubMed] [Google Scholar]
- Torii H., J. Phys. Chem. A 110, 4822 (2006). 10.1021/jp060014c [DOI] [PubMed] [Google Scholar]
- Kwac K., Lee H., and Cho M., J. Chem. Phys. 120, 1477 (2004). 10.1063/1.1633549 [DOI] [PubMed] [Google Scholar]
- Ganim Z., Chung H. S., Smith A. W., DeFlores L. P., Jones K. C., and Tokmakoff A., Acc. Chem. Res. 41, 432 (2008). 10.1021/ar700188n [DOI] [PubMed] [Google Scholar]
- Chung H. S., Ganim Z., Jones K. C., and Tokmakoff A., Proc. Natl. Acad. Sci. U.S.A. 104, 14237 (2007). 10.1073/pnas.0700959104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFlores L. P. and Tokmakoff A., J. Am. Chem. Soc. 128, 16520 (2006). 10.1021/ja067723o [DOI] [PubMed] [Google Scholar]
- Mukherjee P., Kass I., Arkin I. T., and Zanni M. T., Proc. Natl. Acad. Sci. U.S.A. 103, 3528 (2006). 10.1073/pnas.0508833103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krummel A. T., Mukherjee P., and Zanni M. T., J. Phys. Chem. B 107, 9165 (2003). 10.1021/jp035473h [DOI] [Google Scholar]
- Krummel A. T. and Zanni M. T., J. Phys. Chem. B 110, 13991 (2006). 10.1021/jp062597w [DOI] [PubMed] [Google Scholar]
- Lee C., Park K. -H., Kim J. -A., Hahn S., and Cho M., J. Chem. Phys. 125, 114510 (2006). 10.1063/1.2213259 [DOI] [PubMed] [Google Scholar]
- Cowan M. L., Bruner B. D., Huse N., Dwyer J. R., Chugh B., Nibbering E. T. J., Elsaesser T., and Miller R. J. D., Nature (London) 434, 199 (2005). 10.1038/nature03383 [DOI] [PubMed] [Google Scholar]
- Kraemer D., Cowan M. L., Paarmann A., Huse N., Nibbering E. T. J., Elsaesser T., and Miller R. J. D., Proc. Natl. Acad. Sci. U.S.A. 105, 437 (2008). 10.1073/pnas.0705792105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge N. -H., Zanni M. T., and Hochstrasser R. M., in Ultrafast Phenomena XIII, edited by Miller R. J. D., Murnane M. M., Scherer N. F., and Weiner A. M. (Springer-Verlag, New York, 2003), pp. 592–594. [Google Scholar]
- Paarmann A., Hayashi T., Mukamel S., and Miller R. J. D., J. Chem. Phys. 128, 191103 (2008). 10.1063/1.2919050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanni M. T., Ge N. -H., Kim Y. S., and Hochstrasser R. M., Proc. Natl. Acad. Sci. U.S.A. 98, 11265 (2001). 10.1073/pnas.201412998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voronine D. V., Abramavicius D., and Mukamel S., J. Chem. Phys. 126, 044508 (2007). 10.1063/1.2424706 [DOI] [PubMed] [Google Scholar]
- Mukamel S., Principles of Nonlinear Optical Spectroscopy (Oxford University Press, Oxford, 1995). [Google Scholar]
- Hayashi T., Jansen T. l. C., Zhuang W., and Mukamel S., J. Phys. Chem. A 109, 64 (2005). 10.1021/jp046685x [DOI] [PubMed] [Google Scholar]
- Jansen T. l. C. and Knoester J., J. Chem. Phys. 124, 044502 (2006). 10.1063/1.2148409 [DOI] [PubMed] [Google Scholar]
- Auer B. M. and Skinner J. L., J. Chem. Phys. 127, 104105 (2007). 10.1063/1.2766943 [DOI] [PubMed] [Google Scholar]
- Schmidt J. R., Corcelli S. A., and Skinner J. L., J. Chem. Phys. 123, 044513 (2005). 10.1063/1.1961472 [DOI] [PubMed] [Google Scholar]
- Jansen T. l. C., Zhuang W., and Mukamel S., J. Chem. Phys. 121, 10577 (2004). 10.1063/1.1807824 [DOI] [PubMed] [Google Scholar]
- Torii H., J. Phys. Chem. A 108, 2103 (2004). 10.1021/jp037603s [DOI] [Google Scholar]
- Mukamel S., Oszwaldowski R., and Abramavicius D., Phys. Rev. B 75, 245305 (2007). 10.1103/PhysRevB.75.245305 [DOI] [Google Scholar]
- Mukamel S. and Abramavicius D., Chem. Rev. 104, 2073 (2004). 10.1021/cr020681b [DOI] [PubMed] [Google Scholar]
- Kosloff R., J. Phys. Chem. 92, 2087 (1988). 10.1021/j100319a003 [DOI] [Google Scholar]
- Torii H., J. Phys. Chem. A 110, 9469 (2006). 10.1021/jp062033s [DOI] [PubMed] [Google Scholar]
- Schweigert I. V. and Mukamel S., Phys. Rev. A 77, 033802 (2008). 10.1103/PhysRevA.77.033802 [DOI] [Google Scholar]
- Mukamel S., J. Chem. Phys. (in press). [Google Scholar]
- Hayashi T. and Mukamel S., J. Phys. Chem. A 107, 9113 (2003). 10.1021/jp030626m [DOI] [Google Scholar]
- Lehoucq R., Sorensen D. C., and Yang C., ARPACK Users Guide: Solution of Large Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods (Society for Industrial and Applied Mathematics, Philadelphia, 1998). [Google Scholar]
- Hayashi T. and Mukamel S., Bull. Korean Chem. Soc. 24, 1097 (2003). [Google Scholar]
- Partridge H. and Schwenke D. W., J. Chem. Phys. 106, 4618 (1997). 10.1063/1.473987 [DOI] [Google Scholar]
- Berendsen H. J. C., van der Spoel D., and van Drunen R., Comput. Phys. Commun. 91, 43 (1995). 10.1016/0010-4655(95)00042-E [DOI] [Google Scholar]
- Woutersen S. and Bakker H. J., Nature (London) 402, 507 (1999). 10.1038/990058 [DOI] [Google Scholar]
- Jansen T. l. C., Cringus D., and Pshenichnikov M. S., J. Phys. Chem. A 113 , 6260 (2009). 10.1021/jp900480r [DOI] [PubMed] [Google Scholar]
- Asbury J. B., Steinel T., Stromberg C., Corcelli S. A., Lawrence C. P., Skinner J. L., and Fayer M. D., Chem. Phys. Lett. 108, 1107 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazonder K., Pshenichnikov M. S., and Wiersma D. A., Opt. Lett. 31, 3354 (2006). 10.1364/OL.31.003354 [DOI] [PubMed] [Google Scholar]
- Spano F. C. and Mukamel S., Phys. Rev. Lett. 66, 1197 (1991). 10.1103/PhysRevLett.66.1197 [DOI] [PubMed] [Google Scholar]
- Abramavicius D., Palmieri B., Voronine D. V., Sanda F., and Mukamel S., Chem. Rev. (Washington, D.C.) (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge N. -H., Zanni M. T., and Hochstrasser R. M., J. Phys. Chem. A 106, 962 (2002). 10.1021/jp011768o [DOI] [Google Scholar]
- Ashihara S., Huse N., Espagne A., Nibbering E. T. J., and Elsaesser T., J. Phys. Chem. A 111, 743 (2007). 10.1021/jp0676538 [DOI] [PubMed] [Google Scholar]