Nonlinear response of vibrational excitons: Simulating the two-dimensional infrared spectrum of liquid water

Abstract

A simulation formalism for the nonlinear response of vibrational excitons is presented and applied to the OH stretching vibrations of neat liquid H₂O. The method employs numerical integration of the Schrödinger equation and allows explicit treatment of fluctuating transition frequencies, vibrational couplings, dipole moments, and the anharmonicities of all these quantities, as well as nonadiabatic effects. The split operator technique greatly increases computational feasibility and performance. The electrostatic map for the OH stretching vibrations in liquid water employed in our previous study [A. Paarmann et al., J. Chem. Phys. 128, 191103 (2008)] is presented. The two-dimensional spectra are in close agreement with experiment. The fast 100 fs dynamics are primarily attributed to intramolecular mixing between states in the two-dimensional OH stretching potential. Small intermolecular couplings are sufficient to reproduce the experimental energy transfer time scales. Interference effects between Liouville pathways in excitonic systems and their impact on the analysis of the nonlinear response are discussed.

INTRODUCTION

Coherent multidimensional spectroscopies^{1, 2, 3} have most recently become a valuable tool for the study of dynamics in complex systems. As the optical equivalent of two-dimensional (2D) nuclear magnetic resonance,⁴ both electronic and vibrational 2D coherent spectroscopies allow investigations of structural dynamics, coupling, dephasing, and relaxation mechanisms. So far, only a few 2D electronic spectroscopy studies have been reported.^{5, 6, 7, 8} Vibrational 2D spectroscopy, on the other hand, usually referred to as 2D infrared (2DIR) spectroscopy, has been successfully used to study a wide range of systems, such as peptides,^{9, 10, 11, 12, 13, 14, 15, 16, 17} proteins,^{18, 19, 20, 21} DNA,^{22, 23, 24} and neat liquids.^{25, 26, 27, 28}

In general, the analysis of 2D spectra is complicated by the large linewidth of the transitions. The resulting overlap and interference between different peaks in the spectra often greatly distort the peak shapes, preventing simple extraction of the dynamic parameters of interest. The 2D spectra become even more convoluted in systems with pronounced intermode couplings which lead to delocalized excitations or formation of excitons. Some experimental approaches have been developed to amplify features of interest and reduce complexity of the spectra.^{29, 30} Still, high level theoretical modeling is required in order to reliably extract physical and chemical information from these data.

Initially, most 2D modeling approaches relied on the assumption of Gaussian statistics for transition frequency fluctuations of spatially localized vibrational or electronic modes. Then, the cumulant expansion can be truncated at second order³¹ and all nonlinear spectroscopic observables are characterized by the frequency correlation function (FCF) C(t)=⟨δω(t)δω(0)⟩. The FCF is usually obtained from molecular dynamics (MD) with various strategies for mapping the MD observables, e.g., electric fields, onto the transition frequencies.^{16, 32, 33, 34} This method was extended to include bath modulation of the transition dipole moments (non-Condon effects).³⁵ In some special cases, approximate descriptions can be found to describe non-Gaussian statistics of the transition frequency fluctuations.¹⁷

Several methods have been developed to treat intermode coupling leading to energy transfer,¹⁶ chemical exchange,³⁶ and formation of excitons.^{24, 37, 38} As long as the charge densities of the coupled states do not overlap, the delocalized states can be described as Frenkel excitons.³⁹ When the site frequency fluctuations are small compared to the intermode couplings, one can describe the system in a fixed exciton basis, with perturbative description of the energy transfer between exciton states.^{34, 39} If the fluctuations and couplings are comparable, exciton transport is a nonadiabatic process and multiple state crossing prevents the use of that basis.¹⁵

Numerical integration of the Schrödinger equation^{16, 28, 36} (NISE) is well suited to describe such complex dynamics. The major drawback of the method has so far been the high computational cost since it required diagonalizing the two-particle Hamiltonian. For that reason, the method was limited to either linear response calculations or small systems. In Sec. 2, we show that by introducing the split operator technique^{28, 40} the computational cost of NISE can be dramatically reduced enabling this method to be applied to a wide range of molecular systems.

The first application of this approach was made to model the 2DIR spectrum of the OH stretching vibration in neat liquid H₂O.²⁸ Our recent experimental studies²⁶ demonstrated that the OH stretching vibration shows extremely fast dynamics with no clear separation of time scales between the dephasing, energy transfer, and relaxation dynamics. Even more interesting, it was observed that the OH vibrational modes have a pronounced excitonic character at temperatures near freezing. In Sec. 3, we report on the simulations of the 2DIR response of liquid water. We present an ab initio electrostatic map of the OH stretching vibrations in water, as well as nonlinear response calculations that are in good agreement with experiment.

In the last section (Sec. 4) we discuss interference effects between the different Liouville pathways as they appear in simulations of the nonlinear response of excitons. These prevent simple interpretation and analysis of the individual pathways.

NONLINEAR RESPONSE OF VIBRATIONAL EXCITONS

In the following we present our NISE model which employs the split operator technique to calculate the third order optical response of vibrational excitons. This method can also be adapted straight forwardly to model electronic excitations.

The fluctuating Hamiltonian and dipole operator

We consider a system of M coupled vibrational oscillators described by the Hamiltonian

$$\widehat{H}\left(\tau \right)={\widehat{H}}_S\left(\tau \right)+{\widehat{H}}_I\left(\tau \right),$$ (1)

where ${\widehat{H}}_S$ describes the vibrational system and ${\widehat{H}}_I$ contains the interaction with the optical fields. The vibrational system is described by the effective Hamiltonian (we set ℏ=1 throughout this paper):

$${\widehat{H}}_S\left(\tau \right)=\sum _m{\omega }_m\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_m+\sum _{m^{\prime }\ne m}{J}_{m,m^{\prime }}\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_{m^{\prime }}+\sum _{mn,m^{\prime }{n}^{\prime }}{V}_{mn,m^{\prime }{n}^{\prime }}\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_n^{†}{\widehat{B}}_{m^{\prime }}{\widehat{B}}_{n^{\prime }}.$$ (2)

All bath interactions are incorporated into the Hamiltonian parameters. The first two terms describe the free harmonic system, where ω_m(τ) is the fundamental transition frequency of mode m, ${\widehat{B}}_m^{†}\left({\widehat{B}}_m\right)$ is the Boson creation (annihilation) operator for mode m, $\left[{\widehat{B}}_m^{†},{\widehat{B}}_n\right]={\delta }_{m,n}$. The second term contains the intermode coupling J_m,m^′. The last term describes quartic anharmonicities V. Most commonly, only diagonal anharmonicities of local overtones V_mm,mm are considered. These give the anharmonicity shift between the 0→1 and 1→2 transitions. However, the above Hamiltonian allows for a description of combination band frequency shifts V_mn,mn and coupling anharmonicities (off-diagonal elements of V) as well.

The dipole operator is given by

$$\widehat{\mu }\left(\tau \right)=\sum _m{\mu }_m\left(\tau \right)\left({\widehat{B}}_m^{†}+{\widehat{B}}_m\right)+\sum _{mn{m}^{\prime }}\Delta {\mu }_{mn{m}^{\prime }}\left(\tau \right)\left({\widehat{B}}_n^{†}{\widehat{B}}_{m^{\prime }}^{†}{\widehat{B}}_m+{\widehat{B}}_m^{†}{\widehat{B}}_{m^{\prime }}{\widehat{B}}_n\right).$$ (3)

Here, μ_m is the fundamental 0→1 transition dipole moment of mode m, and Δμ represents the dipole moment anharmonicities. In the Condon approximation, the time averaged amplitudes ⟨∣μ∣⟩_τ are used, neglecting fluctuations and anharmonicities of the transition dipole moments. Non-Condon effects can be included³⁵ by explicitly treating the bath influence and time dependence of μ_m. The second term in Eq. 3 allows for treatment of anharmonicities of the local 1→2 transition dipole moments Δμ_mmm, as well as anharmonicities of dipole moments involving intermode combination bands (other elements of Δμ).

The third order vibrational response

The third order contribution to the system’s polarization induced by the laser fields can be written as^{31, 38}

$$P^{\left(3\right)}\left(\mathbf{r},{\tau }_3\right)=\int \int \int d{\tau }_{2}d{\tau }_{1}d{\tau }_{0}S\left({\tau }_3,{\tau }_2,{\tau }_1,{\tau }_0\right)\times \mathbf{E}\left(\mathbf{r},{\tau }_2\right)\mathbf{E}\left(\mathbf{r},{\tau }_1\right)\mathbf{E}\left(\mathbf{r},{\tau }_0\right),$$ (4)

where S(τ₃,τ₂,τ₁,τ₀) is the third order response function.

$$S\left({\tau }_3,{\tau }_2,{\tau }_1,{\tau }_0\right)=i^3⟨\widehat{\mu }\left({\tau }_3\right)\left[\widehat{\mu }\left({\tau }_2\right),\left[\widehat{\mu }\left({\tau }_1\right),\widehat{\mu }\left({\tau }_0\right)\right]\right]⟩.$$ (5)

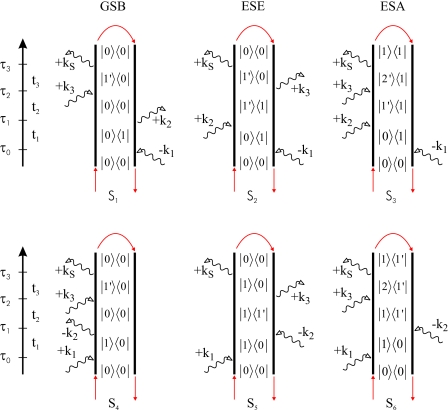
Sorting out the possible time orderings and invoking the rotating wave approximation, S can be written in terms of Liouville pathways for the different signal directions. We shall focus on k_I=−k₁+k₂+k₃ and k_II=k₁−k₂+k₃, also referred to as rephasing and nonrephasing pathways, respectively, represented by the double sided Feynman diagrams given in Fig. 1. The respective Green’s function expressions for the k_I pathways (S₁,S₂,S₃) and the k_II pathways (S₄,S₅,S₆) are given in Eq. 6. These diagrams are often referred to as ground state bleach (GSB) (S₁ and S₄), excited state emission (ESE) (S₂ and S₅), and excited state absorption (ESA) (S₃ and S₆).

$$S_1=-⟨{\widehat{\mu }}^{-}\left({\tau }_0\right){\widehat{G}}_1^{†}\left({\tau }_1,{\tau }_0\right){\widehat{\mu }}^{+}\left({\tau }_1\right){\widehat{G}}_0^{†}\left({\tau }_3,{\tau }_1\right){\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_1\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{+}\left({\tau }_2\right)⟩,$$ (6)

$$S_2=-⟨{\widehat{\mu }}^{-}\left({\tau }_0\right){\widehat{G}}_1^{†}\left({\tau }_2,{\tau }_0\right){\widehat{\mu }}^{+}\left({\tau }_2\right){\widehat{G}}_0^{†}\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_1\left({\tau }_3,{\tau }_1\right){\widehat{\mu }}^{+}\left({\tau }_1\right)⟩,$$

$$S_3=-⟨{\widehat{\mu }}^{-}\left({\tau }_0\right){\widehat{G}}_1^{†}\left({\tau }_3,{\tau }_0\right){\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_2\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{+}\left({\tau }_2\right){\widehat{G}}_1\left({\tau }_2,{\tau }_1\right){\widehat{\mu }}^{+}\left({\tau }_1\right)⟩,$$

$$S_4=-⟨{\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_1\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{+}\left({\tau }_2\right){\widehat{G}}_0\left({\tau }_2,{\tau }_1\right){\widehat{\mu }}^{-}\left({\tau }_1\right){\widehat{G}}_1\left({\tau }_1,{\tau }_0\right){\widehat{\mu }}^{+}\left({\tau }_0\right)⟩,$$

$$S_5=-⟨{\widehat{\mu }}^{-}\left({\tau }_1\right){\widehat{G}}_1^{†}\left({\tau }_2,{\tau }_1\right){\widehat{\mu }}^{+}\left({\tau }_2\right){\widehat{G}}_0^{†}\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_1\left({\tau }_3,{\tau }_0\right){\widehat{\mu }}^{+}\left({\tau }_0\right)⟩,$$

$$S_6=-⟨{\widehat{\mu }}^{-}\left({\tau }_1\right){\widehat{G}}_1^{†}\left({\tau }_3,{\tau }_1\right){\widehat{\mu }}^{-}\left({\tau }_3\right){\widehat{G}}_2\left({\tau }_3,{\tau }_2\right){\widehat{\mu }}^{+}\left({\tau }_2\right){\widehat{G}}_1\left({\tau }_2,{\tau }_0\right){\widehat{\mu }}^{+}\left({\tau }_0\right)⟩.$$

Figure 1.

Double sided Feynman diagrams for the k_I(S₁−S₃) and k_II(S₄−S₆) phase matching conditions, see text. The red arrows indicate the closed time path loops used to calculate the contributions from these diagrams.

The Green’s functions ${\widehat{G}}_0,{\widehat{G}}_1,{\widehat{G}}_2\left({\tau }_b,{\tau }_a\right)$ propagate the ground, the singly excited, and the doubly excited state, respectively, from τ_a to τ_b. The dipole excitation and de-excitation operators ${\widehat{\mu }}^{+}$ and ${\widehat{\mu }}^{-}$ are derived from Eq. 3 and are given by

$${\widehat{\mu }}^{+}\left(\tau \right)=\sum _m{\mu }_m\left(\tau \right){\widehat{B}}_m^{†}+\sum _{mn{m}^{\prime }}\Delta {\mu }_{mn{m}^{\prime }}\left(\tau \right){\widehat{B}}_n^{†}{\widehat{B}}_{m^{\prime }}^{†}{\widehat{B}}_m,$$ (7)

$${\widehat{\mu }}^{-}\left(\tau \right)=\sum _m{\mu }_m\left(\tau \right){\widehat{B}}_m+\sum _{mn{m}^{\prime }}\Delta {\mu }_{mn{m}^{\prime }}\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_{m^{\prime }}{\widehat{B}}_n.$$

The third order response functions for the two techniques are given by the sum of the respective diagrams:

$$S_{\text{I}}=S_1+S_2+S_3,$$ (8)

$$S_{\text{II}}=S_4+S_5+S_6.$$

Harmonic systems [V≡0 in Eq. 2 and Δμ≡0 in Eq. 3] are linear; these contributions then cancel exactly and the signals vanish. The finite nonlinear response is induced by the anharmonicities V and Δμ.

The response functions in Eq. 6 are evaluated by a series of dipole operations and propagations of the many body system as indicated by the closed time path loops in Fig. 1. The challenging tasks in these operations are the propagations, in particular, for doubly excited states in diagrams S₃ and S₆.

Direct numerical propagation of vibrational excitons

All propagators are calculated using NISE:^{15, 28, 41}

$$\widehat{G}\left({\tau }_b,{\tau }_a\right)=-i\theta \left({\tau }_b-{\tau }_a\right)\prod _{p={\tau }_a}^{{\tau }_b-\Delta \tau }\text{exp}\left(-i\widehat{H}\left(p\right)\Delta \tau \right).$$ (9)

We calculate infinitesimal propagators $\widehat{U}\left(p\right)=\exp \left(-i\widehat{H}\left(p\right)\Delta \tau \right)$, and propagate step wise. Setting the ground state energy to zero, the ground state propagator is simply unity. We can now express $\widehat{U}$ in the local basis for the singly (U⁽¹⁾) and doubly (U⁽²⁾) excited states as given in Eq. 10,

$$U_{m,n}^{\left(1\right)}\left(p\right)=⟨m\mid \widehat{U}\left(p\right)\mid n⟩,$$ (10)

$$U_{mn,m^{\prime }{n}^{\prime }}^{\left(2\right)}\left(p\right)=⟨m,n\mid \widehat{U}\left(p\right)\mid m^{\prime },n^{\prime }⟩,$$

where $\mid m⟩={\widehat{B}}_m^{†}\mid 0⟩$ and $\mid m,n⟩=\left(1∕\sqrt{1+{\delta }_{mn}}\right){\widehat{B}}_m^{†}{\widehat{B}}_n^{†}\mid 0⟩$. For not too large systems, U⁽¹⁾ can be calculated exactly by diagonalizing the single particle Hamiltonian $⟨m\mid {\widehat{H}}_S\mid n⟩$, where the third term in Eq. 2 does not contribute.

However, propagation of doubly excited states ∣m,n⟩ is more challenging due to the large size of the symmetrized two-particle basis being M(M+1)∕2. For M≳40, direct diagonalization and data storage is computationally too expensive. Instead, we use the split operator method^{28, 40} for calculating these matrix exponentials. We split the Hamiltonian into the harmonic part ${\widehat{H}}_0$ [first two terms in Eq. 2] and anharmonic part ${\widehat{H}}_a$ (third term) and calculate the matrix exponential as given in Eq. 11.

$$U_{mn,m^{\prime }{n}^{\prime }}^{\left(2\right)}=\sum _{m^{″},n^{″}}{U}_{0,mn,m^{″}{n}^{″}}^{\left(2\right)}{U}_{a,m^{″}{n}^{″},m^{\prime }{n}^{\prime }}^{\left(2\right)}=\sum _{m^{″},n^{″}}⟨m,n\mid \text{exp}\left(-i{\widehat{H}}_0\Delta \tau \right)\mid m^{″},n^{″}⟩\times ⟨m^{″},n^{″}\mid \text{exp}\left(-i{\widehat{H}}_a\Delta \tau \right)\mid m^{\prime },n^{\prime }⟩.$$ (11)

The harmonic exponential $U_0^{\left(2\right)}$ can be calculated exactly from the single particle propagators, see Appendix A. The anharmonic part is usually small enough to allow first order Taylor expansion. The split operator technique gives good accuracy provided the time steps Δτ are small enough.

We note that in Eq. 11 one can avoid computationally expensive matrix multiplications. Consecutive propagation of the doubly excited states with the two infinitesimal propagators $U_0^{\left(2\right)}$ and $U_a^{\left(2\right)}$ is significantly faster.

Nonlinear signal calculation

If the optical pulses are short compared to the system dynamics, the nonlinear polarization can be described in the impulsive limit. Then, the third order signal along the k_I direction is given by Eq. 12.

$$S^{{\mathbf{k}}_I}\left(t_1,t_2,t_3\right)=\sum _{k=1}^3{S}_k\left(t_1,t_2,t_3\right)+\sum _{k=4}^6{S}_k\left(-t_1,t_2,t_3\right).$$ (12)

The 2DIR correlation spectra are obtained by double Fourier transformation with respect to t₁ and t₃, with t_i=τ_i−τ_i−1:

$$S^{2D}\left({\omega }_1,t_2,{\omega }_3\right)=\mathfrak{I}\left[\int \int d{t}_{1}d{t}_3{e}^{i{\omega }_1{t}_1}{e}^{i{\omega }_3{t}_3}{S}^{{\mathbf{k}}_I}\left(t_1,t_2,t_3\right)\right].$$ (13)

Similarly, the pump probe (PP) signal in the impulsive limit is given by Eq. 14 with t₁=0. Then, the rephasing and nonrephasing contributions are identical. The spectrally resolved PP response is given by Eq. 15.

$$S^{\text{PP}}\left(t_2,t_3\right)=2\sum _{k=1}^3{S}_k\left(0,t_2,t_3\right),$$ (14)

$$S^{\text{PP}}\left(t_2,{\omega }_3\right)=\mathfrak{I}\left[{\int }_0^{\infty }d{t}_3{e}^{i{\omega }_3{t}_3}{S}^{\text{PP}}\left(t_2,t_3\right)\right].$$ (15)

In the impulsive limit, the PP signal is also known as heterodyne transient grating.

The polarization anisotropy (PA) S_PA(t₂) is calculated from the PP signal with parallel (∥) and crossed (⊥) polarization of the pump and probe pulses. This is done using the respective projections of the transition dipole moment vectors in Eq. 3 in the laboratory frame when calculating the nonlinear response functions. Orientational averaging is done numerically.

$$S_{\text{PA}}\left(t_2\right)=\frac{S_{\parallel }^{\text{PP}}\left(t_2\right)-S_{\perp }^{\text{PP}}\left(t_2\right)}{S_{\parallel }^{\text{PP}}\left(t_2\right)+2S_{\perp }^{\text{pp}}\left(t_2\right)}.$$ (16)

Equation 16 can be evaluated for either spectrally resolved or spectrally integrated PP, using the respective PP signals as input.

Similarly, the magic angle (MA) pump probe signal can be obtained spectrally resolved or spectrally integrated.

$$S_{\text{MA}}\left(t_2\right)\propto S_{\parallel }^{\text{PP}}\left(t_2\right)+2S_{\perp }^{\text{PP}}\left(t_2\right).$$ (17)

If the optical pulses are not short compared to the dynamics of the system, the finite length of pulses must be considered. Then, the nonlinear polarization has to be evaluated using Eqs. 4, 8 by convolving the nonlinear response function with the optical pulse temporal shape. The impulsive limit has a great advantage, since it only requires propagation along two time variables (t₁ and t₃ for selected values of t₂ for the 2D spectra; t₂ and t₃ for PP), thus significantly reducing the computational cost compared to finite pulse length calculations. Approximate expressions for well separated pulses with finite bandwidth were derived recently.^{42, 43}

Computational benchmarks

We now present a numerical approach for calculations of the third order vibrational response. The most expensive part of the calculations is the propagation of doubly excited states. Diagonalizing the two-particle Hamiltonian scales ∼M⁶ and will only be feasible for M≲40. With our split operator method, the propagation still scales ∼M⁴, whereas all other operations scale either ∼M² (singly excited state propagation, doubly excited dipole interactions) or ∼M³ (matrix multiplications in the singly excited basis). On the other hand, the signal calculation of a single trajectory already contains an ensemble average (∼M), which results in a total scaling of our method as ∼M³.

In our simulations of H₂O presented in Sec. 3 with M=128, the doubly excited state propagation consumes ≈99% of the calculation time. We found a good signal-to-noise ratio when averaging ≈100 trajectories per dipole orientation for pump and probe pulses. With 100 time steps in each time direction, a single trajectory calculation takes ≈2 h on an AMD Athlon© class processor, resulting in ≈1800 h single processor computation time to gain a 2D spectrum in the impulsive limit.

APPLICATION TO OH STRETCHING VIBRATIONS IN LIQUID WATER

The modeling approach described in Sec. 2 is well suited to simulate the nonlinear vibrational response of liquid water. This is due its capabilities, at least in principle, to reproduce the key features of the nonlinear response observed in the experiment:²⁶ frequency dependent spectral diffusion dynamics, frequency dependent anharmonicities, likely nonadiabatic and partially coherent energy transfer dynamics, i.e., exchange between fluctuating disordered vibrational excitons. In the following we show how we obtain the vibrational Hamiltonian for liquid water and that, indeed, our model does reproduce these key features convincingly.

The effective vibrational Hamiltonian

The vibrational Hamiltonian was constructed according to Sec. 2A. We assumed two fundamental modes per molecular site (symmetric and antisymmetric stretch), as shown in Eq. 18. Here, ${\widehat{B}}_{m,\nu }^{†}$ and ω_m,ν denote the creation operator and the fundamental transition frequency, respectively, for mode ν (ν=2,3, symmetric, antisymmetric) at the molecular site m. The intermolecular couplings J_{mν,m^′ν^′} are calculated using dipole-dipole coupling as given in Eq. 19, where μ_m,1ν are the fundamental transition dipole moments at molecular site m, R_mm^′ is the distance between sites m and m^′, and ${\tilde{\mathbf{R}}}_{m{m}^{\prime }}=\left({\mathbf{X}}_m-{\mathbf{X}}_{m^{\prime }}\right)∕R_{m{m}^{\prime }}$. Since the electrostatic map provides instantaneous local eigenstates, we set all intramolecular couplings to 0.

$$\widehat{H}\left(\tau \right)=\sum _{m=1}^{64}\sum _{\nu =2}^3{\omega }_{m,\nu }\left(\tau \right){\widehat{B}}_{m,\nu }^{†}{\widehat{B}}_{m,\nu }+\sum _{m^{\prime },m=1}^{64}\sum _{\nu ,{\nu }^{\prime }=2}^3{J}_{m\nu ,m^{\prime }{\nu }^{\prime }}\left(\tau \right){\widehat{B}}_{m,\nu }^{†}{\widehat{B}}_{m^{\prime },{\nu }^{\prime }}+\sum _{mn,m^{\prime }{n}^{\prime }=1}^{64}\sum _{\nu \gamma ,{\nu }^{\prime }{\gamma }^{\prime }=2}^3{V}_{m\nu n\gamma ,m^{\prime }{\nu }^{\prime }{n}^{\prime }{\gamma }^{\prime }}\left(\tau \right){\widehat{B}}_{m,\nu }^{†}{\widehat{B}}_{n,\gamma }^{†}{\widehat{B}}_{m^{\prime },{\nu }^{\prime }}{\widehat{B}}_{n^{\prime },{\gamma }^{\prime }},$$ (18)

$$J_{m\nu ,m^{\prime }{\nu }^{\prime }}\left(\tau \right)=\frac{1-{\delta }_{m{m}^{\prime }}}{4\pi ϵ}\cdot \frac{3{\mu }_{m,1\nu }\left(\tau \right)\cdot {\tilde{\mathbf{R}}}_{m{m}^{\prime }}\left(\tau \right){\mu }_{m^{\prime },1{\nu }^{\prime }}\left(\tau \right)\cdot {\tilde{\mathbf{R}}}_{m{m}^{\prime }}\left(\tau \right)-{\mu }_{m,1\nu }\left(\tau \right)\cdot {\mu }_{m^{\prime },1{\nu }^{\prime }}\left(\tau \right)}{R_{m{m}^{\prime }}^3\left(\tau \right)}.$$ (19)

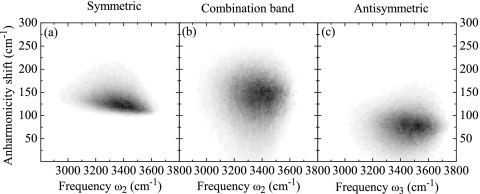
The intramolecular anharmonicities V with m=m^′=n=n^′ are calculated as the difference between the overtone frequencies provided by the electrostatic map and the respective harmonic values. For example, the anharmonicity shift of the antisymmetric overtone on molecule m=1 is V_1313,1313=ω_1,5−2ω_1,3. The distributions of the intramolecular anharmonicities are shown in Fig. 2. We also treat intermolecular anharmonicities, or coupling anharmonicities, that arise from anharmonic transition dipole moments [see below, Eq. 20], affecting the dipole-dipole coupling between local overtones and intermolecular combination bands. Still, the anharmonicity matrix V is rather sparse, greatly reducing the computational effort.

Figure 2.

Diagonal frequency anharmonicities. (a) Symmetric overtone ω₄, (b) antisymmetric overtone ω₅, and (c) intramolecular combination band ω₆, plotted as histograms vs their respective fundamental frequencies.

In a similar way, the transition dipole operator is constructed using Eq. 3 modified to account for the two fundamental modes per molecule, as shown in Eq. 20.

$$\widehat{\mu }\left(\tau \right)=\sum _{m=1}^{64}\sum _{\nu =2}^3{\mu }_{m,1\nu }\left(\tau \right)\left({\widehat{B}}_{m,\nu }^{†}+{\widehat{B}}_{m,\nu }\right)+\sum _{m=1}^{64}\sum _{\nu {\nu }^{\prime }{\nu }^{″}=2}^3\Delta {\mu }_{m,\nu {\nu }^{\prime }{\nu }^{″}}\left(\tau \right)\left({\widehat{B}}_{m,{\nu }^{″}}^{†}{\widehat{B}}_{m,{\nu }^{\prime }}^{†}{\widehat{B}}_{m,\nu }+{\widehat{B}}_{m,\nu }^{†}{\widehat{B}}_{m,{\nu }^{\prime }}{\widehat{B}}_{m,{\nu }^{″}}\right).$$ (20)

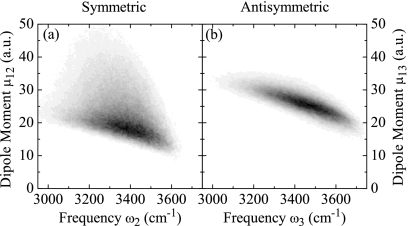
Here, μ_m,1ν are the fundamental transition dipole moments for mode m (transition from ground state into symmetric∕antisymmetric fundamental mode ν=2,3) at molecular site m. The distributions of amplitudes for fundamental transition dipole moments are shown in Fig. 3 as a function of the respective fundamental transition frequencies.

Figure 3.

Histograms of the fundamental transition dipole moment amplitudes as function of the respective transition frequencies. (a) Symmetric mode ν=2. (b) Antisymmetric mode ν=3.

In Eq. 20, we neglected intermolecular anharmonicities of the transition dipole moments. The intramolecular anharmonicities are calculated as the differences between the transition dipole moments involving overtones (μ_m,νν^′,ν=2,3,ν^′=4,5,6) and their harmonic counterparts. This is particularly important for harmonically forbidden transitions μ_m,25 and μ_m,34, which are now enabled due to the anharmonicities.

Ab initio electrostatic map

The electrostatic potential in the vicinity of a single H₂O molecule generated by the surrounding molecules is expanded to second order in Cartesian coordinates (Fig. 4)

$$U\left(\mathbf{X}\right)=U_0-\sum _{\alpha }{E}_{\alpha }{X}_{\alpha }-\frac{1}{2}\sum _{\alpha ,\beta }{E}_{\alpha \beta }{X}_{\alpha }{X}_{\beta }.$$ (21)

Apart from the overall shift U₀, Eq. 21 has nine independent multipole coefficient parameters (note that E_αβ=E_βα). They were arranged in a vector

$$\mathbf{C}=\left(E_x,E_y,E_z,E_{xx},E_{yy},E_{zz},E_{xy},E_{xz},E_{yz}\right).$$ (22)

C was calculated analytically at the origin of the molecular frame coordinate system from the surrounding water partial charges of MD configurations.

Figure 4.

Coordinate system fixed on H₂O.

The anharmonic gas phase vibrational potential surface of H₂O in presence of the multipole field C is expanded in the three normal coordinates Q_i to sixth order

$$V\left(\mathbf{Q};\mathbf{C}\right)=\sum _{k=1}^6{f}_{i_1\cdots i_k}^{\left(k\right)}\left(\mathbf{C}\right)\prod _{i=1}^k-Q_i,$$ (23)

where $f_{i_1\cdots i_k}^{\left(k\right)}\left(\mathbf{C}\right)$ are the anharmonic force constants, which are calculated by the quantum chemical calculations at the MP2∕6-31+G(d,p) level using our modified GAUSSIAN 03 code.³² The Hamiltonian was expanded in a harmonic basis set and was recast into a normal ordered form.⁴⁴ The vibrational eigenstates are calculated by diagonalizing a Hamiltonian using the implicit restarted Arnoldi method.^{44, 45, 46} High energy basis states where the total number of excitations n_T≡n₁+n₂+n₃ are larger than 14 are neglected.

Molecular vibrational frequencies of the six eigenstates (ground state, symmetric O–H stretch, antisymmetric O–H stretch, and their overtones and combinations) and the transition dipole moments between these states were parametrized with the multipole coefficients C.

The calculated gas phase frequencies of these six eigenstates are tabulated and compared to the reference high level calculation⁴⁷ in Table 1. The calculated frequencies are 0.6% to 1.2% higher than the reference calculations which employed higher computational level with larger basis sets. The anharmonicities of symmetric and antisymmetric O–H stretches have good agreement with the reference calculations (103 versus 113 cm⁻¹ and 71 versus 113 cm⁻¹).

Table 1.

Calculated anharmonic frequencies in the gas phase (is in cm⁻¹).

State	Frequency	Reference calc.a	Description
1	0.0	0.0	Ground state
2	3688.2	3657.0	s-δ(O–H)
3	3803.2	3779.5	a-δ(O–H)
4	7273.9	7201.6	s-δ(O–H)v=2
5	7535.1	7445.1	a-δ(O–H)v=2
6	7339.0		s-δ(O–H)+a-δ(O–H)

^aReference ⁴⁷.

The vibrational transition frequency from the ground state to state ν and the transition dipole moments between states ν and ν^′ were parametrized using the multipole coefficient vector C.

$${\omega }_{\nu }={\Omega }_{\text{gas}}^{\nu }+\sum _{\alpha }{\Omega }_{\alpha }^{\nu }{E}_{\alpha }+\frac{1}{2}\sum _{\alpha \beta }{\Omega }_{\alpha ,\beta }^{g\nu }{E}_{\alpha }{E}_{\beta },$$ (24)

$${\mu }_{\nu {\nu }^{\prime }}=M_{\text{gas}}^{\nu {\nu }^{\prime }}+\sum _{\alpha }{M}_{\alpha }^{\nu {\nu }^{\prime }}{E}_{\alpha }+\frac{1}{2}\sum _{\alpha \beta }{M}_{\alpha ,\beta }^{\nu {\nu }^{\prime }}{E}_{\alpha }{E}_{\beta }.$$

Here α and β denote the nine independent Cartesian coefficients α,β=x,y,z,xx,yy,zz,xy,xz,yz of the multipole vector in the molecular frame coordinate system.

The expansion coefficients are calculated by using the central difference formulas.⁴⁴ The calculated map is given in Table 2. Due to the molecular symmetry, the first derivatives with respect to the components E_x, E_y, E_xy, E_xz are 0. The electric field in parallel to the molecular axis (E_z) blueshifts both symmetric and antisymmetric O–H stretch frequencies since the negative charged oxygen moves toward the center of the hydrogens resulting in shorter O–H distances. The calculated map of the transition dipole moments is given in Table 3.

Table 2.

Electrostatic ab initio map of the frequencies of the six states. The state (n,m) represent the n and m quanta on symmetric O–H stretch and antisymmetric O–H stretch modes. Unit is in cm⁻¹ for Ω_gas and cm⁻¹ a.u.⁻¹ for ${\Omega }_{\alpha }^{\left(1\right)}$.

	(1,0)	(0,1)	(2,0)	(0,2)	(1,1)
Ωgas	3 688.2	3 803.3	7 274.0	7 535.1	7 339.1
${\Omega }_x^{\left(1\right)}$	0.0	0.0	0.0	0.0	0.0
${\Omega }_y^{\left(1\right)}$	13.6	−10.0	113.2	−17.7	−70.3
${\Omega }_z^{\left(1\right)}$	718.4	2 468.7	1 621.9	4 410.5	2 983.1
${\Omega }_{xx}^{\left(1\right)}$	3 357.7	3 209.3	6 661.2	6 512.3	6 530.4
${\Omega }_{yy}^{\left(1\right)}$	−2 327.6	−346.0	−4 618.7	−893.1	−3 197.5
${\Omega }_{zz}^{\left(1\right)}$	−898.8	−3 025.0	−2 110.4	−5 706.7	−3 746.5
${\Omega }_{xy}^{\left(1\right)}$	0.0	0.0	0.0	0.0	0.0
${\Omega }_{xz}^{\left(1\right)}$	0.0	0.0	0.0	0.0	0.0
${\Omega }_{yz}^{\left(1\right)}$	−36.8	40.3	−241.0	116.2	123.1
${\Omega }_{x,x}^{\left(2\right)}$	−8 713	−10 288	−15 388	−16 391	−16 668
${\Omega }_{x,y}^{\left(2\right)}$	35	−1 025	−1 495	−952	−5 528
${\Omega }_{x,z}^{\left(2\right)}$	85	−707	1 124	−3 033	−122
${\Omega }_{x,xx}^{\left(2\right)}$	−1 458	−1 139	−4 708	−1 936	−4 474
${\Omega }_{x,yy}^{\left(2\right)}$	−391	−329	−1 534	−2 080	−1 508
${\Omega }_{y,y}^{\left(2\right)}$	−146 732	−18 760	−433 759	−122 156	57 031
${\Omega }_{y,z}^{\left(2\right)}$	−19 598	18 453	−66 921	−1 397	64 275
${\Omega }_{y,yy}^{\left(2\right)}$	−5 335	3 976	−13 762	1 491	4 906
${\Omega }_{y,zz}^{\left(2\right)}$	−4 236	1 661	−16 319	−4 243	4 158
${\Omega }_{y,yz}^{\left(2\right)}$	730 072	−238 293	2 166 068	206 542	−874 097
${\Omega }_{z,z}^{\left(2\right)}$	−51 748	−54 710	−113 723	−107 120	−109 830
${\Omega }_{z,yy}^{\left(2\right)}$	36 402	28 076	68 327	63 670	70 467
${\Omega }_{z,zz}^{\left(2\right)}$	35 784	44 947	81 728	84 202	80 643
${\Omega }_{z,yz}^{\left(2\right)}$	−43 643	41 195	1 784 127	−6 716	62 014
${\Omega }_{xx,xx}^{\left(2\right)}$	−6 302	−5 669	−12 190	−15 493	−11 616
${\Omega }_{yy,yy}^{\left(2\right)}$	−46 859	−54 927	−96 941	−110 177	−101 532
${\Omega }_{yy,zz}^{\left(2\right)}$	17 928	30 437	36 236	59 553	41 087
${\Omega }_{yy,yz}^{\left(2\right)}$	−4 856	7 162	−11 763	11 318	13 978
${\Omega }_{zz,zz}^{\left(2\right)}$	−15 942	−20 310	−33 379	−39 360	−33 977
${\Omega }_{zz,yz}^{\left(2\right)}$	−14 357	15 009	1 667 989	4 962	26 631
${\Omega }_{xy,xy}^{\left(2\right)}$	−30 756	−26 260	−63 808	−52 785	−59 364
${\Omega }_{xz,xz}^{\left(2\right)}$	−23 895	−19 764	−46 442	−38 728	−44 292
${\Omega }_{yz,yz}^{\left(2\right)}$	−134 452 4	952 919	−4 603 900	273 512	3 100 575

Table 3.

Electrostatic ab initio map of the allowed transition dipole moments of the six states (linear part). The state (n₁,n₂)→(m₁,m₂) represents the transition between the state (n₁,n₂) and (m₁,m₂). The x components of the transition dipole moments are always zero and y and z components are shown. Unit is in a.u. for M_gas and $M_{\alpha }^{\left(1\right)}$.

	(0,0)→(1,0)	(0,0)→(0,1)	(1,0)→(2,0)	(1,0)→(1,1)	(0,1)→(0,2)	(0,1)→(1,1)
Mgas	(0.03, 4.11)	(10.66, −0.01)	(0.21, 5.60)	(10.72, −0.10)	(−14.30, 0.02)	(−0.03, 4.24)
${\mathbf{M}}_x^{\left(1\right)}$	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)
${\mathbf{M}}_y^{\left(1\right)}$	(−447.6, −0.4)	(1.3, −127.1)	(−840.6, −0.4)	(9.8, −12.7)	(0.8, 246.4)	(−80.8, 0.2)
${\mathbf{M}}_z^{\left(1\right)}$	(−1.1, −172.2)	(−154.9, 0.8)	(−10.8, −224.7)	(−155.4, 8.6)	(188.6, −0.7)	(5.9, −176.1)
${\mathbf{M}}_{xx}^{\left(1\right)}$	(0.1, −9.9)	(−35.2, −0.1)	(0.7, −14.1)	(−35.2, −0.4)	(−25.9, 0.2)	(−0.4, −10.2)
${\mathbf{M}}_{yy}^{\left(1\right)}$	(0.6, 170.1)	(297.9, −0.4)	(2.6, 234.2)	(298.9, −3.0)	(−416.9, 0.9)	(1.9, 171.0)
${\mathbf{M}}_{zz}^{\left(1\right)}$	(0.7, 64.7)	(6.3, −0.5)	(8.1, 80.7)	(6.7, −5.6)	(12.5, 0.2)	(−5.2, 67.7)
${\mathbf{M}}_{xy}^{\left(1\right)}$	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)
${\mathbf{M}}_{xz}^{\left(1\right)}$	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)	(0.0, 0.0)
${\mathbf{M}}_{yz}^{\left(1\right)}$	(1000.8, −0.1)	(−1.7, −49.7)	(1872.9, −1.1)	(−5.1, −285.0)	(1.8, −216.9)	(−121.6, 1.0)

In order to construct the vibrational Hamiltonian, we performed a MD simulation of a small (M=64 molecules) simple point charge extended water system at room temperature and constant volume using the GROMACS-3.3.1 program.⁴⁸ The electric fields generated by the solvent environment were calculated analytically³² at every molecular site and time step. The electrostatic map was applied to calculate the transition frequencies and dipole moments for each molecule and time step.

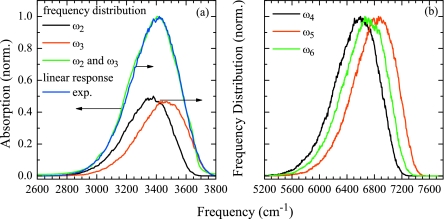
Comparing the resulting distributions of the fundamental transition frequencies ω₂ and ω₃ to the experimental absorption spectrum, we found the solvent shifts generated by the electrostatic map insufficient. We compensated for this effect by scaling all electric fields with a factor of 2.2 to match the maximum of the fundamental frequency distribution to the maximum of the linear spectrum of H₂O, as shown in Fig. 5a. In Fig. 5b we show the resulting overtone frequency distributions.

Figure 5.

(a) Fundamental frequency distribution of the symmetric ω₂ (black), antisymmetric ω₃ (red) OH stretching vibration, and combined symmetric and antisymmetric frequency distribution (green), blue: experimental linear spectrum (Ref. ⁵⁶). (b) Overtone frequency distributions, symmetric overtone ω₄ (black), antisymmetric overtone ω₅ (red), and combination band ω₆ (green).

Nonlinear infrared response

Our recent study of liquid water²⁸ focused on the effect of intermolecular coupling on the dynamics and the 2DIR correlation spectra of the OH stretching vibrations. We used the dielectric constant ϵ in the resonant dipole-dipole coupling Eq. 19 as a scaling factor to reproduce the PA decay regime of ≈80 fs observed experimentally,^{25, 26, 49} evident for the fully resonant coupling regime in liquid H₂O. Good agreement with experiment was found for an average next neighbor coupling κ=12 cm⁻¹.²⁸ We will describe these results and discuss the effects observed in the context of the simulation method.

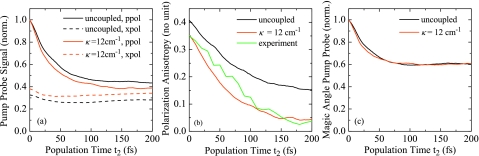
In Fig. 6a, we show the spectrally integrated PP signal for parallel and crossed polarization of pump and probe pulses for two coupling regimes. Figures 6b, 6c show S_PA and S_MA calculated from these signals, respectively. Also shown in Fig. 6b is the experimentally observed PA in H₂O.²⁶

Figure 6.

Spectrally integrated signals. (a) PP transients for parallel (ppol) and crossed (xpol) polarization of pump and probe pulses for two coupling regimes. (b) S_PA calculated from (a), green: experimental PA (Ref. ²⁶). (c) S_MA calculated from (a).

For the uncoupled system, all dynamics observed in Fig. 6 are caused by modulations of the transition dipole moments, since all energy transfer pathways are blocked and all populations remain constant. The PA reflects orientational modulations of the transition dipole moments which are caused by two major effects—(i) fluctuations of the transition dipole moments and (ii) librational motion and rotational diffusion. The former is found to be very strong in H₂O, accounting for ≈1∕2 of the signal decay. On the other hand, the S_MA signal shows a fast initial decay that is entirely due to amplitude fluctuations of the transition dipole moments. This effect has not been addressed before, and we note that it should be considered when population relaxation dynamics are extracted from MA data.

When adding the intermolecular coupling, the anisotropy decay Fig. 6b speeds up with increasing coupling strength and the long-lived components vanish. This effect can be clearly assigned to intermolecular energy transfer. We expect that the transfer process is at least partially coherent, and has to be understood as randomized energy transport between the disordered excitons. Since the total exciton population remains unchanged, the S_MA signal is unaffected by these processes, as can be seen in Fig. 6c.

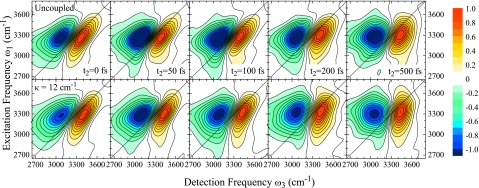
In Fig. 7, we show a series the 2DIR correlation spectra for two coupling regimes, uncoupled and κ=12 cm⁻¹, for different population times t₂. All spectra exhibit two peaks. The positive peak on the diagonal corresponds to the fundamental 0→1 transition. The negative peak originating from 1→2 ESA is red shifted due to anharmonicities. Strong interference between these two peaks results in significant signal cancellation and distortion of the peak shapes in the overlap region. Despite these distortions, we observe a clear V-shape of the ESA peak that, in part, is caused by the distributions of diagonal anharmonicities as shown in Fig. 2.

Figure 7.

2DIR correlation spectra of the OH stretching vibration in H₂O for population times t₂=0, 50, 100, 200, and 500 fs. Top panel: uncoupled system, bottom panel: κ=12 cm⁻¹. Each spectrum is normalized to its maximum.

In both coupling regimes, the fundamental peak is stretched along the diagonal at population time t₂=0 fs, indicative of initial inhomogeneity in the sample. This inhomogeneity is lost as with t₂ on very similar time scales for both systems. However, no single time scale for loss of correlations can be extracted from these spectra. We instead observe these dynamics to vary across the spectrum. For both regimes, the red side loses correlations faster than the blue side. For the uncoupled system, we observe mainly two spectral components showing different dynamics which we attribute to the symmetric stretch on the red side and the antisymmetric OH stretch on the blue side. Extraction of the respective time scales is, however, difficult due to the spectral overlap of the two modes. For κ=12 cm⁻¹, no such separation is observed. The excitonic energy transfer instead smoothes out the dynamics across the spectrum. This is most obvious from the bending of the fundamental peak shape and the nodal line between the peaks in the t₂=100 and 200 fs spectra.

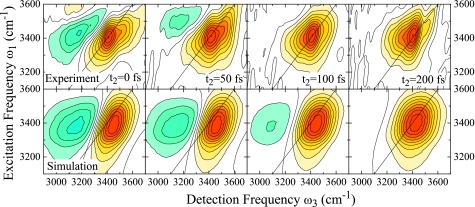
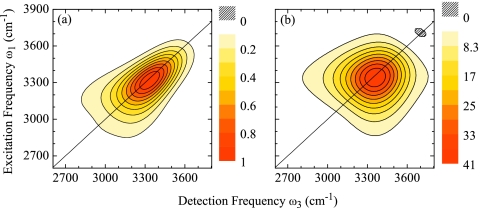
For direct comparison with experiment, we corrected our simulation results for κ=12 cm⁻¹ to match the experimental conditions by multiplication of the frequency domain response with the experimental excitation pulse spectra along ω₁ and ω₃. Additionally, we included population relaxation effects using ad hoc description of the population relaxation with a population lifetime of T₁=200 fs.²⁵ We also model the persisting GSB observed in the experiment.²⁶ The extraction of the GSB contribution to the total nonlinear response is, however, difficult for excitonic systems. This is discussed in Sec. 4. We instead use an approximate description for the GSB contribution as described in Appendix B. With these assumptions, we find close agreement between our simulations and experiment as is shown in Fig. 8.

Figure 8.

2DIR correlation spectra of the OH stretching vibration in H₂O for population times t₂=0, 50, 100, and 200 fs. Top panel: experimental data (Ref. ²⁶), bottom panel: κ=12 cm⁻¹ corrected for experimental pulse spectrum and ad hoc population relaxation, see text. Each spectrum is normalized to its maximum. Figure adapted from Ref. 28.

Discussion of the nonlinear vibrational response of H₂O

The features and dynamics observed in the nonlinear vibrational response of neat H₂O can be assigned to two major contributions—local intramolecular effects and excitonic effects. The former are caused by the local 2D OH stretching potential. Fluctuations in the local environment lead to modulations of the mixing between the states resulting in strong fluctuations of the fundamental dipole moments as well as the overtone frequencies and dipole moments. This can to some extent be interpreted as intramolecular energy transfer. Also, the strong local anharmonicities lead to breakdown of harmonic selection rules, enabling additional pathways contributing to the nonlinear response. Additionally, we observe faster fluctuations for the symmetric stretch mode on the red side of the spectrum, see Fig. 7, compared to the antisymmetric mode on the blue side. Very similar effects have been observed for water in acetonitrile,⁵⁰ where this is attributed to non-Gaussian dynamics caused by local mode couplings. Similarly, modulations of the Fermi resonance of the symmetric mode with the OH bending mode overtone is likely to impact the fast fluctuation time scales observed. This is included in our model through the quantum chemical calculations leading to the electrostatic map.

Apart from all those dynamical effects, the distributions of transition frequencies and dipole moments and their anharmonicities also have significant impact on the peak shapes observed in the 2DIR correlation spectra. The dipole moment distributions as shown in Fig. 3 lead to amplitude distortion. The distributions of local frequency anharmonicities (see Fig. 2) create a distinct ESA peak shape and also lead to significant cancellation in the peak overlap region, see Fig. 10. The combination of all these effects makes it quite clear why a simple analysis of the spectra,^{51, 52} e.g., nodal line slope or dynamic line width analysis is likely to fail for H₂O, even for the uncoupled system.

The intermolecular coupling on the other hand, mainly affects the PA dynamics. Here, the fast transfer time scales observed experimentally are reproduced for an average next neighbor coupling as small as 12 cm⁻¹. We find that the large number of acceptor modes, as well as anharmonicities and fluctuations in the system open up many intermolecular transfer pathways, leading to a full decay of the PA on these fast time scales, even for these small couplings. It is not possible to estimate the coherence contributions to the energy transfer process from our simulations. No clear physical model of energy transfer and dynamic delocalization for such fluctuating disordered excitons has been developed to date.

Excitonic effects on the 2DIR correlation spectra are rather subtle. The overall dynamics are almost unaffected by the excitonic coupling. Rather than speeding up dynamics as one might expect, the excitonic interactions smooth out the fluctuations across the spectrum leading to a continuous distribution of spectral diffusion time scales from ≈100 fs on the red side to >200 fs on the blue side of the spectrum. These time scales are in close agreement with the experimental results.²⁶

We show here that indeed a very high level of theory is necessary to satisfactorily model the nonlinear vibrational response of the OH stretching vibration of liquid H₂O. Non-Gaussian distributions and dynamics, non-Condon effects, distributions of anharmonicities, and excitonic interactions all significantly affect the signal, and therefore must be accounted for. The NISE approach combined with our split operator technique provides all this functionality at manageable computational cost, and in its generality is highly adaptable to any excitonic system.

INTERFERENCE BETWEEN LIOUVILLE PATHWAYS IN EXCITONIC SYSTEMS

In this section, we will address interference effects as they appear in simulations of the nonlinear response of excitonic systems, and how they affect the interpretation of the signal. We note that these interferences are a purely theoretical phenomenon but may affect the total signal through numerical accuracy. This can be avoided by building in the interferences from the outset using a quasiparticle representation and the nonlinear exciton equation.⁵⁴

The third order response of a three band exciton model has three Liouville pathways—GSB, ESE, and ESA—contributing to the total response along a given phase matching direction as shown in Fig. 1. For localized excitations these pathways can be analyzed and interpreted separately, i.e., the GSB pathway can be written such that it reproduces the dynamics and spectral features of a bleached vibrational ground state. For excitons this is not generally possible due to subtle interferences between the different pathways. Only the total signal as the sum of all pathways can be obtained. We will describe and discuss this phenomenon below.

Let us consider a collection of N vibrational chromophores, where the dipole moments are localized on each chromophore. The Green’s function expressions Eq. 6 are written in this local basis. For simplicity, we here apply the Condon approximation (μ_m(τ)≡μ) and will only look at the rephasing GSB diagram S₁:

$$S_1\left(t_1,t_3\right)=-{\mu }^4\sum _{ijkl}{\left(G_{ij}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}{G}_{kl}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right).$$ (25)

In the absence of vibrational coupling between these chromophores, i.e., localized excitations, G⁽¹⁾ is a diagonal matrix, and Eq. 25 simplifies even more.

$$S_1\left(t_1,t_3\right)=-{\mu }^4{\left(\sum _i{G}_{ii}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}\left(\sum _k{G}_{kk}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right)\right).$$ (26)

Equation 26 can be interpreted as follows: if we think of the third order response as the correlation of coherences at different times, the two terms describe the coherences on modes k and i during t₁ and t₃, respectively. However, in Eq. 26 we not only sum over coherences of the same mode (i=k) but also over coherences between different modes (i≠k). For illustration, we recast Eq. 26:

$$S_1\left(t_1,t_3\right)=-{\mu }^4\sum _i{\left(G_{ii}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}\left(G_{ii}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right)\right)-{\mu }^4\sum _{i\ne k}{\left(G_{ii}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}\left(G_{kk}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right)\right).$$ (27)

The first term resembles what is usually discussed as GSB. It locally measures the correlations between coherences during t₁ and t₃ and then performs an ensemble average (∑_i). Double Fourier transforming this first term alone produces a 2D spectrum with one peak on the diagonal and a peak shape according to the spectral diffusion dynamics of the system, as illustrated in Fig. 9a.

Figure 9.

Double Fourier transform of the first (a) and second (b) terms of Eq. 27. As an example, we used the t₂=0 fs, κ=12 cm⁻¹ water data shown in Fig. 7.

The second term of Eq. 27 on the other hand, measures correlations between coherences of different modes i and k. Even in the extreme case of a purely inhomogeneously broadened system, the 2D spectrum of this contribution alone would show a round shape (no stretching along the diagonal). An example is shown in Fig. 9b.

However, for localized excitations this second term does not produce nonlinear signal. It can be shown straight forwardly that it is cancelled exactly with equivalent terms in S₂ and S₃. Thus, by only considering these diagonal contributions to the response the usual picture and interpretation of the GSB, ESE, and ESA can be recovered.

For excitons, it is hard to extract the individual contributions to the total response. We can write down and interpret the response similarly to Eq. 27, but taking into account the vibrational couplings, resulting in nonzero off-diagonal elements of the Green’s functions:

$$S_1\left(t_1,t_3\right)=-{\mu }^4\sum _{ij}{\left(G_{ij}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}\left(G_{ij}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right)\right)-{\mu }^4\sum _{i\ne k,j\ne l}{\left(G_{ij}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right)\right)}^{†}\left(G_{kl}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right)\right).$$ (28)

The first term of Eq. 28 still resembles a GSB-like peak shape. The second term, however, does not cancel out exactly with the other diagrams S₂ and S₃ as soon as V≠0 or μ≠0, i.e., in the case of any anharmonicity in the system. This effect occurs due to energy transfer in the S₃ diagram that essentially leads to redistribution of anharmonic effects. The nonlinear signal contribution emerging from these off-diagonal terms is neither GSB, ESE, nor ESA. It only emerges as a subtle interference and incomplete cancellation between the diagrams.

In general, these off-diagonal contributions scale as N⁴ since each dipole can act on a different chromophore. However, nonlinear signal is generated only when all four interactions occur within the coherence size of the exciton. Otherwise the contributions cancel due to destructive interference between all pathways. This partial destructive interference prevents a simple interpretation of the signal in terms of the individual pathways.⁵³

We note that, in general, the total signal will be significantly weaker than the individual diagrams depending on the ratio between the total system size and the coherence size of the excitons. This interference reflects the fact that individual pathways scale as N⁴ whereas the overall response only scales as N². It should be done carefully since it may affect the numerical accuracy of simulations. The quasiparticle representation and the nonlinear exciton equations build this interference from the outset and avoid this difficulty.^{38, 54}

CONCLUSIONS

We presented a simulation formalism for calculations of the nonlinear optical response of excitons based on numerical integration of the Schrödinger equation. This protocol is highly versatile, enabling explicit treatment of nonadiabatic exciton transport, fluctuations of the transition frequencies, transition dipole moments, intermode couplings and the diagonal, and off-diagonal anharmonicities of all these quantities. The split operator technique greatly reduces computational cost, opening up a wide range of excitonic systems to be treated. Even though we here fully developed the model for vibrational excitons, it can be straight forwardly adapted to treat electronic excitations, as well.

We used the method to simulate the third order response of the OH stretching vibration in neat liquid water. An ab initio electrostatic map for the OH stretching vibrations in water is presented. The simulation results are in good agreement with the experimental data. It is found that intramolecular effects owing to the sensitivity of the two-dimensional OH stretching potential are the major cause of the dynamics observed. The experimental energy transfer times are reproduced for surprisingly small intermolecular couplings.

APPENDIX A: FACTORIZATION OF THE HARMONIC TWO-PARTICLE PROPAGATOR

In the following, we will consider the harmonic part of the effective Hamiltonian denoted as ${\widehat{H}}_0\left(\tau \right)$, i.e., the first two terms of Eq. 2:

$${\widehat{H}}_0\left(\tau \right)=\sum _m{\omega }_m\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_m+\sum _{m^{\prime }\ne m}{J}_{m,m^{\prime }}\left(\tau \right){\widehat{B}}_m^{†}{\widehat{B}}_{m^{\prime }}.$$ (A1)

The infinitesimal propagators for singly excited states used in Eq. 9 are now denoted as $U_0^{\left(1\right)}$ written in the singly excited local basis $\mid m⟩={\widehat{B}}_m^{†}\mid 0⟩$:

$$U_{0,mn}^{\left(1\right)}\left(\tau \right)=⟨m\mid {\widehat{U}}_0\left(\tau \right)\mid n⟩=⟨m\mid \text{exp}\left(-i{\widehat{H}}_0\left(\tau \right)\Delta \tau \right)\mid n⟩.$$ (A2)

The doubly excited infinitesimal propagator $U_0^{\left(2\right)}\left(\tau \right)$ can be calculated by factorization of $U_0^{\left(1\right)}\left(\tau \right)$. In the following, we omit the explicit τ dependence for clarity.

$$U_{0mn,m^{\prime }{n}^{\prime }}^{\left(2\right)}=⟨m,n\mid {\widehat{U}}_0\mid m^{\prime },n^{\prime }⟩={\delta }_{mn}{\delta }_{m^{\prime }{n}^{\prime }}{U}_{0,m{m}^{\prime }}^{\left(1\right)}{U}_{0,n{n}^{\prime }}^{\left(1\right)}+\sqrt{2}\left({\delta }_{mn}\left(1-{\delta }_{m^{\prime }{n}^{\prime }}\right)U_{m{m}^{\prime }}^{\left(1\right)}{U}_{m{n}^{\prime }}^{\left(1\right)}+{\delta }_{m^{\prime }{n}^{\prime }}\left(1-{\delta }_{mn}\right)U_{m{m}^{\prime }}^{\left(1\right)}{U}_{n{m}^{\prime }}^{\left(1\right)}\right)+\left(1-{\delta }_{mn}\right)\left(1-{\delta }_{m^{\prime }{n}^{\prime }}\right)\left(U_{m{m}^{\prime }}^{\left(1\right)}{U}_{n{n}^{\prime }}^{\left(1\right)}+U_{n{m}^{\prime }}^{\left(1\right)}{U}_{m{n}^{\prime }}^{\left(1\right)}\right),$$ (A3)

where $\mid m,n⟩=\left(1∕\sqrt{1+{\delta }_{mn}}\right){\widehat{B}}_m^{†}{\widehat{B}}_n^{†}\mid 0⟩$. This rather complicated structure of the two-particle propagator arises from the properties of the symmetrized two-particle basis. It can be shown straight forwardly that any basis transformation matrix in a symmetrized two-particle basis has the given structure.

APPENDIX B: AD HOC POPULATION RELAXATION FOR VIBRATIONAL EXCITONS

The phenomenon described in Sec. 4 has a direct impact on ad hoc description of population relaxation for vibrational excitons. Population relaxation is included by adding relaxation factors Γ to Eq. 8.

$$S_{\text{I}}\left(t_1,t_2,t_3\right)=\left(\sum _{k=1}^3{S}_k\left(t_1,t_2,t_3\right){\Gamma }_k\left(t_1,t_2,t_3\right)\right),$$ (B1)

$$S_{\text{II}}\left(t_1,t_2,t_3\right)=\left(\sum _{k=4}^6{S}_k\left(t_1,t_2,t_3\right){\Gamma }_k\left(t_1,t_2,t_3\right)\right).$$

It is often assumed that the different levels of excitation have different decay times,¹⁵, ⁵⁵ i.e., T₁ for ground and excited state populations ∣0⟩⟨0∣ and ∣1⟩⟨1∣, T₁∕2 for ∣0⟩⟨1∣ coherences, and 3T₁∕2 for ∣1⟩⟨2∣ coherences, as shown in Eq. B2.

$${\Gamma }_{1,2,4,5}\left(t_1,t_2,t_3\right)=\text{exp}\left(\frac{-t_1-2t_2-t_3}{2T_1}\right),$$ (B2)

$${\Gamma }_{3,6}\left(t_1,t_2,t_3\right)=\text{exp}\left(\frac{-t_1-2t_2-3t_3}{2T_1}\right).$$

No such procedure is possible when treating vibrational excitons. If different ad hoc factors as shown in Eq. B2 are applied to the different diagrams, the proper cancellation between the diagrams is prevented and the resulting nonlinear signal is physically wrong. Consequently, for excitons one can only use one relaxation factor for all the diagrams, e.g.,

$${\Gamma }_{1–6}\left(t_1,t_2,t_3\right)=\text{exp}\left(\frac{-t_1-2t_2-t_3}{2T_1}\right).$$ (B3)

This effect poses serious difficulties when trying to describe a persisting GSB as observed experimentally in the case of H₂O discussed in Sec. 3C. Using a different T₁ time for the GSB diagrams S₁ and S₄ is not possible since this would prevent proper cancellation of the off-diagonal elements of the response [second term in Eq. 28], and thus lead to wrong results.

We instead propose an approximate description for the GSB, that is the first term in Eq. 28 only. This can be expressed by rewriting the rephasing nonlinear response S_I as follows. We now again include intermolecular couplings and fluctuations of the transition dipole moments.

$$S_{\text{I}}=-\sum _{ijkl}{\left({\mu }_i\left({\tau }_3\right)G_{ij}^{\left(1\right)}\left({\tau }_3,{\tau }_2\right){\mu }_j\left({\tau }_2\right)\right)}^{†}\left({\mu }_k\left({\tau }_1\right)G_{kl}^{\left(1\right)}\left({\tau }_1,{\tau }_0\right){\mu }_l\left({\tau }_0\right)\right)\text{exp}\left(\frac{-t_1-t_3}{2T_1}\right)\text{exp}\left(\frac{-t_2}{T_1^{ijkl}}\right)+\left(S_2\left(t_1,t_2,t_3\right)+S_3\left(t_1,t_2,t_3\right)\right)\text{exp}\left(\frac{-t_1-2t_2-t_3}{2T_1}\right),$$ (B4)

where we choose $T_1^{ijkl}$ as

$$T_1^{ijkl}=\{\begin{array}{ll}{T}_{1,\text{GSB}}\hfill & \text{for}i=k\text{and}j=l\hfill \\ T_1\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (B5)

The nonrephasing response S_II is done equivalently. Here, T_1,GSB is the lifetime of the GSB and T₁ is the excited state population lifetime. Using Eqs. B4, B5, we can now choose different times T_1,GSB and T₁ without preventing the proper cancellation of the off-diagonal elements of the response, i.e., we can describe a ground state bleach that persists beyond the excited state population time T₁, by using a, respectively, larger value T_1,GSB. For the data shown in Fig. 8 we chose T₁=200 fs and T_1,GSB=∞.

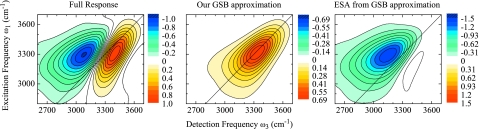
For illustration, we show the different contributions for the t₂=0 fs, κ=12 cm⁻¹ H₂O data in Fig. 10. The GSB contribution as discussed above is shown in (b). At t₂=0 fs, the ESE is identical to the GSB. It is therefore possible at this population time only, to fully dissect the response into the different contributions. In Fig. 10c we show the resulting ESA contribution. From the amplitudes of the signals we see that about 50% of the total amplitude is lost in the full response due to cancellation between the peaks. Similarly, the antidiagonal width of the peaks is significantly narrower in the full response compared to the individual contributions, greatly distorting simple analysis of the dynamics.

Figure 10.

2DIR correlation spectra of H₂O at t₂=0 fs for κ=12 cm⁻¹. (a) Full response, (b) GSB only, and (c) ESA extracted from (a) and (b). All spectra are normalized to the full response amplitude. Note the scales for each spectrum.