Abstract
The paper deals with a diffusing particle that escapes from a cavity to the outer world through a narrow cylindrical tunnel. We derive expressions for the Laplace transforms of the particle survival probability, its lifetime probability density, and the mean lifetime. These results show how the quantities of interest depend on the geometric parameters (the cavity volume and the tunnel length and radius) and the particle diffusion coefficients in the cavity and in the tunnel. Earlier suggested expressions for the mean lifetime, which correspond to different escape scenarios, are contained in our result as special cases. In contrast to these expressions, our formula predicts correct asymptotic behavior of the mean lifetime in the absence of the cavity or tunnel. To test the accuracy of our approximate theory we compare the mean lifetime, the lifetime probability density, and the survival probability (the latter two are obtained by inverting their Laplace transforms numerically) with corresponding quantities found by solving numerically the three-dimensional diffusion equation, assuming that the cavity is a sphere and that the particle has the same diffusion coefficient in the cavity and in the tunnel. Comparison shows excellent agreement between the analytical and numerical results over a broad range of the geometric parameters of the problem.
INTRODUCTION
In the present paper we study a diffusing particle that escapes from a cavity to the outside world through a narrow cylindrical tunnel. While earlier studies of the problem1, 2, 3 are focused on the mean particle lifetime, which is only the first moment of the distribution, we develop a theory that allows us to derive expressions for the Laplace transforms of the particle lifetime probability density and its survival probability. The former is used to obtain an expression for the mean lifetime that contains the results earlier reported in the literature as special cases, which correspond to different escape scenarios. This is a consequence of the fact that our approach is quite general in the sense that it does not assume any particular scenario. The results obtained in the paper show how the escape kinetics depends on the geometric and transport parameters of the system, namely, the cavity volume, the length and radius of the tunnel, and the particle diffusion coefficients in the tunnel and cavity, which may be different.
The model of a diffusing particle escaping from a cavity through a narrow tunnel has been proposed and used when discussing escape of signaling ions and proteins from dendritic spines,1, 2, 3, 4 which are small, micrometer in size protrusions on dendrites. Although there is enormous variability in spine morphology,5 the classical dendritic spine consists of a bulbous head connected to the parent dendrite by a narrow neck. It is believed that dendritic spines are important for communication between nerve cells, since the majority of excitatory synapses in the brain are on spines rather than dendrites. Cells use spines as sites where sufficiently high concentrations of signals can be generated and kept long enough to initiate signaling cascades.1, 2, 3, 4 Therefore, the signal lifetime in the spine is an important parameter.
The dependence of the mean lifetime on spine geometry has been considered in Refs. 1, 2, 3. Denoting the volume of the head by V and the length and radius of the cylindrical spine neck by L and a, we can write the formula for τ suggested in Ref. 1 as
| (1) |
where D is the particle diffusion coefficient in the neck. This formula fails when L or V tends to zero. An alternative formula, which has correct asymptotic behavior in both limiting cases, was suggested in Ref. 2 assuming the same diffusion coefficient of the particle in the head and neck of the spine,
| (2) |
In Ref. 3 this result was modified and the following formula was suggested:
| (3) |
where α=0.84 is a parameter found by fitting the formula to the results for τ obtained in Brownian dynamics simulations with 500–1000 trajectories which started from the center of the spherical cavity used as a model of the spine head. The lifetime τ[3] like τ[1] vanishes as L→0 in contrast to τ[2], which remains finite in this limit.
The results in Eqs. 1, 2, 3 correspond to different scenarios of the escape process. The expression in Eq. 1 can be obtained assuming that the rate of escape is controlled by the signal passage through the neck. Imposing absorbing boundary conditions at the neck-dendrite boundary and assuming that the neck volume is small compared to that of the head, one can write the flux escaping from the cavity containing N(t) particles as Dπa2N(t)∕(LV). Then variation of the number of particles in the spine satisfies the following rate equation:
| (4) |
which leads to the result for τ[1] in Eq. 1.
Expression in Eq. 2 was obtained for a different escape scenario, which assumes that a particle entering the neck could not return to the head. As a consequence, Eq. 2 gives the mean lifetime as the sum of two mean first passage times, τneck and τhead. The former is the mean first passage time through the neck to the dendrite while the latter is the mean first passage time from the head to the neck entrance. The expression for τneck can be obtained by solving one-dimensional diffusion equation on the interval of length L terminated by reflecting and absorbing end points. For a particle starting from the reflecting boundary (blocked entrance from the neck to the cavity), the result is τneck=L2∕(2D). To find τhead one has to consider a particle diffusing in a cavity with a small circular absorbing spot (entrance to the neck) on the wall. When the spot size is small enough and the particle starting position is not too close to the spot, the particle lifetime in the cavity is much larger than the longest intracavity relaxation time. As a consequence, the particle survival probability decays as a single exponential with the rate constant, which is equal to the inverse of the mean particle lifetime τhead. One can find a heuristic, back-of-the-envelope derivation, which leads to τhead=V∕(4Da) and explains why the mean lifetime depends only on the cavity volume and is independent of the shape of the cavity in Ref. 6. In this work the formula for τhead was also compared with the mean lifetimes obtained in Brownian dynamics simulations. It was found that numerical results for spherical and cubic cavities were in excellent agreement with the formula when the spot radius is small enough. Rigorous analysis of the problem, which validates the formula for τhead, can be found in Refs. 2b, 7, 8.
When deriving the expression in Eq. 3, the authors of Ref. 3 dropped the hypothesis that the particle entering the neck could not return, which underlies the result in Eq. 2. They considered the scenario, in which a particle entering the neck either went through and escaped to the dendrite (reached the absorbing neck-dendrite boundary) or returned to the spine head and entered the neck again later. Eventually, after several unsuccessful attempts, this particle escapes. However, when the length of the neck significantly exceeds its radius, L⪢a, it takes the particle much more time to escape than it is suggested by the no return scenario, which leads to the estimate in Eq. 2. Note that the ratio 4α∕π is very close to unity. Therefore, the second term in τ[3] is practically identical to τ[1].
We will see that the general, scenario-independent expression for the mean lifetime reduces to the sum of the mean lifetimes given in Eqs. 1, 2, τ=τ[1]+τ[2], if the diffusion coefficient does not change when the particle enters the tunnel from the cavity. This expression is obtained in Sec. 2 using the approximate solution for the Laplace transform of the particle lifetime probability density. To check the accuracy of our approximate theory, we compare theoretical predictions with the results obtained by solving numerically the three-dimensional diffusion equation. This is done in Sec. 3 assuming that the cavity is of the spherical shape and that the particle has the same diffusion coefficient in the tunnel and in the cavity. Excellent agreement between analytical and numerical results over a broad range of the geometric parameters of the problem can be considered as corroboration of our approximate theory. In Sec. 4 we summarize our results and the approximations that are used when developing the theory. In this section we also discuss possible applications of the theory and its relation to diffusion in spiny dendrites.
THEORY
Consider a particle diffusing in a cavity of volume V with a cylindrical sleeve (tunnel) of length L and radius a, which ends in a perfectly absorbing spot. The particle is trapped as soon as it reaches the spot for the first time that models escape of the particle to the outer world. We assume that radius a is much smaller than all other characteristic lengths associated with the cavity. In addition, we assume that the particle starting point is located sufficiently far away from the tunnel entrance, so that the first passage time to the entrance is much larger than the longest relaxation time in the isolated cavity.
To derive the probability density of the particle lifetime, one has to find the particle propagator in the cavity and in the tunnel and to match the two propagators at the tunnel entrance. This problem is too complicated to be solved exactly. Two approximations are used to bypass the difficulties. (i) We replace diffusion in the cylindrical tunnel by diffusion on a line between absorbing and radiation boundaries. The former describes trapping of the particle by the tunnel end facing the outer world, while the latter describes escape of the particle from the tunnel back to the cavity. Such replacement was suggested and validated by three-dimensional Brownian dynamics simulations in Ref. 9. (ii) Using the fact that a is small, we ignore the intra-head relaxation and describe escape of the particle from the cavity to the tunnels as a single-exponential process characterized by the rate constant k=4Dcava∕V, where Dcav is the particle diffusion coefficient in the cavity. These two approximations allow us to find analytical solutions for the Laplace transforms of the particle lifetime probability density and its survival probability as well as the mean lifetime of the particle.
Let G(x,t) and P(t) be the two components of the particle propagator. The former is the probability density of finding the particle at distance x from the absorbing end of the tunnel at time t, while the latter is the probability of finding the particle in the cavity at time t. Taking that the perfectly and partially absorbing ends of the tunnel are located at x=0 and x=L, respectively, we can write the evolution equations for G(x,t) and P(t) as
| (5) |
| (6) |
where Dtun is the particle diffusion coefficient in the tunnel and κ=4Dcav∕(πa).9 In addition, G(x,t) satisfies absorbing boundary condition at x=0, G(0,t)=0, and the initial conditions are G(x,0)=0 and P(0)=1.
The probability density of the particle lifetime, φ(t), which is one of the quantities of our interest, is given by
| (7) |
Its Laplace transform , respectively, is
| (8) |
where is the Laplace transform of G(x,t). Another quantity of our interest is the particle survival probability for time t, S(t), defined as
| (9) |
As follows from Eq. 9 the Laplace transform of the survival probability, , is given by
| (10) |
To find we first find by solving the equations obtained by the Laplace transformation of Eqs. 5, 6,
| (11) |
| (12) |
Then we substitute the solution into Eq. 8 and obtain
| (13) |
where . The Laplace transform of the survival probability can be obtained by substituting this expression for into Eq. 10. The mean particle lifetime can be found using the relation
| (14) |
which leads to
| (15) |
As might be expected, the mean lifetime increases when the cavity volume gets larger and∕or the tunnel gets longer and∕or narrower. When Dtun=Dcav=D, Eq. 15 reduces to the sum of the mean lifetimes given in Eqs. 1, 2, τ=τ[1]+τ[2].
When L=0, Eq. 13 takes the form
| (16) |
This corresponds to the single-exponential probability density of the particle lifetime in the cavity with a circular absorbing spot of radius a on the cavity wall,
| (17) |
The mean lifetime of the particle in this case is τ∣L=0=V∕(4aDcav).
When V=0 the Laplace transform in Eq. 13 reduces to
| (18) |
One can check that this is the Laplace transform of the lifetime probability density for a particle diffusing in a cylindrical tube with perfectly reflecting and absorbing ends. The particle starts from the reflecting end of the tube and is trapped at the first contact with the absorbing end. The mean particle lifetime in this case is given by τ∣V=0=L2∕(2Dtun). The fact that Eq. 13 has correct asymptotic behavior when V=0 is kind of surprising since the theory has been developed assuming that a is much smaller than all characteristic lengths associated with the cavity.
In contrast to Eqs. 1, 3, the lifetime in Eq. 15 has correct asymptotic behavior when L or V tends to zero. When L⪢a and V⪢Vtun, where Vtun=πa2L is the volume of the tunnel, the mean lifetime in Eq. 15 reduces to τ[1] given in Eq. 1. This happens since under such conditions the rate-limiting step determining the escape kinetics is just passage of the particle through the tunnel to its end opened to the outside world. In this case in Eq. 13 is well approximated by the dependence
| (19) |
Inverting this Laplace transform we obtain
| (20) |
and
| (21) |
These expressions agree with the kinetics predicted by Eq. 4, which is based on the scenario that realizes when L⪢a and V⪢Vtun.
The mean lifetime in Eq. 15 reduces to τ[2] given in Eq. 2 when Dtun=Dcav and L⪡a. In the opposite limiting case, L⪢a, the last term in Eq. 15 can be neglected and the mean lifetime in Eq. 15 reduces to τ[3] in Eq. 3, in which parameter α=0.84 is replaced by π∕4.
NUMERICAL TEST
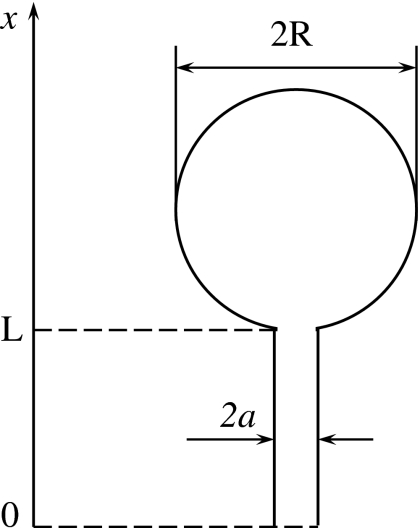
To check the accuracy of the approximate theory developed in Sec. 2, we compare theoretical predictions with the results obtained by solving the three-dimensional diffusion equation numerically (finite element method) assuming that the cavity has the spherical shape as shown in Fig. 1. In our numerical study we take that Dcav=Dtun=D and choose time and length scales so that a=D=1. The numerical solutions were found for several lengths of the tunnel, L=0, 1, 2, 3, 5, 7, 10, 20, and several values of the cavity radius, R=2, 5, 10, 20.
Figure 1.
Spherical cavity of radius R connected to the outside world by a narrow cylindrical tunnel of radius a and length L. The tunnel end opened to the outside world is considered as a perfectly absorbing boundary. When solving the problem numerically we choose the length and time scales so that a=D=1.
When developing the theory we neglect the intra-cavity relaxation. This implies that we have assumed that our results are independent of the particle initial position inside the cavity. (Of course, this assumption fails when the particle starts very close to the tunnel entrance.) To test this assumption we compare numerical results found for two initial distributions of the particle starting point, namely, (1) the particle starts from the center of the cavity and (2) the particle starting points are uniformly distributed over the cavity volume. We saw some differences only in the lifetime probability densities φ(t) at the very early stage of the process and only for the smallest cavity, R=2, at L=1 and 2. For all other values of the parameters the results for φ(t) obtained for the two distributions of the particle initial position are practically indistinguishable. The results for S(t) and τ are indistinguishable for all value of the parameters.
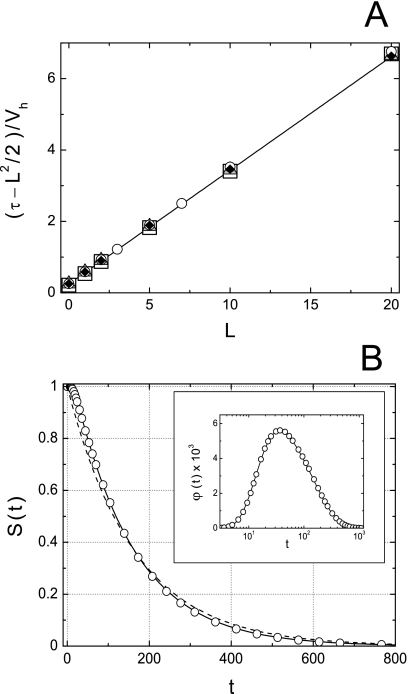
Our numerical results are presented in Fig. 2. In Fig. 2a we compare our theoretical predictions for the mean lifetime, Eq. 15, with the numerical results. The solid line in this figure represents the dependence (τ−L2∕2)∕V. According to Eq. 15 this is a linear function of the tunnel length,
| (22) |
which is independent of the cavity volume. Symbols are the values of (τ−L2∕2)∕V obtained using τ found numerically at different values of the tunnel length and the cavity volume. One can see that our numerical results are in excellent agreement with the theoretically predicted dependence, Eq. 22.
Figure 2.
Numerical test of the theory. (a) Solid curve corresponds to function (τ−L2∕2)∕V, which is 0.25+L∕π independently of V, Eq. 15. Symbols are numerical results for cavities of different head radii: R=2 (squares), 5 (triangles), 10 (circles), and 20 (diamonds). (b) Solid cures are survival probability S(t) and the probability density φ(t) (inset) obtained by inverting numerically and , Eqs. 10, 13, for the cavity and tunnel with R=2 and L=10. The circles are numerical results. The dashed line, which provides a reasonably good approximation for S(t), is S(t)=exp(−t∕τ), with τ given by Eq. 15. Deviations from Markovian behavior at short times are clearly seen in the inset.
In Fig. 2b by the solid lines we show the particle survival probability S(t) and the probability density of its lifetime φ(t) (insert) obtained by inverting numerically the Laplace transforms in Eqs. 10, 13 at R=2 and L=10, while circles show our numerical results. One can see excellent agreement between the theoretical and numerical results. Dashed line in Fig. 2b is the single-exponential approximation for the survival probability, S(t)=exp(−t∕τ), with the mean lifetime τ found by means of Eq. 15. One can see that the single-exponential S(t) provides a good approximation for the survival. At the same time, deviations from the single-exponential Markovian behavior at short times are clearly seen in the inset.
The case of R=2 and L=10 is not special. We found excellent agreement between our numerical results and theoretically predicted S(t) and φ(t) for other values of the geometric parameters also. The only exception was the behavior of φ(t) at very short times in the case of R=2 with L=1 and 2. Here the theoretical curves lied in between the numerical results obtained for the two distributions of the particle starting points. These distinctions in the behavior of φ(t) did not manifest themselves in the behavior of the survival probability since they occurred at the very beginning of the process when the particle had not had enough time to escape and, therefore, deviations of S(t) from unity were negligibly small.
CONCLUDING REMARKS
In summary, we have developed a theory that describes escape of diffusing particles from a cavity to the outside world through a narrow tunnel. One of the main results of our analysis is the expression for the Laplace transform of the probability density of the particle lifetime, Eq. 13. This expression allows one to find the Laplace transform of the particle survival probability, Eq. 10, and its mean lifetime, Eq. 15, i.e., the time it takes a diffusing particle to reach the end of the tunnel opened to the outside world. This time is found as a function of the geometric parameters (volume of the cavity, radius, and length of the tunnel) and diffusion coefficients of the particle in the cavity and in the tunnel, which may be different. The expression in Eq. 15 contains the results for the mean lifetime previously reported in the literature1, 2, 3 as special cases.
Two approximations were made when developing the theory. (i) Three-dimensional diffusion of the particle in the tunnel is described as one-dimensional diffusion on a line terminated by perfectly and partially absorbing end points. The former models exit of the particle from the tunnel to the outside world while the latter models its return to the cavity. (ii) Transition of the particle from the cavity to the tunnel is described as a single-exponential Markov process with a prescribed escape rate. This implies that we neglect the effect of the intra-cavity relaxation on the escape kinetics.
To test our approximate theory we compare its predictions with the results obtained by solving the three-dimensional diffusion problem numerically. This was done for the particle survival probability, its lifetime probability density, and the mean lifetime. Excellent agreement between the theoretical predictions and numerical results over a broad range of the geometric parameters of the problem validates the applicability of the theory developed in the paper.
Concerning possible application of the theory to signal diffusion in dendritic spines, we note that although our analysis above is focused on the geometric aspect of the problem, there are some other factors that may affect the fate of the signal in the spine. These factors include reversible binding of the signal to buffers and intracellular stores, hydrodynamic effects due to the signal interaction with the crowded intracellular environment and the neck walls, spine motility, as well as escape from the spine through different pumps located on the walls of the spine head and neck. To analyze how these factors affect the fate of the ligand in the spine, it is necessary to know what happens with the ligand in the absence of these factors. The theory developed in the present paper provides an answer to this question. Therefore, this theory can be considered as a first step on the way to a comprehensive theory, in which all these factors will be taken into account.
While earlier studies1, 2, 3 were focused on the mean signal lifetime in the spine, our results allow one to analyze complex kinetics which is not necessarily single exponential. This may be important since multiexponential escape kinetics has been observed in some experiments. Based on the expression for , Eq. 13, it can be shown that the kinetics becomes multiexponential when the mean time spent by the signal in the neck is comparable with time τhead=V∕(4Da). Using the fact that the former time is proportional to La∕D,10 we find that deviations from single-exponential behavior of S(t) are important only when the neck volume Vneck=πa2L becomes comparable with the head volume V. Typically Vneck is much smaller than V, and the escape kinetics is single exponential. Therefore, when nonexponential decay of S(t) is observed in spines with Vneck⪡V, one can be sure that there are some other factors different from the spine geometry, which are responsible for this nonexponential decay.
Our results show how the kinetics of the signal escape from the spine depends on the geometric parameters. It turns out that the only geometric parameter of the spine head entering into the expressions for , Eq. 13, and τ, Eq. 15, is the head volume. This implies that the kinetics is independent of the shape of the spine head. This is true only when the intra-head relaxation is fast in the sense that the characteristic relaxation time is much smaller than the mean time required for the signal to find the entrance to the neck.6 Assuming that the spine head is not too asymmetric, we can roughly estimate the relaxation time by V2∕3∕D. Comparison of this relaxation time with τhead leads to the inequality a⪡V1∕3 that restricts the range of applicability of the theory to spines, which satisfy this inequality, for example, spines with bulbous heads studied in Ref. 1. Surprisingly, the theory also leads to the exact results for and τ in the opposite limiting case when V=0 and the spine is purely cylindrical.
While our discussion above is focused on the signal compartmentalization in the spines, we note that spines can also play a different role, namely, they can affect diffusion of signals in the parent dendrite.11, 12 The model suggested in Ref. 11 treats signal diffusion in a spiny dendrite as diffusion in a tube with dead ends. A particle diffusing in such a tube occasionally enters the dead ends. This leads to slowdown of its spreading along the tube. The problem of diffusion in tubes with dead ends has much in common with the problem analyzed in the present paper. To see this one can compare the analysis above with that in Ref. 13 devoted to time-dependent diffusion in tubes with periodic dead ends. The spine effect on diffusion in the parent dendrite should be taken into account when analyzing experiments that monitor the time course of diffusional exchange between the spine head and dendrite.1 Such experiments are important since they allow direct characterization of the diffusional coupling between spines and dendrites that is crucial for understanding neuronal integration and synaptic plasticity.1, 2, 3, 4
ACKNOWLEDGMENTS
This study was supported by the Intramural Research Program of the NIH, Center for Information Technology. We are grateful to Professor Stas Shvartsman for useful suggestions.
References
- Svoboda K., Tank D. W., and Denk W., Science 272, 716 (1996) 10.1126/science.272.5262.716 [DOI] [PubMed] [Google Scholar]; Majewska A., Tashiro A., and Yuste R., J. Neurosci. 20, 8262 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Korkotian E., Holcman D., and Segal M., Eur. J. Neurosci. 20, 2649 (2004) 10.1111/j.1460-9568.2004.03691.x [DOI] [PubMed] [Google Scholar]; Holcman D., Korkotian E., and Segal M., Cell Calcium 7, 467 (2005) 10.1016/j.ceca.2005.01.015 [DOI] [PubMed] [Google Scholar]; (b) Singer A., Schuss Z., Holcman D., and Eisenberg R. J. Stat. Phys. 122, 437 (2006) 10.1007/s10955-005-8026-6 [DOI] [Google Scholar]; Schuss Z., Singer A., and Holcman D., Proc. Natl. Acad. Sci. U.S.A. 104, 16098 (2007). 10.1073/pnas.0706599104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biess A., Korkotian E., and Holcman D., Phys. Rev. E 76, 021922 (2007). 10.1103/PhysRevE.76.021922 [DOI] [PubMed] [Google Scholar]
- Nimchinsky E. A., Sabatini B. L., and Svoboda K., Annu. Rev. Physiol. 64, 313 (2002) 10.1146/annurev.physiol.64.081501.160008 [DOI] [PubMed] [Google Scholar]; Helmchen F., in Dendrites, edited by Stuart G., Spruston N., and Hausser M. (Oxford University Press, Oxford, NY, 2008), pp. 251–285 [Google Scholar]; Carter A. and Sabatini B., in Dendrites, edited by Stuart G., Spruston N., and Hausser M. (Oxford University Press, Oxford, NY, 2008), pp. 287–308 [Google Scholar]; Holmes W. R., Modeling in the Neurosciences, edited by Reeke G. N., Bell J., Poznanski R. R., Lindsay K. A., Rosenberg J. R., and Sporns O. (CRC, Boca Raton, FL, 2005), pp. 25–59 [Google Scholar]; Koch C., Biophysics of Computation (Oxford University Press, Oxford, NY, 1999). [Google Scholar]
- Fiala J. C., Spacek J., and Harris K. M., in Dendrites, edited by Stuart G., Spruston N., and Hausser M. (Oxford University Press, Oxford, NY, 2008), pp. 1–41. [Google Scholar]
- Grigoriev I. V., Makhnovskii Yu. A., Berezhkovskii A. M., and Zitserman V. Yu., J. Chem. Phys. 116, 9574 (2002). 10.1063/1.1475756 [DOI] [Google Scholar]
- Ward M. J. and Keller J. B., SIAM J. Appl. Math. 53, 770 (1993). 10.1137/0153038 [DOI] [Google Scholar]
- Singer A., Schuss Z., and Holcman D., Phys. Rev. E 78, 051111 (2008). 10.1103/PhysRevE.78.051111 [DOI] [PubMed] [Google Scholar]
- Bezrukov S. M., Berezhkovskii A. M., Pustovoit M. A., and Szabo A., J. Chem. Phys. 113, 8206 (2000). 10.1063/1.1314862 [DOI] [Google Scholar]
- Berezhkovskii A. M., Pustovoit M. A., and Bezrukov S. M., J. Chem. Phys. 119, 3943 (2003). 10.1063/1.1590957 [DOI] [Google Scholar]
- Santamaria F., Wils S., De Schutter E., and Augustine G. J., Neuron 52, 635 (2006). 10.1016/j.neuron.2006.10.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedotov S. and Mendez V., Phys. Rev. Lett. 101, 218102 (2008). 10.1103/PhysRevLett.101.218102 [DOI] [PubMed] [Google Scholar]
- Dagdug L., Berezhkovskii A. M., Makhnovskii Yu. A., and Zitserman V. Yu., J. Chem. Phys. 127, 224712 (2007) 10.1063/1.2805068 [DOI] [PubMed] [Google Scholar]; Dagdug L., Berezhkovskii A. M., Makhnovskii Yu. A., and Zitserman V. Yu., J. Chem. Phys. 128, 184706 (2008). 10.1063/1.3010709 [DOI] [PMC free article] [PubMed] [Google Scholar]