Abstract
This paper suggests that critical ratios obtained in noise-masked tone studies are not good indicators of critical bandwidths obtained in both human and nonhuman animal subjects. A probe-tone detection study using chinchilla subjects suggests that they may be broadband processors in detection tasks as opposed to human subjects who use narrow-band, critical-band processing. If chinchilla and other nonhuman animal subjects are wideband processors, this can partially explain why their critical ratios are significantly greater than those measured in human subjects. Thus, large critical ratios obtained for nonhuman animals may indicate processing inefficiency rather than wide critical bands.
INTRODUCTION
A fundamental measure of auditory function is frequency selectivity, the ability of an animal to discern the frequency of one sound in the presence of sound(s) of different frequencies. Obtaining direct psychophysical measures of frequency selectivity [e.g., estimates of critical bandwidth (CBW)] can be time consuming, and, thus, such CBW measures of frequency selectivity have only been obtained for a few animals (see Fay, 1988). An indirect measure of frequency selectivity, the critical ratio (CR), is simple to obtain as it requires a single masked threshold measurement. The CR has been obtained for many animals (Fay, 1988). In this paper, we explain why the CR is probably a poor indicator of frequency selectivity in that the estimates of frequency selectivity derived from direct measurements (e.g., CBW) do not agree with those derived from the indirect CR method. For nonhuman animal subjects, estimates of CRs are considerably greater than those obtained for human subjects, and as such they imply that frequency selectivity in these nonhuman animal subjects would be much worse than in human subjects. The sharpness of tuning of auditory filters between human and nonhuman animals has recently been the subject of controversy in the literature (see Shera et al., 2002; Ruggero and Temchin, 2005). We describe the outcome of an experiment, which might provide one reason why the CRs obtained for most nonhuman animal subjects are considerably larger than those obtained for human subjects.
The concept of the critical band and the use of the CR to estimate the CBW were developed during the 1930s and 1940s at Bell Laboratories directed by Fletcher.1Fletcher (1940) used a band-narrowing procedure and showed that only a “critical band” of frequencies centered on the tone to be detected affected a tone’s noise-masked threshold. That is, the masked threshold of a tone remained unchanged as the bandwidth of a masking noise was decreased (holding the spectrum level of the masking noise constant) until the bandwidth was narrower than a critical value, and then the threshold of the tone decreased as the noise bandwidth was made narrower than this critical value. The masker bandwidth at which the tone’s thresholds began to decrease as the bandwidth was narrowed was used as an estimate of the CBW. Fletcher (1940) showed that the CBW increased as the frequency of the signal tone increased, implying a widening of the CBW with increasing frequency. This and other observations were consistent with frequency selectivity measured at the auditory periphery, and it was assumed that the critical band reflected the biomechanical and neural processes occurring in the cochlea and auditory nerve.
Fletcher (1940) made a general assumption that a tone’s masked threshold was proportional to the power of the noise within the critical band that spectrally surrounded the tone. He also observed that the power of the noise within the critical band was approximately equal to the power of the signal at the masked threshold. This second observation is often couched as a second assumption that the power of the signal at the masked threshold is equal to the power within the critical band. These two assumptions allowed Fletcher (1940) to derive the CR as an indirect estimate of the CBW. The derivation is as follows:
Assumption 1: Masked threshold is proportional to the power in the critical band:
-
(1)
Pt=K*Pcb, where Pt is the power of the tone at masked threshold, Pcb is the power within the critical band, and K is the proportionality constant.
-
(2)
Or Pt∕Pcb=K.
-
(3)
Pcb can be rewritten as Pcb=No*CBW, where No is the spectrum level (noise power per unit bandwidth) of the noise (which is held constant).
-
(4)
Thus, from (2) Pt∕(No*CBW)=K.
-
(5)
Or CBW=Pt∕(K*No).
Assumption 2: The power of the tone at the masked threshold equals the power of the noise within the critical band:
-
(6)
Pt=Pcb.
-
(7)
From (1) above Pt∕Pcb=K.
-
(8)
Thus, from (6) K=1.
-
(9)
Then, from (5) above CBW=Pt∕No.
The value of CBW that equals the ratio Pt∕No, the signal-to-noise ratio at the masked threshold, is called the CR, and CR=CBW. Note that CR only requires a single estimate of the signal-to-noise ratio (expressed as the power of the tonal signal, Pt, at the masked threshold divided by the noise masker’s spectrum level, No, in units of power).2 However, for the CR to be equal to the CBW requires that both assumptions listed above are true. Using only Assumption 1, the CBW is a function of both the signal-to-noise ratio at the masked threshold and K, where K can be viewed as an efficiency value (see Patterson et al., 1982). Let us examine the evidence that Assumption 2 is true. That is, the power of the signal at the masked threshold equals the power of the masking noise within the critical band, and thus K=1. Obtaining an estimate of K requires that the CBW is known.
Measures of the critical band in noise masking experiments have been studied extensively over the past 70 years. We will not attempt to review this history (see Moore, 1986). Scharf (1970) provided a thorough review of the critical band and CR, and he argued based on several data sets that the value of K measured for human subjects is about 0.4, and therefore the CR for human subjects is about 2.5 times the signal-to-noise ratio at the masked threshold, i.e., CR=2.5*Pt∕No. Perhaps Assumption 2 should be changed to CR=2.5*Pt∕No, and as such this revised CR ratio can be used to estimate CBW. However, Patterson et al. (1982) argued that the CR does not allow one to accurately estimate the CBW of elderly subjects in that the CRs obtained in this experiment were more a function of efficiency, the proportionality constant K, than they were of the CBW. Thus, the CR would not accurately estimate the CBW measured as a function of age.
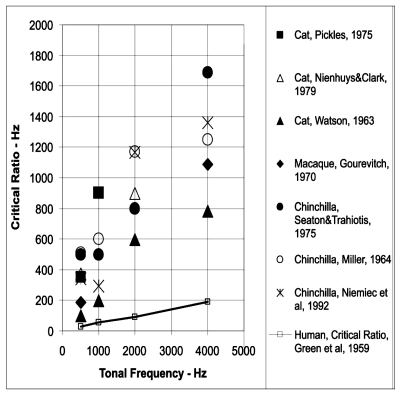
We now deal with how well the CR accounts for critical bands in nonhuman animal subjects. First, almost all studies of noise masking of a tonal signal in nonhuman animal subjects indicate that the signal-to-noise ratio required for threshold performance (i.e., the CR when appropriately calculated) is substantially higher than that measured for human subjects. Figure 1 compares estimates of CRs for several mammalian species based on the summary provided by Fay (1988). Data from several mammals (Gourevitch, 1970; Green et al., 1959; Miller, 1964; Nienhuys and Clark, 1979; Niemiec et al., 1992; Pickels, 1975; Seaton and Trahiotis, 1975; Watson, 1963) are shown in Fig. 1. As can be seen, the CR measures for several nonhuman mammalian species are much larger than the CRs obtained for human subjects. Since the signal-to-noise ratio at threshold is used to calculate the CR as an indirect estimate of the CBW the large masked thresholds obtained for nonhuman animal subjects imply that they have wider critical bands than human subjects.
Figure 1.
CRs in Hz plotted as a function of signal (center) frequency (Hz) for several mammals. Adapted from Fay (1988).
As stated previously, there are very few studies of direct measures of CBWs in nonhuman animal subjects. Niemiec et al. (1992) directly measured the critical band using several different methods along with the CR for the chinchilla. Table 1 summarizes some of these data [those using the notched-noise estimate of the equivalent rectangular bandwidth (ERB),3 as defined in the procedures used by Glasberg and Moore (1990)], and they indicate that the value of K is greater than 1 for the chinchilla, sometimes far greater than 1. The work by Niemiec et al. (1992) showed that, on average, the estimates of the CBW for the chinchilla derived from direct estimates (e.g., notched-noise estimates of the ERB) were about 5%–10% larger than those measured for human subjects. On the other hand, the values of the CR obtained for the chinchilla were, on average, more than 300% larger than the CRs obtained for human subjects (Green et al., 1959; see also Fig. 1). Evans et al. (1992) also measured critical bands for the guinea pig and found that the ERBs for the guinea pig were only about 12% larger than the ERB measured for human subjects. And, recently May et al. (2006) measured filter bandwidths in the mouse using a notched-noise masker and found narrower filter bandwidths than those reported by Ehret (1976) using CR estimates. Thus, it appears as if direct estimates of the critical band for some nonhuman animal subjects are much less than those based on CR measures and only somewhat larger than those estimated for human subjects, while the estimates of CRs for most mammals deviate greatly from those estimated for human subjects. Thus, the CR for nonhuman animal subjects may significantly overestimate the width of the actual critical band that could be directly measured in these animals.
Table 1.
CR measurements and critical band–ERB measurements for the chinchilla from Niemiec et al. (1992) along with the calculated value of K (see text also).
| Signal frequency (Hz) | CR (Hz) | ERB (Hz) | K |
|---|---|---|---|
| 500 | 341 | 59 | 5.8 |
| 1000 | 293 | 185 | 1.6 |
| 2000 | 1166 | 304 | 3.8 |
| 4000 | 1359 | 335 | 4.1 |
The fact that the CR is considerably larger than the critical band in nonhuman animal subjects implies that these animals are inefficient in detecting a tonal signal in a background of noise, not necessarily that these animals have wide critical bands. In the next section we describe an experiment that suggests that chinchillas are inefficient in detecting tonal signals in a noise background because they operate like wideband4 detectors, whereas human subjects use the narrow-band critical band for detecting noise-masked tonal signals.
Probe-tone experiment
In detecting a tonal signal in a background of wideband noise, a detector can maximize its sensitivity if it processes the noise in a narrow band centered on the frequency of the tonal signal (Green and Swets, 1974). That is, using a wideband process4 is inefficient for detecting a tonal signal in a background of broadband noise. It has been shown in several experiments that human subjects appear to use the critical band for detecting tonal signals masked by wideband noise (e.g., Green, 1961).
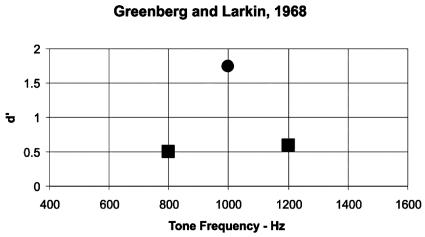
Greenberg and Larkin (1968) measured the ability of human subjects to detect probe tones of different frequencies that were presented at levels of equal detectability but were presented infrequently and at frequencies that the subject was not trained to detect. The general paradigm is that the detectability5 of noise-masked tones of different frequencies was obtained in a baseline experiment. In the test experiment, one of these tones with frequency (fs) was presented as “the signal” during a practice session and on 75% of signal trials during the test condition. The remaining 25% of the signal trials contained probe tones with frequencies different from fs but at levels that were previously determined to yield equal detectability. One example of a typical result is shown in Fig. 2. The detection of the probe tones was lower than that of the signal tone (fs), and detection performance tended to follow a form that is consistent with a critical-band filter function. That is, the data suggested that human subjects use a filter centered on the frequency of the expected tonal signal for detection of that signal, and the level of the probe tones was attenuated by this detection filter. The filter has a bandwidth consistent with that measured for the critical band.4 Thus, the Greenberg and Larkin (1968) probe-tone experiment reinforces the idea that human subjects process a tonal signal masked by a broadband noise using a narrow band characterized by the critical band. Several additional studies have been conducted using variations in the probe-tone technique (e.g., see Hafter and Saberi, 2001; Hafter et al., 1993; Dai et al., 1991; see Hafter et al., 2007, for a review), and these studies consider the filter used by subjects in these experiments to be an “attention filter,” reflecting the idea that a subject’s attention is focused on the frequency of the tonal signal. The results from all of these experiments indicate that human subjects process masked tonal signals in a narrow band, even when the subjects are aware that several different tones may be presented during the probe-tone experiment (Hafter et al., 1993).
Figure 2.
Data from Greenberg and Larkin (1968) showing d′ as a function of tone frequency in Hz. The circled point at 1000 Hz is the test signal, and the d′ values for probe tones at 800 and 1200 Hz are shown as squares. Greenberg and Larkin (1968) plotted their data in terms of percent correct. Percent correct was converted to d′ based on assuming a symmetric criterion and using the tables in Swets (1964).
The probe-tone technique is very similar to the stimulus generalization procedure often used in the animal behavior literature (Malott and Malott, 1970). In a stimulus generalization task, an animal subject is trained (e.g., reinforced) to respond to one value of a stimulus (e.g., one tonal frequency). During testing, sounds that differ from that used during training (e.g., test tones that differ in frequency from that used in training) are occasionally presented without reinforcement, and the responses of the animal to these infrequent test stimuli are recorded. If the animal responds to the test sounds with the same response magnitude that they responded to the training sound, the animal is described as generalizing to the test sounds. That is, the animals presumably perceive the test and training sounds as similar, leading to all sounds being responded to somewhat equally. The degree to which an animal does not generalize suggests the degree to which the animal does not perceive the test and training sounds as similar. The signal tone, fs, in the Greenberg and Larkin (1968) paradigm is similar to a training tone in the generalization task, and the probe tones are similar to the test tones.
We used a task such as the Greenberg and Larkin (1968) procedure to test the generalization of the chinchilla to noise-masked tones of different frequencies. We intended this to be a baseline experiment for additional tests of generalization by the chinchilla as a means to explore aspects of pitch perception in the chinchilla (see, Shofner et al., 2005). That is, we expected chinchilla subjects to show a lack of generalization when the test (fs) and probe tones were considerably different in frequency, as indicated by the previous measures of CBW (Niemiec et al., 1992) or even the CR. The fact that the animals showed strong generalization rather than a lack of generalization was surprising to us and led to our hypothesis that these data are evidence that the chinchilla is a wideband detector in experiments in which tones are masked by noise. Thus, we also conducted a probe-tone experiment with human subjects using the same procedure as was used for the chinchilla subjects to be able to compare performance in the probe-tone task for the two species.
METHOD
Chinchilla subjects
Participants. Four adult chinchillas (Chinchilla lanigera) were maintained at body weights of approximately 400–450 g. Animals were trained to detect a tone in the presence of a continuous low-level background noise. Animals were free to move around their cage that was placed inside of a single-walled sound-proof chamber, and they were not restrained in any manner. A pellet dispenser (Gerbrands G5120) with a reward chute attached to a response lever was located at one end of the cage.
Stimuli. Broadband noise was presented from a noise generator (Grayson-Stadler model 455C) and was low-pass filtered (Tucker-Davis Technologies, TDT, PF1) at a cutoff frequency of 10 kHz. Sine tones were synthesized digitally (TDT AP2) and presented through a 16-bit digital-analog converter (TDT DD1) at a conversion rate of 50 kHz. The output was low-pass filtered at 15 kHz. The 10-kHz noise was on continuously and was presented at a constant spectrum level of 10 dB [approximately 50 dB SPL (sound pressure level) over all levels], which was approximately 12 dB above the detection level of a wideband noise in the experimental setup (see Shofner et al., 1993). The level of the tone was adjusted using a programmable attenuator (TDT PA4). The mixed tone and noise were played through a Realistic Minimus (3.5) loudspeaker placed near the pellet dispenser approximately 6 in. in front of the animal and approximately 30° to the right of the center. The sound level in the cage was monitored with an Ivie Technologies (1133) sound level meter.
Procedure. The behavioral task was a modified “yes∕no” task. The animal initiated a trial by pressing down on the response lever. After the trial was initiated, there was a holdtime of 1.15–8.15 s, which varied randomly for each trial. At the end of the holdtime, either a tone trial or a catch trial was presented. If the animal released the lever before the random holdtime, then the trial was aborted and the countdown for the holdtime was halted. That trial began again with the next lever press using the same holdtime. For a tone trial, two bursts of the tone signal were presented in the presence of the background noise masker; the tones were 500 ms in duration shaped with 10-ms rise∕fall times, presented with an interburst interval of 500 ms and a 500-ms interval after the second tone presentation. During a catch trial, only the continuous background noise was presented. The entire duration of each tone or catch trial was 2.0 s. The response window coincided with the duration of the trial but began 150 ms after the onset of the first tone burst. The resulting response window was therefore 1.85 s. When the animal released the lever during the response window, the response was recorded as a “yes.” A “yes” response during a tone trial was treated as a hit, and that during a catch trial was treated as a false alarm. If the animal continued to hold down the lever throughout the response window, the response was treated as a “no.” A ‘no’ response during a catch trial was treated as a correct rejection and as a miss during a tone trial. Chinchillas received food pellets (Noyes: Formula N) for hits and correct rejections only.
Psychometric functions for tones of 500, 1000, and 2000 Hz were obtained using a method of constant stimuli. Animals ran in a block of 40 trials and generally completed two to five blocks per day. Within a block of 40 trials, eight different tone levels in 5-dB steps were randomly presented. Each level was presented four times, and there were eight catch trials per block (20% of the trials). Each psychometric function was based on at least 50 blocks of data. The psychometric functions obtained at all three frequencies allowed us to ensure that all tones presented during the probe-tone test experiment were equally detectable.5
After all of the data had been collected for the psychometric functions, animals ran in the probe-tone paradigm. During testing using the probe-tone method, the broadband noise was again presented continuously at a 10-dB spectrum level (No), and the duration, shaping, and frequency of the tones as well as the response window and variable holdtime were the same as previously described. The signal tone (fs) was 1000 Hz, and the probe tones were 500 and 2000 Hz. The sound level of all three tones was fixed to be equally detectable based on the psychometric functions. For animals C16, C18, and C24 the levels were chosen to give d′ of 1.3, while for animal C12 the levels were set to yield a d′ of 1.1. The value of d′ was computed from the hit and false alarm rates obtained from each animal and each condition as the z-score associated with the hit rate minus that from the false alarm rate (see Green and Swets, 1974).
A block of 40 trials contained 32 tone trials (80%) and 8 catch trials (20%). Of the 32 tone trials, 24 (60% of 40 and 75% of 32) contained the signal tone (fs=1000 Hz), 4 (10% of 40 and 12.5% of 32) contained the 500-Hz probe tone, and 4 (60% of 40 and 75% of 32) contained the 2000-Hz probe tone. All tones appeared randomly throughout a block. Any correct detection of the tone during tone trials was counted as a hit, but only hits for the signal tone (fs=1000 Hz) were rewarded with a food pellet. Hits for the probe tones of 500 and 2000 Hz were not rewarded. Correct rejections for catch trials were also rewarded with a food pellet. Detection performance to signal and probe tones was measured using d′, as described previously. The false alarms for the signal and probe trials were based on the same values obtained by Greenberg and Larkin (1968).
Human subjects
Participants. Three college students (one male and two females ranging in age from 21 to 25) served as subjects. They all reported that they had normal hearing and were experienced in performing in psychoacoustic tasks. They were paid $10∕h for their participation in the experiment. Since it is not possible to have the human subjects run in the small animal sound-proof chambers, the human subjects ran in a single-walled sound-proof room that had about the same attenuation characteristics as the single-walled animal chambers.
Stimuli. The equipment, stimuli, and stimulus conditions used for the human subjects were very similar to those used for the chinchilla subjects, except that a TDT waveform generator (WG2) was used instead of the Grayson Stadler noise generator. A Realistic Minimus (3.5) loudspeaker was placed near the subject’s head approximately 22 in. in front of the subject and approximately 30° to the right of the center (similar to what was done for the chinchilla subjects). The sound levels at the place of the middle of the subject’s head were measured with an Ivie Technologies (IE-33) sound level meter.
Procedure. The psychometric procedures and analyses used for the human subjects were the same as those used for the animal subjects with the following exceptions. A computer mouse was used by the subject to enter responses. As for the chinchilla subjects, the human subjects initiated a trial by clicking on a box on a computer terminal that said “Ready.” Following the random holdtime and during the response window, a release of the mouse button was used to indicate that they perceived the presence of a signal sound. Keeping the mouse button down during the response window indicated that the signal was not presented. Eight point psychometric functions (varying from a signal-to-noise ratio of 8–22 dB in 2-dB steps; these values were determined from preliminary data) were first obtained for all subjects at the three frequencies, and then the level required for a d′ of 1.3 (calculated in the same way as explained above) was used in the probe-tone test experiment. All other procedures for obtaining the psychometric functions for the human subjects were the same as for the chinchilla subjects.
During the probe-tone test experiment, each block of 40 trials began with three presentations of the 500-ms 1000-Hz signal tone presented at a 40-dB signal-to-noise ratio. Subjects were instructed that the object of the experiment was to be as correct as possible in detecting the presence of the signal when it was presented and in detecting its absence when it was not presented. Unlike in the chinchilla study, no feedback was provided, as was consistent with the procedures used by Greenberg and Larkin (1968). If feedback is viewed as similar to food reward, it is not possible to provide feedback only for hits during signal trials and for all correct rejections (as was done with food reinforcement for the chinchilla subjects) since this would mean that feedback would not be provided on some trials (probe-tone trials). The presentation of the 1000-Hz signal before each block is similar to a procedure used by Greenberg and Larkin (1968) and was intended to serve some of the functions of using food reward to “focus attention” on 1000 Hz. All other procedures were the same for the human subjects as they were for the chinchilla subjects.
RESULTS
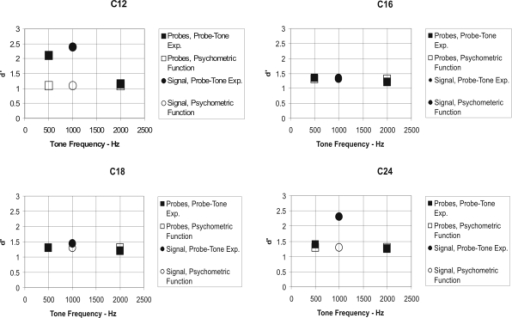
The major results obtained from four chinchillas are shown in Fig. 3 as d′ for the signal-tone (circles) and probe-tone (squares) frequencies. The open symbols are the values of d′ obtained from the psychometric functions during the initial baseline experiments used to determine the signal-to-masker-noise ratio at each tonal frequency required for d′ of 1.1 for C12 and of 1.3 for the other three animals. The closed symbols represent d′ performance during the probe-tone test experiment. As can be seen, all four animals responded to all tones with values greater than d′=1, and they generalized to the probe tones with about the same level of performance (d′) as they did to the test tone. The data also indicate that two animals (C12 and C24) performed with a higher d′ during the test experiment than they did during the initial baseline experiment.
Figure 3.
Probe-tone experimental data for four chinchilla subjects (C12, C16, C18, and C24) showing d′ as a function of tone frequency in Hz. Circled data points at 1000 Hz are for the signal frequency, and the squares are for the 500- and 2000-Hz probe frequencies. Open symbols are for estimates from the psychometric-function baseline experiment, and closed symbols are for the probe-tone test experiment.
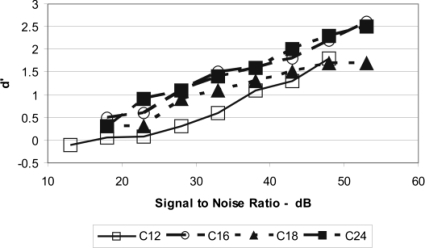
Figure 4 shows the psychometric functions for the four animals measured for fs of 1000 Hz. All psychometric functions obtained at all frequencies were monotonically increasing functions, indicating improved detection with increasing signal-to-noise ratio. Psychometric functions obtained at the probe frequencies were very similar to those obtained at fs, although different signal-to-noise ratios were required to obtain d′ of 1.1 and 1.3. In all conditions the false alarm rate was low (maximally approximately 20%) and relatively consistent from animal to animal and over blocks of trials, and it decreased as the signal level increased. These data also indicate that the signal-to-noise ratio for a d′ of 1.0 is between 25 and 33 dB, which is consistent with the results from other studies of the CR in chinchilla (e.g., Niemiec et al., 1992; Miller, 1964; Seaton and Trahiotis, 1975; see also Fig. 1).
Figure 4.
Psychometric functions for the four chinchilla subjects (C12, C16, C18, and C24) showing d′ as a function of signal-to-noise ratio (dB) for the 1000-Hz tonal signal.
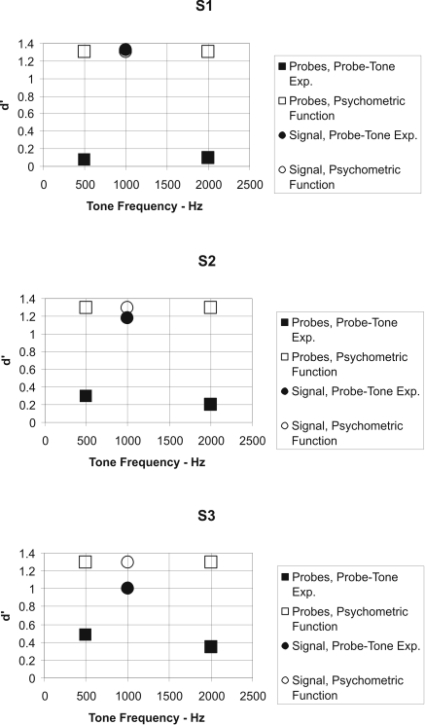
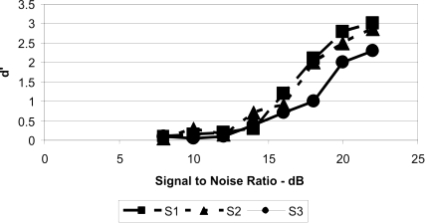
Figures 56 display the data for the three human subjects using the same formant as was used for Figs. 34. As can be seen, the human subjects responded to the two probe tones (500 and 2000 Hz) with much lower values of d′ during the probe-tone experiment than they did in the baseline experiment (Fig. 5), indicating a clear difference from the performance of the chinchilla subjects. The psychometric functions at 1000 Hz indicate that d′=1.0 was obtained at signal-to-noise ratios between 15 and 18 dB, which is higher than that often obtained for human subjects (e.g., Reed and Bilger, 1973). Also, the psychometric functions for the human subjects (Fig. 6) were considerably steeper than those for the chinchilla subjects (Fig. 4), and their slopes are consistent with those found in the literature (e.g., Green, 1961).
Figure 5.
Data from the three human subjects (S1, S2, and S3) using the same format as was used in Fig. 3.
Figure 6.
Data from the three human subjects (S1, S2, and S3) using the same format as was used in Fig. 4.
DISCUSSION
The major results shown in Figs. 35 are that the chinchilla subjects generalized to the probe tones with approximately the same level of performance (d′) as they did to the test tone, but the human subjects did not. We consider this evidence that the chinchilla is not a narrow-band detector, using something like the critical band, in detecting a tonal signal masked by a broadband noise. The fact that two animals responded at higher values of d′ during testing than they did in the initial baseline experiment in which the psychometric functions were obtained might be due to an underestimation of the sensitivity of these animals to the signal tone during the baseline psychometric-function experiment. To test this hypothesis we ran all animals on an additional method of constant stimuli procedure to re-estimate the psychometric functions. Two animals (C12 and C24, but not C16 and C18) performed with higher values of d′ during this second constant stimulus test experiment than they did during the initial baseline experiment, suggesting that indeed the original estimate of performance during the baseline experiments was too low for these two animals. The values of d′ obtained during the retest of the psychometric-function experiment were very similar to those obtained in the probe-tone test experiment. We also compared the psychometric functions obtained during the first ten blocks of trials during the baseline psychometric-function experiment with those obtained during the last ten blocks. Again, only animals C12 and C24 showed improved performance between the first and last ten blocks, also suggesting that these animals were still improving in their performance. A similar comparison of the first ten blocks of trials to the last ten blocks during the follow-up psychometric-function experiment did not reveal any differences in performance for all four animals. While all of the data for C12 and C24 shown in Figs. 34 may not accurately represent their absolute level of detection, the comparison of performance between probe tone and signal tones shown in Fig. 3 is similar to that from the other two animals in indicating broadband processing in a noise-masked tone detection task.
The retest of the psychometric functions indicated that at least for two of the chinchillas the estimate of thresholds is reliable. And even for the two animals whose initial threshold estimates appeared high, their thresholds appeared to be stable after the probe-tone test experiment. Since the thresholds obtained in this study are well within the range of thresholds measured for chinchilla subjects in other experiments (see Fig. 1), the present results would seem to be valid estimates of chinchilla subjects’ performance in this masked threshold experiment.
Since the performance for the signal frequency (1000 Hz) for the three human subjects did not differ between the probe-tone experiment and the baseline psychometric-function experiment (Fig. 5), we did not obtain an additional estimate of the psychometric functions as we did for the chinchilla subjects. The higher signal-to-noise ratios obtained for the human subjects compared to those reported in other studies are probably due to the psychophysical procedure, which is substantially different from that typically used to estimate masked thresholds in human subjects. It is the case that the threshold signal-to-noise ratios are still, on average, approximately 12 dB lower for the human subjects than for the chinchilla subjects. This is consistent with the data in the literature (e.g., see Fig. 1).
Perhaps the chinchilla subjects generalized to the probe tones because of their prior experience with these tones during the baseline psychometric-function experiment. In all of the past probe-tone experiments with human subjects, including the one conducted for this paper, the human subjects have also had prior experience listening to the probe tones before being tested in the probe-tone test experiment.4 In some studies the subjects are aware that information other than that provided by the signal may occur during an experimental run (Hafter et al. 1993). Despite these experiences, in none of the past experiments do human subjects generalize to the probe tones at anywhere near the level that the chinchilla subjects did in the chinchilla experiment reported in this paper. One explanation for these differences that we feel is worth pursuing is that the chinchilla subjects are wideband processors in these tasks and human subjects are narrow-band processors, although we cannot completely rule out other reasons why chinchilla subjects generalize and human subjects do not.
If the data in Fig. 3 indicate broadband processing in noise-masked tone detection tasks, then this could explain why the CR is large in these animals. That is, chinchilla subjects require a larger signal-to-noise ratio for tonal detection than human subjects because chinchilla subjects are wideband processors, while human subjects are narrow-band, critical band processors in noise-masked tone detection tasks. Green (1961) calculated that wideband detection could increase the signal-to-noise ratio by as much as 10 dB over that achieved with narrow-band processing. The results of the present study suggest that the chinchilla subjects required about 12-dB larger signal-to-noise ratio (CR) to detect the tonal signals than did the human subjects. However, if the critical bands for the chinchilla are 10%–12% larger than those for humans as the data of Niemiec et al. (1992) and Evans et al. (1992) suggest, then the difference due to wideband listening for the chinchilla subjects could be less than 10 dB. This difference is roughly consistent with Green’s calculations of the decrement in signal-to-noise ratio that might occur if a wideband listening strategy was employed. While there may be other reasons why the chinchilla subjects perform poorer in detecting a noise-masked tonal signal than human subjects, the results of the present study appear consistent with the hypothesis that a contributing factor for the chinchilla subjects’ poorer performance is that chinchillas are “wideband processors.” Thus, it is possible that chinchilla subjects use, for whatever reason, wider bands to detect tonal signals masked by broadband noise than do human subjects. The same may be true for other nonhuman animal subjects whose CRs are much larger than those measured in human subjects. It is also interesting to note that human infants respond to probe tones with higher response rates than do adult humans, indicating that infants process tones-in-noise with a wideband listening strategy (see Bargones and Werner, 1994).
Greenwood (1990) argued that the larger CRs reflect wider critical bands in many nonhuman animals, and the differences in CR estimates of critical bands can be explained on the basis of the length of the cochlea in these animals and his assumptions regarding the relationship between the cochlear map of frequency and frequency selectivity. Greenwood (1990) produced a compelling series of detailed articles and arguments supporting these relationships. His work implies that frequency selectivity in many nonhuman animal subjects is somewhat accurately represented by the CR.
The analysis presented in this paper argues that the CR is not a good indicator of frequency selectivity. Thus, it is worth asking if the critical-band estimates of Niemiec et al. (1992), Evans et al. (1992), and May et al. (2006) are more indicative of frequency selectivity than the CR. Since several different procedures were used in several of these studies to directly estimate the critical band and since these procedures produced similar estimates of the critical band, which were much narrower than the CR estimates, these critical-band estimates appear to be reliable and valid.
One can use measures other than the critical band or ratio to infer an animal’s frequency-selectivity ability. Measures of tonal frequency discrimination produce results that suggest that nonhuman animal subjects are poorer at tonal frequency discrimination than are human subjects (see Fay, 1988), which might imply that nonhuman animals are poorer at frequency resolution than human subjects. However, frequency discrimination is known to be variable across human subjects (Jesteadt and Bilger, 1974), so it is not clear how much difference there may be between a human subject who is poor at frequency discrimination and a nonhuman animal’s frequency discrimination ability. Moreover, frequency discrimination performance may reflect more than processing based on frequency selectivity (e.g., temporal processing; see Dye and Hafter, 1980). Tone-on-tone psychophysical simultaneous masking functions have been obtained for several nonhuman animal species. In general, the shapes of these psychophysical tonal masking tuning curves obtained for nonhuman animal subjects are similar to those that have been measured for human subjects (see Fay, 1988). This would imply that nonhuman animal and human subjects have similar frequency selectivities. Thus, it is our view that the direct measurements of frequency selectivity do suggest that frequency selectivity in the chinchilla is only slightly worse than that measured for human subjects, while the CR measurements differ greatly.
Why might the chinchilla (and perhaps other animals) use wider band processing in detecting a tonal signal masked by a noise masker? Both positive [e.g., food reinforcement used by Niemiec et al. (1992)] and negative reinforcers [e.g., shock avoidance used by Seaton and Trahiotis (1975)] have been used to estimate the CR and both types of motivation produce approximately the same CRs. Thus, it is unlikely that performance in these detection tasks is related to the type of motivation used in psychophysical tasks. In most studies the animal subjects appear to have reached asymptotic performance during training, so it is unlikely that additional training might improve performance. Thus, we do not have a compelling explanation as to why chinchilla subjects appear to be wideband detectors and human subjects appear to be narrow-band, critical-band detectors. It might be possible to induce narrow-band processing in the chinchilla by using some sort of cuing technique. Such cuing has been shown to improve performance in some detection tasks using human subjects (Richards and Neff, 2004). It is also possible that animals such as the chinchilla process signals as a wideband processor in order to not “miss” potential signals that might indicate a predator. That is, they may trade sensitivity for detecting a particular signal for an ability to process many different signals.
If the chinchilla and other nonhuman animal subjects are not using a narrow-band critical band to process a noise-masked tone, then the first assumption of Fletcher (1940) does not appear to hold for these animals. That is, the detection of a tone masked by a broadband noise may not appear to depend in any direct way on a critical band. While such nonhuman animal subjects show evidence of critical bands with bandwidths similar to those of human subjects, they may not use them in the same way as human subjects when they are asked to detect sinusoids in noisy environments.
CONCLUSIONS
Comparison of CR measures as an indirect indication of frequency selectivity to the direct measures of the critical band suggests that CRs are probably not a good indicator of frequency selectivity as measured in both human and nonhuman animal subjects.
The probe-tone masking experiment suggests that it is possible that the large CRs measured in nonhuman animal subjects, such as the chinchilla, are due to these animals using a broader band for signal processing in noise-masked detection tasks than human subjects use.
ACKNOWLEDGMENTS
The chinchilla experiment was conducted while both authors were at the Parmly Hearing Institute, Loyola University Chicago, Chicago, IL. The experiment with human subjects was conducted by W.A.Y. at Parmly after W.P.S. had left Parmly for Indiana University. The work was supported by a NIDCD Program Project Grant awarded to Loyola. The writing of this paper was supported by a NIDCD grant awarded to W.A.Y. at ASU.
Footnotes
Rankovic, C. M., and Allen, J. B., Study of Speech and Hearing at Bell Telephone Laboratories, CD-ROM from the Acoustical Society of America (www.asa.aip.org), Melville, NY.
Since No, spectrum level, is noise power per unit bandwidth, No actually has energylike units (power×time). In decibels, 10 log CBW=Pt in dB—No in dB.
The term critical band is often used in a general sense to indicate a spectral region critical for determining masked threshold. Measures such as the ERB are specific calculations based on particular experimental and measurement procedures. Thus, the ERB is one of several ways to estimate the CBW and is not necessarily synonymous with the critical band.
Wideband processing can mean one of two things in this paper. It could mean that the animal actually uses a wider band. Or it could mean that the animal uses several different narrow-band critical bands and sums or samples the outputs of these bands in making a detection decision. In either case, the signal level required for a constant level of performance would be greater than that required if the subject used a single narrow band (Green, 1961).
Thresholds for all tones (signal and probes) are obtained in order to ensure that all tones are equally detectable in the probe-tone test experiment. Without such thresholds, performance for the probe tones may be based only (or partially) on their overall detectability rather than on narrow-band versus wideband processing.
References
- Bargones, J. Y., and Werner, L. A. (1994). “Adults listen selectively: Infants Do Not,” Psychol. Sci. 5, 170–174. [Google Scholar]
- Dai, H., Scharf, B., and Buus, S. (1991). “Effective attenuation of signals in noise under focused attention,” J. Acoust. Soc. Am. 10.1121/1.400721 89, 2837–2842. [DOI] [PubMed] [Google Scholar]
- Dye, R. H., Jr., and Hafter, E. R. (1980). “Just-noticeable differences of frequency for masked tones,” J. Acoust. Soc. Am. 10.1121/1.384301 67, 1746–1753. [DOI] [PubMed] [Google Scholar]
- Ehret, G. (1976). “Critical bands and filter characteristics of the ear of the house mouse (Mus musculus),” Biol. Cybern. 10.1007/BF00365592 24, 35–42. [DOI] [PubMed] [Google Scholar]
- Evans, E. F., Pratt, S. R., Spenner, H., and Copper, N. P. (1992). “Comparisons of physiological and behavioural properties: Auditory frequency selectivity,” in Auditory Physiology and Perception, edited by Cazals Y., Demany L., and Horne K. (Pergamon, Oxford: ), pp. 159–170. [Google Scholar]
- Fay, R. R. (1988). Hearing in Vertebrates: A Psychophysics Databook (Hill-Fay Associates, Winnetka, IL: ). [Google Scholar]
- Fletcher, H. (1940). “Auditory patterns,” Rev. Mod. Phys. 10.1103/RevModPhys.12.47 12, 47–65. [DOI] [Google Scholar]
- Glasberg, B. R., and Moore, B. C. J. (1990). “Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 10.1016/0378-5955(90)90170-T 47, 103–138. [DOI] [PubMed] [Google Scholar]
- Gourevitch, G. A. (1970). “Detectability of tones in quiet and in noise by rats and monkeys,” in Animal Psychophysics: The Design and Conduct of Sensory Experiments, edited by Stebbins W. C. (Appleton-Century-Crofts, New York: ), pp. 67–97. [Google Scholar]
- Green, D. M. (1961). “Detection of auditory sinusoids of uncertain frequency,” J. Acoust. Soc. Am. 10.1121/1.1908839 33, 897–903. [DOI] [Google Scholar]
- Green, D. M., Mckey, M. J., and Licklider, J. C. R. (1959). “Detection of a pulsed sinusoid in noise as a function of frequency,” J. Acoust. Soc. Am. 10.1121/1.1907648 31, 1446–1452. [DOI] [Google Scholar]
- Green, D. M., and Swets, J. A. (1974). Signal Detection Theory and Psychophysics (Krieger, New York: ). [Google Scholar]
- Greenberg, G. Z., and Larkin, W. (1968). “Frequency-response characteristic of auditory observers detecting signals of a single frequency in noise: The probe-signal method,” J. Acoust. Soc. Am. 44, 5513–5520. [DOI] [PubMed] [Google Scholar]
- Greenwood, D. D. (1990). “A cochlear frequency-position function for several species—29 years later,” J. Acoust. Soc. Am. 10.1121/1.399052 87, 2592–2605. [DOI] [PubMed] [Google Scholar]
- Hafter, E. R., Sarampalis, A., and Loui, P. (2007). “Auditory attention and filters,” in Auditory Perception of Sound Sources, edited by Yost W. A., Popper A. N., and Fay R. R. (Springer, New York: ), pp. 115–143. [Google Scholar]
- Hafter, E. R., and Saberi, K. (2001). “A level of stimulus representation model for auditory detection and attention,” J. Acoust. Soc. Am. 10.1121/1.1394220 110, 1489–1497. [DOI] [PubMed] [Google Scholar]
- Hafter, E. R., Schlauch, R. S., and Tang, J. (1993). “Attending to auditory filters that were not stimulated directly,” J. Acoust. Soc. Am. 10.1121/1.408203 94, 743–747. [DOI] [PubMed] [Google Scholar]
- Jesteadt, W., and Bilger, R. C. (1974). “Intensity and frequency discrimination in one- and two-interval paradigms,” J. Acoust. Soc. Am. 10.1121/1.1914696 55, 1266–1276. [DOI] [PubMed] [Google Scholar]
- Malott, R. W., and Malott, M. K. (1970). “Perception and stimulus generalization,” in Animal Psychophysics: The Design and Conduct of Sensory Experiments, edited by Stebbins W. C. (Appleton-Century-Crofts, New York: ), pp. 363–400. [Google Scholar]
- May, B. J., Kimar, S., and Prosen, C. A. (2006). “Auditory filter shapes of CBA/CaJ mice: Behavioral assessments,” J. Acoust. Soc. Am. 10.1121/1.2203593 120, 321–330. [DOI] [PubMed] [Google Scholar]
- Miller, J. D. (1964). “Auditory sensitivity of the chinchilla in quiet and in noise,” J. Acoust. Soc. Am. 36, 2010–2016. [Google Scholar]
- Moore, B. C. J. (1986). Frequency Selectivity in Hearing (Academic, London: ). [Google Scholar]
- Niemiec, A. J., Yost, W. A., and Shofner, W. P. (1992). “Behavioral measures of frequency selectivity in the chinchilla,” J. Acoust. Soc. Am. 10.1121/1.404380 92, 2636–2649. [DOI] [PubMed] [Google Scholar]
- Nienhuys, T. W., and Clark, G. M. (1979). “Critical bands following the selective destruction of the cochlear inner and outer hair cells,” Acta Oto-Laryngol. 88, 350–358. [DOI] [PubMed] [Google Scholar]
- Patterson, R. D., Nimo-Smith, I., Weber, D. L., and Milroy, R. (1982). “The deterioration of hearing with age: Frequency selectivity, the critical ratio, the audiogram, and speech threshold,” J. Acoust. Soc. Am. 10.1121/1.388652 72, 1788–1803. [DOI] [PubMed] [Google Scholar]
- Pickels, J. O. (1975). “Normal critical bands in the cat,” Acta Oto-Laryngol. 80, 245–254. [DOI] [PubMed] [Google Scholar]
- Reed, C. M., and Bilger, R. C. (1973). “A comparative study of S/No and E/No,” J. Acoust. Soc. Am. 10.1121/1.1913421 53, 1039–1044. [DOI] [PubMed] [Google Scholar]
- Richards, V. M., and Neff, D. L. (2004). “Cuing effects for informational masking,” J. Acoust. Soc. Am. 10.1121/1.1631942 115, 289–300. [DOI] [PubMed] [Google Scholar]
- Ruggero, M. A., and Temchin, A. N. (2005). “Unexceptional sharpness of frequency tuning in the human cochlea,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0509323102 102, 18614–18619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharf, B. (1970). “Critical bands,” in Foundations of Modern Auditory Theory, edited by Tobias J. V. (Academic, New York: ), Vol. 1, pp. 157–202. [Google Scholar]
- Seaton, W. H., and Trahiotis, C. (1975). “Comparison of critical ratios and critical bands in the monaural chinchilla,” J. Acoust. Soc. Am. 10.1121/1.380414 57, 193–199. [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2002). “Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.032675099 99, 3318–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shofner, W. P., Whitmer, W. M., and Yost, W. A. (2005). “Listening experience with iterated rippled noise alters the perception of ‘pitch’ strength of complex sounds in the chinchilla,” J. Acoust. Soc. Am. 10.1121/1.2049107 118, 3187–3197. [DOI] [PubMed] [Google Scholar]
- Shofner, W. P., Yost, W. A., and Sheft, S. (1993). “Increment detection of bandlimited noises in the chinchilla,” Hear. Res. 66, 67–80. [DOI] [PubMed] [Google Scholar]
- Swets, J. A. (1964). Signal Detection and Recognition by Human Observers (Wiley, New York: ). [Google Scholar]
- Watson, C. S. (1963). “Masking of tones by noise for the cat,” J. Acoust. Soc. Am. 10.1121/1.1918429 35, 167–172. [DOI] [Google Scholar]