Implicit Reference-Based Group-wise Image Registration and Its Application to Structural and Functional MRI

Abstract

In this study, an implicit reference group-wise (IRG) registration with a small deformation, linear elastic model was used to jointly estimate correspondences between a set of MRI images. The performance of pair-wise and group-wise registration algorithms was evaluated for spatial normalization of structural and functional MRI data. Traditional spatial normalization is accomplished by group-to-reference (G2R) registration in which a group of images are registered pair-wise to a reference image. G2R registration is limited due to bias associated with selecting a reference image. In contrast, implicit reference group-wise (IRG) registration estimates correspondences between a group of images by jointly registering the images to an implicit reference corresponding to the group average. The implicit reference is estimated during IRG registration eliminating the bias associated with selecting a specific reference image. Registration performance was evaluated using segmented T1-weighted magnetic resonance images from the Nonrigid Image Registration Evaluation Project (NIREP), DTI and fMRI images. Implicit reference pair-wise (IRP) registration—a special case of IRG registration for two images—is shown to produce better relative overlap than IRG for pair-wise registration using the same small deformation, linear elastic registration model. However, IRP-G2R registration is shown to have significant transitivity error i.e., significant inconsistencies between correspondences defined by different pair-wise transformations. In contrast, IRG registration produces consistent correspondence between images in a group at the cost of slightly reduced pair-wise RO accuracy compared to IRP-G2R. IRG spatial normalization of the fractional anisotropy (FA) maps of DTI is shown to have smaller FA variance compared with G2R methods using the same elastic registration model. Analyses of fMRI data sets with sensorimotor and visual tasks show that IRG registration, on average, increases the statistical detectability of brain activation compared to G2R registration.

Introduction

Inter-subject spatial normalization is an important process in medical image analysis and in particular brain image analysis. The traditional approach to spatially normalize a group of medical images is to use pair-wise image registration in which all images are individually registered to a target image. The problem with this approach is that it introduces a bias according to the target image used. In contrast, group-wise image registration jointly estimates the correspondences between a group of images. Many group-wise registration techniques naturally estimate transformations from individual subjects to a common coordinate space eliminating the bias associated with registering to a target image. Applications that use group-wise image registration have increased in recent years including creation of atlases (Frangi et al., 2002; Christensen et al., 2006b), building shape models (Cootes et al., 1995, 1999; Rueckert et al., 2003), motion tracking along time series (Crum et al., 2004), aging population studies (Mega et al., 2005; Pieperhoff et al., 2008) and disease population analysis (Zhang et al., 2007).

Reference-based group-wise registration is a normalization approach in which each image in the group is registered to a selected reference image. A limitation of this approach is that the selected reference may not adequately capture common structure in the population, and therefore the spatial normalization to this reference may induce bias into later analysis. To minimize the bias caused by the reference selection, some methods have been proposed (Guimond et al., 2000; Christensen et al., 2006b) to iteratively update the selected reference image based on averaging the deformed images or transformation fields.

A strategy to avoid reference selection is to simultaneously estimate transformations for each subject in the group that map them into a common space without choosing any reference image. Different criteria such as joint probability distribution (Studholme, 2003; Studholme and Cardenas, 2004; Bhatia et al., 2004), voxel-wise entropy (Zollei et al., 2005), Jensen-Shannon divergence (Wang et al., 2006), squared voxel intensity difference (Avants and Gee, 2004; Joshi et al., 2004), and the minimum description length (Twining et al., 2005) have been utilized as similarity costs to define the objective function and estimate transformations. Group-wise registration of non-scalar images, such as tensor components in diffusion tensor imaging (DTI) can also be formulated in a similar way (Zhang et al., 2007). Many of these methods compute and update the unbiased reference image by averaging the deformed images during the estimation procedure.

This paper uses an implicit reference group-wise (IRG) registration framework which avoids bias caused by reference selection and evaluates its performance with various image modalities. The method jointly estimates transformations from each image in the group to a “hidden” reference by optimizing the intensity difference of each pair of deformed images. The basis of the method is that transformations take each image to a common coordinate, therefore, the images after deformation should have similar shapes to each other, and the intensity difference at the corresponding location should be minimized. This framework is based on the work in Christensen and Johnson (2001) in terms of using the same small elastic deformation model, while expansion and modification of the similarity cost function are made to enable the method to map a set of more than two images to a common space instead of estimating transformations from one image directly to another.

The group-wise registration algorithm used in this work is similar to the large deformation group-wise registration algorithm used in Joshi et al. (2004). In contrast, the algorithm used in this work assumes a small deformation linear elastic model and uses the Fourier series to parametrize the deformation field. We show in the discussion section that minimizing the similarity cost function used in this paper is equivalent to minimizing the similarity function used in Joshi et al. (2004).

A set of annotated T1-weighted MRI data (Christensen et al., 2006a) were used to evaluate the performance of the IRG registration method. Results show that the implicit reference method produced smaller registration errors compared to reference based methods that directly register each image to a reference. Moreover, experiments were designed to compare the directly estimated transformations from one image to another and the composed transformations from each image to the implicit reference, and results indicate that the improvement of the implicit reference method is partly due to the composition of two small deformations.

This paper demonstrates the potential of IRG registration for group analyses of DTI and functional MRI (fMRI). DTI enables the non-invasive study of white matter integrity and anatomical connectivity (Basser and Pierpaoli, 1996). Fractional anisotropy (FA), a scalar index of fiber directionality derived from DTI data sets, was used for image normalization and analyses. The performance of various group-wise registration methods was compared, and the results show that the implicit reference technique, with the small deformation elastic model, provides better transformations compared to reference-based methods in terms of smaller within-group variance after registration.

Functional MRI techniques provide non-invasive study of neural activity detected by blood oxygen level dependent (BOLD) or other signals (Ogawa et al., 1990). The accuracy of spatial normalization is crucial for group analyses of functional activation. Most current fMRI normalization techniques follow a standard approach that utilizes a lower order registration model under a reference-based framework. A motivation of this work was to examine whether improved spatial normalization would enhance the statistical detectability of brain activation (Miller et al., 2005). The implicit reference method and reference-based methods were applied to a set of fMRI data sets with sensorimotor and visual tasks. Results demonstrate that the smaller within-group variance using the implicit reference method resulted in improved statistics for brain activation detection.

Methods

Pair-wise (PW) image registration

We focus on estimating diffeomorphic transformations between two or more images under a small deformation model (Christensen et al., 1997). Let I_i represent an image volume with voxel dimensions of D₁ × D₂ × D₃. The Eulerian transformation from the coordinate system of I_i to that of I_j can be parameterized as a set of vectors in Euclidean space, and described as a function h_ij : Ω → Ω, where Ω = {(x₁, x₂, x₃)|0 ≤ x₁ ≤ D₁; 0 ≤ x₂ ≤ D₂; 0 ≤ x₃ ≤ D₃}. Under the transformation h_ij, I_i(x) is deformed to I_i(h_ij(x)).

Conventional pair-wise image registration methods define the registration problem as finding the transformation h_ij from image I_i to I_j by minimizing an objective function such as

$$C(I_{\text{i}}(h_{ij}),I_j)=D(I_i(h_{ij}),I_j)+R(h_{ij})$$

where D is a similarity cost function and R is a regularization term to penalize transformations with large and unsmooth distortion. In this paper, PW will be used to refer to pair-wise registration with a sum of squared differences similarity cost function denoted as $D(I,J)={\int }_{\Omega }\parallel I(x)-J(x){\parallel }^{2}dx$ and linear elastic regularization function as in Eq. 1. The PW registration algorithm used in this paper is equivalent to the unidirectional, small deformation, linear elastic registration method described in Christensen and Johnson (2001). Alternatively, the pair-wise image registration problem can be formulated in a symmetric fashion to minimize the asymmetry caused by structural differences between the images being registered (Christensen and Johnson, 2001; Leow et al., 2007) and can use many different similarity cost functions (Studholme, 2003; Studholme and Cardenas, 2004; Bhatia et al., 2004; Zollei et al., 2005; Wang et al., 2006; Joshi et al., 2004).

Implicit reference pair-wise (IRP) image registration

Implicit reference pair-wise (IRP) registration is a special case of IRG registration (see below) when only two images are registered. Instead of directly estimating transformations between images I_i and I_j, IRP registration estimates transformations h_iR from I_i to a common reference space halfway between the images. Similar approaches with large deformation registration model were proposed in previous studies (Avants and Gee, 2004; Avants et al., 2008; Beg and Khan, 2007). The similarity cost becomes D(I_i(h_iR), I_j(h_jR)), and the total cost function is defined by

$$C(h_{iR},h_{jR})=D(I_i(h_{iR}),I_j(h_{jR}))+R(h_{iR})+R(h_{jR}).$$

For this paper, the sum of squared differences was used for D and R was chosen to be a linear elastic regularization function as in Eq. 1.

Group-to-Reference (G2R) image registration

Traditional spatial normalization is accomplished by group-to-reference (G2R) registration in which a group of images are registered pair-wise to a target or reference image. Throughout the rest of the paper, the terms PW-G2R and IRP-G2R will refer to G2R registration computed using the PW and IRP registration algorithm, respectively. G2R registration allows images from different individuals to be compared in a standard reference frame, i.e., the image space of the target or reference image. The drawback of G2R image registration is that the results are biased by factors such as the shape of the structures in the target image and noise in the image.

Implicit reference group-wise (IRG) image registration

The implicit reference group-wise (IRG) image registration problem can be stated as: estimate the N > 2 transformations h_iR from each image I_i in a population to an unknown common space by minimizing the summation of the intensity difference between each pair of deformed images. The unknown common space is defined as the implicit reference space. The objective function for this registration problem can be stated as follows:

$$C=\sigma \sum _i\sum _{j,i<j}{\int }_{\Omega }\parallel I_i(h_{\mathrm{iR}}(x))-I_j(h_{\mathrm{jR}}(x)){\parallel }^2\mathrm{dx}+\rho \sum _i{\int }_{\Omega }\parallel L(u_{iR}(x)){\parallel }^{2}dx,$$ (1)

where h_iR(x) = u_iR(x) + x is the transformation from image i to the implicit reference R, u_iR(x) is the displacement field from i to R, L(u_iR(x)) is a linear differential operator regularization constraint, and σ and ρ are weighting parameters. In this work, we chose L to be the linear elasticity operator with the form $Lu(\text{x})=-\alpha {\nabla }^{2}u(x)-\beta \nabla (\nabla \cdot u(x))+\gamma u(x),$ where $\nabla =\left[\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2},\frac{\partial }{\partial x_3}\right]$ and ${\nabla }^2=\nabla \cdot \nabla =\left[\frac{{\partial }^2}{\partial x_1^2}+\frac{{\partial }^2}{\partial x_2^2}+\frac{{\partial }^2}{\partial x_3^2}\right]$ (Christensen and Johnson, 2001). Each displacement field u_iR(x) is a 3×1 vector-valued function parameterized by the 3D Fourier series $u_{iR}(x)={\sum }_{k=0}^{d-1}{\mu }_{i,k}{e}^{j2\pi k\cdot x/d}$ where $j=\sqrt{-1},k={\left[k_1,k_2,k_3\right]}^T,d-1={\left[d_1-1,d_2-1,d_3-1\right]}^T,x/d={\left[x_1/d_1,x_2/d_2,x_3/d_3\right]}^T$ and ${\mu }_{i,k}={\left[{\mu }_{i,k,1},{\mu }_{i,k,2},{\mu }_{i,k,3}\right]}^T$. The basis coefficients μ_i,k = a_i,k + jb_i,k are initialized to be 0s, and determined by gradient descent using

$$a_{i,k}^{n+1}=a_{i,k}^n+\in \frac{\partial C({\mu }_{i,k}^n)}{\partial a_{i,k}},\text{and}{b}_{i,k}^{n+1}=b_{i,k}^n+\in \frac{\partial C({\mu }_{i,k}^n)}{\partial b_{i,k}},$$ (2)

where ∈ is the step size, and the superscript n corresponds to the value of the parameters at the nth iteration. The estimation details can be found in Christensen and Johnson (2001). The weighting parameter σ of the similarity cost was set to be 1, and the weighting parameter ρ of the regularization constraint was set to be 0.00025 through out the optimization procedure. A spatial and frequency multi-resolution procedure was used to estimate the full resolution registration to avoid local minima. Different levels of resolutions were applied for different image modalities with various voxel dimensions. At each resolution level, the initial and final number of harmonics and the number of iterations were set differently as described in Table 1. When the number of harmonics, r, is set, the triple summation of u_iR over k where k = [0 ≤ k ≤ d − 1] is replaced by k = [0 ≤ k ≤ r − 1,d − r − 1 ≤ k ≤ d − 1]. The calculation of forward and reverse fast Fourier transforms (FFT) of h_iR dominates the computational time at each iteration. Despite the double summation in the similarity cost term, the computational cost is still approximately linear to the number of images, since the number of transformations is equal to the number of images. For example, this algorithm takes about 3 hours to register 15 images with voxel dimensions of 80 × 95 × 75, while it takes about 6 hours to register 30 images with the same dimensions on a 2.4 GHz AMD Opteron Linux system.

Table 1.

Multi-resolution IRG registration parameters used to register T1-weighted MRI, DTI and fMRI images with different voxel dimensions.

voxel dims	resolution	initial num of harmonics	final num of harmonics	iterations
256 × 300 × 256	1/8	1	5	500
	1/4	5	9	500
	1/2	9	13	250
	1	13	17	50
80 × 95 × 75	1/4	1	5	500
	1/2	5	9	500
	1	9	13	250
54 × 64 × 50	1	5	9	500

Fig. 1 illustrates the IRG registration method for mapping images to a common space and mapping any pair of images. The transformation h_iR and the inverse of h_jR are concatenated to compute the transformation between a pair of images I_i and I_j. The inverse transformation was computed using the method described in Christensen and Johnson (2001).

Figure 1.

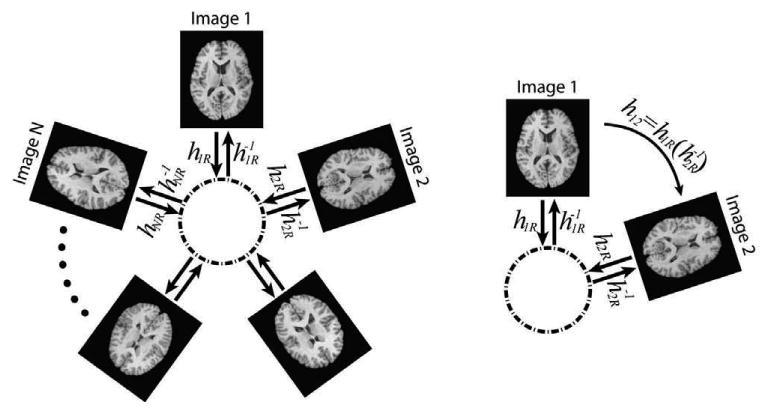
Implicit reference group-wise (IRG) registration method framework. Transformations h_iR from each image to an implicit space are estimated; the transformation h_ij between every pair of images is obtained by concatenating transformations, $h_{\mathrm{ij}}(x)=h_{\mathrm{iR}}(h_{\mathrm{jR}}^{-1}(x))$.

Fig. 2 illustrates the IRG registration method applied to a population of four 2D shapes that consisted of a circle, two ellipses, and a square. It is shown that the transformations bring each shape to the average shape of all the shapes and the deformed shapes are similar to each other.

Figure 2.

IRG registration of four 2D phantom shapes. The top row shows the original four shapes that were registered with the IRG method. The middle row shows the deformed images produced by applying the estimated transformation h_iR to image i above it. The images in the middle row correspond to the implicit reference image. The bottom row shows the transformation h_iR applied to a rectangular grid.

Evaluation using NIREP

In order to evaluate the performance of registration algorithms, it is necessary to have a wide collection of consistently annotated image data sets and evaluation statistics. The NA0 database from the registration evaluation package of the Non-Rigid Image Registration Evaluation Project (NIREP) (Christensen et al., 2006a) was used to evaluate the IRG registration method. The NA0 database consists of MRI data from 16 subjects that include gray matter segmentations (Damasio, 2005; Allen et al., 2002, 2003). The images were initially segmented with Brainvox (Frank et al., 1997). The segmentations, including gray and white matter, were then restricted to the gray matter by applying the gray matter segmentation generated using the approach described in Grabowski et al. (2000) to avoid arbitrary boundaries in white matter. The final regions of interest (ROIs) include gray matter regions in the frontal lobe: frontal pole, superior frontal gyrus, middle frontal gyrus, inferior frontal gyrus, orbital frontal gyrus, precentral gyrus; parietal lobe: postcentral gyrus, superior parietal lobule, inferior parietal lobule; temporal lobe: temporal pole, superior temporal gyrus, infero-temporal region, parahippocampal gyrus; occipital lobe; cingulate gyrus; and insula. The 16 data sets were rigidly rotated and translated using the anterior commissure, posterior commissure, and inter-hemispheric fissure as landmarks.

The relative overlap (RO), which is also called the Jaccard or Tanimoto coefficient, was used to evaluate registration performance. The RO is computed for each ROI and measures how well the two ROIs agree with each other. The RO is defined as the number of voxels in the intersection of two ROIs divided by the number of voxels in the union. Stated mathematically, the RO of the kth ROI when image I_j is registered to I_i is defined as:

$$R{O}_{\mathrm{ij}}^k=\frac{{\sum }_{x=1}^M\mathrm{RO}{I}_i^k(x)\cap \mathrm{RO}{I}_j^k(h_{\mathrm{ji}}(x))}{{\sum }_{x=1}^M\mathrm{RO}{I}_i^k(x)\cup \mathrm{RO}{I}_j^k(h_{\mathrm{ji}}(x))},$$ (3)

where $\mathrm{RO}{I}_i^k(x)$ returns 1 if x is in the kth ROI in I_i, and returns 0 if is not, ∩ and ∪ denote AND and OR operations respectively, and M is the number of voxels in the image. Note that h_ji is estimated directly for pair-wise (PW) registration and obtained by $h_{\mathrm{ji}}=h_{\mathrm{jR}}(h_{\mathrm{iR}}^{-1})$ for IRP and IRG registrations.

The average relative overlap (ARO) of the kth ROI using I_i as reference is defined as:

$$\mathrm{AR}{O}_i^k=\frac{1}{N-1}\sum _{j=1,j\ne i}^{N}R{O}_{\mathrm{ij}}^k,$$ (4)

where N is the number of images in the group being averaged. The ARO using implicit reference method is defined as:

$$\mathrm{AR}{O}_R^k=\frac{1}{N\times (N-1)}\sum _{j=1,j\ne i}^N\sum _{i=1}^N\frac{{\sum }_{x=1}^M\mathrm{RO}{I}_i^k(h_{\mathrm{iR}}(x))\cap \mathrm{RO}{I}_j^k(h_{\mathrm{jR}}(x))}{{\sum }_{x=1}^M\mathrm{RO}{I}_i^k(h_{\mathrm{iR}}(x))\cup \mathrm{RO}{I}_j^k(h_{\mathrm{jR}}(x))}.$$ (5)

Note that $\mathrm{AR}{O}_R^k$ is defined in the implicit reference space while $\mathrm{AR}{O}_i^k$ is defined in the coordinate system of image I_i. Care must be taken when comparing ARO values that are computed in different coordinate systems due to coordinate system specific biases such as different sizes and shapes of the ROIs between different coordinate systems.

The transitivity error (Christensen and Johnson, 2003; Christensen et al., 2006a) of a set of transformations that register a group of images is a measure of consistency between the correspondences defined by the transformations. Ideally, transformations that define correspondence between three images should project a point from image A to B to C to A back to the original position. The transitivity error for a set of transformations is defined as the squared error difference between the composition of the transformations between three images and the identity map. The cumulative transitivity error (CTE) with respect to template image k is computed as

$$\mathrm{CT}{E}_k(x)=\frac{1}{(N-1)(N-2)}\sum _{\begin{array}{c}i=1\\ i\ne k\end{array}}^N\sum _{\begin{array}{c}j=1\\ j\ne i\\ j\ne k\end{array}}^N\Vert h_{ki}(h_{ij}(h_{jk}(x)))-x\Vert ,$$ (6)

where N is the number of images in the population. The average CTE of each ROI for different methods were computed for pair-wise, IRP and IRG registration. Transformations h_ijs were directly estimated using pair-wise registration, and were composed by h_iR and $h_{jR}^{-1}$ using IRP and IRG registration.

Application to diffusion tensor images

Thirty healthy subjects were recruited as part of a protocol approved by the Institutional Review Board (IRB) of the National Institute on Drug Abuse Intramural Research Program and provided written informed consent. All data were scanned on a Siemens 3T Allegra scanner. An EPI-based spin-echo pulse sequence was used to acquire diffusion-weighted MRI images. For each subject, 35 axial images were prescribed to cover the whole brain with a 128×128 in-plane matrix at a resolution of 1.719×1.719×4mm³. Besides the non-diffusion-weighted reference image, 12 directions were used to apply the diffusion-sensitive gradients with a b-factor of 1000s/mm². For EPI, TR/TE = 5000/87ms, BW= 1700Hz/Pixel, and NEX=4. Three-dimensional T1-weighted anatomical images were also acquired.

Each structural image was automatically normalized to Talairach space using the AFNI software package (Cox, 1996). The 12 diffusion weighted images (DWIs) were aligned to their corresponding structural images for correction of motion and image artifacts using mutual information based affine registration (Jenkinson and Smith, 2001), provided by the FSL package (Smith et al., 2004). Normalization matrices were applied to DWIs, and FA images were then calculated from the diffusion tensor. After the preprocessing, all FA images have a 2 × 2 × 2mm³ voxel resolution and a 80 × 95 × 70 matrix.

A comparison of IRG and pair-wise G2R registration was performed to evaluate registration of FA images. Two different non-rigid registration models were applied for G2R registration: the B-spline based free form deformation (FFD) model (Rueckert et al., 1999) used in FSL and the small deformation elastic (SDE) model utilized in this work. The FFD method with a cross correlation similarity measure and the default parameters for FA registration in FSL was used: full resolution registration with a control point spacing of 20 mm resulting a 9 × 10 × 8 mesh of control points. The parameters used in the SDE model are listed in Table 1 for the voxel dimensions of 80 × 95 × 75. The reference was chosen in two different ways. One was to use the standard FA image provided by FSL, which is the average of 58 well-aligned high quality FA images with a 1 × 1 × 1mm³ resolution. The other was to select the “most representative” image. After obtaining all transformations (30 × 29 = 870) using FFD, the image with the smallest amount of average warping, which was necessary to align all other images to it, was selected as the “most representative” image. Including the IRG method, a total of 5 different non-rigid group-wise registration approaches were used: G2R registration using the standard image as reference with the FFD model and the SDE model; G2R registration using the “most representative” image as reference with the FFD model and the SDE model; and IRG registration with the SDE model. The FFD registration was used as a benchmark to evaluate the performance of the IRG method instead of a like-for-like comparison of the FFD and SDE models.

The standard deviation of deformed FA maps were used to measure the registration performance. Although the FA statistics are unknown in normal subjects, it is reasonable to assume that FA values consist of separate distributions for white matter and gray matter. For misaligned structures, this mixture of distributions with unequal means would produce larger sample variance than a single distribution for well aligned structures. Therefore, the cross subject variance is a reasonable indicator of how well the image structures are aligned.

Applications to fMRI studies

Twenty-nine different healthy controls provided written informed consent and were scanned on the same scanner using the same IRB approved protocol as the DTI study. The functional data were acquired using a single-shot gradient-echo EPI sequence with a TR of 4 s and a TE of 27 ms. Thirty-nine contiguous 4-mm thick oblique slices (30° axial to coronal) were prescribed to cover the whole brain with a 64 × 64 in-plane matrix at a resolution of 3.44 × 3.44 × 4mm³. Subjects performed a block-design finger tapping task cued by a flashing checkerboard, which started with 20s “off” (watching a cross on the screen without moving fingers) and followed by 7 cycles of 20s “on” (watching a flashing checkerboard on the screen and moving fingers) and 20s “off” states. High resolution T1-weighted anatomical images were also acquired with a TR of 2.5 s, a TE of 4.38 ms, a FA of 7°, and a voxel size of 1 × 1 × 1mm³.

EPI data preprocessing included slice-timing correction, motion correction and linear detrending. All functional data were spatially normalized to the standard Talairach space using affine registration with a resampled resolution of 3×3×3mm³. Spatial smoothing with a 6-mm Gaussian kernel was performed to increase spatial signal to noise ratio (SNR) after affine alignment and before the non-rigid group registration. All data preprocessing were conducted in AFNI.

Both IRG and pair-wise G2R registration were applied to the affine aligned EPI data. A 3D volume (i.e., at the fourth time point) from the EPI time series was selected from each subject as the registration input. The transformation fields obtained from the volume was then applied to all volumes along the time series. The results from affine registration were used as the baseline. For G2R registration, each subject in the group was selected as the reference, and the rest of the subjects were registered to it, resulting in 29 groups of reference-based normalized images. Including the implicit reference registration, there were a total of 31 groups of registration approaches (1 affine, 29 G2R and 1 implicit reference registration). After registration, across-subject image intensity standard deviation maps were computed for all registration groups. No further smoothing was applied after non-rigid registration. The general linear model was then exploited for analyzing the functional activation, and the linear regression coefficient β maps were obtained from each deformed 4D fMRI data.

For each group of the registered data sets, a one-sample t-test was applied to the β maps to test if the activation coefficients were significantly different from zero. A threshold of t > 5.3 with a cluster size greater than 54 mm³ (p_corrected < 0.01) was used to generate group functional activation maps. Four activated regions were selected as ROIs including visual cortex, left sensorimotor, right sensorimotor cortices and supplementary motor area (SMA). Common ROIs were obtained by taking the intersection of the corresponding 31 ROIs. The average of intensity standard deviation, β weights and the corresponding t-statistics on the four common ROIs were computed and compared.

Results

NIREP evaluation

Fig.3 shows intensity averages of registered images using the IRG algorithm (bottom row), rigid G2R registration (top top) and the PW group-to-reference (PW-G2R) registration in which MRI images 2-16 were registered to image 1 (middle row). The average intensity images produced by the PW-G2R and IRG registrations are much sharper than that produced by rigid G2R registration, showing that both approaches produce similar registration results. Note that the registered images in Fig.3(b) are shown in the coordinate system of the reference image whereas the registered images in Fig.3(c) are shown in the coordinate system of the implicit reference or group average (see Discussion).

Figure 3.

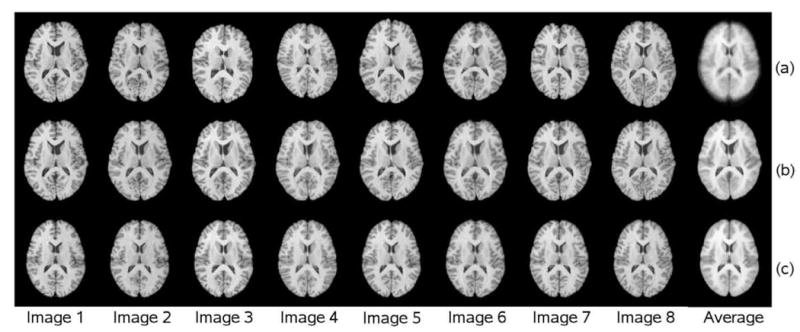
G2R and IRG registration results. Row (a) shows 8 of the 16 MRI images from the NA0 database after rigid G2R registration and the average intensity of the 16 images after rigid registration. Row (b) shows the corresponding 8 deformed images after PW-G2R registration using the first image as the reference and the average intensity computed from the 16 images in the coordinate space of image 1. Row (c) shows the corresponding 8 deformed images after IRG registration and the average of the 16 IRG registered images in the coordinate system of the implicit-reference space.

Fig. 4 shows the voxel-wise overlap produced by mapping the ROIs from 15 of the NA0 data sets to the 16th target reference image. The reference image and the ROIs associated with this reference coordinate system are displayed in Fig. 4(a) and (b) respectively. The other 15 MRI images have similar ROIs that were mapped to the reference coordinate system. The images in Fig. 4(c) show the number of ROIs that agree with the target ROI for rigid, PW, and IRP registration. This figure shows that PW registration is an improvement over rigid registration and IRP registration is an improvement over PW registration. Moreover, visualization of the overlap shows where the registration methods are more and less accurate with respect to the shape and complexity of the reference MRI image.

Figure 4.

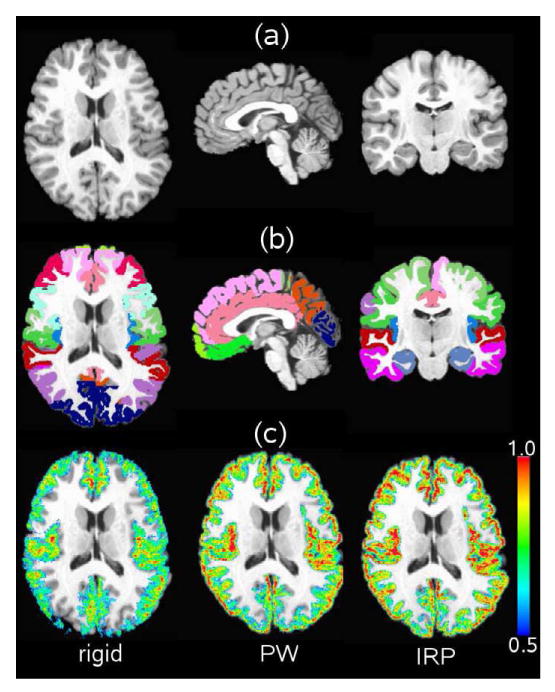
Region of Interest (ROI) overlap comparison between rigid, PW, and IRP registration. Panel (a) shows the T1-weighted MRI reference image; panel (b) shows the gray matter ROIs associated with the reference image; and panel (c) shows the overlap of the ROIs produced by mapping the other 15 MRI data sets to the reference image using rigid, PW, and IRP registration. The overlap of the the ROIs are show for a range of 0.5 to 1.0 where 0.5 corresponds to 50% agreement and 1.0 corresponds to 100% agreement.

Fig. 5 compares IRG to G2R image registration performance using the ARO statistic for 32 ROIs. The G2R image registration was computed using the PW and IRP registration algorithms and will be referred to as PW-G2R and IRP-G2R, respectively. Due to the bias associated with picking a reference image, registration was repeated 16 times for PW-G2R and IRP-G2R registration using a different image (1-16) as the reference. Producing the PW-G2R and IRP-G2R results required computing and storing 2×16×15 = 480 transformations, i.e., all the pair-wise registrations between the 16 images for both the PW and IRP methods. This is in contrast to the 16 transformations computed using the IRG approach. The PW-G2R, IRP-G2R, and IRG approaches used the same small deformation elastic model and same set of parameters (see Table 1 for the voxel dimensions of 256 × 300 × 256).

Figure 5.

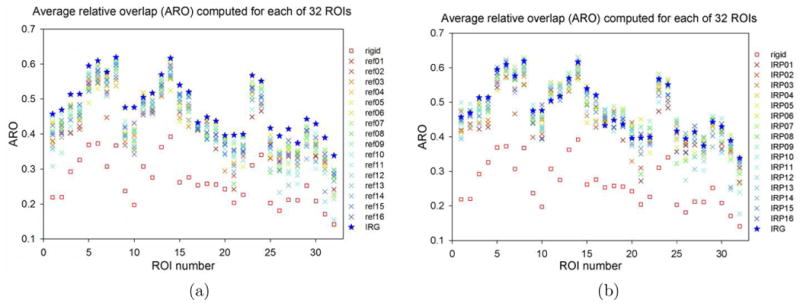
Comparison of (a) IRG to PW-G2R registration and (b) IRG to IRP-G2R registration methods by average relative overlap (ARO) for the 32 region of interests (ROIs) in the NIREP NA0 evaluation database. For each ROI, the square represents the ARO after rigid alignment, the star denotes the ARO using IRG registration, and the 16 “X”-shaped points denote to AROs using G2R registrations, where each color corresponds to a reference-based registration using one of the 16 images as the reference.

For each of the 32 ROIs, the ARO was measured in the implicit reference space for the IRG method and in the reference image coordinate system for G2R registration. In general, it is difficult to compare the ARO values across different spaces due to varying sizes and shapes of the ROIs. However, for this experiment, the ROIs are roughly the same shape and size in each of the coordinate systems making for a less than perfect but still meaningful comparison of the methods.

The results in Fig. 5 show that the IRG registration always outperforms the PW-G2R registration with respect to the ARO independent of the reference used. However, the IRG registration does not always outperform the IRP-G2R registration with respect to ARO. The reason for this is that the IRP registration is a special case of the IRG registration in which only two images are registered. In some cases, adding additional images to the registration helps improve the registration by giving additional information to get out of local minima. In other cases, adding additional images may produce additional local minima or other errors that reduce registration performance. Given that the ROIs have small and complex shapes (Geng, 2007), the relative overlap values are reasonable.

Fig. 6 shows a comparison between the pair-wise registrations produced by PW, IRP, and IRG registration with respect to RO and transitivity error (TE). The purpose of this analysis was to examine the trade-offs between estimating pair-wise registrations directly using PW and IRP registration and estimating pair-wise registration indirectly using IRG registration. The transformations h_ij from image I_i to I_j were computed directly for PW registration and computed by composing transformations using the formula $h_{ij}=h_{iR}\left(h_{jR}^{-1}\right)$ for IRP and IRG registration approaches. Note that the implicit reference for each IRP registration is different and can be thought of roughly as the coordinate system halfway between the coordinate systems of images I_i and I_j. In contrast, the implicit reference for the IRG method can be thought of as the coordinate system corresponding to the average shape of the group. The RO calculated using Eq.3 and its standard deviation were compared for each ROI. The top bar chart of Fig. 6 shows that there is no significant difference of the average ROs between PW and IRG registration for registering two images together. For 9 out of 32 ROIs, the PW registration produced slightly larger RO values, while for the rest ROIs, the IRG registration generated larger values. In contrast, IRP outperforms the IRG method by 5% – 15% suggesting that IRP registration is better to use for pair-wise registration than either PW or IRG registration.

Figure 6.

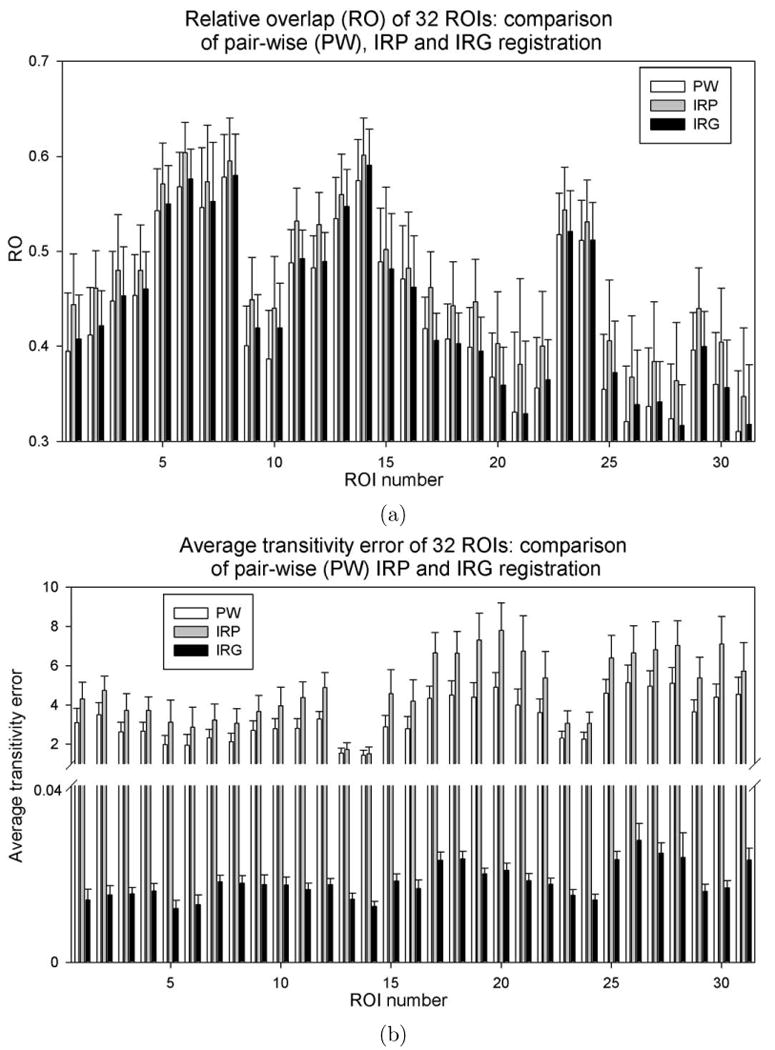
Comparison of pair-wise transformations produced by the PW, IRP, and IRG registration methods with respect to (a) relative overlap (RO) and (b) average transitivity error (ATE). Average and standard deviation of RO and ATE are plotted for each ROI corresponding to 16 × 15 pair-wise transformations in the population.

The bottom bar chart in Fig.6 compares the average transitivity error (ATE) for each ROI for the PW-G2R, IRP-G2R, and IRG methods. The ATE was computed using Eq. 6. Results show that the ATE range is from 2 to 10 voxels for the PW-G2R and IRP-G2R registrations whereas the ATE for IRG registration are all smaller than 0.04 voxel. IRG registration produces much less transitivity error compared to the PW-G2R and IRP-G2R registration indicating that IRG generates a consistent set of transformations between a group of images.

To summarize, results shown in Fig. 6 suggest that IRP registration produces better relative overlap than IRG for pair-wise registration at the cost of significant transitivity error for IRP-G2R registration, i.e., significant inconsistencies between correspondences defined by different pair-wise transformations. In contrast, IRG registration produces consistent correspondence between images in a group at the cost of slightly reduced pair-wise RO accuracy compared to IRP-G2R. Thus, it is better to use IRP registration if the task is to register two images, but it is better to use IRG registration if the task is to register a group of images. Furthermore, the IRP registration should be favored over PW registration when registering two images.

DTI data sets

The mean and standard deviation of the deformed FA maps using different registration methods are displayed in Fig. 7. The average standard deviation (ASD) of FA values in the whole brain and a white matter ROI are presented in Table 2. The white matter ROI was generated by thresholding the average deformed FA images obtained from each of the five methods at 0.3 and taking the overlap region of the five white matter masks. As shown in Table 2, the B-spline FFD model reduced the ASD approximately 30 percent compared to the affine model, and the SDE model reduced ASD approximately 10 percent compared to the FFD model. Within the SDE model, the IRG method further reduced the ASD 6 percent in white matter as well as in the entire brain compared with the G2R registration using either the standard image or the “most representative” image as the reference. Note, since the SDE model with the parameters used in this work generates transformations with more degrees of freedom compared to the FFD model with the default parameters in FSL (3 × 13 × 13 × 13 vs. 3 × 9 × 10 × 8), the reduced ASD does not necessarily indicate that the SDE model is superior to the FFD model. The results give a sense of how good the IRG registration is compared to a standard method in a software package with a large number of users.

Figure 7.

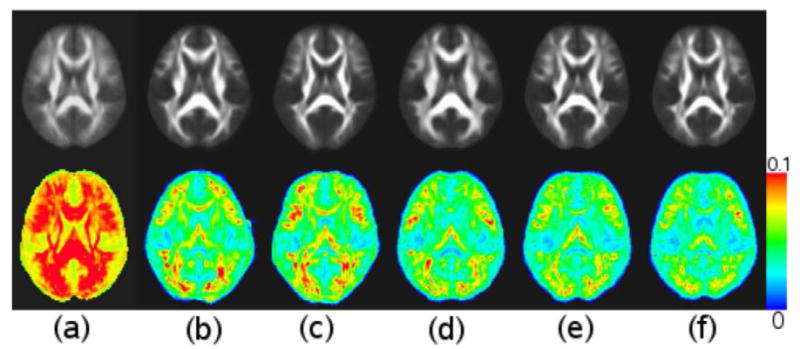
Comparison of average and standard deviation of deformed FA images after different registration methods. Top row includes average deformed FA images after (a) affine registration, (b) G2R registration using standard image as reference with B-spline free form deformation (FFD) model, (c) G2R registration using “most representative” image as reference with FFD model, (d) G2R registration using standard image as reference with small deformation elastic (SDE) model, (e) G2R registration using “most representative” image as reference with SDE model, and (f) IRG registration with SDE model. Bottom row contains standard deviation of FA images after registrations in the same order as in the top row.

Table 2.

Average standard deviation of deformed FA maps in white matter and whole brain under different registration methods.

Ave std dev	Affine	FFD		SDE
		std ref	sel ref	std ref	sel ref	IRG
white matter ROI	.09690	.05997	.06450	. 05278	.05306	.05006
whole Brain	.06685	.04659	.04860	.04125	.04147	.03887

Note: “std ref” refers to the G2R registration using the standard FA image provided by FSL as the reference; “sel ref” refers to the G2R registration selecting the “most representative”image as the reference. The number of degrees of freedom used in SDE model is 3 × 13 × 13 × 13, whereas it is 3 × 9 × 10 × 8 in the FFD model with default parameter setup in FSL.

fMRI data sets

The functional activation maps are shown in Fig. 8. Compared with affine alignment, the non-rigid elastic registration using both G2R and IRG registration methods provide larger β values in the left and right sensorimotor cortices and visual cortex. Fig.8(d) contains the log-Jacobian map of a typical transformation from one image to the implicit reference. The log Jacobian map shows that the IRG method generated large deformations in some locations indicating that affine registration for normalizing fMRI data may not sufficiently account for local variation.

Figure 8.

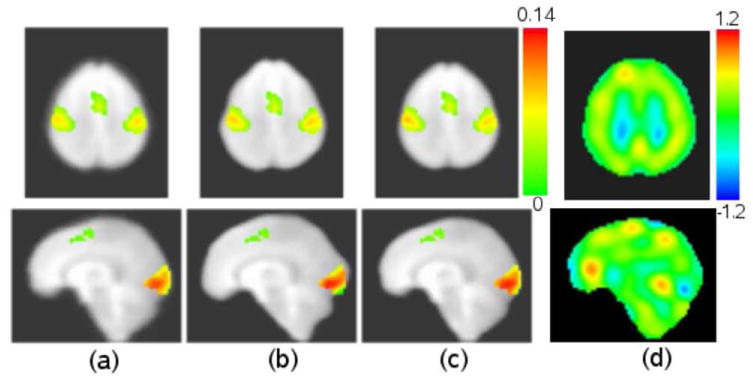
Functional activation maps with different registration methods: (a) affine alignment; (b) G2R registration with one of the group images as reference; (c) IRG registration; (d) log-Jacobian of a transformation from one image to the implicit reference. All activation maps are overlaid on the average of the deformed EPI data sets using IRG registration. (a), (b) and (c) are color coded by β values.

Fig.9(a) shows the ASD of the image intensity in the whole brain and in each ROI under different registration methods. The G2R registration reduced the ASD 30 percent, on average, in the whole brain compared to the affine alignment. The IRG registration further reduced the ASD approximately 2 percent compared to the average performance of the G2R registration in the whole brain. The IRG registration provides a consistent improvement in terms of smaller ASD in the four ROIs as well. Because fMRI data have lower resolution and less structural information compared to structural data such as T1-weighted and DTI images, the improvement of IRG registration using fMRI data is smaller than that using structural data.

Figure 9.

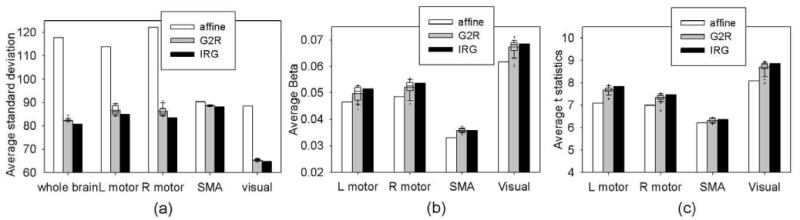
The average of (a) intensity standard deviation, (b) the β weights, and (c) t-statistics on different regions. In each panel, the first bar displays the measurement using affine alignment, the second bar shows the average measurements using 29 G2R registrations (with box plot on the top showing the median, the 5th, 25th, 75th, and 95th percentiles and outliers) and the third bar displays the measurement using IRG registration.

Fig.9(b) and (c) show the average of β weights and t-statistics in the four ROIs under different registration methods. Compared with the affine alignment, the elastic registration methods increased the average β and the t-statistics in each ROI. The IRG registration further increased the β values in the regions of right and left sensorimotor cortices and visual cortex, and the t-statistics in all ROIs compared with the G2R registration.

Discussion

Analysis of reference-based and implicit reference registration errors

The registration results of T1-weighted anatomical images, DTI and fMRI images in this study consistently showed that the implicit reference registration method produced smaller registration errors. This can be explained by the following theoretical analysis. Starting with the registration of two images, the similarity objective function for the implicit reference method is defined as D(I₁(h_1R), I₂(h_2R)), and the similarity cost for the reference-based method can be written as D(I₁(h₁₂), I₂), which is equal to D(I₁(h₁₂), I₂(h_id)), where h_id is the identity map from I₂ to I₂. The optimization of the former cost function searches the optimal transformations h_1R and h_2R to minimize the similarity cost between I₁(h_1R) and I₂(h_2R). The optimization of the latter cost function searches the optimal transformation h₁₂ that minimizes the similarity cost between I₁(h₁₂) and I₂(h_id). Therefore, the minimizer of the latter can be considered as a local minimizer of the former, which means that the similarity error between I₁(h₁₂) and I₂ is no smaller than the error between I₁(h_1R) and I₂(h_2R). Similar analysis can be extended to the registration of more than two images.

Comparison of PW, IRP, and IRG registration

The results in Fig.6 suggest that IRP registration produces better pair-wise registration than using the PW approach with respect to relative overlap. To see why this may be the case, consider that the IRP transformation from I_i to I_j is produced by composing the two transformations h_iR with $h_{Rj}=h_{jR}^{-1},$ where the implicit reference I_R is roughly halfway between I_i and I_j. One reason for the better performance could be that there is less error for smaller deformations. In this case, h_iR and h_Rj have less error combined than the transformation h_ij since both h_iR and h_Rj have roughly half the shape differences to accommodate compared h_ij. Another reason for the better performance could be that estimating h_iR and h_jR solves the registration problem from both directions as opposed to one direction. Solving the registration from both directions could help reduce the number of local minima and may reduce the impact of getting stuck in a local minima since only half the distance between the shapes in the two images is accommodated.

When considering more than two images, the implicit reference is similar to the average of all images, and its shape is likely to be different from the average shape of I_i and I_j. As the population average diverges in shape from the average shape of I_i and I_j, the registration performance of the IRG transformations from I_i to I_j may be similar or even worse than direct pair-wise registration. The registration performance is similar if I_i or I_j has similar shape as the mean and worse when the population average is very different from the average shape of I_i and I_j. To see this, assume that I_i is similar in shape to the population mean, then the transformation from I_i to the reference is close to the identity mapping and the transformation from the reference to I_j will be close to the direct pair-wise registration between I_i and I_j. Now, assume that the population average is different than the average shape of I_i and I_j and that the registration error is proportional to the shape differences. In this case, the error in registering I_i to the reference is added to the error registering the reference to I_j, which could have more error than directly registering I_i to I_j. However, in terms of computation cost, the pair-wise method estimates and stores N(N - 1) transformations, while the IRG methods only computes N transformations.

An experiment using the 16 images from the NA0 NIREP database was used to test the hypothesis that the IRG performance of the composed transformations $h_{iR}\left(h_{jR}^{-1}\right)$ is affected by the distance between the reference and the average of the two images. The distance of ROI^k of two images was defined to be $1-\text{RO}\left({\text{ROI}}_1^k,{\text{ROI}}_2^k\right)$ where 0 means perfect overlap and 1 means no overlap. We also made a crude simplification that for ROI^k, the distance between I_R and the average of I₁ and I₂ to be $1-\frac{1}{2}\left(\mathrm{RO}\left(\mathrm{RO}{I}_R^k,\mathrm{RO}{I}_1^k\right)+\mathrm{RO}\left(\mathrm{RO}{I}_R^k,\mathrm{RO}{I}_2^k\right)\right)$. Assume the registration input has three images. To reduce computations, one image was fixed from the 16 images, and two more images were randomly chosen from the rest of the images. A total of $\left(\begin{array}{c}15\\ 2\end{array}\right)$ registrations were computed. In each registration, we computed the distance between I_R and the average shape of I_i and I_j, and the distance between I_i and deformed I_j which measures the performance of $h_{\mathrm{iR}}\left(h_{\mathrm{jR}}^{-1}\right)$. After least square linear regression, the β coefficient between the two distances is 0.175 with p < 0.001, indicating that the accuracy of $h_{\mathrm{iR}}\left(h_{\mathrm{jR}}^{-1}\right)$ is correlated to the distance between the reference image and the average of I_i and I_j.

Inverse consistency and transitivity

A set of transformations that define correspondences between a group of images should satisfy desirable properties such as inverse consistency and transitivity (Christensen and Johnson, 2003; Geng, 2007). Based on the implicit reference registration method, the transformations between any two images I_i and I_j can be calculated as

$$h_{\mathrm{ij}}=h_{\mathrm{iR}}\circ h_{\mathrm{jR}}^{-1},\text{and}{h}_{\mathrm{ji}}=h_{\mathrm{jR}}\circ h_{\mathrm{iR}}^{-1}.$$

Theoretically, $h_{\mathrm{ij}}=h_{\mathrm{ji}}^{-1}$ by construction for the implicit reference registration method implying no inverse consistency error. However, in practice there are small errors due to computing the inverse and composing the transformations such that the implicit reference methods have some small inverse consistency error.

Theoretically, the IRG registration has no transitivity error. To see this, let I_i, I_j, and I_k represent three images in the group such that

$$h_{\mathrm{ij}}=h_{\mathrm{iR}}\circ h_{\mathrm{jR}}^{-1},h_{\mathrm{jk}}=h_{\mathrm{jR}}\circ h_{\mathrm{kR}}^{-1},\text{and}{h}_{\mathrm{ik}}=h_{\mathrm{iR}}\circ h_{\mathrm{kR}}^{-1}.$$

Combining equations gives

$$h_{\mathrm{ik}}\circ h_{\mathrm{kj}}=h_{\mathrm{iR}}\circ h_{\mathrm{kR}}^{-1}\circ \left(h_{\mathrm{kR}}\circ h_{\mathrm{jR}}^{-1}\right)=h_{\mathrm{iR}}\circ h_{\mathrm{jR}}^{-1}=h_{\mathrm{ij}}$$

which shows theoretically no transitivity error. In practice, the IRG registration has transitivity error due to errors in inverting the transformations and composing the transformations. Results in Fig. 6(b) show that the transitivity error of IRG is less than 0.04 and much less than other registration methods.

Inverse consistency and transitivity are necessary but not sufficient properties for a set of transformations to define meaningful correspondences between images in a group. For example, a set of identity transformations have zero inverse consistency and transitivity errors but they provide meaningless correspondences. Likewise, a set of transformations can be constructed to have near zero inverse consistency and transitivity error using the method described in Skrinjar and Tagare (2004). The drawback of their approach is that correspondence errors present in the original transformations are still present in the newly constructed set of transformations.

Improvement of group analysis

The motivation of this work was to find a registration framework that estimates “good” correspondences between a group of images and improves the sensitivity of group analysis. The result that the IRG registration reduces across-subject variation of FA images suggests that the sensitivity in detecting white matter alterations between populations, as reflected by FA changes at a group level, should be improved by more accurate registration methods. When the IRG registration was applied to fMRI data sets, the increase of the regression coefficient β and t-statistics reflected the enhancement of the functional signal contrast (signal intensity during task vs. resting) and the detection power respectively. Since the registration method only deforms the shape of the input images but does not change the signal intensity, the resulting larger signal contrast can be attributed to a better alignment of the fMRI images across subjects in the group. Based on the assumption that brain structures correspond well to specific functions, it is reasonable to expect that stronger activation signals at a group level should be observed when the corresponding structures are aligned more accurately across all subjects in the group. The stronger t-statistics on the activated regions may be due to the larger average β values or the smaller group variance of β values. The smaller β variance within the group may be caused by the better alignment of the group subjects. The IRG registration provides the potential to improve group analyses of DTI and fMRI data in terms of better sensitivity and detectability.

The IRG registration in the current work assumes that the intensity values at each voxel follow a fixed Gaussian distribution with equal mean and variance across the population. This assumption may not always hold since the distribution of tissues at a particular voxel is not always Gaussian and the intensities at a voxel may not follow the same distribution across the population. Further improvement may be achieved if the intensity distribution used by the similarity term is characterized from the population, i.e., using the sum of voxel-wise entropies (Zollei et al., 2005) as the similarity term. Moreover, this modification will allow registering images from different modalities as well.

Similarity Cost Function Comparison

The similarity cost function in Eq. 1 is similar to the similarity cost $C_{\mathrm{Atlas}}={\sum }_i{\int }_{\Omega }\parallel I_i(h_i(x))-I(x){\parallel }^{2}dx$ with $I(x)=\frac{1}{N}{\sum }_i{I}_i(h_i(x))$ used in the unbiased atlas construction method developed by Joshi et al. (2004). At first glance the cost functions appear to be different since Eq. 1 computes the difference between pairs of images while the cost function C_Atlas computes the difference between each image and the mean image I(x). However, C_Atlas can be manipulated in the following manner:

$$\begin{array}{l}{C}_{\mathrm{Atlas}}=\sum _i{\int }_{\Omega }\Vert I_i(h_{\mathrm{iR}}(x))-\frac{1}{N}\sum _j(I_j(h_{\mathrm{jR}}(x))){\Vert }^{2}dx\\ =\sum _i{\int }_{\Omega }\Vert \frac{1}{N}(N{I}_i(h_{\mathrm{iR}}(x))-\sum _j{I}_j(h_{\mathrm{jR}}(x))){\Vert }^{2}dx\\ =\frac{1}{N^2}\sum _i{\int }_{\Omega }\Vert \sum _{j,i\ne j}(I_i(h_{\mathrm{iR}}(x))-I_j(h_{\mathrm{jR}}(x))){\Vert }^{2}dx\\ =\frac{2}{N^2}\sum _i{\int }_{\Omega }\Vert \sum _{j,i<j}(I_i(h_{\mathrm{iR}}(x))-I_j(h_{\mathrm{jR}}(x))){\Vert }^{2}dx.\end{array}$$ (7)

Notice that the similarity cost function in Eq. 7 differs from the cost function in Eq. 1 only in the order of the square and summation operators and the constant 2/N². This implies that the gradients of the cost functions are the same (up to transformation model), thus the gradient descent optimizer will result in the same minimization. Another difference between the registration algorithm used in this work and that in Joshi et al. (2004) is due to the transformation parametrization and how the transformations were regularized. In this work the transformations were parameterized using a Fourier series and regularized using a small deformation linear elastic model where as the work presented in Joshi et al. (2004) used a large deformation model.

The choice of using a small or large deformation model depends on the application. In general, a large deformation registration approach provides more degrees of freedom for registration than a small deformation model at the cost of increased computation and parameters. Increasing the model complexity and computational requirements may not always be needed to answer a particular scientific question.

Conclusions

An implicit reference group-wise (IRG) registration method was used in which transformations from each image in the group to a hidden reference were estimated using a small deformation linear elastic registration model. The performance of pair-wise and group-wise registration algorithms was evaluated for spatial normalization of T1-weighted MRI from NIREP, DTI and fMRI data. Results with the NA0 evaluation database from NIREP show that implicit reference pair-wise (IRP) registration produces better relative overlap (RO) than implicit reference group-wise (IRG) for pair-wise registration. However, IRP-G2R registration was shown to have a significantly larger transitivity error than IRG registration, i.e., IRP-G2R registration had significant inconsistencies between correspondences defined by different pair-wise transformations compared to IRG registration. In contrast, IRG registration produced consistent correspondence between images in a group at the cost of slightly reduced pair-wise RO accuracy compared to IRP-G2R. Thus, it is better to use IRP registration if the task is to register two images, but it is better to use IRG registration if the task is to register a group of images. Furthermore, the IRP registration should be favored over PW registration when registering two images. IRG spatial normalization of the fractional anisotropy (FA) maps of DTI were shown to have smaller FA variance compared with G2R methods using the same elastic registration model. Analyses of fMRI data sets with sensorimotor and visual tasks showed that IRG registration, on average, increases the statistical detectability of brain activation compared to G2R registration.