Automated MRI-based classification of primary progressive aphasia variants

Abstract

Degeneration of language regions in the dominant hemisphere can result in primary progressive aphasia (PPA), a clinical syndrome characterized by progressive deficits in speech and/or language function. Recent studies have identified three variants of PPA: progressive non-fluent aphasia (PNFA), semantic dementia (SD) and logopenic progressive aphasia (LPA). Each variant is associated with characteristic linguistic features, distinct patterns of brain atrophy, and different likelihoods of particular underlying pathogenic processes, which makes correct differential diagnosis highly clinically relevant. Evaluation of linguistic behavior can be challenging for non-specialists, and neuroimaging findings in single subjects are often difficult to evaluate by eye. We investigated the utility of automated structural MR image analysis to discriminate PPA variants (N=86) from each other and from normal controls (N=115). T1 images were preprocessed to obtain modulated grey matter (GM) images. Feature selection was performed with principal components analysis (PCA) on GM images as well as images of lateralized atrophy. PC coefficients were classified with linear support vector machines, and a cross-validation scheme was used to obtain accuracy rates for generalization to novel cases. The overall mean accuracy in discriminating between pairs of groups was 92.2%. For one pair of groups, PNFA and SD, we also investigated the utility of including several linguistic variables as features. Models with both imaging and linguistic features performed better than models with only imaging or only linguistic features. These results suggest that automated methods could assist in the differential diagnosis of PPA variants, enabling therapies to be targeted to likely underlying etiologies.

Introduction

Primary progressive aphasia (PPA) is a clinical syndrome in which degeneration of language regions in the dominant hemisphere is associated with progressive deficits in speech and/or language function (Mesulam, 1982, 2001). PPA cases can be classified into variants based on linguistic features (Hodges and Patterson, 1996; Neary et al., 1998; Gorno-Tempini et al., 2004), and each variant is associated with distinct patterns of atrophy (Gorno-Tempini et al., 2004) and different likelihoods of underlying pathologies such as taopathies, ubiquitin- and TDP-43-related changes, or Alzheimer’s disease (Davies et al., 2005; Josephs et al., 2008; Mesulam et al., 2008).

The two most-studied variants are progressive non-fluent aphasia (PNFA) and semantic dementia (SD). PNFA is characterized by apraxia of speech and agrammatism in both production and comprehension, but preserved single word comprehension (Grossman et al., 1996; Hodges and Patterson, 1996; Neary et al., 1998). PNFA is associated with atrophy and hypometabolism in left inferior frontal regions (Nestor et al., 2003; Gorno-Tempini et al., 2004). In contrast, SD patients demonstrate profound anomia and poor single-word comprehension, as well as a wider loss of semantic knowledge, but retain fluent, grammatical speech (Snowden et al., 1989; Hodges et al., 1992). SD is associated with atrophy of anterior and inferior temporal regions bilaterally, usually more extensive in the left hemisphere (Mummery et al., 2000; Rosen et al., 2002; Gorno-Tempini et al., 2004). A third PPA variant is logopenic progressive aphasia (LPA), characterized by slow but grammatical speech with word-finding difficulties, phonological paraphasias, and deficits in sentence repetition (Weintraub et al., 1990; Kertesz et al., 2003; Gorno-Tempini et al., 2004, 2008). Atrophy in LPA is predominantly left temporo-parietal (Gorno-Tempini et al., 2004; 2008).

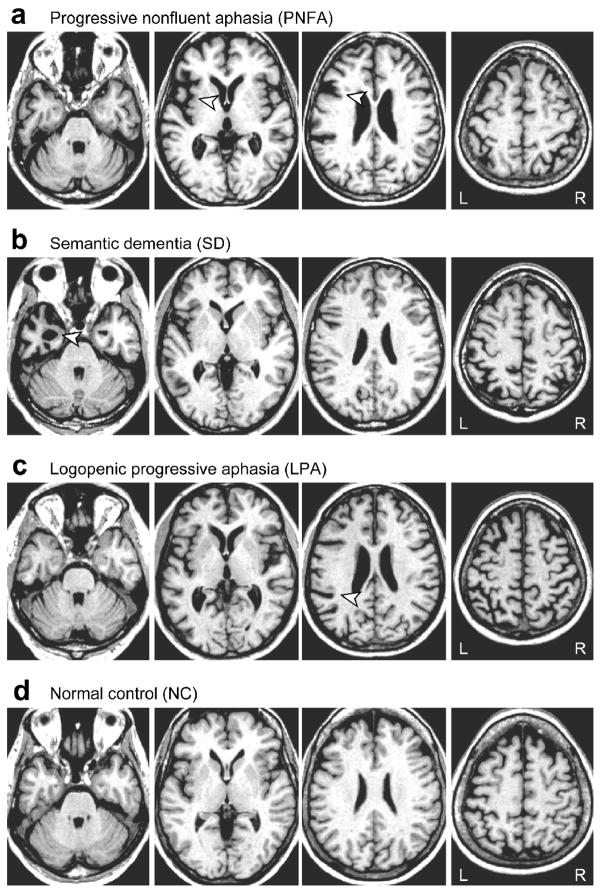
Because different PPA variants typically reflect different underlying etiologies, distinguishing between them is important from a clinical point of view, and will become even more so with the emergence of therapies targeted to particular disease mechanisms. Although the atrophy patterns associated with each variant have been documented (Mummery et al., 2000; Rosen et al., 2002; Gorno-Tempini et al., 2004, 2008), the fact that statistical differences exist at the population level does not imply that structural imaging can be easily used to diagnose individual cases. Examples of single cases with relatively mild atrophy characteristic of each variant are shown in Fig. 1. The subtlety of changes observable on structural MRI is reflected in the fact that neuroimaging remains only a supportive feature for clinical diagnosis of PPA variants (Neary et al., 1998). Furthermore, because PPA is not common, only neurologists and radiologists in large specialized dementia centers are likely to have sufficient experience to recognize and discriminate PPA and its variants. An automated image analysis procedure could prove clinically relevant because it would allow the objective assessment of even mild atrophy.

Figure 1.

T1-weighted MRI scans of patients with relatively mild atrophy representative of each PPA variant, and a normal control subject. (a) A typical PNFA patient, aged 74 years. The arrowheads show asymmetric left-lateralized atrophy in the insula and inferior frontal junction. (b) A typical SD patient, aged 57 years. The arrowhead shows left-lateralized atrophy in the anterior temporal lobe, however atrophy is not always left-lateralized in SD. (c) A typical LPA patient, aged 63 years. The arrowhead shows left-lateralized atrophy in the ascending part of the Sylvian fissure. (d) A typical normal control, aged 67 years.

In this study, we developed an automated procedure for distinguishing PPA variants from each other and from normal controls based on structural MR images. In brief, our algorithm entails preprocessing (bias correction, segmentation and normalization) to derive grey matter (GM) probability maps in standard space; principal components analysis (PCA) to extract features from these maps; and classification of feature vectors with linear support vector machines (SVMs). For the discrimination between PNFA and SD, we also examined the utility of including linguistic variables as additional features alongside the imaging data. A number of recent studies have used similar pattern classification methods to classify patients with Alzheimer’s disease, behavioral variant fronto-temporal dementia (bvFTD), and mild cognitive impairment (MCI) (Teipel et al., 2007; Davatzikos et al., 2008a, 2008b; Fan et al., 2008; Klöppel et al., 2008b; Lerch et al., 2008; Misra et al., 2009; Vemuri et al., 2008). Automated classification algorithms have been shown to perform as well or better than radiologists (Klöppel et al., 2008a). To our knowledge, the current study is the first to use pattern classification methods on MR images to discriminate variants of PPA.

Materials and methods

Subjects

Patients and normal control (NC) subjects were recruited through the Memory and Aging Center at the University of California, San Francisco (UCSF). All subjects, including normal controls, received a comprehensive evaluation including neurological history and examination, neuropsychological testing of memory, executive function, visuospatial skills, language and mood, interview with an informant or caregiver regarding activities of daily living, and neuroimaging. This evaluation was performed by a multidisciplinary team of neurologists, neuropsychologists, psychiatrists and nurses.

A diagnosis of PPA required progressive deterioration of speech and/or language functions, and that deficits be largely restricted to speech and/or language for at least two years. Patients were then diagnosed with PNFA or SD according to established criteria (Neary et al., 1998). Patients were diagnosed with LPA when they met criteria for PPA, but did not meet criteria for either PNFA (due to well-articulated and grammatical speech) or SD (due to preserved single word comprehension). LPA patients have word-finding difficulties in the context of fluent and grammatical speech and show a typical pattern of sentence repetition and comprehension problems due to a phonological short-term memory deficit (Gorno-Tempini et al., 2008). Neuroimaging results were not used for diagnostic purposes, but only to rule out other causes of focal brain damage, including extensive white matter disease. Between May 2001 and November 2008, 96 patients were diagnosed with PPA. Of these, 10 were excluded from the present study for unclear subdiagnosis (N = 4), MMSE ≤ 8 (N = 4) or no MRI scan (N = 2). The remaining 86 patients were classified as PNFA (N = 32), SD (N = 38), or LPA (N = 16).

In the same period, normal controls were recruited through advertisements in local newspapers and talks at local senior community centers. 115 subjects aged 50 to 80 were judged to be clinically normal based on the comprehensive evaluation described above, and had no abnormalities on neuroimaging. Although extensive white matter disease was an exclusionary criterion, presence of atrophy, which varies on a continuum in a population of this age, was not.

Demographic, linguistic and neuropsychological measures for each group are shown in Table 1.

Table 1.

Demographic information and linguistic and neuropsychological measures

	PNFA	SD	LPA	NC
Age	68.1 (6.8)	63.2 (6.9)	63.9 (7.7)	66.0 (7.6)
Males/females	8/24	21/17	8/8	47/68
Years of education	15.0 (2.7)	15.6 (2.8)	17.0 (3.2)	17.1 (2.6)
Mini Mental State Examination (30)	24.9 (5.0)	22.7 (6.1)	20.5 (6.0)	29.6 (0.6)
Clinical Dementia Rating	0.5 (0.4)	0.7 (0.4)	0.6 (0.2)
Years from first symptom	3.8 (1.4)	4.8 (2.8)	3.4 (1.5)
Language production
Boston naming test (15)	12.1 (2.7)	4.1 (3.1)	10.2 (3.8)	14.4 (1.0)
Phonemic fluency	4.5 (2.9)	7.2 (3.9)	8.4 (4.1)	15.7 (4.7)
Semantic fluency	9.8 (4.7)	7.1 (5.0)	8.6 (4.7)	22.2 (5.6)
Spontaneous speech fluency (WAB) (10)	6.2 (3.2)	9.0 (0.8)	8.4 (1.6)
Apraxia of speech (7)	3.1 (2.4)	0.0 (0.0)	0.6 (1.3)
Dysarthria (7)	2.4 (3.0)	0.0 (0.0)	0.0 (0.0)
Repetition (WAB) (100)	77.6 (25.5)	87.9 (13.6)	77.6 (7.7)
Repetition (3 items) (3)	1.9 (1.1)	2.3 (0.8)	1.5 (0.8)
Language comprehension
Auditory word comprehension (WAB) (60)	58.8 (2.6)	50.6 (11.3)	58.3 (2.5)
Sequential commands (WAB) (80)	69.5 (11.7)	72.8 (10.5)	65.5 (15.6)
Pyramids and palm trees (52)	47.5 (4.6)	38.5 (7.5)	47.1 (5.0)	51.4 (0.8)
Visuospatial function
Modified Rey copy (17)	14.6 (1.7)	15.4 (1.4)	14.2 (2.7)	15.7 (1.3)
Delayed Rey recall (17)	9.4 (4.3)	7.3 (4.1)	6.0 (3.4)	11.7 (3.1)
Visual Object and Space Perception	8.6 (1.3)	9.3 (1.0)	8.3 (1.3)	9.2 (1.1)
Verbal memory
CVLT first four (36)	22.4 (6.9)	14.3 (7.0)	13.1 (6.3)	29.3 (3.8)
CVLT 30″ (9)	6.1 (2.2)	2.6 (2.3)	2.9 (2.1)	7.9 (1.4)
CVLT 10′ free recall (9)	6.0 (2.5)	2.0 (2.4)	2.2 (2.3)	7.4 (1.8)
CVLT 10′ recognition (9)	8.3 (0.9)	6.0 (2.5)	7.6 (1.5)	8.5 (0.8)
Executive function
Digits backwards	2.9 (1.2)	4.5 (1.2)	3.1 (0.9)	5.2 (1.2)
Modified trails (lines per minute)	9.8 (10.3)	21.3 (15.0)	8.2 (9.6)	32.8 (13.1)

Values shown are mean (standard deviation). WAB: Western Aphasia Battery; CVLT: California Verbal Learning Test.

Each of the six possible pairwise comparisons between groups was considered as a separate problem, i.e. (i) PNFA vs NC; (ii) SD vs NC; (iii) LPA vs NC; (iv) PNFA vs SD; (v) PNFA vs LPA; (vi) SD vs LPA. In order to match group sizes for each pairing, we included all subjects from whichever was the smaller of the two groups, then used an algorithm to select subjects from the larger group so as to match the smaller group as closely as possible in terms of age, scanner, and where possible, gender. After subset selection, no pair of groups differed significantly in age, duration of disease (where applicable) or MMSE (where applicable) (all ps > 0.05), except that the PNFA group was older than the SD group (68.1 vs 64.4 years, p = 0.034). Note however that age was covaried out prior to model construction (see below), so age-related differences could not be used by models to aid discrimination.

All participants gave written informed consent according to the Declaration of Helsinki, and the study was approved by the Committee on Human Research at UCSF.

Image acquisition

Structural images were acquired on two different scanners. For 171 subjects, T1 images were acquired on a 1.5T Siemens Magnetom VISION system (Siemens, Iselin, NJ) equipped with a standard quadrature head coil, using a magnetization prepared rapid gradient echo (MPRAGE) sequence (164 coronal slices; slice thickness = 1.5 mm; FOV = 256 mm; matrix 256 × 256; voxel size 1.0 × 1.5 × 1.0 mm; TR = 10 ms; TE = 4 ms; flip angle = 15°).

For the remaining 30 subjects, images were acquired on a 4T Bruker MedSpec system with an 8 channel head coil controlled by a Siemens Trio console, using an MPRAGE sequence (176 sagittal slices; slice thickness = 1 mm; FOV = 256 × 256 mm; matrix = 256 × 256; voxel size = 1.0 × 1.0 × 1.0 mm; TR = 2300 ms; TE = 3 ms; flip angle = 7°).

The number of subjects scanned on the 1.5T and 4T scanners were: PNFA: 26/6; SD: 34/4; LPA: 14/2; NC: 97/18. The proportions of subjects studied using each scanner did not differ across groups (χ²(3) = 1.070, p = 0.78), and scanner type was also covaried out prior to model construction (see below). An additional analysis restricted to only those subjects scanned on the 1.5T scanner resulted in classification performance that was comparable to the main analysis.

Image preprocessing

Images were corrected for bias field, segmented into grey matter (GM), white matter and CSF, and normalized to MNI space with the Unified Segmentation procedure (Ashburner and Friston, 2005), implemented in SPM5 running under MATLAB 7.4 (Mathworks, Natick, MA). Modulated GM probability maps scaled by Jacobians were then smoothed with a Gaussian kernel of 8 mm FWHM.

For each of the six pairs of groups, a GM mask was created to include only voxels where mean GM probability was greater than 0.25. A general linear model was fit at each voxel to remove covariates of age, sex, scanner (1.5T or 4T), and total intracranial volume. The residuals from this regression were used for subsequent analysis.

We experimented with different degrees of smoothing (0 mm, 4 mm, 12 mm), as well another segmentation method: Diffeomorphic Anatomical Registration using Exponentiated Lie algebra (DARTEL) (Ashburner, 2007). Model classification performance did not significantly differ as a function of these preprocessing options.

Feature selection

The goal of feature selection is to reduce each patient’s image to a feature vector which effectively summarizes the image. We used principal components analysis (PCA), which expresses each patient’s image as the weighted sum of a number of principal component (PC) images, such that the variance explained by each successive PC is maximized (Jackson, 1991). The component images encode patterns of GM volume differences, and the feature vector which characterizes each patient’s image is made up of the weighting coefficients for the PCs.

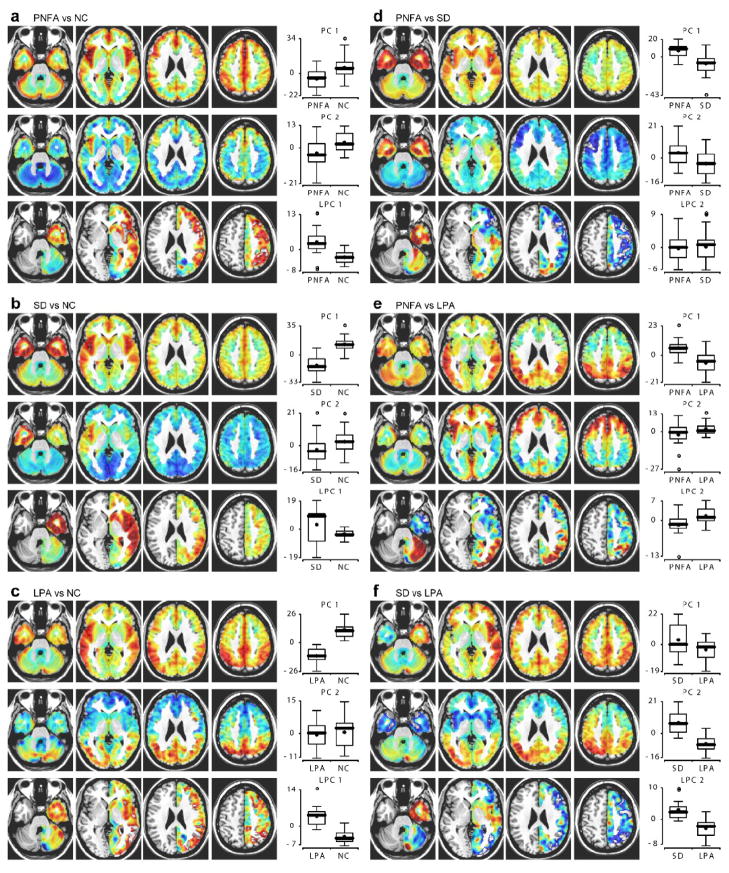
For each pair of groups, patients from both groups were pooled, and PCA was carried out via singular value decomposition in MATLAB, based on the covariance matrix. (Similar results were obtained with PCA based on the correlation matrix.) PCA was carried out only on images in each training set (see cross-validation methods below), and images from testing sets were then projected onto the principal components obtained, except for Fig. 3 which is based on all patients in each pair of groups.

Figure 3.

Principal components analysis. PCA was carried out separately for each pair of groups: (a) PNFA vs NC; (b) SD vs NC; (c) LPA vs NC; (d) PNFA vs SD; (e) PNFA vs LPA; (f) SD vs LPA. The first and second principal components (PCs) are shown for all pairs. The first PC typically captured global degree of atrophy, whereas the second PC typically captured regionally specific patterns of atrophy reflecting differences between the two groups. A “lateralization” PC (LPC) is also shown, which quantifies asymmetrical GM volume differences. For comparisons of patient groups to controls, the first LPC, which essentially captured global lateralization of atrophy, is shown. For comparisons between pairs of patient groups, the second LPC, which typically captured between-group regional differences in lateralization of atrophy, is shown. Boxplots show the distribution of coefficients for each component shown in the two groups (thick line: median; star: mean; circles: outliers).

Since all PPA variants are characterized by asymmetric atrophy (Mummery et al., 2000; Rosen et al., 2002; Nestor et al., 2003; Gorno-Tempini et al., 2004, 2008), we wanted to derive features which would directly encode lateralization of atrophy and regional differences in this lateralization. A “lateralization image” was calculated for each subject by subtracting the modulated GM map for the left hemisphere from the right hemisphere. PCA was performed on these lateralization images. We refer to the principal components from this analysis as lateralization principal components (LPCs).

Each subject’s image was encoded by a feature vector containing coefficients for PCs from the GM images, and LPCs from the lateralization images. Scores for each feature were demeaned and normalized. The numbers of PCs and LPCs included were systematically varied as described below.

We also compared PCA-based feature selection to a simpler method where images were reduced to 116 features representing mean modulated GM volumes in 116 anatomical regions of interest (ROIs) based on the Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002).

Linguistic variables

For the discrimination between PNFA and SD, we investigated whether performance could be improved by including linguistic variables as features alongside imaging features derived with PCA. Only these two groups were employed here, because most controls were at ceiling on the relevant measures, and several LPA subjects were missing data, making the number of subjects in the potential LPA group too small. Three variables were used: (i) Number of items correct on a 15-item version of the Boston Naming Test (BNT) (Kaplan et al., 1978). Short forms of the BNT have proved to be reliable in numerous studies (Kent and Luszcz, 2002). (ii) Auditory word recognition, from the 60-item test in the Western Aphasia Battery (Kertesz, 1982). Patients must indicate which of an array of six items matches a word spoken by the examiner. (iii) Repetition of the three phrases “down to earth”, “pry the tin lid off” and “no ifs, ands or buts”. Responses were scored as correct when all words were intelligible and in the correct order, and there were no extraneous words.

These variables were available for 26 of the 32 patients with PNFA, and 32 of the 38 patients with SD. Therefore, models were constructed to discriminate between these 26 PNFA patients, and 26 of the 32 SD patients, selected so as to match the PNFA group in age as far as possible. Linguistic variables were demeaned and normalized. Models were constructed with imaging features only, linguistic features only, or both imaging and linguistic features.

Machine learning and cross-validation

To classify patients, we used linear support vector machines (SVMs) (Vapnik, 1995, 1998) implemented with libsvm version 2.86 (Chang and Lin, 2001), running under MATLAB. Patients were represented as points in n-dimensional feature space, where n is the length of the feature vectors. SVMs identify an optimal separating hyperplane in this space such that patients from each group lie on opposite sides of the hyperplane, as far as this is possible. Once the hyperplane has been defined, novel cases can be classified as belonging to one group or the other depending on which side of the hyperplane their feature vectors fall on. It is also possible to obtain the probability that a new case belongs to one group or the other, which depends on how far from the hyperplane it falls. Probabilities were derived based on the method described by Platt (2000), and were used to construct Receiver Operating Characteristic (ROC) curves. We used a cross-validation procedure to determine classification accuracy, using expert clinical diagnosis as the gold standard.

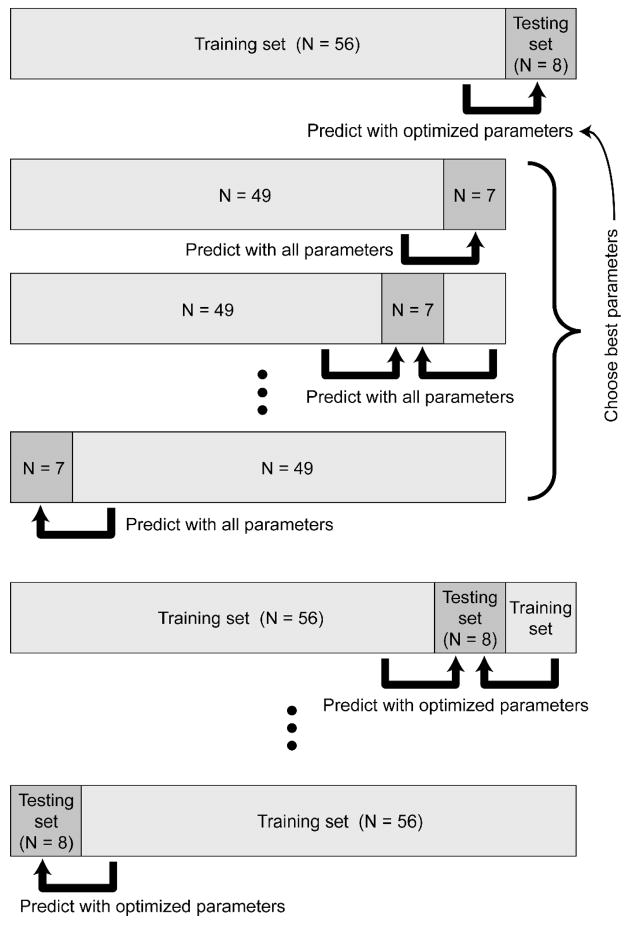
Linear SVMs were chosen because they require the optimization of only a single parameter C, which adjusts the penalty assigned to misclassification errors during model construction. The optimal number of PCs (nPCs) and the optimal number of LPCs (nLPCs) were also unknown, so we treated these as parameters also. We designed a two-level cross-validation procedure implemented in MATLAB to optimize these three parameters and assess generalizability (Fig. 2). In brief, the purpose of the first level of cross-validation was to ensure that each patient was classified based on models which had been constructed without reference to that patient, i.e. to properly determine generalizability. The purpose of the second level was to optimize the three unknown parameters.

Figure 2.

Two-level cross-validation procedure. For each pair of groups (e.g. PNFA vs NC), the patients were first divided into 8 partitions. In this example, there were 64 patients (32 PNFA and 32 NC), so each partition contained 8 patients (4 PNFA and 4 NC). One partition was held out to serve as the testing set. The other 7 partitions (56 patients) comprised the training set. In a parameter optimization stage, the training set was then re-divided into 8 sub-partitions of 7 patients each. Each sub-partition was left out in turn, and all possible sets of parameter values were used to train models based on the other 7 sub-partitions (49 patients) to predict the left-out sub-partition (7 patients). Whichever set of parameters proved best overall was then used to train a model on the whole training set (56 patients) to predict the testing set (8 patients). This whole process was repeated 8 times leaving out a different partition (8 patients) each time. Parameters were optimized again on each training set (not shown). This two-level procedure allowed as many subjects as possible to be used in model construction, while ensuring that every patient was classified based on models and parameters which were determined without reference to the “novel” patients being classified. See text for details.

Specifically, for each pair of groups, the set of patients (half belonging to one group and half to the other) was first divided into 8 partitions, each containing equal numbers from each group except where odd-sized partitions were required in which case the numbers differed by 1. Each of these partitions would in turn constitute the testing set, with the other 7 partitions constituting the training set. Ideally the number of partitions should be as high as possible so as to use as many subjects as possible for model construction; the only limiting factor is computational efficiency. The images and diagnoses for each testing set were set aside in turn, and the following procedure was performed on the training set:

First, the training set was re-divided into 8 partitions at random, again keeping partitions balanced according to group membership as far as possible. Then, the parameters C, nPCs and nLPCs were systematically varied over the ranges C ∈ [2⁻⁵, 2⁻⁴, 2⁻³, …, 2⁸], nPCs ∈ [1, 2, …, 10] and nLPCs ∈ [0, 1, 2]. These ranges for nPCs and nLPCs were determined with reference to scree plots: eigenvalues decreased in an approximately straight line after about the 10th PC or the 2nd LPC, suggesting that further components do not reflect meaningful variability (Jackson, 1991). For each set of parameters, a model was constructed based on 7 of the 8 partitions, and used to predict the diagnoses of the 8th partition. This was repeated leaving out a different partition each time, and total accuracy over the training set as a function of C, nPCs and nLPCs was recorded. This procedure was repeated 12 times (with variability arising due to repartitioning at random), and accuracies were averaged across the iterations, in order to obtain better estimates of which parameters were likely to provide good generalizability.

Now for each value of nPCs and nLPCs, a model was constructed based on the whole training set, using the optimal value of C for each given value of nPCs and nLPCs. This model was applied to the testing set, and we recorded the predicted group memberships and probabilities for each subject. Finally, the predictions arising from the optimal values of nPCs and nLPCs (as determined only on the training set) were recorded.

This whole procedure was repeated 20 times for each pair of groups. Variability across iterations arises because each subject is predicted based on a different training set each time. The final decision value for each subject was determined by averaging across the probabilities obtained for each of the 20 repetitions of the procedure.

The accuracy of each classifier was compared to chance performance by the binomial test. Binomial confidence intervals were calculated as Wilson intervals. ROC curves were calculated and plotted with a custom MATLAB program. The performance of different classifiers was compared with a non-parametric test based on the differences between the areas under the curves (AUC) (Vergara et al., 2008).

Results

For each pair of groups, PCA was carried out on GM images and also on “lateralization” images reflecting regional asymmetries in GM volume (Fig. 3). The first PC typically reflected GM volume fairly uniformly across the brain and so captured global atrophy. In each case where a patient group was compared with controls, patients showed reduced coefficients for the first PC, reflecting global atrophy (Fig. 3a–c, first rows, boxplots). The second PC usually captured large-scale differences between the two groups, i.e. regionally specific atrophy. For PNFA vs NC, this component peaked in the insula, especially in the left hemisphere (Fig. 3a, middle row). For SD vs NC, the second component peaked in the anterior temporal lobes, especially in the left hemisphere (Fig. 3b, middle row). For LPA versus NC, the second PC reflected GM volume in posterior temporal and parietal regions, again left lateralized (Fig. 3c, middle row). For PNFA vs SD, the second component contained opposite signed values in the anterior temporal lobes and frontal lobe (Fig. 3d, middle row). For PNFA vs LPA, the second PC contained opposite signed values in frontal versus parietal regions (Fig. 3e, middle row). For SD vs LPA, it contained opposite signed values in anterior temporal versus parietal regions (Fig. 3f, middle row). In each case, the second PC captured gross differences between the two groups comprising the sample, as reflected in the boxplots. Further PCs also contained important information, as revealed by the fact that their inclusion increased classification accuracies (see below), however rarely did they have such straightforward interpretations as the first and second components.

The first lateralization PCs (LPCs) also tended to capture global differences in asymmetries of GM volumes. Except for about a quarter of SD cases (Seeley et al., 2005), all PPA variants involve left-lateralized atrophy; this is reflected by lower coefficients in patient groups than controls for the first LPC (Fig. 3a–c, third rows, boxplots). Note the wide range of SD coefficients (Fig. 3b, third row, boxplot); this reflects the fact that some SD patients have right-lateralized atrophy.

There was only one case (the first component for LPA vs NC) where the two groups could be perfectly separated based on a single component. This underscores the need for classification algorithms such as SVMs that operate in high dimensional space and can combine information from multiple components.

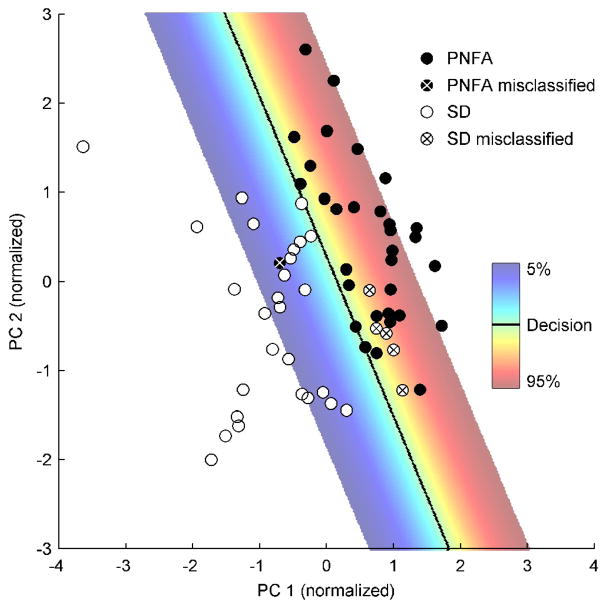
An example of how an SVM can do a reasonable job of separating patients with PNFA and SD with only the first two PCs is shown in Fig. 4. The first component captured global GM volumes, with a focus in the anterior temporal lobes and the insula. Patients with SD had lower coefficients on this component, reflecting more atrophy. The second component had a positive focus in the anterior temporal lobes and a negative focus in the frontal lobe, especially in the left hemisphere. Patients with SD also had lower coefficients on this component, reflecting the fact that they have relatively less temporal and more frontal GM. In this simplified example, all patients were used to construct the model, i.e. no attempt was made to leave patients out and estimate generalizability. The decision surface (in this case a line) separates the patients better than they could be separated by either component alone, but there were still six misclassified cases.

Figure 4.

Example of SVM decision surface in feature space. PNFA and SD patients can be separated reasonably well by the first two components, though 6 of the 64 patients were misclassified. The decision surface (in two dimensions, a line) is shown in grey, and the probability of classifying a patient as PNFA is shown by the color scale for probabilities between 5% and 95%. Probabilities depend on distance from the decision surface.

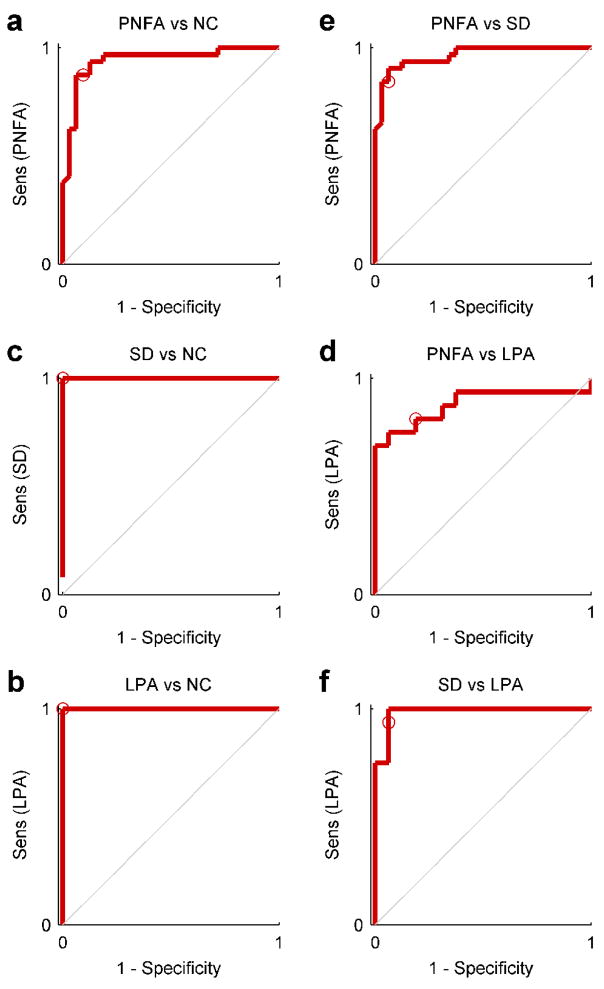
Each of the six pairings of groups were classified by the procedure described above, whereby the parameters C, nPCs, nLPCs were all optimized based on training sets only. The ROC curves for each classifier are shown in Fig. 5. Accuracies, binomial confidence intervals, confusion matrices, sensitivity and specificity for a decision threshold of 50% are shown in Table 2. The mean accuracy across groups was 92.2%, ranging from 81.3% for PNFA vs LPA, to 100% for the discrimination of SD from NC and of LPA from NC. All classifiers were significantly better than chance (binomial test, all ps < 0.001). Areas under the ROC curves are also reported in Table 2; this is an alternative accuracy metric equivalent to the probability that the classifier will assign a higher probability to a randomly chosen positive instance to a randomly chosen negative one (Fawcett, 2006).

Figure 5.

ROC curves for each pair of groups: (a) PNFA vs NC; (b) SD vs NC; (c) LPA vs NC; (d) PNFA vs SD; (e) PNFA vs LPA; (f) SD vs LPA. These plots reveal tradeoffs between sensitivity and specificity. The ROC curve is plotted by varying the decision threshold for probability outputs between 0 and 1. The middle point of 0.5 used to quantify accuracy in Table 2 is denoted by a circle.

Table 2.

Classifier performance

Actual	Predicted		Sens (%)	Spec (%)	Acc (%)	Conf int (%)	AUC
	PNFA	NC
PNFA	28	4	87.5	90.6	89.1	79.1 – 94.6	0.941
NC	3	29
	SD	NC
SD	38	0	100.0	100.0	100.0	95.2 – 100.0	1.000
NC	0	38
	LPA	NC
LPA	16	0	100.0	100.0	100.0	89.3 – 100.0	1.000
NC	0	16
	PNFA	SD
PNFA	27	2	84.4	93.8	89.1	79.1 – 94.6	0.964
SD	5	30
	PNFA	LPA
PNFA	13	3	81.3	81.3	81.3	64.7 – 91.1	0.879
LPA	3	13
	SD	LPA
SD	15	1	93.8	93.8	93.8	79.9 – 98.3	0.984
LPA	1	15

Sens: Sensitivity; Spec: Specificity; Acc: Accuracy; Conf int: Confidence interval; AUC: Area under curve.

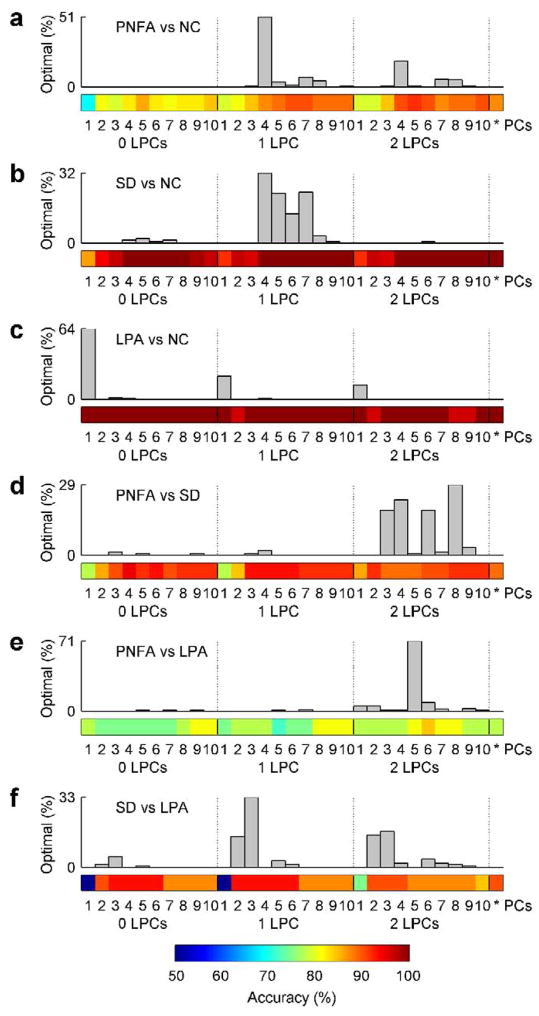
The optimal number of PCs and LPCs depended on which particular groups were being classified. We plotted the number of times each combination of values for nPCs and nLPCs was chosen as optimal for each subject in one of the 20 iterations, based on training sets alone (Fig. 6). The color map below the histogram shows the accuracy that would be obtained if given values for nPCs and nLPCs were used for all subjects, except for the cell on the right, which shows the accuracy resulting from the optimization procedure. These are the most realistic accuracy measures since in practice the optimum number of features for classifying an unlabelled new case can only be determined with reference to existing labeled cases. The optimum number of PCs ranged from 1, in the case of LPA vs NC where the first PC separated the groups perfectly, to 8, in the case of PNFA vs SD. The optimum number of LPCs was 1 for three pairs of groups, 2 for two pairs of groups, and 0 for LPA vs NC. The values of nPCs and nLPCs which would yield the highest accuracy across all subjects (as depicted in the images in Fig. 6), were not always obtained during parameter optimization, however the optimization step usually succeeded in identifying good values, even if they were not the best.

Figure 6.

Optimal numbers of PCs and LPCs as determined by cross-validation on training sets. All six pairs of groups are shown: (a) PNFA vs NC; (b) SD vs NC; (c) LPA vs NC; (d) PNFA vs SD; (e) PNFA vs LPA; (f) SD vs LPA. The number of PCs (between 1 and 10) and LPCs (between 0 and 2) are shown on the horizontal axis. The histograms show how frequently each pair of parameter values (number of PCs, number of LPCs) was selected as optimal for a subject on one of the 20 iterations. The color maps below show the accuracy obtained with each pair of parameter values, except for the rightmost color square which shows the accuracy obtained using the optimal number of PCs and LPCs as determined “on the fly”.

In the follow-up analysis based on 116 anatomical ROIs instead of PCA, the mean accuracy across groups was somewhat lower, at 88.8%. Accuracies were exactly equal for SD vs NC, LPA vs NC and SD vs LPA, but poorer for PNFA vs NC (85.9%, p = 0.083), PNFA vs SD (87.5%, p = 0.27) and PNFA vs LPA (65.6%, p = 0.013).

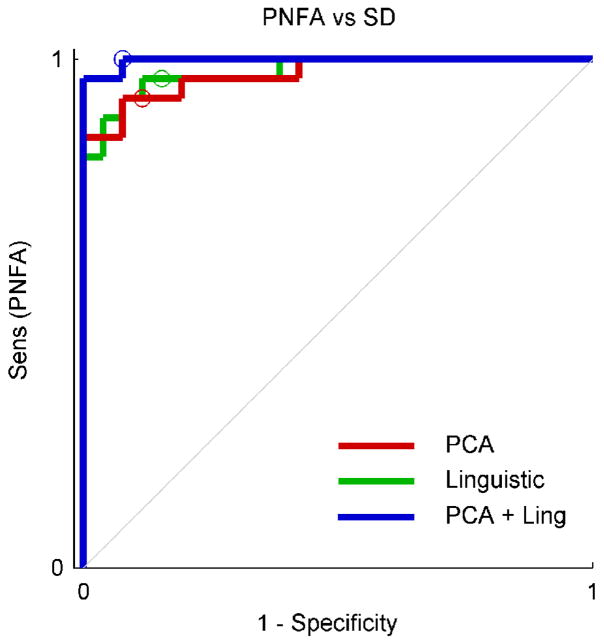
For discrimination between PNFA and SD, we investigated the utility of including linguistic variables (naming, single word comprehension, and repetition) as additional features (Fig. 7, Table 3). Accuracy was 90.4% when imaging features alone were used, and also when linguistic features alone were used. The inclusion of both types of features simultaneously boosted accuracy to 96.2%. The difference between the ROC curves was not significant (p = 0.18 versus imaging alone; p = 0.13 versus behavior alone) due to the small number of subjects (5 subjects were misclassified by the models with one type of feature, improving to 2 misclassified when both types of feature were included). The trend towards improved performance suggests that combining both types of information could result in more accurate classification than either imaging or linguistic information alone.

Figure 7.

ROC curves for additional models discriminating between the PNFA and SD groups, with and without the inclusion of linguistic features.

Table 3.

Classifier performance with and without linguistic data

Actual	Predicted		Sens (%)	Spec (%)	Acc (%)	Conf int (%)	AUC
	PNFA	SD
Imaging only
PNFA	25	1	96.2	84.6	90.4	79.4 – 95.8	0.975
SD	4	22
Linguistic only
PNFA	24	2	92.3	88.5	90.4	79.4 – 95.8	0.970
SD	3	23
Imaging and linguistic
PNFA	26	0	92.3	96.2	96.2	87.0 – 98.9	0.997
SD	2	24

Sens: Sensitivity; Spec: Specificity; Acc: Accuracy; Conf int: Confidence interval; AUC: Area under curve.

Discussion

We have described an automated procedure for distinguishing PPA variants from each other and from normal controls, based on structural MR images alone, or in combination with linguistic variables. The accuracies obtained were sufficiently high to suggest that procedures such as this are potentially relevant to clinical practice. A two-level cross-validation scheme ensured firstly that each patient was classified using models constructed without reference to that patient, and secondly that the model parameters—the number of PCs, the number of “lateralization” PCs, and the SVM constant C—were also optimized on training data alone. This procedure implies that the 92.2% accuracy obtained should generalize to new cases.

Prediction accuracy was bolstered by including features which were guided by previous findings regarding the patient groups of interest, specifically the use of “lateralization” PCs. The use of these features ensured that SVMs would be particularly sensitive to global and local left-right asymmetries in GM volume, which is known to be a feature of PPA (Mummery et al., 2000; Rosen et al., 2002; Nestor et al., 2003; Gorno-Tempini et al., 2004; Gorno-Tempini et al., 2008). In five of the six pairs of groups, lateralization PCs were frequently selected during the optimization stage because they led to increased accuracy.

Recently several groups have used high-dimensional pattern classification of MRI to predict group membership of individual neurodegenerative patients. Patient cohorts studied have included AD (Teipel et al., 2007; Davatzikos et al., 2008b; Klöppel et al., 2008b; Lerch et al., 2008; Vemuri et al., 2008), bvFTD (Davatzikos et al., 2008b; Klöppel et al., 2008b) and MCI (Teipel et al., 2007; Davatzikos et al., 2008a). Classification algorithms have been used to predict conversion of MCI to AD (Fan et al., 2008). One study directly compared the performance of an automated classification algorithm to the judgments of neuroradiologists of various levels of experience, and found that the algorithm performed as well or better than even the most experienced radiologists (Klöppel et al., 2008a). Accuracy rates in these studies typically ranged from 80% to 95%, depending on factors such as how groups were defined, stage of disease, etc. We used the earliest image available for each patient, in order to most closely mimic the potential real-world application of an algorithm like this where we would hope to facilitate correct diagnosis as early as possible.

Although PNFA and LPA are difficult to distinguish based on neuroimaging by even the most experienced clinician, SD has such a characteristic pattern of atrophy that SD patients can be distinguished from other variants and from controls with high accuracy by even a moderately experienced neurologist or neuroradiologist. Although our algorithm separated SD from NC perfectly, accuracy rates were only 89.1% versus PNFA and 93.8% versus LPA. Several factors are likely responsible for the erroneous classifications. One is imperfect segmentation and normalization, which sometimes result in overestimates of anterior temporal volumes in SD patients, or underestimates in the other two variants. A second factor is that some patients have more globalized atrophy, so for instance an SD patient with an exceptional degree of frontal atrophy may be misclassified as PNFA. A more disease-specific feature extraction process would weight anterior temporal changes more highly for identification of SD, but the global nature of the PCA approach we employed is susceptible to errors of this kind.

Imaging measures are not the only means of differentiating dementia subtypes. Cognitive and behavioral measures can also be used for the differential diagnosis of neurodegenerative diseases, including primary progressive aphasia. Recently, a simple measure called the Repeat and Point test has been shown to discriminate well between SD and PNFA based on differential impairments in comprehension and repetition of single words (Hodges et al., 2008). While discriminant function analysis was able to perfectly classify patients in this case, sample sizes were small (15 patients with SD and 6 with PNFA) and cross-validation was not performed to assess generalizability. Despite these caveats, our clinical experience would suggest that this test or similar ones would be highly accurate on populations of these patients. Larger batteries of cognitive, behavioral and linguistic measures can also discriminate PPA variants from each other and/or from other neurodegenerative diseases (Kramer et al., 2003; Knibb et al., 2006; Davies et al., 2008), however the inclusion of linguistic measures (as opposed to general neuropsychological measures) is essential to obtain accurate discrimination (Heidler-Gary et al., 2007).

For the discrimination between PNFA and SD, we found that inclusion of three linguistic variables—naming, auditory word comprehension, and repetition—alongside features derived from imaging, led to improved performance. These measures were chosen because they are clinically useful, and because they require little expertise to quantify (unlike, for example, apraxia of speech, which would be an even more reliably predictive variable). Although assessing classification performance based on linguistic features alone is somewhat circular, because patients were diagnosed in part on linguistic data including these, it is noteworthy that performance was better when imaging data was included alongside linguistic variables than when based on linguistic variables alone.

There are several limitations to this study. First, most of the patients’ diagnoses have not been confirmed at pathology. Predicting clinical gold standard diagnosis and predicting pathology are actually two separate problems, and here we have focused only on the first. Although the accuracy of our clinical diagnoses cannot be quantified precisely, in part due to the complex array of pathologies which underlie different PPA variants (Davies et al., 2005; Josephs et al., 2008; Mesulam et al., 2008), our diagnoses have nevertheless proved highly reliable in predicting [¹¹C]-Pittsburgh compound B (PIB) binding suggestive of Alzheimer’s pathology (Rabinovici et al., 2008) and in predicting subsequent clinical course (Gorno-Tempini et al., 2004, 2008). Second, although we used two different scanners, we covaried out scanner type and did not attempt to evaluate how well models constructed based upon images from one scanner would perform on images from other scanners. This would be an important step in developing a clinically applicable procedure (Klöppel et al., 2008b). Third, the sample size in one of the three groups (LPA) was quite small (N = 16). Possibly as a consequence of this, the model for discriminating between LPA and PNFA had the least accurate performance. A larger group of LPA patients should enable better discrimination of this group. Fourth, we did not systematically investigate linguistic, cognitive or behavioral variables in the way that we did for preprocessing methods or selection of appropriate numbers of components. In principle, other investigations such as genetic markers and Aβ amyloid imaging could also be readily represented as additional features, which may contribute to more accurate performance. Fifth, we considered an idealized situation in which we discriminated between pairs of groups, where half of the patients belonged to each group. A practical algorithm would extend this to the multiclass situation where there are numerous possibilities with different prior probabilities. The SVM framework is already established to handle this problem (Wu et al., 2004). Sixth, although we found that feature selection with PCA led to more accurate classification than features based on parcellation of the whole brain into anatomical ROIs, it is certainly possible that other ROI-based approaches, such as disease-specific ROIs, could lead to better performance, instead of or in conjunction with PCA. Finally, although we used a rigorous two-level cross-validation scheme to quantify generalizability, it would be important to test the accuracy of models on a completely independent dataset, such as patient cohorts from a different institution.

Despite these limitations, our results suggest that automated methods have great potential to assist in the discrimination of PPA variants from each other and from normal controls. As therapies emerge targeted to particular neurodegenerative disease mechanisms, automated algorithms will provide a crucial tool in facilitating correct early differential diagnoses.