Simple group fMRI modeling and inference

Abstract

While many advanced mixed-effects models have been proposed and are used in fMRI, the simplest, ordinary least squares (OLS), is still the one that is most widely used. A survey of 90 papers found that 92% of group fMRI analyses used OLS. Despite the widespread use, this simple approach has never been thoroughly justified and evaluated; for example, the typical reference for the method is a conference abstract, (Holmes and Friston, 1998), which has been referenced over 400 times.

In this work we fully derive the simplified method in a general setting and carefully identify the homogeneity assumptions it is based on. We examine the specificity (Type I error rate) of the OLS method under heterogeneity in the one-sample case and find that the OLS method is valid, with only slight conservativeness. Surprisingly, a Satterthwaite approximation for effective degrees of freedom only makes the method more conservative, instead of more accurate. While other authors have highlighted the inferior power of the OLS method relative to optimal mixed effects methods under heterogeneity, we revisit these results and find the power differences very modest.

While statistical methods that make the best use of the data are always to be preferred, software or other practical concerns may require the use of the simple OLS group modeling. In such cases, we find that group mean inferences will be valid under the null hypothesis and will have nearly optimal sensitivity under the alternative.

1 Introduction

The analysis of multisubject fMRI data presents a number of challenges, in particular the need to account for two sources of variance: “measurement error” variability in the estimated response in each subject, and the “individual differences” variability in the true response between subjects. Appropriately modeling these within- and between-subject variances have motivated a number of papers on the best way to perform group modeling of fMRI data (Friston et al., 2002, 2005; Woolrich et al., 2004; Worsley et al., 2002; Beckmann et al., 2003; Mumford and Nichols, 2006; Penny and Holmes, 2006). Most of these methods individually weight data from each subject, down-weighting subjects with relatively high intrasubject variability, possibly even shrinking intrasubject estimates towards a population estimate. We refer to such weighted methods generically as generalized least squares (GLS) (Searle, 1971). Although the GLS methods make fewer assumptions about the distribution of the data, they are computationally more complicated to employ.

While several software packages have implemented such voxel-wise GLS methods¹, the simpler method, of simply modeling 1st level contrast data with an un-weighted, ordinary least squares (OLS) analysis is still in widespread use. For example, a small survey of 90 papers matching the keyword “group fmri” anywhere in the text in NeuroImage, Human Brain Mapping and Cerebral Cortex ² found that 92% of group fMRI analyses used OLS. Further, OLS also forms the core of other methods. For example permutations are generally based on OLS (though see Mriaux et al. (2006)) and region of interest analyses typically are based on OLS.

The original reference for OLS analysis for group fMRI is a conference abstract, (Holmes and Friston, 1998), which has been referenced 448 times according to Google Scholar. While there are publications on GLS methods that compare to OLS, these comparisons have focused on the sensitivity but not the specificity (the ability to control false positives accurately) of the OLS model. Friston et al. (2005) compared thresholded test statistics from both the GLS and OLS models to determine how robust the OLS model was to violations of the assumption of homoscedasticity; their study focused on a single real dataset and did not consider the specificity of OLS when the assumptions were violated. Likewise Beckmann et al. (2003) compared the power of OLS and GLS under heteroscedasticity and they showed a moderate increase in power when using GLS. Instead of formally estimating power, their work looked at the percent change in the Z statistic, which is an approximation to the t-statistic that is used in standard analyses.

In this paper we provide a detailed description of OLS as it is typically used, focusing on the assumptions of this model and how well they hold for fMRI data. In particular, we highlight that the OLS approach always provides unbiased estimates of effect magnitude and, for the frequently-used one-sample model, unbiased variance estimates. The other possible problem caused by heterogeneity is disturbance of the distributional accuracy of t- or F-statistics, which can affect p-value accuracy. The traditional solution is to alter the degrees-of-freedom (DF) as part of a Satterthwaite adjustment (Satterthwaite, 1946). Satterthwaite has been found to be useful with the OLS model to protect against false positives in single subject fMRI analysis when data are temporally autocorrelated (Worsley and Friston, 1995; Kiebel et al., 2003), and we consider the performance of the Satterthwaite approximation in group fMRI analysis.

2 Methods

2.1 Model for Group fMRI data

Group fMRI data are typically analyzed in a two-stage process. In the 1st level intrasubject models are fit independently to each subject, and in the 2nd level summary measures from each subject are modeled.

2.1.1 First Level: Within-subject Model

For a given voxel, there is a first stage model for each subject k:

$$Y_k=X_k{\beta }_k+{\epsilon }_k,$$ (1)

where Y_k is the T × 1 vector containing the blood oxygen level dependent (BOLD) time series, X_k is the T × p design matrix containing p regressors of interest, β_k is a p × 1 vector of parameters and ε_k is the T × 1 vector error term. Since fMRI data are temporally autocorrelated, we allow non-independent errors and write $\text{Var}({\epsilon }_k)={\sigma }_k^2{V}_k$, where ${\sigma }_k^2$ is the within-subject error variance and V_k is the temporal correlation of the error. For a review of temporal autocorrelation models used for V_k, see Mumford and Nichols (2006). We assume normally distributed errors and, at this first level, regard the β_k as fixed effects; hence the model can be concisely written as $Y_k\sim \mathcal{N}(X_k{\beta }_k,{\sigma }_k^2{V}_k)$, where “~” denotes the distribution of a random variable. Note that model (X_k) and noise ( ${\sigma }_k^2$ & V_k) are subject-specific.

While many regressors are needed to fit complex experimental designs and nuisance effects, an individual research question is usually addressed with 1-dimensional contrast³ c, forming a linear combination of parameter estimates cβ_k. The effect magnitude cβ_k and its variance are estimated with generalized least squares (GLS) as cβ̂_k,

$$c{\widehat{\beta }}_k=c{(X_k^{\prime }{V}_k^{-1}{X}_k)}^{-1}{X}_k^{\prime }{V}_k^{-1}{Y}_k$$ (2)

and its sample variance, for fixed true β_k, is

$$\widehat{\text{Var}}(c{\widehat{\beta }}_k)=c{(X_k^{\prime }{V}_k^{-1}{X}_k^{\prime })}^{-1}{c}^{\prime }{\widehat{\sigma }}_k^2,$$ (3)

$${\widehat{\sigma }}_k^2=(Y-X{\widehat{\beta }}_k{)}^{\prime }{V}_k^{-1}(Y-X{\widehat{\beta }}_k)/(T-p).$$ (4)

Though not recommended, ordinary least squares (OLS) can be used instead of GLS at the first level by (incorrectly) assuming V_k = I_T. This will produce biased standard errors ( $\text{E}\widehat{\{\text{Var}}(c{\widehat{\beta }}_k)\}\ne \text{Var}(c{\widehat{\beta }}_k)$) and effect magnitude estimates that have sub-optimal precision (Var(cβ̂_k) higher than with GLS). As will be seen below, biased standard errors only affect 2nd level GLS not OLS.

2.1.2 Second Level: Between-subject Model

At the “2nd level” we would ideally regress the true subject responses, γ = {cβ_k}_k, on a group model

$$\gamma =X_G{\beta }_G+{\epsilon }_G$$ (5)

where X_G is N × p_G group-level design matrix, β_G is the group level parameter vector and ε_G is the group error vector with $\text{Var}({\epsilon }_G)={\sigma }_G^2{I}_N$, where ${\sigma }_G^2$ is the between-subject variance and I is the identity matrix. Crucially, the true subject responses are now regarded as random, with $\gamma \sim \mathcal{N}(X_G{\beta }_G,{\sigma }_G^2{I}_N)$. While X_G is often just a column of ones (for a one-sample t-test) it can take any form in general.

2.1.3 Second Level: Estimation with OLS

Unfortunately, we only have the estimated contrasts, Y_G = {cβ̂_k}_k, and so the OLS 2nd level model in practice has the form

$$Y_G=X_G{\beta }_G+{\epsilon }_G^{\ast }$$ (6)

where ${\epsilon }_G^{\ast }$ is the mixed-effects error, ${\epsilon }_G^{\ast }=(Y_G-\gamma )+{\epsilon }_G$, containing variation from both imperfect intrasubject fit (Y_G − γ) and the distribution of true responses in the population (ε_G). Specifically we have $\text{Var}({\epsilon }_G^{\ast })={\text{Var}}_{\beta }(Y_G)+{\sigma }_G^2{I}_N$, where ${\text{Var}}_{\beta }(Y_G)=\text{diag}\{{\sigma }_1^{2}c{(X_1^{\prime }{V}_1^{-1}{X}_1)}^{-1}{c}^{\prime },\dots ,{\sigma }_N^{2}c{(X_N^{\prime }{V}_N^{-1}{X}_N)}^{-1}{c}^{\prime }\}$, where diag is the diagonal matrix operator, and the β subscript denotes that this is an intrasubject variance.

Write the OLS estimate of β_G, ${\widehat{\beta }}_{\text{OLS}}=X_G^{-}{Y}_G$, where ⁻ denotes pseudo inverse, and ${\widehat{\sigma }}_{\text{OLS}}^2=(Y_G-X_G{\widehat{\beta }}_{\text{OLS}}{)}^{\prime }(Y_G-X_G{\widehat{\beta }}_{\text{OLS}})/(N-p_G)$ is the estimate of the mixed-effects error variance.

For the OLS approach, it is assumed that the first level variance is homogeneous, ${\sigma }_i^{2}c{(X_i^{\prime }{V}_i^{-1}{X}_i)}^{-1}{c}^{\prime }={\sigma }_j^{2}c{(X_j^{\prime }{V}_j^{-1}{X}_j)}^{-1}{c}^{\prime }$ for all i, j and therefore the second level error variance can be expressed as $\text{Var}({\epsilon }_G^{\ast })=({\sigma }_{\mathit{win}}^2+{\sigma }_G^2)I_N$, where ${\sigma }_{\mathit{win}}^2$ is the common within-subject variance. Therefore the variance can be simplified to $\text{Var}({\epsilon }_G^{\ast })={\sigma }_{\text{OLS}}^2{I}_N$, where ${\sigma }_{\text{OLS}}^2$ is the combined within- and between-subject variance term. Since there is just a single variance term, this model is much easier to estimate and does not require iterative maximization techniques.

Without the homogeneity assumption the OLS estimates may not have optimal precision, though they are unbiased (E(β̂_OLS) = β_G). While the standard errors are not unbiased in general, in the widely-used one-sample t-test the standard errors are unbiased (See Appendix A for full details).

2.1.4 Second Level: Estimation with GLS

In the GLS approach to the multistage mixed model, the assumption at the second stage is that $\text{Var}({\epsilon }_G^{\ast })={\sigma }_G^2{I}_N+{\text{Var}}_{\beta }(Y_G)$. For fMRI software packages that use a GLS approach, such as FSL or fmristat, the estimates of the variance ${\sigma }_k^2$ and correlation V_k from the first level analysis are used for ${\widehat{\text{Var}}}_{\beta }(Y_G)=\text{diag}\{{\widehat{\sigma }}_1^{2}c{(X_1^{\prime }{\widehat{V}}_1^{-1}{X}_1)}^{-1}{c}^{\prime },\dots ,{\widehat{\sigma }}_N^{2}c{(X_N^{\prime }{\widehat{V}}_N^{-1}{X}_N)}^{-1}{c}^{\prime }\}$, where the diagonal elements correspond to the individual estimated variances from equation 3, and ${\sigma }_G^2$ is estimated as part of an iterative model estimation algorithm, such as restricted maximum likelihood (Harville, 1974).⁴ GLS estimates of group-level effects are unbiased and have minimum variance among all linear unbiased estimates (Searle, 1971).

2.1.5 Model for Evaluating Heteroscedasticity in the Second Level Model

This note focuses on the one-sample t-test under the OLS approach, so from this point on we can assume that x₁,…, x_N are the N first level contrast estimates from N subjects, previously referred to as Y_G. The OLS test statistic is given by

$$T_{\mathit{OLS}}=\frac{\overline{x}}{\sqrt{S^2/N}},$$ (7)

where $\overline{x}={\sum }_{i=1}^N{x}_i/N$ orresponds to and β̂_OLS and

$$S^2=\sum _{i=1}^N{(x-\overline{x})}^2/(N-1)$$ (8)

corresponds to ${\widehat{\sigma }}_{\text{OLS}}^2$. Inference is carried out by comparing T to a t-distribution with N − 1 degrees of freedom (T_N−1).

2.1.6 Satterthwaite Correction to Address Heteroscedasticity

Although the OLS variance estimate is unbiased in the case of the one-sample t-test (See Appendix A), the distributional assumptions change under heteroscedasticity. Under homoscedasticity the sample variance S² (equation 8) is proportional to a ${\chi }_{N-1}^2$ random variable, where the degrees of freedom also define the t-distribution used to test the null hypothesis of the t-statistic (equation 7). Under heteroscedasticity the sample variance is only approximately proportional to a χ² random variable. The motivation of the Satterthwaite approach is to estimate the effective degrees of freedom (eDF) such that the sample variance is proportional to ${\chi }_{\mathit{eDF}}^2$.

The Satterthwaite degree of freedom approximation is based on matching the first and second moments of S² and a scaled χ² distribution, solving for the χ² degrees-of-freedom ν_SAT (Satterthwaite, 1946),

$${\nu }_{\mathit{SAT}}=\frac{2E^2(S^2)}{\text{Var}(S^2)}.$$

Using the values in Table 1 and after some algebra, one finds that

Table 1.

First two moments of a ${\chi }_{\nu }^2$ random variable and S²

Moment	${\chi }_{\nu }^2$	S2
First	ν	$\frac{1}{N}{\sum }_i{\sigma }_i^2$
Second	ν(ν + 2)	$3\frac{N^2-2N-1}{N^2}{\sum }_i{\sigma }_i^4+\frac{N^2-2N+3}{N^2}{\sum }_i{\sum }_j{\sigma }_i^2{\sigma }_j^2$

$${\nu }_{\mathit{SAT}}=\frac{{(N-1)}^2{\sum }_i{\sum }_j{\sigma }_i^2{\sigma }_j^2}{N(N-2){\sum }_i{\sigma }_i^4+{\sum }_i{\sum }_j{\sigma }_i^2{\sigma }_j^2}.$$ (9)

In the real data analyses below, we use the FSL estimates for ${\sigma }_i^2={\widehat{\sigma }}_i^2+{\widehat{\sigma }}_B^2$ to compute ν_SAT. (FSL’s FEAT analysis software uses GLS to find these quantities and saves these estimates as var_filtered_func_data and stats/mean_random_effects_var1.)

2.2 Real data analysis

2.2.1 Data and variance estimation

Our data are from a finger tapping experiment of the right hand involving 12 normal subjects (Johansen-Berg et al., 2002). This was a block design study consisting of blocks of rest and 3 pseudorandomly cued tasks: tapping of the index finger, sequentially tapping fingers, randomly tapping fingers.

The data were analyzed using the fMRIB software library (FSL), using a two-level “FLAME” model. This model produced 12 contrast estimates, and 12 subject specific mixed-effects variance estimates for each of the 226,000 voxels. The contrast of interest for our study tested the difference between the response when randomly tapping the fingers and sequentially tapping the fingers. For each voxel the p-value for the OLS statistic was calculated using the Satterthwaite correction and two other methods that are described in the following sections.

2.2.2 Permutation test

The permutation p-values were obtained by comparing the test statistic, T, to an empirical t-distribution based on permutations. Since we are making inference on contrasts of parameter estimates involving differences, the order of differencing does not matter under the null hypothesis of no activation; for example β₁ − β₂ is equivalent to β₂ − β₁. Therefore, by permuting the signs on the contrasts we can construct the null distribution of the contrast (Nichols and Holmes, 2002). Specifically, all possible 2^N permutations are created by the different +/− combinations of the N contrasts and a test statistic for each permutation is calculated and P_perm = % of the 2^N permuted test statistics as large or larger than the test statistic T.

2.2.3 Monte Carlo simulation details

Since the true null distribution is unknown under the heteroscedastic case, we used Monte Carlo to calculate “correct” p-values at each voxel, assuming the variances of the contrast for each subject, ${\sigma }_i^2$, to be known. For each realization, we generated 10,000 sets of N(0, ${\sigma }_i^2$) data for each of the i subjects and used it to calculate 10,000 test statistics. P_MC = % of 10,000 test statistics as large or larger than the test statistic, T, for that voxel.

2.3 Simulated data analysis methods

Simulations were used to study different sample sizes with differing numbers of outliers and varying degrees of outlying variances. To simulate outlying within-subject variances we used a mixture of χ² random variables where, with probability 0.9, the variance was chosen from a ${\chi }_{{\sigma }_{in}^2}^2$ distribution and, with a probability of 0.1 it was chosen from a ${\chi }_{{\sigma }_{\mathit{out}}^2}^2$ distribution, where ${\sigma }_{in}^2$ and ${\sigma }_{\mathit{out}}^2$ are the within-subject variances for the non-outlying and outlying subjects, respectively. Between-subject variances were chosen such that the overall variance for each simulation was kept constant. Therefore across different variance settings a given effect size would correspond to equivalent statistical power.

Variances that have been found in real data are shown in Table 2 and the range of values for ${\sigma }_{in}^2$, ${\sigma }_{\mathit{out}}^2$ and ${\sigma }_B^2$ were chosen to include these values. The details are described in Appendix B. While the overall standard deviation was fixed, varying sample sizes required different effect magnitudes Δ to maintain 80% power across simulations. Specifically, Δ was set to 28.14, 19.04, and 15.34, for 10, 20, and 30 subjects, respectively.

Table 2.

Average estimated variances from real data analyses with outlying variances where variance estimates resulted from a mixed effects analysis using FSL. Averages shown are for voxels within the interquartile range of the nonzero between-subject variances. For comparison purposes, numbers were scaled such that ${\sigma }_{in}^2$ was 400 across studies. The last column corresponds to the values on the x-axis of Figure 3. Data used in the rows of the table came from Stover et al. (2006), Harley et al. (2009), Foerde et al. (2006), Cazalis et al. (2004), and Harley et al. (2009), respectively.

Study type	# subjects	# outliers	mean ${\sigma }_B^2$	mean ${\sigma }_{in}^2$	mean ${\sigma }_{\mathit{out}}^2$	$100\frac{{\sigma }_{\mathit{out}}^2-{\sigma }_{in}^2}{{\sigma }_{\mathit{out}}^2+{\sigma }_B}$
Blocked	16	1	1138.1	400	3558.5	67.3
Blocked	20	2	179.6	400	1134.4	55.9
Blocked	15	1	465.3	400	1499.5	56.0
Event Related	14	2	971.3	400	910.4	27.1
Event Related	20	2	488.1	400	1992.4	64.2

3 Results

3.1 Real Data

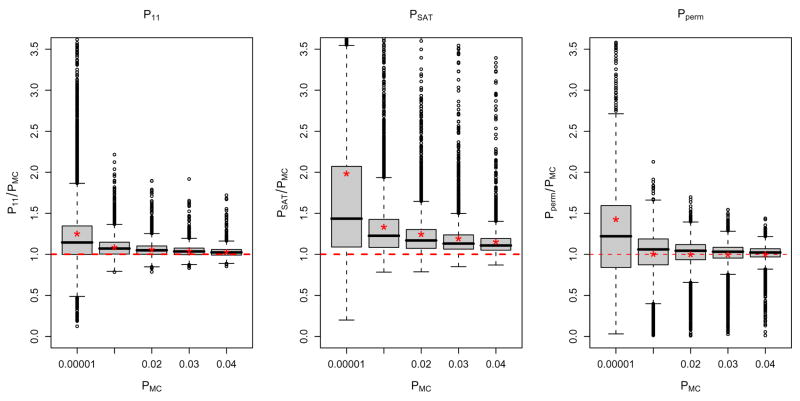
Using the subject-specific first level contrast estimates we calculated T_OLS (eq 7) and obtained four different P-values: P₁₁ found with the usual t-distribution with N − 1 = 11 DF, P_SAT found with a t-distribution with Satterthwaite DF (ν_SAT ), P_MC created with the Monte Carlo simulated t-distribution, and P_perm computed with the permutation driven null distribution. To evaluate the accuracy of the p-values at potential signal voxels, we compared both P₁₁ and P_SAT to P_MC in the voxels that were found to be significant with P_MC < 0.05. The left two panels of Figure 1 show the boxplots of the ratios of P₁₁/P_MC and P_SAT/P_MC over different ranges of P_MC. The mean corresponding to each boxplot is indicated by a red star. Surprisingly, P₁₁ is slightly conservative and P_SAT is even more conservative, having values larger than P_MC on average. Since ν_SAT ≤ 11 this indicates that the true degrees of freedom of the null distribution tends to be larger than N − 1. P-values that are too large indicate that the null distribution used has tails that are too heavy, in particular, that both DF values of ν_SAT and 11 are too small and the effective degrees of freedom that best match the true distribution are yet larger than the nominal DF.

Figure 1.

Comparisons of P₁₁, P_SAT, and P_perm with P_MC over values of P_MC < 0.05. The x-axis show the lower bound of the interval for P_MC and the red stars indicate the means of the distributions.

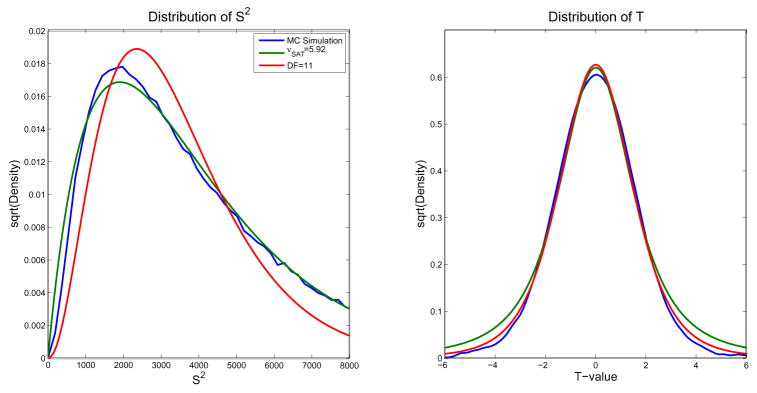
In order to understand the poor performance of P_SAT, we examined the implied distribution of S² and T for each method. Figure 2 shows these two distributions, where the blue line is the probability density estimate based on the Monte Carlo simulation values. The distribution of S² under 11 and ν_SAT degrees of freedom (or in general ν_method) are χ₂ distributions scaled by E(S²)/ν_method, which is a gamma distribution with shape parameter ν_method/2 and scale parameter 2E(S²)/ν_method. The distribution of S² based on the Monte Carlo simulation is quite similar to the distribution of S² under ν_SAT, with the mean and variance of the two distributions matching. Even so, the corresponding t-distributions do not agree in the tails of the distribution, which is important since it affects the p-values of interest. This is due to the distributions of S² not matching well for values near zero. There is a much higher probability of obtaining near-zero values of S² under ν_SAT, which leads to a higher probability of getting larger values in the corresponding t-distribution, explaining the fatter tails.

Figure 2.

The distribution of S² (left) and T (right). Although the mean and variance of the distributions of S² for the MC simulation and ν_SAT are similar, the lower tails do not match as well as ν₁₁. The larger lower tail of the distribution of S² causes the tails of the distribution of T to be too large.

The distribution of S² based on 11 DF does not look as similar to that based on the Monte Carlo simulation overall, but for the values of S² that we are interested in, the lower values, the distributions are much closer and hence p-values are more similar. While nonparametric inferences are known to be exact, we confirmed this by comparing P_perm to P_MC. In the right panel of Figure 1, the mean of the ratio P_MC/P_perm is nearly 1 (means marked with asterisks), except for the smallest P-values which likely are exhibiting discreteness-induced conservativeness. One possible limitation of our Monte Carlo simulations is that they assume that the FLAME-derived variance estimates are the true values of the variances in the real data. To assess this assumption, we repeated the Monte Carlo simulation using t-statistic values based on samples from a Normal distribution with known variances and obtained similar results (see Supplementary Material), suggesting the FLAME variance estimates are accurate.

3.2 Simulations

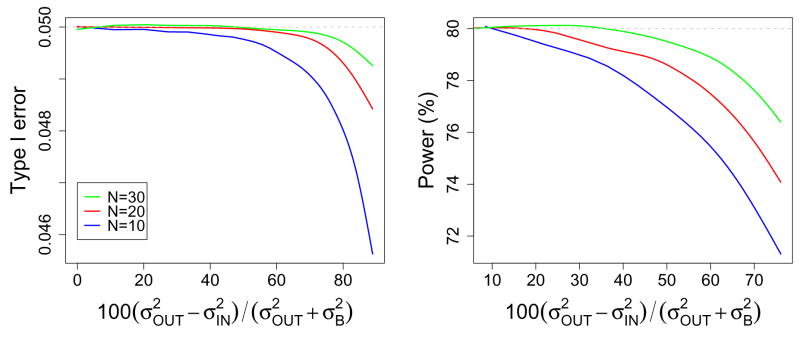
Simulations were used to study type I error rate and power over a range of degrees of outlying variance when using T_OLS versus T_GLS and a null distribution t_N−1. Figure 3 shows the type I error rate and power as a function of the percent difference between the mixed effects variance for the outliers and non-outliers, $100\ast ({\sigma }_{\mathit{out}}^2-{\sigma }_{in}^2)/({\sigma }_{\mathit{out}}^2+{\sigma }_B)$. The left panel of Figure 3 supports the finding of our real data analysis, in that when using OLS the type I error rate is close to the desired level and may be slightly conservative (though note the very tight range of the y-axis). The type I error is most conservative for smaller sample sizes and larger outlying variances. Note in each sample size there were 10% outliers.

Figure 3.

Type I error rate (left) and power (right) as a function of the % difference in the mixed effects variances of outlying and non-outlying variances, $100({\sigma }_{\mathit{out}}^2-{\sigma }_{in}^2)/({\sigma }_{\mathit{out}}^2+{\sigma }_B^2)$, for sample sizes of 10, 20 and 30. Overall variance was held constant for each sample size over the range of the x axis to ensure power for each sample size reflected the same effect size.

The right panel of Figure 3 shows the power under the OLS model, where the true power (under GLS) was 80% in each case. As found in Beckmann et al. (2003) and Friston et al. (2005) power can be lost when using OLS under heteroscedasticity. The decrease was as high as 9% and was worst for the smaller sample size and larger outlying variances.

The x-axis range of Figure 3 can be compared to the values found from real data shown in the last column of Table 2. We searched over 12 data analyses that were analyzed using the Feat analysis tool of FSL, including event related and blocked designs and found that 5 of these studies had subjects with outlying variances. This was determined by subsetting voxels with nonzero between-subject variances and plotting boxplots of the voxel-averaged within-subject variances. In cases where outlying variances were found, the within-subject variance distributions were similar for voxels where the between-subject variance was 0. Table 2 lists the average within-subject variances for outlying and non-outlying subjects within the interquartile range of the nonzero between-subject variances, scaled such that ${\sigma }_{in}^2=400$ for all studies.

4 Discussion

We hypothesized that when using a one-sample t-test for a group contrast mean of fMRI data, simply using N − 1 degrees of freedom would lead to invalid p-values due to the heterogeneity of variances. Surprisingly, in our data analysis, we found N − 1 degrees of freedom to be slightly conservative and hence valid when compared to p-values calculated with a Monte Carlo simulation or permutation test. The 2 moment matching Satterthwaite approximation was even more conservative than using N − 1 degrees of freedom. Although the Satterthwaite approximation has been shown to give valid hypothesis tests in single subject fMRI analysis (Kiebel et al., 2003), it did not perform well in the given situation where observations are uncorrelated, but have heterogeneous variance. This is even more surprising since the Satterthwaite approximation was originally developed to handle cases of heteroscedasticity, but suggests that the approach may not perform well with low degrees-of-freedom. As shown in our comparison of distributions of S² and T in Figure 2, the Satterthwaite approximation only matches the first two moments of the distribution, which does not ensure the left tails of the distributions of S² for Satterthwaite and the true distribution match; hence the tails of the T distributions will not match. Therefore the Satterthwaite approximation tends to be too conservative in this application.

A three moment matching eDF approach of Scariano and Davenport (1986) was also considered, but similar to the Satterthwaite approximation the effective degrees of freedom are always less than N − 1 and so this method was not considered. The permutation test is the only test that does not assume the T test statistics follow a specific distribution, and its only limitation is discrete P-values for very small sample sizes (e.g. for 6 subjects all P-values are multiples of 1/2⁶ = 0.015625).

Our simulation study allowed us to study type I error and power under a range of sample sizes and outlying variances that are representative of real data findings. Our findings for type I error supported our real data analysis finding that the OLS-based hypothesis test on the sample mean was slightly conservative under heteroscedasticity. Although the true type I error rate was most conservative for small sample sizes and/or the presence of very large outliers, the smallest we found in our simulations was 0.0456 when the goal type I error rate was 0.05.

Although previous studies by Beckmann et al. (2003) and Friston et al. (2005) implied there was a loss in power under the OLS model, they did not formally quantify the loss. Our results show that although there is a loss in power, it was not found to be larger than a 9% in our simulations and this was for a small sample size of 10 subjects with a very large outlying variance.

Although we have shown the OLS model is robust to violations of the heteroscedasticity assumption for the 1-sample t-test, it is probably not the case that this result would also hold in the case of simple linear regression as the slope of a line is easily influenced by outliers. It is likely that in the case of simple linear regression the GLS model should be used to ensure outliers are properly down-weighted.

Finally, we note that these results for fMRI also inform group analyses in other modalities. In particular, in PET or EEG, where it may be impractical or undesirable to estimate intrasubject variance, it is useful to know that the OLS model is performing well in the face of any potential heteroscedasticity.

In conclusion, while a weighted, GLS mixed effects model is the more optimal modeling approach, we find “plain old” OLS surprisingly robust for the widely-used one-sample model. We have provided evidence that an OLS model used with varying designs or outlier-induced heteroscedasticity actually controls false positive risk and has near-optimal power.

Appendices

A Bias of OLS variance estimators

In this appendix we find the bias of the OLS variance estimators under (unmodeled) heterogeneous variance. Writing the second level model originally shown in equation 6 using a simplified notation we have,

$$Y=X\beta +\epsilon$$ (10)

where Y is the N-vector of contrast data fed up from the first level, X is N × p second-level design matrix, and β are the group-level parameters, and ε are the second-level errors. We assume that Var(ε) = V σ², where σ² is the average mixed effects variance, V = diag(v_i), Σ_i v_i = 1 are the scaling factors for each subject, allowing for heteroscedasticity. Under this model of the variance we are interested in the properties of the OLS estimators:

$${\widehat{\beta }}_{\text{OLS}}={(X^{\prime }X)}^{-1}{X}^{\prime }Y$$ (11)

$${\widehat{\sigma }}_{\text{OLS}}^2=(Y-X{\widehat{\beta }}_{\text{OLS}}{)}^{\prime }(Y-X{\widehat{\beta }}_{\text{OLS}})/(N-p)$$ (12)

$${\widehat{\text{Var}}}_{\text{OLS}}(\widehat{\beta })={(X^{\prime }X)}^{-1}{\widehat{\sigma }}_{\text{OLS}}^2$$ (13)

First essential result is that E(β̂_OLS) = β, that is, the estimates of the regression coefficients are unbiased. However, the estimates of error and parameter variance are not necessarily unbiased. First

$$\text{E}({\widehat{\sigma }}_{\text{OLS}}^2)=\text{trace}((I_N-H)V)/(N-p)$$ (14)

$$=\frac{{\sum }_i(1-h_i)v_i}{N-p}{\sigma }^2$$ (15)

where H = X(X′X)⁻¹X′ is the so-called hat matrix, and h_i is the ith diagonal element of H, the leverage of observation i. A basic result of linear models gives Σ_i(1 − h_i) = N − p (Harville, 2008). Thus if the variance scaling factors are not all equal (to unity), then the requirement for unbiased ${\widehat{\sigma }}_{\text{OLS}}^2$ is that all leverages h_i are all equal. A one-sample model has equal leverage values, as does any balanced ANOVA design. Except for this balanced ANOVA case, a regression model will not have all equal leverages.

The estimator variance is

$$\text{Var}({\widehat{\beta }}_{\text{OLS}})={(X^{\prime }X)}^{-1}{X}^{\prime }VX{(X^{\prime }X)}^{-1}{\sigma }^2$$ (16)

while

$$\text{E}({\widehat{\text{Var}}}_{\text{OLS}}(\widehat{\beta }))={(X^{\prime }X)}^{-1}\text{E}({\widehat{\sigma }}_{\text{OLS}}^2).$$ (17)

If there is no bias in ${\widehat{\sigma }}_{\text{OLS}}^2,{\widehat{\text{Var}}}_{\text{OLS}}(\widehat{\beta })$, is unbiased when

$$X^{\prime }X=X^{\prime }VX.$$ (18)

This is true for a one-sample problem, but not even for a balanced ANOVA model. However, for balanced ANOVA models and typical contrasts of interest, there may be no bias. For example, for a balanced two sample t-test, with design matrix

$$X^{\prime }=\left[\begin{array}{lllllll}1\hfill & 1\hfill & \cdots \hfill & 0\hfill & 0\hfill & \cdots \hfill & 0\hfill \\ 0\hfill & 0\hfill & \cdots \hfill & 1\hfill & 1\hfill & \cdots \hfill & 1\hfill \end{array}\right]$$ (19)

and contrast c = [−1 1] can be shown to have $c{\widehat{\text{Var}}}_{\text{OLS}}(\widehat{\beta })c^{\prime }$ unbiased for cVar(β̂_OLS)c′.

B Simulation details

Using GLS, the group mean and estimated variance have the following form,

$${\widehat{\mu }}_{\mathit{GLS}}={\left(\sum _{i=1}^N\frac{1}{{\sigma }_i^2}\right)}^{-1}\sum _{i=1}^N\frac{x_i}{{\sigma }_i^2}$$ (20)

$$\text{Var}({\mu }_{\mathit{GLS}})={\left(\sum _{i=1}^N\frac{1}{{\sigma }_i^2}\right)}^{-1},$$ (21)

where ${\sigma }_i^2$ is the sum of the within- and between-subject variance for subject i. When the variance is known, this yields the z statistic, $Z_{\mathit{GLS}}={\widehat{\mu }}_{\mathit{GLS}}/\sqrt{\text{Var}({\mu }_{\mathit{GLS}})}$. Assuming 90% and 10% of the within-subject variances are ${\sigma }_{in}^2$ and ${\sigma }_{\mathit{out}}^2$, respectively, that ${\sigma }_B^2$ is the between-subject variance and that x_i = Δ for all subjects,

$$Z_{\mathit{GLS}}=\sqrt{N}\mathrm{\Delta }{\left(0.9\frac{1}{{\sigma }_{in}^2+{\sigma }_B^2}+0.1\frac{1}{{\sigma }_{\mathit{out}}^2+{\sigma }_B^2}\right)}^{1/2},$$ (22)

which corresponds to a test statistic for a group mean whose value is Δ with N subjects and a standard deviation of

$${\left(0.9\frac{1}{{\sigma }_{in}^2+{\sigma }_B^2}+0.1\frac{1}{{\sigma }_{\mathit{out}}^2+{\sigma }_B^2}\right)}^{-1/2}.$$ (23)

For our simulations we chose a constant ${\sigma }_{in}^2=400$ across all simulations and varied the outlying variance across the range between 400–3600 and the between subject variance was chosen so that the overall standard deviation in equation 23 was held constant at 33. This range included variance combinations that were found in real data analyses with outlying variances shown in Table 2.