Image charge approximations of reaction fields in solvents with arbitrary ionic strength

Abstract

In this paper, we report a new development of image charge approximations of reaction fields for a charge inside a dielectric spherical cavity immersed in an ionic solvent with arbitrary ionic strength. This new development removes the requirement of low ionic strength of the solvent in a previous result [S. Deng, W. Cai, Extending the fast multipole method for charges inside a dielectric sphere in an ionic solvent: high-order image approximations for reaction fields, J. Comput. Phys. 227 (2007) 1246–1266], thus extending the applicability of the image charge approximations of reaction fields in the modeling of bio-molecular solvation.

1. Introduction

Image charge methods are important numerical approaches for calculating electrostatic interactions among charges inside a dielectric cavity immersed in an aqueous solution. In hybrid explicit/implicit solvent models [1] of biomolecular simulations, spherical cavities are often used to enclose biomolecules of irregular shapes with a few layers of surrounding water molecules. For a spherical cavity, the reaction field can be expressed by the well-known Kirkwood series expansion [2,3] in terms of Legendre polynomials. However, image charge methods can offer a more efficient calculation of the electrostatic interactions.

When no salt effects are present in the solvent, Friedman [4] developed a single image charge approximation for the reaction field in the Poisson equation model, and later an improved version was obtained by Abagyan and Totrov [5]. These image charge methods have been widely applied in biomolecular simulations. Recently, a multiple image charge approximation was proposed [6] to represent the reaction field for the pure water solvent and found to perform about 20–30 times faster than the direct Kirkwood expansion. Moreover, this method can be combined with the fast multipole method [7,8] in a straightforward manner so that the electrostatic interactions among N charges inside the dielectric cavity can be calculated in an O(N) complexity. For an ionic solvent, high-order accurate multiple image charge approximations were also developed [9,10] for the reaction field provided that the ionic strength is low so that u = λa < 1, where λ is the inverse Debye screening length and a is the spherical radius. In this paper, we shall present new image charge approximations for the reaction field for solvents with arbitrary ionic strength such that no restriction on u will be imposed.

The paper is organized as follows. In Section 2, the Kirkwood series representation of the reaction field in the Poisson–Boltzmann theory is reviewed. In Section 3, we present new line image approximations and multiple discrete image charge approximations. Numerical results and analysis are given in Section 4, and a conclusion is drawn in Section 5.

2. Reaction field of a point charge

In the Poisson–Boltzmann theory, the electrostatic potential Φ inside a dielectric spherical cavity embedded in a dissimilar dielectric continuum is given by the Poisson equation

$$\nabla ·({\epsilon }_{\mathrm{i}}\nabla \Phi (\mathbf{r}))=-{\displaystyle \sum _k{q}_k\delta (\mathbf{r}-{\mathbf{r}}_k), \mathbf{r}\in {\Omega }_{\mathrm{i}},}$$ (1)

where Ω_i is the interior region of the spherical cavity centered at the origin with radius a, ε_i is the interior dielectric constant, and r_k is the position of the kth point charge with strength q_k. In the exterior medium with salt effects, from the Debye–Hückel theory, the potential is given by the Poisson–Boltzmann equation after linearization

$${\nabla }^2\Phi (\mathbf{r})-{\lambda }^2\Phi (\mathbf{r})=0, \mathbf{r}\in {\Omega }_{\mathrm{e}},$$ (2)

where Ω_e = ℝ³ \ Ω_i, and λ is the inverse Debye screening length determined by the ionic strength of the solvent and the exterior dielectric constant ε_o. On the surface of the cavity, two boundary conditions for the continuities of the potentials and the fluxes along the normal direction hold, i.e.

$$\Phi ({\mathbf{r}}^{-})=\Phi ({\mathbf{r}}^{+}), {\epsilon }_{\mathrm{i}}\frac{\partial \Phi ({\mathbf{r}}^{-})}{\partial \mathbf{n}}={\epsilon }_{\mathrm{o}}\frac{\partial \Phi ({\mathbf{r}}^{+})}{\partial \mathbf{n}} \text{for}|\mathbf{r}|=a,$$ (3)

where r⁻ and r⁺ are, respectively, the inner and outer limits at position r, and n is the unit outward vector normal to the surface of the cavity.

Due to the principle of linear superposition, we only need to consider the reaction field of one point charge q located at r _s=(r_s, 0, 0) inside the sphere. The solution Φ(r) inside and outside the sphere for the Poisson–Boltzmann system can be written in the following form of the classical Kirkwood series expansion [2,3] in a spherical coordinate system (r,φ, θ) as

$$\Phi (\mathbf{r})=\{\begin{array}{cc}{\displaystyle {\sum }_{n=0}^{\infty }\left[\frac{q}{4\pi {\epsilon }_{\mathrm{i}}{r}_{\mathrm{s}}}{\left(\frac{r}{r_{\mathrm{s}}}\right)}^n+A_n{r}^n\right]P_n(\text{cos}\theta ),}\hfill & \text{when}0\le r<r_{\mathrm{s}},\hfill \\ {\displaystyle {\sum }_{n=0}^{\infty }\left[\frac{q}{4\pi {\epsilon }_{\mathrm{i}}r}{\left(\frac{r_{\mathrm{s}}}{r}\right)}^n+A_n{r}^n\right]P_n(\text{cos}\theta ),}\hfill & \text{when}{r}_{\mathrm{s}}\le r<a,\hfill \\ {\displaystyle {\sum }_{n=0}^{\infty }{B}_n{k}_n(\lambda r)P_n(\text{cos}\theta ),}\hfill & \text{when}r\ge a\hfill \end{array}$$ (4)

in which

$${\Phi }_{\text{RF}}(\mathbf{r})={\displaystyle \sum _{n=0}^{\infty }{A}_n{r}^n{P}_n(\text{cos}\theta ),}$$ (5)

defines the potential of the reaction field inside the dielectric cavity. Here, P_n(x) are the Legendre polynomials, and k_n(r) are the modified spherical Hankel functions [11] of order n defined by

$$k_n(r)=\frac{\pi {\mathrm{e}}^{-r}}{2r}{\displaystyle \sum _{k=0}^n\frac{(n+k)!}{k!(n-k)!}\frac{1}{{(2r)}^k}.}$$ (6)

The expansion coefficients A_n and B_n are found from the boundary conditions in Eq. (3) to be

$$A_n=\frac{q}{4\pi {\epsilon }_{i}a}\frac{1}{r_{\mathrm{k}}^n}\frac{\epsilon (n+1)k_n(u)+u{k}_n^{\prime }(u)}{\epsilon n{k}_n(u)-u{k}_n^{\prime }(u)}=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}\frac{1}{r_{\mathrm{k}}^n}\frac{\epsilon (n+1)S_n(u)+1}{\epsilon n{S}_n(u)-1},$$ (7)

$$B_n=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}{\left(\frac{r_{\mathrm{s}}}{a}\right)}^n\frac{\epsilon (2n+1)}{\epsilon n{k}_n(u)-u{k}_n^{\prime }(u)},$$ (8)

where r_k=a²/r_s, ε = ε_i/ε_o and $S_n(u)=\frac{k_n(u)}{u{k}_n^{\prime }(u)}.$

3. Image charge approximations for the reaction field

3.1. Previous image charge approximations

Although the Kirkwood expansion can be used [12], its convergence rate is slow, particularly near the boundary of the spherical cavity. For a pure water solvent (the term S_n(u) in (7) simplifies to −1/(n + 1)), some literature [4,5] approximated the reaction field due to a point charge inside the sphere as the potential of an image charge, known as the Kelvin image charge [13], at the conventional Kelvin image point

$${\mathbf{r}}_{\mathrm{K}}=(r_{\mathrm{K}},0,0)\text{and}{r}_{\mathrm{k}}=a^2/r_{\mathrm{s}},$$ (9)

plus a correction term. These treatments speed up the calculation and have been used in many applications of molecular dynamics and Monte Carlo simulations (see [14–16] for examples). However, approximation with only one image charge is inaccurate in many simulations. Based on the remarkable results [17–20] which extended the Kelvin image for a conducting sphere to the case of a dielectric one, the reaction field for the pure water solvent can be represented exactly by a line image charge in addition to the Kelvin image charge. Recently, using the line image results, a multiple discrete image charge approximation for the reaction field was obtained [6].

To extend the multiple image approximation to ionic solvents, an asymptotic approach was adopted. For an ionic solvent, the modified spherical Hankel function holds the following asymptotic expansion in terms of u = λa < 1

$$k_n(u)=\pi \frac{(2n)!}{n!}\frac{1}{{(2u)}^{n+1}}+O\left(\frac{1}{u^{n-1}}\right) \text{for}n\ge 1$$ (10)

and

$$k_n(u)=\pi \frac{(2n)!}{n!}\frac{1}{{(2u)}^{n+1}}-\frac{\pi }{2}+O\left(\frac{1}{u^{n-1}}\right) \text{for}n=0.$$ (11)

We then have

$$\begin{array}{c}{S}_n(u)=\frac{k_n(u)}{u{k}_n^{\prime }(u)}=-\frac{1}{n+1}+O(u^2), n\ge 1,\hfill \\ S_0(u)=\frac{k_0(u)}{u{k}_0^{\prime }(u)}=-\frac{1}{1+u}.\hfill \end{array}$$ (12)

Applying these asymptotic expansions, a second-order line image charge approximation [9] to the reaction field was obtained as

$${\Phi }_{\text{RF}}(\mathbf{r})=\frac{q_{\mathrm{K}}}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-{\mathbf{r}}_{\mathrm{K}}|}+{\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{q_{\mathrm{A}}^{\text{line}}(x)}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-\mathbf{x}|}\mathrm{d}x+{\Phi }_{\mathrm{A}}^{\text{cor}}+O(u^2),}$$ (13)

where x = (x, 0, 0), q_K and q_A^line(x) denote, respectively, the Kelvin image charge and a line image charge extending from the Kelvin image point to infinity along the radial direction. ${\Phi }_{\mathrm{A}}^{\text{cor}}$ is a position-independent constant correction potential which comes from the additional term in (11) for the case of n = 0. The image charges are defined by

$$q_{\mathrm{K}}=q\gamma \frac{a}{r_{\mathrm{s}}}, q_{\mathrm{A}}^{\text{line}}(x)=q\frac{{\delta }_{\mathrm{A}}}{a}{\left(\frac{x}{r_{\mathrm{k}}}\right)}^{-{\sigma }_{\mathrm{A}}} \text{for} r_{\mathrm{K}}\le x$$ (14)

and

$${\Phi }_{\mathrm{A}}^{\text{cor}}=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}(\frac{\epsilon }{1+u}-1-\gamma -\frac{{\delta }_{\mathrm{A}}}{{\sigma }_{\mathrm{A}}})=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}(\frac{\epsilon }{1+u}-\epsilon )$$ (15)

with

$$\gamma =-\frac{1-\epsilon }{1+\epsilon }, {\sigma }_{\mathrm{A}}=\frac{1}{1+\epsilon }, {\delta }_{\mathrm{A}}=\gamma (1-{\sigma }_{\mathrm{A}}).$$

Here the subscript “A” is used to distinguish this method from the new image charge methods to be presented later in this paper.

Higher-order accurate image charge approximations can be further obtained by expanding the modified spherical Hankel functions to higher order with respect to u. For example, by using the Kelvin image charge and two line image charges together with a position-independent and a position-dependent correction potentials, a fourth-order image charge approximation has been developed in [10].

3.2. Image charge approximations for solvents of high ionic strength

It can be seen that the key in developing the above image charge methods is to approximate the function S_n (u) in (12) with some simple rational functions of n and u = λa in the order of O(u^m) for a certain positive integer m. Therefore, the product of the inverse Debye screening length λ (which is proportional to the square root of the ionic concentration) and the sphere radius a being small is the precondition for the success of the previous image charge approximations for ionic solvents. However, in circumstances of high salt concentration or large sphere radius or both, it is possible that the product λa is greater or much greater than 1.

Nevertheless, when u is large, in fact we can expand asymptotically the function S_n (u) in terms of O(1/u^m), instead. In particular, for a second-order expansion, we have

$$S_n(u)=-\frac{1}{n+1+u}+O\left(\frac{1}{u^2}\right) \text{for}n\ge 0,$$ (16)

which is a better approximation than that given by (12) for large u because S_n(u) tends to −1/u as u tends to infinity. In addition, when u tends to zero, the approximation will still be analytical; that is, the reaction field will reproduce the Born formula [6].

Order of Convergence

The order of convergence can be verified by a simple analysis. On the one hand, when u tends to infinity, since $k_n(u)/k_n^{\prime }(u)=-1+O(1/u)$, we have S_n (u) = −1/u + O(1/u²), then,

$$S_n(u)+\frac{1}{n+1+u}=-\frac{n+1}{u(n+1+u)}+O\left(\frac{1}{u^2}\right)=O\left(\frac{1}{u^2}\right).$$ (17)

On the other hand, as u tends to zero, the approximation is in the order of convergence O(u), because of S_n (u) = −1/(n + 1) + O(u²)and

$$\frac{1}{n+1}-\frac{1}{n+1+u}=\frac{u}{(n+1)(n+1+u)}=O(u).$$

Plugging (16) into (7) leads to an approximation of the expansion coefficient A_n as

$$A_n\approx \frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}\frac{1}{r_{\mathrm{K}}^n}(\gamma +\frac{{\delta }_{\mathrm{B}}}{n+{\sigma }_{\mathrm{B}}}),$$ (18)

where

$$\begin{array}{cc}{\sigma }_{\mathrm{B}}=\frac{1+u}{1+\epsilon },& {\delta }_{\mathrm{B}}=\gamma (1-{\sigma }_{\mathrm{B}})-\frac{u}{1+\epsilon }.\end{array}$$

Because σ_B and r_K are both positive real constants, a simple calculation yields the identity

$$r_{\mathrm{K}}^{n+{\sigma }_{\mathrm{B}}}{\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{1}{x^{n+{\sigma }_{\mathrm{B}}+1}}\mathrm{d}x=\frac{1}{n+{\sigma }_{\mathrm{B}}}.}$$ (19)

With this identity, we can rewrite the approximation of the reaction field (5) as

$${\Phi }_{\text{RF}}(\mathbf{r})\approx \frac{q\gamma a}{4\pi {\epsilon }_{\mathrm{i}}{r}_{\mathrm{s}}}\frac{1}{r_{\mathrm{K}}}{\displaystyle \sum _{n=0}^{\infty }{\left(\frac{r}{r_{\mathrm{K}}}\right)}^n{P}_n(\text{cos}\theta )}+{\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{q{\delta }_{\mathrm{B}}}{4\pi {\epsilon }_{\mathrm{i}}a}}{\left(\frac{x}{r_{\mathrm{K}}}\right)}^{-{\sigma }_{\mathrm{B}}}\frac{1}{x}{\displaystyle \sum _{n=0}^{\infty }{\left(\frac{r}{x}\right)}^n{P}_n(\text{cos}\theta )\mathrm{d}x.}$$ (20)

Then, using the expansion of the reciprocal distance

$$\frac{1}{|\mathbf{r}-\mathbf{x}|}=\frac{1}{x}{\displaystyle \sum _{n=0}^{\infty }{\left(\frac{r}{x}\right)}^n{P}_n(\text{cos}\theta ), \text{when} 0\le r<x,}$$ (21)

we obtain the following line image approximation for the reaction field

$${\Phi }_{\text{RF}}(\mathbf{r})\approx \frac{q_{\mathrm{k}}}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-{\mathbf{r}}_{\mathrm{K}}|}+{\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{q_{\mathrm{B}}^{\text{line}}(x)}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-\mathbf{x}|}\mathrm{d}x},$$ (22)

where q_K is defined in (14) and the line image charge is now as

$$q_{\mathrm{B}}^{\text{line}}(x)=q\frac{{\delta }_{\mathrm{B}}}{a}{\left(\frac{x}{r_{\mathrm{K}}}\right)}^{-{\sigma }_{\mathrm{B}}} \text{for}{r}_{\mathrm{K}}\le x.$$ (23)

We remark that, when n = 0, because the approximation to S₀(u) exactly equals −1/(1 + u), no correction term is required for the reaction field.

3.3. Line image charge approximation with one correction term

The accuracy of the line image approximation (22) can be improved by modifying the asymptotical formula of S_n(u) for large u as

$$S_n(u)=-\frac{1}{(n+1)+\frac{u^2}{1+u}}+O\left(\frac{1}{u^2}\right).$$ (24)

The second-order accuracy can be analyzed in the same way as u tends to infinity. Furthermore, when u tends to zero, the approximation is at an order of O(u²); therefore this new image charge approximation can cover the low ionic strength case as well [9]. In this case, the approximation (24) is analytical for n = 1. And we need to add a position-independent correction term for n = 0. Performing a similar deduction yields an approximation to the reaction field

$${\Phi }_{\text{RF}}(\mathbf{r})\approx \frac{q_{\mathrm{K}}}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-{\mathbf{r}}_{\mathrm{K}}|}+{\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{q_{\mathrm{C}}^{\text{line}}(x)}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-\mathbf{x}|}\mathrm{d}x+{\Phi }_{\mathrm{C}}^{\text{cor}}}$$ (25)

with a line image charge

$$q_{\mathrm{C}}^{\text{line}}(x)=q\frac{{\delta }_{\mathrm{C}}}{a}{\left(\frac{x}{r_{\mathrm{K}}}\right)}^{-{\sigma }_{\mathrm{C}}} \text{for}{r}_{\mathrm{K}}\le x,$$ (26)

where

$$\begin{array}{ccc}{\sigma }_{\mathrm{C}}=\frac{1+\tilde{u}}{1+\epsilon },& {\delta }_{\mathrm{C}}=\gamma (1-{\sigma }_{\mathrm{C}})-\frac{\tilde{u}}{1+\epsilon },& \tilde{u}=\frac{u^2}{1+u}.\end{array}$$

Here, the constant correction term is

$${\Phi }_{\mathrm{C}}^{\text{cor}}=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}(\frac{\epsilon }{1+u}-1-\gamma -\frac{{\delta }_{\mathrm{C}}}{{\sigma }_{\mathrm{C}}})=\frac{q}{4\pi {\epsilon }_{\mathrm{i}}a}(\frac{\epsilon }{1+u}-\frac{\epsilon }{1+\tilde{u}}).$$ (27)

Remark 1

Higher order asymptotic approximation for S_n(u) can be derived through the Mathematica software [21]. Actually by using the software, a higher-order approximation can also be obtained as

$$S_n(u)\approx -\frac{(2n-1)(1+u)+(n-1)u^2}{(2n-1)(n+1)(1+u)+n^2{u}^2+(n-1)u^3},$$ (28)

which is O(u³) when u tends to 0 and O(1/u²) when u tends to infinity. The approximation is analytical when n = 1 and 2. Consequently, the reaction field can be represented by a point charge and two line charges together with a position-independent correction term; see [10] for the treatment of multiple line image charges.

3.4. Discrete image charge approximations

To obtain multiple discrete image charge approximations to the reaction field, each line image charge introduced in (13), (22), or (25) is approximated with a set of discrete point image charges through Gauss integration quadratures, i.e.

$${\displaystyle {\int }_{r_{\mathrm{K}}}^{\infty }\frac{q_{\mathrm{X}}^{\text{line}}(x)}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-\mathbf{x}|}\mathrm{d}x\approx {\displaystyle \sum _{m=1}^M\frac{q_m^{\mathrm{X}}}{4\pi {\epsilon }_{\mathrm{i}}|\mathbf{r}-{\mathbf{x}}_m^{\mathrm{X}}|},}}$$ (29)

where ${\mathbf{x}}_m^{\mathrm{X}}=(x_m^{\mathrm{X}},0,0)$ and for m = 1, 2, …, M,

$$\begin{array}{cc}{q}_m^{\mathrm{X}}=\frac{{\delta }_{\mathrm{X}}}{2{\sigma }_{\mathrm{X}}}\frac{W_m{X}_m^{\mathrm{X}}}{a}q,& x_m^{\mathrm{X}}=r_{\mathrm{K}}{\left(\frac{2}{1-s_m}\right)}^{1/{\sigma }_{\mathrm{X}}}\end{array}$$

and s_m, w_m, m = 1, 2, …, M, are Jacobi–Gauss quadrature points and weights on the interval [−1, 1] (see [10] for details). Here, the label X represents “A”, “B”, or “C”. We remark that the main objective to formulate discrete image charge approximations is to apply the well-known fast multipole methods [7,8] which are of O(N) complexity in calculating the electrostatic interactions among N charges.

4. Numerical results

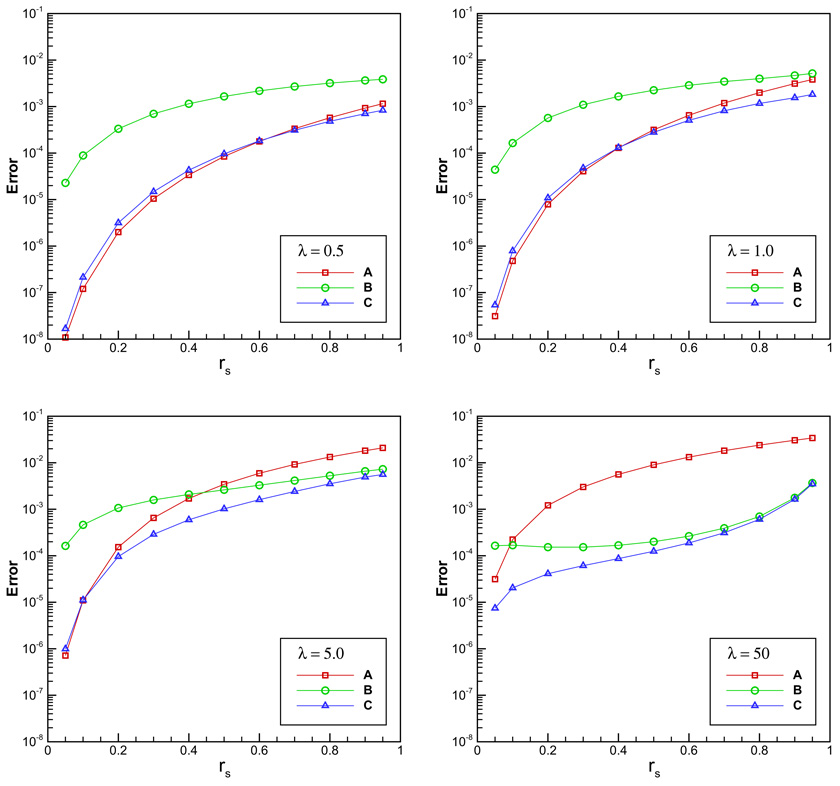
A test example is implemented by taking a = 1 and increasing the salt concentration related parameter λ. The dielectric constants chosen are ε_i = 2 and ε_o = 80, respectively. In all the numerical tests, the results obtained by the direct series expansion with 800 terms are taken to be the exact solutions, and we calculate the maximum relative error of image charge approximations at 10,000 observation points uniformly distributed inside the sphere. We compare the new image charge methods with the original second-order image charge method (Approach A) with a position-independent correction term in (13) [9]. Approaches B and C represent the new methods without correction term (Eq. (22)) and with one position-independent correction term (Eq. (25)), respectively.

4.1. Accuracy of new line image approximations

We first test the accuracy of the line image approximations versus the source location. For this purpose, we take M = 20 quadrature points for the line image integrals, and four different inverse Debye screening lengths λ = 0.5, 1, 5 and 50. We remark that usually 2–4 quadrature points can keep the approximation to the line image integral within a very small error [6], and thus 20 discrete images can be regarded as an exact calculation of the line image. The errors of the three approaches are shown in Fig. 1. It is seen that at low ionic concentrations (λ = 0.5 and 1), the second-order approaches A and C have less errors than the first-order approach B. Approaches A and C have almost the same performance. The errors increase gradually when the source location r_s tends to 1. However, the overall errors of Approach C are less than 0.1%, and in contrast, the original method (Approach A) has some errors greater than 0.1% with r_s close to 1 for λ = 1. With the increase of λ, the merit of the new method is clearer. At λ = 5, the largest error of the original method is bigger than 1% while those of Approaches B and C are 0.73% and 0.56%, respectively. In particular, when λ is very large (λ = 50), the advantage of the new method is much more clear. Approaches B and C have almost the same behavior when r_s is close to 1, and their largest errors are both less than 0.4%. In comparison, Approach A has the largest error over 3% which is unacceptably large in many practical simulations.

Fig. 1.

Accuracy comparison for the methods vs. the source location r_s. A, B and C, respectively, represent the original method, the new method without correction term and the new method with one constant correction term.

4.2. Accuracy of new discrete multiple image approximations

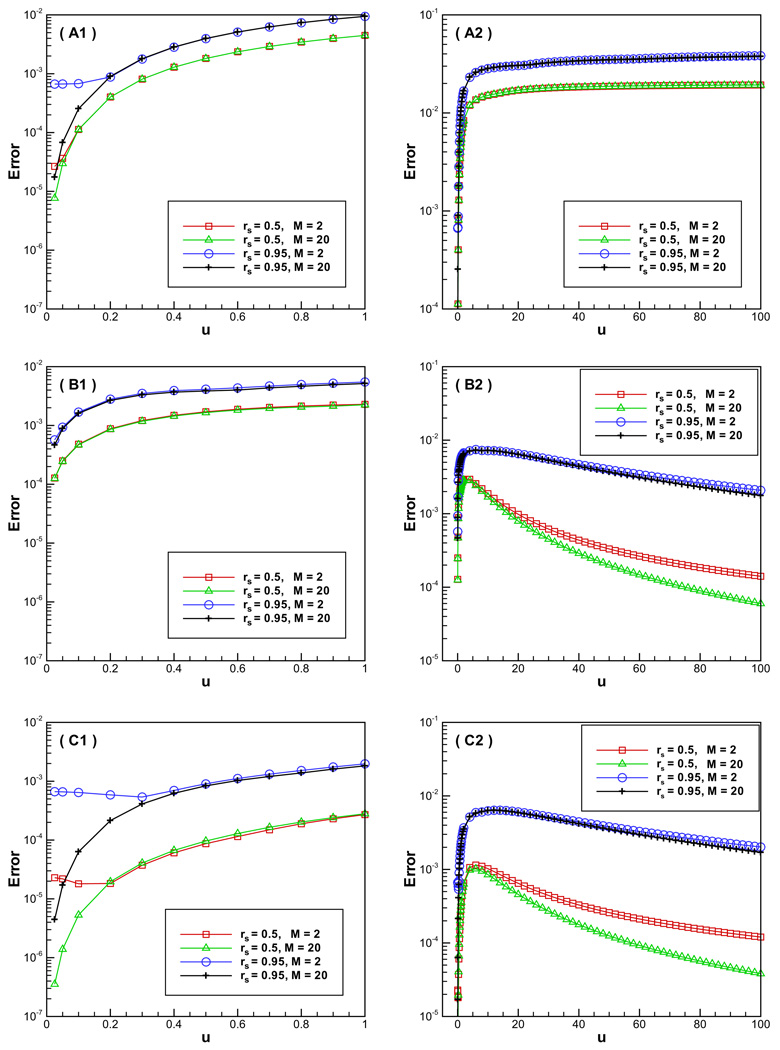
To investigate the accuracy of discrete multiple image approximations in relation to the inverse Debye screening length λ, we use two different charge locations r_s = 0.5 and r_s = 0.95. For each value of u = λa, we take M = 2 and 20 quadrature points (corresponding to 2 and 20 image charges), respectively. A comparison of accuracy with the increase of u is made in Fig. 2. As predicted from analysis, we can see that the new image methods perform well for large u; an almost second-order of convergence is confirmed numerically. On the other hand, although using 20 discrete image charges can achieve better accuracy, the errors with only two image charges are already small. The results agree with those of Table 2 in Ref. [9], indicating that only several image charges are needed to achieve high accuracy in the reaction field with the multiple image charge approximations. More importantly, the original method does not converge with the increase of u. It has an error over 1% for both r_s = 0.5 and 0.95 for a relatively large u, and for r_s = 0.95 the errors are even over 3% when u reaches 20. Thus, the original method will produce inaccurate results for solvents with high salt effects. Moreover, the new methods work as well for u < 1. In particular, Approach C with one correction term has smaller errors than Approach A does, and they are both second-order accurate with respect to u for M = 20. Though it should be noted that for M = 2 the accuracy for both the original method (Approach A) and the new method (Approach C) does not decrease further as u tends to zero. This is due to the fact that the discretization error of the line image integral by M = 2 quadrature points becomes the dominating error while the asymptotic error O(u²) becomes negligible. Still the overall errors for the reaction fields are less than 0.1%.

Fig. 2.

Accuracy comparison for the methods vs. u = λa where a is fixed to be 1. A, B and C, respectively, represent the original method, the new method without correction term and the new method with one constant correction term. Left: u ε [0, 1]; right: u ε [0, 100].

As expected, the new methods should have their worst performance for u ≈ 1. Still, they are superior to the original one, as seen in Fig. 2. An error less than 0.8% for r_s = 0.95 is usually acceptable in applications for both Approaches B and C with M = 2. Even when r_s reaches 0.99, additional tests show that the error is less than 1% for both cases. Moreover, we can always obtain better approximation by adjusting the size of the sphere in the hybrid explicit/implicit solvent bio-molecular simulations to avoid the situation of u ≈ 1, of course at the expense of a larger simulation system inside the sphere when the size of the sphere is increased.

5. Conclusions

In this paper, high-order accurate multiple discrete image charge approximations have been extended to calculate the reaction field inside a dielectric spherical cavity immersed in a continuum solvent of arbitrary ionic strength. These approximations can be used for rapid and accurate electrostatic computations of large molecules in solvent with high salt effects. Numerical results confirm the validity and improved performance of the new image charge approximations for the whole range of ionic strength of the solvent.