Validating CHARMM parameters and exploring charge distribution rules in structure-based drug design

Abstract

Using an extensive series of TIBO compounds that are non-nucleoside inhibitors of HIV-1 reverse transcriptase, we have systematically evaluated the quality of recently developed ligand parameters that are consistent with the CHARMM22 force field. Thermodynamic integration simulations for 44 pairs of TIBO compounds achieve a high level of success with an overall average unsigned error (AUE) in the relative binding affinities of 1.3 kcal/mol; however, the accuracy is strongly dependent on the size differential between the substituents sampled as well as the class of functional group. Low errors are observed among the alkyl, allyl, aldehyde, nitrile, trifluorinated methyl, and halide TIBO derivatives and large systematic errors among thioether derivatives. We have also investigated how different charge assignment schemes for small molecules impact the quality of computed binding affinities for a subset of this series. This study demonstrates the advantage of using model compounds to derive physically meaningful charge distributions and bond-charge increments for rapidly expanding fragment libraries for drug development applications. Specifically, in the absence of a bond-charge increment for a given pair of atom types, the strategy of adopting CHELPG charges from localized regions of model compounds provides reliable results when modeling with the CHARMM force field.

Introduction

Computational methods have become important resources in structure-based drug design^1,2. Three-dimensional structures can be used to model the interactions between protein targets and potential new drugs and to predict their binding free energies^3–5. Empirical all-atom force fields that are used to represent proteins in these simulations have matured to a significant level^6,7. However, due to the enormity of chemical space, it is still challenging to develop force field parameters that cover a wide range of compounds that might be encountered in drug design and development efforts⁷.

Ligand parameterization procedures are traditionally computationally intensive and can represent a bottleneck in structure-based drug design strategies. To develop force field parameters that are tailored for a new compound, the specific parameters required for the intra- and intermolecular energy terms must be optimized. This process may require several iterations until the parameters yield appropriate conformational energies, hydration free energy, dipole moment or other molecular properties of the modeled compound. These ligand parameterization efforts may be accelerated if information about well-parameterized compounds can be leveraged to describe new compounds under investigation. However, individual force fields have been developed with different philosophies which means that, in general, ligand parameters are not immediately transferable among the biomolecular force fields^8,9.

Each of the major biomolecular force fields have programs that read in the coordinates of a compound and assign atom types, partial charge distributions and energy parameters based on information in template libraries^10–15. For example, the molecular modeling package IMPACT¹⁰ and the utility software script, hetgrp_ffgen (Schrödinger, LCC), as well as the BOSS and MCPRO¹⁶ molecular modeling systems (Cemcomco, LLC) facilitate modeling with the OPLS-AA¹⁷ force field; Antechamber¹¹ was developed as an auxiliary program in the AMBER¹² molecular modeling packages; PRODRG^13,14 prepares ligands for modeling with the GROMOS force field¹⁸; and the recently developed MATCH suite of tools (unpublished, D.J. Price and C.L. Brooks III) constructs ligand files that are compatible with the CHARMM¹⁹ force field. The success of these automated parameterization programs depends on the extent of the classes of compounds that are covered within the template libraries, the quality of the parameters themselves and the transferability of parameters from the modeled compounds or fragment to a novel context.

Significant progress has been made to develop ligand parameters that are compatible with the CHARMM22 force field and are transferable from smaller model compounds into more complicated chemical structures. Mackerell and coworkers have most recently introduced newly optimized halide and ether parameters to this CHARMM General Force Field (CGenFF) (private communication, K. Vanommeslaeghe and A.D. Mackerell). Often, the quality of force field parameters is assessed by their ability to reproduce the hydration free energies of small molecules or thermodynamic properties of bulk solutions^20–23. However, the primary end-use of these ligand parameters is to model the interactions between putative drug compounds and larger biomolecules, like proteins and nucleic acids. In this study, we will evaluate a variety of CGenFF parameters for their ability to reproduce relative binding affinities for a series of compounds. To our knowledge, this work represents the first large-scale assessment of the quality of CGenFF parameters in the context of binding free energy calculations.

We have chosen the TIBO class of non-nucleoside inhibitors of HIV-1 reverse transcriptase (RT) because of the availability of extensive experimental data and because it has been used in a variety of contexts^24–26 as a benchmark for evaluating the quality of free energy models using AMBER and OPLS-AA force fields. Specifically, Linear Interaction Energy (LIE) models as well as molecular dynamics simulations coupled with MM-PBSA simulations have also achieved high levels of success in computing absolute binding affinities for series of these TIBO-like compounds bound to HIV-1 RT. Smith et al.²⁵ examined 12 TIBO derivatives using the OPLS-AA force field and their best linear response approximation models obtained root-mean squared errors of 0.9 kcal/mol; though no test set was included to provide a more unbiased estimate of the uncertainty in the calculations. Wang et al.²⁴ tested this same set of 12 compounds and with molecular dynamics and MM-PBSA calculations governed by the AMBER force field predicted binding affinities with errors on the order of ∼1 kcal/mol and the largest error was 1.9 kcal/mol. Su et al.²⁶ computed binding affinities for 37 TIBO compounds using the OPLS-AA force field and achieved average LIE model errors as low as 1.2 kcal/mol for predicting the binding affinity of one compound given the LIE parameters that were fit to the remaining 36 compounds. The high quality of these results irrespective of method and force field suggests that the HIV-1 RT:TIBO system is relatively well-behaved and, thus, serves as a good benchmark for evaluating the quality of new ligand parameters. In contrast to these previous studies, we perform series of thermodynamic integration calculations so that we can readily identify systematic errors that relate to specific classes of compounds and ascertain where improved force field parameters are warranted and so that we do not need to estimate entropy contributions.

Charge distribution rules in structure-based drug design

Arguably, partial charges are the most difficult ligand parameters to transfer among force fields or to adopt from other “known” molecules within a given force field due to their dependence on their local bonded environment. Yet, assigning appropriate charge distributions in novel compounds is of profound importance in effectively representing the nonbonded interactions in binding free energy calculations²⁷. Atomic partial charges are the primary components of the electrostatic energy terms and are critical for adequately describing the correct desolvation penalty when a small molecule is transferred from solution into a binding pocket. Certainly polarization effects influence the magnitude of the desolvation penalty as well as the strength of the protein-ligand interaction energy and will play a more significant role in the presence of larger differences in the dielectric properties between the solvent and the binding pocket. While polarizable force fields are being developed^28,29, most biomolecular force fields rely predominantly on fixed-charge models.

Two main strategies have been suggested for generating partial charge assignments that are compatible with current biomolecular force fields. In one fixed-charge strategy, charges are adopted for an entire molecule, often based on ab initio calculations. For example, a restrained electrostatic potential (RESP) charge fitting procedure or a semi-empirical method that mimics these charge distributions is advised for assigning partial charges to novel ligands in a manner that is consistent with the Generalized AMBER force field (GAFF)^30,31. Systematic studies using Lennard-Jones parameters from the OPLS or AMBER force fields demonstrated that partial charge distributions that were fit to electrostatic potentials (ESP) or scaled CM1A partial charges yield hydration free energies for small molecules that have average errors on the order of 1 kcal/mol^21–23. However, several chemical classes, especially the more polar compounds, exhibit larger individual errors. The largest unsigned error observed for solvation free energies modeled by GAFF using semi-empirical AM1 charges with Bayly and coworkers’ parameterized bond-charge corrections (AM1-BCC) was about 3 kcal/mol²² while the results for the OPLS-AA force field with the Cramer/Truhlar CM1A charge model scaled by 1.14 led to maximal errors of about 2.5 kcal/mol²¹.

In the second fixed-charge strategy, generally employed by CHARMM and OPLS-AA force fields, bond charge increment (BCI) “rules” are employed such that optimal charges are determined for fragments of molecules and then these fragments are pieced together to construct charge distributions for novel compounds³². In addition to variations in the specific force field parameters, these programs differ in how the bonded environment is determined, how the specific BCI rules are defined for matching the fragments in the new molecule with those “known” fragments and how excess charges are distributed throughout the molecule.

In developing these libraries of fragments, it is important to ascertain whether more automated processes could effectively determine charge distribution for the fragments themselves and where these optimization strategies could be transferable across a variety of functional groups. In addition, it is imperative that sufficient information about the charge distributions from these well-parameterized fragments be included to adequately describe new compounds under investigation. If too little information about the chemical context of the fragment is included, properties of the subsequent compounds may lack appropriate specificity and binding affinities may be unreliable. On the other hand, if too much specificity about the chemical context is required then the modeled fragments become less transferable to new compounds. Both of these issues are addressed in this study in attempts to focus subsequent ligand parameterization efforts.

In the present manuscript we examine the range of questions discussed above. First, we validate a variety of CGenFF parameters for use in structure-based drug design. Thermodynamic integration (TI) simulations are used to compute the relative binding affinities for select pairs of these 21 TIBO derivatives. These TIBO compounds possess a common chemical core structure and only differ from one another at one of two substituent sites. Therefore, systematically evaluating this series of compounds mimics a chemical optimization strategy in which various substituents or fragments are evaluated at specific sites on a promising new therapeutic lead compound.

Second, we explore the effect of different charge distribution rules in structure-based drug design for constructing new bond-charge increments. Four charge distribution schemes are investigated to determine what features of the charges of the constitutive fragments contribute to the accuracy of the computed binding affinities of the TIBO derivatives. These schemes differ in how the charges are assigned and the extent to which a given fragment influences that charge distribution in the rest of the molecule.

Methods

Ligand set and experimental binding affinities

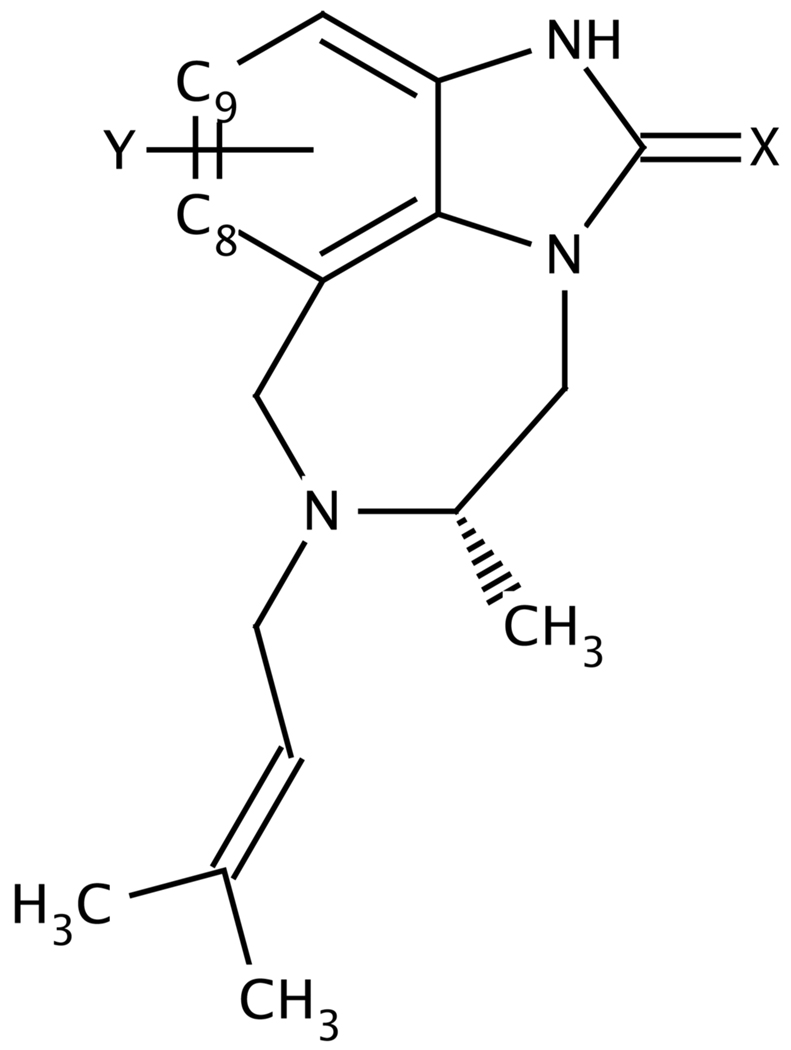
Figure 1 and Table 1 show the molecular structures and the experimental binding free energies of the 21 TIBO compounds that were included in these calculations. These ligands and their corresponding IC₅₀ values were compiled from Ho et al.³³ and Smith et al.²⁵. Differences among the compounds are limited to two variations at the X site (C=O and C=S) and 14 variations at the Y site (alkanes, alkynes, halides, trifluorinated methyls, nitriles, aldehydes, ethers and thioethers) on the TIBO core.

Figure 1.

The TIBO core structure.

Table 1.

Molecular structures and the corresponding experimental IC₅₀ and binding free energies of the TIBO analogues.

Compound	X	Ya	IC50b(µM)	ΔGbindingc (kcal/mol)
1	S	Br	0.0030	−12.09
2	S	Cl	0.0043	−11.87
3	S	SCH3	0.0050	−11.78
4	S	F	0.0058	−11.69
5	S	CH3	0.0136	−11.16
6	S	9-F	0.0250	−10.79
7	S	CCH	0.0296	−10.69
8	S	9-Cl	0.0340	−10.60
9	S	OCH3	0.0340	−10.60
10	S	H	0.0440	−10.44
11	S	I	0.0474	−10.39
12	O	Br	0.0473	−10.39
13	S	CN	0.0563	−10.29
14	O	I	0.0880	−10.01
15	S	CHO	0.1880	−9.54
16	O	CCH	0.4376	−9.02
17	S	9-CF3	0.4850	−8.96
18	O	CH3	0.9890	−8.52
19	O	CN	1.1396	−8.43
20	O	H	3.1550	−7.81
21	O	9-CF3	5.9190	−7.42

^aY is attached to C8 unless otherwise indicated.

^bref²⁵,³³

^bcalculated from ΔG_binding=RTlnIC₅₀ at 310 K.

Binding free energy calculations

Relative binding free energies were computed via thermodynamic cycles by performing TI simulations for pairs of ligands both in solvent and while bound to the non-nucleoside reverse transcriptase inhibitor (NNRTI) binding pocket in HIV-1 RT. For the solvation simulations, the hybrid molecule was solvated in a 20 Å cubic box of TIP3P³⁴ water molecules and periodic boundary conditions were employed. For the bound simulations, the pdb structure, 1TVR³⁵, was truncated so that only residues within ∼20 Å of the crystallographic TIBO compound were retained and the truncated protein-ligand system was solvated in a 37 Å sphere of water. Stochastic boundary conditions using a solvent boundary potential³⁶ of 25 Å with a 5 Å buffer region were employed; 244 and 6101 water molecules were explicitly included in the solvated and bound simulations respectively. A non-bonded cutoff of 15 Å was used and van der Waals switching and electrostatic force shifting functions were implemented between 10 Å and 12 Å. In all simulations, the temperature was maintained near 310 K by coupling the water molecules to a Langevin heat bath using a frictional coefficient of 62 ps⁻¹. Hydrogen bonds were restrained using the SHAKE³⁷ algorithm and the time step was 2 fs. Heating phases were 10 ps regardless of the environment while equilibration phases were 30 and 60 ps for the solvated and bound simulations respectively. The production runs were 300 ps and the coordinates were saved every 300 steps. Simulations were performed for 11 different λ values: 0.025, 0.05, 0.1, 0.2, 0.3, 0.5, 0.7, 0.8, 0.9, 0.95, and 0.975. Linear scaling by λ applied to all energy terms except the bond and angle terms which were treated at full strength regardless of λ value. All simulations were performed in triplicate and the resulting mean and standard deviations are reported. All calculations were performed using the BLOCK module in the CHARMM molecular dynamics package v35a1 on dual 2.66 GHz Intel Quad Core Xeon processors. On a single processor, each solvated and bound simulation required 1 and 22 CPU hours respectively. Since each simulation window was generated independently from the others all simulations could be performed simultaneously on a computer cluster.

TIBO Parameter assignments

Atom types for the TIBO compounds were assigned using MATCH (unpublished, D.L. Price and C.L. Brooks III) with the extended CHARMM22³⁸ force field and CGenFF (private communication, K. Vanommeslaeghe and A.D. Mackerell). Where possible, bonded parameters which were absent in CGenFF and the CHARMM22 force field were approximated by those from the OPLS-AA force field taken from BOSSv4.2¹⁶. Bonded parameters for which there were no analogous assignments in existing CHARMM of BOSS parameter files were obtained by fitting ab initio energy calculations from Gaussian 03³⁹. Equilibrium bond lengths, angles and dihedral were determined by energy minimization of the corresponding molecular fragments at the MP2 level of theory using the 6–31G* basis set. The respective force constants were determined by systematically distorting the structures away from the optimal values at the MP2 level of theory. Van der Waals energy parameters (i.e. atomic radii, r_i, and energy well-depths, ε_i) were taken from analogous atom types in CHARMM22 and CGenFF.

Initial TIBO Charge assignments

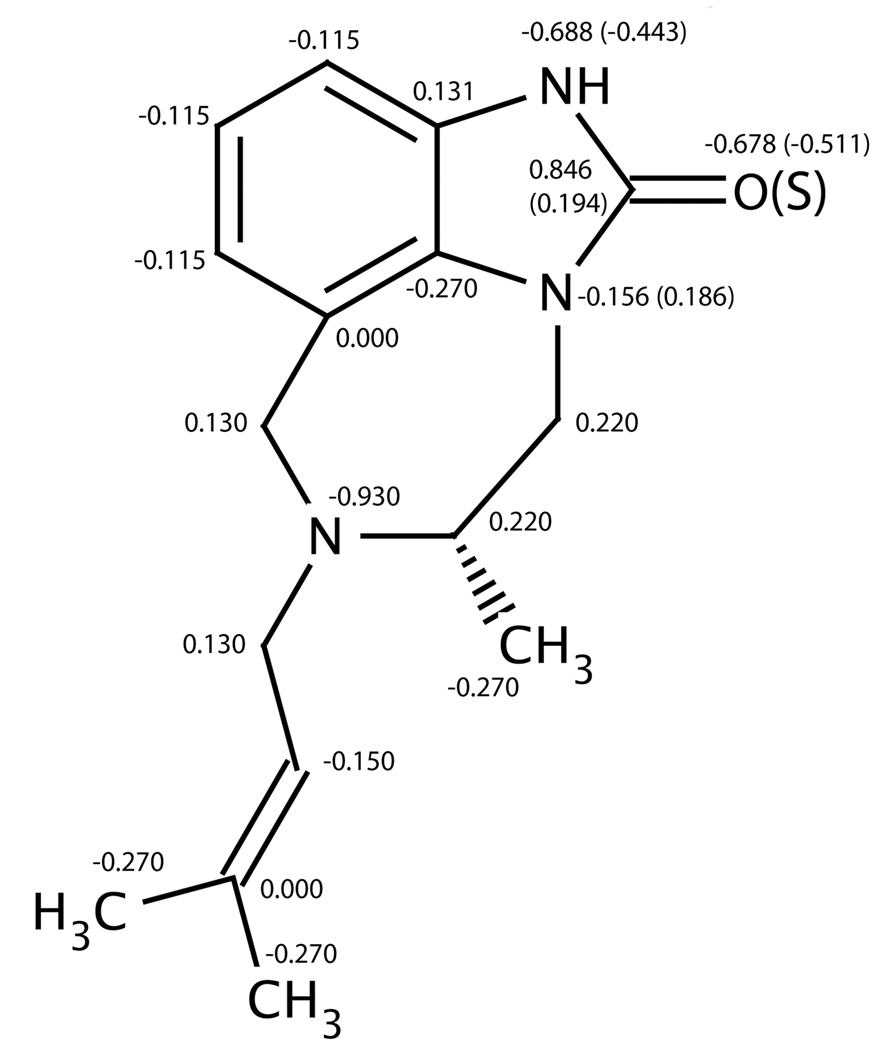
Initial partial charges were assigned using MATCH with the extended CHARMM22³⁸ force field and CGenFF. Partial charges for most of the Y-site fragments (i.e. hydrogen, alkyl, halides, aldehydes and ethers) were adopted from their corresponding benzene derivatives. Partial charges for the nitrile and trifluorinated methyl fragments were adopted from alkylated derivatives. No optimized partial charges existed for the allyl and thioether fragments, so they were estimated from CHARMM parameters for alkene and methoxybenzene derivatives respectively. CHARMM22 did not have a template which corresponded to the C=S fragment, so pairs of molecules that differed only at the X site (i.e. X=O or S) were geometry-optimized in Gaussian 03 at the MP2/6–311+G** level of theory and partial charges were fit to the electrostatic potential using the CHELPG algorithm (Breneman and Wiberg 1990). The largest differences in the CHELPG assigned partial charges (i.e. Δq_O→!S>0.2e) between pairs of compounds were localized in five atoms in the five-member ring (H-N-C(=O/S)-N), therefore the partial charges of these five atoms in the X=O and X=S TIBO derivatives were approximated directly from the CHELPG charges. The charge assignments for the TIBO core are illustrated in Figure 2.

Figure 2.

Initial partial charges assigned for heavy atoms on the TIBO core with X=O and Y=H. Partial charges associated with X=S are labeled in parenthesis. Hydrogen atoms bonded to alkanes, alkenes, and aromatic carbons have partial charges of 0.09e, 0.150e and 0.115e respectively. The amide hydrogen has partial charges of 0.415e with X=O and 0.313e with X=S.

Alternate fragment charge assignments: CHELPG

Partial charges for four Y fragments (i.e. Y=CN, CHO, OCH₃ and SCH₃) were reassigned based on CHELPG assigned partial charges for MP2/6–311+G**geometry-optimized structures of the corresponding benzene derivatives in Gaussian 03. In “CHELPG2” simulations, the charges of the Y fragment atoms along with the charge of the ipso carbon atom were re-assigned. In “CHELPG4” simulations, the charges of the ortho carbons and hydrogen atoms were also re-assigned. The CHELPG partial charges for a given benzene derivative were uniformly offset such that the sum of the re-assigned charges equaled zero. The re-assigned charges are listed in Table 4. (note: the “2” denotes fragment+ipso site and the “4” denotes fragment+ipso site+2 ortho sites)

Table 4.

Effect of the partial charge distributions on the quality of the computed relative binding free energies: Errors in the computed relative binding free energies are reported in kcal/mol (ΔΔG_calc-ΔΔG_expt).

		Errors in Charging schemes
Ligand 1 X, Y	Ligand 2 X, Y	Initial	CHELPG2	CHopt2	CHELPG4	CHopt4	Control
O, H	O, CN	1.50	−0.23	0.03	1.73	1.63	4.18
O, CH3	O, CN	1.80	−0.08	0.91	1.95	1.01	3.16
S, H	S, CN	−0.28	0.05	−0.73	0.33	0.18	3.44
S, CH3	S, CN	−0.93	−0.97	−0.96	−0.42	−0.59	2.08
O, CN	S, CN	0.03	−0.15	−0.28	0.42	−2.95	−2.70
	AUE(Y=CN):	0.9	0.3	0.6	1.0	1.3	3.1
S, H	S, CHO	0.25	1.40	1.87	3.04	0.39	4.50
S, CH3	S, CHO	−2.16	−1.30	−2.05	−0.14	−0.19	1.23
	AUE(Y=CHO):	1.2	1.4	2.0	1.6	0.3	2.9
S, H	S, OCH3	2.66	1.79	2.15	2.14	3.31	3.83
S, CH3	S, OCH3	0.48	0.92	−0.15	0.39	0.28	3.09
	AUE(Y=OCH3):	1.6	1.4	1.2	1.3	1.8	3.5
S, H	S, SCH3	5.38	2.72	3.26	4.05	3.91	5.39
S, CH3	S, SCH3	3.05	2.04	2.56	2.73	2.94	4.22
	AUE(Y= SCH3):	4.2	2.4	2.9	3.4	3.4	4.8

Alternate fragment charge assignments: CHopt

Based on the strategy outlined by MacKerell et al.³⁸ for parameterizing ligands to be consistent with the CHARMM22 force field, the partial charges of the same four fragments at the Y site (i.e. Y=CN, CHO, OCH₃ and SCH₃) were optimized in the context of the corresponding benzene derivatives to yield molecular properties that were consistent with experimental hydration free energy data⁴⁰ as well as components of the dipole moment. The dipole moments were obtained in Gaussian 03 at the HF/6–31+G* level of theory and were scaled by 15%.

A Monte Carlo (MC) sampling strategy was employed in CHARMM in which many configurations of partial charges were evaluated for the atoms in the benzene derivative. In “CHopt2” simulations, the charges of the Y fragment atoms, along with the charge of the ipso carbon atom were optimized. In “CHopt4” simulations, the charges of the ortho carbon and hydrogen atoms were also optimized. Partial charges of each of the atoms of interest were sampled such that each −1e<q_i<1e (note: methoxy- and thiomethoxy- hydrogen atoms retained their charge of 0.09e throughout). Once trial partial charges were assigned, the components of the dipole were computed and the atomic coordinates were minimized in vacuum for 100 steps using the Adopted Basis Newton-Raphson algorithm and then re-minimized for 100 steps using Steepest Descent algorithm using the GBMV implicit solvent model^41,42. The hydration free energy was approximated as the difference between the solvent and vacuum energy minima²⁰. The scoring function, S, for each configuration of partial charges, q, was defined by:

$$S_q=\frac{{(\mathrm{\Delta }\mathrm{\Delta }{G}_{hydr}^q-\mathrm{\Delta }\mathrm{\Delta }{G}_{hydr}^{\text{target}})}^2}{2{\sigma }_{\mathrm{\Delta }\mathrm{\Delta }G}^2}+\frac{{({\mu }_x^q-{\mu }_x^{\text{target}})}^2+{({\mu }_y^q-{\mu }_y^{\text{target}})}^2+{({\mu }_z^q-{\mu }_z^{\text{target}})}^2}{2{\sigma }_{\mu }^2}$$

where ΔΔG_hydr denotes the hydration free energy relative to benzene and μ_x, μ_y and μ_z are the components of the molecular dipole (σ_ΔΔG=0.25 kcal/mol and σ_μ=0.25 D). The scoring function for CHopt4 optimizations included additional restraints to keep the partial charges near the initial MATCH-or CGenFF-assigned partial charges by imposing a fixed penalty of 5.5 whenever a trial partial charge deviated more than 0.1e from the initial charge. 40 000 trial configurations were sampled and trial configurations were accepted with probability, P:

$$P=\text{min}\left(1,{\text{exp}}^{-\left(\frac{S_{trial}-S_{previous}}{k_{B}T}\right)}\right)$$

The effective temperature, k_BT, was gradually decreased every n steps using an exponential cooling schedule such that, k_BT_t+1=ak_BT_t. The initial temperatures and cooling schedules were optimized to ensure that the best-scored solutions were not dependent on the initial charge assignments (i.e. CHopt2: n=500, k_BT₀=200 and a=0.75; CHopt4: n=1000, k_BT₀=20 and a=0.9). The charge distributions that yielded the lowest-scored solutions were identified as the CHopt2 and CHopt4 charge models. The charge distribution that yielded the most poorly scored solution sampled was used as the “control” charge distribution.

Results & Discussion

Overall high quality of computed binding affinities

Relative binding affinities were computed for 44 pairs of TIBO compounds (Table 2). This dataset encompasses 21 unique TIBO molecules and includes all transformations from Y=H and Y=CH₃. Eleven additional pairs were assessed: seven pairs that involved Y=halide→halide transformations and four pairs that involved X=O→S transformations. All possible combinations of pairwise relative binding affinities among the 21 TIBO compounds could theoretically be reconstructed from these representative calculations.

Table 2.

Quality of computed binding free energies^a using thermodynamic integration for a selection of pairs of TIBO compounds.

Pair No.	Ligand 1 X, Y	Ligand 2 X, Y	ΔΔGexpt	ΔΔGsolv		ΔΔGbound		ΔΔGcalc	Error
				mean	stddev	mean	stddev
1	O, H	O, CH3	−0.71	0.18	0.12	0.73	1.21	0.55	1.26
2	S, H	S, CH3	−0.72	0.05	0.17	1.10	0.41	1.05	1.77
3	O, H	S, H	−2.63	3.75	0.17	1.92	0.43	−1.83	0.80
4	O, CH3	S, CH3	−2.64	3.98	0.07	1.67	0.50	−2.31	0.33
5	O, H	O, CCH	−1.21	14.44	0.22	13.10	0.26	−1.34	−0.13
6	S, H	S, CCH	−0.25	14.66	0.14	13.93	0.60	−0.73	−0.48
7	O, CH3	O, CCH	−0.50	14.63	0.08	14.09	1.10	−0.54	−0.04
8	S, CH3	S, CCH	0.47	15.03	0.10	15.33	0.62	0.30	−0.17
9	S, H	S, F	−1.25	3.30	0.07	3.29	0.37	−0.01	1.24
10	S, 9H	S, 9F	−0.35	−9.31	0.07	−9.33	0.68	−0.03	0.32
11	S, CH3	S, F	−0.53	2.50	0.05	0.00	0.27	−2.50	−1.97
12	S, F	S, Cl	−0.40	−0.88	0.08	0.34	0.26	1.23	1.63
13	S, 9F	S, 9Cl	0.19	2.44	0.02	2.56	0.26	0.12	−0.07
14	S, H	S, Cl	−1.43	2.04	0.05	3.16	0.24	1.12	2.55
15	S, 9H	S, 9Cl	−0.16	−7.35	0.02	−6.90	0.44	0.45	0.61
16	S, CH3	S, Cl	−0.71	1.47	0.03	0.52	0.13	−0.95	−0.24
17	S, Cl	S, Br	−0.22	−0.08	0.02	0.79	0.31	0.87	1.09
18	O, H	O, Br	−2.58	3.55	0.11	4.63	0.60	1.08	3.66
19	S, H	S, Br	−1.65	1.62	0.19	2.53	1.01	0.91	2.56
20	O, CH3	O, Br	−1.87	3.20	0.08	2.99	0.14	−0.21	1.66
21	S, CH3	S, Br	−0.93	1.23	0.04	1.65	0.52	0.42	1.35
22	O, Br	S, Br	−1.70	3.77	0.02	1.90	0.21	−1.87	−0.17
23	O, Br	O, I	0.38	−0.76	0.03	0.05	0.05	0.81	0.43
24	S, Br	S, I	1.70	−0.50	0.08	−0.21	0.31	0.29	−1.41
25	O, H	O, I	−2.20	2.49	0.09	4.64	0.88	2.15	4.35
26	S, H	S, I	0.05	0.53	0.10	3.14	0.46	2.61	2.56
27	O, CH3	O, I	−1.49	2.33	0.01	2.97	0.47	0.64	2.13
28	S, CH3	S, I	0.77	0.63	0.16	1.76	0.33	1.13	0.36
29	O, I	S, I	−0.38	3.52	0.12	2.40	0.30	−1.11	−0.73
30	O, 9H	O, 9CF3	0.39	2.68	0.19	4.10	0.19	1.41	1.02
31	S, 9H	S, 9CF3	1.48	2.65	0.17	4.64	0.13	1.99	0.51
32	S, 9F	S, 9CF3	1.83	12.95	0.11	14.62	0.09	1.68	−0.15
33	S, 9Cl	S, 9CF3	1.64	10.69	0.04	12.70	0.33	2.01	0.37
34	O, H	O, CN	−0.62	8.42	0.20	9.30	0.81	0.88	1.50
35	S, H	S, CN	0.15	8.62	0.08	10.57	1.34	1.95	1.80
36	O, CH3	O, CN	0.09	8.68	0.05	8.49	0.52	−0.19	−0.28
37	S, CH3	S, CN	0.87	9.16	0.09	9.10	0.31	−0.06	−0.93
38	O, CN	S, CN	−1.86	4.00	0.18	2.17	0.21	−1.83	0.03
39	S, H	S, CHO	0.90	7.23	0.06	8.38	0.87	1.15	0.25
40	S, CH3	S, CHO	1.62	7.27	0.11	6.73	0.34	−0.54	−2.16
41	S, H	S, OCH3	−0.16	9.03	0.08	11.53	0.97	2.50	2.66
42	S, CH3	S, OCH3	0.54	9.31	0.18	10.33	0.87	1.02	0.48
43	S, H	S, SCH3	−1.34	2.48	0.04	6.53	0.29	4.04	5.38
44	S, CH3	S, SCH3	−0.62	3.10	0.12	5.52	0.35	2.43	3.05

^aMeans and standard deviations are reported for three independent sets of simulations where each set includes 11 simulations at λ values: 0.025, 0.05, 0.1, 0.2, 0.3, 0.5, 0.7, 0.8, 0.9, 0.95, and 0.975.

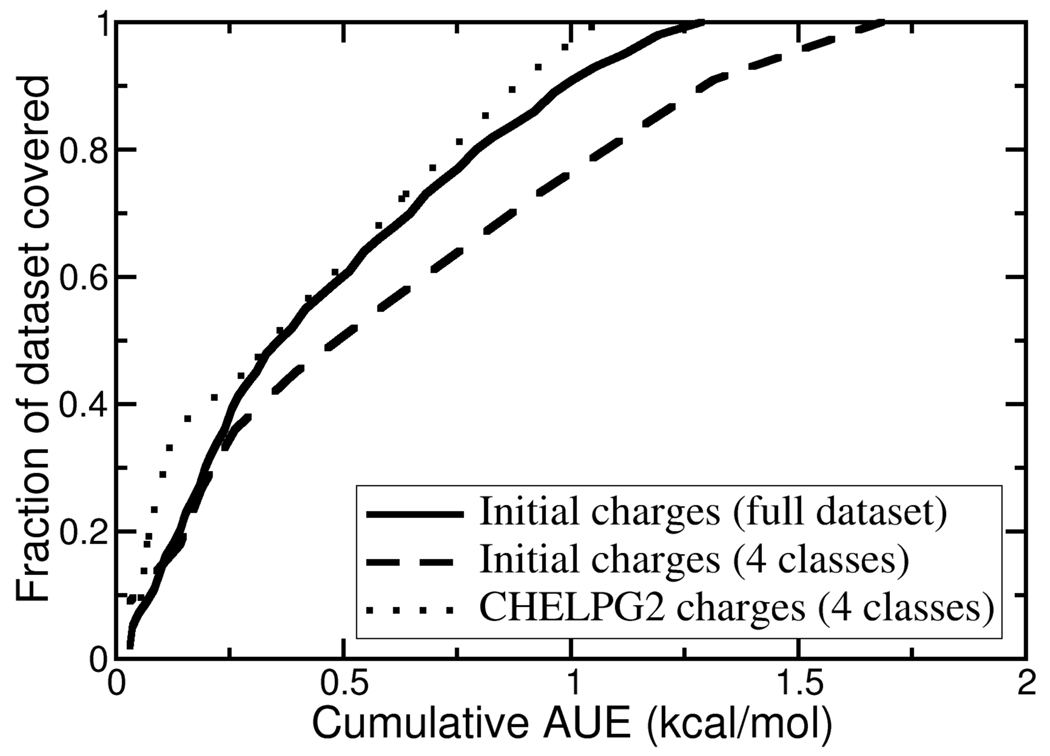
The average unsigned error (AUE) for the entire dataset is 1.29 kcal/mol and half of the TIBO pairs have computed binding affinities with individual errors of less than 1 kcal/mol while the maximum unsigned error (MUE) is 5.38 kcal/mol. Figure 3 illustrates that by ranking the TIBO pairs by their difference in the predicted relative to the experimental binding free energy, the cumulative AUE for the top 89% of the dataset is less than 1 kcal/mol. Computed binding affinities in this study have uncertainties on the order of −0.7 kcal/mol (Table 2). The majority of the simulations of the solvated ligands show standard deviations of less than 0.2 kcal/mol; most of the bound simulations show increased diversity yet with standard deviations of less than 0.6 kcal/mol. Based on a comparison between computed and experimental hydration free energies of small molecules, Mobley et al.²² suggest that it will be difficult with current force fields to achieve average errors in binding affinities of less than 1 kcal/mol. Furthermore, it is estimated that experimental binding affinities have uncertainties of ∼0.5 kcal/mol³. Therefore, a cumulative AUE in our study of 1 kcal/mol represents quite a conservative threshold of “success”.

Figure 3.

Cumulative errors in computed binding affinities for pairs of TIBO compounds ordered by absolute error. The full dataset includes all 44 pairs of TIBO compounds listed in Table 2. The “4 classes” includes 11 pairs of TIBO compounds (pairs 34 through 44 in Table 2) which involve transformations for Y=CN, CHO, OCH₃ or SCH₃.

Reproducibility of binding free energies is size- and class-dependent

Large differences in the substituent size between pairs of compounds provides a more challenging context for adequately sampling relevant protein conformations in free energy calculations. Indeed, in this study, both the precision and the accuracy are deleteriously affected for simulations that involve large size differentials in the TIBO derivatives. Among most of the 11 pairs of TIBO derivatives whose transformations are less conservative in size (i.e. where the transformation at the Y-site involves an addition of more than one heavy atom or a transformation from H→Br or H→I), their standard deviations for simulations of the bound “arm” of the thermodynamic cycle are significantly larger than those for more conservative transformations. The AUE for simulations modeling larger size differentials is 2.3 kcal/mol whereas the AUE for simulations involving more conservative transformations at the Y-site is 1.0 kcal/mol. These systematic errors are likely related to the λ-scaling scheme that was used in the TI calculations⁴³. For example, simulations involving large substituent size differentials, the values of the integrand, ∂H/∂λ, and their standard deviations from independent trajectories at very low and very high λ, values (i.e. λ=0.025 and 0.975) are significantly larger than for those simulations involving substituents that are more similar in size. For structure-based drug design applications, longer simulation trajectories and more extensive soft-core scaling techniques⁴⁴ may be required to achieve adequate sampling with the anticipation of improving the quality of the estimated binding affinities.

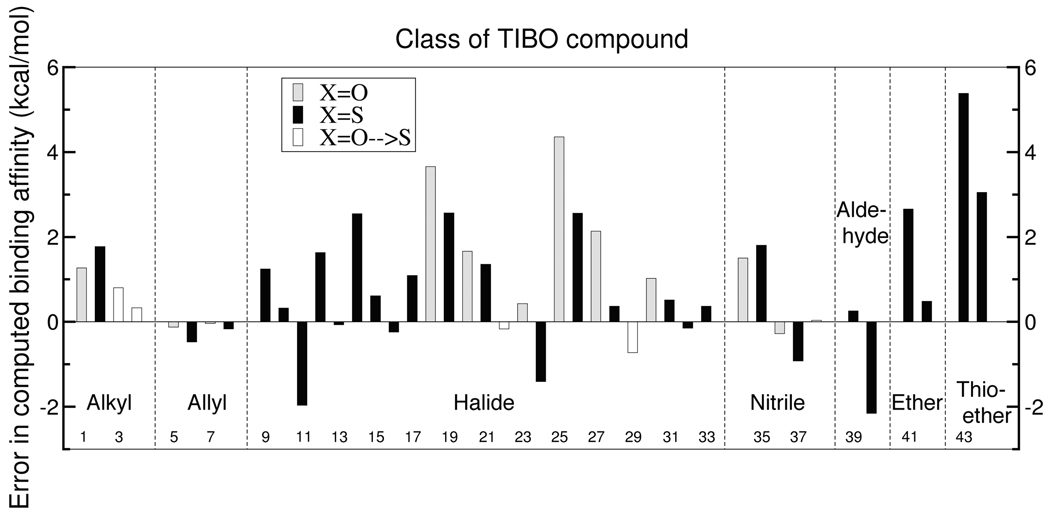
Representatives from all classes of functional group at the Y-site, except for the thioether moiety, reliably reproduce experimental binding affinities for the TIBO NNRTIs. Figure 4 depicts the free energy errors for chemical transformations by functional group at the Y-site. A positive error indicates that the hydrogen or methyl TIBO derivative in the transformation (or the smaller halide in the case of Y=halide→halide transformations or oxygen in the case of X=O→S transformations) is overfavored relative to experiment. The eight pairs of compounds that contain only hydrogen, alkyl and allyl groups at the Y site have individual errors that are less than 1.8 kcal/mol and have an AUE of 0.6 kcal/mol. The thirteen pairs of compounds which contain either fluoride, chloride or trifluorinated methyl groups at the Y position demonstrate random errors in the computed binding free energies and collectively have an AUE of 0.9 kcal/mol. The quality of the modeled bromide and iodide substituents at the Y-site is degraded relative to the rest of the dataset, but this is primarily due to the large size differential in four of the simulations. The AUE of the latter four simulations which involve transformations from hydrogen to either bromide or iodide at the Y-site is 3.3 kcal/mol whereas the AUE for all other bromide and iodide transformations is 1.0 kcal/mol. The Y=H→OCH₃ transformation also suffers from a relatively large error of 2.7 kcal/mol, but the Y=CH₃→OCH₃ transformation is accurately computed with an error of 0.5 kcal/mol. The majority of the binding affinities among the nitriles and aldehydes TIBO derivatives are computed reliably with AUEs of 0.9 and 1.2 kcal/mol respectively. By contrast, simulations of pairs of compounds that contain the thioether fragment yield the largest individual and collective errors in the dataset. Specifically, the Y=H→SCH₃ and Y=CH₃→SCH₃ transformations systematically underestimate the relative binding affinities of the thioether TIBO derivative and have errors of 5.4 and 3.1 kcal/mol respectively.

Figure 4.

Errors in binding affinities enumerated by pair number (see Table 2) and categorized by identity of the Y fragment.

The success of the hydrogen and alkyl TIBO derivatives is not surprising given that these atoms have analogues in well-parameterized amino acid sidechains in the CHARMM22 force field. The high quality of the binding affinities for the halide and methoxy TIBO derivatives validates the bonded and nonbonded parameters that were recently optimized by Vanommeslaeghe and Mackerell for methoxybenzene and the halobenzenes. The consistently large and systematic errors for the thioether derivative are not surprising given that, in the absence of parameters for thiomethoxybenzene, their initial charges were estimated from methoxybenzene. This finding suggests that optimization efforts could be targeted towards improving the parameterization of the thioether TIBO derivatives.

Overall, the success of the X=O→S transformations indicates that the balance of the charge distributions between the oxygen and sulfur TIBO derivatives is reasonable. Yet, the large percentage of positive errors for transformations at the Y-site (29 out of 41 cases) suggests a systematic overfavoring of the hydrogen or methyl substituent (or the smaller halide in the Y=halide→halide transformations) relative to experiment. These predominantly represent the favoring of the smaller of the two substituents under consideration in a given simulation. This bias could be due to charges associated with the amide hydrogen that results in a strong hydrogen bond with the K101 backbone carbonyl oxygen at the mouth of the binding pocket. The strength of this hydrogen bond may prevent sufficient relaxation of the TIBO compound such that the interactions with the protein environment at the other end of the binding pocket are too restrictive and, thus, unfavorable for the bulkier substituent.

Charge optimization strategies improve thioether computed binding affinities

Based on these results, the atomic partial charges associated with the thioether fragment were targeted for further optimization. Partial charges of the nitrile, aldehyde and ether fragments were also optimized as controls to confirm the transferability of any proposed charging scheme across a variety of functional groups. To ensure that these charge distributions would be generalizable beyond the TIBO compounds, each of these four functional groups was investigated as a substituent at a single site on a benzene ring.

The four optimization strategies that have been investigated explore how the charges are assigned and the extent to which a given fragment influences that charge distribution in the rest of the molecule. In the first strategy (CHELPG), charges were adopted from the CHELPG charges that were fit to the electrostatic potential. In the second strategy (CHARMM optimization—CHopt), partial atomic charges were optimized via a Monte Carlo procedure to yield good agreement with the components of the QM molecular dipole as well as experimental hydration free energies relative to benzene. As a first approximation (CHELPG2 and CHopt2), partial charge distributions are assumed to be local in nature and, thus, charge assignments are limited to atoms in the functional group and the ipso carbon on the benzene ring. More extensive charge delocalization was also investigated (CHELPG4 and CHopt4) such that the charge assignments for each of these four functional groups was specific for the ortho carbon and hydrogen atoms on the benzene ring as well as the atoms in the functional group and the ipso carbon. (note: the “2” denotes functional group+ipso site and the “4” denotes functional group+ipso site+2 ortho sites). From the CHopt2 MC trajectories, a “control” charging scheme was identified which yielded the poorest fit to the targeted physical properties of the model benzene derivatives. Table 3 describes the molecular properties that result from these different charge distributions in the respective benzene derivatives. Table 4 summarizes the errors in the relative binding affinities that were recomputed for these four classes of TIBO derivatives.

Table 3.

Partial charge assignments from various charge optimization schemes and their respective molecular properties^a.

			Charging schemes
Benzene Substituent		Atomname/ Targets	Initial	CHELPG2	CHopt2	CHELPG4	CHopt4	Control
Y=SCH3	Charges:	CA	0.220	0.206	0.039	0.218	0.291	0.468
		S	−0.390	−0.305	−0.186	−0.292	−0.292	−0.432
		CT3	−0.100	−0.005	−0.122	0.007	−0.110	−0.305
		HA	0.090	0.035	0.090	0.046	0.090	0.090
		CA	−0.115	−0.115	−0.115	−0.185	−0.214	−0.115
		HP	0.115	0.115	0.115	0.150	0.134	−0.115
	ΔΔGhydr	−1.83 (expt)	−3.27	−1.20	−1.37	−1.86	−1.80	−5.46
	μx	−0.04 (HF)	−1.42	−1.76	−0.03	−0.65	−0.11	−4.29
	μy	1.72 (HF)	2.34	1.52	1.74	1.70	1.93	1.35
Y=CN	Charges:	CA	0.130	0.097	0.425	0.084	0.132	−0.475
		CN	0.400	0.370	−0.238	0.357	0.308	−0.451
		NC	−0.530	−0.467	−0.187	−0.480	−0.440	0.024
		CA	−0.115	−0.115	−0.115	−0.124	−0.019	−0.115
		HP	0.115	0.115	0.115	0.143	0.308	0.115
	ΔΔGhydr	−2.66 (expt)	−5.30	−3.70	−3.04	−4.47	−3.70	−5.53
	μx	−5.84 (HF)	−4.49	−3.90	−4.58	−4.13	−2.80	2.82
Y=CHO	Charges:	CA	0.120	0.051	0.252	0.055	0.177	−0.264
		CD	0.160	0.465	−0.017	0.469	0.099	0.581
		O	−0.330	−0.536	−0.332	−0.531	−0.378	−0.530
		HR1	0.050	0.021	0.098	0.025	0.092	0.213
		CA	−0.115	−0.115	−0.115	−0.152	−0.016	−0.115
		HP	0.115	0.115	0.115	0.142	0.022	0.115
	ΔΔGhydr	−3.18 (expt)	−1.98	−5.63	−3.31	−5.83	−3.30	−11.39
	μx	3.19 (HF)	2.28	3.16	2.68	3.09	2.92	3.53
	μy	−3.05 (HF)	−2.02	−2.11	−2.80	−1.78	−3.01	0.71
Y=OCH3	Charges:	CA	0.220	0.458	−0.022	0.513	0.318	0.020
		O	−0.390	−0.515	−0.093	−0.460	−0.290	−0.503
		CT3	−0.100	0.148	−0.155	0.203	−0.065	0.213
		HA	0.090	−0.030b	0.090	0.025	0.090	0.09
		CA	−0.115	−0.115	−0.115	−0.326	−0.135	−0.115
		HP	0.115	0.115	0.115	0.160	0.019	0.115
	ΔΔGhydr	−0.20 (expt)	−1.92	−2.43	−0.57	−2.17	−0.43	−7.73
	μx	0.68 (HF)	−0.75	−3.26	0.49	1.07	0.53	2.02
	μy	1.53 (HF)	1.64	1.15	0.93	1.57	1.48	2.71

^aExperimental hydration free energies (ΔΔG_hydr) relative to benzene in kcal/mol taken from ref ⁴⁰. Computed relative hydration free energies are approximated from the difference between GBMV and vacuum energy-minimized energies. Dipole moments are reported in units of Debye from the standard Gaussian 03 orientation and their HF/6-31+G* values have been scaled by 15%.

^bThe negative charges assigned to the methyoxy hydrogen atoms are a result of the offset factor used to require that the overall charge of the re-assigned atoms sums to zero.

The CHELPG2 charge distribution for thioether benzene is similar to that of the initial charges; yet, it yields a better estimate of the hydration free energy than the initial charges. When these CHELPG2 charges are transferred to the TIBO compound, there is a marked improvement in the thioether computed binding free energies; the error for each of the two thioether transformations improves by at least 1 kcal/mol when the initial charge estimates are replaced by the CHELPG2 charges. The CHopt2 charge model also has an improved fit to the experimental hydration free energy and QM dipole moment relative to the initial charge model. This charge distribution in the TIBO derivative elicits an improvement in the computed binding affinities by 0.5 to 2.1 kcal/mol relative to the initial charge, though it is not overall as favorable as the result for the CHELPG2 charge model. Increasing the scope of the charge delocalization in the CHELPG4 and CHopt4 models yields better agreement with the targeted molecular properties for the thioether benzene derivatives; yet, these charge models do not improve the computed binding affinities for the corresponding TIBO derivatives (errors of 2.7 and 4.1 kcal/mol) over the CHELPG2 and CHopt2 models. However, the quality of the CHopt4 charge model may be unduly hindered since the initial charges to which the CHopt4 partial charges are restrained were approximated from the methoxybenzene charge distribution. The “control” charge model which has the poorest agreement to the targeted molecular properties of any of the charge models exhibits the worst binding free energies when it is transferred to the TIBO compound (errors of 4.2 and 5.4 kcal/mol).

Charge optimization strategies adequate for nitriles, aldehydes and ethers

Results from the other three classes of fragments (Y=CN, CHO and OCH₃) demonstrate that charge models obtained from either schemes that fit charges to the electrostatic potential or that optimize charge distributions to mimic hydration free energies and molecular dipole moments are sufficient to compute reliable estimates of binding free energies. The AUEs for each of these four functional groups and charge models range from 0.3 to 2.0 kcal/mol. The CHELPG2 models perform favorably in which all but one computed binding free energy has an error of less than 1.4 kcal/mol. Figure 3 illustrates the significant improvement in the overall quality of the computed binding affinities for the CHELPG2 models relative to the initial charges for the functional groups investigated. The overall AUE for these 11 pairs of TIBO compounds improves from 1.68 to 1.06 kcal/mol and the MUE is reduced from 2.66 to 1.80 kcal/mol.

Even though CHELPG2 and CHELPG4 charges were assigned from the same set of CHELPG charges that were fit to the electrostatic potential of the model benzene compounds, the atomic charges differ slightly among the CHELPG2 and CHELPG4 charge sets due to approximations that were introduced to restrain the sum of the re-assigned charges to be zero. For each substituent, the CHELPG4 charges are within 0.06e of the CHELPG2 assigned charges for the fragment and the ipso carbon, though most vary by less than 0.02e. It was anticipated that these more delocalized charge distributions in the CHELPG4 models, which increase the specificity of the context of the functional group in the benzene derivatives relative to the CHELPG2 models, would improve the quality of the corresponding TIBO binding affinities. In fact, the relative to the CHELPG2 models, CHELPG4 charge distributions tend to degrade the quality of the computed binding affinities for the nitriles, aldehydes and ethers derivatives.

The alternative CHopt2 scheme for assigning localized partial charges results in charge distributions that differ substantially from the initial as well as the CHELPG2 charges; these resulting charge distributions yield relative hydration free energies and components of the QM dipole moments that are closer to the target values than either the initial or the CHELPG2 charges. We assumed that the set of charges that are optimized by this scheme would result in higher quality computed binding affinities for the respective TIBO compounds due to the increased ability of the charges to mimic physical properties of the corresponding model benzene compound. Indeed, these CHopt2 charge distributions slightly improve the binding affinities for most of the pairs of TIBO derivatives relative to the initial charge models. The one exception is the relatively large error for the Y=H!CHO transformation. Interestingly, the partial charge assignments for Y=CN and Y=OCH₃ differ by up to 0.3e relative to the initial charges, yet the high quality of the binding affinities is still achieved.

By permitting optimization of the charges of the carbon and hydrogen atoms in the ortho position, the CHopt4 partial charge assignments in the benzene derivatives yielded better agreement with the experimental hydration free energies and QM dipole moments than the CHopt2 charges. Though, restraining the partial charges to the initial charges resulted in poorer fits with the targeted molecular properties for Y=CN. With the increased ability of the charge distributions of the TIBO fragments to mimic critical molecular properties, it was assumed that the CHopt4 charges would result in greater improvements in the corresponding binding affinities than the other models. In fact, the quality of the computed binding affinities tend to be degraded relative to the CHopt2 charge models; although both transformations involving Y=CHO achieve remarkably low errors (AUE of 0.3 kcal/mol). The AUE is degraded slightly from 0.6 to 1.3 kcal/mol and from 1.2 to 1.8 kcal/mol for Y=CN and Y=OCH₃ respectively.

Given the relative success of the charge optimization schemes for these nitrile, aldehyde and ether functional groups and the inability of these schemes to improve the quality of the binding affinities for the thioether TIBO derivatives beyond 2 kcal/mol, we suggest that further optimization of the other non-bonded parameters (i.e. atomic radius and energy well-depth) are likely required in conjunction with improved partial charges, but is beyond the scope of this study.

The importance of physically meaningful charge distributions

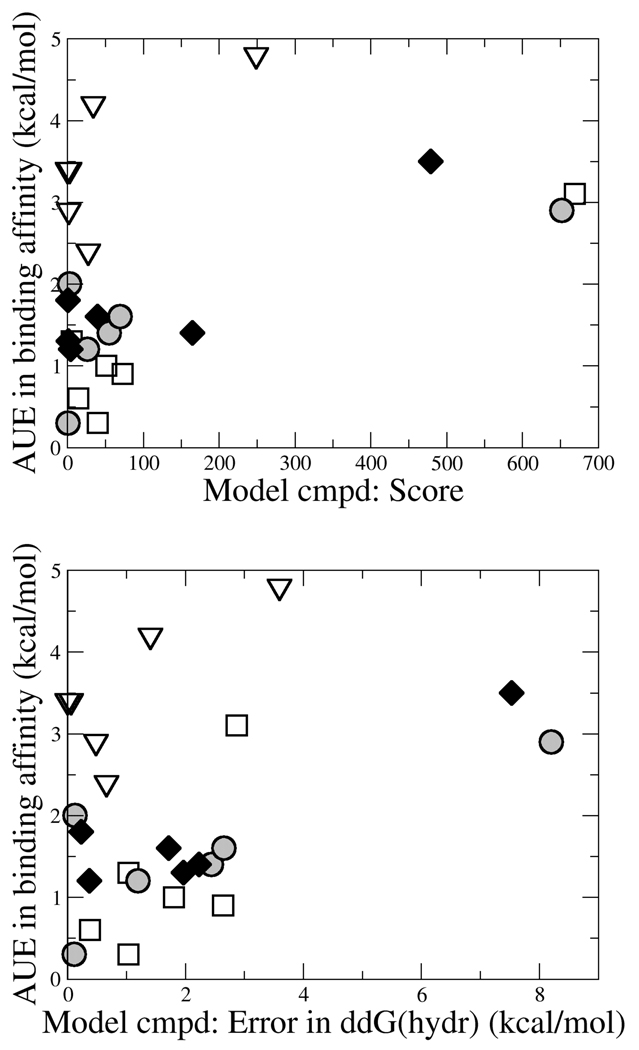
A “control” charging scheme was selected for each functional group to ascertain the importance of physically-relevant charge distributions for effectively modeling binding affinities for these TIBO derivatives. The “control” charging schemes exhibit poor agreement with experimental hydration free energies and QM dipole moments and yield very poor quality results among the TIBO binding affinities. In fact, the AUE for each class degrades to more than 2.9 kcal/mol and all but one individual binding free energy has an error of more than 2 kcal/mol. Figure 5 illustrates the correlation that is observed between the quality of the charge distributions in the modeled compound (as measured by the score used in the MC optimization or by the error in the hydration free energy relative to benzene) and the quality of the computed binding affinities in the corresponding TIBO derivatives. From figure 5, it is clear that reasonable physical properties for model compounds (i.e. low MC scores or low errors in hydration free energies) are required for achieving high quality binding free energies. In fact, the lowest errors in predicted binding affinities result from charge distributions that predict hydration free energies of their model compounds within 1 kcal/mol. However, achieving accurate experimental hydration free energies or good scores in model compounds does not guarantee success in reproducing experimentally binding affinities as is demonstrated by the consistently poor performance of any of the charge distributions for the thiomethoxy TIBO derivatives. A larger set of data for each functional group as well as additional classes of compounds would need to be explored to more fully describe the relationship between molecular properties and the quality of the computed binding affinities in the regime where the charge distributions are physically-meaningful (i.e. the distributions spanned by the CHELPG and CHopt models in this study). In addition, other charging schemes like the scaled CM1A charge model and the AM1-BCC charges which have proved effective for modeling with OPLS-AA and AMBER respectively could also be investigated for their compatibility with the CHARMM force field and is under investigation in our group. It is also worth emphasizing that the inclusion of experimental hydration free energies and scaled dipole moments in our scoring function was designed to be compatible with other CHARMM22 force field parameter development efforts³⁸, so likely minor modifications or inclusion of other key molecular properties would be required for the appropriate transferability of measures of model quality to other biomolecular force fields.

Figure 5.

Correlation between the physical properties of the model benzene derivatives and the quality of the resulting binding free energies of the corresponding TIBO compounds for Y=CN (open squares), Y=CHO (shaded circles), Y=OCH₃ (filled diamonds) and Y=SCH₃ (open triangles). The score (top) that is used in the MC simulations can be understood as a “penalty” such that the lower the number, the better the agreement between the targeted molecular properties. The error in the hydration free energy (bottom) is approximated from the difference between GBMV and vacuum-minimized energies.

Developing charge distributions in model compounds

In molecular modeling, there is always the need to balance chemical rigor with computational efficiency. This is especially relevant in a discussion about ligand parameterization where the need for transferability of parameters to novel drug-like molecules must be held in tension with the demand for high-quality estimates of binding affinities in investigating these new compounds in silico. At one end of the spectrum, new parameters could be optimized for each novel compound under investigation. While this strategy may produce more reliable results, given the enormity of chemical space, it is too time consuming to be realistically pursued. Recently, Åqvist and coworkers investigated the plausibility of adopting charge distributions for complete drug molecules that were estimated from automated semi-empirical and ab initio methods. Their study showed that several charge schemes (including CHELPG charge distributions) were reasonably compatible with the OPLS-AA force field for computing binding affinities with linear interaction energy (LIE) models⁴⁵. While these charge schemes did not achieve the same level of success as OPLS-AA-optimized charges, they suggest that these automated schemes could be used as reasonable approximations in high-throughput calculations.

An alternative strategy involves optimizing charge distributions on fragments or model compounds that could be used to build up any new molecule. Maciel and Garcia have examined how the molecular context affects charge assignments to identify the smallest context that is required to reliably reproduce CHELPG charge assignments from a molecule’s constitutive fragments⁴⁶. Using a large test set of 324 molecules, they determined that five or more heavy-atom neighbors are typically required for accurately transferring charge assignments from one molecule or molecular fragment to another. This “five-atom neighborhood” could represent the ideal conditions for partial charge transferability; however, it is still significantly beyond the scope of current fragment library development efforts.

Generally, automated parameter assignment schemes use atom types that are obtained by matching molecular fragments that describe functional groups covered by the force field. A molecular fragment is associated with a given set of BCIs that describe the magnitude and direction of the partial charges associated with a covalent bond between any two atom-types. The high quality of the individual and collective binding affinity results for the well-parameterized initial charges, as well as the CHELPG2 and CHopt2 schemes, are a promising indication that bond charge increment rules and their associated partial charge distributions that are derived from physically-meaningful charge distributions on model compounds can be transferred successfully to novel compounds. Furthermore, these results suggest that the important “neighborhood” is relatively local in nature. Of course, there may be exceptions to this finding, as demonstrated by the halide substituents whose influence is modeled to extend to the charges on the ortho carbon and hydrogen atoms in the recently optimized CGenFF parameters. However, for the most part, as fragment libraries are developed the bond charge increment rules that include the identity of the atoms that attach fragments to one another (e.g. the ipso carbon on the benzene ring) will likely be sufficient.

In our opinion, the CHopt2 charge models do not perform sufficiently well to warrant the added computational expense that is required to develop these charge distributions. Due to the success of the CHELPG2 charge distributions in computing binding free energies and how readily the model may be obtained (within minutes to a few hours on a standard desktop machine), this works supports the use of charge distributions that are derived from the ESP of model compounds for rapidly generating new bond-charge increments to investigate novel compounds or to expand current fragment libraries.

Conclusions

Here, we have performed a systematic assessment of the quality of binding affinities than can be achieved with current and recently optimized CGenFF parameters for a large series of non-nucleoside inhibitors which bind to HIV-1 RT. Thermodynamic integration simulations were performed to compute relative binding affinities for 44 pairs of TIBO compounds which cover 21 unique molecules. These calculations achieve a high level of success with average errors in the binding affinities of 1.29 kcal/mol for the entire dataset and half of the pairs of compounds exhibit individual errors of less than 1 kcal/mol. While representatives of each of the CGenFF functional groups that were tested performed well, the quality of the results depended significantly on the size of the modeled substituents. TI simulations that modeled the transformation between substituents of similar sizes tended to be more successful (AUE of 1.0 kcal/mol for 33 pairs) than transformations that involved larger size differentials (AUE of 2.3 kcal/mol for 11 pairs). Binding affinities for TIBO derivatives containing alkyl, allyl, aldehydes, nitriles, trifluorinated methyl, and conservative halide transformations were reliably computed and had AUEs between 0.6 and 1.2 kcal/mol. By contrast, the thioethers whose partial charge assignments were approximated from methoxybenzene demonstrated large and systematic errors that consistently overfavored the binding of the hydrogen or methyl TIBO derivative relative to the thioether counterparts; their individual errors were greater than 3 kcal/mol and the AUE was 4.2 kcal/mol.

Due to its large and systematic errors and the fact that thioether CHARMM parameters have not yet been developed, parameters of the thioether TIBO compound was targeted for optimization. Three additional classes of compounds were selected as controls: the nitriles, aldehydes and ethers. We have investigated how different charging schemes for small molecules in conjunction with the CHARMM force field impact the quality of the computed binding affinities for this subset of TIBO compounds. The four charge distribution schemes that we tested each improved the quality of the computed binding affinities for the thioether TIBO derivative relative to its initial charges and performed reasonably well for the nitriles, aldehydes and ethers. The CHELPG2 charge optimization scheme which adopted localized partial charges that were fit to the QM electrostatic potential of model benzene yielded the smallest average binding affinity error among the pairs of TIBO compounds investigated; the AUE of the 11 pairs of TIBO compounds was reduced from 1.7 kcal/mol with the initial charge distributions to 1.1 kcal/mol with the CHELPG2 charge assignments and the MUE for these 11 pairs was reduced from 5.4 to 2.7 kcal/mol. By contrast, the “control” charge distributions which specifically did not mimic experimental or QM target molecular properties for the model benzene compounds resulted in extremely poor quality binding affinities with an AUE of 3.4 kcal/mol and MUE of 5.4 kcal/mol across the 11 pairs of TIBO compounds. Since the thioethers were still consistently underfavored relative to their alkyl counterparts in each of the charge optimization schemes, we suggest that other non-bonded parameters will likely need to be optimized before further improvements in the corresponding binding affinities are observed.

This study demonstrates the quality of recently developed CGenFF parameters as well as the advantage of using model compounds to derive physically meaningful charge distributions in the absence of parameterized bond-charge increments for a given compound. Due to the high quality of the binding affinities computed using the CHELPG2 partial charge assignments, we suggest that this kind of charge optimization strategy can be used either to rapidly generate charge distributions for specific drug-like models of interest and to expand bond-charge increments and fragment libraries of current force fields.