Why Do We Test Multiple Traits in Genetic Association Studies?

Abstract

In studies of complex disorders such as nicotine dependence, it is common that researchers assess multiple variables related to a disorder as well as other disorders that are potentially correlated with the primary disorder of interest. In this work, we refer to those variables and disorders broadly as multiple traits. The multiple traits may or may not have a common causal genetic variant. Intuitively, it may be more powerful to accommodate multiple traits in genetic traits, but the analysis of multiple traits is generally more complicated than the analysis of a single trait. Furthermore, it is not well documented as to how much power we may potentially gain by considering multiple traits. Our aim is to enhance our understanding on this important and practical issue. We considered a variety of correlation structures between traits and the disease locus. To focus on the effect of accommodating multiple traits, we examined genetic models that are relatively simple so that we can pinpoint the factors affecting the power. We conducted simulation studies to explore the performance of testing multiple traits simultaneously and the performance of testing a single trait at a time in family-based association studies. Our simulation results demonstrated that the performance of testing multiple traits simultaneously is better than that of testing each trait individually for almost models considered. We also found that the power of association tests varies among the underlying models. The advantage of conducting a multiple traits test is minimized when some traits are influenced by the gene only through other traits; and it is maximized when there are causal relations between the traits and the gene, and among the traits themselves or when there are extraneous traits.

1 Introduction

For complex diseases, their characterization often requires us to consider multiple factors. For example, one of the instruments for studying nicotine dependence is the Fagerstrom Test for Nicotine Dependence (FTND) (Fagerstrom, 1978). An overall score is generated by FTND after asking about ten questions.

The determinants of complex diseases are also multi-factorial and tend to be inadequately understood. For example, in studies of smoking, people may smoke because of nicotine dependence, but smoking may also be a behavioral adjustment to stress, depression, and other mental health problems. Furthermore, when people smoke, they may also drink and use other substance or vice versa. Understanding such a kind of comorbidity is a very important, very challenging issue. Therefore, when we conduct genetic studies of complex diseases, we should keep in mind the complex characterization and etiology of the diseases. In fact, to this end, multi-dimensional data are frequently collected (Beyene, & Tritchler on behalf of Group 12, 2007). As a result, we have data from a batch of traits that may be mutually correlated, and some or all of them may be associated with common genetic markers (Lange, Lyon, DeMeo, Raby, Silverman, & Weiss, 2003; Lange, Silverman, Xu, Weiss, & Laird, 2003). When that happens, namely, if multiple traits are simultaneously affected by a single gene or DNA variant, the phenomenon is referred to as pleiotropy.

In addition to the need to consider the complexity of complex diseases, there is potentially another advantage of testing multiple traits simultaneously. Testing the traits one at a time requires adjustments for type I error using single-trait based tests, and the adjustments are generally made by Bonferroni correction or Hochberg correction. It is well known that these corrections tend to be conservative and may reduce our chance to reveal underlying associations.

Various methods have been developed to gain more power by considering multiple traits in mapping complex disease genes. Using the composite interval mapping, Jiang and Zeng (1995) proposed a method for mapping quantitative trait loci (QTL) when multiple traits and their correlation structure are considered. For family-based association tests (FBATs), Lange, Silverman, Xu, Weiss, and Laird (2003) proposed a generalized-estimation equation (GEE) method to test multiple traits simultaneously, extending the single trait based FBATs (Schaid, 1996; Allison, 1997; Laird, Horvath, & Xu, 2000). Some authors have reported increased power as a result of testing multiple traits simultaneously (Jiang & Zeng, 1995; Lange, Lyon, DeMeo, Raby, Silverman, & Weiss, 2003; Lange, Silverman, Xu, Weiss, & Laird, 2003; Xu, Tian, & Wei, 2003).

Despite the motivation highlighted above for considering multiple traits, it is not entirely clear as to how beneficial such a strategy is and when it makes the most sense to use this strategy. One drawback to consider multiple traits is that the method of analysis is inevitably more complicated (Liang & Zeger, 1986; Prentice & Zhao, 1991; Lange, Whittaker, & Macgregor, 2002).

Our aim is to enhance our understanding on this important and practical issue. We consider a variety of correlation structures between traits and the disease locus. To focus on the effect of accommodating multiple traits, we examine genetic models that are relatively simple so that we can pinpoint the factors affecting the power. We conduct simulation studies to explore the performance of testing multiple traits simultaneously and the performance of testing a single trait at a time in family-based association studies.

The magnitude of correlation among multiple traits depends on the underlying genetic mechanism as well as environmental covariates. When data are observed, in general, we can only assess the association among the traits. However, it is possible that the potential benefit of analyzing multiple traits simultaneously may depend on the causal relations among them. Hence, we simulated data using directed acyclic graphs (DAGs) to examine whether the directions of the causal relations have impact on the power of the association test. Specifically, we impose a linear structural equation model (SEM) on each DAG. While analyzing the simulated data and assessing the power, however, we do not make use of the casual effects among the traits.

For clarity, we will not consider covariates in our simulation studies or other complications in association studies such as population admixture, because our purpose is to compare the multiple-trait based versus the single-trait based tests. We consider both quantitative traits and binary traits.

2 Methods and Simulation Models

Suppose that data are collected from n independent nuclear families consisting of parents and their offspring. For each member of a family, we observe m disease traits. For clarity, we focus on genotypes at one di-allelic (allele A or α) marker and also restrict our attention to trios (two parents and one child).

For the ith family, let y_i = (y_i1, …, y_im) denote the m traits of the child. Let X_i be the number of copies of allele A for the child at the marker, and let $G_i^p$ denote the observed genotypes of the parents in the ith family. To explore the performance of testing multiple traits simultaneously and the performance of testing each trait individually, we consider two testing strategies using the family-based association test.

2.1 Testing Strategies

First, we consider testing the association between the genetic marker and each of the m traits by using the univariate FBAT (Lange, Silverman, Xu, Weiss, & Laird, 2003). For the jth trait, the corresponding univariate FBAT is ${\chi }_F^2=\frac{{(S-E(S))}^2}{V_S},$ where $S={\displaystyle {\sum }_{i=1}^n{t}_{\mathit{\text{ij}}}{X}_i,}E(S)={\displaystyle {\sum }_{i=1}^n{t}_{\text{ij}}E(X_i\text{|}{G}_i^p}),\text{and}{V}_S={\displaystyle {\sum }_{i=1}^n{t}_{ij}^2\text{Var}(X_i\text{|}{G}_i^p).}$ $E(X_i\text{|}{G}_i^p)\text{and}\text{Var}(X_i\text{|}{G}_i^p)$ are computed conditional on the parental genotypes under Mendel’s laws. Moreover, t_ij = y_ij − ȳ_j for quantitative trait, where ȳ_j is the average of the jth trait in all children (Rabinowitz, 1997), and t_ij = y_ij − r for binary trait, where r is the population prevalence of the disease (Whittaker & Lewis 1998).

Because we need to perform m individual tests, we apply Bonferroni correction to adjust for multiple testing.

Second, to test the association between the m traits and the marker, we use the FBAT-GEE method, an extension of FBATs for multivariate phenotypes (Lange, Silverman, Xu, Weiss, & Laird, 2003). The FBAT-GEE statistic is ${\chi }_G^2={\tilde{\mathbf{S}}}^T{\mathbf{V}}_{\tilde{\mathbf{S}}}^{-1}\tilde{\mathbf{S}},$ where $\tilde{\mathbf{S}}={\displaystyle {\sum }_{i=1}^n{\mathbf{t}}_i(X_i-E(X_i\text{|}{G}_i^p)),}{\mathbf{V}}_{\tilde{\mathbf{S}}}={\displaystyle {\sum }_{i=1}^n{\mathbf{t}}_i{\mathbf{t}}_i^T\text{Var}}(X_i\text{|}{G}_i^p),\text{and}{\mathbf{t}}_i=(t_{i1},\dots ,t_{\mathit{\text{im}}}{)}^T.$ Note that ${\chi }_G^2$ is asymptotically ${\chi }_k^2$-distributed with the degrees of freedom k defined as rank $({\mathbf{V}}_{\tilde{\mathbf{S}}}).$

2.2 Graphical Structures for Simulation Studies

To compare the two testing strategies introduced above, we conducted a series of simulations. For clarity, we assume a di-allelic disease susceptibility locus with alleles D (disease allele) and d. We consider three traits Y₁, Y₂ and Y₃.

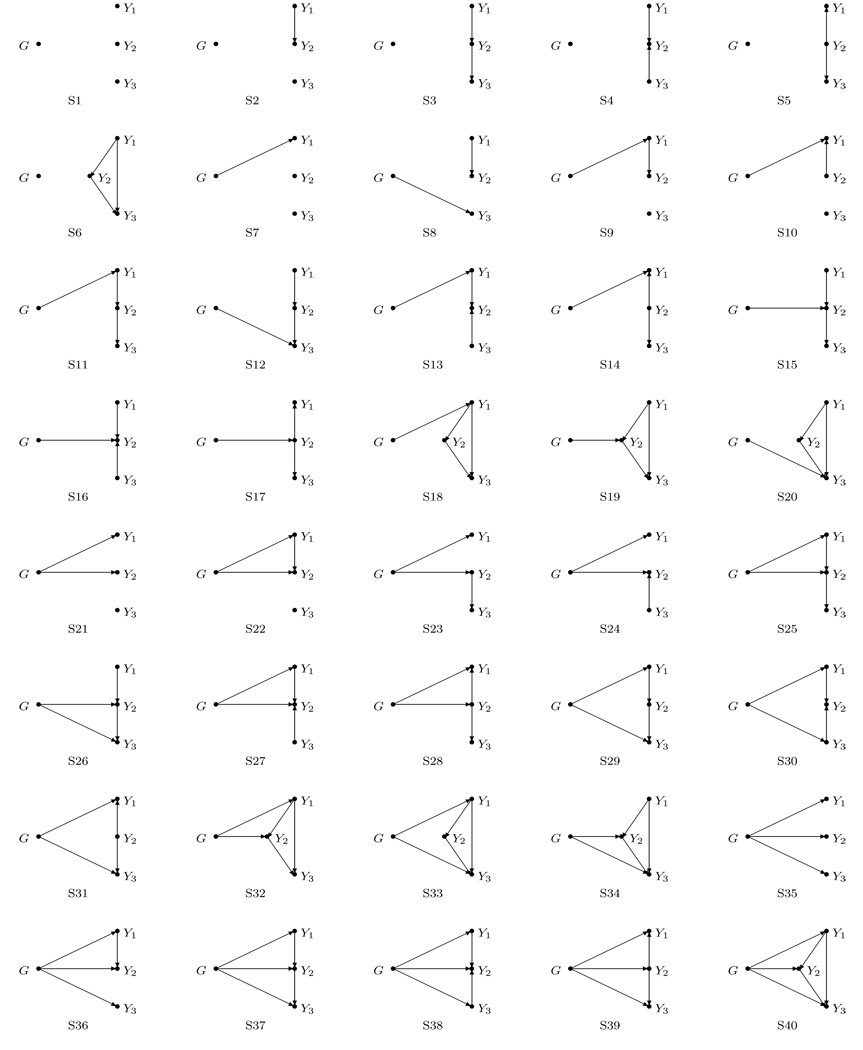
Although we may not observe the causal relationship between the genotypes and traits or among the traits, we generate the data from 40 directed acyclic graphs (DAGs) to understand how the directions may impact the performance of the tests. Those DAGs are displayed in Figure 1. An arrow between any two elements points to a causal relationship. The 40 DAGs can be summarized in four categories according to the number of traits that are directly affected by the disease susceptibility locus. The structures in the first category (S1–S6) imply that none of the three traits are caused by the gene (the null hypothesis). In the second category (S7-S20), one of the three traits is induced by the gene. In the third category (S21–S34), two of the three traits are induced by the gene. Finally, in the fourth category (S35–S40), all of the three traits are induced by the gene.

Figure 1.

Forty causal structures among one disease gene G and three traits Y₁, Y₂ and Y₃ that are illustrated by DAGs. The arrows from G to Y_j and from Y_k to Y_j represent that there exist direct effects of G on Y_j and Y_k on Y_j for j, k = 1, 2, 3. The locations of Y₁, Y₂ and Y₃ can be exchanged arbitrarily in each structure.

2.3 Models for the Traits

With the directional relationship defined in Figure 1, we explain here how to generate the trait values.

First, we consider quantitative traits. We impose linear SEMs on each DAG. For Y_j in a DAG, if there exist some arrows pointing to Y_j, say, an arrow from gene G to Y_j and an arrow from Y_k to Y_j, we reflect these relationships through a linear regression model as follows:

$$Y_j={\mu }_j+{\beta }_j{X}_D+{\gamma }_{kj}{Y}_k+{\epsilon }_j,\hspace{1em}\text{for}j,k=1,2,3$$ (1)

where ${\epsilon }_j~N(0,{\sigma }_j^2),$ ε₁, ε₂, ε₃ are mutually independent, and X_D is the number of disease allele D. In addition, μ_j denotes the intercept, β_j represents the additive effect of disease allele D for the trait Y_j, and γ_kj represents the effect of trait Y_k on the trait Y_j. Conditional on X_D and Y_k, Y_j can be generated from the normal distribution $N({\mu }_j+{\beta }_j{X}_G+{\gamma }_{kj}{Y}_k,{\sigma }_j^2).$

If there are no arrows pointing to Y_j in a DAG, Y_j is independent of the disease gene and other traits, and distributed as a normal distribution $N({\mu }_j,{\sigma }_j^2).$

For clarity, we set μ_j = 0, ${\sigma }_j^2=1$ for j = 1, 2, 3 throughout the simulation.

2.4 Heritability

We presented our simulation models in the regression framework. However, for ease of interpretation, we discuss the relationship between the regression parameters and heritability. Without loss of generality, we use the following models for illustration.

$$\begin{array}{c}{Y}_1={\beta }_1{X}_D+{\epsilon }_1,\hfill \\ Y_2={\beta }_2{X}_D+{\gamma }_{12}{Y}_1+{\epsilon }_2,\hfill \\ Y_3={\beta }_3{X}_D+{\gamma }_{13}{Y}_1+{\gamma }_{23}{Y}_2+{\epsilon }_3.\hfill \end{array}$$ (2)

Heritability of trait Y_j, denoted by $h_j^2,$ is defined as the proportion of phenotypic variation that is attributable to the genetic variation, i.e.,

$$h_j^2=\frac{\text{Var}({\beta }_j{X}_D)}{\text{Var}(Y_j)}.$$

Similar to the definition of heritability, we define interability as

$$t_{kj}^2=\frac{\text{Var}({\gamma }_{kj}{Y}_k)}{\text{Var}(Y_j)}$$

for j, k = 1,2,3. This interability reflects the ratio of the phenotypic variation of the jth trait explained by the kth phenotypic variation.

After some simple algebra, we have

$$\begin{array}{c}{\beta }_1=\frac{1}{\sqrt{2p(1-p)}}\sqrt{\frac{h_1^2}{1-h_1^2}},\hfill \\ {\beta }_2=\frac{1}{\sqrt{2p(1-p)}}\sqrt{\frac{h_2^2}{1-t_{12}^2-h_2^2}},\hfill \\ {\gamma }_{12}=\sqrt{\frac{t_{12}^2}{1-t_{12}^2-h_2^2}}\text{,}\hfill \\ {\beta }_3=\frac{1}{\sqrt{2p(1-p)}}\sqrt{\frac{h_3^2}{1-t_{13}^2-t_{23}^2-h_3^2}}\text{,}\hfill \\ {\gamma }_{13}=\sqrt{\frac{t{}_{13}^2}{1-t_{13}^2-t_{23}^2-h_3^2}},\hfill \\ {\gamma }_{23}=\sqrt{\frac{t_{23}^2}{1-t_{13}^2-t_{23}^2-h_3^2}}.\hfill \end{array}$$

Therefore, given heritabilities and interabilities, we can determine the regression co-efficients and then follow model (2) to generate Y₁, then Y₂, and lastly Y₃.

2.5 Extraneous Variables

In the discussions above, we considered the situations where the three traits either are independent or directly affect each other or correlated through the gene. However, there may exist one or more extraneous variables that are not included in the traits under consideration and that result in correlations among the the traits under consideration. To accommodate this situation, we need to consider correlated ε₁, ε₂, ε₃. To be more specific, we let (ε₁, ε₂, ε₃)′ ~ N(0, Σ) in the model for traits, where Σ = (σ_kj)_3×3 represents the correlation among the traits under consideration that is induced by extraneous variables. Furthermore, let σ_jj = 1, then σ_kj = ρ_kj for k, j = 1,2,3. We control the covariance structures of (ε₁, ε₂, ε₃)′ by changing ρ_kj.

2.6 Binary Traits

To simulate binary traits $(Y_1^{*},Y_2^{*},Y_3^{*}),$ we first simulate quantitative traits (Y₁, Y₂, Y₃) as describe above, then we let $Y_j^{*}=1$ if Y_j > c_j and $Y_j^{*}=0$ otherwise, j = 1, 2, 3. We need to select suitable cut-off points c_j in our simulations to reflect the prevalence. Note that c_j = Φ⁻¹(1 − r), where Φ is the cumulative distribution function of the standard normal distribution.

2.7 Simulation Settings

As in Zhang, Wang, and Ye (2006), the parents’ genotypes at trait and marker loci were generated according to a specified coefficient of linkage disequilibrium, δ = 0.11, and the haplotype frequencies for AD, Ad, aD, and ad were 0.2, 0.1, 0.1, and 0.6 if we let P(A) = P(D) = 0.3.

The offspring genotypes were generated using the parental genotypes. For estimating the empirical type I error, under the null hypothesis, the traits are not associated with the disease susceptibility locus. For evaluating the power, the trait and marker loci are 1 cM apart.

We let the significance level be 0.01 and the number of nuclear family be 400 in our simulations, and replicated each simulation 10,000 times for power comparisons and 50,000 times for type I error comparisons. It should be pointed out that the significance level of each single-trait test is set to be α = 0.01/3 based on the Bonferroni adjustment, and then each single-trait test was counted on its own, giving rise to, for example, 30,000 tests under the null hypothesis. For the case of quantitative traits, we considered the heritability of $h_j^2=0.05.$ In absence of any extraneous variables, we considered three choices for $t_{kj}^2,$ i.e., 0.05, 0.15, and 0.35.

In presence of extraneous variables, we considered two different covariance structures for (ε₁, ε₂, ε₃)′ by choosing ρ_kj = 0.2, and −0.2.

For the case of binary traits, we replaced the value of $h_j^2$ with 0.10 and let the population prevalence r = 0.10.

3 Results

3.1 Type I Error Comparison

Type I error comparisons are listed in Table 1 for quantitative traits and in Table 2 for binary traits based on structures S1–S6. Table 1 and Table 2 show that the empirical type I errors of the two testing methods are relatively close to the nominal significance level. The estimated type I errors for the multiple traits based test are closer to the nominal significance level than those of the single trait based test, especially when the magnitude of the directed effects among the traits become large and/or the extraneous variables result in correlations among the traits under consideration. Because the tests performed on each trait are usually not independent due to the correlations among the traits. This violation of the independence assumption limits the ability of Bonferroni adjustment to control type I error effectively.

Table 1.

Estimated type I errors of two testing methods based on structures S1–S6 for quantitative traits.

	Structure	$t_{kj}^2=0.05$		$t_{kj}^2=0.15$		$t_{kj}^2=0.35$
ρkj	No.	S	M	S	M	S	M
–	S1	0.0099	0.0100	0.0099	0.0100	0.0099	0.0100
	S2	0.0096	0.0096	0.0085	0.0092	0.0101	0.0097
	S3	0.0088	0.0095	0.0092	0.0091	0.0081	0.0089
	S4	0.0098	0.0095	0.0095	0.0098	0.0092	0.0093
	S5	0.0095	0.0091	0.0094	0.0091	0.0098	0.0099
	S6	0.0090	0.0093	0.0091	0.0091	0.0070	0.0085
0.2	S1	0.0090	0.0097	0.0090	0.0097	0.0090	0.0097
	S2	0.0100	0.0101	0.0094	0.0097	0.0094	0.0097
	S3	0.0101	0.0101	0.0092	0.0096	0.0084	0.0096
	S4	0.0095	0.0099	0.0101	0.0102	0.0087	0.0102
	S5	0.0099	0.0100	0.0092	0.0101	0.0085	0.0095
	S6	0.0093	0.0092	0.0080	0.0092	0.0078	0.0096
−0.2	S1	0.0095	0.0097	0.0095	0.0097	0.0095	0.0097
	S2	0.0102	0.0101	0.0095	0.0097	0.0094	0.0097
	S3	0.0104	0.0089	0.0098	0.0096	0.0093	0.0096
	S4	0.0098	0.0096	0.0094	0.0097	0.0103	0.0102
	S5	0.0090	0.0096	0.0095	0.0097	0.0093	0.0097
	S6	0.0093	0.0091	0.0094	0.0096	0.0078	0.0097

‘S’ and ‘M’ denote the single-trait and multiple-trait tests, respectively. ρ_kj= –, 0.2, and −0.2 represent the case of no extraneous variables, and the cases of having extraneous variables that result in positive and negative correlations among traits, respectively. The nominal significance level is 0.01.

Table 2.

Estimated type I errors of two testing methods based on structures S1–S6 for binary traits.

	Structure	$t_{kj}^2=0.05$		$t_{kj}^2=0.15$		$t_{kj}^2=0.35$
ρkj	No.	S	M	S	M	S	M
–	S1	0.0088	0.0092	0.0088	0.0092	0.0088	0.0092
	S2	0.0090	0.0089	0.0087	0.0093	0.0088	0.0085
	S3	0.0096	0.0096	0.0093	0.0086	0.0093	0.0087
	S4	0.0085	0.0085	0.0089	0.0094	0.0085	0.0086
	S5	0.0088	0.0090	0.0089	0.0086	0.0095	0.0092
	S6	0.0092	0.0089	0.0088	0.0094	0.0090	0.0088
0.2	S1	0.0086	0.0090	0.0086	0.0090	0.0086	0.0090
	S2	0.0097	0.0095	0.0097	0.0094	0.0090	0.0093
	S3	0.0085	0.0093	0.0089	0.0089	0.0092	0.0095
	S4	0.0092	0.0092	0.0097	0.0087	0.0098	0.0098
	S5	0.0093	0.0093	0.0098	0.0098	0.0089	0.0093
	S6	0.0092	0.0092	0.0098	0.0094	0.0082	0.0088
−0.2	S1	0.0092	0.0096	0.0092	0.0096	0.0092	0.0096
	S2	0.0080	0.0085	0.0083	0.0087	0.0093	0.0096
	S3	0.0089	0.0094	0.0089	0.0087	0.0083	0.0089
	S4	0.0094	0.0097	0.0090	0.0092	0.0095	0.0092
	S5	0.0090	0.0089	0.0087	0.0090	0.0093	0.0093
	S6	0.0082	0.0083	0.0081	0.0085	0.0080	0.0088

‘S’ and ‘M’ denote the single-trait and multiple-trait tests, respectively. ρ_kj= –, 0.2, and −0.2 represent the case of no extraneous variables, and the cases of having extraneous variables that result in positive and negative correlations among traits, respectively. The nominal significance level is 0.01.

3.2 Power Comparison

To compare the power of the two testing methods, we need to carry out simulations based on S7–S40. We should note that although all DAGs include three traits, power can only be assessed when there exists an association between a trait and the gene. For example, for S7, we considered the association between G and Y₁. For S13, we considered the associations between G and Y₁ and between G and Y₂. In this graph, Y₁ affects Y₂ and hence G affects Y₂. However, Y₃ affects Y₂ independent of Y₁ and hence G. All eligible associations are counted individually in the power calculation.

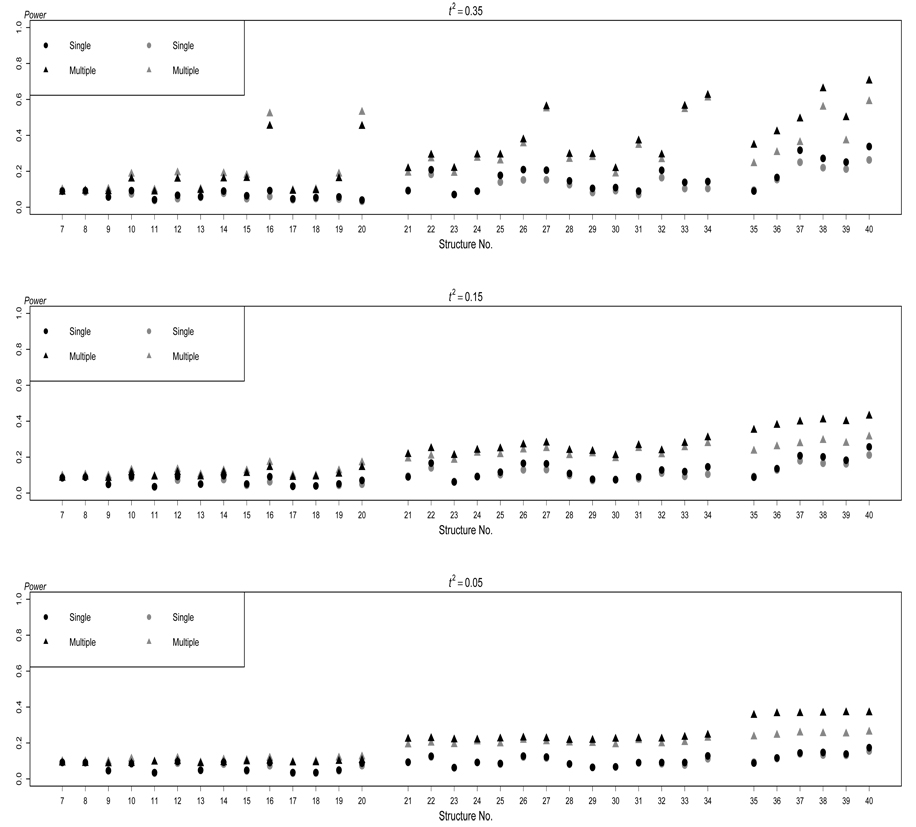
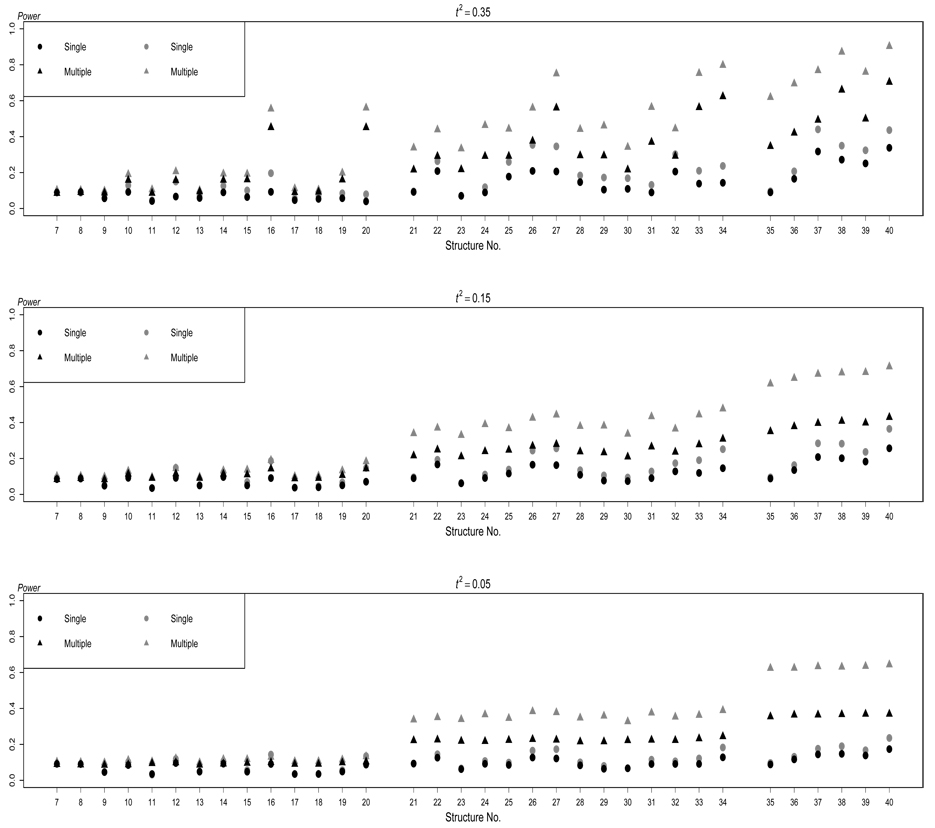
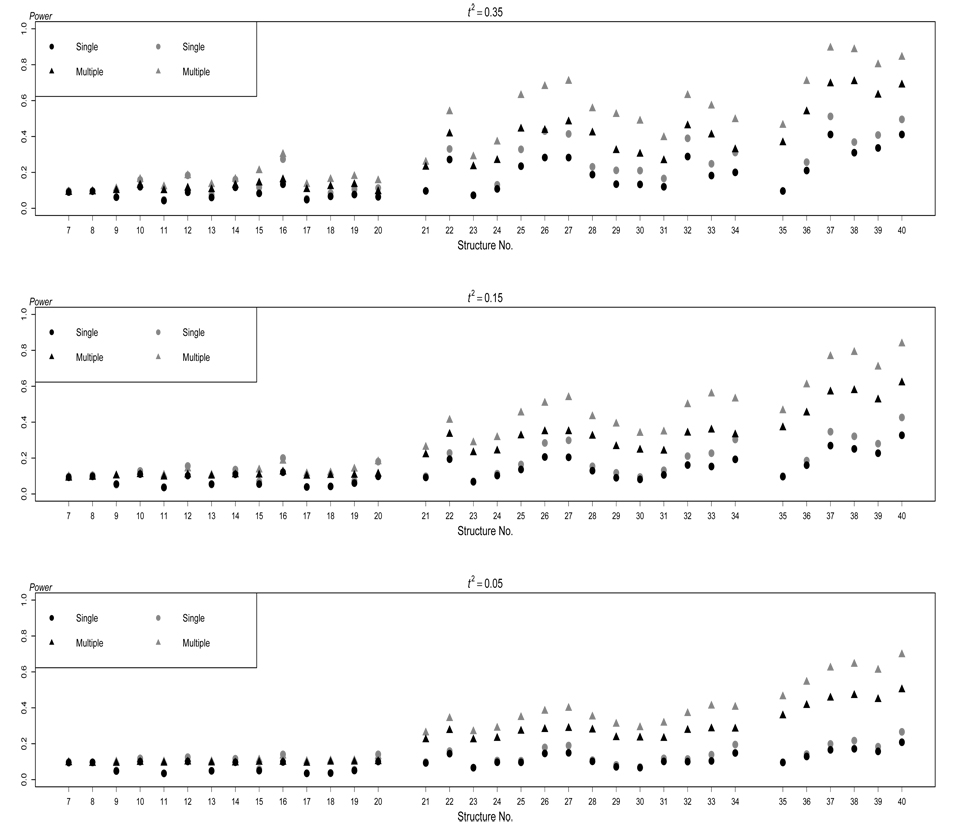
In presence of extraneous variables, the results are displayed in Figure 2 for ρ_kj = 0.2 and in Figure 3 for ρ_kj = −0.2 for quantitative traits. For the purpose of comparison, the results without extraneous variables are also listed in Figure 2 and Figure 3. Overall, as expected, the power of both testing methods increases when there are more traits that are directly affected by the disease susceptibility locus, and when the magnitude of the direct effect among multiple traits is greater.

Figure 2.

Power of the two testing methods based on structures S7–S40 for quantitative traits. The black dots and the black triangles respectively represent the performance of single-trait test and multiple-trait test in absence of any extraneous variables, and the gray dots and the gray triangles respectively represent the performance of single-trait test and multiple-trait test in presence of extraneous variables, which result in positive correlations among traits. The nominal significance level is 0.01.

Figure 3.

Power of the two testing methods based on structures S7–S40 for quantitative traits. The black dots and the black triangles respectively represent the performance of single-trait test and multiple-trait test in absence of any extraneous variables, and the gray dots and the gray triangles respectively represent the performance of single-trait test and multiple-trait test in presence of extraneous variables, which result in negative correlations among traits. The nominal significance level is 0.01.

In absence of extraneous variables, from Figure 2 and Figure 3 we can see that, testing multiple traits simultaneously outperforms testing each trait individually for most of the DAGs, especially when more than one trait are induced by the disease locus. The improvement is much more pronounced for some structures (see S16, S20, S27, S33, S34, S38, and S40) when the correlation between the traits that are directly or indirectly affected by the gene is stronger $(\text{i.e.},t_{kj}^2=0.35).$ As pointed out by Lange, Silverman, Xu, Weiss, and Laird (2003), FABT-GEE gains power more by using traits simultaneously than depending on the information of one trait. When the correlation between the traits that are directly or indirectly affected by the gene is low $(\text{i.e.},t_{kj}^2=0.05),$ the traits are nearly independent. The method of testing multiple traits simultaneously remains superior to the single-trait test by avoiding Bonferroni correction.

We should note, however, that the performance of testing multiple traits simultaneously varies across different causal structures. When only one trait is directly induced by the disease locus, the power of testing multiple traits simultaneously is lower for S9, S11, S13, S17, and S18 than for other structures. This is not surprising because structures S9, S11, S13, S17, and S18 share one thing in common: G directly affects Y₁ and then Y₁ directly affects other trait(s). Because the other traits are independent of G conditional on Y₁, they do not add much information in the test of multiple traits, at least not enough to compensate the increase of the degrees of freedom of the test. For this reason, testing multiple traits becomes less and less attractive as $t_{kj}^2$ increases if the underlying model is S9, S11, S13, S17, or S18. The situation is similar in structures S30 and S32 although two traits are directly induced by the disease locus, where the third one are conditionally independent of G given the other two traits. The presence of Y₃ in the multiple-trait test adds both information and noise in the test. In contrast, for S10, S12, S14-S16, S19, and S20, the power of testing multiple traits simultaneously is relatively high. In S10, for example, Y₂ is actually an extraneous variable to Y₁ and G. By testing multiple traits, the influence of this extraneous variable is taken into account, which is not possible by testing a single trait. As a result, the power of testing multiple traits is much enhanced.

When more than one trait are induced by the disease locus, both testing methods become more powerful. Besides the genetic cause, if the traits also have a causal relationship, the power of both testing methods (see S22, S25–S28, S32–S34, and S36–S40) are even greater. For example, the power of testing multiple traits simultaneously is high for S27, S33, S34, S38, and S40 in which the magnitude of the direct effect is large $(\text{i.e.},t_{kj}^2=0.35).$ We illustrate some of the reasons. In S27, not only does G directly cause Y₁ and Y₂, but also there is a cause relationship between Y₁ and Y₂. Furthermore, Y₃ is the extraneous variable to Y₁ and Y₂. In S31 and S34, one trait acts as the extraneous variable to the other two traits directly induced by G. Hence, as expected, the power of testing multiple traits is greater than testing a single trait, because again the former considers the extraneous variable and the latter does not.

We have seen the advantage of including the extraneous variable in the multipletrait test over the single-trait test. However, in practice, we do not have information about all extraneous variables, and hence we cannot really consider all of them in the multiple-trait test. For this reason, we examine the consequence of without including all extraneous variables in the multiple-trait test. Figure 2 and Figure 3 show that the general patterns are similar to those we revealed above. As expected, however, extraneous variables do impact on the power of both testing methods in all structures. We have seen that the failure to consider the extraneous variable in the single-trait test reduces the power of the test. Likewise, the failure to consider the extraneous variables in the multiple-trait test also reduces the power of the test. When the extraneous variables result in positive correlations among the traits under consideration, the power of both testing methods is reduced even more (see Figure 2). To the contrary, the power of both tests increases when the extraneous variables cause negative correlations among the traits under consideration (see Figure 3). Therefore, in practice, efforts should be made to consider and collect data from the extraneous variables.

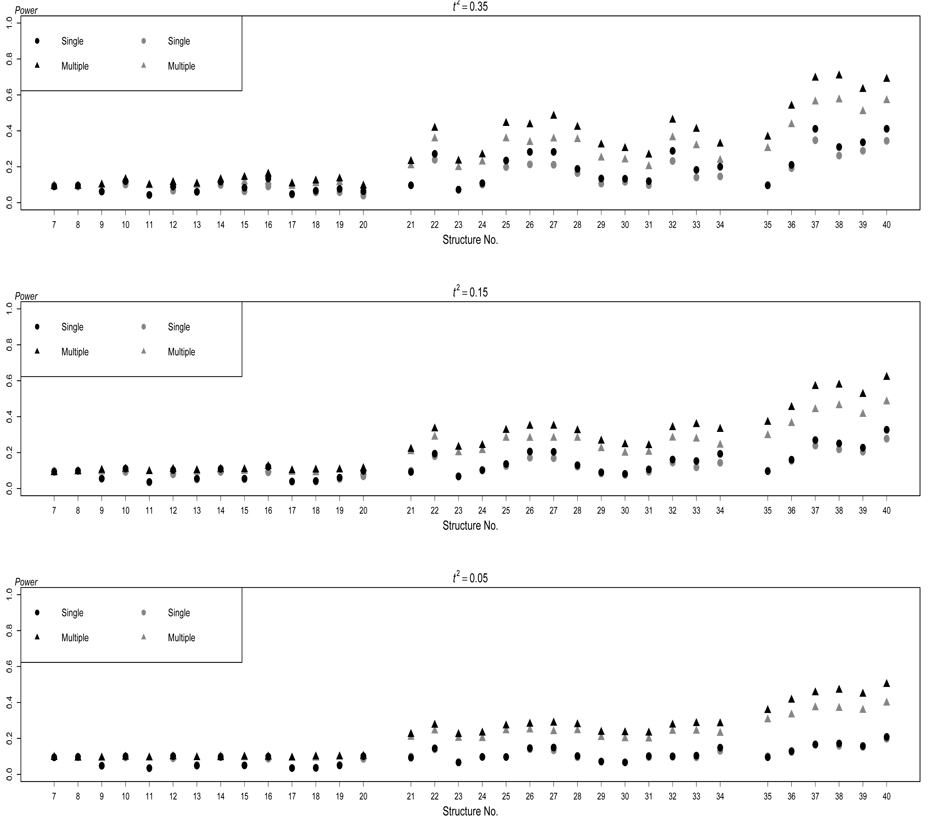
The power comparison for binary traits is presented in Figure 4 and Figure 5, which are similar to Figure 2 an Figure 3 for quantitative traits. However, the superiority of the multiple traits based test over the single trait based test is less substantial. Lange, Silverman, Xu, Weiss, and Laird (2003) discussed a similar observation. This is most due to the loss of information from thresholding the underlying quantitative traits.

Figure 4.

Power of the two testing methods based on structures S7–S40 for binary traits. The black dots and the black triangles respectively represent the performance of singletrait test and multiple-trait test in absence of any extraneous variables, and the gray dots and the gray triangles respectively represent the performance of single-trait test and multiple-trait test in presence of extraneous variables, which result in positive correlations among traits. The nominal significance level is 0.01.

Figure 5.

Power of the two testing methods based on structures S7–S40 for binary traits. The black dots and the black triangles respectively represent the performance of singletrait test and multiple-trait test in absence of any extraneous variables, and the gray dots and the gray triangles respectively represent the performance of single-trait test and multiple-trait test in presence of extraneous variables, which result in negative correlations among traits. The nominal significance level is 0.01.

4 Discussion

We carried out extensive simulations to compare the performance of two testing methods in the family-based association studies where multiple traits are of interest: one tests one trait at a time and the other tests multiple traits simultaneously. To understand when and how testing multiple traits may be helpful, we considered a variety of data-generating models to reflect the causal relations among the traits and the gene. Those models are presented in the form of directed acyclic graphs. Within each structure, we utilized linear structure equation models to accommodate the direct effects between different traits and between traits and disease locus. In practice, we usually do not observe the data for inferring a causal relation. But, it is useful to examine whether such a causal relationship has any impact on the power of the multiple-trait based testing.

Our simulation results demonstrated that the performance of testing multiple traits simultaneously is better than the performance of testing each trait individually for almost casual structures. Meanwhile, we found that the power of association tests varies among causal structures. The advantage of conducting a multiple traits test is minimized when some traits are influenced by the gene only through other traits; and it is maximized when there are causal relations between the traits and the gene, and among the traits themselves or when there are extraneous traits.

While the data were generated from known causal models, we should point out that neither tests make use of the casual effects. In practice, if the existing literature suggests a causal pathway, our simulation result can help select a powerful testing strategy. In absence of this knowledge, our simulations underscore the importance of developing more effective testing methods that accommodate multiple traits simultaneously.

Although we designed the simulation studies by assuming one di-allelic disease gene and three traits, the simulation method can be extended to involve more loci and more traits. However, we expect the general conclusions will not be changed by those extensions. In the linear regression structural equation models, for clarity, we did not consider complex causal relationship. For example, in theory, there can be interactions between some traits and the disease gene when they induce the other traits. We did not consider this complex causal relationship, also because it is unlikely to be detectable in most association studies.

We only considered a few choices for the magnitude of causal effect and two levels of correlation induced by an extraneous variable. In practice, underlying mechanisms are more complex. Thus, despite our extensive simulations, it warrants further studies to understand the power of testing statistic under more realistic and complex genetic models.

The topic we presented is rather timely, as there is an increasing interest in developing testing procedures for multiple traits in statistical genetics. As we discussed in the introduction, there is a strong motivation as to why it is important from a scientific point of view. Here, we demonstrated that the potential benefit can be real. Furthermore, we are at a stage in which data are available to conduct association analysis of multiple traits.