Abstract
Recent advances in the theoretical treatment of proton-coupled electron transfer (PCET) reactions are reviewed. These reactions play an important role in a wide range of biological processes, as well as in fuel cells, solar cells, chemical sensors, and electrochemical devices. A unified theoretical framework has been developed to describe both sequential and concerted PCET, as well as hydrogen atom transfer (HAT). A quantitative diagnostic has been proposed to differentiate between HAT and PCET in terms of the degree of electronic nonadiabaticity, where HAT corresponds to electronically adiabatic proton transfer and PCET corresponds to electronically nonadiabatic proton transfer. In both cases, the overall reaction is typically vibronically nonadiabatic. A series of rate constant expressions have been derived in various limits by describing the PCET reactions in terms of nonadiabatic transitions between electron-proton vibronic states. These expressions account for the solvent response to both electron and proton transfer and the effects of the proton donor-acceptor vibrational motion. The solvent and protein environment can be represented by a dielectric continuum or described with explicit molecular dynamics. These theoretical treatments have been applied to numerous PCET reactions in solution and proteins. Expressions for heterogeneous rate constants and current densities for electrochemical PCET have also been derived and applied to model systems.
I. Introduction
The coupling between electrons and protons plays a vital role in biological processes such as photosynthesis, respiration, and enzyme reactions, as well as in fuel cells, chemical sensors, and electrochemical devices. Proton-coupled electron transfer (PCET) reactions involving the transfer of an electron and a proton may be sequential, where either the electron or the proton transfers first, or concerted, where the electron and proton transfer simultaneously. This general definition of PCET includes hydrogen atom transfer (HAT), in which the electron and proton transfer simultaneously between the same donor and acceptor. These distinctions are not rigorously defined because the electron and proton behave quantum mechanically and hence are not localized to a single point at any given time. Thus, to maintain generality, all of these types of mechanisms can be viewed within the unified framework of PCET reactions.
A wide range of experiments have been designed to probe PCET reactions in solution,1–14 proteins,15–21 and electrochemistry.22–24 These experiments have uncovered complex behavior of PCET systems, including large deuterium kinetic isotope effects (KIEs) at room temperature,9,16 weak or even inverse temperature dependences of the KIEs,14,16 and unusual pH dependences of the rates5 or current densities.22 Structural and energetic aspects of PCET in solution and proteins have been studied computationally with quantum chemistry calculations and molecular dynamics simulations.24–36 In addition, the intriguing experimental kinetic data have motivated the development of theoretical approaches to model PCET reactions37–39 and to calculate the rates and KIEs in solution, proteins, and electrochemistry.
From a historical perspective, the theoretical treatment of PCET reactions has been strongly motivated by Marcus theory for electron transfer,40,41 as well as related theories for vibrationally nonadiabatic proton transfer.42–45 Cukier and coworkers proposed a PCET theory that is a direct extension of Marcus theory for electron transfer, in which the proton transfer coordinate is treated as an inner-sphere solute mode.46–48 The resulting rate expressions include a Franck-Condon overlap of the proton vibrational wavefunctions, which are localized in asymmetric double well potentials for the reactant and product states. Subsequently, we generalized this theory by introducing two collective solvent coordinates corresponding to electron and proton transfer.49–51 In this generalized theory, the reaction is described in terms of nonadiabatic transitions between mixed electron-proton vibronic states. The initial form of this theory represented the solvent environment by a dielectric continuum, but later forms utilized an explicit molecular solvent and protein environment. Further extensions of this theory included the dynamical effects of the proton donor-acceptor motion,52 which has been shown to play an important role in proton transfer reactions.43,53,54 These nonadiabatic PCET theories have been applied to PCET in solution and proteins.16,17,48,55,56
Related theoretical approaches have also been used to study electrochemical PCET. The advantage of electrochemical systems is that the reaction can be controlled through the electrode potential, and observables such as current density can be measured directly as a function of the overpotential without the complexities inherent to homogeneous reactions in solution and proteins. Costentin, Savéant, and coworkers have modified portions of the homogeneous nonadiabatic PCET theory to reflect the electrochemical environment in certain limits.57 Subsequently, we derived a series of expressions for heterogeneous rate constants and current densities for electrochemical PCET that account for the effects of extended ET in the diffuse layer, as well as the effects of the proton donor-acceptor vibrational motion in various well-defined limits.58 Schmickler and coworkers have developed an alternative approach based on the Anderson-Newns model Hamiltonian used widely in the theory of electrochemical ET.59,60 Recently, we developed an extension of this model Hamiltonian in a basis of electron-proton vibronic states including the effects of the proton donor-acceptor vibrational motion.61 This general model provides the framework for the inclusion of the coupling of electrochemical PCET reactions to the breaking and forming of other chemical bonds and for the derivation of rate constant expressions for adiabatic as well as nonadiabatic electrochemical PCET reactions.
Although HAT can be viewed as a type of PCET reaction, historically the theoretical treatment of HAT has evolved separately. Traditionally, HAT has been studied with electronic structure methods and multidimensional tunneling calculations in the gas phase.62,63 More recently, Mayer and coworkers have applied adiabatic Marcus theory to HAT reactions in solution.10,13 Other groups have described HAT with a nonadiabatic formulation analogous to the theories developed for PCET.51,64,65 In this unified framework for describing both HAT and PCET, proton transfer is electronically adiabatic for HAT but electronically nonadiabatic for PCET, leading to different methods for calculating the vibronic coupling between mixed electron-proton vibronic states.66 We have proposed a quantitative diagnostic for differentiating between HAT and PCET in terms of the degree of electronic nonadiabaticity.66 This diagnostic is based on an adiabaticity parameter defined by Georgievskii and Stuchebrukhov within a semiclassical framework for calculating the vibronic couplings.67 The adiabaticity parameter depends on the electronic coupling, as well as other characteristics of the potential energy surface and the tunneling quantum particle. The distinguishing topographical characteristics of the potential energy surfaces for HAT and PCET have also been examined recently.68
An outline of this article is as follows. Section II summarizes a general theory of PCET reactions, including the definitions of the electronic and vibronic states, the mechanisms, and the rate constant expressions in various well-defined limits. Section III discusses a unified theory for PCET and HAT, as well as a quantitative diagnostic for differentiating between these two types of mechanisms. Sections IV and V describe representative applications of these theoretical formulations to PCET in solution and proteins, respectively. Section VI summarizes a theory for electrochemical PCET and discusses the characteristics of the current density that differentiate electrochemical PCET from ET. Future directions are discussed in Section VII.
II. General Theory
A. Electronic and vibronic states
A general PCET reaction involving the transfer of one electron and one proton can be described in terms of four diabatic electronic states:49
| (1) |
where 1 and 2 denote the ET state, and a and b denote the PT state. This model can describe sequential mechanisms, where the proton transfers prior to the electron (i.e., 1a → 1b → 2b) or the electron transfers prior to the proton (i.e., 1a → 2a → 2b), as well as concerted mechanisms, where the electron and proton transfer simultaneously (i.e., 1a → 2b). Depending on the relative energies of the four diabatic states, as well as the couplings between them, all of these mechanisms are possible.
Experimental measurements of PCET reaction rates usually focus on the electron transfer rates by monitoring, for example, the absorbance or emission of the electron donor or acceptor. For comparison to these types of experimental data, the overall PCET reaction can be described in terms of reactant and product states that correspond to the electron being localized on the donor and acceptor, respectively. In terms of the diabatic electronic states defined above, the reactant states (I) can be defined as mixtures of the 1a and 1b states, and the product states (II) can be defined as mixtures of the 2a and 2b states. In this case, a transition from a reactant to a product state corresponds to either ET or PCET, depending on the relative contributions of the PT diabatic states a and b.
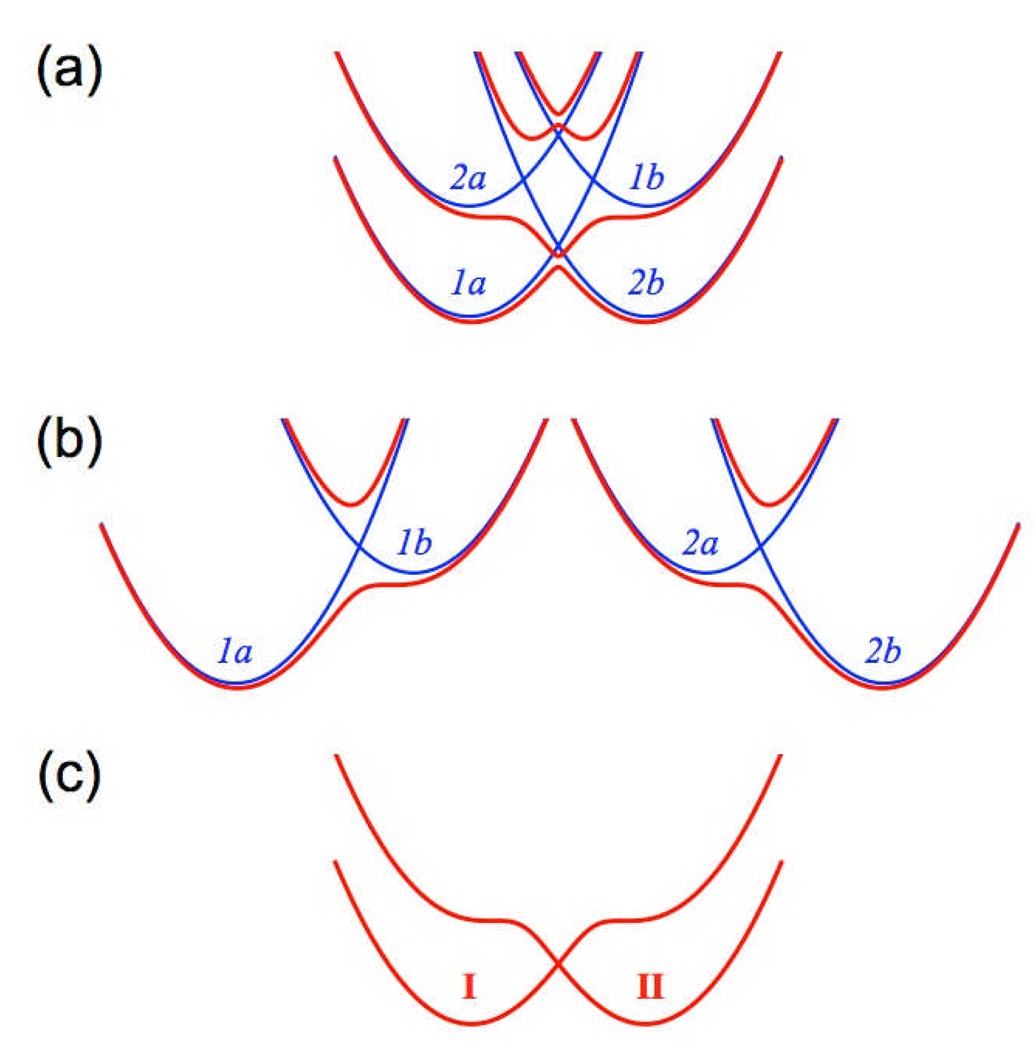
Figure 1 illustrates the physical meaning of the four diabatic states and the overall PCET reactant and product states. Figure 1a depicts the energy profiles along the proton coordinate for the four diabatic states defined above and the adiabatic states that are obtained by diagonalizing the 4×4 Hamiltonian matrix in the basis of these four diabatic states. Typically the second and third excited adiabatic states are much higher in energy than the ground and first excited adiabatic states and therefore can be neglected. In principle, the lowest two electronic adiabatic states could be obtained from a conventional multiconfigurational electronic structure calculation, in which the hydrogen is moved along a grid between the donor and acceptor. Figure 1b depicts the two sets of diabatic states 1a/1b and 2a/2b and the corresponding electronic states obtained by block diagonalization of the 1a/1b and 2a/2b blocks of the 4×4 Hamiltonian matrix. The electronic couplings between the PT diabatic states a and b are usually large enough so that the excited states from each 2×2 block diagonalization are much higher in energy than the ground states and therefore can be neglected. Thus, the two ground electronic states from the 1a/1b and 2a/2b block diagonalizations correspond to the reactant and product diabatic states I and II, respectively, for the overall PCET reaction, as depicted in Figure 1c. In this limit, diagonalization of the 2×2 Hamiltonian matrix in the basis of the two states I and II depicted in Figure 1c would lead to the lowest two adiabatic states depicted in Figure 1a.
Figure 1.
(a) Diabatic and adiabatic electronic states as functions of the proton coordinate. The diabatic states (blue) are labeled 1a, 1b, 2a, and 2b. The adiabatic states (red) are obtained by diagonalizing the 4×4 Hamiltonian matrix in the basis of the four diabatic states. (b) Two pairs of diabatic states 1a/1b and 2a/2b and associated electronic states obtained by block diagonalization of the 1a/1b and 2a/2b blocks of the 4×4 Hamiltonian matrix. The diabatic states are labeled as in part (a) and are shown in blue, while the electronic states obtained by block diagonalization are shown in red. (c) The two ground electronic states from part (b) are the reactant (I) and product (II) diabatic states for the overall PCET reaction.
Due to the quantum mechanical nature of the proton, PCET reactions are described in terms of mixed electron-proton vibronic states rather than purely electronic states.49 The vibronic states can be determined by calculating the proton vibrational states for the electronic states I and II depicted in Figure 1c. Solution of the timeindependent Schrödinger equation for the proton moving in each of these potentials leads to two sets of proton vibrational wavefunctions ϕ Iμ (r p) and ϕ IIν (r p), associated with the electronic wavefunctions ΨI (r e;r p) and ΨII (r e;r p), respectively. The double adiabatic vibronic states are defined as products of the electronic and proton vibrational wavefunctions: the reactant vibronic states are ΨI (r e;r p)ϕIμ(r p), and the product vibronic states are ΨII (r e;r p)ϕIIν(r p). Note that these vibronic states are double adiabatic only within each set of vibronic states corresponding to the reactant (I) or the product (II).
The energies of the electronic and vibronic states depend on the other nuclear coordinates of the system, including the other solute nuclei and the solvent or protein nuclear degrees of freedom. Diagonalization of the Hamiltonian matrix in a basis of the double adiabatic vibronic states leads to a set of adiabatic vibronic states as functions of these nuclear coordinates. We have shown that the nonadiabatic couplings between the electrons and the proton can be included in the Hamiltonian matrix elements to remove the double adiabatic approximation in the generation of the adiabatic vibronic states.69 In practice, however, these electron-proton nonadiabatic effects have been found to be negligible for the PCET systems studied. If all of the excited adiabatic vibronic states are sufficiently high in energy so that they can be neglected, the PCET reaction will occur on the ground adiabatic vibronic state. In general, however, the effects of excited vibronic states must be taken into account. In the context of explicit classical molecular dynamics simulations for the nuclei moving on the adiabatic vibronic surfaces, nonadiabatic transitions among the adiabatic vibronic states can be incorporated using surface hopping methods.70
Sequential and concerted PCET mechanisms can be differentiated by defining a sequential mechanism as a reaction involving a stable intermediate arising from single electron or proton transfer. A stable intermediate can be thermally equilibrated or defined in terms of a specified lifetime. In this paper, all PCET reactions that do not involve a stable intermediate are denoted concerted, although the term concerted is not rigorously applicable because the electron and proton behave quantum mechanically and hence are not localized to a single point at any given time. A PCET reaction is typically concerted when the energies of the intermediates arising from single electron and single proton transfer are significantly higher than the energies of the reactant and PCET product. Within the theoretical framework described above, the mechanism is determined mainly by the relative energies of the four diabatic states and the couplings between them. A PCET reaction will be concerted when the 1b and 2a diabatic states are significantly higher in energy than the 1a and 2b diabatic states.
The remainder of this article will center on concerted PCET reactions according to the above definition. In this case, the diabatic reactant (I) and product (II) sets of vibronic states provide a more physically meaningful representation than the adiabatic surfaces discussed above. Note that the reactant and product states correspond to the electron being localized on the electron donor and acceptor, respectively. As shown in Figure 1c, typically the proton potential energy curve for the reactant diabatic state I is asymmetric with the minimum near the proton donor, and the proton potential energy curve for the product diabatic state II is asymmetric with the minimum near the proton acceptor. As a result, the proton vibrational ground state wavefunction is localized near the donor for the reactant state I and near the acceptor for the product state II. In this case, the couplings between the diabatic reactant and product vibronic states are often significantly smaller than the thermal energy due to the small overlap between the reactant and product proton vibrational wavefunctions, as discussed below. Thus, concerted PCET reactions are typically in the vibronically nonadiabatic regime and can be described in terms of nonadiabatic transitions between the reactant and product sets of vibronic states.
B. Mechanism
PCET reactions in the condensed phase can be described in a framework analogous to Marcus theory for electron transfer. In this framework, the charge transfer reaction is driven by reorganization of the solvent and protein environment. (For the remainder of this article, we use the term solvent to denote both solvent and protein.) We have generalized a multistate continuum theory developed for electron transfer71 to the case of PCET reactions in a solvent environment represented by an isotropic dielectric continuum.49,50 In this theory, the free energy surfaces corresponding to the reactant and product vibronic states obtained from the four diabatic states defined in Eq. (1) depend on two collective solvent coordinates associated with solvent reorganization upon electron and proton transfer, respectively. Each collective solvent coordinate is defined to be the difference between the interaction energies of the charge distribution corresponding to the two relevant diabatic states with the inertial polarization of the solvent environment. These two solvent coordinates are linearly independent because the charge densities of the relevant diabatic states are linearly independent.49
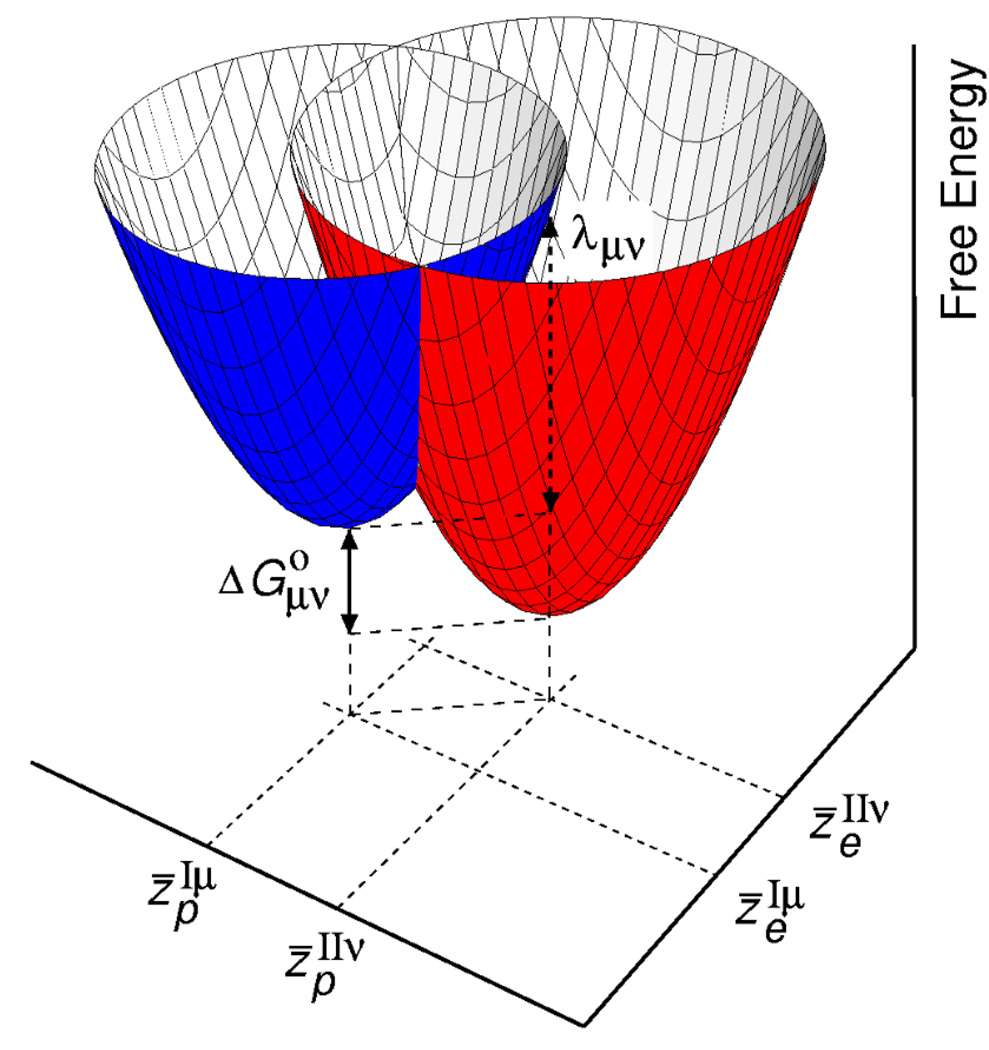
Figure 2 depicts a pair of reactant and product free energy surfaces as functions of the two collective solvent coordinates. Note that these surfaces correspond to mixed electron-proton vibronic states, and the overall PCET reaction is described in terms of two sets of stacked surfaces corresponding to the different proton vibrational states for each electronic state. These free energy surfaces can also be generated from molecular dynamics simulations with explicit solvent molecules.72 Moreover, the multistate continuum theory can be generalized to reactions involving the transfer of a total of N protons and electrons, where the number of diabatic states is 2N and the number of collective solvent coordinates is N.49,73
Figure 2.
Pair of two-dimensional vibronic free energy surfaces as functions of two collective solvent coordinates for a PCET reaction. The lowest energy reactant (I) and product (II) free energy surfaces are shown. The free energy difference and outer-sphere reorganization energy λ µvare indicated. Figure reproduced with permission from Ref. 56.
In the vibronically nonadiabatic limit, the mechanism of PCET can be described in terms of these two-dimensional free energy surfaces. For a given pair of vibronic states, the system is initially at thermal equilibrium on the reactant surface. Due to fluctuations of the solvent environment, the system evolves to the intersection between the two surfaces. A nonadiabatic transition from the reactant to the product surface occurs with a probability proportional to the square of the vibronic coupling. Subsequently, the system undergoes relaxation to thermal equilibrium on the product surface as a result of the reorganization of the solvent environment. Note that in the nonadiabatic limit, the thermal fluctuations of the environment are assumed to occur on a much faster time scale than the nonadiabatic transitions in the crossing region, thereby allowing the utilization of perturbation theory in the form of Fermi’s golden rule to calculate the rate constant.
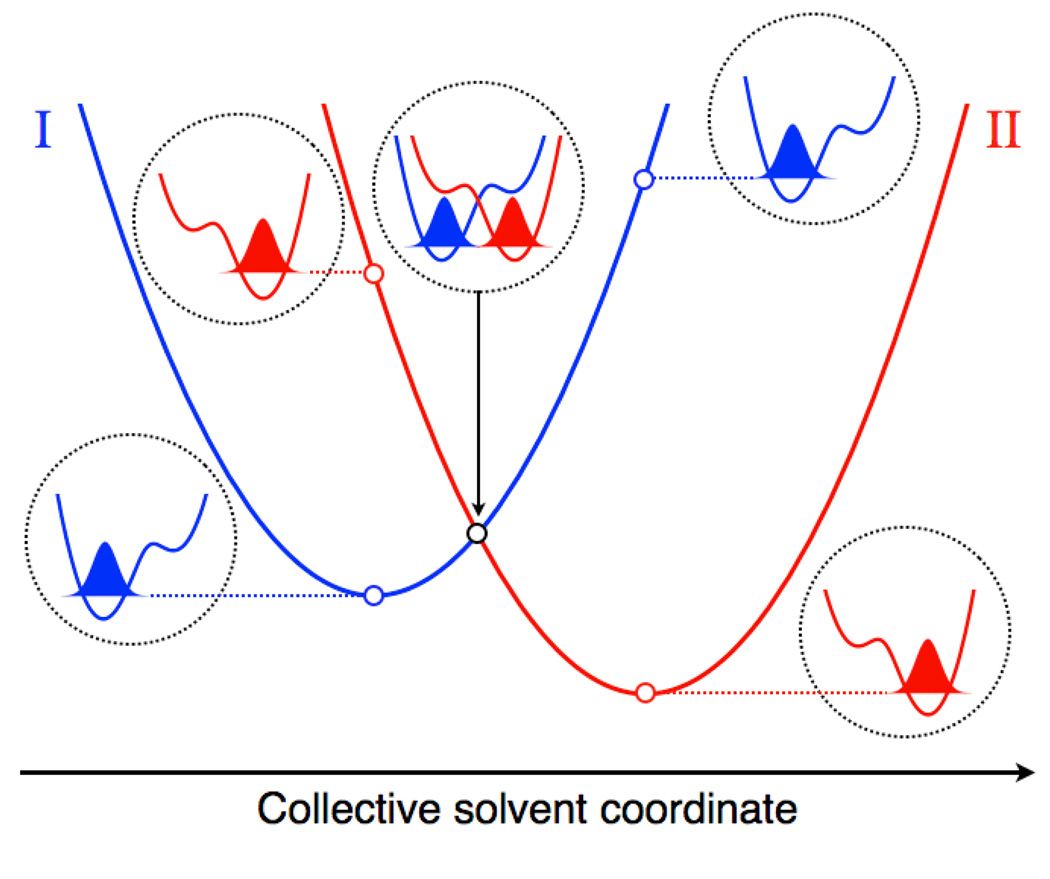
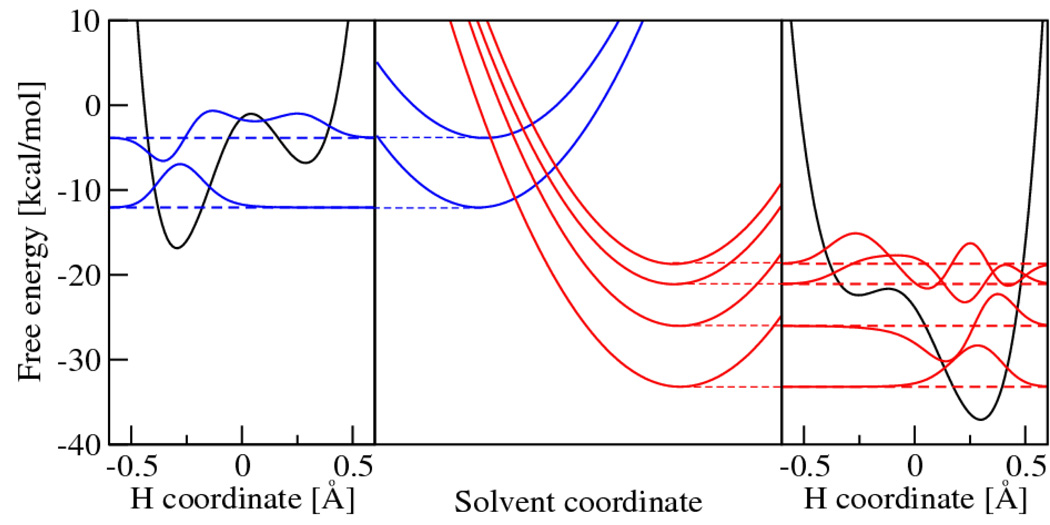
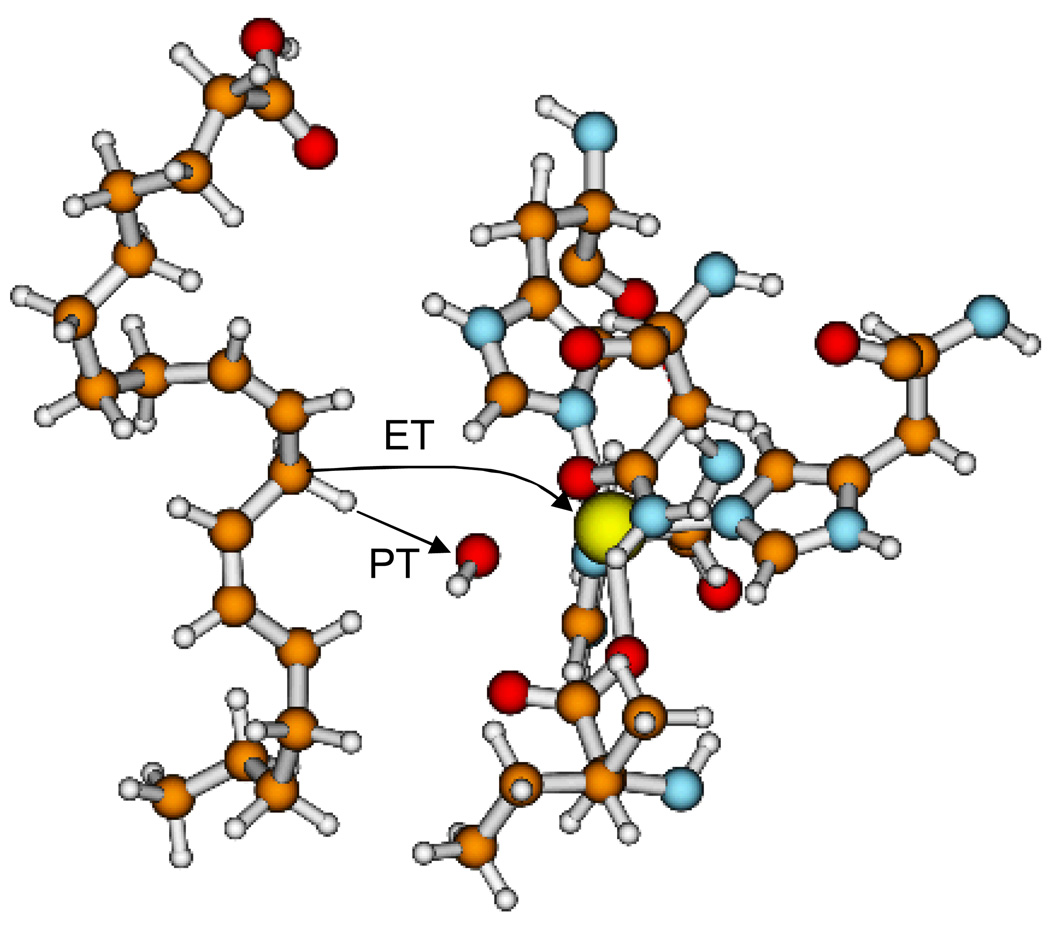
The details of this mechanism can be elucidated by viewing a slice of the free energy surfaces along the line connecting the two minima of the paraboloids, as shown in Figure 3. This figure also shows the proton potential energy curves and associated proton vibrational states for the solvent coordinates corresponding to the reactant minimum, the crossing point, and the product minimum. The shapes of the proton potential energy curves are not significantly affected by the solvent coordinates in the region of interest. However, the changes in the solvent coordinates along the reaction path strongly impact the relative energies of the proton potential energy curves. For a given pair of vibronic states in the normal Marcus regime, the reactant vibronic state is lower in energy at the reactant minimum, the product vibronic state is lower in energy at the product minimum, and the reactant and product vibronic states are degenerate at the crossing point. As mentioned above, the proton vibrational ground state wavefunction is localized near the donor for the reactant state and near the acceptor for the product state. In general, the excited vibronic states may also play an important role in PCET reactions. Figure 4 depicts slices of the free energy surfaces and the corresponding proton vibrational wavefunctions for two reactant and four product vibronic states for PCET in a rhenium-tyrosine complex, which will be discussed below.
Figure 3.
Slices of the free energy surfaces for the ground reactant (I) and product (II) vibronic states along a collective solvent coordinate. The proton potential energy curves along the proton coordinate and the corresponding ground state proton vibrational wavefunctions are depicted for the reactant minimum, the crossing point, and the product minimum of the free energy curves. The energies of these proton vibrational states correspond to the open circles on the free energy curves. The proton potential energy curves associated with the crossing point are shifted higher in energy for clarity.
Figure 4.
Free energy surfaces for the PCET reaction in a rhenium-tyrosine complex.88 In the center frame are slices of the free energy surfaces along a collective solvent coordinate. In the left frame is the reactant (I) proton potential energy curve and the corresponding proton vibrational wavefunctions along the proton coordinate evaluated at the minimum of the ground state reactant free energy surface. In the right frame is the product (II) proton potential energy curve and the corresponding proton vibrational wavefunctions along the proton coordinate evaluated at the minimum of the ground state product free energy surface. Figure reproduced with permission from Ref. 88.
As mentioned above, the probability of a nonadiabatic transition between two vibronic states is determined by the square of the vibronic coupling between these two states. This coupling is defined as the Hamiltonian matrix element between the reactant and product vibronic wavefunctions. In the electronically nonadiabatic regime, the vibronic coupling is the product of the electronic coupling between the reactant and product electronic states and the overlap between the reactant and product proton vibrational wavefunctions. In general, however, this simple factorization is not valid. This issue will be discussed below in the context of differentiating between HAT and PCET mechanisms.
C. Rate constant expressions
A series of expressions for PCET rate constants have been derived in various well-defined limits.50,52 All of the expressions given here are based on Fermi’s Golden rule formalism, which is valid in the vibronically nonadiabatic limit, in conjunction with linear response theory. The input quantities for these rate constant expressions can be calculated with a dielectric continuum representation of the solvent or with molecular dynamics simulations based on an explicit molecular representation of the solvent.
For fixed proton donor-acceptor distance R, the rate constant is:50
| (2) |
where the summations are over reactant and product vibronic states, Pμ is the Boltzmann probability for the reactant state μ, Vμν is the vibronic coupling between the reactant and product vibronic states μ and ν, λμν, is the solvent reorganization energy for states μ and ν, and is the free energy of reaction for states μ and ν. The latter two parameters are defined in Figure 2. All of these quantities depend on the fixed proton donor-acceptor distance R. The free energy of reaction can be expressed as the sum of the value for the ground states and the difference between the product and reactant energy levels ν and μ relative to their respective ground states. Note that Eq. (2) is related to the Marcus-Levich-Dogonadze expression74–76 for electron transfer with the proton treated as an inner-sphere quantum solute mode.77 Since the formulation leading to Eq. (2) includes the coupling between the proton and the solvent, however, the quantities in Eq. (2) are defined in terms of two-dimensional paraboloids rather than one-dimensional parabolas, the reorganization energies can vary for different pairs of states, and the vibronic coupling does not rigorously factor into the product of an electronic coupling and a Franck-Condon overlap. The effects of varying R may be included by thermally averaging this rate constant over R. This thermal averaging procedure involves calculating the rate constant in Eq. (2) for a range of R values and integrating over the R coordinate, weighting each rate constant by the Boltzmann probability for that value of R.52
We have also derived rate constant expressions that include the dynamical effects of the R coordinate and the solvent.52 In this formulation, the rate constant is represented by the time integral of a time-dependent probability flux correlation function. This formulation accounts for correlations between the fluctuations of the R mode and the vibronic couplings. Specifically, the vibronic coupling is assumed to depend exponentially on R:
| (3) |
where R̅μ is the equilibrium value of R for the reactant state μ, and is the vibronic coupling between states μ and ν at distance R̅μ. This form of the coupling is a reasonable approximation in the region of R near its equilibrium value, as illustrated by expanding in a Taylor series around R = R̅μ and retaining only the linear terms.78
In this dynamical formulation, the probability flux correlation function is expressed in terms of the vibronic coupling and the time correlation functions of the R coordinate, the energy gap, and the derivative of the energy gap with respect to the R coordinate. The rate constant is then obtained by numerical integration of the time integral of the probability flux correlation function. In practice, these time correlation functions can be calculated from classical molecular dynamics simulations of the entire system moving on the reactant surface. The advantage of this formulation is that it can be used in conjunction with any potential energy surface and includes the dynamical effects of the solvent and R mode. The disadvantage of this rate constant expression is that it requires numerical integration over time, and its complicated form is not conducive to the analysis of experimental data.
Closed analytical expressions for the rate constant have been obtained in a number of well-defined limits. Using the short-time, high-temperature approximation for the solvent modes and representing the R-mode time correlation function by that of a quantum mechanical harmonic oscillator, the rate constant can be expressed as:52
| (4) |
with the dimensionless parameters defined as
| (5) |
Here is the coupling reorganization energy defined as , and λR is the R-mode reorganization energy defined as λR = MΩ 2 δR, where M and Ω are the R-mode effective mass and frequency, respectively, and δR = R̅ν–R̅μ. According to this notation, δR is assumed to be the same for all pairs of states, although in general it could be allowed to vary for different pairs of states. Moreover, the solvent reorganization energy is assumed to be the same for all pairs of states (i.e., λμν = λs for all pairs of states). The short-time, high-temperature approximation for the solvent is valid when the solvent reorganization energy λs is large enough to ensure that the time decay of the probability flux correlation function is dominated by the strong damping term originating from the equilibrium solvent fluctuations. In this limit, the dynamics of the solvent fluctuations are fast on the time scale of the coherent nonadiabatic transitions. Eq. (4) provides the rate constant in terms of physically meaningful parameters, rather than general time correlation functions, but it still requires the numerical integration over time.
This rate constant expression can be simplified further in certain limiting regimes pertaining to the R-mode frequency. In the high-temperature (low-frequency) limit for the R mode (hΩ <<k B T), the rate constant simplifies to58
| (6) |
where the total reorganization energy is defined as . This expression can be derived from Eq. (4) above by performing a short-time expansion of the trigonometric functions and subsequently evaluating the time integral analytically. Alternative derivations based on different mathematical approximations lead to slight differences in the expression.52,79 Related expressions have been derived for vibrationally nonadiabatic proton transfer reactions43,44 and for electron transfer reactions.80
The rate constant expression in Eq. (6) can be further simplified by assuming that δR = 0 (i.e., the equilibrium R value is the same for the reactant and product vibronic states) and , which is equivalent to the replacement of the R-mode time correlation function with its value at zero time. The simplified rate constant expression is79
| (7) |
The only difference between Eq. (7) and the original expression in Eq. (2) for fixed R is the temperature-dependent exponential prefactor , which arises from the dependence of the vibronic coupling on R. This prefactor leads to non-Arrhenius behavior at high temperatures. Moreover, if the R dependence of the rate constant in Eq. (2) is assumed to arise solely from the vibronic coupling, which in turn is assumed to depend exponentially on R, Eq. (7) is identical to the thermal average of the rate constant in Eq. (2) over R.81
In the low-temperature (high-frequency) limit for the R mode (βhΩ>>1), the rate constant has the following form:52
| (8) |
This analytical expression is derived using the stationary phase method and is valid only in the strong solvation regime (i.e., for all relevant pairs of states). In this limit, the R-mode remains predominantly in its ground state, and the excited states become inaccessible due to the large vibrational energy level splittings hΩ. For this reason, the R-mode cannot effectively participate in the energy dissipation mechanism, so its reorganization does not contribute to the activation energy. In this limit, the sole effect of the R-mode on the rate constant is that the vibronic coupling is averaged over the ground state vibrational wavefunction of the R-mode.
The effects of intramolecular solute modes (i.e., inner-sphere reorganization) may easily be incorporated within this theoretical framework. We have extended the rate constant expression given in Eq. (2) to include quantum mechanical harmonic solute modes uncoupled to the solvent and the proton coordinate by utilizing the corresponding theoretical developments for electron transfer reactions.50,77,82,83 In the high-temperature approximation for the uncoupled solute modes, the rate constant expressions given above are modified by adding the inner-sphere reorganization energy to the solvent reorganization energy. The inner-sphere reorganization energy can be calculated with standard methods based on the frequencies and changes in equilibrium bond lengths for the solute modes84 or from other quantum mechanical methods.85
Analysis of the rate constant expressions given above enables the prediction of qualitative trends for the dependence of the rate constant and the KIE (i.e., the ratio of the rate constant for hydrogen to the rate constant for deuterium) on the proton donor-acceptor distance R. As will be discussed in Section III, the vibronic coupling can be approximated as the product of an electronic coupling and the overlap Sμν between the reactant and product proton vibrational wavefunctions in the electronically nonadiabatic regime. For a given pair of vibronic states, the rate constant is proportional to the square of the vibronic coupling, which in turn is proportional to , the square of the hydrogen vibrational wavefunction overlap for that pair of states. Thus, the rate constant decreases as the hydrogen overlap SH decreases (i.e., as the proton donor-acceptor distance R increases). The KIE is proportional to , the ratio of the squares of the hydrogen overlap and the deuterium overlap, for a given pair of vibronic states. Due to the larger mass of deuterium, the deuterium overlap decreases faster than the hydrogen overlap as the proton donor-acceptor distance R increases. Thus, the ratio , and therefore the KIE, increase as the distance R increases when only the ground reactant and product vibronic states contribute to the total reaction rate. For many systems, however, excited vibronic states contribute to the total reaction rate. The relative weighting of the contribution from each pair of reactant and product vibronic states is determined by a combination of the Boltzmann population of the reactant state, the free energy barrier, and the vibronic coupling. These relative weightings are often different for hydrogen and deuterium, and they are influenced by the distance R in a complex manner. Moreover, the dominant mechanism will become single ET when R becomes too large for proton transfer to be favorable. Thus, the dependence of the KIE on R is not always straightforward.
These rate constant expressions may also be used to predict the temperature dependence of the KIE. This analysis is facilitated by a simple expression for the KIE obtained from Eq. (7) including only the ground reactant and product vibronic states:79
| (9) |
This expression indicates that the temperature dependence of the KIE is determined mainly by the proton donor-acceptor frequency and the distance dependence of the vibronic couplings. The magnitude of the KIE is determined by these parameters, as well as the ratio of the overlaps. According to Eq. (9), the temperature dependence of the KIE increases as the frequency of the proton donor-acceptor mode decreases. As mentioned above, however, excited vibronic states often contribute to the total reaction rate, so this trend may not always be followed. Moreover, Eq. (9) is valid only in the low-frequency limit for the R-mode.
III. Distinguishing between HAT and PCET mechanisms
Traditionally, reactions in which the electron and proton transfer between the same donor and acceptor are denoted HAT, and reactions in which the electron and proton transfer between different donors and acceptors are denoted PCET. This criterion is not rigorous because the electron and proton behave quantum mechanically and hence are not localized to a specific point at any given time. Within the general theoretical framework based on the four diabatic states given in Eq. (1), HAT is a type of PCET reaction with De ≡ Dp and Ae ≡ Ap. From a mechanistic perspective, however, HAT and PCET reactions are fundamentally different and may require different rate constant expressions. In particular, HAT does not involve significant charge redistribution, so the solvent reorganization energy is very small. Thus, the collective solvent coordinates used in Marcus theory may not provide a physically meaningful description of these systems, and an explicit treatment of the dynamics of the specific modes coupled to hydrogen transfer may be required. The traditional nonadiabatic approaches based on the application of Fermi’s golden rule may also require special treatment such as the inclusion of the coupling between the proton donor-acceptor vibrational mode and the solvent modes to avoid divergent integrals within the probability flux correlation function formalism.86 In addition, typically HAT reactions are electronically adiabatic, while PCET reactions are electronically nonadiabatic, leading to different expressions for the vibronic couplings.66,67
We have proposed a quantitative diagnostic for differentiating between HAT and PCET mechanisms based on the degree of electronic nonadiabaticity for the proton transfer reaction.66 Both HAT and PCET mechanisms are usually vibronically nonadiabatic because the overall vibronic coupling between reactant and product states is much less than the thermal energy k B T (i.e., the quantum subsystem comprised of the electrons and transferring proton does not respond instantaneously to the solvent motions). Even for vibronically nonadiabatic reactions, however, the proton transfer can be electronically adiabatic, electronically nonadiabatic, or in the intermediate regime. Here the electronically nonadiabatic and adiabatic limits for general PCET reactions refer to the relative timescales of the rearranging electrons and the transferring proton. The electrons respond instantaneously to the proton motion in the electronically adiabatic limit but not in the electronically nonadiabatic limit.
The degree of electronic nonadiabaticity can be determined using the semiclassical formulation developed by Georgevskii and Stuchebrukhov.67 Their formulation can be analyzed in the context of the two proton potential energy curves corresponding to the diabatic electronic states I and II, as depicted schematically in Figure 1c. Georgevskii and Stuchebrukhov derived a semiclassical expression for the general vibronic coupling in terms of the adiabatic vibronic coupling : 67
| (10) |
where the factor κ is defined as
| (11) |
Here Γ(x) is the gamma-function, and p is the proton adiabaticity parameter defined as
| (12) |
where Vel is the electronic coupling between the diabatic electronic states, νt is the tunneling velocity of the proton at the crossing point of the two proton potential energy curves, and |ΔF| is the difference between the slopes of the proton potential energy curves at the crossing point. The tunneling velocity νt can be expressed in terms of the energy Vc at which the potential energy curves cross, the tunneling energy E, and the mass m of the proton: . In the electronically adiabatic limit, p>>1, κ = 1, and the vibronic coupling simplifies to . In the electronically nonadiabatic limit, p<<1, , and the vibronic coupling reduces to , where Sμν is the overlap between the reactant and product proton vibrational wavefunctions. The input quantities for the adiabaticity parameter can be calculated with conventional electronic structure methods.
The electronic nonadiabaticity of a general PCET reaction can be characterized in terms of the relative timescales for the proton tunneling and the electronic transition. Within the semiclassical framework, the time spent by the tunneling proton in the crossing region (i.e., the proton tunneling time) is τp ∼V el/|ΔF|νt, and the time required to change the electronic state (i.e., the electronic transition time) is τe ∼hV el. The adiabaticity parameter is simply the ratio of these two times: p=τp/τe. When the proton tunneling time is much longer than the electronic transition time, the electronic states have enough time to mix completely, and the proton transfer occurs on the electronically adiabatic ground state surface (i.e., the reaction is electronically adiabatic). When the proton tunneling time is much less than the electronic transition time, the reaction is electronically nonadiabatic because the electronic states no longer have enough time to mix completely during the proton tunneling process.
Within this theoretical framework, the adiabaticity parameter p given in Eq. (12) can be used to distinguish between the HAT and PCET mechanisms. Specifically, the HAT mechanism corresponds to the electronically nonadiabatic limit (i.e., p<<1), and the PCET mechanism corresponds to the electronically adiabatic limit (i.e., p>>1). In principle, some reactions could be in the intermediate regime between the HAT and PCET mechanisms. Characterization of the mechanism for a given reaction has important implications for calculating the vibronic coupling and understanding the fundamental physical properties of the system.
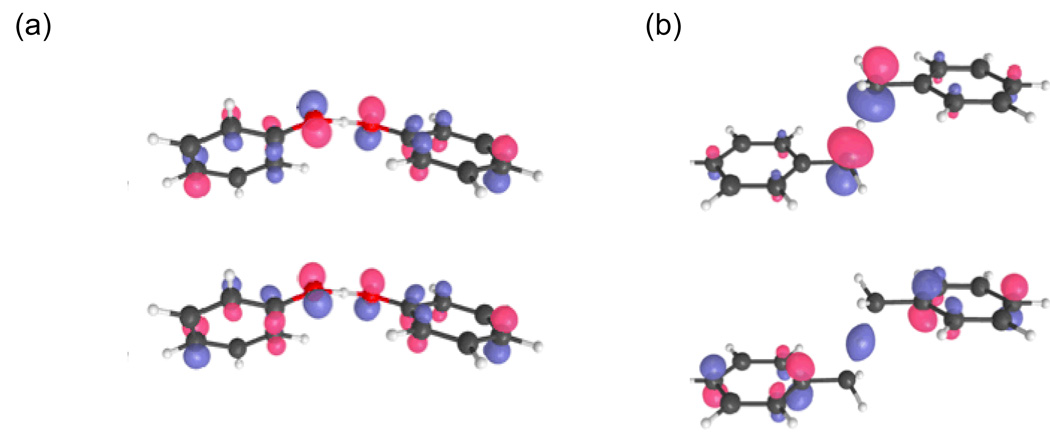
The distinction between HAT and PCET mechanisms is illustrated by a comparison between the phenoxyl/phenol and benzyl/toluene self-exchange reactions.66 As shown in Figure 5, the transition state geometries of the phenoxyl/phenol and the benzyl/toluene systems are qualitatively different. The phenoxyl/phenol transition state has C 2 symmetry, and the OΛHΛO bond is approximately planar with the phenol rings and represents a strong hydrogen bond. The benzyl/toluene transition state has C 2h symmetry, and the C(H(C bond is orthogonal to the planes of the benzene rings and does not form a strong hydrogen bond. Mayer, Borden, and coworkers distinguished between these two types of reactions by analyzing the singly occupied molecular orbitals (SOMOs) from density functional theory calculations of the transition state structures.28 The SOMO is dominated by 2p orbitals that are perpendicular to the proton donor-acceptor axis for the phenoxyl/phenol system, while the SOMO is dominated by atomic orbitals oriented along the donor-acceptor axis for the benzyl/toluene system. They concluded that the electron and proton are transferred between different sets of orbitals for the phenoxyl/phenol system but between the same sets of orbitals for the benzyl/toluene system, leading them to identify the former as PCET and the latter as HAT.
Figure 5.
The singly occupied molecular orbital (SOMO) for (a) the phenoxyl/phenol and (b) the benzyl/toluene system for the transition state structures. Figure reproduced with permission from Ref. 66.
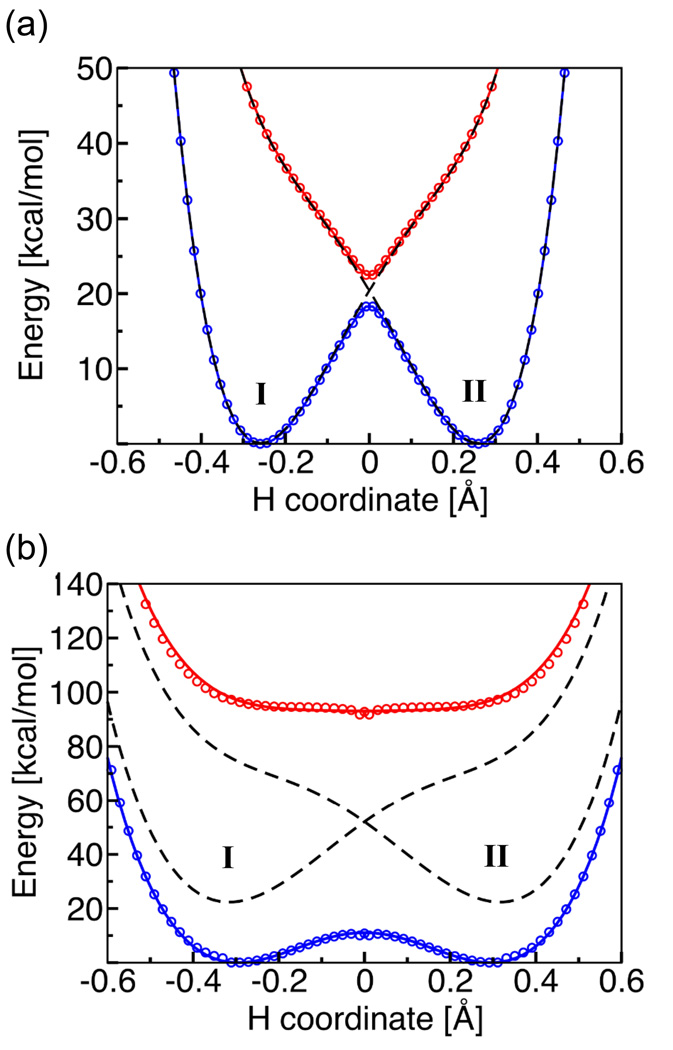
We analyzed these two reactions in terms of the degree of electronic nonadiabaticity, as determined by calculation of the adiabaticity parameter defined above.66 Our calculations indicated that the phenoxyl/phenol reaction involves electronically nonadiabatic proton transfer and corresponds to PCET, whereas the benzyl/toluene reaction involves electronically adiabatic proton transfer and corresponds to HAT. The input quantities for the adiabaticity parameter were obtained from the CASSCF (complete active space self consistent field) electronically adiabatic ground and excited state potential energy curves and the associated electronically diabatic potential energy curves depicted in Figure 6. Note that these diabatic curves are analogous to those depicted schematically in Figure 1c for the reactant and product states I and II. The mixing of these two diabatic states with the appropriate electronic coupling leads to the CASSCF electronically adiabatic curves. Figure 6 illustrates that the splitting between the electronically adiabatic ground and excited states at the transition state is more than an order of magnitude larger for the benzyl/toluene system than for the phenoxyl/phenol system. This larger splitting is associated with a larger electronic coupling between the two diabatic states.
Figure 6.
State-averaged CASSCF ground and excited state electronically adiabatic potential energy curves along the transferring hydrogen coordinate for (a) the phenoxyl/phenol and (b) the benzyl/toluene system. The coordinates of all nuclei except the transferring hydrogen correspond to the transition state geometry. The CASSCF results are depicted as open circles that are blue for the ground state and red for the excited state. The black dashed lines represent the diabatic potential energy curves corresponding to the two localized diabatic states I and II. The mixing of these two diabatic states with the electronic coupling V el leads to the CASSCF ground and excited state electronically adiabatic curves depicted with solid colored lines following the colored open circles. For the phenoxyl/phenol system, the solid colored lines and the black dashed lines are nearly indistinguishable because the adiabatic and diabatic potential energy curves are virtually identical except in the transition state region. Figure reproduced with permission from Ref. 66.
The calculated values of the adiabaticity parameter clearly differentiate these two self-exchange reactions. For the phenoxyl/phenol system, the adiabaticity parameter p is very small, with τe≈|80τp. In this case, the electronic transition time is significantly greater than the proton tunneling time, so the electrons are not able to rearrange fast enough for the proton to remain on the electronically adiabatic ground state surface. For the benzyl/toluene system, the adiabaticity parameter p is larger, with τp≈4τe. In this case, the electronic transition time is less than the proton tunneling time, so the electrons can respond instantaneously to the proton motion, allowing the proton to remain on the electronically adiabatic ground state surface. This analysis indicates that the proton tunneling is electronically nonadiabatic for the phenoxyl/phenol system but electronically adiabatic for the benzyl/toluene system, leading to the designation of a PCET mechanism for the phenoxyl/phenol system and an HAT mechanism for the benzyl/toluene system. This characterization is consistent with the qualitative analysis based on the SOMOs.
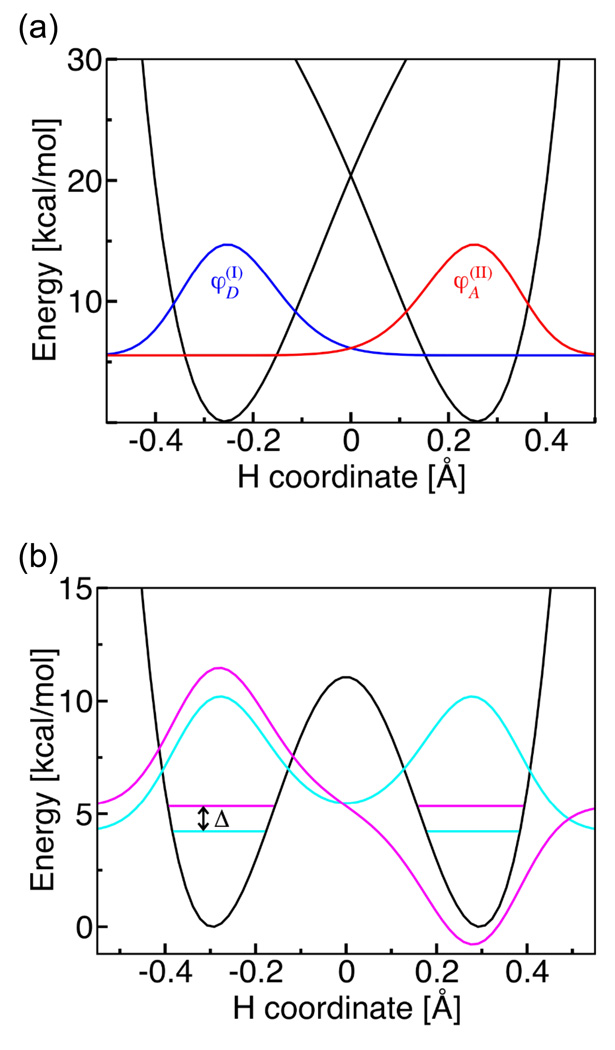
These two self-exchange reactions can also be used to illustrate the methods for calculating the vibronic coupling for general PCET reactions in the electronically nonadiabatic and electronically adiabatic limits. As indicated by the rate constant expressions given in Section II, the rate constant for vibronically nonadiabatic PCET reactions depends strongly on the vibronic coupling. Although the splittings between the ground and excited electronic states are significantly larger than the thermal energy k B T at room temperature for both self-exchange systems, the overall vibronic couplings for both systems were found to be smaller than k B T, indicating that the reactions are vibronically nonadiabatic with respect to a solvent environment. The qualitative difference between the methods for calculating the vibronic couplings for these two types of reactions is illustrated in Figure 7. For the electronically nonadiabatic phenoxyl/phenol reaction, the vibronic coupling is the product of the electronic coupling between the diabatic states and the overlap of the reactant and product proton vibrational wavefunctions corresponding to these diabatic states. For the electronically adiabatic benzyl/toluene reaction, the vibronic coupling is half the tunneling splitting (i.e., the energy splitting between the states corresponding to the symmetric and antisymmetric proton vibrational wavefunctions) for the electronically adiabatic ground state. For systems in the intermediate regime, the semiclassical expression in Eq. (10) can be used to calculate the vibronic coupling.
Figure 7.
(a) Diabatic potential energy curves corresponding to the two localized diabatic states I and II and the corresponding proton vibrational wavefunctions (blue) and (red) for the phenoxyl/phenol system. Since this reaction is electronically nonadiabatic, the vibronic coupling is the product of the electronic coupling V el and the overlap of the reactant and product proton vibrational wavefunctions . (b) Electronically adiabatic ground state potential energy curve and the corresponding proton vibrational wavefunctions for the benzyl/toluene system. Since this reaction is electronically adiabatic, the vibronic coupling is equal to half of the energy splitting Δ between the symmetric (cyan) and antisymmetric (magenta) proton vibrational states for the electronic ground state potential energy surface. For illustrative purposes, the excited vibrational state is shifted up in energy by 0.8 kcal/mol. Figure reproduced with permission from Ref. 66.
IV. Applications to PCET in solution
We have applied the theory described in Section II to numerous PCET reactions in solution.55 These studies include PCET in amidinium-carboxylate salt bridges, iron biimidazoline complexes, ruthenium-polypyridyl complexes, osmium-benzoquinone systems, ruthenium-polypyridyl-tyrosine systems, rhenium-polypyridyl-tyrosine systems, and thymine-acrylamide complexes. These calculations have reproduced the trends in rates and kinetic isotope effects, as well as the temperature and pH dependences in some cases. More importantly, they have elucidated the fundamental principles underlying PCET reactions and have assisted in the interpretation of unusual experimental data. In this section, we summarize the results of calculations on ruthenium-polypyridyl complexes and rhenium-polypyridyl-tyrosine complexes.
A. Ruthenium-polypyridyl complexes
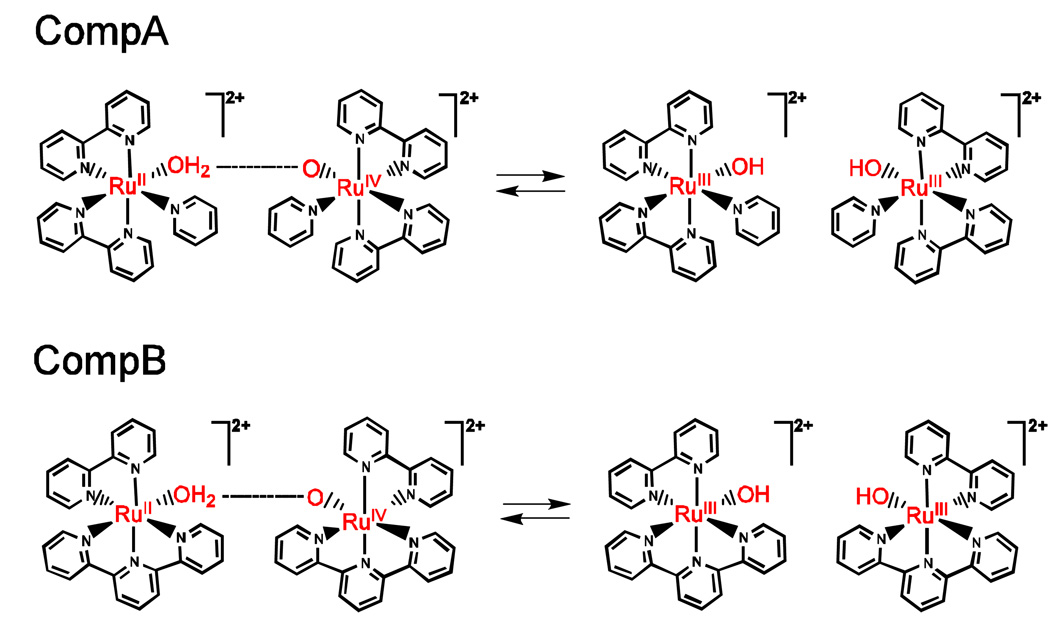
An experimental study of PCET in the ruthenium polypyridyl complexes7 shown in Fig. 8 revealed that the CompB rate is nearly one order of magnitude larger than the CompA rate, and the CompA KIE of 16.1 is larger than the CompB KIE of 11.4. These experimentally observed differences in rates and KIEs are quite significant given the relatively small chemical difference between the two systems. These trends can be explained within the framework of the PCET theory described above. The physical basis for these trends is the dependence of the rate constant on the overlap SH between the reactant and product proton vibrational wavefunctions and the increase in the overlap SH as the proton donor-acceptor distance R decreases. The dependence of PCET rate constants and KIEs on the distance R was analyzed in Section IIC.
Figure 8.
PCET comproportionation reactions in ruthenium polypyridyl complexes.
Based on this analysis, the qualitative trends in the rates and KIEs for the ruthenium polypyridyl systems can be explained in terms of differences in the proton donor-acceptor distance R. Density functional theory calculations on the acceptor complex illustrated that the steric crowding near the oxygen proton acceptor is significantly greater for CompA than for CompB, suggesting that the proton donor-acceptor distance R is greater for CompA than for CompB.87 We calculated the rate of PCET for these two systems using Eq. (2) in conjunction with a dielectric continuum representation of the solvent and an empirical valence bond representation of the solute. These calculations implied that the proton donor-acceptor distance is ∼0.06 Å larger for CompA than for CompB, leading to smaller proton vibrational wavefunction overlap for CompA than for CompB. Although excited vibronic states contribute to the total reaction rate, especially for deuterium transfer, the qualitative trends predicted by the analysis in Section IIC for PCET reactions involving only the ground vibronic reactant and product states are followed. According to this analysis, the larger distance and smaller overlap lead to the smaller rate and the larger KIE for CompA. Thus, the theory provides a simple explanation for the experimental observations.
B. Rhenium-tyrosine complex
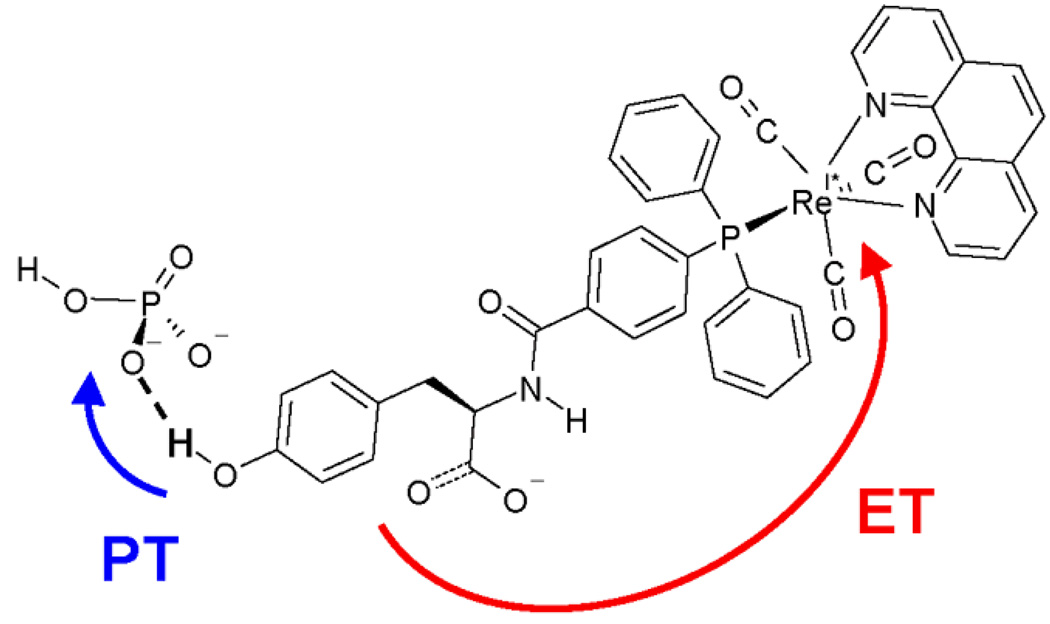
PCET in the tyrosine-bound rhenium polypyridyl complex shown in Figure 9 has been studied by photoexcitation of the metal-to-ligand charge transfer (MLCT) excited state of the ReYOH complex. Reese and Nocera analyzed the pH dependence of the rate constant for emission quenching in this complex following photoexcitation.2,4 The rate constant increases with pH in the range 4 < pH < 9 in the presence of phosphate buffer, indicating a PCET rather than an ET mechanism. In addition, the rate constant is independent of pH for 4 < pH < 8 in the absence of the phosphate buffer, suggesting that the phosphate buffer is the proton acceptor. Furthermore, the dependence of the rate on phosphate buffer concentration is absent at low pH, where the dominant buffer species is H2PO4 −, suggesting that the proton transfers to HPO4 2− but not to H2PO4 −. These experimental observations are consistent with a PCET mechanism in which the proton is transferred from the tyrosine to the phosphate buffer species HPO4 2− for 4 < pH < 9.
Figure 9.
Structure of the rhenium-tyrosine complex2 hydrogen bonded to a phosphate HPO4 2− acceptor. The proton transfer and electron transfer reactions are indicated with arrows. Figure reproduced with permission from Ref. 88.
We performed calculations aimed at explaining the preference for proton transfer to the phosphate buffer rather than to a water molecule.88 Density functional theory calculations of the ReYOH complex hydrogen bonded to HPO4 2− or to water indicated that the proton donor-acceptor distance R OO is ∼0.02 Å smaller for the phosphate acceptor due to its negative charge. This smaller proton donor-acceptor distance leads to a larger vibronic coupling because of the greater overlap between the reactant and product proton vibrational wavefunctions. Other important factors differentiating these two mechanisms include the differences in driving forces for PCET and the slightly smaller solvent reorganization energy for PCET when phosphate is the proton acceptor.
The pH-dependence of the overall rate can be explained in terms of a titration between the HPO4 2− and H2PO4 − forms of the phosphate buffer, where the proton is assumed to transfer to HPO4 2− but not to H2PO4 −. In this case, the overall rate constant for tyrosine oxidation can be expressed as4
| (13) |
where [Phosphate]T is the total concentration of phosphate buffer and is the mole fraction of , which can be calculated as a function of pH using the relation with pKa of 7.2 for HPO4 2−. In Eq. (13), is the bimolecular rate constant for the PCET reaction in which the proton is transferred to HPO4 2−, and k ET is the rate constant for an ET reaction that is followed by rapid PT to the solvent. The ET rate constant was determined from experimental measurements in the absence of phosphate buffer, and the bimolecular PCET rate constant was determined from measurements of kq as a function of phosphate buffer concentration at different pH values. The H/D KIE for the bimolecular PCET rate constant was determined to be ∼3.0 from measurements of kq as a function of phosphate buffer concentration at high pH in H2O and D2O.
We calculated the overall rate kq for hydrogen and deuterium transfer using the expression in Eq. (13) in conjunction with our PCET expression in Eq. (2) with a dielectric continuum representation of the solvent. The experimental and calculated data are depicted in Figure 10. We used the experimentally determined k ET and fit two parameters in the empirical valence bond potential to reproduce the experimentally determined and H/D KIE for . The rate constant expression in Eq. (2) applies to the unimolecular PCET reaction in a hydrogen-bonded complex. The calculated unimolecular PCET rate constant was converted to a bimolecular rate constant according to , where K eq is the known equilibrium association constant to form the hydrogen-bonded complex.
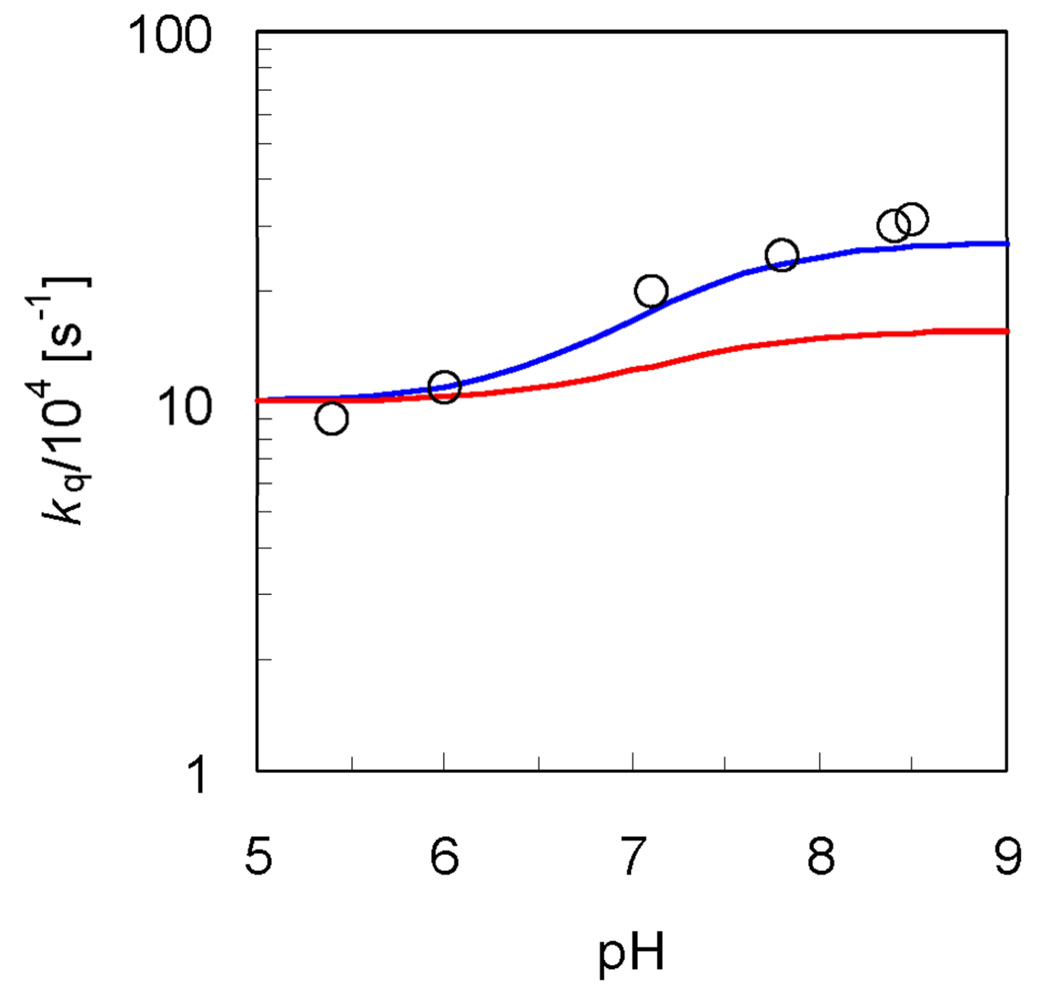
Figure 10.
pH-dependence of the overall rate constant k q for the rhenium-tyrosine complex in H2O and D2O. The experimental data for k q measured with 10mM phosphate buffer in H2O (Figure 3 in Ref. 2) are depicted with open circles (○). The rate constants for the phosphate-acceptor model with 10mM phosphate buffer calculated using Eq. (13) are depicted with blue and red lines for the reaction in H2O and D2O, respectively. The rate constant for the reaction in H2O or D2O is plotted as a function of pH or pD, respectively, where the mole fraction or is calculated as a function of pH or pD with pKa = 7.2 or 7.8, respectively. Figure reproduced in color with permission from Ref. 88.
Analysis of the PCET calculations provided insight into the reorganization energies, reaction free energies, activation free energies, and vibronic couplings for the various pairs of reactant/product vibronic states for both hydrogen and deuterium transfer. Based on experimental measurements for a related system,89 the inner-sphere reorganization energy was estimated to be 9.8 kcal/mol. The calculated outer-sphere reorganization energy for the overall PCET reaction was ∼33 kcal/mol for all pairs of vibronic states. The dominant contribution to the rate arose from nonadiabatic transitions between the ground reactant state and the third product state for hydrogen transfer and the fourth product state for deuterium transfer. These contributions exceed the contributions from the nonadiabatic transition between the ground reactant and product states because the larger vibronic coupling overrides the slightly higher activation free energy barrier. The larger vibronic coupling is due mainly to the greater overlap between the reactant and product proton vibrational wavefunctions for excited vibrational states. This effect is more pronounced for deuterium than for hydrogen. Figure 4 depicts the free energy surfaces and the corresponding proton vibrational wavefunctions for this system.
The physical basis for the experimentally observed pH dependence of PCET rates has been an issue of debate. In the case of the rhenium system discussed above, the proton acceptor has been clearly identified as a buffer species in solution, and therefore the pH dependence arises from the protonation equilibrium of the buffer.4 Similar behavior has been observed for tyrosine oxidation in other systems.90 In contrast, the pH dependence of tyrosine oxidation for one specific ruthenium-polypyridyl-tyrosine system has been observed to be independent of the buffer and has been interpreted in terms of proton transfer to bulk water.4,5 These data have been modeled with a pH-dependent driving force,5 which provides a phenomenological but not rigorous description of bulk solvent effects.91 As pointed out by Krishtalik,92 the driving force in the Marcus expression for the activation energy cannot depend on the mixing entropy of protons in bulk solution because the driving force is defined as the configurational free energy difference between the product and reactant hydrogen-bonded complexes. Moreover, as pointed out by Matyushov,93 when the driving force depends on pH without a compensating dependence of the reorganization energy on pH in Marcus theory, the mixing entropy of the protons appears in the vertical transition energy, which is nonphysical because the nuclei do not move on the timescale of electronic transitions. Thus, the explanation for the observed pH-dependence of tyrosine oxidation4,5 when the proton is transferred to bulk water is still not fully resolved. In general, the pH dependence may be due to several factors, including the kinetic complexity of the competing concerted and sequential PCET reaction pathways,94,95 deviations from the linear response relation in Marcus theory due to additional pH-dependent terms in the expressions for the free energies as functions of the energy gap,93 and the impact of pH on the physical properties of the proton transfer interface, such as hydrogen bond strength, proton donor-acceptor distance, and frequencies.
V. Application to PCET in proteins
PCET reactions also play a vital role in a variety of biological processes, including photosynthesis, respiration, and enzyme reactions. In this section, we summarize the results of our theoretical studies of the enzyme soybean lipoxygenase (SLO).79,96 Kinetic studies have shown that the hydrogen abstraction step for the oxidation of linoleic acid by SLO is rate-limiting above 32 °C.97 In this step, the pro-S hydrogen atom from carbon atom C11 of the linoleic acid substrate is transferred to the Fe(III)–OH cofactor, forming a radical intermediate substrate and Fe(II)–OH2.98 The deuterium KIE of this reaction was observed to be unusually high, with a value of 81 at room temperature,16,98 and the temperature dependences of the rates and KIEs were found to be relatively weak.16 The SLO reaction has been studied with a variety of theoretical approaches.16,26,38,79,96,98–106
The hydrogen abstraction step of the reaction catalyzed by SLO is depicted in Figure 11. Quantum mechanical calculations indicate that this step occurs by a PCET mechanism, in which the electron transfers from the π-system of the substrate to the iron of the cofactor, while the proton transfers from the C11 carbon of the substrate to the hydroxyl ligand of the cofactor.103 This PCET mechanism is also supported by a thermodynamic analysis based on electrochemical data indicating that the single proton and electron transfer reactions are highly endothermic by 30–40 kcal/mol, whereas the PCET reaction is slightly exothermic by ∼5 kcal/mol.16,96 Thus, the concerted PCET mechanism avoids the high-energy intermediates of the sequential mechanism.
Figure 11.
The hydrogen abstraction step of the reaction catalyzed by soybean lipoxygenase with its natural substrate linoleic acid. In this step, a hydrogen is abstracted from the linoleic acid to the iron cofactor. Figure reproduced with permission from Ref.79.
We applied the multistate dielectric continuum theory for PCET reactions to the reaction catalyzed by SLO.96 The inner-sphere reorganization energy of the iron cofactor was determined to be ∼19 kcal/mol from density functional theory calculations on a model system. The outer-sphere reorganization energy of the protein was calculated to be ∼2.5 kcal/mol with an electrostatic dielectric continuum model for conformations obtained from docking simulations. The total reorganization energy was estimated to be the sum of these inner-sphere and outer-sphere components. The gas phase empirical valence bond matrix elements were represented by standard molecular mechanical terms. The relative energies of the valence bond states were fit to electrochemical data, and the ET and PT couplings were fit to the experimental rate and KIE at 303 K.
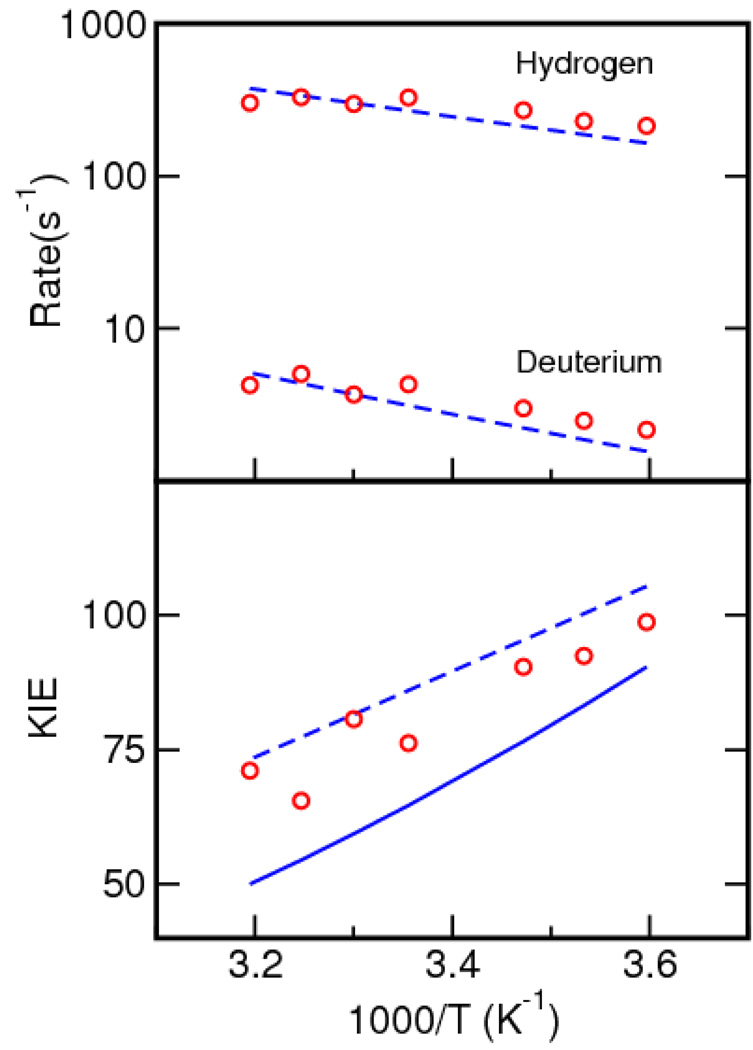
As shown in Figure 12, the calculations reproduced the experimentally determined temperature dependence of the rates and KIEs.16 The weak temperature dependence of the rate is due to the small free energy barrier, which arises from a balance between the total reorganization energy and the driving force. The unusually large KIE of 81 at room temperature results from the relatively small overlap of the reactant and product vibrational wavefunctions and the dominance of the lowest energy reactant and product vibronic states for the tunneling process. The overlap is relatively small because of the weak hydrogen bond between the carbon donor and the oxygen acceptor.
Figure 12.
Temperature dependence of the rates and KIE for soybean lipoxygenase. The dashed lines depict the rates and KIE obtained with Eq. (2) in conjunction with the multistate continuum theory. The solid line depicts the temperature dependence of the KIE obtained with Eq. (7) in conjunction with molecular dynamics simulations of the entire solvated enzyme to obtain the solvent reorganization energy and the average value and frequency of the R coordinate, as well as quantum calculations on a model system to obtain the vibronic coupling parameters. The experimental data are depicted with circles.16 The theoretical data were obtained from Ref. 96 and 79.
We also investigated the dependence of the rate on the proton donor-acceptor distance. In this early work, we calculated the rate constant using Eq. (2) and performing a thermal average over the R coordinate. The maximum contribution to the rate was found to occur at a C–O distance of ∼2.7 Å. The equilibrium C–O distance is significantly larger than this dominant distance, and the Boltzmann probability at 2.7 Å is extremely small. On the other hand, the coupling between the vibronic states increases dramatically as the C–O distance decreases. The dominant distance is determined by a balance between the larger coupling and the smaller Boltzmann probability as the C–O distance decreases. The rate is dominated by a relatively low-probability C–O distance because of the larger coupling. If the system were frozen, the C–O distance would not be able to decrease enough to allow efficient catalysis. Thermal motions of the enzyme are critical to ensure sampling of these smaller C–O distances to enable effective catalysis.
To further explore the role of enzyme motion in the SLO reaction, we applied the probability flux correlation function formalism to this system.79 This formulation includes the explicit solvent and protein environment, as well as the dynamical effects of the R mode and the solvent and protein. As discussed in Section IIC, the rate constant is represented by the time integral of a probability flux correlation function that depends on the vibronic coupling and on the average values and time correlation functions of the R coordinate, the energy gap, and the derivative of the energy gap with respect to the R coordinate. The vibronic couplings were estimated to within a constant factor by calculating the overlaps between reactant and product hydrogen vibrational wavefunctions for model systems, and the other quantities were calculated from classical molecular dynamics simulations of the entire solvated enzyme at atomic resolution.
Based on these molecular dynamics simulations, we analyzed the dynamical behavior of the protein, substrate, and cofactor. We found that the dynamical behavior (i.e., the time dependence) of the probability flux correlation function is dominated by the equilibrium protein and solvent motions and is not significantly influenced by the proton donor-acceptor motion. The magnitude of the overall rate, however, is strongly influenced by the frequency of the proton donor-acceptor motion and the protein/solvent reorganization energy. Typically, a lower frequency of the proton donor-acceptor motion leads to a faster rate because it enables the system to sample smaller values of R that correspond to greater vibronic coupling. Morever, a larger protein/solvent reorganization energy leads to a faster decay of the probability flux correlation function and therefore a slower rate.
Following this analysis, we calculated the rate using the analytical expression given in Eq. (6), which is based on the short-time, high-temperature approximation for the solvent/protein and the R-mode. We verified that these approximations are valid for this system. This analysis illustrated that only the equilibrium motions, specifically the average value and the variance, of the energy gap and the R-mode impact the rate. We determined the frequency of the R motion and the total reorganization energy from the variance of the R coordinate and energy gap distributions, respectively, in the molecular dynamics simulations. These simulations provided an estimate of 39 kcal/mol for the total reorganization energy. As shown in Figure 12, these calculations lead to KIEs that are in excellent agreement with the experimental data. The advantage over our earlier calculations with the multistate continuum theory is that no fitting to the kinetic data was required, but rather all input was determined from the molecular dynamics simulations and the coupling calculations. Note that this analysis provides the KIE, but not the independent rate constants for hydrogen and deuterium transfer, because we did not calculate the value of the electronic coupling V el, which is assumed to be the same for hydrogen and deuterium and therefore is not required for calculating the KIE.
The analysis of the magnitude and temperature dependence of the KIE was facilitated by the simple expression for the KIE given in Eq. (9). As discussed in Section IIC, the temperature dependence of the KIE is strongly influenced by the proton donor-acceptor frequency. The magnitude of the KIE is also determined by the ratio of the overlaps, where a smaller overlap tends to lead to a larger KIE. Consistent with our earlier calculations, we found that the large KIE for SLO is due to the relatively small overlap between the reactant and product proton vibrational wavefunctions and the dominance of the ground vibronic states. The new insight provided by these dynamical calculations was that the weak temperature dependence of the KIE arises from the local nature of the R motion. As indicated by Eq. (9), the KIE becomes less temperature dependent as the proton donor-acceptor mode frequency increases, and a higher frequency is typically associated with a more localized, constrained motion.
VI. Electrochemical PCET
Electrochemical methods are highly suitable for probing the detailed mechanisms of PCET reactions because the reaction can be controlled through the electrode potential, and observables such as current density can be measured with high precision. The ability to measure the current density as a function of a continuous variable, namely the overpotential, without changing any other parameters in the system eliminates many of the complexities inherent to PCET reactions in solution and proteins. Recently we have extended the theory for homogeneous PCET described above to electrochemical PCET using the methods and techniques developed for electrochemical ET.58 The systematic derivations based on well-defined approximations provide a series of analytical expressions for the heterogeneous rate constants and current densities that are valid in specified regimes. They also provide a diagnostic for differentiating electrochemical PCET from ET.
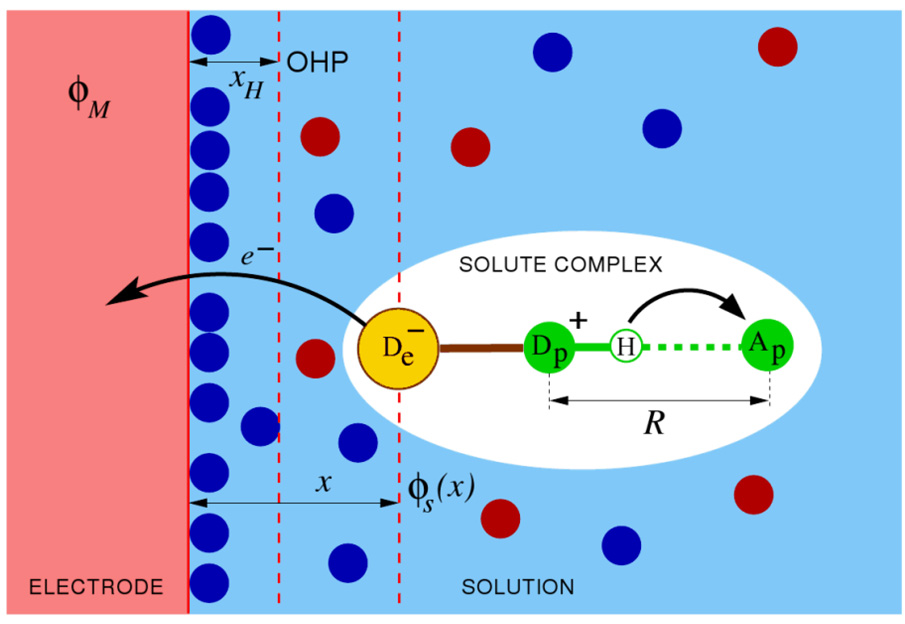
Figure 13 depicts the electrochemical PCET system under consideration. This system consists of a metal electrode immersed in a solution containing electrolyte ions and solute molecules capable of exchanging electrons with the electrode concurrently with a proton transfer reaction. The proton transfer is assumed to occur within a hydrogen-bonded solute complex, and the electron transfer reaction is assumed to occur only when the hydrogen-bonded solute complex is formed. The solute complex could be either a single solute molecule with an internal hydrogen bond or a solute molecule hydrogen bonded to another molecule, such as buffer or solvent.
Figure 13.
Schematic picture of the electrochemical PCET reaction system comprised of a solute complex near the surface of a metal electrode in solution. The electron transfers from the electron donor De of the solute complex to the electrode, and the proton transfers from Dp to Ap within the solute complex. Filled circles represent the ions of the supporting electrolyte in the solvent, φM is the inner potential of the electrode, φ S(x) is the electrostatic potential in solution at a distance x from the electrode surface, x H is the distance to the outer Helmholtz plane (OHP), and R is the proton donor-acceptor distance within the solute complex. Figure reproduced with permission from Ref. 58.
As in the homogeneous PCET theory, the electrochemical reaction is described in terms of nonadiabatic transitions between reactant and product electron-proton vibronic states. The transition probability W SC→m(x, ε)of PCET from the reduced solute complex located at a distance x from the electrode surface to a one-electron state in the metal electrode with energy ε was derived using the methods described in Section IIC. This procedure led to expressions analogous to Eq. (4) in the high-temperature limit for the solvent modes and then to Eq. (6) and Eq. (8), respectively, in the high-temperature and low-temperature limits for the R mode. The only significant difference is that the free energy of reaction is replaced by ΔGμν(x, ε), which depends on the overpotential η:58
| (14) |
where ΔUμν is the free energy difference between the product and reactant vibronic states for the solvated solute complex, and Q I and Q II are the total partition functions of the reduced and oxidized solute complexes, respectively, in bulk solution. Note that K B Tin(Q II/Q I)=–ΔU 00 when only the ground vibronic states are included in the partition functions, which is a reasonable approximation for the relatively high proton vibrational frequencies of ∼3000 cm−1. In Eq. (14), ϕ s(x) is the potential in solution at a distance x from the electrode surface due to the electrical double layer formed by the supporting electrolyte ions in the absence of the solute complex. The potential ϕ s(x) is defined to be zero for bulk solution [i.e.,ϕ s(∞)=0 ].
The most relevant expression for the oxidation transition probability W SC→M(x, ε) is analogous to Eq. (6) with the replacement of the reaction free energy by Eq. (14). The analogous reduction transition probability WM→SC+ (x,ε) corresponding to PCET from the metal one-electron state in the electrode with energy ε to the oxidized solute complex is different in two important ways. First, the term 2αμνδR k B T in the effective activation energy has the opposite sign. Second, the overall rate constant expression includes an additional prefactor exp[–2αμνδR]. These differences arise from the definition of the vibronic coupling in Eq. (3) relative to the equilibrium value of R for the reactant state. As discussed below, they lead to interesting physical characteristics of the current densities for electrochemical PCET reactions.
Given these expressions for the transition probabilities, the total first order rate constants are obtained by integrating over the energy levels in the conduction band of the electrode, weighting the transition probability according to the Fermi distribution f(ε)=[1+exp(βε)]−1 and the density of states ρ(ε) of the electrode. The resulting expressions for the oxidation and reduction rate constants are:
| (15) |
The anodic and cathodic current densities ja and jc defined for oxidation and reduction processes, respectively, are obtained by integrating the product of the rate constant and the relevant solute complex concentration over the distance x to the electrode surface:
| (16) |
where F is the Faraday constant, xH is the distance corresponding to the outer Helmoltz plane, and C SC(x) and C SC +(x) are the molar concentrations of the reduced and oxidized solute complexes, respectively, at a distance x from the electrode surface.
The integrals in Eq. (16) can be evaluated analytically under several well-defined assumptions. First, the rate constants are assumed to decrease exponentially with the distance x. This approximation is justified by noting that the nonadiabatic transition probabilities are proportional to the square of the vibronic coupling. As discussed in Section III, the vibronic coupling can often be approximated by the product of the proton vibrational wavefunction overlap and the electronic coupling, which is typically assumed to decrease exponentially with x as exp[–β′x]. Second, the solute complex concentration is assumed to maintain an equilibrium distribution in the diffuse layer and beyond. This assumption holds for low currents and a relatively low concentration of solute complexes in solution. Third, the Gouy-Chapman-Stern model of the double layer107,108 is used to obtain the potential ϕ s(x) in the diffuse layer. At low concentrations of the electrolyte, the current is dominated by PCET occurring at the outer Helmholtz plane, and the current densities are given by the expression:109
| (17) |
where and are the bulk concentrations of reduced and oxidized solute complex, respectively, and z is the charge of the reduced solute complex. At higher electrolyte concentrations, the current is dominated by PCET occurring outside the very thin diffuse layer, and the double layer corrections can be neglected so ϕ s(xH).
A simplified expression for the total current density as a function of the overpotential is obtained based on a series of additional assumptions. The effects of the double layer are neglected, the density of states is approximated by its value ρM at the Fermi energy, the proton potentials are assumed to be harmonic with frequency ωH, the proton transfer is assumed to be electronically nonadiabatic, and the electronic coupling V el is approximated by its value at the Fermi energy. In this case, the expression for the current density simplifies to:58
| (18) |
where is the proton vibrational wavefunction overlap evaluated at R̅μ.
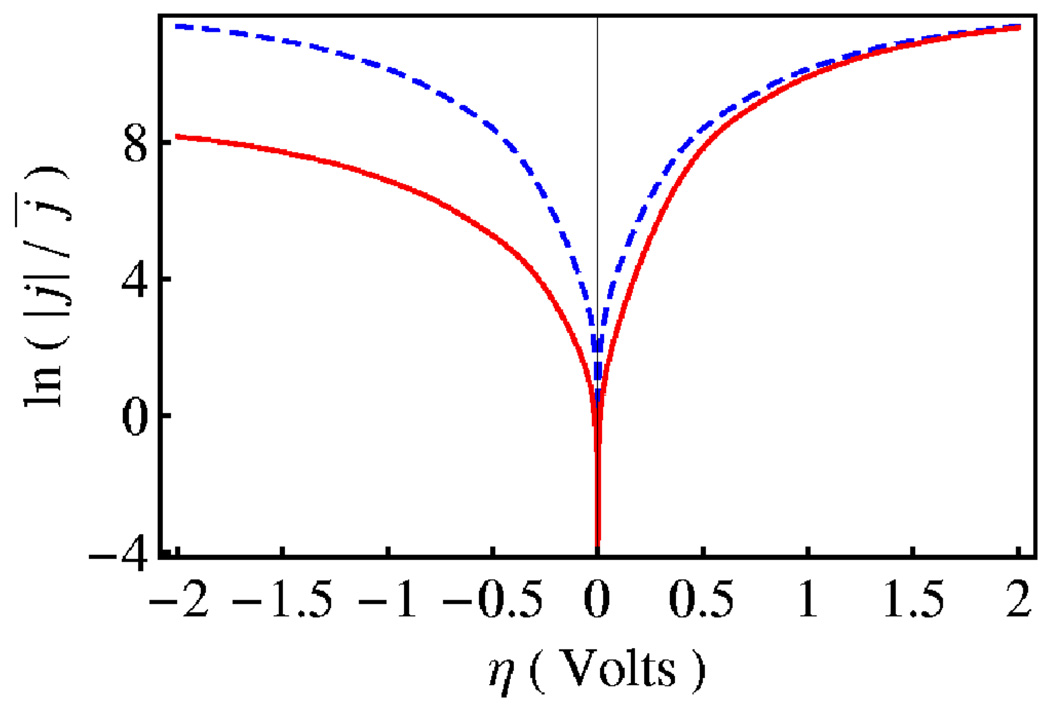
Although these expressions for current density are similar to those describing nonadiabatic electrochemical ET,40,110 a number of important differences arise for electrochemical PCET processes. The electrochemical PCET rate constants are calculated by summing over the reactant and product electron-proton vibronic states, and the excited vibronic states become particularly important at high voltages. As in electrochemical ET, the electronic coupling depends exponentially on the distance between the solute complex and the electrode surface. An important difference is that the vibronic coupling for PCET also depends strongly on the proton donor-acceptor distance. The modulation of the vibronic coupling by the proton donor-acceptor vibrational motion leads to three significant differences in the electrochemical PCET rate constant expressions. First, the total reorganization energy includes two additional contributions, namely the reorganization energy of the proton donor-acceptor mode and a coupling term associated with the modulation of the vibronic coupling by this mode. Second, the rate constants include an additional exponential temperature-dependent prefactor that depends on the frequency of this mode and the α parameter characterizing the modulation of the vibronic coupling by this mode. This prefactor leads to non-Arrhenius behavior of the rate constant at higher temperatures. Third, the effective activation energies contain temperature-dependent terms arising from the change in the equilibrium proton donor-acceptor distance upon electron transfer. This term has a different sign for the cathodic and anodic processes, leading to asymmetries of the theoretical Tafel plots even for small changes in the equilibrium proton donor-acceptor distance. This behavior is illustrated in Figure 14 for a model system.58 This asymmetry of the Tafel plot provides a diagnostic for differentiating between electrochemical PCET and ET. Thus, characteristics of electrochemical PCET are kinetic isotope effects, pH dependence, and asymmetric Tafel plots. These characteristics have been observed experimentally for osmium complexes attached to self-assembled monolayers on gold electrodes.22
Figure 14.
Logarithm of the scaled current density as a function of overpotential at T=300 K for a model electrochemical PCET system. The solid red and dashed blue curves correspond to δR= 0.05 Å and δR= 0, respectively. Data obtained from Ref. 58.
To facilitate the extension of this theory in a variety of directions, we developed a model system-bath Hamiltonian for electrochemical PCET.61 This model Hamiltonian is an extension of the Anderson-Newns-Schmickler model for electrochemical PCET59,60 but differs in a number of significant aspects. We have derived a Hamiltonian in a basis of electron-proton vibronic states defined within a double adiabatic approximation for the electrons, transferring proton, and bath modes.61 The vibronic coupling terms responsible for electronic transitions between the solute complex and the electrode depend on the proton donor-acceptor vibrational mode within the solute complex. The quasi-free electrons of the electrode are included explicitly in the model Hamiltonian, thereby allowing a detailed description of the electronic structure of the electrode and the description of semiconductor as well as metal electrodes. The vibronic structure of the Hamiltonian allows the inclusion of additional effects, such as the coupling of electrochemical PCET to the breaking and forming of other chemical bonds. This model Hamiltonian is currently being utilized for the derivation of general rate constant expressions valid in the adiabatic and nonadiabatic limits, as well as the intermediate regime.61
VII. Concluding remarks and future directions
This article has summarized some of the recent theoretical advances in the field of PCET. The elucidation of the fundamental physical principles underlying PCET reactions will enhance our understanding of many biological processes and has important implications for the design of effective catalysts, fuel cells, solar cells, and chemical sensors. Further progress in the field will benefit from feedback between theory and experiment, where theoretical calculations are used to make predictions that are tested experimentally, leading to further refinement of the theory. A long-term objective is to use theoretical treatments of PCET to design chemical systems that harness the energetic advantages of coupling electrons and protons.
Acknowledgments
S.H.-S. would like to acknowledge all of her group members who have worked on PCET and related topics over the past decade: Jian-Yun Fang, Hélène Decornez, Nedialka Iordanova, Ivan Rostov, Mark Kobrak, Claudio Carra, Elizabeth Hatcher, Yasuhito Ohta, Jonathan Skone, Hiroshi Ishikita, Charulatha Venkataraman, Irina Navrotskaya, Michelle Ludlow, and Sarah Edwards. This work has been supported over the years by NSF, NIH, and AFOSR.
Biographies
Sharon Hammes-Schiffer is the Eberly Professor of Biotechnology and Professor of Chemistry at The Pennsylvania State University. She received her B.A. in 1988 from Princeton University and her Ph.D. in Chemistry at Stanford University in 1993. She was a postdoc at AT&T Bell Laboratories and was appointed the Clare Boothe Luce Assistant Professor of Chemistry and Biochemistry at the University of Notre Dame in 1995. She has been at Pennsylvania State University since 2000, when she was appointed the Shaffer Associate Professor of Chemistry and subsequently appointed the Eberly Professor of Biotechnology in 2006. She is a Senior Editor for The Journal of Physical Chemistry. Hammes-Schiffer’s research centers on the investigation of proton and electron transfer reactions in chemical and biological processes. Her work encompasses the development of analytical theories and computational methods, as well as applications to a wide range of experimentally relevant systems. To simulate enzyme reactions, her group has developed a hybrid quantum/classical molecular dynamics approach. These simulations have provided insights into the roles of hydrogen tunneling and protein motion, as well as the impact of distal mutations. Her group has also contributed to the theory of proton-coupled electron transfer reactions in solution, proteins, and electrochemistry. In addition, her group has developed the nuclear-electronic orbital approach for including the quantum effects of selected nuclei in electronic structure calculations. A recent direction of her research is the development of electron-proton density functionals in multicomponent density functional theory.
Alexander V. Soudackov received his M.S. degree in chemistry in 1986 from Moscow State University and Ph.D. degree in physics and mathematics in 1992 from Karpov Institute of Physical Chemistry, Moscow. After completing his stay at the University of Hannover, Germany as an Alexander von Humboldt research fellow in 1994–1996 where he worked in the field of electronic structure of transition metal compounds, he worked in the group of Professor Basilevsky at Karpov Institute where he was involved in theoretical studies of dynamics of charge transfer reactions in condensed media, in particular proton transfer reactions in polar solvents. In 1998 he moved to the United States to join the group of Professor Hammes-Schiffer at the University of Notre Dame where he was involved in the development of the theory of proton-coupled electron-transfer reactions in solution. In 2000–2002 he also worked in the group of Professor Voth at the University of Utah developing the multistate empirical valence bond methodology for molecular dynamics simulations of proton transfer processes in condensed phase and studying the proton transfer processes in enzymes. He is currently a research assistant professor in the group of Professor Hammes-Schiffer at the Pennsylvania State University and his research interests include theory of proton-coupled electron transfer reactions in biological and electrochemical systems.
References
- 1.Roberts JA, Kirby JP, Nocera DG. Journal of the American Chemical Society. 1995;117:8051. [Google Scholar]
- 2.Reece SY, Nocera DG. Journal of the American Chemical Society. 2005;127:9448. doi: 10.1021/ja0510360. [DOI] [PubMed] [Google Scholar]
- 3.Rosenthal J, Nocera DG. Accounts of Chemical Research. 2007;40:543. doi: 10.1021/ar7000638. [DOI] [PubMed] [Google Scholar]
- 4.Irebo T, Reece SY, Sjodin M, Nocera DG, Hammarstrom L. Journal of the American Chemical Society. 2007;129:15462. doi: 10.1021/ja073012u. [DOI] [PubMed] [Google Scholar]
- 5.Sjodin M, Styring S, Akermark B, Sun L, Hammarstrom L. Journal of the American Chemical Society. 2000;122:3932. [Google Scholar]
- 6.Sjodin M, Irebo T, Utas JE, Lind J, Merenyi G, Akermark B, Hammarstrom L. Journal of the American Chemical Society. 2006;128:13076. doi: 10.1021/ja063264f. [DOI] [PubMed] [Google Scholar]
- 7.Binstead RA, Meyer TJ. Journal of the American Chemical Society. 1987;109:3287. doi: 10.1021/ja000517a. [DOI] [PubMed] [Google Scholar]
- 8.Fecenko CJ, Thorp HH, Meyer TJ. Journal of the American Chemical Society. 2007;129:15098. doi: 10.1021/ja072558d. [DOI] [PubMed] [Google Scholar]
- 9.Huynh MH, Meyer TJ. Chemical Reviews. 2007;107:5004. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roth JP, Lovel S, Mayer JM. J. Am. Chem. Soc. 2000;122:5486. [Google Scholar]
- 11.Mayer JM. Annual Review of Physical Chemistry. 2004;55:363. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 12.Rhile IJ, Mayer JM. Journal of the American Chemical Society. 2004;126:12718. doi: 10.1021/ja031583q. [DOI] [PubMed] [Google Scholar]
- 13.Roth JP, Yoder JC, Won T-J, Mayer JM. Science. 2001;294:2524. doi: 10.1126/science.1066130. [DOI] [PubMed] [Google Scholar]
- 14.Cape JL, Bowman MK, Kramer DM. Journal of the American Chemical Society. 2005;127:4208. doi: 10.1021/ja043955g. [DOI] [PubMed] [Google Scholar]
- 15.Stubbe J, Nocera DG, Yee CS, Chang MCY. Chemical Reviews. 2003;103:2167. doi: 10.1021/cr020421u. [DOI] [PubMed] [Google Scholar]
- 16.Knapp MJ, Rickert KW, Klinman JP. Journal of the American Chemical Society. 2002;124:3865. doi: 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]
- 17.Meyer MP, Klinman JP. Chemical Physics. 2005;319:283. doi: 10.1016/j.chemphys.2005.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tommos C, Tang X-S, Warncke K, Hoganson CW, Styring S, McCracken J, Diner BA, Babcock GT. Journal of the American Chemical Society. 1995;117:10325. [Google Scholar]
- 19.Hoganson CW, Lydakis-Simantiris N, Tang X-S, Tommos C, Warncke K, Babcock GT, Diner BA, McCracken J, Styring S. Photosynthesis Research. 1995;47:177. doi: 10.1007/BF00020428. [DOI] [PubMed] [Google Scholar]
- 20.Diner BA, Babcock GT. Structure, dynamics and energy conversion efficiency in photosystem II. In: Ort DR, Yocum CF, editors. Oxygenic Photosynthesis: The Light Reactions; Kluwer: Dordrecht: The Netherlands; 1996. p. 213. [Google Scholar]
- 21.Malmstrom BG. Accounts of Chemical Research. 1993;26:332. [Google Scholar]
- 22.Madhiri N, Finklea HO. Langmuir. 2006;22:10643. doi: 10.1021/la061103j. [DOI] [PubMed] [Google Scholar]
- 23.Costentin C, Robert M, Saveant J-M. Journal of the American Chemical Society. 2006;128:4552. doi: 10.1021/ja060527x. [DOI] [PubMed] [Google Scholar]
- 24.Li B, Zhao J, Onda K, Jordan KD, Yang J, Petek H. Science. 2006;311:1436. doi: 10.1126/science.1122190. [DOI] [PubMed] [Google Scholar]
- 25.Blomberg MRA, Siegbahn PEM, Styring S, Babcock GT, Akermark B, Korall P. Journal of the American Chemical Society. 1997;119:8285. [Google Scholar]
- 26.Olsson MHM, Siegbahn PEM, Warshel A. Journal of the American Chemical Society. 2004;126:2820. doi: 10.1021/ja037233l. [DOI] [PubMed] [Google Scholar]
- 27.Moore DB, Martinez TJ. Journal of Physical Chemistry A. 2000;104:2367. [Google Scholar]
- 28.Mayer JM, Hrovat DA, Thomas JL, Borden WT. Journal of the American Chemical Society. 2002;124:11142. doi: 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
- 29.Stuchebrukhov AA. Journal of Theoretical and Computational Chemistry. 2003;2:91. [Google Scholar]
- 30.Gunner MR, Mao JJ, Song YF, Kim J. Biochimica et Biophysica Acta-Bioenergetics. 2006;1757:942. doi: 10.1016/j.bbabio.2006.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Siegbahn PEM, Blomberg MRA, Crabtree RH. Theoretical Chemistry Accounts. 1997;97:289. [Google Scholar]
- 32.Sproviero EM, Gascon JA, McEvoy JP, Brudvig GW, Batista VS. Current Opinion in Structural Biology. 2007;17:173. doi: 10.1016/j.sbi.2007.03.015. [DOI] [PubMed] [Google Scholar]
- 33.Jones ML, Kurnikov IV, Beratan DN. Journal of Physical Chemistry. 2002;106:2002. [Google Scholar]
- 34.Xu J, Voth GA. Biochimica et Biophysica Acta. 2008;1777:196. doi: 10.1016/j.bbabio.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Peluso A, Di Donato M, Saracino GAA. Journal of Chemical Physics. 2000;113:3212. [Google Scholar]
- 36.Yamamoto T, Kato S. Journal of Chemical Physics. 2007;126:224514. doi: 10.1063/1.2737048. [DOI] [PubMed] [Google Scholar]
- 37.Peluso A, Brahimi M, Carotenuto M, Del Re G. Journal of Physical Chemistry A. 1998;102:10333. [Google Scholar]
- 38.Siebrand W, Smedarchina Z. Journal of Physical Chemistry B. 2004;108:4185. [Google Scholar]
- 39.Mincer JS, Schwartz SD. Journal of Chemical Physics. 2004;120:7755. doi: 10.1063/1.1690239. [DOI] [PubMed] [Google Scholar]
- 40.Marcus RA. Annual Reviews of Physical Chemistry. 1964;15:155. [Google Scholar]
- 41.Marcus RA, Sutin N. Biochimica et Biophysica Acta. 1985;811:265. [Google Scholar]
- 42.Kuznetsov AM, Ulstrup J. Canadian Journal of Chemistry. 1999;77:1085. [Google Scholar]
- 43.Borgis D, Lee S, Hynes JT. Chemical Physics Letters. 1989;162:19. [Google Scholar]
- 44.Borgis D, Hynes JT. Journal of Chemical Physics. 1991;94:3619. [Google Scholar]
- 45.Warshel A, Chu ZT. Journal of Chemical Physics. 1990;93:4003. [Google Scholar]
- 46.Cukier RI. Journal of Physical Chemistry. 1994;98:2377. [Google Scholar]
- 47.Cukier RI. Journal of Physical Chemistry. 1996;100:15428. [Google Scholar]
- 48.Cukier RI, Nocera DG. Annual Reviews of Physical Chemistry. 1998;49:337. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]
- 49.Soudackov A, Hammes-Schiffer S. Journal of Chemical Physics. 1999;111:4672. [Google Scholar]
- 50.Soudackov A, Hammes-Schiffer S. Journal of Chemical Physics. 2000;113:2385. [Google Scholar]
- 51.Hammes-Schiffer S. Accounts of Chemical Research. 2001;34:273. doi: 10.1021/ar9901117. [DOI] [PubMed] [Google Scholar]
- 52.Soudackov A, Hatcher E, Hammes-Schiffer S. Journal of Chemical Physics. 2005;122:014505. doi: 10.1063/1.1814635. [DOI] [PubMed] [Google Scholar]
- 53.Trakhtenberg LI, Klochikhin VL, Pshezhetsky SY. Chemical Physics. 1982;69:121. [Google Scholar]
- 54.Suarez A, Silbey R. Journal of Chemical Physics. 1991;94:4809. [Google Scholar]
- 55.Hammes-Schiffer S, Iordanova N. Biochimica et Biophysica Acta-Bioenergetics. 2004;1655:29. doi: 10.1016/j.bbabio.2003.07.009. [DOI] [PubMed] [Google Scholar]
- 56.Hammes-Schiffer S. Accounts of Chemical Research. 2006;39:93. doi: 10.1021/ar040199a. [DOI] [PubMed] [Google Scholar]
- 57.Costentin C, Robert M, Saveant J-M. Journal of Electroanalytical Chemistry. 2006;588:197. [Google Scholar]
- 58.Venkataraman C, Soudackov AV, Hammes-Schiffer S. Journal of Physical Chemistry C. 2008;112:12386. doi: 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Grimminger J, Bartenschlager S, Schmickler W. Chemical Physics Letters. 2005;416:316. [Google Scholar]
- 60.Grimminger J, Schmickler W. Chemical Physics. 2007;334:8. [Google Scholar]
- 61.Navrotskaya I, Soudackov AV, Hammes-Schiffer S. Journal of Chemical Physics. 2008;128:244712. doi: 10.1063/1.2940203. [DOI] [PubMed] [Google Scholar]
- 62.Benderskii VA, Goldanskii VI, Makarov DE. Physics Reports. 1993;233:195. [Google Scholar]
- 63.Garrett BC, Truhlar DG. Journal of Physical Chemistry. 1991;95:10374. [Google Scholar]
- 64.Cukier RI. Journal of Physical Chemistry B. 2002;106:1746. [Google Scholar]
- 65.Hammes-Schiffer S. ChemPhysChem. 2002;3:33. doi: 10.1002/1439-7641(20020118)3:1<33::AID-CPHC33>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 66.Skone JH, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2006;128:16655. doi: 10.1021/ja0656548. [DOI] [PubMed] [Google Scholar]
- 67.Georgievskii Y, Stuchebrukhov AA. Journal of Chemical Physics. 2000;113:10438. doi: 10.1063/1.1796751. [DOI] [PubMed] [Google Scholar]
- 68.Tishchenko O, Truhlar DG, Ceulemans A, Nguyen MT. Journal of the American Chemical Society. 2008;130:7000. doi: 10.1021/ja7102907. [DOI] [PubMed] [Google Scholar]
- 69.Soudackov AV, Hammes-Schiffer S. Chemical Physics Letters. 1999;299:503. [Google Scholar]
- 70.Fang J-Y, Hammes-Schiffer S. Journal of Chemical Physics. 1997;107:8933. [Google Scholar]
- 71.Basilevsky MV, Chudinov GE, Newton MD. Chemical Physics. 1994;179:263. [Google Scholar]
- 72.Kobrak MN, Hammes-Schiffer S. Journal of Physical Chemistry B. 2001;105:10435. [Google Scholar]
- 73.Rostov I, Hammes-Schiffer S. Journal of Chemical Physics. 2001;115:285. [Google Scholar]
- 74.Marcus RA. Journal of Chemical Physics. 1956;24:966. [Google Scholar]
- 75.Marcus RA. Journal of Chemical Physics. 1957;26:867. [Google Scholar]
- 76.Levich VG, Dogonadze RR. Dokl. Akad. Nauk SSSR. 1959;124:123. [Google Scholar]
- 77.Kestner NR, Logan J, Jortner J. Journal of Physical Chemistry. 1974;78:2148. [Google Scholar]
- 78.Hatcher E, Soudackov A, Hammes-Schiffer S. Chemical Physics. 2005;319:93. doi: 10.1063/1.1814635. [DOI] [PubMed] [Google Scholar]
- 79.Hatcher E, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2007;129:187. doi: 10.1021/ja0667211. [DOI] [PubMed] [Google Scholar]
- 80.Matyushov DV. Chemical Physics. 1992;164:31. [Google Scholar]
- 81.Hammes-Schiffer S, Hatcher E, Ishikita H, Skone JH, Soudackov AV. Coordination Chemistry Reviews. 2008;252:384. doi: 10.1016/j.ccr.2007.07.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bixon M, Jortner J. Advances in Chemical Physics. 1999;106:35. [Google Scholar]
- 83.Ulstrup J, Jortner J. Journal of Chemical Physics. 1975;63:4358. [Google Scholar]
- 84.Marcus RA. Journal of Physical Chemistry. 1963;67:853. [Google Scholar]
- 85.Basilevsky MV, Chudinov GE, Rostov IV, Liu Y-P, Newton MD. Journal of Molecular Structure (Theochem) 1996;371:191. [Google Scholar]
- 86.Ohta Y, Soudackov A, Hammes-Schiffer S. Journal of Chemical Physics. 2006;125:144522. doi: 10.1063/1.2354500. [DOI] [PubMed] [Google Scholar]
- 87.Iordanova N, Hammes-Schiffer S. Journal of the American Chemical Society. 2002;124:4848. doi: 10.1021/ja017633d. [DOI] [PubMed] [Google Scholar]
- 88.Ishikita H, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society (in press) 2007 doi: 10.1021/ja072708k. [DOI] [PubMed] [Google Scholar]
- 89.Reece SY, Seyedsayamdost MR, Stubbe J, Nocera DG. Journal of the American Chemical Society. 2006;128:13654. doi: 10.1021/ja0636688. [DOI] [PubMed] [Google Scholar]
- 90.Fecenko CJ, Meyer TJ, Thorp HH. Journal of the American Chemical Society. 2006;128:11020. doi: 10.1021/ja061931z. [DOI] [PubMed] [Google Scholar]
- 91.Carra C, Iordanova N, Hammes-Schiffer S. Journal of the American Chemical Society. 2003;125:10429. doi: 10.1021/ja035588z. [DOI] [PubMed] [Google Scholar]
- 92.Krishtalik LI. Biochimica et Biophysica Acta. 2003;1604:13. doi: 10.1016/s0005-2728(03)00020-3. [DOI] [PubMed] [Google Scholar]
- 93.Matyushov DV. arXiv:0710.2875. 2007 [Google Scholar]
- 94.Costentin C, Robert M, Saveant J-M. Journal of the American Chemical Society. 2007;129:5870. doi: 10.1021/ja067950q. [DOI] [PubMed] [Google Scholar]
- 95.Finklea HO. Journal of Physical Chemistry B. 2001;105:8685. [Google Scholar]
- 96.Hatcher E, Soudackov AV, Hammes-Schiffer S. Journal of the American Chemical Society. 2004;126:5763. doi: 10.1021/ja039606o. [DOI] [PubMed] [Google Scholar]
- 97.Glickman MH, Klinman JP. Biochemistry. 1995;34:14077. doi: 10.1021/bi00043a013. [DOI] [PubMed] [Google Scholar]
- 98.Rickert KW, Klinman JP. Biochemistry. 1999;38:12218. doi: 10.1021/bi990834y. [DOI] [PubMed] [Google Scholar]
- 99.Kuznetsov AM, Ulstrup J. Canadian Journal of Chemistry. 1999;77:1085. [Google Scholar]
- 100.Tresadern G, McNamara JP, Mohr M, Wang H, Burton NA, Hillier IH. Chemical Physics Letters. 2002;358:489. [Google Scholar]
- 101.Knapp MJ, Klinman JP. European Journal of Biochemistry. 2002;269:3113. doi: 10.1046/j.1432-1033.2002.03022.x. [DOI] [PubMed] [Google Scholar]
- 102.Olsson MHM, Siegbahn PEM, Warshel A. Journal of Biological Inorganic Chemistry. 2004;9:96. doi: 10.1007/s00775-003-0503-2. [DOI] [PubMed] [Google Scholar]
- 103.Lehnert N, Solomon EI. J. Biol. Inorg. Chem. 2003;8:294. doi: 10.1007/s00775-002-0415-6. [DOI] [PubMed] [Google Scholar]
- 104.Borowski T, Krol M, Chruszcz M, Broclawik E. Journal of Physical Chemistry B. 2001;105:12212. [Google Scholar]
- 105.Borowski T, Broclawik E. Journal of Physical Chemistry B. 2003;107:4639. [Google Scholar]
- 106.Tejero I, Eriksson LA, Gonzalez-Lafont A, Marquet J, Lluch JM. Journal of Physical Chemistry B. 2004;108:13831. [Google Scholar]
- 107.Bard AJ, Faulkner LR. Electrochemical Methods: Fundamentals and Applications. New York: Wiley; 1980. [Google Scholar]
- 108.Shaw DJ. Introduction to Colloid and Surface Chemistry. Boston: Butterworth-Heinemann; 1992. [Google Scholar]
- 109.Feldberg S, Sutin N. Chemical Physics. 2006;324:216. [Google Scholar]
- 110.Levich VG. In: Physical Chemistry: An Advanced Treatise; Eyring H, Henderson D, Jost W, editors. Vol. IXB. New York, London: Academic Press; 1970. p. 985. [Google Scholar]