Crystal Structure Prediction (CSP) of Flexible Molecules using Parallel Genetic Algorithms with a Standard Force Field

Abstract

This paper describes the application of our distributed computing framework for crystal structure prediction (CSP), Modified Genetic Algorithms for Crystal and Cluster Prediction (MGAC) to predict the crystal structure of flexible molecules using the General Amber Force Field (GAFF) and the CHARMM program. The MGAC distributed computing framework which includes a series of tightly integrated computer programs for generating the molecule’s force field, sampling crystal structures using a distributed parallel genetic algorithm, local energy minimization of the structures followed by the classifying, sorting and archiving of the most relevant structures. Our results indicate that the method can consistently find the experimentally known crystal structures of flexible molecules, but the number of missing structures and poor ranking observed in some crystals show the need for further improvement of the potential.

INTRODUCTION

Are crystal structures predictable? Since Angelo Gavezzotti posted this question in his 1994 review,¹ several research groups have been working towards the goal of predicting the crystal structures of molecules prior to their experimental determination. The prediction of crystal structures for organic molecules is of great importance for many industries such as pharmaceuticals, agrochemicals, pigments, dyes, explosives and specialty chemicals^2–4 due to the strong dependence of material properties on the crystal structure. Crystal structure prediction (CSP) is complicated by the fact that for many organic crystals a number of different polymorphic forms may exist. Polymorphism is the ability of a molecule to crystallize in more than one structure and thus having different values for properties such as solubility, bio-availability, shelf life, crystal size and color, vapor pressure, and shock sensitivity. The existence of polymorphic structures was originally thought to be a rarity but now it is known to be widely observed.^3,5–9 Moreover, CSP shares many similarities with the more popular protein-folding prediction problem,¹⁰ as both face unsolved questions such as the choice of force field, existence of many energy minima, and understanding of thermodynamic and kinetic factors.¹⁰

The ability to readily and reliably predict crystal structures has become a desirable goal for the modeling and crystal engineering communities. The periodic blind tests^10–12 of CSP organized by the Cambridge Crystallographic Data Centre (CCDC) have been the focal point for this community and they reflect the overall progress in the field. The tests show a continuous improvement in the capabilities for predicting the crystal structures of simple rigid molecules and indicate that the methods should now be extended to the more complex systems such as flexible molecules and co-crystals.^10–12 It is important to note that while the definition of success for the blind tests is to have the experimental structure within the top three ranked structures, much less stringent success criteria can be very useful in practical applications. For instance, when no single crystals are available and the experimental structure must be determined by other techniques like X-ray powder diffraction or solid state NMR, to have a reliable list of even several hundred possible candidate structures can be extremely valuable.^{13, 14}

CSP of flexible molecules is a great challenge for computational modeling because the energies of some of the inter- and intra- molecular interactions are of the same order of magnitude, whereas among rigid molecules the energies of intermolecular interactions are much smaller than the ones associated with the internal degrees of freedom.^3,6 Successful predictions of crystal structures of flexible molecule have been reported in the literature,^{3,10,11,15,16,17–22} but no universal approach has emerged as a good candidate method for high throughput studies, an important goal for the pharmaceutical industry.

There are several approaches used to search for possible crystal packing arrangements of unknown crystals using global optimization algorithms. These include simulated annealing (SA),^23,24 random crystal packing method (by Schmidt and Englert),²⁵ a new algorithm by using selected symmetry operators,^26,27 and genetic algorithms (GAs). ^5,28–30 Our research has been concentrated in using GAs, which are based on the idea of Darwinian natural evolution.^31,32 Populations of candidate individuals (i.e., feasible solutions to the problem) compete with one another through selection, crossover, and mutation operations to produce individuals that have higher fitness, thereby concentrating the search towards the global minimum.³³ The advantage of GAs is that they extensively search the “good regions” of the configuration space because genetic operators create children whose structures can greatly differ from their parents, but belong to provable regions in the configurational space.³⁴ In addition, GAs are naturally amenable to parallelization schemes, an important feature for computationally intensive problems like CSP. Our previous work ^{5, 28, 29} presented the development and use of the Modified Genetic Algorithms for Crystal and Cluster structures (MGAC) method, in which all the crystal structures considered by the GA are locally optimized, i.e. they correspond to a local minimum in the potential energy with respect to all intra and intermolecular parameters defining the crystal structure even those not included in the GA global search.

Due to computational intractability as well as issues related to the proper description of the dispersion forces by DFT methods,^35–39 most of the work in CSP has been limited to using empirical force fields to calculate both inter- and intra- molecular interactions. A great deal of work has been done to improve the completeness and accuracy of force field descriptions by modeling the electrostatic interactions. In addition, improvements have been made to increase the speed of the necessary calculations.^40–43 Brodersen and his colleagues⁴⁴ tested distributed multipole models for evaluating electrostatic interaction between atoms in force field calculations. The methods were applied to large scale test sets and the results were compared to experiment. Their technique was able to improve the accuracy for rigid molecules, but not for flexible molecules. Karamertzanis et al.¹⁶ recently introduced a new methodology for the accurate minimization of crystal structures of flexible molecules; in this approach the intra- molecular interactions, which mostly determine the accuracy of flexible molecule crystal structures, are calculated from ab initio calculations and the intermolecular interactions are evaluated via a conformation-dependent distributed multipole model in conjunction with a realistic electrostatic model.¹⁶ However, both tests^{16, 44} concentrated only in local optimizations and were limited to show that for these methods the experimental structures correspond a the local minima of their potential function. Neumann et al.^12,17,45,46 presented a novel force field approach based on the detailed fitting of energies calculated using their dispersion corrected DFT calculations.⁴⁵ Similar work has been reported recently by Misquita et al. ⁴⁷ for the prediction the structure of 1,3-dibromo-2-chloro-5-fluorobenzene. In these approaches individual force fields have to be developed for each molecule; this is a time consuming and labor intensive process⁴⁸ that has been very successful, but it is unclear how they can be applied to any high throughput studies.

In our previous papers we reported the implementation and testing of our distributed computing environment for CSP. Our method uses a standard force field (the general AMBER force field, known as GAFF)⁴⁹ and while it is as computationally demanding as other methods in the literature, MGAC requires much less human labor. While this makes our method suitable for high throughput studies, the use of standard potentials may, to some extent, limit its predictive capabilities. The assessment of these limitations is the thrust of the research presented here.

In this paper we describe the use of MGAC to predict the structures for a set of flexible molecules representative of compounds of pharmaceutical interest that has been previously used as a benchmark set in Ref. 16. These molecules have been selected because they represent most of the functional groups and conformational flexibility typical of many pharmaceutical compounds. The results obtained allow for a better understanding of the limits of our method and act to highlight the areas that require improvement in order to provide a reliable CSP method with wide applicability to pharmaceutical problems.

COMPUTATIONAL METHODS

Here we present a brief description of distributed computing method for crystal structure prediction used in this work. A full and more detailed description is given in Ref. 3.

Modified Genetic Algorithms for Crystal Structure Model

The crystal structures are encoded in a genome that allows for both the manipulation of the structures by the genetic operators and for the calculation of the energy of the crystal structure. The genome is the representation of Z molecules, or any arbitrary number of molecules, per unit cell in the crystal.²⁹ The genome for rigid molecules is given by the crystallographic parameters (α, β, γ), the position of the center of mass of each molecule in the cell (r₁, r₂, r₃, …, r_z), and the orientation of the molecular axes with respect to the unit cell (Φ₁, Φ₂, Φ₃, …, Φ_z). For flexible molecules, the genome also needs to include the values of the dihedral angles that can be significantly affected by the intermolecular interactions during the global optimization.

Note that the MGAC program only considers the lattice angles (α, β, γ) as independent parameters whereas the lattice lengths (a, b, c) are dependent parameters in the GA optimization.³ The lattice lengths are determined from the molecular coordinates in the unit cell. A minimal intermolecular distance, by default 3 Å, is used to minimize the chance of producing very short intermolecular distances between molecules and their neighbors when the initial guesses of lattice lengths are chosen.³ This parameter will not affect the final structures since all inter- and intra- molecular parameters are locally optimized in every GA generations.³

Several GA operators, including the one-point-crossover, two-point-crossover, n-point-crossover, uniform-crossover, arithmetic-crossover, inversion-crossover, geometric-crossover, and gaussian mutation which have been proposed by Niesse et al.,^34,50 are implemented in MGAC. The initial generation or population is started from a set of randomly selected crystal structures, and then the GA operators are used to create a new set of crystal structures for the next generation. At each GA evolution, all the crystal structures are relaxed to their local minima of the potential energy surface using the local optimization routines in CHARMM. This evolution is repeated until either a predefined number of generations is reached or the data convergence process is achieved.

MGAC can search for solutions in any of the 230 space groups, however for this project the search was restricted to the 14 most common space groups⁵¹ to produce a representative sampling of possible packing arrangements. The global parallelization scheme for GA was implemented in MGAC to reach the high sampling power for these searches.³

Force-Field Generator

The automatic force field generator, charmmgen, was implemented based on the antechamber program.^49,52,53 This software package calculates the molecular parameters using GAFF^49,53 which has parameters suitable for most organic and pharmaceutical molecules composed of H, C, N, O, S, P, and halogens. The potential energy function (U(R)) is shown below:⁵³

$$\begin{array}{ll}U(R)=\sum _{\mathit{bonds}}{K}_r{(r-r_{eq})}^2\hfill & \mathit{bonds}\hfill \\ +\sum _{\mathit{angles}}{K}_{\theta }{(\theta -{\theta }_{eq})}^2\hfill & \mathit{angles}\hfill \\ +\sum _{\mathit{dihedrals}}\frac{V_n}{2}(1+cos[n\phi -\gamma ])\hfill & \mathit{dihedrals}\hfill \\ +\sum _{i<j}^{\mathit{atoms}}\frac{A_{ij}}{R_{ij}^{12}}-\frac{B_{ij}}{R_{ij}^6}\hfill & \mathit{van}\mathit{der}\mathit{Waals}\hfill \\ +\sum _{i<j}^{\mathit{atoms}}\frac{q_i{q}_j}{\epsilon R_{ij}}\hfill & \mathit{electrostatic}\hfill \end{array}$$

where r_eq and θ_eq are equilibrium structural parameters. K_r, K_θ, and V_n are force constants, n is multiplicity, and γ the phase angle for the torsional angle parameters. In addition, A, B, and q are parameters related to the non-bonded potentials. For the non-bonded part, the electrostatic parameters (q_i, q_j) are calibrated using the restrained electrostatic potential fit (RESP) model.^54,55 The Gaussian 03 package⁵⁶ is used to perform the calculation of these atomic charges at the optimized geometry (HF/6-31G* level).

Therefore, for all of the crystal structures in this paper the energy calculation and local optimization are performed using CHARMM^57,58 with the GAFF⁴⁹ parameters and RESP charges.^54,55 These charges were calculated using the optimized HF/6-31G* geometries obtained when the experimental conformation was used as the starting one. But our previous work shows that do not significantly depend on the molecular conformation. ³ A cutoff of 14 Å was used to compute short range non-bonded interactions and the Ewald technique was then applied to calculate the electrostatic interactions including at least two unit cells in the simulation box in every direction.

Search Protocols

While the crystal structure of the compounds studied here are all known, the calculations were done as if performing a blind test, i.e., no information of the experimental structure was used a priori in our calculations. A series of ten MGAC runs for each of the 14 most common space groups in organic molecules (P1, P−1, P2₁,C2, Pc, Cc, P2₁/c, C2/c, P2₁2₁2₁, Pca2₁, Pna2₁, Pbcn, Pbca, and Pnma) were completed, with five done on structures with one molecule per asymmetric unit and five on structures with two molecules per asymmetric unit. The parameter values describing the initial population are randomly selected, this include the dihedral angles included in the global optimization. Each GA run produced 130 generations with 30 crystal structures each, using a crossover probability of 1.0 and a mutation probability of 0.001. This process generates approximately 500,000 structures for each compound studied here.

To generate these structures requires running approximately 140 independent optimizations, each one taking between 12 to 72 hrs on 14 processors; this translates in a total of 23,000 to 140,000 processor hours per molecule.

Analysis of the Results

After a series of MGAC runs has been finished, the results were filtered using a series of utilities developed and/or integrated into our analysis environment in order to obtain a set (ranging in size from 300 to 2000 as discussed in the results section) of unique lowest energy structures.³ These utilities first detect and remove duplicate crystal structures from the final set, since the set of structures from the MGAC runs have many similar structures with small energy differences, and then select the lowest energy structures for further analysis.

We employed the well-known methodology of COMPACK⁵⁹ (COSET) for comparison of the computed three-dimensional crystal structures with the experimental one, and we report the rms between these structures using the default COMPACK settings of a cluster of 15 molecules and a 20% tolerance; the rms values do not include the hydrogen atoms. A few exceptions to this procedure are indicated in the text. We then used the ADDSYM algorithm from PLATON⁶⁰ to find additional symmetries in the calculated structures, as it is a common occurrence that higher symmetries are found in less restricted searches.³

Fig. 1 shows a schema of the 18 compounds, which provide 22 different crystal structures when considering the different known polymorphs, studied in this paper and indicates the dihedral angles that were allowed to freely vary in the GA searches along with the CCDC reference code for the experimental structure. In the four cases in which there are experimentally known polymorphs it was observed that the intra molecular conformation of all the polymorphs is the same and they do not introduce any additional complexity of our analysis. The experimental structures were obtained from the CCDC files, where the references to the original work can be found. Finally it should be noted that the dihedral angles depicted in Fig. 1 are those included in the GA global optimization procedure; the rest of the dihedral angles in the molecule as well as the bond lengths and angles are always locally minimized, i.e., all the structures reported here always correspond to local minima for the force field potential used in the calculation of the energies.

Figure 1.

Schema of the molecules studied in this paper, indicating the dihedral angles allowed to freely vary in the GA search.

RESULTS AND DISCUSSION

In this section we present a detailed discussion of the results obtained for each molecule studied. MGAC matches were found for 16 of the 22 different known crystal structures available for the compounds in Fig. 1. The overall results, including ranking, the match rms, cell parameters, cell volume, and space group for these 16 structures are given in Table I. In the following each molecule is designated by the CCDC reference code of the experimental structure. The energies of the experimental structures discussed below correspond to the energies of the locally optimized experimental structure calculated with the same GAFF parameters. It was always found that the local minimization did not significantly change the experimental structure, i.e. all the experimental structures correspond to a local minimum in the GAFF potential surface.

Table I.

Comparison of calculated and experimental structures.

	rank	rms Å	a Å	b Å	c Å	α	β	γ	volume Å3	space group
NOZKES	78	0.18	4.789	6.763	9.232	90	90	90	299.58	P212121
(exp.)			5.013	6.915	9.271	90	90	90	321.38	P212121
NOREPH01	1	0.32	12.447	8.293	7.808	90	104.63	90	779.87	P21/c
(exp.)			12.507	8.771	8.130	90	106.20	90	856.44	P21/c
CYACHZ01a	196	0.56	7.258	9.309	8.144	90	121.65	90	467.93	P21/c
(exp.)			7.247	8.678	7.855	90	116.80	90	440.93	P21/c
CBOHAZ02b	110	0.42	3.453	9.196	11.614	90	97.631	90	365.47	P21/c
(exp)			3.618	8.789	12.487	90	106.43	90	380.85	P21/c
GAHPIO	1162	1.99	20.150	14.913	5.374	90	90	90	1615.02	P212121 (Z=8)
(exp.)			14.003	5.425	10.495	90	93.70	90	795.60	P21/a (Z=4)
BZAMID02	37	0.64	5.090	4.871	23.31	90	95.58	90	575.15	P21/c
(exp.)			5.529	5.033	21.343	90	88.73	90	593.77	P21/c
HBIURT10	106	0.32	11.115	10.386	3.646	90	90	90	420.89	P212121
(exp.)			10.868	11.698	3.603	90	90	90	458.06	P212121
HISTAN	2	0.25	7.128	7.253	5.626	90	106.18	90	279.33	P21
(exp.)			7.249	7.634	5.698	90	104.96	90	304.63	P21
ACYGLY11b	482	0.51	4.895	11.044	10.333	90	101.63	90	547.11	P21/c
(exp.)			4.859	11.546	14.633	90	138.29	90	546.22	P21/c
KAYTUZ b	22	0.44	10.280	8.807	10.604	90	119.99	90	831.59	P21/c
(exp.)			10.668	8.958	10.308	90	115.75	90	887.25	P21/c
HUYYOP	12	0.40	4.738	12.237	18.928	90	90	90	1097.37	P212121
(exp.)			5.145	12.326	18.536	90	90	90	1175.45	P212121
BANGOM01	380	0.29	24.563	7.539	5.962	90	90.33	90	1103.33	C2(Z=4)
(exp.)			12.738	7.263	6.039	90	98.15	90	553.06	P21 (Z=2)
HAMTIZ	3	0.15	12.521	4.879	17.411	90	100.92	90	1026	P21/c
(exp)			12.569	4.853	17.266	90	99.16	90	1039.81	P21/n
ACSALA13b	1	0.25	12.371	6.301	11.279	90	112.58	90	811.84	P21/c
(exp)			12.095	6.491	11.323	90	111.51	90	827.05	P21/c
CBMZPNXYb	11	0.41	27.023	6.478	14.398	90	112.03	90	2336.30	C2/c
(exp) XY=12			26.609	6.926	13.957	90	109.70	90	2421.92	C2/c
	127	0.29	7.490	10.638	29.602	90	90	90	2358.63	Pna21 (Z=8)
(exp) XY=10			7.537	11.156	13.912	90	92.86	90	1168.30	P21/n (Z=4)

^aMatch found in search performed with some flexibility locked.

^bMatch found in search performed using a rigid model at the experimental conformation.

NOZKES

Ethylene glycol was run with three independent dihedrals: one describing the rotation about the central C-C bond and the other two describing the orientation of the two hydroxyl hydrogen atoms. The energy range of the 300 lowest energy structures was −18.39 to −12.73 kJ/mol; the experimental structure matches a structure that was found at 3.85 kJ/mol above the lowest energy structure (rank 78). The rms of the match calculated with COSET for 15 molecules was 0.18 Å. As it is depicted in Fig. 2, this is an excellent match of the structures. While a match at rank 78 may be consider non-optimal it is remarkable that the method can find this excellent match when taking into consideration the large number of crystal structures present in a narrow range of energies. As depicted in the histogram in Fig. 3, approximately 50% (150 structures) of the structures from the short list considered for analysis are found within a 5 kJ/mol range from the minimum. As it will be shown later, this is a common occurrence in crystal structure prediction and one of the most formidable hurdles facing the field. This finding also highlights the open issues raised by Dunitz^61,62 and others on the importance of kinetic vs. thermodynamic factors in determining the crystal structure observed in a particular experiment. The results presented here for GAFF are consistent with the ranking issues discussed by Mooij et al. when using other general force fields in their study of ethylene glycol.¹⁹

Figure 2.

Comparison between experimental (gray) and predicted structure (green) of ethylene glycol (NOZKES).

Figure 3.

Histogram showing the distribution density of the crystal structures as a function of energy in the MGAC short list for ethylene glycol (NOZKES).

ATUVIU

The crystal structure prediction of N-acetyl-L-alanine was not successful. The 300 lowest energy crystals ranges from −440.74 to −430.75 kJ/mol, while the energy of locally optimized experimental structure is −415.14 kJ/mol, clearly well above the range of best structures found by MGAC using the GAFF potential. Careful analysis of the predicted structures does not reveal any systematic failure of GAFF to predict the experimental conformation of this molecule.

Moreover, calculations locking the conformations of the side chains to the angles obtained from the experimental structure also failed to find any match with the experimental structure. In the first list of three hundred crystals of this search COSET does, however, find several structures with some similarities to the experimental. For instance, the structure ranked 20 belongs to the correct symmetry group P2₁2₁2₁ but has an rms of 2.85 Å. This structure as well as all other showing some similarities to the experimental show much smaller (~10%) cell volumes than the experimental, while (as discussed in more detail below) most of other structures studied here have predicted cell volumes that are only 3% more compact than their experimental counterparts, leading us believe that GAFF overestimates the hydrogen bond (HB) strength for this compound. This overestimation of the HB energies in this compound is consistent with shorter intermolecular HB distance observed in the predicted structures relative to the HB distances found experimentally. This comparison for the four lowest energy predicted structures is presented in Table II.

Table II.

Comparison of the HB distances observed in the four lowest energy predicted and experimental crystal structures of N-acetyl-L-alanine (ATUVIU). All values are in Å and the reported values correspond to the H…O distances.

	Exp.	Structure #1	Structure #2	Structure #3	Structure #4
N H···.O=C	2.190	1.836	1.810	1.790	1.824
C=O···.HO C	1.793	1.579	1.571	1.701	1.642

NOREPH01

The search for the crystal structure of (+−)-norephedrine (racemic 2-amino-1-phenyl-1-propanol) was performed allowing total flexibility of the molecule, using the six dihedral angles, as shown in the Fig. 1. The energy range for the first 300 hundred structures was −134.27 to −116.65 kJ/mol. The match to the experimental crystal structure was the lowest energy structure, having an rms of 0.32 Å. This excellent match is depicted in Fig. 4 and the cell parameters are compared with the experimental ones in Table I. The success of this prediction is consistent with the lattice energy calculations from Li et al.⁶³

Figure 4.

Matching between the predicted (green) and experimental structures (gray) of norephedrine (racemic 2-amino-1-phenyl-1-propanol, NOREPH01).

CYACHZ01

The searches of the structure of α-cyanoacetohydrazide were performed varying five dihedral angles: OCCC, and four to allow pyramidalization of the two amine nitrogens. While there were a couple of similar structures, there were no good matches found. It was found that in most of the MGAC structures, the terminal primary amine group was inverted such that the hydrogens were on the same side of the molecule as the carbonyl oxygen. However, in the experimental structure as well as in the Gaussian03 optimized (HF/6-31G*) structure, these hydrogen atoms are found on the side opposite of the carbonyl oxygen. In addition, it was noted that the experimental structure has the nitrile and carbonyl group on the same side of the molecule, with a dihedral of about 21°, whereas the optimized Gaussian03 structure has a near 180° dihedral between these two groups, even when the optimization run is started at the known experimental structure. This is the only case in the molecules studied where the Gaussian03 optimized structure did not reproduce the conformation of the experimental structure.

Based on these results a second MGAC run was completed using three dihedrals (OCCC, OCNN, and CNNH), again starting from the Gaussian03 optimized structure. This did have the result that most of the MGAC lowest energy structures had the correct orientation of the terminal amine group hydrogen atoms. The best match in this search was a cluster of 11 molecules (out of 15) match with an rms of 0.56 Å for the structure ranked 196 in energy. MGAC reported this match to be of P21 symmetry, but this was reduced to P2₁/c symmetry by the ADDSYM procedure;⁶⁰ the crystallographic cell parameters of the match are reported in Table I. When expanding the size of the cluster in COSET for the match to 30, a match of 20 molecules was found (rms of 0.53 Å) for this same MGAC structure. The match was good, however it did show divergence in the nitrogen containing end of the molecule.

A third run was also performed on the completely rigid structure. In this case, the Gaussian03 optimized structure was first rotated about the C-C bond to set the dihedral between the nitrile and carbonyl group to the experimental value. This structure was then used to calculate the RESP charges and the MGAC run was done using these values and locking all dihedrals. In this run we were able to find the best match with the structure ranked 742 with a rms of 0.70 Å; as with the previous run, this structure also belonged to the P2₁ symmetry, but after applying the PLATON’s ADDSYM procedure60 the group symmetry was reduced to P2₁/c with cell parameters: a = 7.212 Å, b = 9.983 Å, c = 7.100 Å, α = γ = 90° and β = 119.31°.

CBOHAZ02

The search for the structure of 1,3-diaminourea was performed including the eight dihedral angles depicted in Fig. 1. The first 300 structures have energies in the range from −243.57 to −257.74 kJ/mol, while the locally optimized experimental crystal structure has energy of −273.51 kJ/mol, clearly outside of this range. Visual analysis of the predicted structures shows that all of them have an incorrect conformation of the terminal NH₂ groups relative to the carbonyl group orientation, indicating that the GAFF potential cannot reproduce the energetics of this torsional angle. Therefore calculations were undertaken locking all the dihedral angles to their experimental conformation, which is also reproduced by the Gaussian03 (HF/6-31G*) optimization, in the GA global search. This search produced a match with the structure ranked 110 with a rms of 0.42 Å. The cell parameters of the structure are those entered in Table I.

GAHPIO

The searches of the structure DL-2-(N-acetyl-N-hydroxyamino)butyric acid were performed using all eight dihedral angles depicted in Fig. 1. In order to include the energy of the optimized experimental crystal structure (−240.51 kJ/mol), it was necessary to expand the list of MGAC crystal structures to 2000 structures (energy range from −262.52 to −238.01 kJ/mol). Unfortunately, we were not able to find any crystal in the list that closely matches the experimental structure. The molecular conformation is correctly reproduced by the GAFF potential and it is found in multiple structures in the list. The best matches found in the list correspond to the structures ranked 1162 (seven molecules, rms = 1.99 Å), 1013 (eight molecules, rms = 2.11 Å) and 1899 (seven molecules rms = 2.65 Å). The cell parameters of the best match are compared with the experimental in Table I. Note, that if the axis are properly permuted the predicted cell is almost twice the size of the experimental in one of the dimensions; this leads to the match having a cell volume double of the experimental volume. This finding will be further discussed below.

BZAMID02

The search for the structure of benzamide was performed allowing two dihedral angles, CCCO and CCNH to vary. The 300 lowest energy structures range in energy from −260.15 to −251.16 kJ/mol, while the locally optimized experimental crystal structure has energy of −254.66 kJ/mol, within the range of the list. The best match to the experimental structure ranked 37 with an rms of 0.64 Å; this structure belongs to the P-1 symmetry group with parameters, a = 35.67 Å, b = 10.99 Å, c = 7.04 Å, α = 18.67°, β = 128.23°, and γ = 136.66°. There is also a close match with the structure ranked 38 with rms of 0.63 Å, having cell parameters: a = 4.873 Å, b = 5.089 Å, c = 35.313 Å, and β = 138.95° with a P2₁ symmetry. Comparison of their XRPD (X-ray powder diffraction) spectra show that these structures correspond to the same crystal; moreover, after applying the PLATON’s ADDSYM procedure⁶⁰ both crystals reduce to the P2₁/c symmetry with the cell parameters reported in Table I, which closely match the experimental one.

HBIURT10

The search for the structure of 3-hydroxybiuret was performed allowing the seven dihedral angles depicted in Fig. 1 to vary. The energy of the 300 lowest energy structures ranges from −712.51 to −684.84 kJ/mol and the locally optimized experimental structure has energy of −690.01 kJ/mol, which is within this energy range. The best match to the experimental structure was found for the structure ranked 106 with an rms of 0.32 Å. The comparison of the cell parameters of these structures is given in Table I. The excellent match of these structures is depicted in Fig. 5.

Figure 5.

Matching between the predicted (green) and experimental (gray) structures of 3-hydroxybiuret (HBIURT10).

HISTAN

The search for the structure of histamine was performed allowing the four dihedral angles indicated in Fig. 1 to vary, allowing for total side chain flexibility and inversion about the NH₂ group. The best match with the experimental structure was found for the structure ranked second lowest in energy; this match has an rms of 0.25 Å. The match was found in a P1 search, but after applying PLATON’s ADDSYM procedure⁶⁰ it can be seen that the structure also belongs to P2₁. The comparison of the cell parameters of these structures is given in Table I and their XRPD patterns in Fig. 6. The success of this prediction is consistent with previous results from Williams et al.⁶⁴

Figure 6.

Comparisons between the simulated XRPD patterns of the experimental (top) and predicted (bottom) structures of histamine (HISTAN).

ACYGLY11

The search for the crystal structure of (acetylamino)acetic acid was performed with six dihedral angles allowed to vary during the GA global optimization. The list of the 2000 crystal structures with the lowest energies range from −52.84 to −47.35 kJ/mol. The energy of the locally minimized experimental crystal structure is −33.73 kJ/mol, which is outside of the range of this search. This discrepancy can be attributed to the incorrect molecular conformation of the carboxylic acid predicted by the GAFF. Predictions were also done using the experimental molecular conformation, which is also the conformation predicted by Gaussian03 (HF/6-31G*) optimizations. The 300 lowest energy structures for the rigid molecule search have energies in the range of −41.69 to −34.15 kJ/mol which are all lower than the energy of the locally optimized experimental structure. Å list of the 1000 lowest energy structures takes the energy range up to −32.98 kJ/mol, which includes the energy of the experimental structure. The best match is found for the structure ranked 482 with an rms of 0.51 Å. This structure has P2₁ symmetry, but after applying ADDSYM ⁶⁰ the symmetry is reduced to the experimental P2₁/c; the parameters of this structure are compared with those of the experimentally known in Table I.

KAYTUZ

The search for the crystal structure of N-(p-nitrophenylethylenediamine) was performed allowing the seven dihedrals depicted in Fig. 1 to vary independently during the GA global search. This allows for flexibility of both the orientation of the nitro group and the long side chain; additionally two independent dihedrals were used for each of the C to amine N bonds to allow for inversion at the amine nitrogen. The list of the 300 lowest energy structures produced by the MGAC runs show a great deal of variation in orientation along the side chain; these structures have an energy range from − 45.39 to − 31.31 kJ/mol, while the optimized experimental crystal structure has an energy of − 22.94 kJ/mol, clearly outside of the list’s range. Careful analysis of the structures in the list shows that all exhibit side chains conformations that do not match the experimental structure. Locking the side chain to the experimental conformation, which is also the conformation that Gaussian03 (HF/6-31G*) predicts for the isolated molecule, and re-running the MGAC search as a rigid molecule gave a match of the experimental structure with the structure of rank 22 of the new list. The rms between the experimental and predicted structures is 0.44 Å and both are in the P2₁/c space group. The parameters of this crystal structure are given in Table I. This result shows a clear failure of the GAFF potential to properly describe the torsional potential of the side chain of this molecule. It should also be noted that in the 300 lowest energy structures of the rigid MGAC run a second hit was found with the 119^th structure. However, the crystal structure parameters were not a match to the experimental parameters, nor was there agreement between the experimental and predicted powder diffraction pattern. In this case, the comparison between experimental and the MGAC lowest energy structures when looking for a match of a 30 molecule cluster only the first match was found.

HUYYOP

The searches for the structure of (1R,2R)-(+) -1,2-diphenylethylenediamine were performed using the five dihedral angles depicted in Fig. 1. The energies of the structures with the lowest 300 energy structures range from − 55.34 to − 111.31 kJ/mol. The best match with the experimental structure was found for the structure ranked 12 with energy of − 96.82 kJ/mol and a rms 0.40 Å. The cell parameters are entered in Table I.

BANGOM

The searches for the structure of N-salicylidene-pentafluoroaniline were performed using the three dihedral angles depicted in Fig. 1. The energy of the 2000 lowest energy structures ranged from − 129.98 to − 110.83 kJ/mol, while the energies of the optimized experimental crystal structures of the two known polymorphs are − 110.61 and − 105.25 kJ/mol, respectively. The analysis of the predicted structures show that they exhibit an incorrect molecular conformation in the position of the hydroxyl hydrogen; clearly the GAFF potential underestimates the N^···HO hydrogen bond observed in the experimental structure. The Gaussian03 (HF/6-31G*) optimization, however, reproduces the experimental conformation of the OH group. We therefore ran a rigid molecule search using the experimental conformation of the molecule. In this search a match for the BANGOM01 polymorph was found; this match had an rms of 0.29 Å and was found at rank 380 (there were actually a number of hits of similar quality with the same crystallographic parameters between 344 and 380; the one reported is the best rms). The MGAC crystallographic parameters, however, did not agree well with the known experimental ones. The MGAC match was of C2 symmetry, with cell dimensions of a = 27.229 Å, b = 7.539 Å, and c = 5.96 Å and with angles of α = 90°, β = 115.64° and γ = 90° and a volume of 1103.33 ų. Using the ADDSYM program,⁶⁰ the match kept the space group assignment as C2, but changed the value of a to 24.563 Å and β to 90.33°. These unit cell parameters are very close to those of the P2₁ experimental structure, with the exception of the doubling a dimension and the volume (and also doubling of the number of molecules per unit cell). The match is very good, as shown in Fig. 7, and remains a good match if the sample size is increased to 30 molecules. This type of conflict between a good visual match and non-agreement of the space group of the MGAC match and the experiment crystal structure was previously mentioned for the case of GAHPIO and is also discussed below for the case of CBMZPN and exemplify the issues encountered when comparing crystal structures.⁶⁵ No match was found for the BANGOM02 polymorph.

Figure 7.

Matching between the predicted (green) and experimental (gray) structures of N-salicylidene-pentafluoroaniline (BANGOM01 polymporph).

CERNIW

The searches for the structure of 4-hydroxy-4-phenylpentanamide were performed allowing the eight dihedral angles depicted in Fig. 1 to vary independently in the GA process. The energy of the locally optimized experimental crystal structure, −389.24 kJ/mol, is within the energy range of the 300 lowest energy structures, −394.76 to −377.98 kJ/mol, but no good matches were found between the experimental structure and any of the structures of the list. The MGAC structure conformations are in good agreement with that of the experimental structure. The closest match was a similarity for a cluster of 12 molecules, instead of the 15 used by default in COMPACK,⁵⁹ which had an rms of 0.30 Å. However, the crystallographic parameters of these two structures do not match. A closer look at the comparison between the best MGAC result and the experimental crystal structure shows that there is a nice match in two of the three crystallographic directions, while in the third axis the molecules in the MGAC structure are rotated by 180 degrees from the orientations observed in the experimental structure.

HAMTIZ

The details for the search for the crystal structure of N-(2-dimethyl-4,5-dinitrophenyl) acetamide have been reported in a previous publication.³ The experimental structure shows an excellent match with the third-ranked structure with an rms of 0.15 Å. The comparison of the cell parameters are reported in Table I.

ACSALA05/13

Aspirin crystallization and polymorphism have been extensively studied, demonstrating the complexity of the problem.⁶⁶ The searches for the structure of acetylsalicylic acid (aspirin), with the five independent dihedrals angles depicted in Fig. 1, produced no matches; the energy range of the 300 lowest energy structures is −652.12 to −637.32 kJ/mol, while the energy of the locally optimized crystal structures are −646.34 and −619.25 kJ/mol, for the two known polymorphs ACSALA05 and ACSALA13, respectively. By looking at the molecular conformations of the structures in the list it was noticed that the majority had the carboxylic acid group oriented such that the carbonyl carbon was on the side facing the ether substituent. However, in the experimental crystal structures and in the Gaussian03 (HF/6-31G*) optimized structure it was the hydroxyl group of the acid that was facing the ether, indicating a clear failure of the GAFF to predict the correct molecular conformation of acetylsalicylic acid. Therefore a second run was completed with only four dihedrals, while locking the dihedral between the benzene ring and the carboxylic acid carbon into the conformation of the experimental structure. In this case the lowest energy MGAC structure was a match for the ACSALA13 structure, with an rms between the predicted and experimental structure of 0.24 Å. The cell parameters of these structures are compared in Table I. The energies of both of the locally optimized experimental crystal structures are within the energy range of the 300 lowest energy structures of the second search with three dihedral angles, which is −647.09 to −630.57 kJ/mol, however a good match for ACSALA05 is not found. For this polymorph we found five partial hits (11 out of 15 molecules), two of which are notable. The first partial hit was the match for the ACSALA13 structure, with an rms of 0.27 Å and the second was the 24^th structure, with a low rms of 0.18 Å. However, neither of these partial hits showed agreement, not in the crystallographic parameters nor in the simulated powder diffraction. The reason for the differences between the MGAC and experimental structure in this case is similar to the CERNIW case; there was a nice two dimensional match but the orientation of the next set of molecules in the third dimension was not matched.

IBPRAC01/JEKNOC11

The first crystal structure corresponds to a racemic mixture and the second corresponds to the S (+) enantiomer of ibuprofen, 2-(4-isobutylphenyl) propionic acid; in both cases the MGAC searches using the eight dihedrals shown in Fig. 1 did not find any matches. The energy of the locally minimized experimental crystal structure for IBPRAC01, − 326.84 kJ/mol, was within the range of the lowest energy structures included in the analysis, − 339.24 to − 324.80 kJ/mol. Careful analysis of the structures in the lists identifies the problem to the fact that none of the lowest energy structures found reproduced the herringbone pattern of the aromatic groups found in the experimental structures. Instead, the molecular arrangements in the GAFF evaluated MGAC crystal structures seemed to be dominated by the hydrogen bonding interaction between neighboring molecules, with very few structures depicting the herringbone motif defined by the π^···C–H intermolecular interactions in aromatic compounds.

To assess if this was due to a total neglect of the π^···C–H intermolecular interaction in the GAFF or simple a lack of balance between different intermolecular interactions, a MGAC run was completed on benzene (BENZEN) where the molecular packing is defined by the π^···C–H interaction. Benzene has two polymorphs with known structures. The lowest energy structures were tightly grouped between −23.01 and −21.01 kJ/mol, and there were many matches of similar quality for both of the polymorphs. The comparison between the experimental and the best predicted structures of the two forms of benzene is presented in Table III. Therefore, the GAFF reproduces the π^···C–H interactions, and in the case of IBPRAC the lack of matches is most likely due to a relative imbalance between the strength of the π^···C–H and the hydrogen bonds interactions.

Table III.

Comparison between the experimental and predicted structures of benzene.

	rank	rms Å	a Å	b Å	c Å	α	β	γ	volume Å3	space group
BENZEN04	125	0.23	5.446	5.506	7.747	90	107.3	90	221.8	P21/c
(exp)			5.417	5.376	7.532	90	110.0	90	206.1	P21/c
BENZEN11	188	0.10	6.628	7.458	9.239	90	90	90	456.7	Pbca
(exp)			6.688	7.287	9.200	90	90	90	448.3	Pbca

CBMZPN

The standard runs of MGAC can only find two of the four known polymorphs of carbamazepine: CBMZPN10 and CBMZPN12. One of the other two has four molecules per asymmetric unit; the other is of R-3 symmetry. Neither of these conditions is searched when using MGAC with the protocol used in this paper. The first run was done with the four dihedrals depicted in Fig. 1 freely varying during the GA search. The energies of the experimental crystal structures were −355.04 and −354.33 kJ/mol for the CBMZPN10 and CBMZPN12 polymorphs, respectively; both were in the energy range of the 300 lowest energy predicted structures (−359.61 to −343.93 kJ/mol). In this run a match was found to the CBMZPN12 polymorph. The match was the 14^th structure and the parameters were nominally the same as the structure discussed below.

A second MGAC run was then completed locking the conformation of the molecule to the optimized Gaussian03 (HF/6-31G*) structure which was very close to that in the known crystal structures (within < 5°) to attempt to find the CBMZPN10 polymorph. The analysis of the results of this MGAC run found the same good match for CBMZPN12 (rms 0.41 Å) as the 11^th lowest energy structure. Details of the predicted crystal structure parameters for this match are given in Table I, showing that they agree well with the known structural parameters. There was also a partial match (13/15 molecules) for the CBMZPN10 structure which was not observed in the flexible run. This match had an rms of 0.29 Å and was for the 127^th structure in terms of energy. This match, however, has the same problem as GAHPIO and BANGOM01 had with the crystal parameters. Most of the cell dimensions match, except for the a crystal dimension, which is doubled, and the predicted structure has eight molecules per unit cell instead of four. Also the angles for the match are all 90°, whereas in the experimental structure the beta angle is 92.86°. This difference of less than 3° leads to a predicted orthorhombic crystal system (and Pna²₁) instead of the experimental monoclinic P2₁/n. The cell parameters of this structure are given in Table I.

Summary of all Results

The results presented above show that using a fully flexible molecular model MGAC was able to find the experimental structures for 10 of the 22 molecules (counting four cases with polymorphs as two individual molecules each) studied here. Additionally for six other molecules the experimental crystal structure was found when some or all of the molecular internal degrees of freedom were set to the experimental values, leading to an overall success rate of 16 of the 22 molecules. When matches were found there is generally good agreement between the experimental and predicted cell parameters. However, there were three exceptions to this (BANGOM01, GAHPIO and CBMZPN10); in these cases a visual comparison of the matches looks very good, but there are discrepancies between the crystallographic parameters. In all three cases there was one cell dimension that was doubled in the MGAC structure, along with a doubling of the cell volume and number of molecules in the unit cell.

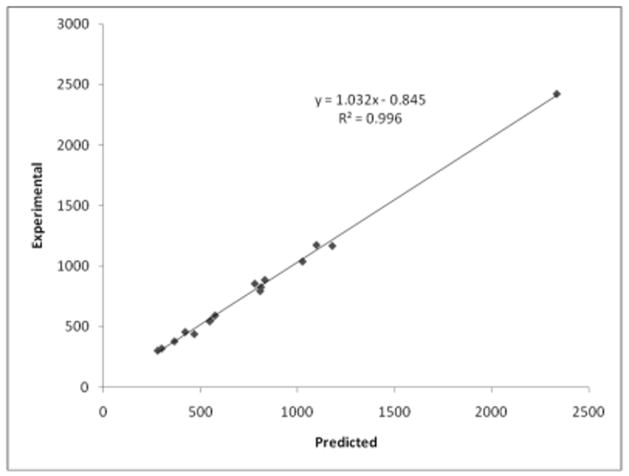
The overall quality of the agreement can be observed by the excellent correlation observed between the experimental and predicted cell volumes, depicted in Fig 8. Most compounds show a predicted cell volume that is about 3 % smaller than the experimental value, i.e., the predicted crystals are denser than the experimental ones. This is consistent with the fact that the predicted structures correspond to zero temperature minima, while the experimental ones reflect the thermal vibrations.

Figure 8.

Correlation between the predicted and experimental cell volumes of the compounds studied here. All values in ų.

Unfortunately, in many cases the energy ranking provided by the GAFF method is quite unreliable, with many good matches ranking well below of what has been considered a successful prediction for the CSP blind tests.^12,15,67 However, short of using custom fit potentials tailored to individual molecules or a significant improvement of the GAFF, it appears that this shortcoming should be addressed by using re-ranking methods⁶⁸ or by incorporating experimental information like solid state NMR or XRPD to further refine the structures.^13,14

Only in six cases were no viable matches found (see Table IV). In all but one of these cases specific problems with the GAFF potentials that may be responsible for these failures have been identified. In ATUVIU it appears that the GAFF overestimates the HB strengths and therefore MGAC produces structures that are systematically too compact. In the case of IBPRAC01 and JEKNOC11 there is a clear imbalance between the π^···C–H intermolecular interaction and HB and van der Waals forces leading to a systematic discrimination of herringbone structures in the GA selection process. Finally, in CERNIW, as in the ACSALA05 polymorph, good agreement was observed in two dimensions of the crystal; perhaps long range intermolecular interactions governing the alignment of rows of molecules in the third crystal dimension is the cause.

Table IV.

Structures for which matches not found

	Reason match not found
ATUVIU	Overestimation of intermolecular HB interaction leading to MGAC structures having smaller unit cell dimensions
BANGOM02	No reason found
CERNIW	Match was found in two dimensions of crystal; possible failure in long range interactions for third crystallographic direction
ASCALA05	Match was found in two dimensions of crystal; possible failure in long range interactions for third crystallographic direction
IBPRAC01	Balance between π···C–H intermolecular and HB intermolecular interactions leading to never seeing herringbone packing found experimentally
JEKNOC11	Balance between π···C–H intermolecular and HB intermolecular interactions leading to never seeing herringbone packing found experimentally

CONCLUSIONS

Our study shows that it is possible to find good matches between predicted and experimental crystal structures of flexible molecules using a standard force field. Unfortunately the ranking of the structures is not as good as desired and there are still cases in which the searches were unsuccessful and the experimental or perhaps ab initio optimized molecular conformation had to be used in order to find good matches. Our results indicate that our search procedure is robust, but there are still significant problems with using standard potentials for crystal structure prediction. In the case of GAFF, studied here, it is clearly that significant improvements in the torsion potentials are needed. Brodersen et al.⁴⁴ and Karamertzanis et al.¹⁶ have also reported large scale tests; however, they concentrated in local optimizations and showed that the potentials used reproduce the local minima of the experimental structures. This is also true for GAFF, even for the molecules for which MGAC does not find the experimental structure, the locally optimized (GAFF) experimental structures are very close, to the experimental ones, i.e. all the experimental structures correspond to a local minimum of the GAFF energy, but in many cases this minimum is not the global one. This is depicted in detail in the supplementary material were we provide a Table with the rms, ranging from 0.18 Å to 0.66 Å, between the experimental and its locally optimized structure, figures comparing these structures and all the cif files for the locally minimized experimental structures.

Our results show that the correct prediction of the experimental structure as a local minimum may not be sufficient information about the existence of different structures with much lower energies. As we show here this is not an uncommon issue. The potential function can well reproduce the experimental structure as local minima, but this structure can rank well above many predicted structures.

Finally, we acknowledge that better crystal structure prediction can be accomplish using potentials tailored to individual molecules;^16,45,46 however, these methods are not well suited for high throughput studies, as they involve a significant amount of manual labor in developing the potentials for specific compounds. Our method is quite low in its requirements of manual labor; the crystal structure prediction of one compound, including set up and analysis, can be accomplished with only a few hours of manual labor. This makes it very appropriate for high throughput studies, but more work is needed to improve its computational efficiency and the reliability of the potential without compromising its wide range of applicability.