Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Aug 7.
Published in final edited form as: J Biomech. 2009 May 30;42(11):1622–1627. doi: 10.1016/j.jbiomech.2009.04.033

Spatial Patterning of Cell Proliferation and Differentiation Depends on Mechanical Stress Magnitude

Bin Li 1, Fang Li 1, Kathleen M Puskar 1, James H-C Wang 1,*
PMCID: PMC2720430  NIHMSID: NIHMS116459  PMID: 19482284

Abstract

Mechanical stress has been proposed as a major regulator of tissue morphogenesis; however, it remains unclear what is the exact mechanical signal that leads to local tissue pattern formation. We explored this question by using a micropatterned cell aggregate model in which NIH 3T3 fibroblasts were cultured on micropatterned adhesive islands and formed cell aggregates (or “cell islands”) of triangular, square, and circular shapes. We found that the cell islands generated high levels of mechanical stresses at their perimeters compared to their inner regions. Regardless of the shape of cell islands, the mechanical stress patterns corresponded to both cell proliferation and differentiation patterns, meaning that high level of cell proliferation and differentiation occurred at the locations where mechanical stresses were also high. When mechanical stretching was applied to cell islands to elevate overall mechanical stress magnitudes, cell proliferation and differentiation generally increased with the relatively higher mechanical stresses, but neither cell proliferation nor differentiation patterns followed the new mechanical stress pattern. Thus, our findings indicate that a certain range of mechanical stress magnitudes, termed window stress threshold, that drives formation of cell proliferation and differentiation patterns and hence possibly functions as a morphogenetic cue for local tissue pattern formation in vivo.

Keywords: Cell aggregate, finite element analysis, mechanical stress, proliferation, differentiation

1. Introduction

A fundamental yet unresolved problem in tissue morphogenesis is the understanding of how a growing tissue “knows” where to branch (Chuang and McMahon, 2003) or bud (Allen et al., 1990) in order to achieve a specific, functional complex structure. Local tissue pattern formation, a fundamental process in tissue morphogenesis, has been mainly explained through genetic mechanisms regulating cell developmental signaling pathways (Gaudilliere et al., 2004; Kashimata et al., 2000; Noselli and Agnes, 1999) and morphogen gradients (Basler and Struhl, 1994; Teleman and Cohen, 2000). In recent years, mechanical stress has also been recognized as a crucial morphogenetic regulator. While external mechanical forces are well known to influence the structure and function of cells and tissues (Grenier et al., 2005; Ingber, 2006; Trepat et al., 2007; Vogel and Sheetz, 2006; Wang and Thampatty, 2006), internal mechanical stresses, or the stresses generated by cells themselves within a cell aggregate, have also been suggested to regulate cell proliferation and differentiation (Huang and Ingber, 1999; Hufnagel et al., 2007; Lecuit and Lenne, 2007; Shraiman, 2005). Even in the case of morphogen gradient, mechanical stresses are expected to arise from the non-uniformity of morphogen distribution that drives tissue growth, leading to stretch at the periphery and compression at the center of a tissue; these stresses then compensate for the non-uniformity of morphogen through certain feedback mechanisms on tissue growth (Hufnagel et al., 2007; Lecuit and Le Goff, 2007; Shraiman, 2005).

A few recent studies (Hufnagel et al., 2007; Nelson et al., 2005; Shraiman, 2005) have started to address the following question through both experimental and modeling approaches: how do internal mechanical stresses generated by a cell aggregate drive cell proliferation pattern formation? Using a micropatterned cell aggregate model, Nelson et al. (2005) have shown that concentrated internal mechanical stresses around the perimeter of a cell aggregate cause endothelial cells to proliferate there, but not in its inner region. They concluded that the mechanical stress pattern, which implies a stress gradient, dictates cell proliferation pattern. We reasoned that, although it appears that the mechanical stress pattern determines cell proliferation pattern, whether a cell aggregate responds to mechanical stress gradient, as suggested in their study, or to mechanical stress magnitude remains an unresolved issue. The latter seems possible, as high and low mechanical stress regions correspond to regions of cell proliferation and no cell proliferation, respectively (Nelson et al., 2005). Furthermore, whether mechanical stress also influences patterning of cell differentiation, an equally vital cellular process in tissue development, remains unknown.

To address the above questions, we tested the hypothesis that mechanical stress determines proliferation and differentiation patterns of cell aggregates in a stress magnitude-dependent manner. We performed computational modeling and experimental studies on cell aggregates of specific shapes (herein referred to as “cell islands”). We grew micropatterned NIH 3T3 cell islands on a deformable poly(dimethylsiloxane) (PDMS) substrate so that mechanical stretching could be imposed to modulate the mechanical stresses generated by the cells, or internal mechanical stresses (Kubicek et al., 2004). Herein we report the findings of our studies.

2. Materials and methods

Mechanical stress patterns of cell islands

Cell islands of three shapes (circular, square, and triangle) were fabricated on PDMS substrates using stencil micropatterning technique (Li et al., 2008a; Li et al., 2008b). Finite element analysis (FEA) method was used to determine the stress distributions of cell islands due to cell contraction alone and a combination with mechanical stretching. An AMPS (Advanced Multi-Physics Simulation) program was used for stress analysis. The cell islands were meshed with eight node brick elements and a grid spacing of 2 to 12 μm between nodes. The substrate to which cell islands were attached was modeled as a large plate, which was meshed with eight node brick elements and a grid spacing of 40 to 48 μm. The cell islands were modeled as two layers of materials (Table 1). The top layer was contractile, which was simulated in the FE model by temperature drop. The bottom layer, on the other hand, was non-contractile and represented the transition between the top layer and its attachment to a substratum plate so that the strain in the top layer was not affected by the boundary condition. The top layer was five times (20 μm) higher than the bottom layer (4 μm), while both shared the same surface. All layers were defined as Mooney-Rivlin material with common Poisson's ratio 0.499. The Young's modulus of the top layer was 500 Pa, whereas that of the bottom layer was 100 Pa, based on the same values taken by a previous study (Nelson et al., 2005). The Young's modulus of the substratum plate was 2 MPa corresponding to a PDMS substrate (Tan et al., 2003). Contraction of cell island was simulated using a 5 K temperature drop. The thermal conductivity (10 kW•m-1•K-1) and linear expansion coefficient (0.002 K-1) were chosen so the overall reduction was consistent with the contraction measured on the actual cell islands. In the case of application of mechanical stretching to cell islands, a triangular cell island was chosen and placed in the substrate in such a way that one side was aligned in parallel to the long axis of plate. A 2% or 8% uniaxial stretch was applied to the ends of the plate as a displacement boundary condition. The von Mises stress at the bottom of fixed layer was reported in this study, but similar stress patterns were seen using the maximum principle stress. To verify mechanical stress predictions of cell islands by FEA, cell traction force microscopy (CTFM) (Wang and Lin, 2007) was used for measuring cell traction forces (CTFs), the mechanical stresses exerted by cell islands to their underlying substrate.

Table 1.

Parameters of FEA model for cell islands

Shape of cell island Side length/diameter (μm) Area (μm2) Height of layer (μm)
Contractile layer Passive layer
Triangle 790 490,000 20 4
Square 700 490,000 20 4
Circle 1,064 490,000 20 4
Open in a new tab

Cell culture experiments

NIH 3T3 fibroblasts (ATCC, Manassas, VA) were maintained in Dulbecco's modified Eagle's medium (DMEM) containing 10% bovine calf serum (BCS) and 1% penicillin-streptomycin at 37 °C in a 5% CO2 atmosphere. Cells were synchronized by incubating in 1% BCS medium for 2 days after they reached confluence (Liu et al., 2006). To culture cells on PDMS substrate, the fibronectin (FN)-micropatterns fabricated were encompassed with a PDMS ring prior to cell seeding. Two hundred microliters of cell suspension (3 × 105 cells/ml) in 1% BCS medium were pipetted in each ring. To culture cells on micropatterned polyacrylamide gel (PAG) substrate for CTF measurement, 200 μl cell suspension (6 × 105 cells/ml) were pipetted onto the gel disk. After 1 hr, non-attached cells were extracted and fresh 1% (for PDMS) or 10% (for PAG) BCS medium was added to the culture dish. Cells were maintained in culture for 2 days until further treatments were applied.

To apply mechanical stretching to cell islands, they were cultured in custom-made silicone dishes, in which FN micro-islands were fabricated on the bottom. Triangular islands were aligned in a way that one side of the triangle was in parallel to the long axis of silicone dish, that is, along the stretching direction. After 2 days, a 2% or 8% uniaxial mechanical stretching was applied to the silicone dishes for 24 hrs using a custom-made stretching apparatus (Wang et al., 2004).

Proliferation and differentiation assays of cell islands

For determining cell proliferation, after cell islands were cultured for 2 days, BrdU labeling reagent (RPN20 kit, GE Healthcare, Piscataway, NJ) was added to the medium at a dilution of 1:1000. Eighteen hours later, cells were fixed using 4% paraformaldehyde for 15 min, followed with incubation in a Blotto buffer for 1 hr. Then, primary antibody (anti-BrdU monoclonal antibody, dilution 1:100) was applied overnight at 4 °C. Next, the sample was washed 3 × 10 min with Blotto. Secondary antibody (goat anti-mouse, Cy3-conjugated, dilution 1:200) was then applied for 1 hr, followed by washing 3 × 10 min. Finally, fluorescence images of cell islands were acquired on a fluorescence microscope (Nikon Eclipse TE2000-U). Overlapping of fluorescence images of the same cell island shape was performed using a SPOT™ imaging software (Diagnostic Instruments, Inc., Sterling Heights, MI).

To determine cell differentiation, cells were fixed for 15 min using 4% paraformaldehyde and washed 2 × 2 min with PBS. After blocking, the primary antibody, anti-mouse α-SMA was applied to cells for 30 min. Cells were then washed 2 × 2 min before incubating with secondary antibody (Cy3-conjugated goat anti-mouse) for 20 min. After washing with PBS, fluorescence microscopy was then performed.

3. Results

Mechanical stress distributions of cell islands

Using stencil micropatterning technique, cell islands were obtained. Cells conformed to the geometry of each island (Fig. 1A-C).

Fig. 1.

Fig. 1

Open in a new tab

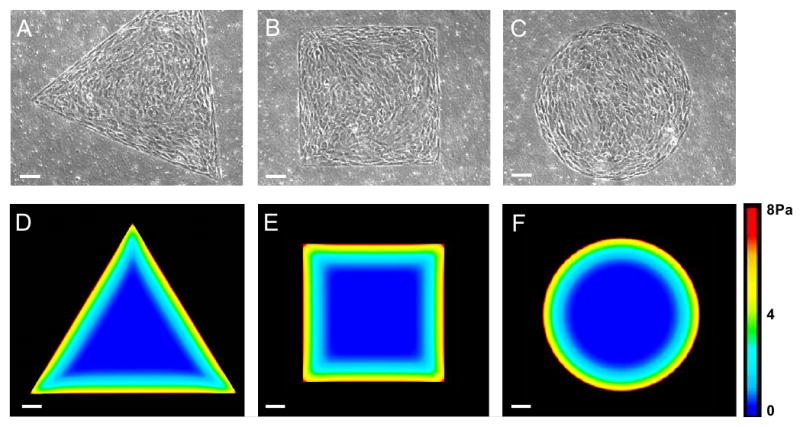
Micropatterned cell islands of distinctive shapes and their mechanical stress patterns. (A-C) Cell islands of triangular, square, or circular shapes, respectively. (D-F) Mechanical stress patterns of cell islands determined by finite element analysis (FEA). Mechanical stress magnitudes are color coded, where red represents the highest stress and blue represents the lowest. As seen, mechanical stresses are concentrated at the perimeters of cell islands, independent of their shape. Note the whole triangular island did not fit in one image due to the imaging area limit of CCD camera. (Scale bars, 100 μm).

As determined by FEA, larger mechanical stresses of cell islands were distributed around their perimeters compared to the inner regions of the islands (Fig. 1D-F). Moreover, even larger mechanical stresses were concentrated at the corners of the triangular and square cell islands.

We reasoned that if a cell island produces large mechanical stresses around the perimeters and corners of the island due to cell contraction, they may also exert large traction stresses to the substrate at these locations because anchorage-dependent cells transmit their contraction to the underlying substrate. Indeed, we found that CTFs were larger at the perimeters than at inner regions (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

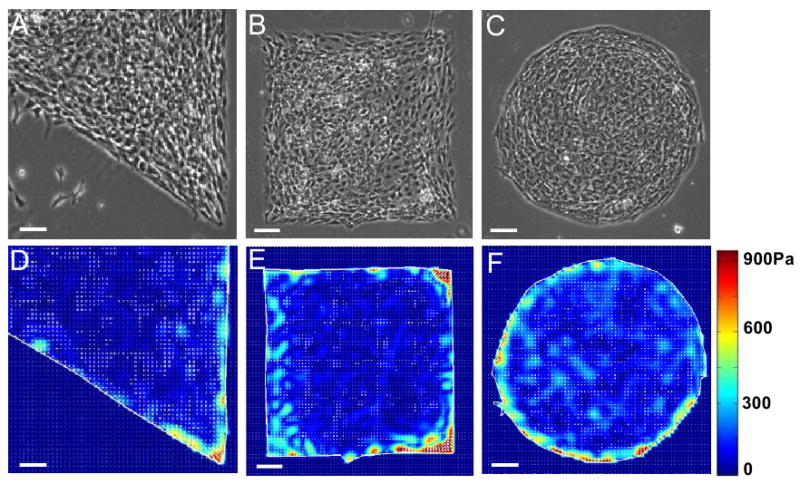
Cell traction force (CTF) distribution of cell islands determined by cell traction force microscopy (CTFM). (A-C) Phase contrast microscopy images of cell islands on polyacrylamide gels (PAGs). (D-F) CTF maps obtained using CTFM. CTF levels are color coded, where red represents the highest stress and blue represents the lowest. (Scale bars, 100 μm).

Proliferation of cell islands

We found that cells around the perimeters of all three islands, but not at the inner regions, exhibited strong BrdU signals, indicating that cells at the perimeters were proliferating (Fig. 3A-I). This can be more clearly seen from the overlapping of a number of BrdU immuno-staining images of similar shapes (Fig. 3J-L). The enhanced cell proliferation at the perimeters of cell islands were not due to the possible nutrient gradients from the edge of each island to its inner region (data not shown).

Fig. 3.

Fig. 3

Open in a new tab

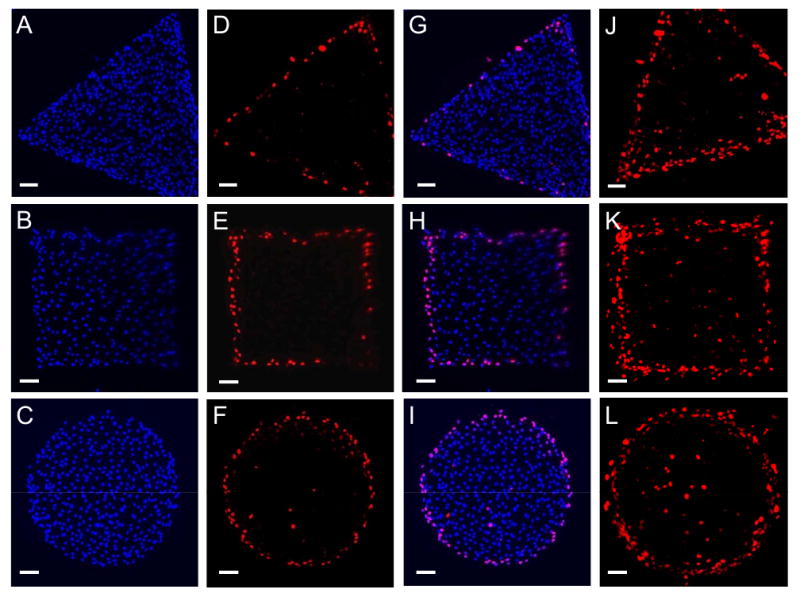
Proliferation patterns of cell islands. (A-C) Stained nuclei indicated uniform distribution of cells throughout the island. (D-F) Proliferating cells were identified through immunofluorescence microscopy for BrdU incorporation. BrdU-positive signals indicated proliferating cells which incorporated BrdU during DNA synthesis. (G-I) Proliferating cells were preferentially located at the perimeters of three cell islands (merged images of nucleus and BrdU staining). (J-L) Stacked images of BrdU signals for triangular, square, and circular shapes, respectively. For each shape 6-10 immunofluorescence microscopy images were overlapped using a SPOT software. (Scale bars, 100 μm).

Moreover, we found that a 2% stretching applied in parallel to one side of a triangular cell island caused mechanical stress in the region close to the perimeter of island to be slightly increased while the overall stress pattern did not apparently change (Fig. 4A-B). Correspondingly, the proliferating cell zone was slightly expanded to inner region of cell island (Fig. 4D-E). Proliferation of the majority of cells in inner region, though, was not apparently affected. However, under an 8% stretching, although the mechanical stress pattern of the cell island still partially resembled the stress pattern of non-stretched cell island, the magnitude of the mechanical stresses increased markedly at all locations (Fig. 4C). For example, with an 8% stretching, the maximum stress in the triangular cell island increased 4.5 times compared with that in the non-stretched cell island (44.6 Pa vs. 8.0 Pa). The mechanical stresses at nearly all locations throughout the stretched island were now higher than the highest stress in non-stretched island. Correspondingly, proliferating cells were distributed throughout the entire stretched island (Fig. 4F) instead of being only concentrated at the perimeter of the cell island without stretching (Fig. 4D) and with 2% stretching (Fig. 4E).

Fig. 4.

Fig. 4

Open in a new tab

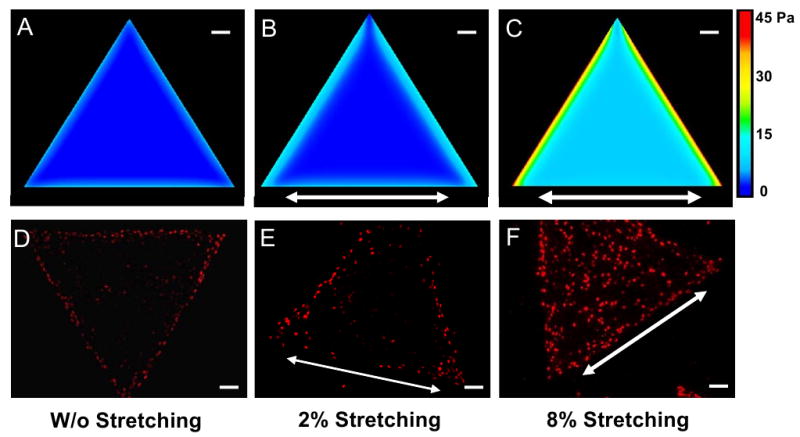
Alteration of mechanical stress and cell proliferation patterns of cell islands. (A-C) Mechanical stress patterns of the triangular cell island without stretching and with 2% or 8% stretching, respectively. (D-F) Cell proliferation patterns of the same cell island without stretching and with 2% or 8% stretching, respectively. Note that arrows indicate stretching directions. (Scale bars, 100 μm).

Differentiation of cell islands

We further investigated whether the internal mechanical stresses generated by cell islands were related to cell differentiation patterning. Using immunofluorescence microscopy, we aimed to detect cellular expression of α-SMA, which is a marker of myofibroblast differentiation (Chen et al., 2007; Hinz et al., 2003). We found that only cells at the perimeter of each island exhibited α-SMA signals, meaning that these cells had differentiated into myofibroblasts. Similar to cell proliferation, the α-SMA expression pattern of each cell island also corresponded to the mechanical stress pattern of the cell island (Fig. 5A-C); that is, cells differentiated into myofibroblasts at high stress magnitudes, whereas they remained as fibroblasts at low magnitudes.

Fig. 5.

Fig. 5

Open in a new tab

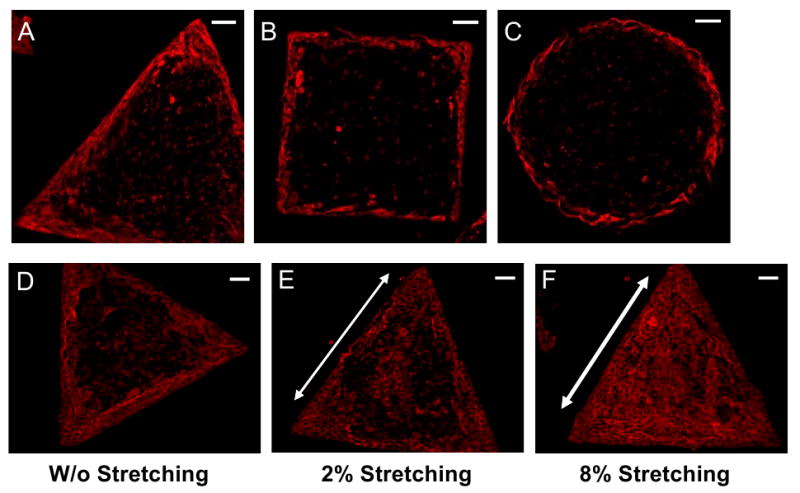
Differentiation patterns of cell islands. (A-C) Non-stretched cell islands of various shapes. The myofibroblast differentiation was assessed by immunofluorescence microscopy for α-SMA expression. (D-F) Triangular cell islands under no stretching, 2%, and 8% stretching, respectively. Arrows indicate the stretching directions. (Scale bars, 100 μm).

To examine whether altered mechanical stresses also led to altered cell differentiation pattern, we applied mechanical stretching to PDMS substrate containing triangular cell islands. Compared to cell islands without stretching (Fig. 5D), more cells expressed α-SMA in islands under 2% stretching (Fig. 5E). However, virtually all cells expressed α-SMA in islands under 8% stretching, indicating that a uniform pattern of cell differentiation occurred throughout the entire island (Fig. 5F).

4. Discussion

While many studies have focused on the effects of mechanical loading on cells, such as gene and protein expression, knowledge is limited in terms of how aggregated cells use internal mechanical stresses generated by themselves to regulate local tissue growth. Nelson et al. (2005) were the first to define the relationship between mechanical stress pattern generated by a cell aggregate and cell proliferation pattern. Using micropatterned NIH 3T3 fibroblasts of different shapes, we showed in this study that these aggregated cells produced specific mechanical stress patterns, and they corresponded to specific cell proliferation patterns. While these results are consistent with the finding by Nelson et al. (2005) using endothelial and epithelial cells, they emphasize that formation of cell proliferation pattern due to internal mechanical stress is not cell type dependent. Furthermore, we have for the first time shown that the specific internal mechanical stress patterns (Fig. 1D-F) match well with cell differentiation patterns (Fig. 5A-C).

Based on the results above, it appears that mechanical stress gradient, or stress pattern formed by contraction of cell island, determines cell proliferation pattern, as suggested by Nelson et al. (2005). To examine the validity of this conclusion, we altered the mechanical stresses of cell islands by applying small or large uniaxial static stretching (2% or 8%). We found that the region of mechanical stress higher than the maximum stress in non-stretched cell island was widened upon a 2% mechanical stretching, although the overall stress pattern did not apparently change. Correspondingly, the region of cell proliferation and differentiation was broadened, but the cell proliferation and differentiation patterns remained largely unchanged. However, upon 8% stretching, the mechanical stresses at all locations of a triangular cell island exceeded the maximum stress in non-stretched cell island. As a result of altered mechanical stress by stretching, both proliferating and differentiated cells were now uniformly distributed throughout the entire island instead of only around the perimeter under non-stretching conditions. Note that, however, mechanical stretching did not eliminate the mechanical stress gradient within the cell island under both 2% and 8% stretching conditions; rather, significantly higher stresses were present along the perimeter of cell island across the stretching direction compared to other regions (Fig. 4B-C). Thus, these results support that it is the mechanical stress magnitude, not the mechanical stress gradient, that dictates spatial patterning of cell proliferation and differentiation.

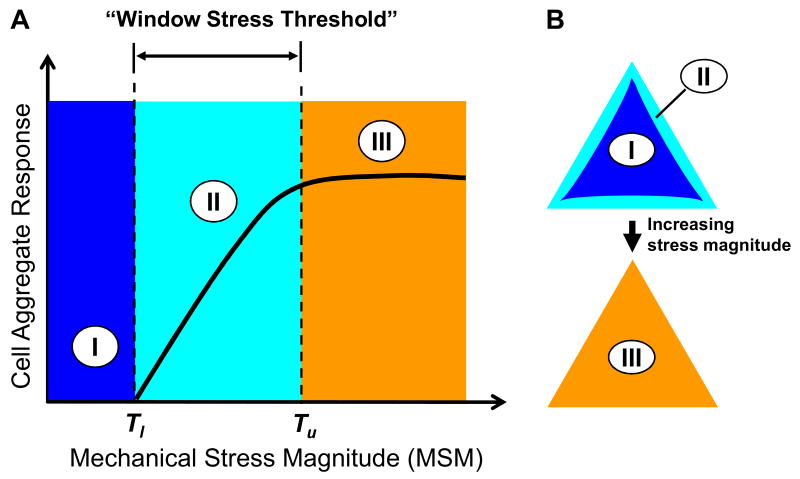
Note that although there were also mechanical stresses in the inner regions of cell islands without stretching, cell proliferation and differentiation events largely occurred at the perimeter regions (Fig. 3 and Fig. 5A-C) where larger mechanical stresses were located (Fig. 1D-F). This observation suggests that there exists a lower mechanical-stress-magnitude (MSM) threshold (Tl) below which aggregated cells were not activated by mechanical stresses to undergo proliferation or differentiation (Fig. 6A, zone I); as a result, cell proliferation and differentiation patterns were not likely formed. On the other hand, that large but non-uniform mechanical stresses due to an 8% stretching induced nearly uniform distribution of cell proliferation and differentiation indicates the presence of an upper MSM threshold (Tu), above which further enhancement of cell proliferation and differentiation did not likely happen (Fig. 6A&B, zone III); consequently, no appreciable changes occurred in cell proliferation and differentiation patterns with increased mechanical stresses. Therefore, the lower and upper thresholds constitute a “window stress threshold” for a cell aggregate to respond to mechanical stresses in terms of the formation of cell proliferation and differentiation patterns (Fig. 6A, zone II). The extent of cell proliferation and differentiation within the window stress threshold can vary, implying that cell proliferation and differentiation patterns may also vary, depending on the magnitude of mechanical stresses. The window stress threshold concept is supported by previous studies using both theoretical and experimental approaches. For instance, modeling a cell aggregate revealed that cell growth stops when the peripheral region falls below a certain stretching threshold (Day, 2007). Cell orientation response has also been found to be strain threshold-dependent (Wang et al., 1995; Wang and Grood, 2000). In other studies, force-induced focal adhesion reinforcement and translocation were found to depend on force magnitude (Balaban et al., 2001; Mack et al., 2004; Riveline et al., 2001). Given the fact that focal adhesions are miniature mechano-sensors that mediate mechanotransduction (Ingber, 2003; Riveline et al., 2001), it seems reasonable to expect that cells respond to mechanical stress in a stress threshold-dependent fashion. Finally, the concept of upper MSM threshold explains why uniform cell proliferation and differentiation patterns were formed in cell islands under 8% mechanical stretching (Fig. 4F and Fig. 5F).

Fig. 6.

Fig. 6

Open in a new tab

Schematic illustration of the concept of mechanical stress magnitude (MSM) thresholds for cell proliferation and differentiation pattern formation. (A) Two MSM thresholds are proposed: a lower MSM threshold (Tl), below which cell aggregates do not respond by formation of cell and differentiation patterns (zone I), and an upper MSM threshold (Tu), above which cell aggregates do not further alter their proliferation and differentiation patterns (zone III). The range from Tl and Tu forms a MSM window (termed “window stress threshold”) within which mechanical stresses dictate the formation of cell proliferation and differentiation patterns (zone II). (B) An example of cell aggregate response. Zones I and II correspond to the inner region and perimeter of the triangular cell island, respectively, while zone III spans across the entire island when mechanical stresses are elevated above Tu such as by application of 8% mechanical stretching.

Despite the interesting findings of this study, there are a few limitations. First, the FE model, similar to that previously utilized (Nelson et al., 2005), considers an aggregated cell island as a continuum, homogenous elastic object. Future research should develop a more representative model of aggregated cells, such as incorporation of viscoelastic property of cells, so that more predictive power can be realized. Second, the molecular mechanisms of the downstream signaling pathways responsible for MSM-regulated cell proliferation and differentiation pattern formation remain unclear and needs to be investigated. In addition, biaxial mechanical stretching may be applied in future studies to see whether changes in cell proliferation and differentiation patterns differ from application of uniaxial mechanical stretching.

In summary, we show that MSM is likely the mechanical signal that is responsible for the spatial patterning of both cell proliferation and differentiation, and hence it may function as a morphological cue for local tissue pattern formation in vivo. We suggest that there are lower and upper MSM thresholds for cell aggregates in their response to mechanical stresses in terms of formation of cell proliferation and differentiation patterns. These findings have important physiological implications, as they imply that by simply invoking “new contraction” and hence altering mechanical stress pattern through autocrine or paracrine mechanisms (e.g., release of soluble factor TGF-β1), cell aggregates may form new patterned tissues in vivo. Moreover, imposing external mechanical stresses (e.g., fluid shear stress) on developing embryonic tissues may also result in changes in tissue forms.

Acknowledgments

The authors thank Drs. M. Szczodry and H. Davitt for their assistance in cell micropatterning experiments. We also thank Dr. T. Lin from AMPS Technologies Company for helpful discussion and technical support with FEA. The AMPS programs were generously donated by AMPS Technologies Company. This research was supported by NIH grants AR049921 and AR049921S1 (JHW).

Footnotes

Conflict of interest statement: The authors have no conflict of interest to declare.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Allen F, Tickle C, Warner A. The role of gap junctions in patterning of the chick limb bud. Development. 1990;108:623–34. doi: 10.1242/dev.108.4.623. [DOI] [PubMed] [Google Scholar]
  2. Balaban NQ, Schwarz US, Riveline D, Goichberg P, Tzur G, Sabanay I, Mahalu D, Safran S, Bershadsky A, Addadi L, Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat Cell Biol. 2001;3:466–72. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
  3. Basler K, Struhl G. Compartment boundaries and the control of Drosophila limb pattern by hedgehog protein. Nature. 1994;368:208–14. doi: 10.1038/368208a0. [DOI] [PubMed] [Google Scholar]
  4. Chen J, Li H, SundarRaj N, Wang JH. Alpha-smooth muscle actin expression enhances cell traction force. Cell Motil Cytoskeleton. 2007;64:248–57. doi: 10.1002/cm.20178. [DOI] [PubMed] [Google Scholar]
  5. Chuang PT, McMahon AP. Branching morphogenesis of the lung: new molecular insights into an old problem. Trends Cell Biol. 2003;13:86–91. doi: 10.1016/s0962-8924(02)00031-4. [DOI] [PubMed] [Google Scholar]
  6. Day C. Mechanical force may determine the final size of tissues. Physics Today. 2007;60:20–21. [Google Scholar]
  7. Gaudilliere B, Konishi Y, de la Iglesia N, Yao G, Bonni A. A CaMKII-NeuroD signaling pathway specifies dendritic morphogenesis. Neuron. 2004;41:229–41. doi: 10.1016/s0896-6273(03)00841-9. [DOI] [PubMed] [Google Scholar]
  8. Grenier G, Remy-Zolghadri M, Larouche D, Gauvin R, Baker K, Bergeron F, Dupuis D, Langelier E, Rancourt D, Auger FA, Germain L. Tissue reorganization in response to mechanical load increases functionality. Tissue Eng. 2005;11:90–100. doi: 10.1089/ten.2005.11.90. [DOI] [PubMed] [Google Scholar]
  9. Hinz B. Masters and servants of the force: the role of matrix adhesions in myofibroblast force perception and transmission. Eur J Cell Biol. 2006;85:175–81. doi: 10.1016/j.ejcb.2005.09.004. [DOI] [PubMed] [Google Scholar]
  10. Hinz B, Dugina V, Ballestrem C, Wehrle-Haller B, Chaponnier C. Alpha-smooth muscle actin is crucial for focal adhesion maturation in myofibroblasts. Mol Biol Cell. 2003;14:2508–19. doi: 10.1091/mbc.E02-11-0729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Huang S, Ingber DE. The structural and mechanical complexity of cell-growth control. Nat Cell Biol. 1999;1:E131–8. doi: 10.1038/13043. [DOI] [PubMed] [Google Scholar]
  12. Hufnagel L, Teleman AA, Rouault H, Cohen SM, Shraiman BI. On the mechanism of wing size determination in fly development. Proc Natl Acad Sci USA. 2007;104:3835–40. doi: 10.1073/pnas.0607134104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ingber DE. Mechanosensation through integrins: cells act locally but think globally. Proc Natl Acad Sci USA. 2003;100:1472–4. doi: 10.1073/pnas.0530201100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ingber DE. Mechanical control of tissue morphogenesis during embryological development. Int J Dev Biol. 2006;50:255–66. doi: 10.1387/ijdb.052044di. [DOI] [PubMed] [Google Scholar]
  15. Kashimata M, Sayeed S, Ka A, Onetti-Muda A, Sakagami H, Faraggiana T, Gresik EW. The ERK-1/2 signaling pathway is involved in the stimulation of branching morphogenesis of fetal mouse submandibular glands by EGF. Dev Biol. 2000;220:183–96. doi: 10.1006/dbio.2000.9639. [DOI] [PubMed] [Google Scholar]
  16. Kubicek JD, Brelsford S, Ahluwalia P, Leduc PR. Integrated lithographic membranes and surface adhesion chemistry for three-dimensional cellular stimulation. Langmuir. 2004;20:11552–6. doi: 10.1021/la0487646. [DOI] [PubMed] [Google Scholar]
  17. Lecuit T, Le Goff L. Orchestrating size and shape during morphogenesis. Nature. 2007;450:189–92. doi: 10.1038/nature06304. [DOI] [PubMed] [Google Scholar]
  18. Lecuit T, Lenne PF. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat Rev Mol Cell Biol. 2007;8:633–44. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
  19. Li B, Lin M, Tang Y, Wang B, Wang JH. A novel functional assessment of the differentiation of micropatterned muscle cells. J Biomech. 2008a;41:3349–53. doi: 10.1016/j.jbiomech.2008.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Li F, Li B, Wang QM, Wang JH. Cell shape regulates collagen type I expression in human tendon fibroblasts. Cell Motil Cytoskeleton. 2008b;65:332–41. doi: 10.1002/cm.20263. [DOI] [PubMed] [Google Scholar]
  21. Liu WF, Nelson CM, Pirone DM, Chen CS. E-cadherin engagement stimulates proliferation via Rac1. J Cell Biol. 2006;173:431–41. doi: 10.1083/jcb.200510087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mack PJ, Kaazempur-Mofrad MR, Karcher H, Lee RT, Kamm RD. Force-induced focal adhesion translocation: effects of force amplitude and frequency. Am J Physiol Cell Physiol. 2004;287:C954–62. doi: 10.1152/ajpcell.00567.2003. [DOI] [PubMed] [Google Scholar]
  23. Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS. Emergent patterns of growth controlled by multicellular form and mechanics. Proc Natl Acad Sci USA. 2005;102:11594–9. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Noselli S, Agnes F. Roles of the JNK signaling pathway in Drosophila morphogenesis. Curr Opin Genet Dev. 1999;9:466–72. doi: 10.1016/S0959-437X(99)80071-9. [DOI] [PubMed] [Google Scholar]
  25. Riveline D, Zamir E, Balaban NQ, Schwarz US, Ishizaki T, Narumiya S, Kam Z, Geiger B, Bershadsky AD. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J Cell Biol. 2001;153:1175–86. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Shraiman BI. Mechanical feedback as a possible regulator of tissue growth. Proc Natl Acad Sci USA. 2005;102:3318–3323. doi: 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Tan JL, Tien J, Pirone DM, Gray DS, Bhadriraju K, Chen CS. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc Natl Acad Sci USA. 2003;100:1484–9. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Teleman AA, Cohen SM. Dpp gradient formation in the Drosophila wing imaginal disc. Cell. 2000;103:971–80. doi: 10.1016/s0092-8674(00)00199-9. [DOI] [PubMed] [Google Scholar]
  29. Tomasek JJ, Gabbiani G, Hinz B, Chaponnier C, Brown RA. Myofibroblasts and mechano-regulation of connective tissue remodelling. Nat Rev Mol Cell Biol. 2002;3:349–63. doi: 10.1038/nrm809. [DOI] [PubMed] [Google Scholar]
  30. Trepat X, Deng LH, An SS, Navajas D, Tschumperlin DJ, Gerthoffer WT, Butler JP, Fredberg JJ. Universal physical responses to stretch in the living cell. Nature. 2007;447:592–+. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Vogel V, Sheetz M. Local force and geometry sensing regulate cell functions. Nat Rev Mol Cell Biol. 2006;7:265–75. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
  32. Wang H, Ip W, Boissy R, Grood ES. Cell orientation response to cyclically deformed substrates: experimental validation of a cell model. J Biomech. 1995;28:1543–52. doi: 10.1016/0021-9290(95)00101-8. [DOI] [PubMed] [Google Scholar]
  33. Wang JH, Grood ES. The strain magnitude and contact guidance determine orientation response of fibroblasts to cyclic substrate strains. Connect Tissue Res. 2000;41:29–36. doi: 10.3109/03008200009005639. [DOI] [PubMed] [Google Scholar]
  34. Wang JH, Lin JS. Cell traction force and measurement methods. Biomech Model Mechanobiol. 2007;6:361–71. doi: 10.1007/s10237-006-0068-4. [DOI] [PubMed] [Google Scholar]
  35. Wang JH, Thampatty BP. An introductory review of cell mechanobiology. Biomech Model Mechanobiol. 2006;5:1–16. doi: 10.1007/s10237-005-0012-z. [DOI] [PubMed] [Google Scholar]
  36. Wang JH, Yang G, Li Z, Shen W. Fibroblast responses to cyclic mechanical stretching depend on cell orientation to the stretching direction. J Biomech. 2004;37:573–6. doi: 10.1016/j.jbiomech.2003.09.011. [DOI] [PubMed] [Google Scholar]

RESOURCES