MRI diffusion tensor tracking of a new amygdalo-fusiform and hippocampo-fusiform pathway system in humans

Abstract

Purpose

To use MRI diffusion-tensor tracking (DTT) to test for the presence of unknown neuronal fiber pathways interconnecting mid-fusiform cortex and anteromedial temporal lobe in humans. Such pathways are hypothesized to exist because these regions co-activate in functional MRI (fMRI) studies of emotion-valued faces and words, suggesting a functional link that could be mediated by neuronal connections.

Materials and Methods

15 normal human subjects were studied using unbiased DTT approaches designed for probing unknown pathways, including whole-brain seeding and large pathway-selection volumes. Several quality-control steps verified the results.

Results

Parallel amygdalo-fusiform and hippocampo-fusiform pathways were found in all subjects. The pathways begin/end at mid-fusiform gyrus above the lateral occipitotemporal sulcus bilaterally. The superior pathway ends/begins at the superolateral amygdala. The inferior pathway crosses medially and ends/begins at the hippocampal head. The pathways are left-lateralized, with consistently larger cross-sectional area, higher anisotropy, and lower minimum eigenvalue (D-min) on the left, where D-min assesses intrinsic cross-fiber diffusivity independent of curvature.

Conclusion

A previously-undescribed pathway system interconnecting mid-fusiform region with amygdala/hippocampus has been revealed. This pathway system may be important for recognition, memory consolidation, and emotional modulation of face, object, and lexical information, which may be disrupted in conditions such as Alzheimer's disease.

INTRODUCTION

The human brain contains specific structural regions that support functions such as language, social cognition, memory, and abstract reasoning. These structures are likely unique or greatly expanded relative to the non-human primate brain. The anatomical connections involved in these functions are largely unknown in humans, as such connections cannot be directly inferred from invasive tracer studies of non-human primates (e.g., ^1,2). Diffusion tensor tracking (DTT) provides a direct measurement of white matter pathway anatomy and connectivity that previously was not possible. First introduced in fixed rat brain (3) and living humans (4), DTT was subsequently applied to reconstruct several dominant macroscopic pathways in the human brain (5–9). Extension of DTT to discover previously unknown pathways requires specific techniques and unbiased approaches.

Here we use DTT to test the hypothesis that a pathway system exists in humans interconnecting the mid-fusiform region with the amygdala/hippocampus. The mid-fusiform region incorporates a complex high-order cortex associated with visual object recognition, including special "objects" such as faces (in both hemispheres, more so on the right), non-face objects (in both hemispheres, more so on the left), and aspects of visual-lexical function (in the left hemisphere) (10–20). We hypothesize the existence of these pathways based on available human functional and pathological data. In several functional MRI (fMRI) studies, facial recognition tasks that activate human mid-fusiform cortex also activate the amygdala (21–23). Task-driven functional correlation studies (24,25) also show correlations between these structures as well as other areas comprising a distributed cortical network, but high correlation does not necessarily imply a direct anatomical connection. Lesions in the amygdala are associated with a decrease in the fMRI activation of mid-fusiform cortex in response to viewing fearful faces (26). Co-activation of amygdala and mid-fusiform gyrus on fMRI has been observed during experimental manipulations of perceived social fairness, and reduced correlation between these regions has been observed in autism (25), leading to the interpretation that the fusiform gyrus and amygdala are components of a system associated with social cognition (27).

Recent studies have also suggested a role of mid-fusiform and related visual association cortex in episodic memory. Co-activation of hippocampus and fusiform cortex during encoding of novel visual stimuli has been demonstrated by fMRI (28,29). Mid-fusiform cortex shows reduced functional activation during visual confrontation naming in asymptomatic persons at risk for Alzheimer's disease (AD) (30,31), an illness characterized by early pathologic involvement of the amygdala, entorhinal cortex, and hippocampal complex (32), as well as the fusiform gyrus (33). Connections between mid-fusiform gyrus and amygdala/hippocampus could link these observations. While two areas that co-activate or that have a high functional correlation are not necessarily directly connected by a fiber pathway, such a direct pathway connection could explain the frequent co-activation and high functional correlation between the two regions, and could explain the pathological changes in AD.

Primate lesion studies suggest connections between lateral/basal amygdala and inferior temporal cortex (34), but the homology between primate inferior temporal cortex and human mid-fusiform cortex is uncertain. Objective measurement of the hypothesized connections in humans would have strong potential anatomic, functional and pathologic significance. We used DTT in living humans to detect and characterize a parallel amygdalo-fusiform and hippocampo-fusiform pathway system.

MATERIALS AND METHODS

Fifteen healthy, right-handed volunteers (18.3–36.6 years; 7 females, 3 African-Americans, 1 Asian, 1 Hispanic) were imaged under IRB approval. These volunteers were consecutive subjects scanned using the same protocol. Informed consent was obtained after the procedures were fully explained.

DT-MRI Acquisition and Whole-Brain Track Computation

Diffusion-tensor MRI (DT-MRI) data were acquired using a custom single-shot multislice echo-planar imaging (EPI) sequence with tetrahedral-orthogonal diffusion encoding and ten scan repeats. Data were acquired at Washington University using a Siemens Vision 1.5T MRI scanner (Erlangen, Germany) with TE=94 ms, TR=15.75 ms, 2.5-mm slice thickness, and 45 slices, with b-factors of 994.3 (tetrahedral), 331.43 (perpendicular), and 36.83 s/mm² (reference I0 image with b~0). Other sequence parameters were as in (9). Image data were realigned and averaged, and whole-brain track data were computed using a cubic 1-mm grid of seed points and a 0.5-mm step size (4,9). A track was computed from each seed point that met the trackability criterion (A_σ ≥ 0.14, see below). Each track was built by first stepping in both opposite directions from the seed, along the line of fastest diffusion (major eigenvector), to initiate two track arms. Then, each track arm was constructed by continuing to step along the major-eigenvector direction (step-angle ≤90°), laying down pathway beads until the trackability criterion was not met. To ensure recovery of pathway curves, no trackability criteria were set for curvature (dot-product). As opposed to attempts at seeding specific pathways, whole-brain seeding is free of any a priori assumptions about anatomic regions or their connections. All calculations were performed using a SunFire V880 (8×1.2 GHz/64GB RAM/XVR-600 graphics; Sun Microsystems, Santa Clara, CA). In all subjects, the trackability threshold for seeding/stopping was A_σ=0.140 (FA=0.238). Additionally, a trackability threshold of A_σ=0.080 (FA=0.138) was used for detailed visualization near cortex.

In DTT, a "track" refers to a single connected line satisfying the above criteria. For a pathway containing ordered neuronal fibers, a track follows the course of the local bundle of fibers within the pathway (i.e., a track effectively corresponds to a bundle of coherent fibers). In contrast, a "pathway" is biologically defined as a macroscopic group of nerve fibers that are anatomically related, having a common origin/termination/anatomical course/function. Different pathways can course alongside each other inside classically-defined white matter "tracts" and inside larger blocks of white matter, but such pathways eventually diverge to connect to different specific brain areas. As a consequence, distinct pathways cannot be identified merely by color displays of fiber direction, but are defined based on origins and terminations. Accordingly, in DTT, a pathway is represented as a group of track lines that have similar anatomical or functional relationships, selected based on specific anatomic or functional criteria. The pathways were selected as follows.

DTT Pathway Selection

In the initial exploratory phase of this study, large hemispheric spatial selection volumes (SSVs) were used to select large blocks of tracks that contained the pathway of interest, from which the pathway was progressively sub-selected. This approach ensured that the pathway would be identified if it existed in the data, a critical step for probing previously-unknown pathways. For the experimental phase of the study, we designed a procedure to select the pathway in a consistent, objective, unbiased manner, without constraining its spatial extent. For this purpose, large ellipsoidal SSVs were placed at specific coordinates defined in atlas space, then transformed to diffusion-imaging space, and then combined in Boolean logical operations to select groups of tracks representing the hypothesized pathways. Tracks were selected that passed into both an SSV encompassing mid-fusiform area, and an SSV encompassing anteromedial temporal lobe. The SSVs only selected tracks from the independently-generated whole-brain track data, and did not create new tracks. These two SSVs selected the entire pathway, and excluded most of the surrounding pathways. Tracks that passed into an SSV posterior to mid-fusiform region were removed to prevent selection of unrelated pathways. This multi-step SSV approach (4) ensured that the entire pathway contained in the data was selected for each hemisphere, with minimal inclusion of neighboring pathways, and without having to use small anatomically-constraining SSVs that would introduce bias. The detailed selection procedure had the following steps.

First, each subject's anatomic MP-RAGE was registered to brain-atlas MP-RAGE data (Mayo 3D Brain Atlas, AnalyzeAVW 6.0, Mayo Foundation, Rochester MN), and was saved in atlas space. The rostrocaudal (anterior-posterior) location of the anterior commissure (AC) and posterior limit of occipital pole (PO) were recorded in atlas space for each subject. We then defined the anterior/posterior limits of mid-fusiform region (MFR) as: (1) MFR-anterior-limit, MFR_ant = AC -[0.31 × (AC - PO)]; (2) MFR-posterior-limit, MFR_post = AC -[0.74 × (AC - PO)]. The MFR center was defined as MFR_ctr = AC -[0.52 × (AC - PO)], midway between anterior/posterior limits.

This mid-fusiform region is the main part of Brodmann area 37 (BA37). These formulas are based on recent atlases using Brodmann's work and current human anatomic data (35–37), where the anatomical landmarks reported by Harasty et al. were histologically verified in human post-mortem tissue to correspond to cytoarchitectonic BA37 (36). Because there is significant variability in the location/extent of the cytoarchitectonic regions relative to macroscopic landmarks, e.g., sulcal/gyral boundaries (38), we refer to the defined mid-fusiform region as "canonical BA37".

Second, to each subject's atlas-registered MP-RAGE, we added the atlas-defined amygdala and four separate 3-pixel-wide reference planes (perpendicular to AC-PC line) centered at points AC, MFT_ant, MFT_ctr, MFT_post; all saved as an "object map" in atlas space.

Third, the subject's atlas-transformed MP-RAGE was registered (linear transformation) to the subject's I0 volume (T2-weighted EPI) in native diffusion-imaging space. The same transformation was applied to the object map to place the amygdala object and reference planes in the native diffusion-imaging space (native space of the track data) in an unbiased, repeatable manner. This procedure yields a standard anatomic definition of amygdala and mid-fusiform region tailored to each subject. This procedure also avoids errors from transformation/resampling of diffusion-weighted images. The distortions in acquired I0 images were minor in the mid-fusiform/amygdalar regions, and did not limit the registration. The MPRAGE-I0 registration, anatomical location of amygdala object, and subsequent SSV placement (see below) were verified visually in each subject.

Fourth, we defined mid-fusiform and anteromedial-temporal SSVs in each hemisphere (Fig. 1, green ellipses/circles) based on the MFR reference planes and amygdala object. The center of the mid-fusiform ellipsoidal SSV was positioned at MFR_ctr, and its rostro-caudal thickness was conservatively set to only 50% of the anterior-posterior limits of MFR (Fig. 1). This conservative definition was adopted because it includes a region clearly within the rostro-caudal bounds of BA37 as reported in the anatomy, pathology, and functional imaging literature (36,39,40), and includes the part of fusiform gyrus that undergoes rapid changes in AD (33). Although this definition risks excluding some tracks that may connect to more rostral parts of MFR, a selection criterion based on the central-50% of MFR has a sounder anatomical basis in the literature. The careful definition of the rostro-caudal dimension of this SSV is the most critical part of the selection. The superior-inferior and medial-lateral SSV dimensions are less important and were set to span the hemisphere to obtain the complete width/height of the pathway without anatomical constraint (Fig. 1). The anteromedial-temporal SSV was defined as a sphere (22.5-mm diameter) centered on the amygdala object viewed in the transverse plane. This SSV encompassed white matter immediately adjacent to amygdala (sphere border was typically 5-mm lateral to and 6.25-mm posterior to the amygdala-object borders).

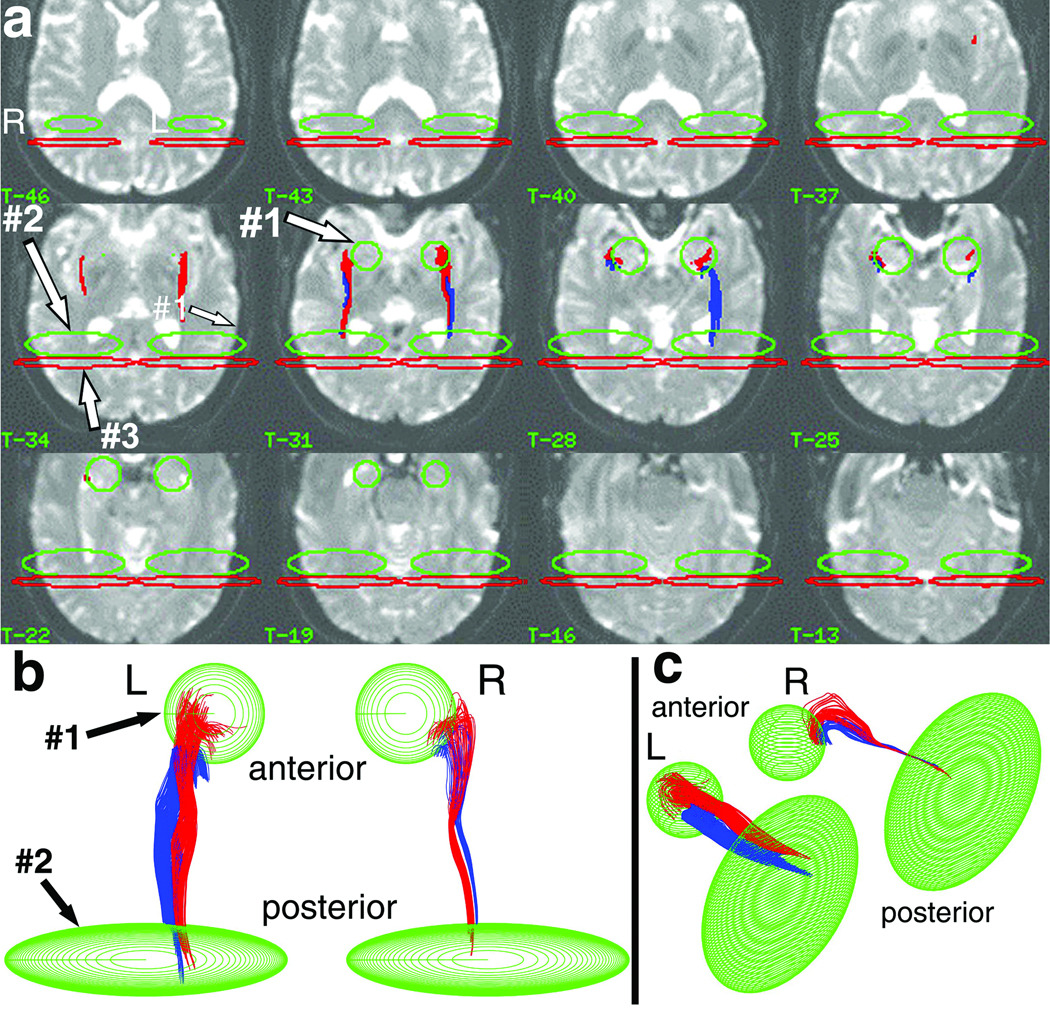
Figure 1.

Pathway selection procedure in one subject. The pathways were selected from whole-brain track data using ellipsoidal SSVs placed at atlas locations in the diffusion imaging space. The SSVs either include (green ellipsoids) or exclude (red ellipsoids) tracks that entered each SSV. The 2D anatomical overlay onto T2-weighted I0 images (a) evaluates the precise anatomical location of the SSVs and resulting tracks (displayed I0 images are every third contiguous 1.25-mm slice). The 3D projection displays viewed from above (b) and from the left-postero-superior oblique viewpoint (c) evaluate the 3D trajectory of the final selected pathways, and the presence of track-free margins [colors in (b,c) are as in (a)]. The combined upper-lower pathway intersects both the anteromedial temporal SSV (green circles, SSV#1) and mid-fusiform region (MFR) SSV (oblong green ellipsoids, SSV#2,), but does not pass beyond the mid-fusiform region (excluded by the red ellipsoids, SSV#3). The anteromedial-temporal SSV (SSV#1) was placed on the I0 images to be centered on and enclose the amygdala atlas object (not shown) as described in text. The MFR SSV (SSV#2) was placed such that the center of the ellipsoid had x,y,z atlas coordinates given by y=MFR_ctr (anterior-posterior direction), z=0 (superior-inferior direction), and × centered exactly between the medial and lateral borders of the temporal lobe, intersected by the MFR-center reference plane (see text). The long medial-lateral axis of the SSV was oriented tangential to the MFR-center reference plane, and spanned the full width of the temporal lobe at z=0. The superior-inferior axis spanned the entire z-extent of the hemisphere. The short anterior-posterior dimension of the MFR ellipsoid was set as 50% of the distance between the MFR-anterior-limit reference plane and MFR-posterior-limit reference plane. The SSV posterior to MFR (SSV#3) was defined as a large disc-like ellipsoid spanning the entire temporal lobe, placed parallel to and immediately posterior to the posterior border of the MFR ellipsoid. The initial "raw" pathway was selected by applying the Boolean operations SSV#1 "AND" SSV#2 "NOT" SSV#3 separately in each hemisphere (using the corresponding right or left SSVs). The "NOT" step using SSV#3 did not remove any of the tracks in the target pathway because, upon applying the SSV#1 "AND" SSV#2 step, no tracks were observed to loop posteriorly into the occipital lobe and back to the MFR destination. The pathways as shown were after further processing and separation into superior/inferior components using heuristic criteria (see text).

Fifth, the MFR and anteromedial-temporal SSVs were combined with Boolean "AND" logic to select tracks intersecting both SSVs (4,41). This step selected the entire pathway, excluding pathways that did not curve medially into the anteriomedial-temporal SSV. Some selected tracks passed posteriorly beyond the MFR SSV [as part of the amygdalo-calcarine pathway (9)], and were removed by placing an SSV posterior to MFR (red ellipses, Fig. 1a) and using "NOT" logic. Errors in atlas registration and MPRAGE-I0 transformation were not expected to affect the resulting pathways, because the selection procedure was insensitive to ~mm SSV offsets (see below).

The selected tracks were visualized by 3D vector-graphic projection display (Matlab, MathWorks, Natick MA) and 2D anatomical overlay onto I0 (Analyze 6.0) to verify that tracks terminated in anteromedial temporal lobe. All logical-AND SSVs were inspected to confirm track-free superior/inferior/lateral margins (e.g., Fig. 1b,c), ensuring that pathway width was not limited or constrained. As an exception, the anteromedial-temporal SSV margins were not track-free near hippocampus, because this SSV was not designed to select all possible connections to hippocampal body/tail. (Because this SSV overlapped with hippocampal head, tracks from/to that structure were selected consistently.)

Nearly identical results were obtained when repeating the above steps within/across observers (<1mm inter-operator variation in SSV positions; <2% inter-operator variation in selected track counts). The low inter-operator variability in pathway selection is indicative of the low bias resulting from whole-brain seeding, large SSVs, and Boolean-logic operations. The same observer performed all pathway selections.

Removal of Non-Pathway Tracks

In some cases, the raw pathway obtained from the above steps contained a few tracks passing anteriorly beyond the anteromedial-temporal SSV, likely as part of another pathway. In these cases, the tracks were removed using individually-placed SSVs and NOT-logic. The fraction of removed tracks was 0.15±0.006 (±1SEM) on the right, 0.17±0.05 on the left. As this right-left difference was insignificant (p=0.81), this removal did not introduce bias or false laterality.

Rebound Cutting

In some instances, rebound occurred adjacent to gray matter as described in (9), typically at the posterior end of the pathway. Rebound tracks meet the selection criteria, then rebound at gray matter, and then pass into other locations (or, rarely, re-enter the pathway). A procedure was developed for cutting the tracks at the rebound, and then retaining the pathway part that initially met the selection criterion (discarding the rebounded part). In most cases, the pathway part was selected by placing an SSV over the anterior portion of the pathway. Occasionally, the rebounded part was directly removed using an SSV or, in rare cases of pathway re-entry, a length histogram. In all cases, track counts confirmed complete removal of rebounded parts. The site to be cut was identified by locally searching for two successive beads that had above-threshold step angles. This criterion was chosen because rebounds are usually caused by the rare statistical event of two large successive step angles (due to noise), causing the track to enter, turn, and exit low-anisotropy areas.

Color Separation

3D-projection views suggested a separation ("cleft") between superior/inferior parts of the pathways (pronounced in a few cases, subtle in most). Another SSV was placed midway along the pathway length (y) to separate the pathway into inferior (AND-logic) and superior (NOT-logic) parts. The SSV had a long × and short y,z dimensions. The SSV z-position (vertical) was adjusted using heuristic criteria. The primary criterion was separation at the cleft (viewed from medial side). When a cleft was not visible, the secondary criterion at any transition in medial temporal lobe (viewed from the side and viewed from above). In most cases where both a cleft and medial-temporal transition were observed, the same z-position met both criteria.

Pathway Metric Measurement and Statistical Analysis

Microstructural pathway metrics were measured to assess the microscopic properties of white matter fiber bundles within the pathway. Anisotropy was measured as A_σ (42), related to the measure FA (43) by a mathematical expression (44). Anisotropy was calculated for all pathway beads (calculating the tensor from diffusion-weighted images interpolated to each bead location). The bead-based pathway anisotropy was determined by averaging A_σ across all the pathway beads. Additionally, a voxel-based pathway anisotropy was measured by calculating the mean A_σ in each voxel (averaging across the beads in that voxel), and then averaging across all voxels containing at least one bead (weighing all voxels equally). Voxel-based measurements weigh all pathway parts equally, and are generally preferred when the pathway is well-defined by the tracks. Bead-based measurements preferentially weigh regions of high track density (typically the more central part of the pathway), and might be preferred in pathology. All metric values herein are voxel-based.

A_σ was used because it responds linearly over the 0–1anisotropy range, important when comparing pathways or calculating laterality. For the main results, we also report FA for literature comparison. Other microstructural metrics were measured similarly: magnitude-sorted minimum/middle/maximum eigenvalues (D-min=λ-min, D-mid=λ-mid, D-max=λ-max); radial diffusivity [D-radial=(D-min+D-mid)/2]; and mean diffusivity [D-bar=(D-min+D-mid+D-max)/3].

Macrostructural pathway metrics were also measured, consisting of pathway volume (sum of voxels traversed by at least one track), mean pathway length (average length of tracks, where the track length is number of beads times step size), and effective mean cross-sectional area (pathway volume divided by mean length).

Pathway metrics are reported as group-mean and standard error of the mean (SEM) (N=15). Differences between left/right pathways, and between upper/lower pathways, were tested for statistical significance using paired 2-tailed t-tests. Paired rather than unpaired t-tests increase statistical power by comparing within the same brain (thus controlling for global factors such as water content). A z-test was used to test for non-zero laterality (see Results).

Negative-Control Selection and Other Quality-Control Procedures

When studying previously-unknown pathways, it is essential to assure that the results are not false findings. Accordingly, several quality-control tests were administered. First, a negative-control selection procedure was performed to confirm that the pathways were not a trivial result of the selection. We defined a control ("foil") SSV by moving the anteromedial-temporal SSV to encompass ipsilateral primary motor cortex. We re-applied the selection procedure to select tracks connecting MFR and motor cortex (regions not expected to be connected). In most subjects, no tracks were selected in either hemisphere. For three subjects, there were only 4,0,0 tracks on the left, and 7,6,11 on the right (~2 foil tracks versus 542 pathway tracks per subject), suggesting a very low likelihood of spurious false-positive track selection. The second quality-control step tested for track-free SSV margins (see above), and assessed specificity by confirming that tracks only passed through focal parts of the SSVs (Fig. 1b,c), rather than filling the SSV (in principle, tracks can enter any part of the SSV). For the third quality-control step, I0 images were inspected for susceptibility-induced signal losses (e.g., petrous bone), and A_σ and skewness [A_ν (42)] images were inspected for regions of artifactually low anisotropy/strongly-negative skewness that occur in regions of crossing fibers. There were no such regions in the vicinity of the pathways. Similarly, the fourth quality-control step involved magnified projection display of track trajectories to screen for sharp turns, zigzags, or other irregularities suggestive of tensor anomalies [e.g., when a track loses a "winner-take-all" computational contest with an adjacent crossing pathway (41)]. No significant irregularities were observed. Fifth, inter-observer variation was tested, and was very low (see above).

RESULTS

Tracks interconnecting mid-fusiform cortex with medial temporal lobe (e.g., amygdala and entorhinal region) were identified bilaterally in all 15 subjects. The two distinct superior/inferior component pathways had characteristic shapes, trajectories, and anatomical locations. Detailed results are shown for one subject (Fig. 2), consistent with results for all subjects (Fig. 3). The tracks in both pathways began/ended in mid fusiform gyrus at the crest of, and medial to, the lateral occipitotemporal sulcus. The tracks then curved slightly dorsally and laterally, passed into the medial temporal lobe, and then hooked inferiorly-medially to end/begin next to amygdala or hippocampus in each hemisphere (Fig. 2). The superior pathway terminated adjacent to the supero-lateral part of amygdala, while the inferior pathway terminated adjacent to the hippocampal head (Fig. 2d,e), seen in all subjects to varying degrees (Fig. 3). Both component pathways have posterior origins/terminations adjacent to mid-fusiform area (Fig. 1a, Fig. 2d), with detailed analysis demonstrating a clear curvature downward toward fusiform cortex in the region of the lateral occipitotemporal sulcus (Fig. 4; A_σ=0.08 threshold). Accordingly, the upper and lower pathways are termed amygdalo-fusiform (AF) and hippocampo-fusiform (HF) pathways, respectively.

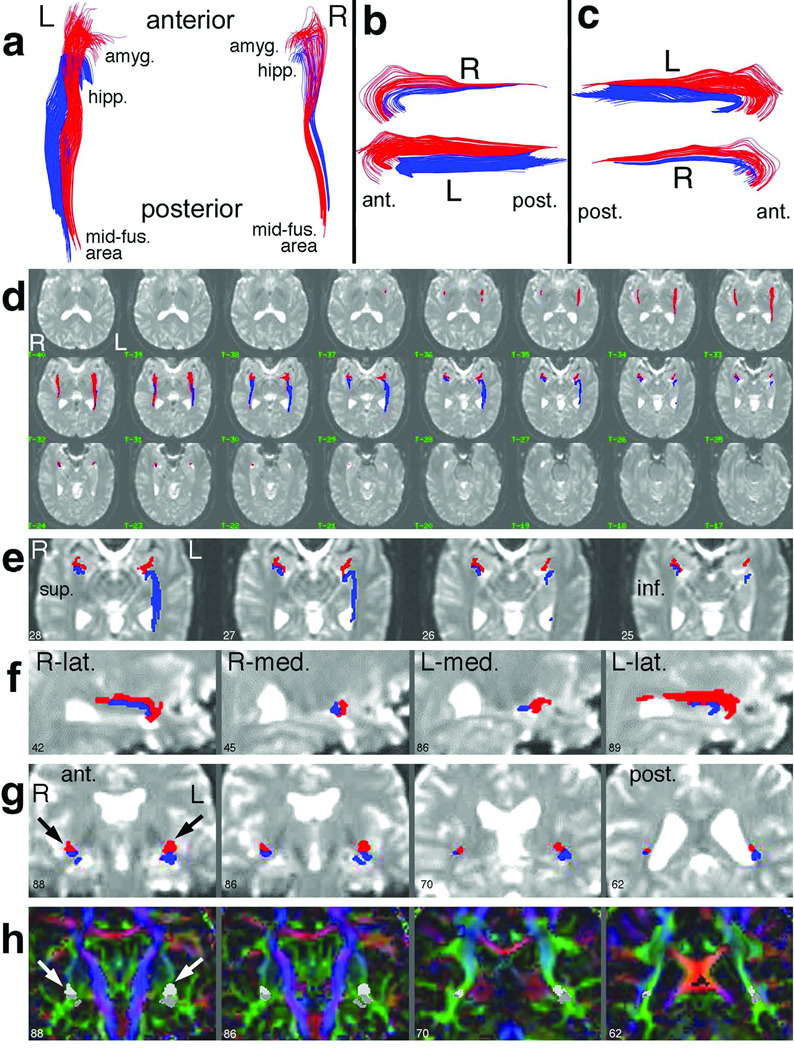
Figure 2.

Typical pathway results for one subject. In (a–c), the amygdalo-fusiform (red) and hippocampo-fusiform (blue) pathways are shown in 3D projection display, viewed from above (a), from the left side (b), and from the right side (c). The views in (b,c) are slightly obliqued (viewing superior-to-inferior by 20°) to better demonstrate the separation at the medial temporal lobe (see anterior parts of b,c). A 2D anatomical overlay of the pathways onto contiguous transverse 1.25-mm I0 images (d) documents the precise anatomical location. In (e), a close-up display of four consecutive slices in (d) shows the pathway terminations in relationship to amygdala and hippocampus. Select sagittal (f) and coronal (g) reformatted images demonstrate the relationship of the pathways to various anatomical structures. Finally, pathways are overlayed onto coronal color-direction images (h), calculated as in (62), to demonstrate the location of the pathways with respect to various white matter structures. The same slices are displayed in (g) and (h), with the red/blue pathways in (g) respectively shown as light/dark gray in (h) (see arrows). In all figures, the image numbers correspond to the sequential number of 1.25-mm sections. Abbreviations: L = left, R = right; ant. = anterior; post. = posterior; sup. = superior; inf. = inferior; lat. = lateral; med. = medial; amyg. = amygdala; hipp. = hippocampus; mid-fus. = mid-fusiform.

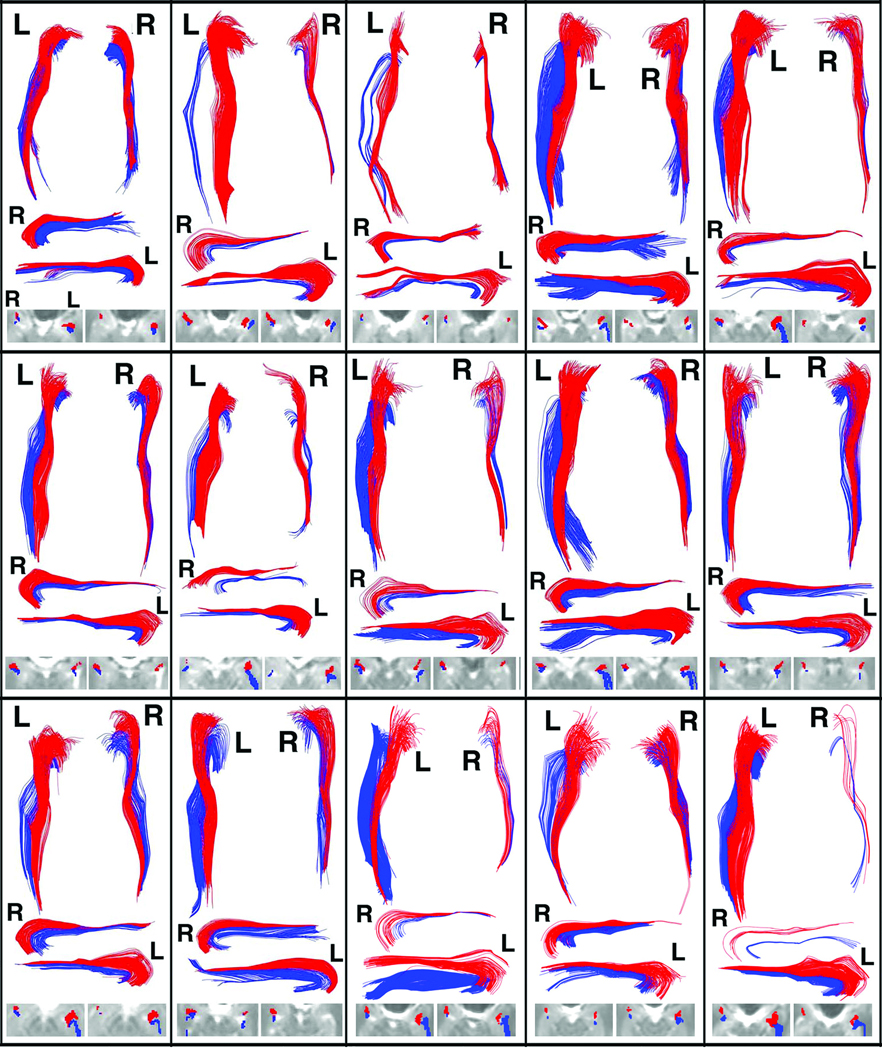
Figure 3.

Montage of pathway results for all 15 subjects in the study. Each rectangular box contains (from top to bottom): a 3D projection view of both sides viewed from above (as in Fig. 2a); a 3D view of the right pathway viewed from the 20° left superior oblique viewpoint (as in Fig. 2b); a 3D view of the left pathway viewed from the 20° right superior oblique viewpoint (as in Fig. 2c); and a close-up of the 2D overlay of pathways onto I0 images in the medial temporal lobe. The views in b,c were chosen to "open" the curve to amygdala/hippocampus for each respective side, and demonstrate that the lower pathway curves inside the upper pathway (i.e., has sharper curvature) near the medial temporal lobe. The 2D overlays are from the two slices (the left one typically more superior) that best illustrate the pathway terminations near amygdala and hippocampus on each side. [Note that pathways can be reconstructed in areas that contain small CSF spaces where, although anisotropy is decreased, the major eigenvector direction is preserved due to partial volume averaging (9)]. A threshold of A_σ=0.14 was used in all cases.

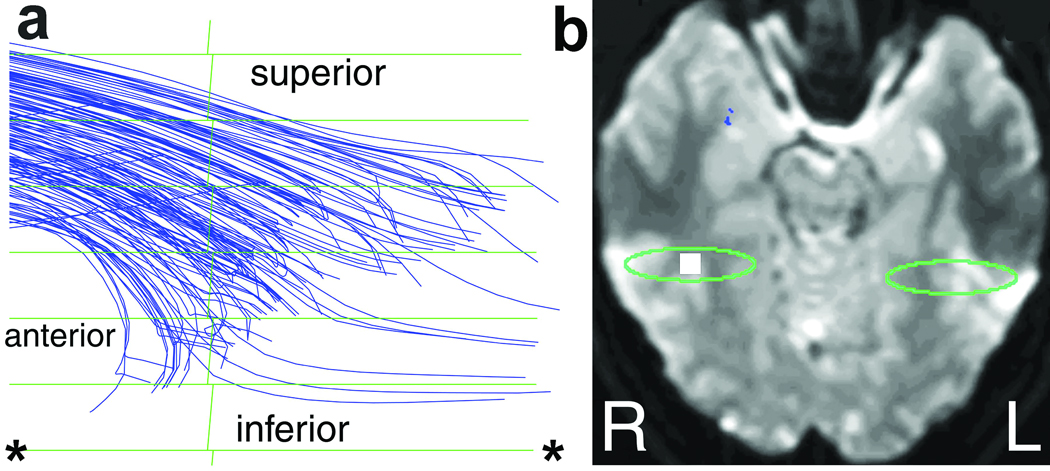
Figure 4.

Detail of the termination of the pathway tracks adjacent to mid-fusiform area in one subject. A magnified 3D projection view (a) shows the posterior termination of the combined right-hemispheric pathway, viewed from the right. (Tracks were computed at a lower threshold of A_σ=0.08, and were not color-separated.) The downward curvature of the pathway toward area-37 cortex is evident in (a). A reference I0 image (b) shows the cubical volume (white square) viewed in (a), in which the tracks terminate. The horizontal green lines in (a) are the ellipsoidal rings seen in Fig. 1b [the rings are spaced 1.25-mm apart and viewed from infinite distance in (a)]. The green ellipse in (b) corresponds to the posterior-most green SSV in Fig. 1a, which is centered on mid-fusiform area. The ellipse in (b) corresponds to the ellipsoidal ring demarcated by asterisks (*) in (a). Most tracks curve downward toward gray matter in the collateral sulcus within area 37, suggesting that they originate or terminate there.

Topologic relationships between the two pathways were very consistent, with mirror-symmetry across hemispheres, a superior-inferior separation along the pathway length (Fig. 2b), and a medial-lateral separation (Fig. 2a). The HF pathway was lateral to the AF pathway posteriorly, and then passed under the AF pathway to lie medial to the AF anteriorly. Near the anterior end of the pathways, the AF pathway broadly curved to terminate more antero-laterally in medial temporal lobe, while the HF pathway hooked more sharply to terminate more posterior-medially (Fig. 2a–c). We did not observe an alternate route between mid-fusiform and medial-temporal regions via the ventral temporal lobe, and no tracks entered the contralateral hemisphere.

Pathway metrics, statistical tests, and lateralities are in Table 1–Table 3, respectively. Pathway size was strongly left-lateralized, with the pathways visually appearing wider on the left in all 15 cases (Fig. 3). Combined upper-lower pathway volume was significantly larger on the left than right (2.41±0.19 cm³ left, 1.25±0.13 right, Table 1) with p=8.7E-6 (Table 2). These volumes were significantly left-lateralized [laterality=(+32.4±4.8)%; p=1.7E-12, Table 3]. On average, (66.2±2.4)% of the total pathway volume was on the left. Volume laterality was equivalent for AF and HF pathways [(28.7±4.3)% upper, (31.2±7.5)% lower; p=0.67, Table 3], significantly non-zero in both cases (p=2.7E-12 and 8.0E-6, Table 3). The similarity in upper and lower lateralities reflects the fact that the upper-lower distribution of volume was similar on both sides [(65.8±3.0)% of the left volume was upper, (72.2±3.4)% of the right volume was upper]. Overall, (67.3±2.5%) of the total volume was in the upper pathways. As a rule-of-thumb, ~2/3 of the total pathway volume was on the left, and ~2/3 was upper.

Table 1.

Voxel-based pathway metrics and DTT statistical counts.^*

	left pathway system						right pathway system
	upper(AF)		lower (HF)		combined (AF-HF)		upper (AF)		lower (HF)		combined (AF-HF)
pathway metrics*	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)
macrostructural metrics
pathway volume	1.550	(0.101)	0.994	(0.124)	2.411	(0.188)	0.879	(0.085)	0.539	(0.083)	1.252	(0.135)
pathway mean length	5.453	(0.146)	4.896	(0.104)	5.248	(0.137)	5.353	(0.174)	4.617	(0.135)	5.111	(0.160)
cross-sectional area	28.40	(1.67)	20.32	(2.47)	46.03	(3.50)	16.28	(1.44)	11.70	(1.76)	24.47	(2.49)
microstructural metrics
anisotropy (A-sigma)**	0.3175	(0.0073)	0.3222	(0.0077)	0.3249	(0.0059)	0.2974	(0.0071)	0.2917	(0.0059)	0.3003	(0.0068)
mean diffusivity (D-bar)	0.7971	(0.0065)	0.8208	(0.0092)	0.8078	(0.0068)	0.8111	(0.0075)	0.8338	(0.0152)	0.8174	(0.0084)
lambda-min (D-min)	0.4466	(0.0099)	0.4383	(0.0118)	0.4405	(0.0092)	0.4827	(0.0079)	0.4929	(0.0154)	0.4810	(0.0098)
lambda-mid (D-mid)	0.6722	(0.0074)	0.6976	(0.0279)	0.6863	(0.0086)	0.6858	(0.0104)	0.7299	(0.0193)	0.6966	(0.0130)
lambda-max (D-max)	1.2731	(0.0146)	1.3043	(0.0099)	1.2965	(0.0104)	1.2646	(0.0160)	1.2786	(0.0160)	1.2744	(0.0120)
radial diffusivity (D-radial)	0.5594	(0.0078)	0.5680	(0.0183)	0.5634	(0.0081)	0.5843	(0.0080)	0.6114	(0.0163)	0.5888	(0.0105)
DTT statistical counts***	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)	mean	(SEM)
number of track beads	24213	(3326)	14659	(3118)	38872	(4236)	9880	(1564)	4964	(1263)	14845	(2648)
number of traversed voxels	793.6	(51.9)	508.8	(63.6)	1234.5	(96.4)	450.2	(43.6)	275.9	(42.7)	640.9	(69.0)

^*Pathway metrics for amygdalo-fusiform (AF) and hippocampo-fusiform (HF) pathways are reported as the group mean and standard error of the mean (SEM) for the 15 subjects in the study. Pathway volume is given in cm³, mean length is in cm, and mean cross-sectional area is in mm². The parameters of mean diffusivity (D-bar), tensor eigenvalues (D-min, D-mid, D-max), and radial diffusivity (D-radial) are in units of µm²/ms.

^**The anisotropy values expressed as FA are (upper, lower, combined): Left -- 0.5017, 0.5078, 0.5113; right -- 0.4748, 0.4671, 0.4787.

^***The statistical counts (number of track beads and number of traversed voxels) are only presented to indicate the sampling statistics of the data underlying the measurement of bead-based and voxel-based pathway metrics. The number of traversed voxels is the number of 1.25×1.25×1.25-mm voxels that contain at least one bead of one track, where the 1.25×1.25×2.5-mm diffusion-weighted images were interpolated in-plane to 1.25-mm isotropic voxels prior to track computation (4,9). The pathway volume is calculated as number of traversed voxels times [(1.25)³ / 1000] cm³ The number of tracks (track count) was typically 70–220 for the four individual pathways. Track counts are due to many technical factors, and should not be interpreted in biological terms (see text).

Table 3.

Lateralities of pathway metrics.^*

	pathway laterality (%)									upper vs
	upper(AF)			lower (HF)			combined (AF-HF system)			lower
pathway metrics	mean	(SEM)	p	mean	(SEM)	p	mean	(SEM)	p	p
macrostructural metrics
pathway volume	28.67%	(4.30%)	2.72E-12	31.25%	(7.50%)	8.02E-06	32.41%	(4.82%)	1.74E-12	0.671
pathway mean length	1.03%	(1.35%)	0.215	3.04%	(1.23%)	0.0051	1.42%	(1.18)%	0.107	0.163
cross-sectional area	27.84%	(4.17%)	2.57E-12	28.64%	(7.44%)	3.38E-05	31.22%	(4.68)%	2.43E-12	0.900
microstructural metrics
anisotropy (A-sigma)	3.28%	(1.25%)	0.0034	4.92%	(1.01%)	2.07E-07	4.00%	(1.03)%	3.04E-05	0.289
mean diffusivity (D-bar)	−0.86%	(0.36%)	0.0060	−0.72%	(0.88%)	0.198	−0.58%	(0.32)%	0.030	0.884
lambda-min (D-min)	−3.96%	(0.97%)	1.26E-05	−5.80%	(1.47%)	2.12E-05	−4.41%	(0.88)%	1.09E-07	0.434
lambda-mid (D-mid)	−0.96%	(0.60%)	0.048	−2.62%	(2.81%)	0.167	−0.69%	(0.61)%	0.121	0.544
lambda-max (D-max)	0.34%	(0.60%)	0.279	1.03%	(0.68%)	0.059	0.87%	(0.42)%	0.016	0.473
radial diffusivity (D-radial)	−2.18%	(0.68%)	4.58E-04	−3.82%	(2.05%)	0.027	−2.17%	(0.66)%	3.24E-04	0.414

^*The mean, SEM, and p-values of lateralities in the pathway metrics in Table 1, reported for amygdalo-fusiform (AF) and hippocampo-fusiform (HF) pathways for the 15 subjects. The laterality of a given metric (M) is calculated as [M(left)-M(right)/M(left)+M(right)], and ranges from +100% (full left-lateralization) to 0 (no lateralization) to −100% (full right-lateralization). In general, a left-lateralized pathway function is indicated by a positive laterality in cross-sectional area and anisotropy, and a negative laterality in D-min and D-radial (see text). The p-value is for a null hypothesis of zero laterality, as tested using the z-test. The p-values < 0.05 are shown in italics. Abbreviations are as in Table 1.

Table 2.

Statistical tests (p values) of differences between pathways, for various pathway metrics^*.

	left vs right pathway			upper vs lower pathway
pathway metric	upper (AF)	lower (HF)	combined (AF-HF)	left	right
macrostrutural metrics
pathway volume	2.23E-06	0.0021	8.73E-06	9.92E-04	2.37E-04
pathway mean length	0.523	0.028	0.294	1.26E-04	1.09E-06
cross-sectional area	4.26E-06	0.0029	1.29E-05	0.0064	0.0060
microstructural metrics
anisotropy (A-sigma)	0.015	2.33E-04	0.0011	0.535	0.335
mean diffusivity (D-bar)	0.023	0.402	0.082	0.010	0.103
lambda-min (D-min)	7.29E-04	0.0015	1.51E-04	0.434	0.392
lambda-mid (D-mid)	0.103	0.356	0.246	0.347	0.0051
lambda-max (D-max)	0.572	0.159	0.050	0.040	0.497
radial diffusivity (D-radial)	0.0044	0.068	0.0051	0.603	0.036

^*All p-values are for a 2-tailed paired t-test. The p-values < 0.05 are shown in bold italics, with p-values < 0.001 reported in scientific notation. Abbreviations are as in Table 1.

The mean pathway length was similar on each side (5.25±0.14 cm left, 5.11±0.16 right; p=0.29, combined upper-lower, Table 1–Table 2), but differed upper-versus-lower (5.41±0.14 cm upper, 4.81±0.12 lower; p=1.1E-6, combined left-right), the lower pathways being (9.9±1.7)% shorter on the left and (13.5±1.6)% shorter on the right. The mean cross-sectional area differed across hemispheres (46.0±3.5 mm² left, 24.5±2.5 right; p=1.3E-5, combined upper-lower, Table 1–Table 2). The total cross-sectional area was strongly left-lateralized (p=2.4E-12, Table 3), with no upper/lower difference [laterality=(27.8±4.2)% upper, (28.6±7.4)% lower; p=0.90, Table 3]. Overall, (65.6±2.3)% of the cross-sectional area was on the right, and (59.4+2.5)% was upper (~2/3 rule-of-thumb). The cross-sectional area (and volume) of the combined pathways was left-lateralized in 15/15 subjects.

The mean A_σ ranged from 0.23–0.35 (FA 0.38–0.54) across subjects and pathways, and was typically 0.30–0.34 (FA 0.48–0.53). A_σ was statistically higher on the left (0.325±0.006 left, 0.300±0.007 right; p=0.0011, combined upper-lower, Table 1–Table 2), resulting in significant left-lateralization [laterality=(+4.00±1.03)%; p=3.0E-5, combined upper-lower, Table 3]. A_σ was equivalent for upper and lower pathways (0.310±0.006 upper, 0.312±0.007 lower; p=0.80, weighted-average left+right), with similar lateralities [(3.3±1.2)% upper, (4.9±1.0)% lower; p=0.29, Table 3].

For D-min, there were left-right differences (0.440±0.009 µm²/ms left, 0.481±0.010 right; p=1.5E-4, combined upper-lower, Table 1–Table 2) and strong laterality [(−4.41+0.88)%; p=1.1E-7, combined upper-lower, Table 3], with slower D-min on the left (consistent with higher anisotropy). There were no upper-lower differences in D-min (0.460±0.008 µm²/ms upper, 0.456±0.010 lower; p=0.53, combined left-right) nor D-min laterality [(−3.96+0.97)% upper, (−5.80+1.47)% lower; p=0.43]. Similar (but weaker) effects were observed for D-radial (Table 1–Table 3). For the other metrics (Table 1–Table 2), there were no significant left-right differences in D-mid or D-bar, but there was a subtle left-right difference in D-max (1.296±0.010 µm²/ms vs. 1.274±0.012; p=0.050).

DISCUSSION

The basic DTT finding is a pathway system consisting of parallel AF-HF pathways that interconnect mid-fusiform gyrus and amygdala/hippocampus bilaterally. The pathway anatomy and general mirror-symmetry support the accuracy of the results. These pathways have not been described previously. The typical range in pathway anisotropy (0.30–0.34) is higher than region-of-interest (ROI) measurements of general association white matter (0.21–0.26), and lower than projection white matter (0.31–0.45) reported in (45). The cross-subject variation in pathway anisotropy (6–8% standard deviation, SD, combined upper-lower) is much less than the 15–21% cross-subject SD in ROI anisotropy in (45) and the general variation across regions (45,46). Thus, the pathways have a very characteristic anisotropy.

The DTT connection pattern is consistent with fMRI data demonstrating functional coupling of amygdala and mid-fusiform region within, but not between, hemispheres (26). Because macroscopic clusters of synapses occur in gray matter or mixed gray-white structures (not subcortical/deep white matter), and the stopping threshold (A_σ=0.14) was well above gray matter values, the results suggest that these pathways are predominantly mono-synaptic (9). Fiber polarity cannot be determined using DTT, and the pathways likely contain both forward/back projections as in the visual system (47).

Precise definition of human pathway connections becomes essential when analyzing the brain in terms of overlapping functional systems, rather than isolated regional modules subserving specific functions (e.g., the hippocampus as spatial map or temporary memory store). The bilateral AF-HF pathways are interpreted as being part of such a functional system, based on two lines of evidence. First, the connected gray matter structures are likely to interact with each other via these pathways in functions that involve interplay between memory and emotion (e.g., emotional modulation of memory). Second, the upper and lower pathways have equivalent laterality for the most functionally-relevant metrics: cross-sectional area, anisotropy, D-min, and D-radial (discussed below). This consistent laterality suggests that the functional causes of (or role for) left lateralization are similar for upper and lower pathways (i.e., the pathways have interrelated functions and participate in the same functional network). Interestingly, the upper and lower pathways have very similar anisotropy/D-min within hemispheres but very different across hemispheres (Table 2), suggesting that the pathways are more functionally related within hemispheres, and more specialized across hemispheres.

The parallel AF-HF pathways are expected to be involved in emotional modulation of higher-order visual functions (including face/object recognition) and visual word-form (lexical) processing, known functions of the mid-fusiform area. The hippocampus and amygdala play intimate roles in both encoding and retrieval of memory, and in memory consolidation (48). The amygdala modulates memory formation partly through encoding emotional salience (49–52) (for example, memories of highly-emotional events to be vivid). The HF pathways may support memory aspects of object/face/lexical recognition, with AF pathways supporting emotional modulation of this process, and detection of emotional content in faces/objects.

The macroscopic anatomical connectivity of this pathway system, observed by DTT, suggests two possible mechanisms by which such emotional modulation may occur: 1) both medial-temporal structures sending related information to BA37 (with modulation occurring in BA37), or 2) both medial-temporal structures receiving parallel information from BA37 [with modulation occurring by local amygdalo-hippocampal connections shown in monkeys (53)]. The 10–13% shorter length of HF compared to AF implies that information originating in mid-fusiform area would arrive at the hippocampus prior to reaching the amygdala (assuming similar myelination, as suggested by anisotropy/D-min). Recent concepts of the functional role of hippocampus emphasize the central importance of putative hippocampal connections with neocortex and amygdala in multimodal association and memory formation (54).

The left lateralization (larger cross-sectional area, higher anisotropy, lower D-min/D-radial on the left) may provide additional functional insights into these pathways. To interpret laterality, the physical meaning of the measurements in Table 1 is considered. Track counts have the weakest relation to physical pathway characteristics. A track line represents the mean internal trajectory of a local bundle of fibers surrounding the track. The set of selected tracks is merely a representation of the trajectory and spatial extent of an ordered neuronal fiber pathway. The track count is not related to the number or density of axonal fibers within a pathway. Track count is determined by a variety of factors such as: seeding density; pathway volume [determining number of seeds in a pathway]; anisotropy level and signal-to-noise ratio [tracks may truncate due to low anisotropy or noise, failing the selection (9)]; pathway width [track counts are disproportionately low for narrow pathways (9)]; and pathway curvature/trajectory. As a result, track counts had higher cross-subject variability (39–65% SD) than pathway volume (29–40%) or cross-sectional area (28–38%), and the latter two measures were more consistently lateralized across subjects.

Pathway volume and cross-sectional area were the most strongly-lateralized metrics (Fig. 2, Table 3). The information-carrying capacity of the pathway is more related to cross-sectional area than volume. Regarding microstructural metrics, anisotropy was left-lateralized, in association with an even stronger D-min lateralization and a relatively weaker D-radial lateralization (Table 3). The higher anisotropy and lower D-min/D-radial on the left are indicative of slower diffusion across fibers, and could be due to microstructural factors such as a higher degree of myelination and/or higher fiber density.

The pattern of A_σ, D-min, D-mid, and D-radial values (Table 1–Table 3) gives further insight into these metrics. The anisotropy laterality is contributed mostly by D-min, and much less by D-mid or D-max, as noted by the relative strengths of laterality in Table 3 (A_σ is proportional to the root-mean-square of D-min/D-mid/D-max). The weak D-mid laterality causes the D-radial laterality to be weaker than the D-min laterality. D-min and D-mid would be expected to be equal in a noise-free, homogeneous, axisymmetric fiber packing arrangement. However, in the case of curved fiber trajectories, there is an intravoxel mixture of directions in the plane of curvature, causing diffusion to appear faster in the curvature plane. Thus, D-mid is elevated by curvature effects, while D-min samples the intrinsic curvature-independent cross-fiber diffusivity. Because both right and left pathways contain sharp anterior curves, the D-mid laterality is weakened by curvature effects (D-mid is elevated on both sides). The weakened D-mid laterality also weakens D-radial laterality and, to a lesser degree, A_σ laterality. Accordingly, D-min is the most strongly-lateralized microstructural metric, and can be taken to reflect the intrinsic cross-fiber diffusivity.

This D-min/D-mid concept is supported by upper/lower pathway comparisons. Anisotropy and D-min show no upper-lower differences (Table 2), indicative of a pathway system. However, D-mid was higher in the lower pathway (Table 1). We interpret this as due to the sharper curvature and shorter straight segment of the lower pathway. Such effects are less apparent in ROI measurements because the underlying curvatures are occult. Thus, while anisotropy, D-radial, D-min, and D-mid all relate to characteristics such as myelination and packing density, we posit that D-min is the most direct indicator of these characteristics.

In contrast to D-min, D-max had very weak laterality (Table 3), and would be expected to be relatively insensitive to factors such as myelination. D-max was modestly increased in the left lower pathway relative to the other pathways (Table 1), producing a weak upper-lower difference (Table 2). D-bar, being a function of D-max, showed similar effects. Increases in D-max might be due to factors such as increased spacing between fibers.

The strong left lateralization in cross-sectional area implies that the left pathways have greater information-carrying capacity compared to the right (assuming that anisotropy is at least as high on the left as right). Anisotropy was higher on the left, which (in normal subjects) suggests a higher degree of myelination.

This left lateralization in pathway size and anisotropy can be explained by the known hemispheric specialization within the domains of social cognition and language (27). The left pathways support the additional functions of the left mid-fusiform region not subserved by the right, e.g., lexical processing of visual word forms and other language-related data (15). Larger left pathways likely reflect a larger number of projections between the left medial-temporal and mid-fusiform areas, which could be necessary for these additional functions. Regarding anisotropy laterality, right-brain processes such as face recognition are slower and more integrative than left-brain processes such as language and object recognition. Thus, the right pathways need not be as myelinated as the left. In several fMRI studies reporting asymmetric left-right amygdala activation, the left is the predominantly-activated side (55). Moreover, while face processing is considered to be right-lateralized, many functional studies that use non-verbal materials, such as expressive faces, demonstrate bilaterally-symmetric co-activation of amygdala and mid-fusiform region (21–23). FMRI lateralization need not coincide with DTT size lateralization. DTT lateralization represents all the functions of a given pathway, while fMRI lateralization depends on the pathways recruited by the task (e.g., objects vs. faces) and the information-load feeding into the pathway system in each hemisphere.

Accurate, unbiased selection of the entire pathway in each hemisphere is critical for quantitation of laterality. We minimized pathway selection bias in four ways. First, we seeded the entire brain and then selected the pathways using Boolean-logic combinations of SSVs. In contrast, when trying to selectively seed the pathway, one may fail to seed the entire pathway cross-section, and seeding only one end of a pathway may limit recovery of the other end [due to finite probability of noise-induced sub-threshold anisotropy (9)]. Second, we used large SSVs that yielded track-free margins, ensuring selection of the entire pathway supportable by the data, without constraining its spatial extent. Third, we defined SSV locations only once in atlas space, then mapped these locations back to each individual's native image space. Thus, we used SSVs matched to each subject's diffusion images, without requiring anatomical identification, manual tracing, or other subjective steps. As a result, pathway selection was insensitive to ~mm displacements in SSVs, and had very low inter-operator variability (see Methods). Fourth, we measured pathway metrics in the "pathway space" of each subject.

Nevertheless, some caveats should be considered when interpreting these data. DTT is limited by factors such as image distortion, susceptibility-induced signal loss, partial-volume averaging with adjacent gray matter or other pathways, noise, and error propagation along lengthy tracks (4–6,9,56–58). These errors can cause early termination of tracks or, theoretically, misattribution of their origin/termination. Some of these error sources were ruled out by visualizing signal intensity and tensor characteristics. However, we cannot exclude the possibility that some parts of the pathway might not have been recovered. Track truncation effects in the lateral border of the pathway (9) cause under-reporting of pathway width, while central tracks remain precise (endpoint errors <0.5mm for long pathways, 9). The trackability threshold was significantly lower than the pathway anisotropy, and was chosen as a balance between track truncation (high threshold) versus rebounding (low threshold). As tracks do not typically enter gray matter, their origin/destination must be inferred from the location and trajectory of their terminal portions, enhanced by low-threshold analysis (Fig. 4).

The detection of AF-HF pathways raises the question of whether similar pathways exist in non-human primates. However, primate-human homologies for higher cortical areas (e.g., mid-fusiform) are unclear and difficult to verify. Specifically, the human mid-fusiform cortex includes cytoarchitectonic BA37, for which there is no definitive primate homologue. In non-human primates, regions possibly homologous to BA37 (TEO,TE) project to the lateral and superior portion of the laterobasal nucleus of amygdala as well as rostral neocortical areas (34). Reciprocal projections from basal/laterobasal nuclei of amygdala to the lateral temporal lobe only partially overlap the TEO,TE input zones (tracer studies do not typically map trajectories, but can assess polarity). Taken in combination with the results herein, the amygdala may receive neural inputs from mid-fusiform area [e.g., socially-important data regarding faces and, in humans, language (12,26,27)] and reciprocally modulate upstream visual processing areas via back-projections.

The demonstration of direct connections between human mid-fusiform region (canonical BA37) and medial temporal lobe (amygdala/hippocampus) has clinical and basic-science implications. Radiologically, white matter lesions in the pathway region (Fig. 1–Fig. 2) should be considered when interpreting images in patients with a history of impaired face/object recognition. Conversely, incidental detection of white matter lesions in this region could motivate clinical workup of face/object recognition. For basic science, the results can help elucidate pathological mechanisms in Alzheimer's disease. Pathologic alterations in the earliest stages of AD occur in allocortical/periallocortical medial-temporal regions (entorhinal cortex, subiculum, and hippocampus), as well as in amygdala and BA37 (33), and may be present prior to symptom onset (32). A direct mediotemporal-fusiform fiber connection is consistent with the functional/histological changes observed in canonical BA37 in asymptomatic subjects at high risk of AD [e.g., BA37 may be reporting dysfunction in medial temporal lobe via this connection (30,31)]. Although speculative, these histopathologic changes may be a consequence of this direct pathway connection through retrograde degeneration. Such a mechanism is supported by a comprehensive histopathologic AD study demonstrating that, when the amygdala was densely affected by neurofibrillary pathology, BA37 was also involved but with less density (59), suggesting early involvement of hippocampus/amygdala later progressing to involvement of BA37. A hallmark of AD is impaired ability to consolidate new memories, a function involving hippocampus and, in a modulatory role, amygdala. In advanced AD, the ability to interpret emotional content in facial expressions is also impaired (60). Such impairments in memory/affect likely involve the hippocampus, amygdala, and HF-AF pathway system. Face processing also declines in normal aging, and has been observed to be associated with decreased anisotropy in inferior fronto-occipital fasciculus (61).

In conclusion, we demonstrate the existence of a pathway system interconnecting mid-fusiform BA37 with amygdala/hippocampus in humans. Identification of this pathway system provides a more complete mechanistic understanding of memory and emotional processing of visual (objects, faces) and lexical information. This pathway system may also have relevance to Alzheimer's disease and other neuropsychiatric disorders such as autism. DTT holds substantial promise for mapping previously-unknown moderate-sized pathways in human brain that would not be observable otherwise. We anticipate that, in the future, a number of other pathways related to new or specifically-expanded human brain regions will be identified by DTT, highlighting characteristic or specifically-expanded human capabilities.