Incorporating Quality into Data Envelopment Analysis of Nursing Home Performance: A Case Study

Abstract

When using data envelopment analysis (DEA) as a benchmarking technique for nursing homes, it is essential to include measures of the quality of care. We survey applications where quality has been incorporated into DEA models and consider the concerns that arise when the results show that quality measures have been effectively ignored. Three modeling techniques are identified that address these concerns. Each of these techniques requires some input from management as to the proper emphasis to be placed on the quality aspect of performance. We report the results of a case study in which we apply these techniques to a DEA model of nursing home performance. We examine in depth not only the resulting efficiency scores, but also the benchmark sets and the weights given to the input and output measures. We find that two of the techniques are effective in insuring that DEA results discriminate between high and low quality performance.

1. Introduction

Like the rest of the United States health care industry, the nursing homes sector is under increasing pressure to improve its productivity. Nursing homes constitute a large, costly and growing portion of the overall health care industry. Expenditures for nursing home care amounted to $115.2 billion in 2004 and are projected to increase by nearly 80% over the next ten years [1]. Beginning in 1998, Medicare switched to a prospective payment system that has increased financial strains within the industry. Nursing home managers are under increasing pressure to control costs while maintaining or increasing the quality and level of care.

Large amounts of data are collected and reported on numerous aspects of nursing home performance including cost, utilization, case-mix severity, and quality. One tool that can be used for converting the vast amounts of available data into information useful to managers is Data Envelopment Analysis (DEA).

DEA, a benchmarking technique based on linear programming, converts multiple input and output measures into a single comprehensive measure of performance (an “efficiency score”) for each of a group of “decision-making units” (DMUs) [2]. A major advantage of DEA is that it does not require that the relative importance or weights of the input and output measures be known a priori. Also, each input and output variable can be measured independently in any useful unit, without being transformed into a single metric [3].

With DEA, each DMU (representing an individual nursing home for this application) is evaluated by comparing its performance with that of other DMUs or with the hypothetical performance of composite DMUs that are constructed as a weighted combination of the other DMUs in its peer group. A DMU is considered to be “inefficient” when another DMU, or hypothetical composite of two or more of them, can produce more outputs with the same inputs (the “output-oriented” model) or can produce the same outputs with fewer inputs (the “input-oriented” model). Otherwise, the DMU is deemed to be “efficient.” DEA assigns an efficiency score of 100% to these efficient DMUs. Inefficient DMUs receive lower scores, based on how efficiently they use their inputs to generate outputs compared to the efficient ones.

Perhaps the greatest value of DEA is that, for each of the inefficient DMUs, DEA identifies a set of efficient units that constitute its benchmark (or reference) set. A composite of the units in the benchmark set provides targets for the inefficient unit that will make its performance efficient. The units in the benchmark set can therefore serve as role models of “best practice” for the inefficient unit.

In order to apply DEA methodology to nursing homes, it is important to select relevant measures from the large amounts of nursing home performance data, and to define these measures as either outputs or inputs. Measures that are typically taken as outputs represent both the quantity and quality of services provided. The output measures used include number of residents and their case-mix severity for quantity of services and various indicators for quality of services. Measures typically taken as inputs are operating costs. To increase productivity, a nursing home would want to increase outputs or decrease inputs, or both.

One of the major problems in evaluating nursing homes using DEA is the selection of quality output measures. Several readily available and acceptable measures exist to represent costs, number of residents and case-mix severity. However, quality, which has received increasing concern and attention from both the government and nursing home managers, remains difficult to measure. As the role of quality measures becomes more prominent in the study of performance improvement in the nursing home industry, this problem requires more study.

In addition to the problem of selecting quality measures, there is also the problem of how to incorporate them into a DEA model. We first became aware of this problem in the context of an ongoing NIH-sponsored project to develop DEA software suitable for use by nursing home managers. Our initial recommendation to users was to treat measures of quality just like measures of the quantity of service [4], in other words, as just additional outputs. However, on closer examination, we found that this was not sufficient—the results from DEA were the same with or without the quality measures.

Therefore, we found it necessary to explore the question of how quality of service measures can and should be treated in a DEA model, focusing on models of nursing home performance. To do this, we performed a case study, applying several techniques suggested in the literature to a specific DEA model of nursing homes using real performance data for a group of homes located in central Massachusetts. This paper reports the results of this study. Section 2 reviews the literature on the treatment of quality in DEA and the concerns that can arise. In Section 3 we present several modeling approaches that address these concerns. Section 4 discusses the data and models used in our case study, and Section 5 presents the results of applying the various modeling approaches. In Section 6 the overall conclusions of this study are presented.

2. Literature Review

DEA models using quality measures have been applied to a variety of managerial contexts. One early DEA study in health care by Morey et al. [5] defined a quality-of-care output measure as the ratio of actual deaths in a hospital for a year in question to the forecasted number of deaths for the hospital. Salinas-Jimenez and Smith [6] studied the quality of services provided by the medical practitioners in family health service authorities in England. They used seven quality indicators as outputs, including, for example, the percentage of general medical practitioners not practicing single-handed and the percentage of female patients who had a cervical smear in the previous five and a half years. In a more recent work evaluating the performance of primary care physicians, Wagner et al. [7] measured quality in terms of the avoidance of readmission and complications for inpatients and satisfaction ratings from a survey of outpatients.

In addition to the area of health care, there are many other DEA applications that have used quality measures. Olesen and Petersen [8] studied primary schools in Denmark and measured outputs using the distribution of grades given to pupils as a quality measure. In another school application by Ray and Mukherjee [9], outputs included two quality measures: the average test score in an equivalency exam and the percentage of graduating students pursuing further education. In a DEA study of airport quality, Adler and Berechman [10] treated levels of customer satisfaction from use of each airport as the output measures. Despotis [11] applied the United Nations’ Human Development Index to benchmark countries of the regional aggregate of Asia and the Pacific.

Kleinsorge and Karney [12] conducted one of the early studies that demonstrated the usefulness of DEA for operational decision-making in nursing homes. It was a pilot study focused on a single nursing home chain that experimented with several models of efficiency based on financial, economic, and quality measures (such as number of bedsore-free days of care provided). In a recent study of nursing home performance by Lenard et al. [4], a group of homes in Massachusetts all belonging to the same national chain were analyzed using DEA where the number of residents without a catheter was used as a quality output measure.

The previous studies have shown that quality is often a difficult concept to define and can vary considerably based upon the context in which it is to be applied. One aspect that is important to recognize in DEA is that there are situations in which quality output measures do not increase with additional input resources. For example, Salinas-Jimenez and Smith [6] found that the increase in gross expenditure on medical services led to a decrease in two of the seven quality indicators that they studied. One can imagine modeling hospital health care in which too much of an input, such as length of stay for inpatient admissions or treatment by hospital staff, may lead to new health problems or illnesses and thus decrease the output as measured by the quality of care. It is important that the choice of quality output measures be appropriately related to the input measures so that the model meets the objectives of the DEA application.

The use of quality measures as outputs in DEA models has come under recent scrutiny for another reason. Thanassoulis et al. [13] used DEA to study perinatal care in England. They used full-time equivalent staff positions as inputs, along with three measures of outputs: activity quantity levels and both service quality and quality of medical outcomes. The authors encountered a problem with the analysis because DEA does not require that the weights of the inputs and outputs be specified a priori (as mentioned in Section 1), but rather it allows each DMU to choose its own weights. As a result of this “freedom of choice”, DMUs with poor quality could achieve high scores and appear efficient by simply ignoring some of the output measures (i.e., assigning very small weights to the quality outputs). The authors believed that this was not appropriate because of the importance of quality in this application.

In applications to the banking industry [14, 15], DEA has traditionally been used to identify low-cost, high-volume branches. More recently, there has been a recognition that service quality also needs to be considered [16]. One particular study by Sherman and Zhu [17] used teller hours and non-personnel expenses as inputs, and number of transactions processed and a quality measure based on a customer questionnaire as outputs. The authors determined that some branches were found to be efficient even though they had low quality. In this case, high productivity compensated for low quality. Furthermore, some of these high productivity/low quality bank branches were used as part of the benchmark set for inefficient branches. If inefficient branches did try to follow the lead of the benchmark set, DEA could result in not only reducing costs but also reducing service quality. Exactly opposite results were found in the study of primary schools in Denmark [7]. That study found some schools that were efficient with regard to quality of grades but inefficient with regard to quantity of pupils.

Applications such as nursing homes require that quality be included among the output measures used in DEA studies. However, inherent problems in DEA may, in fact, result in nursing homes receiving high overall ratings without having high quality. Even worse, homes with high operating efficiency but low quality may be in the reference set for benchmarking. Due to these shortcomings, modified DEA techniques must be developed to assure the primacy of quality in the analysis. In the next section we will present three such techniques.

3. Techniques to Incorporate Quality in DEA

In this section, we discuss three different techniques for incorporating quality measures in DEA and describe how they could be applied to the nursing home industry.

3.1 Two-Model Approach – Separate Quality Efficiency and Operating Efficiency Models

Some researchers have attempted to add the dimension of quality by developing and later integrating separate models [18–20]. In their analysis they introduced a quality efficiency model that used quality outputs and a second operating efficiency model that used quantity outputs. The authors graphed the results, showing the relative positions of the DMUs along the two dimensions in the graph: operating efficiency and quality level. They proposed different implications for the DMUs that were located in each of the four quadrants in the graph. For example, the DMUs in the quadrant representing high operating efficiency and high quality level could be considered as the best practice units and could serve in the reference set for inefficient DMUs. However, those DMUs in the high quality and low operating efficiency quadrant would need to improve their operating efficiency while keeping their quality at the same level.

Sherman and Zhu [17] also looked at operating efficiency and quality level separately in their study of productivity among bank branches. As discussed in Section 2, simply adding quality as an output measure resulted in branches in the benchmark set having high operating efficiency but low quality (that is, high operating efficiency compensated for low quality). To overcome this situation they introduced a method called Quality-adjusted DEA (Q-DEA). The authors first analyzed the operating efficiency using a DEA model without quality measures. They next graphed operating efficiency from the DEA model against a value for service quality based on customer evaluations. Those branches that were efficient in operating efficiency but low in quality were removed from the analysis and the DEA model was run again. Thus, those branches whose productivity was high enough to offset and possibly disguise low quality (perhaps sacrificing quality to achieve lower costs) were removed from the set of benchmark branches. The benchmark set was now comprised of branches that were both high in operating efficiency and service quality.

Elsewhere [21], we have proposed an extension of Q-DEA that we call the Two-Model Approach. The Two-Model Approach treats quality efficiency and operating efficiency as independent dimensions and develops two separate DEA models. In a demonstration applying the Two-Model Approach to nursing homes, both models used the same categories of labor as inputs, but one model (quality efficiency) used quality of service measures as outputs and the second model (operating efficiency) used quantity of service measures as outputs. After obtaining initial results from the two separate models, the Two-Model Approach eliminates from the quality efficiency model any homes in the benchmark set that have low operating efficiency and eliminates from the operating efficiency model any homes in the benchmark set that have low quality efficiency. The Two-Model Approach can utilize the opinion of the nursing home manager to determine the definition of “low” operating and quality efficiency.

3.2 Combined Quality and Operating Efficiency Model with Weight Restrictions

As discussed in Section 2, a popular approach used in DEA has been simply to add quality measures into the model as outputs. However, DEA can assign such low weights to some inputs and/or outputs that the quality output variables are effectively ignored. One way to overcome this problem is to place restrictions on the weights of the input and/or output measures.

Allen et al. [22] classified the methods of employing weight restrictions into three approaches: (1) direct restrictions on the weights; (2) adjusting the observed input-output levels; and (3) restricting the virtual inputs and outputs. Each of the approaches is based upon the idea that weight restrictions are arrived at through value judgments on the part of the experts or those most familiar with the situation being modeled [23].

The first approach, direct restrictions on the weights, is applied by adding additional constraints involving the weights to the existing DEA model. This is done by using absolute limits on weights [24], assurance regions of type I that assumes separate input and output bounds [25], or assurance regions of type II that assumes linked input and output bounds [13]. Adjusting the observed input-output levels, the second approach, involves transforming input-output data to simulate weight restrictions through the use of cone-ratios [26] or ordinal relations [27]. The third method, restricting the virtual inputs and outputs, involves placing restrictions on the “importance” attached by a DMU to a particular output (the proportion of the total virtual output devoted to that output) [28].

Previous studies have successfully applied weight restrictions in DEA to various applications such as banks [29], oil and gas producers [30], textile corporations [31], university departments [32] and farm management [33]. In looking at rates collection departments, Dyson and Thanassoulis [34] developed some simple cases in which the weight restrictions could be found by using regression. Relationships between the weights of inputs and outputs were established so that certain value judgments could be incorporated in the analysis of university departments [35] and perinatal health care [13].

For nursing homes, we propose using a combined quality and operating efficiency model that incorporates weight restrictions for the output measures that have been determined using value judgments from the nursing home manager. This approach, involving the use of type I assurance regions, will assure that the quality output variables are included in the DEA results and may prevent DEA from selecting nursing homes with low quality measures as part of the benchmark set.

3.3 Multiple Objective DEA (MODEA) Models for Quality Efficiency and Operating Efficiency

Klimberg and Puddicombe [36] extended the original single-objective DEA model developed by Charnes et al. [2] to formulate a multiple objective extension called multiple-objective DEA (MODEA). Using data to evaluate the day-to-day performance of a firm that produces and delivers concrete, the authors found that the single-objective model resulted in days in which the firm had a 100% efficiency rating but still experienced low levels in some of their outputs (e.g., yards delivered or number of jobs late). They observed that relatively significant changes in various inputs or outputs did not always influence the efficiency ratings. These problems were similar to those that resulted when quality output measures were used in DEA modeling (as reported in Section 2).

To overcome the shortcomings of single-objective DEA, MODEA permits the creation of multiple models, one for each objective, using different combinations of measures as inputs and outputs. The optimization is performed using the sum of the objectives for the individual models. Then to prevent the solution from decomposing into the solution of the individual single-objective models, MODEA restricts the weights assigned to measures appearing in more than one of the individual models to have values “close” to each other. Some proposals for restricting weights in MODEA can be found in Klimberg et al. [37].

For the concrete firm example presented in their paper, Klimberg and Puddicombe [36] originally worked with a single objective that included four inputs and four outputs. Because the single-objective DEA model did not produce sufficiently discriminating results (i.e., most facilities had very high efficiency scores), they defined three new models measuring different performance objectives (material efficiency, transportation efficiency and scheduling effectiveness) using various combinations of the eight input and output measures. Two measures appeared in all three models – in two of the models as part of the inputs and in one model as the outputs. Weight restrictions were imposed on these common measures which assured that the assigned weights were not significantly different from model to model.

Overall, the MODEA efficiency scores were much more discriminating than the results observed using the single-objective DEA model. Most of the single-objective efficiency scores were greater than 90% with 9 out of 16 DMUs at 100% efficiency. The MODEA results reported efficiencies as low as 20% with only 3, 2 and 1 DMUs at 100% efficiency for the material efficiency, scheduling effectiveness and transportation efficiency objectives, respectively.

The nursing home example with performance objectives measured in terms of both quality efficiency and operating efficiency meets the conditions of MODEA. MODEA can be used to analyze nursing home performance using the two different objectives, while, at the same time, applying weight restrictions to the common measures, namely the labor inputs. The judgment of the nursing home manager can be included in determining the weight restrictions to be used in MODEA.

As is the case with the Two-Model Approach, MODEA provides linkage between the two aspects of performance, while giving the nursing home manager separate information on quality and operating efficiency. An advantage of MODEA over the Two-Model Approach is that the solution is found in one solution of one model, rather than in (potentially) two solutions of two models.

4. Nursing Home Data and Models

There are several sources of nursing home data from which quality measures can be determined. One is the Online Survey, Certification and Reporting (OSCAR) database. It is maintained by CMS (Centers for Medicare and Medicaid Services) and provides information on every nursing home in the United States that is certified by Medicare and/or Medicaid. OSCAR data are collected in two different ways. States are required to conduct inspection surveys of each facility no less often than every 15 months. During the survey, data are gathered on the incidence and severity of nearly 190 facility deficiencies that can result in negative impact on the health and safety of residents. In addition, at the time of the survey, the individual nursing home is required to provide self-reported data that include facility characteristics, resident characteristics and staffing levels.

Another federal source of data is the Minimum Data Set (MDS), a comprehensive patient assessment instrument used by nursing facilities. The MDS is used for care planning, billing and research. Also, CMS has used data from the MDS to generate a set of valid facility-level Quality Measures for both long-term and short-stay residents. CMS maintains an Internet site which presents these quality data for all Medicare and Medicaid certified nursing homes along with a description of the facility deficiencies that have been reported on the state inspection survey from the OSCAR database [38].

We have selected as the basis for our case study OSCAR data for thirty-eight homes, all located in the same county (Worcester County in central Massachusetts), and all having 90 or more total beds. The data we used was taken from the 2003 OSCAR database (i.e., data collected during the survey conducted closest to July 1, 2003).

The primary input category for our model of nursing home performance is labor. The OSCAR database provides many measures of staffing data. We aggregated these into six measures, namely the full-time equivalents (FTEs) of: registered nurses (RN); licensed practical nurses (LPN); nursing aides (AIDES); ancillary non-nursing professional staff (ANCPRO); ancillary non-nursing non-professional staff (ANCNON); and administrative staff (ADMIN).

On the output side, we selected measures of both quantity of services and quality of services provided. To represent the quantity of services provided, we used the total number of residents (TOTRES) in the nursing home along with the case-mix severity, as measured by the number of residents needing assistance with the five Activities of Daily Living (ADLs). Thus, the five measures of case-mix severity are the number of residents who are dependent on assistance with: bathing (BATH_DEP), dressing (DRESS_DEP), transferring (TRANS_DEP), toileting (TOIL_DEP), and eating (EAT_DEP). The choice of these quantity output measures is supported by a number of previous studies [39–41] that report a strong relationship among staffing levels and the number of nursing home residents and resident characteristics measured by case-mix severity.

We chose three measures of quality that focus on the prevalence of various conditions among the residents of a nursing home. The measures chosen are the number of residents with an indwelling or an external catheter, residents who require physical restraints, and residents with pressure sores. A high prevalence of any of these conditions is often taken as an indication of poor quality care by a nursing home. We used the OSCAR variables for the number of residents with catheters, restraints and sores and subtracted these variables from the total number of residents to get the following quality measures: the number of residents without a catheter (NOCATH), number of residents without restraints (NOREST), and number of residents without pressure sores (NOSORE). In this way these quality measures satisfy the DEA assumption that efficiency scores increase when output measures increase.

For our nursing home application, using quality measures as outputs and staffing levels as inputs is an appropriate model. A review of the literature suggests that there is a positive association between quality and staffing in nursing homes. Studies have consistently shown that higher staffing levels were related to improved quality of care measured through a number of outcome indicators [42–48]. In many of these studies quality of care was determined on the basis of the prevalence of resident conditions reported in the OSCAR database, including, but not limited to, the three that we have chosen to use.

Table 1 presents a summary of the input and output measures just described for the thirty-eight nursing homes. The table includes values of the mean, standard deviation, coefficient of variation, minimum and maximum values for each of the input and output measures.

Table 1.

Summary of Nursing Home Measures (N = 38)

Measures	Mean	Standard Deviation	Coefficient of Variation	Min	Max
Inputs:
RN	10.05	4.35	0.43	4.40	22.00
LPN	16.54	4.27	0.26	9.60	24.40
AIDES	59.03	14.98	0.25	27.60	87.10
ANCPRO	18.96	7.03	0.37	10.00	41.60
ANCNON	31.85	14.03	0.44	13.80	83.40
ADMIN	7.47	4.79	0.64	1.30	19.80
Outputs (Quantity):
TOTRES	123.42	23.17	0.19	87	172
BATH_DEP	117.16	21.88	0.19	77	157
DRES_DEP	114.21	21.04	0.18	75	156
TRANS_DEP	101.61	23.26	0.23	51	151
TOIL_DEP	105.03	22.20	0.21	60	157
EAT_DEP	57.11	23.52	0.41	16	116
Outputs (Quality):
NOCATH	116.42	21.11	0.18	82	158
NOREST	117.88	23.58	0.20	76	165
NOSORE	115.24	22.21	0.19	81	165

Throughout this paper, the input-oriented CRS model is used in the analysis. We chose the input orientation because we believe that labor is more directly under the control of management than the output measures. The CRS model represents constant returns to scale among the DMUs. This seemed appropriate because we did not expect scale effects for the size of the nursing homes that we considered in this study.

5. Results

We began by combining all of the measures into a single DEA model, that is, the six labor measures were used as the inputs, and the three measures of quality of services along with the six measures of quantity of services were used as outputs. Column 2 in Table 2 shows the resulting efficiency scores. For this combined quality and operating efficiency model, fifteen nursing homes were found to have 100% efficiency scores. However, when reviewing the weights assigned to the three quality measures for the thirty-eight nursing homes (a total of 114 different weights), all but two of the weights had values that were very small. (We have chosen to use 10⁻⁶ as the threshold for “very small” values of the weights). Thus, the quality measures played a minimal role in determining the efficiency scores and ultimately, the best-practice homes. It is certainly possible, as will be shown, that some nursing homes were found to be 100% efficient while having low quality. To overcome the problems encountered by simply adding quality to the other output measures, we will demonstrate the application of the three techniques for incorporating quality measures into DEA that were discussed in Section 3.

Table 2.

Efficiency Scores (%)

1	2	3	4	5	6	7	8
Facility	Combined Model	Two-Model Approacha			Combined Modelb	MODEAc
		Quality	Quantity	RvQuantity	Wgt Restrictions	Quality	Quantity
1	100.0	100.0	100.0	100.0	100.0	100.0	100.0
2	91.4	86.4	90.3	100.0	86.9	83.9	90.3
3	76.2	72.2	76.2	77.8	72.2	72.2	75.3
4	54.7	38.4	54.7	54.7	41.8	38.4	54.8
5	62.6	55.3	62.6	62.6	55.9	55.3	62.6
6	88.3	81.9	88.3	88.3	85.6	80.9	88.0
7	100.0	100.0	100.0	100.0	100.0	100.0	100.0
8	100.0	100.0	100.0	100.0	100.0	100.0	100.0
9	77.5	67.5	77.5	77.7	70.3	67.5	77.6
10	79.0	67.7	79.0	81.6	68.0	65.5	74.2
11	100.0	80.4	100.0	Removed	85.5	80.4	100.0
12	100.0	94.3	100.0	100.0	98.8	91.8	99.9
13	100.0	100.0	100.0	100.0	100.0	100.0	100.0
14	75.9	67.0	75.9	79.3	67.0	64.6	75.2
15	100.0	49.2	100.0	Removed	54.7	48.8	96.8
16	100.0	88.6	100.0	Removed	91.2	86.1	100.0
17	100.0	100.0	100.0	100.0	100.0	100.0	100.0
18	70.8	53.6	70.8	77.2	55.2	50.0	68.2
19	100.0	100.0	100.0	100.0	100.0	100.0	100.0
20	67.8	67.8	67.8	67.8	67.8	67.8	67.8
21	86.0	70.7	86.0	86.0	72.5	70.7	86.0
22	78.6	59.1	78.6	82.1	62.5	58.4	78.6
23	89.2	70.4	89.2	90.7	74.7	70.4	89.2
24	72.3	69.3	72.3	72.3	70.1	68.5	72.3
25	100.0	100.0	100.0	100.0	100.0	100.0	100.0
26	69.2	67.9	69.2	69.2	67.9	66.5	69.2
27	56.4	51.1	56.4	56.4	52.0	51.1	56.4
28	89.0	64.6	89.0	100.0	67.8	60.1	89.0
29	94.2	49.6	94.2	96.3	55.0	44.5	94.2
30	85.1	78.0	85.1	85.1	78.6	78.0	85.1
31	100.0	67.5	100.0	Removed	71.6	54.2	99.8
32	100.0	94.4	100.0	100.0	97.2	94.4	100.0
33	79.1	55.5	79.1	89.0	60.3	55.4	77.7
34	100.0	100.0	100.0	100.0	100.0	100.0	100.0
35	68.1	45.0	68.1	68.1	48.1	45.0	68.1
36	54.9	47.2	54.9	61.2	49.3	46.2	54.5
37	100.0	100.0	100.0	100.0	100.0	100.0	100.0
38	69.3	62.9	69.3	69.3	63.1	63.0	69.3

^aFacilities removed if quality score less than 90%.

^bWith θ = 1

^cWith φ = 10%

5.1 Results for Two-Model Approach – Separate Quality Efficiency and Operating Efficiency Models

Two separate DEA models were analyzed, one for quality efficiency and one for operating efficiency. The quality efficiency model used the six labor measures as inputs and the three quality measures as outputs. The operating efficiency model used the same six labor measures as the inputs but used the six quantity measures – total number of residents and the five case-mix severity measures – as outputs.

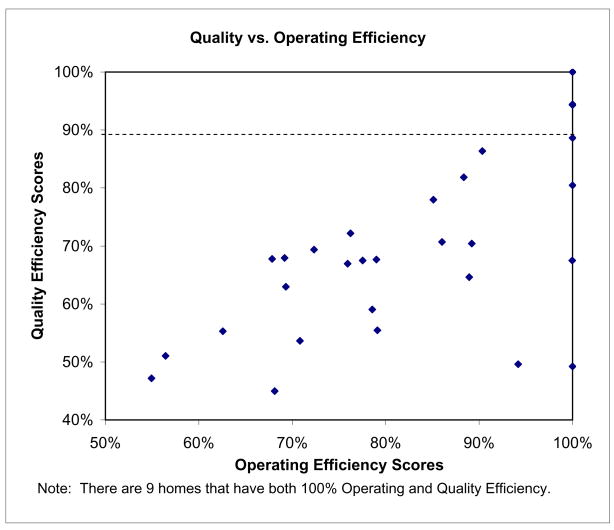
Table 2 shows the results of the two-model DEA approach in terms of efficiency scores. Column 3 presents the scores of the quality efficiency model, in which nine nursing homes were found be efficient with efficiency scores of 100%. The scores from the operating efficiency model in Column 4 shows that fifteen homes had efficiency scores of 100%. Nine nursing homes were efficient in both models and could serve as best practice homes in the reference set of the respective models.

Also, a comparison of Column 4 with Column 2 shows that they are virtually identical. This serves as further illustration that the combined model ignores quality. The results are the same with or without quality measures in the output.

A close examination of Columns 3 and 4 in Table 2 shows the obvious problem with treating quality efficiency and operating efficiency independently. Certainly it would be inappropriate for nursing home 15, with 100% operating efficiency but 49.2% quality efficiency, to serve as a best practice home. While it had the highest possible operating efficiency, it also had one of the lowest quality services of any nursing home. (In this particular example, there were no nursing homes that had a score of 100% with regard to quality efficiency but less than 100% on operating efficiency. Such nursing homes, with high quality efficiency but low operating efficiency, would also not be good choices as best practice benchmark homes.)

In Figure 1, the efficiency scores of the quality and operating models are graphed on separate axes. The homes of interest are those on the top side of the graph, corresponding to 100% quality efficiency, and on the right side of the graph, corresponding to 100% operating efficiency. In order to meet the performance objectives of the facility, the nursing home manager could establish a minimum acceptable level of quality and operating efficiency. In this example, we used 90% quality efficiency as the minimum level for homes to be used as best practice benchmarks in the operating efficiency model. As a result, four nursing homes (homes 11, 15, 16, and 31) were excluded from the operating efficiency model because they had 100% operating efficiency but less than 90% quality efficiency. Now, only homes that were 100% efficient with respect to operating efficiency and at least 90% quality efficiency would be included as benchmark homes. No nursing homes were excluded from the quality efficiency model since all of the homes that had 100% quality efficiency were also 100% operating efficiency.

Figure 1. Efficiency Scores for Two-Model DEA Approach.

Note: There are 9 homes that have both 100% Operating and Quality Efficiency.

The operating efficiency DEA model was rerun with the appropriate nursing homes removed due to low quality efficiency. The results of the revised operating efficiency model are presented in Column 5 of Table 2. This column shows that many of the remaining nursing homes improved their operating efficiency. Two new homes had 100% operating efficiency scores and ten other nursing homes showed improvements in their operating efficiency. The highest increase in the efficiency scores from the results of the operating efficiency model reported in Column 4 occurred in nursing home 28 (11.0%). The average increase in efficiency scores for the revised operating efficiency model was 1.7%. The thirteen efficient nursing homes that now serve as benchmarks in the operating efficiency model also have at least 90% efficiency in quality.

The results of the Two-Model Approach are dependent upon the manager’s choice of the standard used for measuring quality efficiency. For example, the manager could have chosen to relax the standard and to exclude just the two nursing homes whose quality efficiency was less than 80%. The revised results for that case were found to be nearly identical to those of the operating efficiency model in Column 4 of Table 2. No new homes achieved 100% operating efficiency and only one home showed a small increase in its efficiency score of 0.035%. Whereas if the manager were to tighten the standard for quality and exclude any nursing home whose quality efficiency was less than 100%, six homes would be dropped in the revised model. Now fifteen homes showed improvements in their operating efficiency scores, with an average increase of 1.9%.

The Two-Model Approach was also evaluated to determine the impact of the quality standard on the target or benchmark values for the labor input measures. Choosing a minimum of 80% quality efficiency yielded target results for the revised model that were very similar to the targets of the operating efficiency model in Column 4 of Table 2. As the standard for quality efficiency was raised to 100%, the ratio of the targets for the revised model versus the operating efficiency model generally increased. For the six labor input measures, the revised operating efficiency model produced target results that were as much as 5% higher, on average, than the targets of the original operating efficiency model. In other words, removal of the low quality homes from the benchmark set led to labor targets that might be considered more reasonable.

5.2 Results for Combined Quality and Operating Efficiency Model with Weight Restrictions

To demonstrate the use of weight restrictions, we used the combined quality and operating efficiency model that had three quality outputs and six quantity outputs. The results of this model, shown in Column 2 of Table 2, were discussed previously. The effect of the quality outputs was essentially negligible. In order to guarantee that the quality measures will have an impact on the DEA results, we will impose weight restrictions on the output measures (an application of type I assurance regions). There are numerous weight preference “structures” that could be employed (see [22]). Here, we define a structure, or set of constraints on the weights, that, in broad terms, reflects the perceived relative importance of the quality and quantity output measures in the nursing home.

Specifically, if μ_i^quality is the weight on quality measure i, and μ_j^quantity is the weight on quantity measure j, then we require, for some positive value of θ, that

$${min}_{\text{i}}({{\mu }_{\text{i}}}^{\text{quality}})\ge \theta \ast {max}_{\text{j}}({{\mu }_{\text{j}}}^{\text{quantity}})$$

In other words, we require that the minimum weight for quality measures exceed some positive multiple of the maximum weight for quantity measures. So, for example, if θ were chosen to be 1, this restriction ensures that each of the quality measures are accorded at least as much weight as that given to any of the quantity measures. If θ were chosen to be 0.5, then, assuming that the minimum weight for the quantity measures is very small, this restriction ensures that each of the weights given to the quality measures exceeds the mid-range of the weights for the quantity measures. In practice, we would expect that θ would be chosen by management to reflect their assessment of the relative importance of the quantity and quality aspects of performance.

Unlike other approaches that ask managers or other experts to assess the relative importance of each measure individually, we are asking for the relative importance of one category of measures (quality) versus another category (quantity). There are two advantages to this: (1) the manager need only choose one number instead of many, and (2) DEA is still allowed freedom to assign weights to measures within each category. This approach would also be useful in other situations where there are two categories of performance measures. For example, one application might involve operating expenses and capital expenditures as categories of inputs or another might include profit and market share as categories of outputs. It should be noted however that, in our application, the measures of quality and quantity are in the same units (i.e., number of residents) and of comparable magnitude. If that were not the case, the restriction should be applied to the virtual inputs or outputs, rather than to the weights (i.e., the third method of employing weight restrictions discussed in Section 3.2).

To incorporate this weight structure into a DEA model, we converted the restriction above into the following constraints on the ratios of weights:

$${{\mu }_{\text{i}}}^{\text{quality}}/{{\mu }_{\text{j}}}^{\text{quantity}}\ge \theta ,\text{for}\text{all}\text{i}\text{and}\text{j}.$$

For our model, this relationship was applied to all three of the quality output measures and the five quantity output measures representing case-mix severity (the number of residents needing assistance with the five ADLs), for a total of 15 weight restrictions.

Applying the weight preference structure shown above to the combined quality and operating efficiency model, and choosing θ = 1, yielded the results shown in Column 6 of Table 2. Now, nine nursing homes were 100% efficient compared to fifteen efficient homes when no weight restrictions were used. In addition, the efficiency scores of a total of twenty-eight homes that were reported in Column 2 without weight restrictions had decreased now that weight restrictions were being used. The highest decrease in efficiency score for the results of the combined model occurred in nursing home 15 (45.3%). Most importantly, no nursing home had very small weight values (less than 10⁻⁶) for all of its quality output measures. In fact, the overwhelming number of quality measures had weights that were larger than 10⁻⁶ (80.7% or 92 out of 114 total quality output weights using θ = 1). The quality outputs in this DEA model were no longer being overlooked and, in fact, the impact of these quality measures on the DEA results was quite dramatic when comparing the findings in Columns 2 and 6 of Table 2. It should be noted, however, that alternate optima are certainly possible so that the percentage of quality measures with very small weight values may differ from what is reported in our results.

Comparing these results to those of the separate quality and operating efficiency models found in Columns 3 and 4, it can be seen that the efficiency scores for the combined model using weight restrictions falls between the efficiency scores for the two separate models. Therefore, we defined the efficiency scores obtained using weight restrictions for each nursing home as a linear combination of the quality and operating efficiency scores in the following manner:

$$\text{Weight}\text{Restrictions}\text{Score}=\alpha \ast \text{Quality}\text{Score}+(1-\alpha )\ast \text{Operating}\text{Score}$$

Here α represents where the efficiency score with weight restrictions lies on the interval between the quality efficiency score and the operating efficiency score. For any nursing home, a value of α equal to one would mean that the efficiency score for the weight restrictions model would be identical to the score of the quality efficiency model and a value of α equal to zero would mean that the score with weight restrictions would be identical to that of the operating efficiency model.

As we have already observed, when θ is zero (no weight restrictions), the average value of α is zero (the combined score is all but identical to the operating efficiency score). Table 3 shows that higher values of θ (i.e., greater emphasis on quality weights) led to higher average values of α, (i.e., greater weight on the quality score in the combined score).

Table 3.

Weight Restrictions Model--Response to Choice of θ

θ	Average α for Efficiency Scores	Quality Weights		Average α for Labor Targets
		% Very Small Valuesa	Averageb
0.0	0.000	1.8	0.1124	0.000
0.01	0.042	93.0	0.4171	0.057
0.1	0.285	85.1	0.9669	0.173
0.5	0.656	86.0	1.3337	0.639
1.0	0.817	80.7	1.4927	0.828
2.0	0.921	66.7	1.6839	0.921
5.0	0.981	50.0	1.9589	0.980
Separate Q	1.000	33.3	2.1228	1.000

^a< 10⁻⁶

^b× 10⁻³

The choice of a value of θ also affects the weights assigned to the three quality measures for the thirty-eight nursing homes (a total of 114 different weights). As shown in Table 3, the percentage weights with values greater than 10⁻⁶ increases as θ increases. Thus, using weight restrictions has produced a model in which the quality measures play an important role.

Finally, analysis of the target values for the input measures in terms of α yielded a pattern similar to that of the efficiency scores. In general, for larger values of θ, the labor targets from the model with weight restrictions were similar to the targets from the quality efficiency model for each of the six inputs (i.e., the value of α was close to 1). As θ decreased, the targets moved closer to the target values from the operating efficiency model (see Table 3).

It is important that the nursing home manager carefully evaluate the decision to select the weight preference structure and the value of θ to be used in the weight restrictions model, since that decision will move both the efficiency scores and the labor targets towards the results of either the quality or operating efficiency models.

5.3 Results for Multiple Objective DEA (MODEA) Models for Quality Efficiency and Operating Efficiency

The MODEA technique handles quality efficiency and operating efficiency as two separate DEA models. As before, the quality efficiency model uses the three quality measures as outputs, while the operating efficiency model uses the six quantity measures as outputs. The six labor inputs are common to both the quality and operating efficiency models. The two models are linked in two ways. First, they are linked by having a single objective, namely the maximization of the sum of the objectives of the two separate models. (For this application, MODEA maximizes the sum of the value of the quality outputs plus the sum of the value of the quantity outputs.) To prevent the solution for the combined model from decomposing into the solution for the two separate models, MODEA adds another link between the models—namely weight restrictions for the common measures (in this application, the labor inputs) in the two separate models that require them to be “close” to each other.

Specifically, if υ_k^quality is the weight for input measure k in the quality efficiency model and υ_k^operating is the weight for input measure k in the operating efficiency model, then MODEA requires:

$$1-\varphi \le {{\upsilon }_{\text{k}}}^{\text{quality}}/{{\upsilon }_{\text{k}}}^{\text{operating}}\le 1+\varphi \text{for}\text{every}\text{k}.$$

We began by setting φ = 10%, so that the weight restrictions on the input measures in both the quality efficiency and operating efficiency models require that the weights be within 10% of each other. Lower (or higher) values of φ would bring the weights closer (or further apart) and could be chosen to reflect the nursing home manager’s preference for valuing labor resources in two different contexts. A total of six weight restrictions were used, one for each of the respective labor input measures in the quality and operating efficiency

The efficiency scores obtained with MODEA, are shown in Columns 7 and 8 of Table 2. (The contributions from the quality efficiency and operating efficiency models are reported separately). The efficiency scores of many of the nursing homes in the two MODEA models were lower than the scores in the combined model as shown in Column 2 or the scores in the separate models (Columns 3 and 4). The combined model found fifteen nursing homes to have 100% efficiency. Now, the MODEA quality efficiency model yielded nine homes with 100% efficiency and the MODEA operating model yielded twelve homes with 100% efficiency.

Further, we attempted to study the MODEA results in relation to the separate quality and operating models. We defined β^quality and β^operating as the ratio of the efficiency score for each nursing home from the MODEA quality and operating models to that of the separate quality and operating models, respectively. That is, the β^quality and β^operating values were found by taking the ratios of Columns 7 and 8 in Table 2 to Columns 3 and 4, respectively. A value of 1 for either β would mean that the MODEA results were identical to the results from the separate models for quality or for operating efficiency. For this example, where φ = 10%, the average value of β^quality was 0.982 and β^operating was 0.995. The MODEA efficiency scores showed little difference from those of the separate models, particularly with respect to operating efficiency.

Next, we analyzed the MODEA models for additional values of φ (between 0% and 20%). Table 4 shows that as φ varied, the results of the MODEA quality and operating models showed only small differences from the separate quality and operating efficiency models. This was true for the following measures: (1) the efficiency scores where the values of β^quality and β^operating were consistently close to 1; (2) the percentage of weights with values greater than 10⁻⁶ assigned to the three quality measures in the MODEA quality model which was nearly the same (36% = 41/114) for all values of φ; (3) the average of the weights on the quality measures in the MODEA quality model which were consistently between 2.07–2.08 ×10⁻³; and (4) the target values for the labor input measures in the MODEA models, where again the values of β^quality and β^operating were consistently close to 1.

Table 4.

MODEA Model--Response to Choice of φ

φ	Efficiency Scores		Quality Weights		Labor Targets
	Average β for quantity	Average β for quality	% Very Small Valuesb	Averagec	Average β for quantity	Average β for quality	Sum of Squared Differencesd
0%	0.993	0.983	36.0	2.0741	0.992	0.987	1.399
1%	0.993	0.982	36.0	2.0739	0.992	0.988	1.391
5%	0.995	0.981	36.0	2.0712	0.992	0.988	1.385
10%	0.993	0.982	36.0	2.0742	0.992	0.988	1.380
20%	0.995	0.986	36.8	2.0806	0.992	0.988	1.353
Infinitya	1.000	1.000	33.3	2.1228	1.000	1.000	1.281

^aNo restriction--identical to using two separate models.

^b< 10⁻⁶

^c× 10⁻³

^d× 10⁴

Finally, in MODEA, one might expect that restricting the differences in the weights on the common labor input variables in the quality and operating efficiency models would make the differences in labor target levels between the two models smaller than when they are solved separately (i.e., without the use of weight restrictions). In this case study, however, we found that, as φ decreased, the differences between the labor target levels (as measured by the sum of squared differences) actually increased slightly. This is documented in the final column in Table 4.

6. Conclusions

The nursing home industry has been using benchmarking extensively to measure their performance against best practices in order to develop strategies for cost control and performance improvement. One approach that can assist nursing homes in performing benchmarking is Data Envelopment Analysis (DEA). Because of the growing importance and relevance of quality measures in the nursing home industry, it is imperative that they be included as part of the DEA model. Simply using quality measures as additional outputs can result in some serious problems. Some studies reported that the impact of the quality measures on the DEA results was minimal since most of the measures had zero weights. Other researchers found that some DMUs with 100% efficiency scores had low quality measures. Furthermore, these low-quality but efficient DMUs were in the reference set for benchmarking. These problems would make DEA unacceptable for benchmarking nursing home performance.

In this paper, we have considered three techniques to overcome the problems that arise when quality output measures are simply added into the DEA model. Then we performed a case study examining the results of applying these three techniques to a DEA model of nursing home performance.

The Two-Model Approach treats quality efficiency and operating efficiency as two independent models. Using this approach, we removed nursing homes from the operating efficiency model because they were in the benchmark set but had low quality efficiency. Then the two independent models were re-solved. A second technique uses a combined model (that is, a single model with both quality and quantity outputs) but adds weight restrictions on the output measures. We imposed weight restrictions that required the minimum weight on the quality output measures to exceed some multiple (called θ) of the maximum weight on the quantity output measures. Lastly, a third technique treats benchmarking in the nursing homes as a multiple objective DEA study (MODEA). Now, quality efficiency and operating efficiency are treated as two separate models that are solved by maximizing the sum of the two individual objectives. Furthermore, the weights on the common labor input variables in the quality and operating efficiency models are restricted to be close to each other in order to make the weights assigned to the various labor categories in the two models more consistent

Oftentimes DEA applications yield results in which many of the nursing homes are 100% efficient and it is difficult for the decision-maker to determine what area to focus on to bring about performance improvements. One major advantage of the techniques that have been discussed in this paper is that they have the effect of reducing the number of fully efficient nursing homes, thereby providing more discriminating results. For the nursing home manager, there is greater flexibility to focus on quantity output measures or quality output measures or their interrelationship.

All three of the techniques that have been presented require the input of management in the decision process. In the Two-Model DEA Approach, the nursing home manager plays a role in defining acceptable levels of quality efficiency and operating efficiency. Similarly, the value judgment of the manager is necessary to determine the weight preference structure for the output measures in the combined operating and quality efficiency model. Finally, MODEA, as well, necessitates that the manager specify the weight restrictions on common input measures in each of the single-objective DEA models.

Overall, the Two-Model Approach is the easiest technique to understand and to apply. Most nursing home managers will probably be able to express a minimum standard for acceptable quality and/or operating efficiency. The results include separate scores for quality and operating efficiency. The problem with this technique, however, is that the manager must eventually decide whether to focus on quality or operating efficiency, each of which will likely require different staffing targets.

The weight restrictions technique, since it uses a single combined model, yields just a single combined efficiency score and a single set of staffing targets. Compared to the Two-Model Approach, this has the advantage of giving managers guidance on staffing targets without forcing them to choose either quality or operating efficiency as a goal. However, the weight restrictions technique instead requires that the manager decide on a value of θ (an indicator of the relative importance of quality and quantity output measures), which then indirectly causes the model results to be somewhere between those of the quality efficiency model and the operating efficiency model. A manager might find this decision (i.e., choosing the value of θ) to be less intuitive than setting the minimum acceptable standard needed for the Two-Model Approach.

The technique that was the least effective in this case study was MODEA. The results that we obtained were insensitive to the weight restrictions on the input measures. The insensitivity may be due to the nature of the two models used in this study, i.e., all of the inputs (the six labor measures) were common to both models, whereas reported successes of MODEA have been in cases where the two models were less homogeneous [36] (i.e., different combinations of input and output measures were used to define the objectives of three models). Since the results we obtained with MODEA were very similar to those of the separate quality and quantity efficiency models, we conclude that the added complexity of using the MODEA technique in this case is not justified. However, determining under what circumstances MODEA is and is not effective would be an interesting topic for further research.

This case study applied three techniques found in the literature to a specific set of nursing home data. While our analysis has led us to reach certain conclusions about the three techniques, the findings could be different for other data sets. Nevertheless, we have demonstrated some methods for evaluating these techniques that can be used in other situations. Furthermore, we believe we have demonstrated that the inherent problems with using quality measures in DEA models can be overcome, making it possible to use DEA benchmarking for nursing homes.

We have focused on the primacy of quality measures in the nursing home industry. However, the DEA techniques that we have discussed are not limited to quality measures or to this application. Other aspects of performance may be essential in a particular industry and could be incorporated into DEA benchmarking studies using the same techniques

We conclude that the techniques discussed, applied, and evaluated in this paper can be valuable tools in DEA modeling. They offer multiple options to the decision-maker in evaluating performance and working towards continuous improvement and increased efficiency. In the future, it would be worthwhile to explore under what circumstances each of the modeling techniques are most useful in incorporating quality measures into DEA studies.