Comparing measures of model selection for penalized splines in Cox models

Abstract

This article presents an application and a simulation study of model fit criteria for selecting the optimal degree of smoothness for penalized splines in Cox models. The criteria considered were the Akaike information criterion, the corrected AIC, two formulations of the Bayesian information criterion, and a generalized cross-validation method. The estimated curves selected by the five methods were compared to each other in a study of rectal cancer mortality in autoworkers. In the stimulation study, we estimated the fit of the penalized spline models in six exposure-response scenarios, using the five model fit criteria. The methods were compared based on a mean squared-error score and the power and size of hypothesis tests for any effect and for detecting nonlinearity. All comparisons were made across a range in the total sample size and number of cases.

1. Introduction

The Cox regression model [8] is widely used in epidemiological research to examine the association between an exposure and a health outcome. In a typical approach to the analysis of epidemiologic data with a continuous exposure variable, the exposure is transformed to an ordinal or nominal polytomous variable and relative risk (RR) is modeled as a step function of the exposure. This approach is attractive because there are no constraints on the change in RR between exposure categories and because it is conceptually and computationally straightforward to implement. However, the selection of cutpoints used to define the exposure categories influences the shape of the dose-response relationship and this model sensitivity has raised concerns [43]. Moreover, a step function does not take advantage of the information within categories [18,19]. To avoid these pitfalls, as well as to avoid parametric constraints on the shape of the exposure-response curve, a variety of smoothing techniques have been recommended by epidemiologists [16,18,35]. Over the past decade, splines and other smoothing methods have appeared in a wide range of studies, from etiologic investigations of air pollution [31], occupational exposures [36], cancer risk assessment [6], and diet-disease associations [7,15], to microrarray studies [10].

In several recent papers we have examined methods for selecting the optimal amount of smoothing for splines in an occupational cohort study of autoworkers exposed to metalworking fluids (MWF) [12,16,26,39]. The amount of smoothness (degrees of freedom) determines the RR predicted by the model for a given level of exposure and is therefore a critical aspect of model selection. Thurston et al. [39] presented the relative risk of prostate cancer mortality as a smoothed function of cumulative exposure to soluble metalworking fluid using penalized splines with different degrees of freedom. Malloy et al. [26] presented RR for rectal cancer in relation to cumulative exposure to straight metalworking fluid with penalized spline models fit using three different model fit criteria, Akaike information criteria (AIC), a corrected AIC (AICc), and cross-validation (CV), and varying numbers of knots. Classical methods for assessing model fit, such as Mallows’ Cp and Allen’s PRESSp, do not generalize to Cox models [41]. In this paper we examine criteria for assessing model fit that have been used for model selection or smoothing parameter selection in generalized linear models and, more recently, for Cox regression. The methods considered here, AIC, AICc, generalized cross-validation (GCV), and two forms of Bayesian information criteria (BIC) are all based on penalizing the partial likelihood for high degrees of freedom and are computationally efficient to implement. We fit penalized splines in Cox models to the autoworkers dataset previously analyzed by Malloy et al. [26] to compare the results of the five model fit criteria. We then apply the same criteria in a simulation study designed to reflect several plausible scenarios that are typical of epidemiological studies. This allows us to investigate the properties and behavior of the different goodness of fit methods and to assess how well each one captures the true exposure-response curve.

The remainder of the paper is organized as follows. In Section 2, we describe the Cox model with penalized splines. In Section 3, the criteria used to select the smoothing parameter are reviewed. The use of these criteria is illustrated in Section 4 in a study of rectal cancer mortality in an occupational cohort of autoworkers exposed to metalworking fluid. The Monte Carlo simulation study used to examine the properties of these selection criteria is described in Section 5. Results and conclusions follow in Sections 6 and 7, respectively.

2. The Cox model with penalized splines

The Cox model is used to analyze censored survival data. Suppose the observed data are the triplets (t_i, x_i, c_i) where t_i is the possibly censored survival time, x_i the scalar predictor variable, and c_i the event indicator, taking values of 1 if the event of interest occurred and 0 if it did not. Then, the Cox proportional hazards model takes the form

$$\lambda (t\mid x_i)={\lambda }_0(t)exp(\beta x_i)$$

where λ(t|x_i) is the hazard function given the predictor x_i, λ₀(t) is the baseline hazard function and β is the regression coefficient. Methods to model nonlinearities in the covariate have been described by O’Sullivan [27], who used smoothing splines, Sleeper and Harrington [33], who used regression splines, and Gray [17] who used penalized splines. All fit the model

$$\lambda (t\mid x_i)={\lambda }_0(t)exp\left[s(x_i)\right]$$ (1)

where s(x_i) is a linear combination of B-spline basis functions, f_k (x_i),

$$s(x_i)=\sum _{k=1}^K{b}_k{f}_k(x_i).$$ (2)

B-splines are piecewise-defined polynomials joined at knots, with cubic B-splines being the most frequently used basis functions. An algorithm for computing the B-splines is given in de Boor [9] and Eilers and Marx [11] provides an excellent summary of the properties of B-splines and their use in nonparametric regression.

Penalized splines are available in existing software packages such as R and S-PLUS. They are not available, however, in SAS, which is commonly used by epidemiologists, or in Stata, another frequently used package. Estimates for the unknown parameters in the B-spline expansion (2) are found by maximizing the penalized partial log-likelihood,

$$l(b)-\theta \int {\left[s^{″}(x)\right]}^{2}dx,$$ (3)

where b = (b₁,…,b_k)′ is the vector of parameters associated with the spline, l(b) is the partial log-likelihood for the Cox model in (1), and the penalty term includes a smoothing parameter, θ. The smoothing parameter controls the penalty applied to the curvature in s(x) through its second derivative, which in turn determines the behavior of the fitted estimate, ŝ(x). Properties of smoothing parameter selection methods have been examined in the nonparametric regression setting by Lee [25] but no similar study exists for censored survival data. It is the automatic selection of θ in (3) for the Cox regression setting that is of interest in this study. The standard methods used to choose θ in the Cox model are the nonparametric regression counterparts. The most popular and readily available methods are the AIC [1] and a corrected AIC [23]. These are included in the R and S-PLUS penalized spline functions. A closer examination of their use and properties along with those of other methods in an application to the metalworking fluid data and in a comprehensive simulation study is the focus of this paper.

3. Smoothing parameter selection

The model fit criteria used to select the optimal smoothing parameter in (3), θ, can be formulated in terms of the degrees of freedom (df) of the penalized spline. The df is the effective number of parameters estimated in model (1). With no penalty (θ = 0) there are K terms in the spline basis expansion (2) giving df = K. Taking θ → ∞ gives df = 1 and fits s(x)= βx [17]. The remaining possible values of df range between df = 1 and df = K and can be computed using the method discussed in Chapter 5 of Therneau and Grambsch [38]. We examine several measures of model fit for selecting the optimal smoothness, defined in terms of df as displayed in Table 1.

Table 1.

Smoothing parameter selection criteria in terms of model degrees of freedom

Criteria	Formula
AIC	−2log(L) +2df
AICc	$-2log(L)+\frac{r(df+1)}{r-(df+2)}$
BICn	−2log(L) +df log(n)
BICr	−2log(L) +df log(r)
GCV	$-\frac{log(L)}{{(n-df)}^2}$

Notation: df=model effective degrees of freedom

r=number of events (uncensored cases)

n=total same size (cases and non-cases)

log (L) = log-partial likelihood

The AIC method estimates the expected Kullback-Leibler (KL) information [24], a measure of the information lost when using an approximating distribution for estimation and inference instead of the true (unknown) distribution [4]. The degrees of freedom of the model give a bias correction to the expected KL information in large samples and act as a penalty on the number of parameters in the model. The optimal model minimizes AIC with respect to df providing a balance between model fit (via the log-likelihood) and parsimony (df). However, AIC has displayed deficiencies in detecting nonlinearities in Poisson models [28] and AIC tends to under-penalize the spline in nonparametric regression [22], leading to more variability in the fitted curves. A corrected AIC, AICc, adjusts for this over fitting by replacing the degrees of freedom in the AIC formula with a finite sample correction based on the number of events (uncensored cases) as in Therneau and Grambsch [37]. The statistical software packages R and S-PLUS fit the Cox model with penalized splines using AIC by default. AICc is also available in these two packages and implementation of both is straightforward.

We also examine methods based on a Bayesian motivation for model selection and an approximate generalized cross-validation statistic. The Bayesian information criterion (BIC), also known as the Schwarz criterion [32], estimates the Bayes factor for comparing candidate models to one another and can be applied even when no prior distributions are explicitly specified. Volinsky and Raftery [42] examined the use of BIC in Cox regression models for variable selection and used the number of events, r, in place of the sample size, which we denote BICr. For clarity, we denote by BICn the BIC criterion using the sample size. Volinsky and Raftery [42] reported an improvement in prediction using the BICr criterion over the BICn. It is not clear if this behavior generalizes to models fit using the penalized partial likelihood, therefore we consider both definitions of BIC. Finally, we also apply the GCV-type criterion used by Tibshirani [40] in Cox models for variable selection. Both BIC and the GCV criterion are minimized with respect to df. We demonstrate the use of these five criteria, AIC, AICc, BICn, BICr, and GCV, for selecting the optimal degrees of freedom when modeling exposure-response data from a cohort study of autoworkers exposed to metalworking fluids.

4. Data Application

Descriptions of the autoworkers cohort study are discussed in detail in previous publications [13,14]. We present a brief outline of this study here.

The cohort consists of 46,399 autoworkers from three manufacturing plants in Michigan. All employees who worked for at least three years prior to January 1, 1985 were included in the cohort and followed from 1941 to 1995 [13]. An extensive exposure assessment was conducted to retrospectively estimate past levels of particulate exposure to specific types of metalworking fluids [20]. By combining these exposure estimates with employment records, cumulative exposures to straight, soluble and synthetic fluids were estimated for each subject, measured in mg/m³-years.

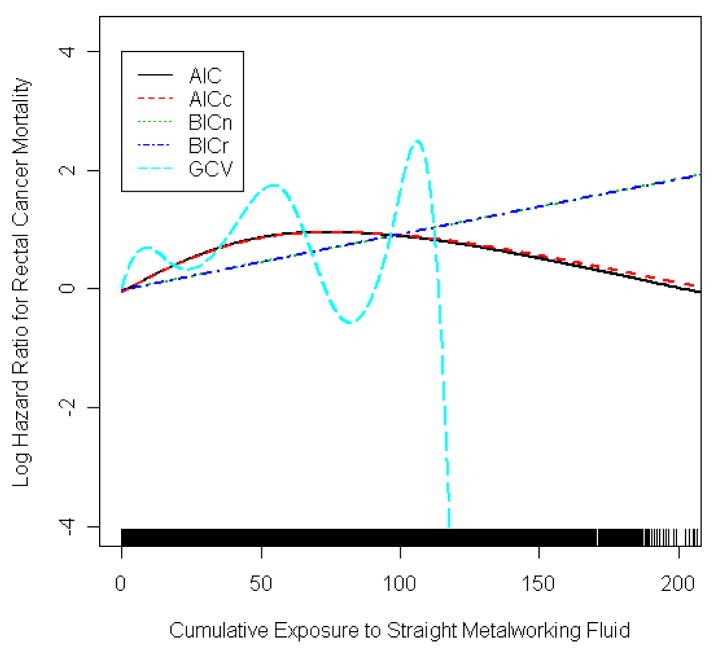
In this paper, we examined the dose-response curves for the association between rectal cancer mortality and particulate exposure to metal working fluids, as reported previously [26]. Because of small numbers of females, we excluded them from this analysis. The distribution of exposure was skewed, with mean of 2.8 mg/m³-years and a median of 0.02 mg/m³-years. Cox models were fit using penalized splines to estimate the exposure-response relationships, where the model in (1) was extended to include a vector of covariates as discussed in chapters 3 and 5 of Therneau and Grambsch [38]. The optimal smoothness was df = 1.99 for AIC, 1.95 for AICc, 1.01 for BICn and BICr, and 7.40 for GCV. AIC and AICc were fairly consistent with each other in both degrees of freedom and shape, as were BICn and BICr. The AIC methods differed from the BIC methods, both by slightly higher degrees of freedom as well as a decline in predicted RR in the higher exposure range. By contrast, the GCV criterion selected very large degrees of freedom, resulting in a biologically implausible fitted dose-response curve. Malloy et al. [26] used a true leave-one-out CV to select the smoothness and found results similar to AIC. We have opted for Tibshirani’s [40] GCV criterion here as it is computationally feasible to implement and is the natural CV counterpart for the linear regression setting. This analysis suggests that GCV has some deficiencies, and we have explored this further in the simulation studies that follow.

5. Design of the simulation study

Data were generated to follow the Cox regression model in (1) with a nonlinear exposure-response relationship, λ(t|x_i) = λ₀ (t) exp[s(x_i)], where t is the survival time, x is the exposure variable, and s(x) is the given function of interest. To mimic the distribution of exposure typically observed in environmental studies, we generated x to follow a half-normal distribution with shape parameter value set to six. This probability density function of x, $f(x)=\frac{2}{\sqrt{2\pi {\sigma }^2}}exp\left(\frac{-x^2}{2{\sigma }^2}\right)$, σ² = 6, x ≥ 0, gives only positive exposure values that are skewed right with median of 4.1 and an IQR of 5.0. We then followed the setup of Bender et al. [2] to generate the survival data, described below.

Let the random variable T denote survival time. If λ(t) is the hazard function, then the cumulative hazard function is $\mathrm{\Lambda }(t)=\underset{0}{\overset{t}{\int }}\lambda (t)dt=e^{s(x)}{\mathrm{\Lambda }}_0(t)$, where Λ₀(t) is the cumulative baseline hazard function. The survivor function is S(t)=e^−Λ(t) so that the cumulative distribution function (CDF) of T is F(t)=1−S(t) = 1 − e^−Λ(t). Using a Weibull distribution for the survival times, λ₀(t)=ωvt^ω−1(ω, v > 0), gives the CDF

$$F(t)=1-exp[-\nu t^{\omega }{e}^{s(x)}].$$ (4)

It is well known that the probability integral transformation F(T)~U(0,1)where U (0,1) is the uniform distribution on the interval from 0 to 1 (see for example, Casella and Berger [5] p. 52). Therefore, to generate survival times, T₁, for the event of interest, we solved (4) for T as $T_1={\left[-\frac{1}{\nu }log(1-U_1)e^{-s(x)}\right]}^{1/\omega }$ where U₁~ U(0,1).

We also included a competing risk time, T₂, and an end-of-study time, τ. The times of the competing risk were found in a manner similar to the method described above except we used an exponential survival time distribution with scale parameter γ so that $T_2=-\frac{1}{\gamma }log(1-U_2)$ with U₂ ~ U (0,1). Therefore, the observed follow-up time, T, was taken to be the minimum of T₁, T₂ and τ. An event indicator was calculated as C=I[T₁≤T_c], where $I[x]=\{\begin{array}{cc}1& \text{if}x\text{is}\text{true}\\ \text{0}& \text{otherwise}\end{array}$ and T_c is the minimum of T₂ and τ. The simulated data consisted of the triples (T, x, C) for each subject, corresponding to the follow-up time, the exposure variable, and the censoring indicator.

The parameters ω,ν,τ, and γ, the form of the true s(x) curves and the exposure covariate x were chosen to reflect situations that typically arise in epidemiologic studies of potential carcinogens, as illustrated by the application in the previous section. Breslow and Day [3] suggested that a value of ω = 5 is typical of many cancers and so we used this value. We fixed γ at 0.01, which corresponds to approximately 1% censoring per year for the competing risk. We chose ν such that the proportion of cases after τ = 20 years of follow-up was 5 to 40%. We used the follow forms for s(x):

1. s(x) = β log(x+1), β > 0 (logarithm)

2. s(x) = βx(x−b_m), β< 0 (quadratic)

3. s(x) = β sin(x/b_p), β> 0 (sine)

4. s(x) = β(x−b_mid)₊, where $x_{+}=\{\begin{array}{l}x,x>0\hfill \\ 0,x\le 0\hfill \end{array},\beta >0(\text{threshold})$

5. s(x) = βx, β > 0 (linear)

6. s(x) = 0 (null)

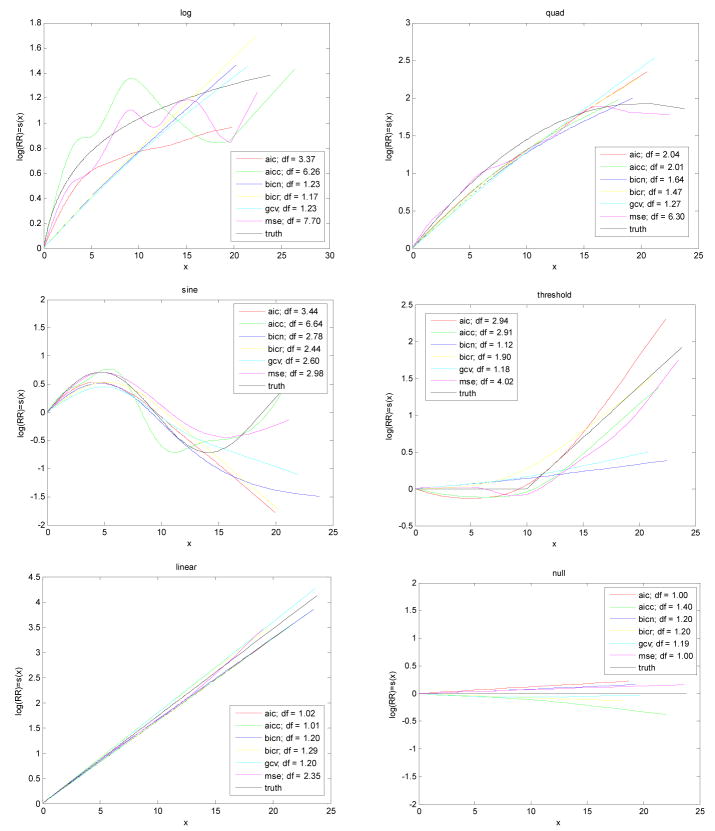
where β was chosen such that the hazard ratio for a given scenario at approximately the median exposure across the 1000 simulated data sets is double that at no exposure, b_m is twice the average of the maximum exposure across the data sets, and b_p gives a period that is approximately the maximum exposure. The sine function was included along with the other plausible exposure-response functions because splines are often used to adjust for confounding by factors with sinusoidal patterns that vary over time with season or diurnally. For the threshold curve, the threshold cut-off b_mid was chosen to be at approximately the midpoint of the exposure interval and β was chosen so that the hazard ratio for the threshold scenario at approximately the 99^th percentile of exposure is four times that at the midpoint. These parameters were selected to keep the behavior of the true exposure-response curves within a plausible range of values for environmental health studies, Figure 2.

Figure 2.

Estimated log(RR) = s(x) curves for each method and high case counts corresponding to those with median RMSE. Black curves are the true exposure-response curves used to generate the response.

One thousand data sets were simulated with n = 2000 subjects per data set using the same exposure variable for each of the six exposure-response curves, with large and small sample sizes and a range of case proportions. Cox regression models were fit in the R software package and each of the five selection criteria (AIC, AICc, BICn, BICr, and GCV) were used to determine the optimal smooth parameter (df) for each simulated data set. The penalized spline function in R was used to automatically select df using AIC and AICc. As R requires 17 cubic B-spline basis functions be used in the basis expansion in (2), we too use these 17 basis functions for all methods and scenarios. This is consistent with the results of Ruppert [30] who found that the number of knots, which determines the number of basis functions in (2), typically has a small effect on the smoothness provided a sufficient number have been chosen. A grid search for θ was used to determine the optimal df for the other three methods. In addition, the Cox model with a linear exposure-response curve was also fit for comparison to the five other methods.

To evaluate and compare the methods, the square root of the mean-squared error (RMSE) was calculated for the fitted curve as compared to the true curve in each simulated data set using

$$\mathit{RMS}{E}_j={\left(\frac{1}{n}\sum _{i=1}^n{\left[s(x_i)-{\widehat{s}}_j(x_i)\right]}^2\right)}^{1/2},$$ (5)

where ŝ_j(x_i) is the estimated curve for the j^th simulated data set evaluated at the i^th subject’s exposure x_i and s(x_i)is the value of the true curve at x_i. Smaller values of RMSE_j indicate the estimated curve is closer to the true curve on average. Furthermore, we also used the RMSE score as a benchmark criterion for comparing the model fits from the five selection criteria. That is, we also found the degrees of freedom that gave a fitted curve which optimized (minimized) the RMSE in (5). To avoid confusion between these two uses of the RMSE score, we denote by MSE the criterion used to select df and use RMSE for the computed values defined by (5). MSE was optimized using a grid search for θ to find the corresponding df.

The performance of these methods can also be assessed by the validity and power of hypothesis tests based on the optimal models selected. We tested two hypotheses using a likelihood ratio test (LRT). We tested the penalized spline fit versus the model with no exposure effect. This is equivalent to testing for any effect in the model with the basis expansion representation in (2). That is, we test H₀: b₁= b₂ = … = b_K = 0 versus H_A: not all b_k are zero. Rejecting the null hypothesis suggests that there is evidence of an association between the exposure and the outcome. The second hypothesis test we examined was a test for nonlinearity. This test is based on the fact that the basis expansion in (2) can be expressed with the linear term explicitly written separately from the sum, $s(x_i)=b_1{x}_i+{\displaystyle \sum _{k=2}^K}{b}_k{f}_k(x_i)[17]$, as there exists a linear combination of the K B-spline basis functions which gives the linear term. The LRT for nonlinearity was performed by forming the LRT statistic which compares the fit of the penalized spline model to the fit of the linear model. Hence, a test rejecting H₀:s(x_i)=b₁ x_i in favor of H_A: $s(x_i)=b_1{x}_i+{\displaystyle \sum _{k=2}^k}{b}_k{f}_k(x_i)$, not all b_k zero, suggests a nonlinearity in the exposure-response curve.

6. Simulation results

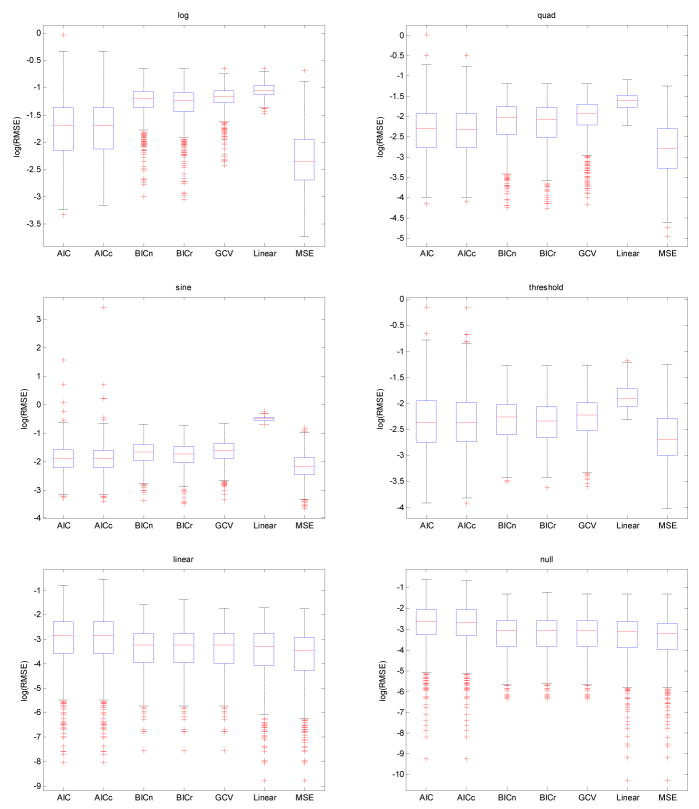
Based on goodness of fit as measured by RMSE in (5), no one method performed the best across all six scenarios. By definition given in the previous section, the MSE criterion has the smallest RMSE as it is designed to minimize the RMSE. It is presented only as a benchmark since it cannot be computed unless the true dose-response is known. For the four scenarios with nonlinearities (logarithm, quadratic, sine, and threshold) and with a high number of cases, the AIC and AICc criteria had the smallest RMSE values and the GCV method had the highest RMSE of all penalized methods, as in Table 2 and Figure 3. Compared to other penalized spline criteria, GCV performed better with a low number of cases (Table 3), having smallest RMSE values for the quadratic, sine and threshold scenarios while AICc had the smallest for the logarithm. Note that GCV did not perform well when the number of cases was dropped to approximately 100, whether 50% or 5% cases (as seen in Table 4), consistent with its poor performance in the application. For a small absolute number of cases, GCV uniformly had the highest and most variable RMSE scores for all scenarios except for the sine. The linear and null scenarios were fit best by the parametric linear exposure-response model with the BICn method providing the best fit of the penalized spline methods for the low case counts and GCV for the high case counts. Regardless of case size, AIC and AICc had the highest RMSE for the linear and null scenarios, although, based on the fits to the linear scenario in Figure 2, the AIC estimated curve still captured the overall linear relationship fairly well.

Table 2.

RMSE Median (IQR) with high case counts

Mean number of cases (%)	Method	AIC	AICc	BICn	BICr	GCV	Linear Fit	MSE*
	Scenario
740 (37.0%)	Logarithm	0.1828 (0.1388)	0.1841 (0.1369)	0.3012 (0.0859)	0.2925 (0.0967)	0.3141 (0.0721)	0.3540 (0.0578)	0.0948 (0.0765)
797 (39.9)	Quadratic	0.0993 (0.0841)	0.0989 (0.0841)	0.1328 (0.0831)	0.1260 (0.0870)	0.1472 (0.0717)	0.1971 (0.0587)	0.0622 (0.0613)
592 (29.6)	Sine	0.1520 (0.0953)	0.1513 (0.0951)	0.1896 (0.1023)	0.1767 (0.0997)	0.1987 (0.1032)	0.6069 (0.0549)	0.1150 (0.0692)
613 (30.7)	Threshold	0.0943 (0.0773)	0.0940 (0.0740)	0.1035 (0.0579)	0.0962 (0.0573)	0.1084 (0.0574)	0.1493 (0.0527)	0.0674 (0.0521)
839 (42.0)	Linear	0.0584 (0.0741)	0.0585 (0.0731)	0.0395 (0.0443)	0.0397 (0.0443)	0.0393 (0.0442)	0.0374 (0.0469)	0.0315 (0.0397)
595 (29.8)	Null	0.0702 (0.0914)	0.0694 (0.0900)	0.0457 (0.0532)	0.0465 (0.0534)	0.0456 (0.0532)	0.0451 (0.0537)	0.0403 (0.0478)

^*MSE criterion optimizes the RMSE and can only be computed when the true exposure-response is known.

Figure 3.

log(RMSE) boxplots for high cases counts.

Table 3.

RMSE Median (IQR) with low case counts

Mean number of cases (%)	Method	AIC	AICc	BICn	BICr	GCV	Linear Fit	MSE*
	Scenario
166 (8.3%)	Logarithm	0.2960 (0.1833)	0.2949 (0.1880)	0.3473 (0.1262)	0.3346 (0.1407)	0.3049 (0.1731)	0.3617 (0.1180)	0.1514 (0.1429)
191 (9.6)	Quadratic	0.1822 (0.1530)	0.1781 (0.1432)	0.1889 (0.1189)	0.1753 (0.1246)	0.1727 (0.1351)	0.2118 (0.1138)	0.0996 (0.1147)
224 (11.2)	Sine	0.2439 (0.1783)	0.2410 (0.1747)	0.3112 (0.1807)	0.2668 (0.1601)	0.2370 (0.1512)	0.6056 (0.0850)	0.1752 (0.1246)
264 (13.2)	Threshold	0.1385 (0.1109)	0.1374 (0.1035)	0.1372 (0.0756)	0.1310 (0.0735)	0.1238 (0.0814)	0.1642 (0.0772)	0.0915 (0.0794)
223 (11.2)	Linear	0.1031 (0.1512)	0.0990 (0.1423)	0.0667 (0.0803)	0.0674 (0.0811)	0.0777 (0.0943)	0.0646 (0.0784)	0.0504 (0.0647)
254 (12.7)	Null	0.1115 (0.1297)	0.1085 (0.1268)	0.0696 (0.0869)	0.0713 (0.0879)	0.0761 (0.0909)	0.0692 (0.0866)	0.0606 (0.0748)

^*MSE criterion optimizes the RMSE and can only be computed when the true exposure-response is known.

Table 4.

RMSE Median (IQR) from logarithmic scenario with different sample sizes and numbers of cases

Mean number of cases	Total sample size	AIC	AICc	BICn	BICr	GCV	Linear Fit	MSE*
73.5	200	0.3389 (0.2487)	0.3296 (0.2249)	0.3285 (0.1873)	0.3281 (0.1880)	0.3333 (0.1885)	0.3490 (0.1860)	0.1997 (0.1779)
96.8	200	0.3251 (0.2166)	0.3108 (0.1978)	0.3183 (0.1676)	0.3151 (0.1693)	0.3293 (0.1655)	0.3437 (0.1681)	0.1811 (0.1592)
100.8	2000	0.3263 (0.2038)	0.3164 (0.1906)	0.3557 (0.1536)	0.3416 (0.1572)	0.3641 (0.2979)	0.3629 (0.1484)	0.1788 (0.1680)
497.4	2000	0.2051 (0.1673)	0.2076 (0.1693)	0.3193 (0.0885)	0.3102 (0.0991)	0.3169 (0.0905)	0.3552 (0.0683)	0.1050 (0.0845)
740.0	2000	0.1828 (0.1388)	0.1841 (0.1369)	0.3012 (0.0859)	0.2925 (0.0967)	0.3141 (0.0721)	0.3540 (0.0578)	0.0948 (0.0765)
739.4	5000	0.1921 (0.1514)	0.1908 (0.1495)	0.3145 (0.0793)	0.3008 (0.0949)	0.2798 (0.1132)	0.3579 (0.0574)	0.0935 (0.0823)

^*MSE criterion optimizes the RMSE and can only be computed when the true exposure-response is known.

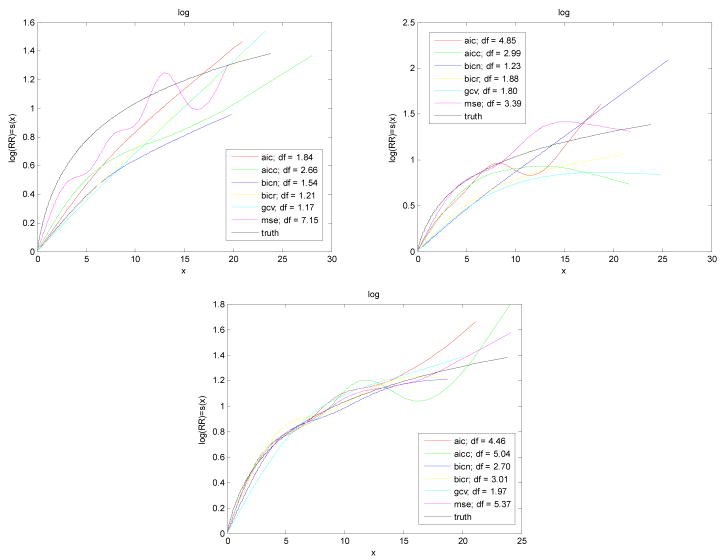
We investigated the logarithmic scenario in more detail than the others because it was similar to the estimated exposure-response in the application and the AIC methods were quite variable for this scenario in the simulations. The plot of the logarithm fits in Figure 2 illustrates a concern with both AIC methods: high curvature of the estimated function reflecting high degrees of freedom and an implausible model fit. Similar behavior was also seen for the logarithm scenario with a low proportion of cases (data not shown). Figure 4 gives further estimated logarithm fits with high case counts. These three plots are the estimated curves corresponding to the 75^th and 25^th percentiles of RMSE (top two plots) in addition to the best fitting curve, that which gave the minimum RMSE for each criterion. From these we see that all methods, even GCV, give smooth fits with low curvature, even for the estimated curves at the 75^th percentile of RMSE. The MSE selected curve has a relatively high degrees of freedom, in particular, df = 5.37 for the MSE curve corresponding to the lowest RMSE.

Figure 4.

Fit of logarithm scenario corresponding to the 75^th percentile of RMSE (top left), 25^th percentile of RMSE (top right), and minimum of RMSE (bottom) for high case counts.

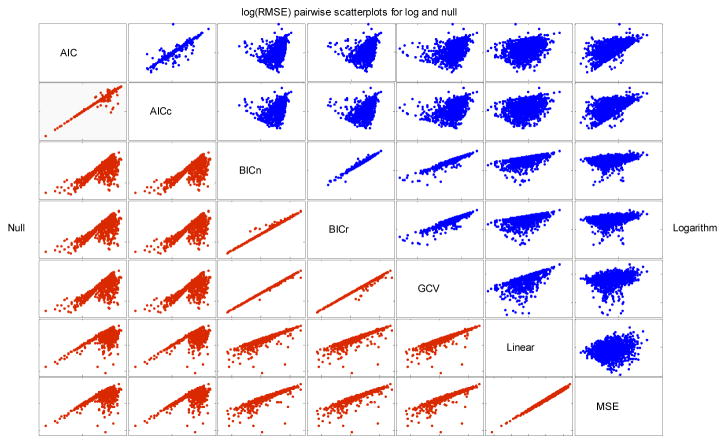
In general, the AIC and AICc methods tended to perform similarly, with AICc having the smaller median RMSE scores for most scenarios and case sizes. This similarity can also be seen in Figure 5, which presents pairwise plots of log(RMSE) values for each criterion, using the logarithm and null scenarios with high case counts as illustrations. (Note that the other scenarios and case numbers provided somewhat similar results and are thus not shown). The AIC and AICc methods also had more variable errors and exhibited more outliers in the right tail of the RMSE distribution, as displayed in Figure 3, indicating more simulated data sets with estimated curves further from the truth than the other methods. Likewise, as expected the BICn and BICr methods performed similarly overall, as demonstrated also in Figure 5. BICr fit better for the four nonlinear models and BICn for linear and null. With low case counts, the BIC methods gave median fits that were close to linear in the logarithm, quadratic, and threshold scenarios with optimal degrees of freedom selected to be approximately 1 in these situations (output omitted). With high case counts, the BIC methods selected less linear fits except for the logarithm scenario, as displayed in Figure 2. Based on Figure 5, the GCV method demonstrated similar behavior as the BICn and BICr for the logarithm and null scenarios. With a high number of cases, this was observed regardless of curve being estimated. For smaller numbers of cases, the GCV was not similar to any of the other methods, except for the linear and null scenarios where all of BICn, BICr, and GCV selected models close to linear.

Figure 5.

Pairwise scatter plots of log(RMSE) values for logarithm scenario (blue graphs above diagonal) and null scenario (red graphs below diagonal).

The results in Table 5 illustrate the power and size of likelihood ratio hypothesis tests of no effect and of a nonlinear dose-response relationship. Results are presented for low case counts. The tests for any effect were similar across the penalized spline methods. There was a high degree of power for the logarithm (93–95%), quadratic (100%), sine (95–100%), and linear (100%) scenarios. There was much less power to detect an effect for the threshold scenario, with AIC and AICc having the highest power (over 75%) and BICn and BICr the lowest (62% and 66%, respectively). The threshold scenario was interesting as the true log relative risk is zero across the first half of the exposure range and then increases linearly. The median fit displayed in Figure 2 shows the difficulty in estimating a function which is non-differentiable at a single value, particularly if the change-point is of interest. Like the penalized spline methods, the parametric linear fit had high power in most scenarios, despite its poor fit, although for the sine and threshold curves the power was particularly low, 37% and 47%, respectively. With respect to the null model, the BICn method had estimated size at the nominal testing level of 5%, BICr was at 6% and the linear fit was at 4%. The AIC and AICc methods were well above the nominal level for both tests at 15% and 14%.

Table 5.

Likelihood ratio hypothesis tests for any effect and for nonlinearity with low case counts

Proportion of significant p-values at the 5% level
	Test for any effect							Test for nonlinearity
Method	AIC	AICc	BICn	BICr	GCV	LinearFit	MSE*	AIC	AICc	BICn	BICr	GCV	MSE*
Scenario
Logarithm	0.95	0.96	0.93	0.93	0.95	0.93	0.86	0.67	0.69	0.41	0.36	0.35	0.24
Quadratic	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.68	0.70	0.42	0.40	0.41	0.32
Sine	1.00	1.00	0.95	0.98	1.00	0.37	0.99	0.99	0.99	1.00	1.00	0.99	0.97
Threshold	0.76	0.75	0.62	0.66	0.70	0.47	0.63	0.74	0.74	0.64	0.64	0.56	0.48
Linear	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.72	0.74	0.10	0.10	0.12	0.03
Null	0.15	0.14	0.05	0.06	0.09	0.04	0.04	0.74	0.75	0.13	0.13	0.10	0.05

^*Notes: MSE criterion optimizes the RMSE and can only be computed when the true exposure-response is known.

Test for any effect: H₀: all coefficients in s(x) = 0 vs. H_A: at least one non-zero.

Test for nonlinearity: H₀: linear relationship vs. H_A: nonlinear relationship.

For the second hypothesis test examined, all methods were able to significantly detect the nonlinearity in the sine curve, with power over 97% for all (including MSE), yet this can be considered one of the most difficult curves to fit based on the high RMSE scores in Tables 1 and 2. For the logarithm curve, which was also hard to fit, however, the methods had low power to detect the nonlinearity. Power was similarly low for the quadratic and threshold scenarios. On the other hand, when the curve was truly linear, the AIC and AICc methods rejected linearity in over 74% of the samples. BICn, BICr, and GCV only did so in about 10–13% of the samples. These three methods also fit the linear scenario slightly better than the AIC methods. Results were not substantially different when case counts increased, with power increasing with increasing case counts and the size of the appropriate test remaining similar to those in Table 5 for the linear and null scenarios.

The results for the test of nonlinearity when there is no effect (the null scenario) are curious. As this is testing a linear relationship versus a nonlinear relationship defined by the basis expansion in equation (2), it is difficult to assess the meaning of these results when there is no true effect. The high number of significant p-values for the AIC and AICc methods (over 74%) suggest nonlinearity is appropriate, yet the RMSE scores in Tables 1 and 2 are only marginally larger than those for the other methods, for the null scenario, suggesting the overall fit from these methods is on par with the others. Furthermore the degrees of freedom selected using AIC and AICc are much higher and more variable than the other methods for this (and all) scenarios (output omitted). Inspection of individual plots suggests that the AIC methods are varying around the horizontal axis in an attempt to fit the null case – using up a large number of degrees of freedom and rejecting linearity in favor of nonlinearity in up to 30% of the 1000 simulated datasets.

To further explore the effect of sample size on the estimates, we also considered a simulation where the total sample size was dropped to 200 but the proportion of cases remained similar to those in Table 2. The first line of Table 5 gives the results for the logarithm scenario, where we see that the median RMSE values are similar across methods. This behavior was also seen in the other non-linear scenarios but there were larger differences between the AIC criteria and the other methods for the linear and null scenarios (output omitted.) Here, for the logarithm curve, we see that when the average number of cases across the 1000 simulated data sets is similar, but the total sample size is not, the RMSE median and IQR are still close, as when there were approximately 100 cases and 740 cases. With the total sample size held constant, the RMSE values decreased in size, on average, and become less variable when the number of cases increased. This was consistent for all dose-response scenarios and model selection criteria examined.

7. Conclusions

In the simulation study, none of these methods, AIC, AICc, BICn, BICr, or GCV, was clearly superior in estimating all of the six exposure-response curves examined here (the sine curve was included to represent a seasonal adjustment). The BIC criteria are conservative in that they tend to choose the degrees of freedom close to 1 with very little variability. The AIC and AICc methods have much more variable df and RMSE scores, displaying a few very large RMSE scores, but also having some of the smallest RMSE values overall, suggesting they are able to achieve good fit. The AIC methods also rejected the null hypothesis of no effect in favor of an association in the null scenario (no true association) too often, incorrectly detecting an association when one does not exist. The GCV criteria had the smallest median RMSE for the quadratic, sine, and threshold curves with a lower proportion of cases but all methods gave similar fits for these scenarios. While the AIC and AICc criteria did display some deficiencies in the models selected, including biologically implausible models with high degrees of freedom, AICc selected fewer degrees of freedom. Thus we consider AICc to be the most reliable and flexible of the criteria for fitting penalized spline curves in the Cox model, particularly if there is strong prior reason to believe a nonlinearity is present.

In the occupational application, both AIC selected curves followed a nonlinear pattern, with the log of the hazard ratio for rectal cancer mortality initially increasing with exposure, followed by a decline. By contrast the curves selected by BIC were more linear. The pattern of attenuation or even decline in RR at high exposure levels is often seen in occupational studies and has been attributed to bias [34]. Thus, when fitting models to occupational data, AICc would be a reasonable choice for a model selection criterion for penalized splines in Cox models. GCV performed erratically in the application.

Researchers interested in estimating exposure-response relationships require tools for accurately examining departures from the assumption of linearity. While the focus of this paper was primarily on the bias in exposure-response curves estimated with penalized splines that used standard model fit criteria for selecting the smoothing parameter, they are by no means the only method. Fractional polynomials, as described by Royston and Altman [29], and restricted cubic splines were examined in a simulation study by Holländer and Schumacher [21] and they found the fractional polynomials to be superior. Their study was limited to two nonlinear exposure-response curves, a step function and a V-shaped curve, and uncensored data simulated using a uniform exposure distribution. We selected nonlinear scenarios that would be familiar to epidemiologists and used a skewed exposure distribution, common in environmental studies. In the simulation study of Lee [25], who examined AICc, GCV, CV, Mallows’ Cp and two risk estimation methods for selecting the smoothing parameter in nonparametric regression, they too found no one method to be best and considered the six criteria to be reasonable. Although our results suggest some deficiencies may exist in using penalized splines with the criteria investigated here, we do see strong evidence of their ability to detect and correctly model nonlinear relationships in Cox models.

Figure 1.

Estimated exposure-response for rectal cancer mortality from a cohort study of male autoworkers using penalized splines of the cumulative exposure variable with degrees of freedom selected using AIC, AICc, BICn, BICr, and GCV.