Abstract
High-resolution small-angle X-ray scattering (SAXS), complemented by small-angle neutron scattering (SANS) and dynamic light scattering (DLS) experiments, was used to study the effect of curvature on the bilayer structure of dioleoyl-phosphatidylcholine (DOPC) and dioleoyl-phosphatidylserine (DOPS) unilamellar vesicles (ULVs). Bilayer curvature, as a result of finite vesicle size, was varied as a function of vesicle radius and determined by DLS and SANS measurements. Unilamellarity of large DOPC ULVs was achieved by the addition of small amounts (up to 4 mol %) of the charged lipid, DOPS. A comparison of SANS data over the range of 0.02 < q <0.2 Å−1 indicated no change in the overall bilayer thickness as a function of ULV diameter (620 to 1840 Å). SANS data were corroborated by high-resolution (0.06 < q <0.6 Å−1) SAXS data for the same diameter ULVs and data obtained from planar samples of aligned bilayers. Both the inner and outer leaflets of the bilayer were found to be indistinguishable. This observation agrees well with simple geometric models describing the effect of vesicle curvature. However, 1220-Å-diameter pure DOPS ULVs form asymmetric bilayers whose structure can most likely be rationalized in terms of geometrical constraints coupled with electrostatic interactions, rather than curvature alone.
Introduction
Phospholipid bilayers are 2D matrices of biological membranes, and information regarding their structure is widely used to understand biomembrane structure and function.1,2 There are two commonly used approaches in obtaining bilayer structural parameters. The first approach uses supported samples, either single bilayers3 or multibilayer arrays,4 that are then studied by a variety of diffraction techniques. However, the interaction between the substrate and lipid bilayer can affect the fluidity of the bilayer, altering some of its physical properties.5 This effect is strongest on the bilayer adjacent to the substrate and decays exponentially. Therefore, a multibilayer stack is a better mimic of a free-standing bilayer, assuming that adjacent bilayers do not affect each other,6,7 than a single bilayer adsorbed to a solid support. Moreover, in the case of scattering experiments, multibilayer systems offer more material to the beam, which results in a concomitantly stronger signal. Because of this increased intensity, data can be collected at higher scattering vectors, q [4π/λ sin(θ/2), where λ is the wavelength and θ is the scattering angle]. Recently, the analysis of diffraction data from multibilayer stacks has focused on diffuse, continuous scattering in the vicinity of Bragg reflections to gain structural information,4,8 instead of the traditionally used discrete Bragg peak refinement. However, in contrast to Bragg peak measurements, this diffuse scattering method cannot be used effectively to analyze low q data.
The second approach used to obtain bilayer structure utilizes multilamellar vesicles (MLVs) or commonly referred to “powder” samples. MLVs are often used in a manner similar to that of oriented multibilayer systems9 with the disadvantage that the in-plane component of the scattering vector is lost through powder averaging. ULV samples are of biophysical interest because their topology is similar to that of a biological cell and their interior and exterior environments can be manipulated. ULV samples are suitable for small-angle scattering experiments where they give rise to a continuous form factor, with the provision that the system is sufficiently dilute so that intervesicle interactions are either minimized or completely eliminated. Unfortunately, compared to aligned bilayers and MLVs, dilute ULV systems are weak scatterers. In addition, powder averaging causes the scattering intensity to decay as q−2 instead of q−1, as is the case for oriented samples. All of these factors taken together result in the poor counting statistics commonly seen in the high-q-region data. Some of the best scattering data extends only up to ~0.3 Å−1 for X-rays10 and ~0.2 Å−1 for neutrons.11
A combined global analysis approach was recently introduced12 that takes advantage of the complementarity of the different sample preparations described. It uses ULVs to obtain the low-q data and oriented multibilayer arrays to provide high-q data, thus enhancing spatial resolution and consequently the bilayer’s structural details. The data from this approach is in good agreement with previous results but at the same time captures more of the features intrinsic to the phospholipid bilayer.13,14 However, an important question raised by this method of combining two different data sets is whether the two different sample preparations are made up of equivalent bilayers. This question was addressed using two independent tests.12 First, both sets of data overlap over a substantial range in q, most notably at the positions of the maxima and minima of the scattering curve. Furthermore, data obtained using MLVs were compared to ULVs and aligned sample data. Even though the MLV data give rise only to discrete form factors, they lie on the same continuous curve obtained from both ULVs and aligned samples.12 This suggests that the bilayers found in all three sample preparations are equivalent, implying that membrane curvature, intrinsic to ULVs, does not influence bilayer structure.
There are other studies that have previously reported the effect of curvature on bilayer structure. The effect of curvature on bilayer thickness has been studied by Kiselev et al.15 and Schmiedel et al.16 using ULVs whose diameters ranged from 500 to 4000 Å. They concluded that with increasing ULV diameter (decreasing bilayer curvature) the bilayer gets thinner. However, increasing ULV size also resulted in the presence of more MLVs, complicating data analysis. In their case, a direct comparison of the primary scattering data could have eliminated the use of complex models. A curvature effect on bilayer structure was also suggested by Brzustowicz and Brunger,17 who observed an asymmetry in the bilayer profile of 1000 Å ULVs. According to their analysis, the inner ULV bilayer leaflet is “rougher” than the outer leaflet. Bilayer structure asymmetry was also detected in monosialoganglio—dipalmitoylphosphatidylcholine mixtures,18 although these studies used very small ULVs (~ 200 Å) having a much larger bilayer curvature. However, photosynthetic membrane ULV that were more than 2 times larger in diameter formed symmetric membranes.19
The influence of ULV size on bilayer thickness strongly impacts membrane biophysics because membrane structure (e.g., bilayer thickness and symmetry) possibly affects both the conformation and function of intrinsic membrane proteins. Therefore, the suggestion that subtle changes in ULV size can lead to changes in bilayer structure has significant implications for biophysical and functional studies of membranes. Furthermore, if bilayer structure does indeed depend on ULV curvature, then this would also preclude the use of a global analysis method that relies on combining data obtained from ULVs and aligned samples. It is therefore of general interest to address the issue of the potential influence of bilayer curvature on structure and to provide data that possibly will resolve some of the recent and seemingly contradictory findings in the literature.15,16
The present study addresses the effect of membrane curvature on the bilayer structure of the well-characterized zwitterionic lipid, dioleoyl-phosphatidylcholine (DOPC). This particular group of neutral lipids (i.e., zwitterionic PC) was previously used in studies that combined and analyzed data from ULVs and aligned samples12–14 and is the primary focus of this work. Extruded ULVs were first characterized with dynamic light scattering (DLS) to determine their size distributions, and structural analysis was performed using data obtained from small-angle neutron scattering (SANS) and small-angle X-ray scattering (SAXS), both of which have proven to be powerful techniques for determining the structure of phospholipid bilayers.2,20 The comparative approach used in our analysis provides a direct result, whereas a model-based analysis is used to interpret our observations. This is in contrast to previous studies that have exclusively used the latter.15–17 In the cases of both pure DOPC bilayers and those doped with small amounts (up to 4%) of the anionic lipid, DOPS, both inner and outer leaflets are essentially the same for a ULV whose diameter is greater than 620 Å. This observation is in agreement with simple geometric models describing vesicle curvature. However, complementary measurements show that 1220 Å ULVs composed entirely of DOPS form asymmetric bilayers whose structure can most likely be explained in terms of geometrical constraints coupled with electrostatic interactions.
Materials and Methods
Sample Preparation
Synthetic DOPC (1,2-dioleoyl-sn-glycero-phosphatidylcholine) and DOPS (1,2-dioleoyl-sn-glycero-phosphatidylserine) were purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Organic solvents were high-performance liquid chromatography grade.
Pure DOPC or DOPS lipid was mixed in a sealed plastic tube with 18 MΩ cm water (Millipore) or D2O (99.9% pure, Chalk River Laboratories) to a total concentration of either 15 or 30 mg/mL, which is the lipid concentration range widely used for ULV studies. At these concentrations, ample water between ULVs is guaranteed, even for the largest-diameter ULV used, where ~75% of the water resides outside the ULV. As expected, the two lipid concentrations scattered similarly (except for an increase in counting statistics at higher concentration) over the measured q range (not shown). In the case of mixed DOPS/DOPC samples, lipids were first dissolved in chloroform and, after mixing, dried in an evacuated desiccator for several hours. Finally, the lipids were hydrated with purified water or D2O. DOPS/DOPC samples were made with either 2 or 4 mol % DOPS. MLVs were prepared by repetitive heating, above the main phase transition, and freezing of the hydrated lipid until a uniform dispersion was obtained. Extruded ULVs were then prepared from this dispersion using an Avanti miniextruder. The MLVs were extruded through two polycarbonate filters with pore diameters of 500, 1000, and 2000 Å to produce vesicles with nominal diameters of 500, 1000, and 2000 Å, respectively. Samples were subjected to 25 passes through a given-size filter while the lipid was above its main phase-transition temperature. An odd number of passes was performed to minimize contamination of the sample by MLVs, which may not have gone through the filter. The typical time between sample preparation and measurement was less than 10 h.
DLS
Dynamic light scattering measurements were performed at 25 °C on a DynaPro-LSR light scattering machine (Protein Solutions, Inc.) using an incident wavelength of 782.7 nm and a scattering angle of 90°. The autocorrelation functions were inverted to give discrete intensity-weighted distributions of hydrodynamic radii using the program Sedfit.21
SANS
Neutron scattering data were taken at the NG-7 station22 of the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR). Neutrons of wavelength λ = 5.5 Å were used for a sample-to-detector distances (SDDs) of 1 and 4 m, whereas neutrons of wavelength λ = 8 Å were used for an SDD of 12 m. Neutron wavelengths were selected using a mechanical velocity selector, with 11% FWHM energy dispersion. Data were collected using a 640 mm × 640 mm 2D 3 He position-sensitive detector with 5 mm × 5 mm resolution. Samples were contained in standard, 2-mm-path-length quartz cylindrical cells. Collected images were corrected using a suite of software supplied by NIST.
SAXS
X-ray data were taken at the D-1 station located at the Cornell High Energy Synchrotron Source (CHESS). Scattered X-rays (λ = 1.18 Å) were collected using a Medoptics charge-coupled device (CCD) with a 1024 × 1024 pixel array and pixels having linear dimensions of 47.19 μm. The SDD was 322 mm and was determined using a silver behenate standard. Collected images were dezingered and processed for CCD distortion and intensity corrections using calibrated files supplied by CHESS. Standard 1.5 mm quartz capillaries were used as sample cells.
Data Reduction
In the case of lipid dispersions, the scattering from water makes a substantial contribution to the total scattered intensity. In fact, its contribution dominates the scattering from other constituents for q > 0.2 Å−1 (Figure 1). Careful subtraction of background scattering is therefore essential.
Figure 1.
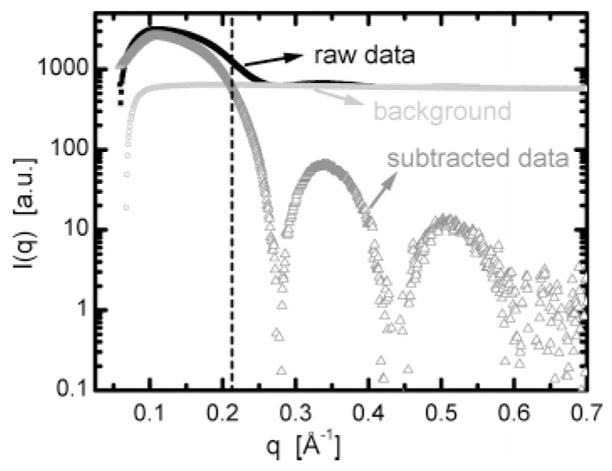
Radially averaged scattering intensities of raw SAXS data from ULVs dispersed in water (dark squares), background scattering from water and the associated sample environment (light circles), and the ULV background-subtracted data (gray triangles). The vertical dashed line demarcates the region where scattering from ULVs dominates (q less than ~0.2 Å−1).
Every data set was normalized using the incident beam intensity and the transmission of the sample (TX) defined as
| (1) |
where IX(0) and IB(0) are the integrated intensities of the direct beam after passing through the sample (X) (i.e., C = empty cell, S + C = cell filled with sample, and W + C = cell filled with water) and in the absence of a sample, respectively. Although transmission is typically determined in a separate measurement, in the case of the present X-ray experiments, we were able to perform simultaneous transmission and scattering measurements by using a semitransparent beam stop made out of a 225-μm-thick molybdenum foil. In this way, all of the necessary information for data normalization is recorded on a single image during the scattering measurement. After proper normalization, the empty cell scattering intensity, IC, is subtracted as follows
| (2) |
where IS+C and IW+C are the scattering intensities from the sample and water, respectively. Note that the IC contribution, which is predominantly scattering from air and helium in the flight path, is ~40% of the total scattering taking place in the high-q region. The scattering from ULVs can then be calculated in terms of the macroscopic cross section as
| (3) |
where F is a scaling factor used to determine the absolute intensity. F was not determined for the present experiments. Finally, kt is the factor for proper normalization of the buffer scattering relative to that of the sample and can be written as
| (4) |
where c is the sample’s lipid concentration. In the case of dilute samples, only a few weight percent, c can be neglected. We have also explicitly addressed the fact that in the case of X-ray experiments not all capillaries have identical inner diameters, thereby resulting in different X-ray path lengths. As such, the scattered intensity from water must be accurately scaled using the thickness ratio of water (tW) and the sample (tS). To minimize the effect of this variable in our analysis of the data, we used the same capillary for measurements with ULVs in water and water only. Nevertheless, ~5% in the average variation of the normalization factor was required for proper background subtraction in the high-q region (0.6 < q < 0.8 Å−1), where the scattering from ULVs is negligible. This variation is mainly due to the experimental uncertainty in the repetitive positioning of capillaries and the truncation in the direct beam integration. A similar correction factor should also be present in eq 2, although its effect is negligible (~2%) considering that in the high-q region scattering from IC accounts for ~40% of the total scattering. Figure 2a,b shows typical examples of corrected and background-subtracted data images.
Figure 2.

(a) Gray scale plot of background-subtracted SANS data taken at an SDD of 4 m; mid-q range data are obtained at this distance. The white spot at the graph’s origin is a result of the beam stop. (b) Gray scale plot of background-subtracted SAXS data. Three distinct darker regions corresponding to the locally maximal intensities are interspersed among the light minima. The rectangular light region in the lower right-hand corner is the absorption from the beam stop.
Results and Discussion
Dynamic Light Scattering
DLS experiments were performed on ULVs with nominal diameters of 500, 1000, and 2000 Å (Figure 3). From Figure 3, it is evident that the width of the size distribution increases with increasing ULV size but the relative polydispersity (Gaussian width/ULV radius ≈ 25%) does not. It can also be seen that the peak positions corresponding to the two smaller ULVs suggest larger vesicles than the nominal sizes, whereas the vesicle diameter for the largest ULV is smaller than the filter pore size, a result consistent with a previous and more systematic study of extruded ULVs.23
Figure 3.
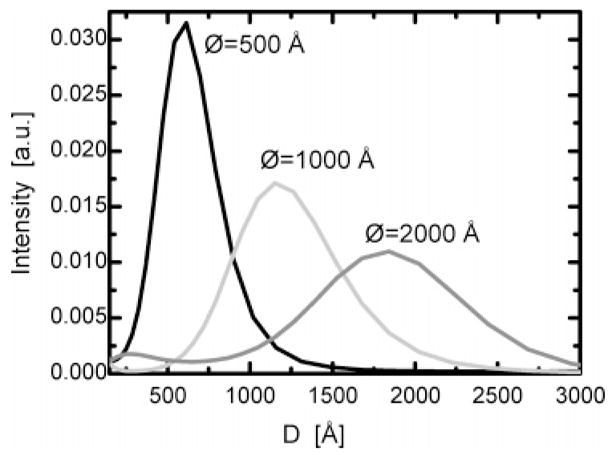
Size distribution functions corresponding to the three extruded ULV systems. The peaks, although getting broader with increasing mean value, have the same relative polydispersity of 25%. Values for the two smaller ULVs are shifted toward larger sizes (620 and 1210 Å) than the filter pore size. However, the peak corresponding to the largest nominal ULV is shifted toward a smaller ULV diameter (1840 Å).
Effect of Charged Lipid
Extruded ULVs are generally contaminated with pauci-lamellar vesicles (PLVs) whose concentration in the sample is determined by such factors as the type of lipid used, the filter’s pore size, the number of passes through the filter, and the temperature at which the extrusion was performed. Previously, for noncharged PC lipids the best results were obtained when using a filter with 500-Å-diameter pores, whereas an increased presence of MLVs was reported for the production of larger ULVs.16 Charged lipid bilayers, however, are repelled by electrostatic interactions and preferentially form ULVs. To ensure the production of large ULVs, we studied three different ULV preparations, namely, pure DOPC ULVs and ULV mixtures of DOPC doped with small amounts (i.e., 2 and 4 mol %) of the charged lipid DOPS. It is interesting that doping DOPC ULVs with DOPS resulted in a significant improvement of unilamellarity whereas bilayer structure apparently remained unaltered.
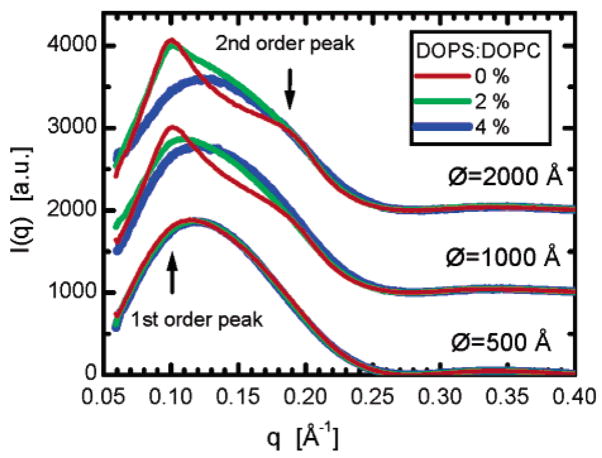
Even small amounts of PLVs in the system can be readily detected in a scattering experiment through a significant distortion of the scattering curve, as a result of Bragg scattering arising from the PLV. Figure 4 shows X-ray scattering curves, grouped according to ULV size, corresponding to the different DOPC/DOPS ratios used. The contribution from PLV is most evident in the data from nominal 1000- and 2000-Å-diameter ULVs. In this case, Bragg scattering overlays the ULV form factor, although the number of layers making up the individual PLVs are few; otherwise, the narrow peaks would be limited only by the instrumental resolution. Doping the DOPC ULVs with 2 mol % DOPS ameliorates this problem, and 4 mol % DOPS eliminates the presence of PLVs entirely. With the exception of Bragg scattering, all measured curves, for a given ULV size, overlap over the entire q range, implying that small amounts of DOPS do not alter the DOPC bilayer. The only change observed is the amount of PLVs in the system whose presence is not detectable at 4 mol % DOPS.
Figure 4.
SAXS curves arising from extruded vesicles containing different DOPS/DOPC molar ratios (pure DOPC, red lines; 2% DOPS, green lines; 4% DOPS, blue lines). Curves corresponding to systems with same diameter vesicles are grouped together and shifted vertically. Two arrows point to the q values where the first-and second-order Bragg peaks are expected.
Effect of Vesicle Size
Structural parameters are typically refined in terms of an iterative model-fitting approach,15,16,24–26 that eventually results in the bilayer profile. This approach also allows for the comparison of various bilayers. However, real space comparisons are intrinsically dependent on the input parameters,27 where no solution is unique, only highly probable. However, in directly comparing experimental data, no assumptions regarding the structure of the system are made.
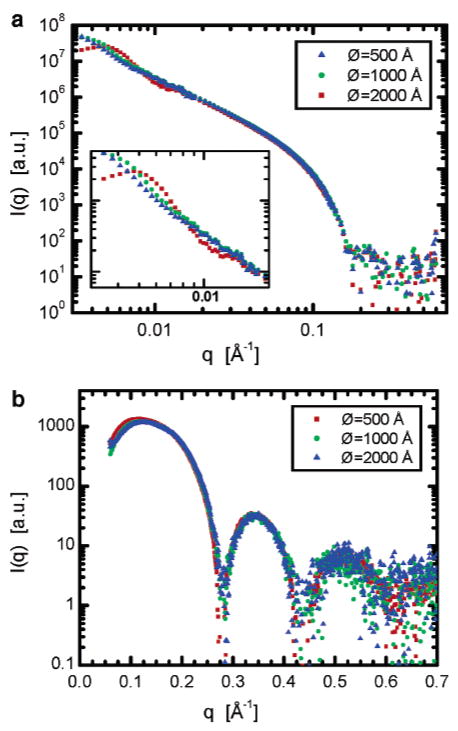
A comparison of SANS curves in Figure 5a reveals differences, in the low-q region, between data sets corresponding to the different sized ULVs. In this region of q, the scattering is sensitive to large scale lengths, i.e. the size of the ULV. It is therefore not surprising to observe deviations in the data, especially in the case of 500 Å ULVs whose form factor has a characteristic minimum at ~0.01 Å−1 (actual vesicle size 620 Å). For the larger ULVs, this feature is shifted to 0.005 and 0.003 Å−1, corresponding to 1210 and 1840 Å ULVs, respectively. Because of the higher polydispersities (Figure 3) and exceedingly low q values, this feature is less obvious for 1210 and 1840 Å ULVs. It should also be mentioned that the probability of vesicle—vesicle interactions increases with ULV size, and if they exist, they make a significant contribution to the scattering curve at these small q values.
Figure 5.
(a) SANS scattering curves collected with samples of different nominal size ULVs (DOPS/DOPC of 4 mol %). Red squares correspond to ULVs extruded through a 500 Å filter pore; green circles, 1000 Å; and blue triangles, 2000 Å. The distribution functions of the actual size ULVs are shown in Figure 3. (b) SAXS scattering curves collected with samples of different nominal size ULVs. Red squares correspond to the DOPC ULV system extruded through a 500 Å pore filter, and green circles and blue triangles correspond to ULVs made from a DOPS/DOPC mixture at 4 mol % and extruded through 1000 and 2000 Å filters, respectively. The actual ULV size distributions were determined by DLS, and the data are shown in Figure 3.
More interestingly, the mid-q scattering range defined as 0.02 < q < 0.17 Å−1 corresponds to the overall thickness of the bilayer and is adequately described by a single-strip model whose scattering-length density (SLD) is that of the averaged bilayer.24 Direct comparison of the scattering curves shows no distinguishable differences over this region of scattering, indicating that there are no differences in the overall bilayer thickness of ULVs of differing size. To reveal more structural detail and to compare this structure as a function of ULV curvature, it is therefore necessary to collect data in the high-q region, where unfortunately SANS counting statistics are poor. To overcome this SANS limitation, high-q data were collected using SAXS (Figure 5b).
Whereas SANS data correspond to the largest distances in the system (i.e., vesicle size), as a result of the extended q range accessed, SAXS data provide intrabilayer information. Also, because X-rays and neutrons scatter from different atomic parts of the bilayer their scattering curves are markedly different. One of the most pronounced differences is in the direct forward scattering, I(0), which relates the integrated contrast of the bilayer SLD to that of water. In the case of neutrons, the bilayer SLD profile has an overall value that is less than that of heavy water, leading to a large I(0) value. For X-rays, this is not the case because the bilayer SLD is approximately the same as that of water, causing a downturn in the SAXS data at small q, as can be seen in Figure 5b. This downturn in the scattering intensity is not the result of beamstop interference.
The present SAXS data are of very high quality with good experimental statistics up to q ≈ 0.6 Å−1, comparable to data obtained from oriented multibilayers (q range ~0.8 Å−1). The SAXS data presented here extend to a higher q than previously published ULV data,13,17 which were typically analyzed using a model-dependent analysis. However, reciprocal space scattering data are related to the real space structure through a simple Fourier transform, with no loss of information. One of the most important “fingerprints” associated primarily with bilayer thickness consists of the positions of the scattering curve minima and maxima.10 The graph in Figure 5b shows all three scattering curves exhibiting the same first minimum (<0.01 Å−1 deviation) and that they overlay in the region of the second maximum. The overall good agreement of the different scattering curves implies no difference in bilayer structure.
Figure 6 shows the form factors ( ) of 620-Å-diameter ULVs (red squares), oriented multibilayers (open green diamonds), and a model-based fit (solid blue line). This way of presenting the data better illustrates the bilayer’s structural features and also allows for a direct comparison with data obtained previously from planar oriented multibilayers13 which possess no intrinsic curvature. The Figure shows excellent agreement between ULVs and oriented samples in the range of 0.2 < q < 0.6 Å−1. Moreover, both experimental data sets comply with the model-based fit using the structural model described in the Appendix. Agreement between the data sets is not only in q, as was discussed, but also in the relative amplitudes of the different lobes. Because no differences between the different data sets were noted here, or in Figure 5b, we conclude that in the case of ULVs with diameters >620 Å the structure of neither DOPC bilayers nor those doped with small amounts of DOPS are affected by bilayer curvature.
Figure 6.
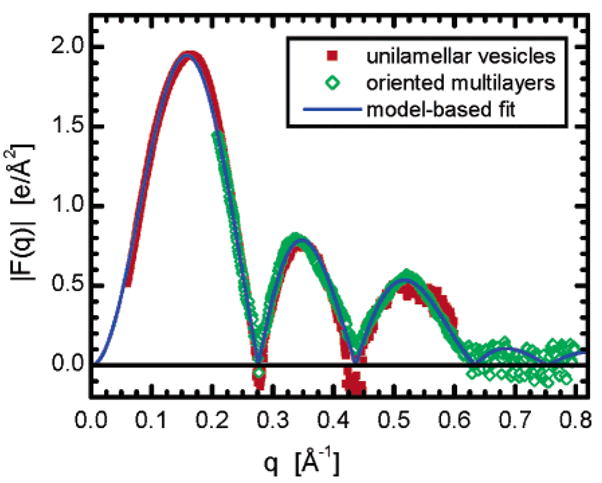
Form factors for 620-Å-diameter ULVs (red squares) and oriented multibilayers (open green diamonds), both made up of pure DOPC. The blue line is a best fit to the data and corresponds to the bilayer structure presented previously by Kučerka et al.13 Negative values for |F(q)| are the result of poor counting statistics as the form factor approaches zero.
Effect of Bilayer Asymmetry
The calculated form factor shown in Figure 6 (blue line) is based on a model that describes a symmetric bilayer and is taken from the well-known Fourier transform of the SLD profile. This expression is given as
| (5) |
where Δρ (z) is the difference SLD between the bilayer and the solvent, and the integration extends from the bilayer center to a point (D/2) beyond which Δρ(z) = 0. The behavior of F(q) for a typical lipid bilayer is characterized by periodic oscillations that cross zero (shown as absolute values in Figure 6). The scattered intensity is then calculated as the square of this expression and multiplied by an additional function that includes the particle’s “sphericity” as well as the system’s polydispersity.28 I(q) is thus written as
| (6) |
| (6a) |
where s = Rm/σR2 and z = Rm2/σR2 − 1 are the products of the ULV mean radius Rm and σR represents the system’s polydispersity. PTS, however, affects only the region where q < 0.03 Å−1 and in our SAXS experiment remained constant over the measured range of q values. The bilayer’s form factor plays a dominant role because its characteristic oscillations are responsible for many of the features seen in the scattering intensity, including the typical extinctions in intensity. A lack of zero intensity indicates bilayer asymmetry, as can be deduced from the following expression of the Fourier transform:
| (7) |
The calculation corresponds to the complete form of the Fourier transform with a complex exponential. For an asymmetric lipid bilayer, its amplitude will not go to zero.
This is exactly what was observed in the case of pure DOPS lipid (Figure 7)—a lipid similar to SOPS used by Brzustowicz and Brunger,17 which they concluded forms asymmetric bilayers. Our result is supported by the fit to the experimental data in Figure 7, and the reconstructed bilayer profile (using the model given in the Appendix) is shown in the inset to the Figure. It should be mentioned that no constraints (e.g., various lipid volumes, number of electrons, and headgroup thickness) were used in the fit to the data, as was done previously by Kučerka et al.,12–14 and only a qualitative picture is given. Moreover, eq 7 does not distinguish between inner and outer bilayer leaflets, thus it does not provide any information with regard to the bilayer’s overall orientation.
Figure 7.
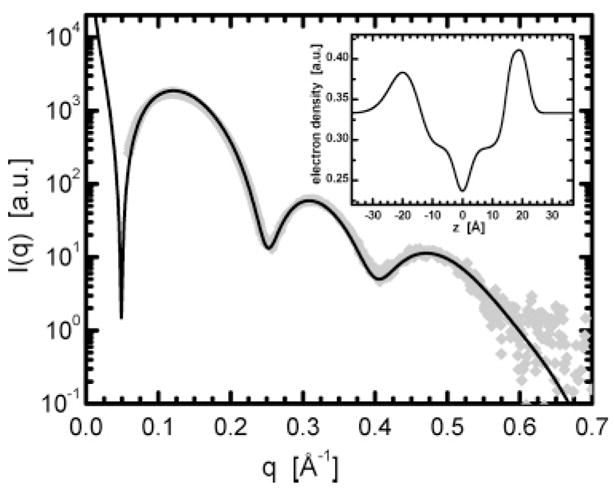
SAXS data from nominal 1000 Å extruded DOPS ULVs. Note that unlike the scattering from DOPC ULVs (Figure 5b) the first and second minima do not decay to zero intensity, suggesting the presence of an asymmetric bilayer. The inset shows the resultant 1D electron density profile obtained from the best fit to the data.
Discussion
In contrast to DOPS bilayers, there is no bilayer asymmetry found in pure DOPC bilayers and DOPC bilayers doped with 2 and 4 mol % DOPS. SAXS data from DOPC ULVs (Figures 5b and 6) show that the scattering intensity approaches zero in the vicinity of the scattering minima, indicative of symmetric bilayers. Thus, bilayer curvature (in the q range examined here) appears to have no effect on the bilayer structure of zwitterionic lipids. Nevertheless, because curvature does play a role in the asymmetry of anionic lipid membranes, we examine possible mechanisms where curvature may affect the bilayer’s symmetry. One scenario is that the inner and outer leaflet lipids are of equal volume. If this is the case, then according to a simple set of geometrical equations the bilayer midplane will be shifted from 225 to 228 Å (assuming a 500-Å-diameter ULV and a 50-Å-thick bilayer), making the inner leaflet thicker than the outer leaflet by a factor of 1.24. Here, the assumptions are that the volume per lipid is conserved and that the number of lipid molecules is the same in both leaflets. However, there is nothing that requires the number of lipids in both leaflets to be the same because lipids are free to exchange between the two monolayers. Decreasing the number of lipid molecules in the inner leaflet by 20% allows for the conservation of volume per lipid without changing the thickness of either monolayer. A similar calculation for 1000 Å ULVs gives a thickness ratio of 1.11 and an ~10% difference between the number of lipids in the two bilayer leaflets.
A different geometrical model accounting for structural changes in a curved bilayer was proposed by Kučerka et al.24 In addition to a constant molecular volume, they assumed, for both leaflets, the same lipid area at the interface between the hydrocarbon chains and headgroup, because the hydrocarbon chains are flexible and can better accommodate curvature effects than the head-groups. For 500-Å-diameter ULVs, this constraint resulted only in a minor distortion in bilayer thickness, making the outer monolayer negligibly thicker by about 3%. Both models agree well with our observations of DOPC bilayers where no effect of curvature on the bilayer’s structural properties was detected. It should be stressed, however, that the discussed molecular arrangements are only a rough representation of a system with interacting molecules. Besides the above-mentioned geometrical constraints, no others were assumed.
Electrostatic interactions present in ULVs composed of lipids with a net charge add another layer of complexity to the models already described. The results from a molecular dynamics simulation of dipalmitoyl-phosphatidylserine (DPPS) bilayers containing Na+ counterions,29 showed that counterions play a crucial role in determining the structural and electrostatic properties of DPPS bilayers. The net negative surface charge present on PS bilayers is balanced by the positively charged Na+ counterions in solution. When there is no added salt, as in our experiments, the electrostatic interaction is long-range,30 comparable to the size of the ULV. The counterion distribution and the partitioning of surface charge density between the inner and outer monolayers that minimizes the electrostatic free energy are nontrivial and might provide a mechanism that would induce asymmetry in ULVs. An unequal distribution of lipid molecules between the two monolayers of charged SOPS vesicles was reported by Brzustowicz and Brunger,17 although their experiments were performed in 50 mM salt, which reduces the range of the electrostatic interactions, but introduces yet more complexity to the system.31
For the present DOPS experiments it was shown that the electrostatic effects affecting bilayer structure and those due to curvature are coupled. Whereas aligned, charged bilayers are symmetric, our experimental results show a significant effect of curvature on bilayer asymmetry. However, we have conclusively shown that similarly sized neutral ULV bilayers are not affected by curvature.
Conclusions
From simple, straightforward SAXS and SANS experiments, we were able to characterize the effect of curvature on bilayer structure in ULVs composed of neutral DOPC and charged DOPS lipids. The actual ULV size was determined from DLS measurements and complemented with low-q SANS data. The mid-q range was covered using a combination of SANS and SAXS, of which SAXS was also used to determine the presence of PLV. Data with characteristic PLV peaks were not used in the comparative analysis in order to avoid any misrepresentation of the bilayer structure. Unilamellarity of large DOPC vesicles was achieved by the addition of small (up to 4 mol %) amounts of the charged lipid, DOPS. This additive molecule eliminated the presence of PLV without altering the structure of the DOPC bilayer. We found that the neutral DOPC bilayers were unaffected by bilayer curvature, a result supported by simple geometrical arguments.
The question of lipid bilayer asymmetry recently seen in charged ULVs17 was also addressed. After considering electrostatic interactions between charged lipid molecules, the curvature effect seems to manifest itself in the formation of an asymmetric bilayer, described by the unequal distribution of lipids between the bilayer’s two monolayers. This bilayer asymmetry was borne out by SAXS data for 1220-Å-diameter DOPS ULVs. From these experiments, bilayer asymmetry was readily detectable because of the distinct scattering effects associated with this bilayer morphology. This data is presently described in a qualitative manner, and we defer a more quantitative picture to future work that will require more systematic data from charged lipids organized in a curved bilayer.
Acknowledgments
We thank Dr. Stephanie Tristram-Nagle for stimulating discussions, Thalia Mills for help in collecting the synchrotron data, and Dr. Detlef M. Smilgies for assistance with the SAXS setup at the CHESS D-line. Access to the instruments at the National Institute of Standards and Technology (NIST) through the Cold Neutrons for Biology and Technology (CNBT) partnership and the Cornell High Energy Synchrotron Source (CHESS) funded by National Science Foundation grant DMR-0225180 is gratefully acknowledged.
J.F.N. was funded by grant GM 44976 from the General Medicine Institute of the U S National Institutes of Health.
Appendix
Symmetric Bilayer
The bilayer structure model used to fit the data was inspired by the one previously published by Klauda et al.26 For symmetric bilayers it describes one monolayer, where two Gaussians represent the probability distributions of the phosphate + choline (PC) groups, and the carbonyl + glycerol (CG) group. An additional Gaussian describes the probability of the terminal methyl (M) groups. The Gaussian function is
| (8) |
where the amplitude c is determined by the volumetric constraints (V = Acσ, where A is the area per lipid molecule). The hydrocarbon (HC) region of the bilayer is best approximated by the classical Error function26 that defines the probability of just methylene (MN) groups as
| (9) |
Finally, the water (W) probability in the present model is defined as a residual part of the total probability, which is unity across the bilayer
| (10) |
Probability distributions of every group contribute to the total neutron and/or electron SLD profile via
| (11) |
where ρW is the SLD of water and Δρi = ρi − ρW is the average SLD contrasts of particular groups compared to ρW.
The bilayer form factor is then calculated via eq 5 as
| (12) |
Asymmetric Bilayer
For a symmetric bilayer there are two distinct Gaussians used to describe the headgroup region of one bilayer leaflet. In the case of asymmetric bilayers, two additional Gaussians are used for a total of four distinct Gaussians. These define the headgroup regions of the two structurally different leaflets found in an asymmetric bilayer. The functions describing the HC and M regions for asymmetric bilayers are the same as for symmetric bilayers. The SLD across the entire bilayer is thus represented by
| (13) |
The symmetric part of the Fourier transform of eq 7 can be written in term of the cosines as
| (14) |
and for the sine terms as
| (15) |
References
- 1.Balgavý P, Dubničková M, Kučerka N, Kiselev MA, Yaradaikin SP, Uhríková D. Biochim Biophys Acta. 2001;1512:40–52. doi: 10.1016/s0005-2736(01)00298-x. [DOI] [PubMed] [Google Scholar]
- 2.Katsaras J, Gutberlet T. Lipid Bilayers: Structure and Interactions. Springer-Verlag; New York: 2001. [Google Scholar]
- 3.Krueger S, Ankner JF, Satija SK, Majkrzak CF, Gurley D, Colombini M. Langmuir. 1995;11:3218–3222. [Google Scholar]
- 4.Liu Y, Nagle JF. Phys Rev E. 2004;69:040901. doi: 10.1103/PhysRevE.69.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wong JY, Majewski J, Seitz M, Park CK, Israelachvili JN, Smith GS. Biophys J. 1999;77:1445–1457. doi: 10.1016/S0006-3495(99)76992-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Katsaras J. Biophys J. 1997;73:2924–2929. doi: 10.1016/S0006-3495(97)78320-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Katsaras J. Biophys J. 1998;75:2157–2162. doi: 10.1016/S0006-3495(98)77658-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lyatskaya J, Liu Y, Tristram-Nagle S, Katsaras J, Nagle JF. Phys Rev E. 2001;63:011907. doi: 10.1103/PhysRevE.63.011907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pabst G, Rappolt M, Amenitsch A, Laggner P. Phys Rev E. 2000;62:4000–4009. doi: 10.1103/physreve.62.4000. [DOI] [PubMed] [Google Scholar]
- 10.Lewis BA, Engelman DM. J Mol Biol. 1983;166:211–217. doi: 10.1016/s0022-2836(83)80007-2. [DOI] [PubMed] [Google Scholar]
- 11.Pencer J, Hallett FR. Phys Rev E. 2000;61:3003–3008. doi: 10.1103/physreve.61.3003. [DOI] [PubMed] [Google Scholar]
- 12.Kučerka N, Liu Y, Chu N, Petrache HI, Tristram-Nagle S, Nagle JF. Biophys J. 2005;88:2626–2637. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kučerka N, Tristram-Nagle S, Nagle JF. J Membr Biol. 2005;208:193–202. doi: 10.1007/s00232-005-7006-8. [DOI] [PubMed] [Google Scholar]
- 14.Kučerka N, Tristram-Nagle S, Nagle JF. Biophys J Lett. 2006;90:L83–L85. doi: 10.1529/biophysj.106.086017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kiselev MA, Zemlyanaya EV, Aswal VK, Neubert RHH. Eur Biophys J. 2006;35:477–493. doi: 10.1007/s00249-006-0055-9. [DOI] [PubMed] [Google Scholar]
- 16.Schmiedel H, Almásy L, Klose G. Eur Biophys J. 2006;35:181–189. doi: 10.1007/s00249-005-0015-9. [DOI] [PubMed] [Google Scholar]
- 17.Brzustowicz MR, Brunger AT. J Appl Cryst. 2005;38:126–131. [Google Scholar]
- 18.Hirai M, Iwase H, Hayakawa T, Koizumi M, Takahashi H. Biophys J. 2003;85:1600–1610. doi: 10.1016/S0006-3495(03)74591-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sadler DM, Worcester DL. J Mol Biol. 1982;159:485–499. doi: 10.1016/0022-2836(82)90297-2. [DOI] [PubMed] [Google Scholar]
- 20.Nagle JF, Tristram-Nagle S. Biochim Biophys Acta. 2000;1469:159–195. doi: 10.1016/s0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schuck P. Biophys J. 2000;78:1606–1619. doi: 10.1016/S0006-3495(00)76713-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Glinka CJ, Barker JG, Hammouda B, Krueger S, Moyer JJ, Orts WJ. J Appl Cryst. 1998;31:430–445. [Google Scholar]
- 23.Patty PJ, Frisken BJ. Biophys J. 2003;85:996–1004. doi: 10.1016/S0006-3495(03)74538-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kučerka N, Nagle JF, Feller SE, Balgavý P. Phys Rev E. 2004;69:051903. doi: 10.1103/PhysRevE.69.051903. [DOI] [PubMed] [Google Scholar]
- 25.Wiener MC, White SH. Biophys J. 1992;61:434–437. doi: 10.1016/S0006-3495(92)81849-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Klauda JB, Kučerka N, Brooks BR, Pastor RW, Nagle JF. Biophys J. 2006;90:2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sachs JN, Petrache HI, Woolf TB. Chem Phys Lipids. 2003;126:211–223. doi: 10.1016/j.chemphyslip.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 28.Pencer J, Krueger S, Adams C, Katsaras J. J Appl Cryst. 2006;39:293–303. [Google Scholar]
- 29.Pandit SA, Berkowitz ML. Biophys J. 2002;82:1818–1827. doi: 10.1016/S0006-3495(02)75532-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Petrache HI, Tristram-Nagle S, Gwrisch K, Harries D, Parsegian VA, Nagle JF. Biophys J. 2004;86:1574–1586. doi: 10.1016/S0006-3495(04)74225-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sachs JN, Nanda H, Petrache HI, Woolf TB. Biophys J. 2004;86:3772–3782. doi: 10.1529/biophysj.103.035816. [DOI] [PMC free article] [PubMed] [Google Scholar]