Shape Analysis with Overcomplete Spherical Wavelets

Abstract

In this paper, we explore the use of over-complete spherical wavelets in shape analysis of closed 2D surfaces. Previous work has demonstrated, theoretically and practically, the advantages of over-complete over bi-orthogonal spherical wavelets. Here we present a detailed formulation of over-complete wavelets, as well as shape analysis experiments of cortical folding development using them. Our experiments verify in a quantitative fashion existing qualitative theories of neuro-anatomical development. Furthermore, the experiments reveal novel insights into neuro-anatomical development not previously documented.

1 Introduction

In this paper, we explore the use of overcomplete spherical wavelets [1,16] for shape analysis of closed 2D surfaces. Wavelets offer a tradeoff between entirely local and global features more commonly used in shape analysis.

In the Euclidean space, a pixel representation of an image provides precise pointwise features, but suffers from noise and can benefit from a multiscale representation using global contextual information. At the other extreme, the Fourier transform creates a global summary of an image at the expense of localization ability. The orthogonal/bi-orthogonal wavelet transform [5] provides a tradeoff between pixel-wise and Fourier representation by projecting an image onto basis functions with compact support, at different spatial scales and locations.

Unfortunately, each level of the multi-scale orthogonal/bi-orthogonal wavelet transform suffers from sampling aliasing. Practically, this results in a loss of translational invariance: translation of an image by even one pixel causes dramatic changes in the wavelet coefficients [13]. A related problem is unidentifiability [13,18]. Suppose a tumor of a certain size exists at a certain spatial location. Ideally, one would want a large wavelet coefficient at that particular scale and spatial location. But due to undersampling, the tumor's location might not be sampled at that scale, resulting in two moderate wavelet coefficients on either side of the actual tumor. Considering coefficients from that scale leads to a false hypothesis of the existence of two moderate-sized tumors.

Over-complete wavelets resolve these problems by ensuring each wavelet scale is sufficiently sampled [13]. Overcomplete transforms result in more coefficients than pixels, hence the name “overcomplete”. This inefficiency is compensated for by their increased accuracy and robustness.

Pioneering work using landmarks for shape analysis include the Procrustes method [8] and active shape models (ASM) [4]. The individual landmarks provide precise local information about the shape, but lack global contextual information. ASM performs principal component analysis on the landmarks of training images, thus avoiding some limitations of landmark-based methods. However, this requires training data, while we are interested in generic shape representations.

The desire for a global shape representation motivates the introduction of global basis functions. Since closed 2D shapes can be spherically parameterized, one can treat each coordinate function {x, y, z} of a closed 2D surface as a spherical image and project it onto spherical bases, such as spherical harmonics [2] and polynomials [14].

Schroder and Sweldens [12] proposed the bi-orthogonal spherical wavelet transform for scalar spherical images. The application of these wavelets to closed 2D surfaces demonstrated great utility in both segmentation and shape analysis [11,17]. Unfortunately, the bi-orthogonal wavelet transform on the sphere suffers from the same aliasing problems observed in Euclidean images. Over-complete spherical wavelets [1,16] overcome these problems by ensuring sufficient sampling at each scale and have been shown to be both more robust and more sensitive to group differences than bi-orthogonal spherical wavelets in shape analysis [18].

In this paper, we present a detailed formulation of overcomplete spherical wavelets and incorporate them into the growth model of neonatal cortical folding, extending the experiments in the workshop paper [18]. Our analysis yields quantitative characterizations of cortical folding development consistent with previous studies, which were based on visual inspection of post-mortem brains [3]. The results also provide novel insights into neuro-anatomical development, suggesting directions for future experimental verification, and potentially providing a basis for early detection of neurodevelopmental disorders.

2 Overcomplete Spherical Wavelets for Shape Analysis

In this section, we outline the theory and implementation details of overcomplete spherical wavelets for shape analysis. While several related formulations of wavelet transforms on the sphere exist, we follow the continuous spherical filter bank and sampling framework of [16].

Continuous Spherical Filter Bank Theory

In the Euclidean domain, convolution is defined as the inner product of two functions translated relative to each other. In the spherical domain, we define spherical convolution as the inner product between spherical functions rotated relative to each other.

Let I(θ, φ) be a spherical scalar image (function) and ${\left\{{\tilde{h}}_n(\theta ,\varphi )\right\}}_{n=1}^N$ be a set of N spherical scalar filters (functions) parameterized by the spherical coordinates (θ, φ). We apply each filter ${\tilde{h}}_n$ to the image via spherical convolution, resulting in the continuous outputs $w_n=I{\tilde{h}}_n$. In wavelet theory, $\left\{{\tilde{h}}_n\right\}$ are called the analysis filters. We can then convolve {w_n} with another set of spherical filters {h_n}, called the synthesis filters, producing reconstructed image components $\widehat{I}=w_n{h}_n$. We define $\widehat{I}={\sum }_n{\widehat{I}}_n$ to be the reconstructed image.

If ${\{{\tilde{h}}_n,h_n\}}_{n=1}^N$ are such that $\widehat{I}=I$ for all input images I, the analysis-synthesis filter bank is invertible and {w_n is a lossless representation the original image I. In particular, if the filters $\left\{{\tilde{h}}_n\right\}$ are dilated versions of a template filter, then {w_n} is a continuous wavelet transformation (CWT) that captures the original image properties at multiple scales. While conceptually similar to the Euclidean case, there are significant differences between planar and spherical convolutions. For example, unless ${\tilde{h}}_n$ is axisymmetric (i.e., radially symmetric about the north pole), w_n is a function on SO(3) rather than a spherical function.

For a general non-axisymmetric analysis-synthesis filter bank, the relationship between the input and reconstructed image is as follows [16]:

$${\widehat{I}}^{l,m}=I^{l,m}\frac{8{\pi }^2}{2l+1}\sum _{n=1}^N\sum _{m^{\prime }=-l}^l\left[h_n^{l,m^{\prime }}\right]{\left[{\tilde{h}}_n^{l,m^{\prime }}\right]}^{\ast }$$ (1)

where I^l,m is the degree l and order m spherical harmonic coefficient of function I(θ, φ)and * denotes complex conjugation. We define the frequency response of a filter bank to be

$$H_{\tilde{h},h}\left(l\right)=\frac{8{\pi }^2}{2l+1}\sum _{n=1}^N\sum _{m=-l}^l\left[h_n^{l,m}\right]{\left[{\tilde{h}}_n^{l,m}\right]}^{\ast }.$$ (2)

It is easy to see that a filter bank is invertible if and only if its frequency response $H_{\tilde{h},h}\left(l\right)$ is equal to 1 for all l such that I^l,m ≠ 0.

We now construct a spherical continuous wavelet transform (SCWT). We define the analysis filters ${\tilde{h}}_n=D_n\psi$ to be dilations of a template wavelet ψ and

$$h_n^{l,m}=\{\begin{array}{cc}\frac{1}{H_{\tilde{h},\tilde{h}}\left(l\right)}{\tilde{h}}_n^{l,m}\text{for}\hfill & H_{\tilde{h},\tilde{h}}\left(l\right)>0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (3)

One can verify that this analysis-synthesis filter bank is invertible for frequencies (l, m) for which $H_{\tilde{h},\tilde{h}}\left(l\right)\ne 0$.

Sampling Theory for SCWT

In the above formulation, the spherical images, filters and SCWT are defined continuously. While fast algorithms exist for computing and representing these continuous functions via coefficients of basis functions (e.g., spherical harmonics, and wigner-D functions), in practice, effective analysis requires sampling the SCWT. The sampling scheme and the discrete convolution between the wavelet samples and the continuous synthesis filter bank must be defined in a way that ensures invertibility.

It turns out that for axisymmetric analysis-synthesis filter banks of a finite spherical harmonic degree, latitude-longitude (lat-lon) sampling – at a sufficient rate dependent on the maximum spherical harmonic degree – guarantees that the filter bank has the same frequency response under the continuous and discrete convolution [16]. Thus an invertible continuous filter bank remains invertible under sampling and discrete convolution. The sampling guarantee implies that we can sample the SCWT defined in Eq. (3) while maintaining invertibility.

Implementation

In practice, we first establish a minimal metric-distortion spherical coordinate system [6] for an input shape consisting of mesh vertices {x_i, y_i, z_i}, resulting in the coordinate samples {x(θ_i, φ_i), y(θ_i, φ_i), z(θ_i, φ_i)}. Fast spherical convolution requires representing the coordinate functions in the spherical harmonic domain. We interpolate the coordinate samples onto the latlon grid and use the fast spherical harmonic transform [9] to obtain the spherical harmonic coefficients {x^l,m, y^l,m, z^l,m}. We verify by visual inspection and by computing percentage errors that interpolation errors are small.

For multi-scale shape analysis, we choose the template wavelet ψ to be the Laplacian-of-Gaussian [18]. We compute the SCWT of each coordinate function via convolutions with the analysis-synthesis filter bank in the spherical harmonic domain. As required by the sampling theories, the wavelet coefficients are sampled onto the lat-lon grid. For computational convenience, we interpolate the sampled wavelet coefficients onto a subdivided icosahedron grid (160k vertices). Theoretically, the coarser wavelet scales require smaller number of samples to prevent aliasing. In this work, we over-sample the wavelets coefficients on the same dense grid at all scales to increase the precision of our analysis. By re-interpolating the wavelet coefficient samples from the subdivided icosahedron back to the lat-lon grid, we again verify that interpolation errors are small.

Since metric distortion is invariant under rotations of the coordinate system, the resulting shape analysis is also rotation invariant, unlike bi-orthogonal wavelets. Rotational invariance of the overcomplete wavelet transform was theoretically and experimentally demonstrated in [18].

To summarize, given an input shape as a set of mesh vertices {x_i, y_i, z_i}, the spherical wavelet transforms output a set of wavelet coefficients samples $\{w_n^j\left(x\right),w_n^j\left(y\right),w_n^j\left(z\right)\}$ on the subdivided icosahedron grid, where j denotes the vertex index on the grid and n denotes the index of the filter, which corresponds directly to the resolution level of the wavelet transform.

3 Experiments and Discussion

Cortical folds in humans start developing at about 9 weeks in gestation and change dramatically until birth. The mechanism involved remains unclear. Cortical folds are known to correlate with function and cytoarchitecture [7]. The study of the folding formation process can therefore deepen our understanding of structure-function relationship and neurological diseases originating from abnormal structural and functional connectivity in neuro-development. A previous postmortem study reports regional and hemispheric differences in folding patterns in gestation [3]. Recent advances in MR imaging allow us to study the cortical folding pattern of premature newborns in-vivo.

We consider 11 MRI scans of eight normal neonates at gestational ages of 30.57, 31.1, 34, 37.71, 38.1, 38.4, 39.72, and 40.43 weeks, and three children (2, 3 and 7 years old). The cortical surfaces corresponding to the gray-white matter boundary were manually segmented, automatically registered [6] and manually checked for correspondence. We then apply the overcomplete spherical wavelets and employ the Gompertz function [15] to characterize the folding development:

$$F\left(t\right)=m{e}^{-e^{-r(t-p)}}+∊\left(t\right)$$ (4)

where F(t) is some feature derived from the wavelet coefficients w_t(x), w_t(y), w_t(z) at age t [17]. m is the maximum value of F at maturity, r is the maximum growth rate, p is the age of fastest growth and ∊(t) is i.i.d. zero mean Gaussian noise. We assume a zero mean Gaussian prior on m, p, and r and estimate them using the maximum-a-posteriori framework. The variance of the Gaussian noise and priors on m, p and r are tuned via cross-validation. We estimate the confidence intervals of the estimated parameters using the Laplace approximation [10] and measure the goodness-of-fit with an R² statistic. An R² of 0.6 implies the model explains 60% of the variation in the data, and is considered a good fit.

Global Analysis of Folding Development

At each frequency level n ∈ {0,..., 4}, for each cortical surface, we compute $F_n\left(t\right)={\sum }_{j=1}^J{w}_{n,t}^j{\left(x\right)}^2+w_{n,t}^j{\left(y\right)}^2+w_{n,t}^j{\left(z\right)}^2$, where t is the age of the subject and J is the number of sampled wavelet coefficients per level. F_n(t) summarizes the amount of cortical folding at the n-th scale: coefficients on the coarser level add details to the primary folds while coefficients on the finer level contribute to the smaller folds. For each wavelet level n, we then regress F_n(t) against time t using Eq. (4). A good fit indicates that folding development at that scale obeys the characteristic of the Gompertz curve: fast exponential growth followed by slowing down and tapering off.

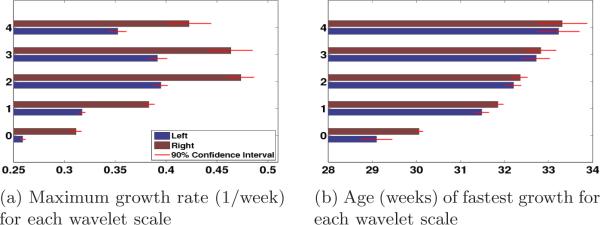
The estimated model parameters provide intuitive notions of growth. Fig. 1 shows that the speed of folding development r increases from level 0 to level 2 in both hemispheres and the age of fastest folding development p increases monotonically with frequency levels from approximately 29 to 33 weeks. The maximum development ages and speeds are significantly different across frequency levels. This temporal developmental order from the larger scale folds to smaller scale folds is consistent with the postmortem study [3] and more salient than in the previous imaging study based on bi-orthogonal spherical wavelets [17].

Fig. 1.

Summary of Gompertz model fit to the global wavelet energies for wavelet scales {0,...,4}. Parameters of the Gompertz model provide intuitive notion of growth. Red bars indicate 90% confidence intervals.

Furthermore, we find that in the left hemisphere, the fastest folding development occurs at a younger age than in the right at all levels (Fig. 1b), suggesting that cortical folds in the left hemisphere develop earlier, but slower than the right (Fig. 1a). In the postmortem study [3], structures in the temporal lobe, including the superior frontal, superior temporal and transverse temporal gyri were found to appear at an earlier gestational age on the right hemisphere. In contrast, our result predicts an earlier folding development age, but a slower development speed on the left. The inconsistency between the two studies is probably due to a difference in definitions. For example, the definition of age of appearance in [3] is different from the age of fastest development in our model.

Regional Analysis of Folding Development

At each frequency level n ∈ {0,...,4}, for each cortical surface, and for each spatial location j, we compute $F_{n,j}\left(t\right)=w_{n,t}^j{\left(x\right)}^2+w_{n,t}^j{\left(y\right)}^2+w_{n,t}^j{\left(z\right)}^2$. Once again, we regress F_n,j(t) against t using Eq. (4) and study both when and where folding of the cortical surface occurs at different spatial scales.

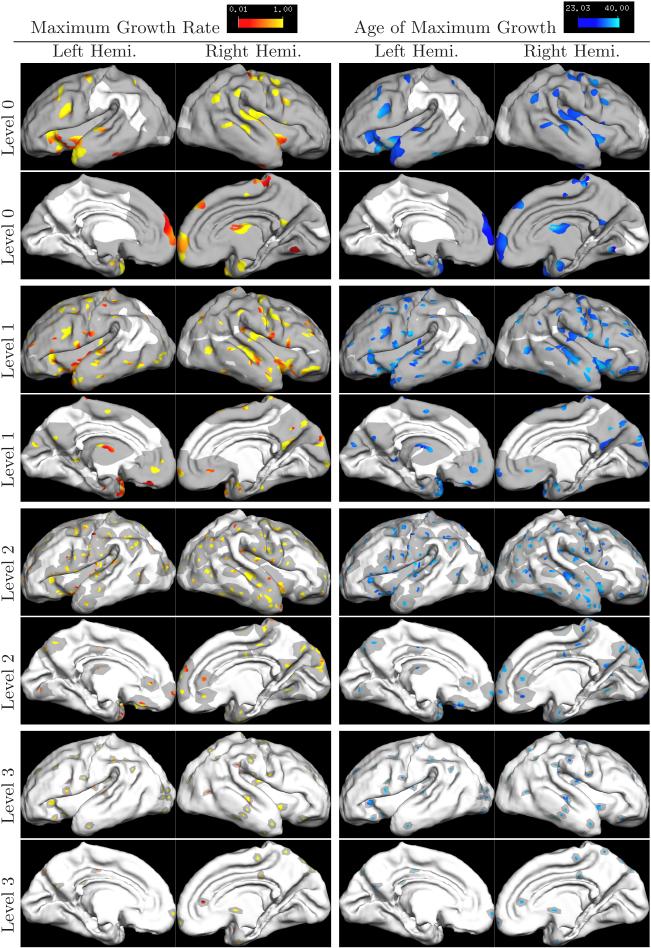
Fig. 2 shows the results of the regional analysis. At each frequency scale, spatial locations with R² > 0.6 are color-coded with the corresponding development speed and age, and superimposed on the youngest newborn surface. To visualize the different spatial scales, the support of the corresponding wavelet basis function at that scale is shown in dark gray around each color-coded vertex.

Fig. 2.

Regional Growth Pattern. Colored regions indicated areas whose wavelet coefficients fit well to the Gompertz model. Each region has an accompanying support region shown in dark gray. The size of the supports correspond to the support of the wavelet basis at that scale, which decreases with increasing level.

Consistent with the global development results, regions that develop earlier (darker blue) also grow more slowly (more red). For example, the lateral side of the parietal lobe on the left hemisphere develops earlier than the right, but at a slower speed. In particular, the post-central sulcus and inter-parietal sulcus develop two weeks earlier in the left hemisphere than in the right.

Also consistent with the global analysis, we find that larger folds develop earlier but slower. On the lateral side, the pre- and post-central gyri develop the fastest during 30−31 weeks in both hemispheres while smaller structures such as supramarginal and angular gyri develop the fastest at much later time, as can be seen on level 3. Another example is the superior temporal gyrus developing much earlier than the smaller middle and inferior temporal gyri.

Discussion

Modeling cortical folding in the wavelet domain allows us to localize and study its regional development. Consistent with previous studies, we find that larger cortical folds develop at younger gestational ages with slower speeds. We also find that the left hemisphere develops earlier but slower than the right. The study of individual wavelet coefficients detects and quantifies the regional differences in folding development at different spatial scales.

Because the overcomplete wavelet bases are not orthogonal, the correlation between wavelet coefficients at different levels should be taken into account, requiring further development of computational methods that model such dependencies. We note that for orthogonal representations, this problem is avoided at the price of losing rotational invariance and sensitivity.

While more analysis is needed to characterize the probability of false positives in the local analyses, our general agreement with the postmortem study [3] is encouraging. Furthermore, the improvement over biorthogonal wavelets is grounded in rigorous wavelet theory that cannot be attributed to multiple comparisons.

4 Conclusion

In this work, we explore the use of over-complete spherical wavelets in cortical shape analysis. We present a theoretic formulation of over-complete spherical wavelet filter banks and demonstrate their application on a study of cortical folding in newborns. Our experiments quantitatively verify previous experiments based on visual examination of postmortem brains and offer new insights into neuro-anatomical development.