Determination of the Solution Bound Conformation of an Amino-acid Binding Protein by NMR Paramagnetic Relaxation Enhancement: Use of a Single Flexible Paramagnetic Probe with Improved Estimation of Its Sampling Space

Abstract

We demonstrate the feasibility of elucidating the bound (“closed”) conformation of a periplasmic binding protein, the glutamine-binding protein (GlnBP), in solution, using paramagnetic relaxation enhancements (PREs) arising from a single paramagnetic group. GlnBP consists of two globular domains connected by a hinge. Using the ligand-free (“open”) conformation as a starting point, conjoined rigid-body/torsion-angle simulated annealing calculations were performed using backbone ¹H^N-PREs as a major source of distance information. Paramagnetic probe flexibility was accounted for via a multiple-conformer representation. A conventional approach where the entire PRE data set is enforced at once during simulated annealing yielded poor results due to inappropriate conformational sampling of the probe. On the other hand, significant improvements in coordinate accuracy were obtained by estimating the probe sampling space prior to structure calculation. Such sampling is achieved by refining the ensemble of probe conformers with intra-domain PREs only, keeping the protein backbone fixed in the open form. Subsequently, while constraining the probe to the previously found conformations, the domains are allowed to move relative to each other under the influence of the non-intra-domain PREs, giving the hinge region torsional degrees of freedom. Thus, by partitioning the protocol into a “probe sampling” and a “backbone sampling” stage, structures significantly closer to the X-ray structure of ligand-bound GlnBP were obtained.

Introduction

Many proteins display, as an essential feature for their function, large conformational changes that consist in the relative movement of (quasi-) rigid structural elements. A textbook example is the quaternary structure of hemoglobin, where the difference between several distinct crystallographic states can be explained by rigid-body motion of the subunits.¹ Another example is the periplasmic binding protein (PBP) structural superfamily, whose members are involved in transport and signaling processes in both prokaryotic and eukaryotic cells. Typically, PBPs are characterized by (i) two similar globular domains connected by two or three linker segments, and (ii) a ligand binding site located at the interface between the domains.² A ligand-free PBP usually exhibits an “open” conformation, whereas its liganded counterpart adopts a “closed” state, the conformational change consisting in a hinge-bending motion at the linker region that alters the relative position and orientation of the domains, bringing them closer to each other.

Given a protein structure of the above-described type, it is possible to elucidate an alternative conformation by experimentally restrained rigid-body molecular dynamics. Paramagnetic relaxation enhancement (PRE) via chemical modification of engineered cysteines has emerged as a reliable tool for the estimation of paramagnetic center–¹H nucleus distances by solution nuclear magnetic resonance (NMR) spectroscopy.³ PRE presents advantages over the nuclear Overhauser effect (NOE), the most common source of NMR structural restraints, in that it provides longer distance information, and the experimental data are easier to acquire and interpret. In particular, since J-correlated experiments are used for measuring PREs, their assignment to specific ¹H nuclei in the protein is straightforward vis-à-vis the assignment of NOEs to ¹H–¹H pairs, which can be seriously compromised by chemical shift degeneracy. On the other hand, a factor that complicates PRE data interpretation is that covalent attachment of an extrinsic paramagnetic group to the protein is usually achieved via a flexible linker, which may exhibit a large conformational sampling space. If not properly accounted for, such sampling may lead to coordinate distortions in the course of structure calculations due to a break down of the commonly used approximation where the paramagnetic group is represented by a single point.⁴ Indeed, some nuclei may effectively sense one region of the probe’s sampling space, while other nuclei may be affected by another region of such space, thus hindering the description of the effect in terms of a single probe position. A solution to this problem has been proposed by Iwahara et al.,⁴ whereby the paramagnetic probe is represented in simulated annealing calculations by an ensemble of non-self-interacting conformers. Application of this approach to the refinement of a DNA/protein complex, where the DNA was paramagnetically labeled with dT-EDTA-Mn²⁺ at three different positions, resulted in a good agreement between experimental and back-calculated PRE data, and significant gains in coordinate accuracy. In contrast, although refinement via the single-conformer representation using the same data set also yielded a good experimental/back-calculated PRE fit, this was achieved in detriment of coordinate accuracy.⁴

Here, we demonstrate the use of PRE data arising from a single paramagnetic group in the calculation of the bound conformation of the glutamine-binding protein (GlnBP; a 25-KDa member of the PBP superfamily), using the X-ray crystallographic coordinates of the Gln-free, open state⁵ as a starting point (Figure 1). It is shown that conjoined rigid-body/torsion-angle simulated annealing calculations^6,7 with a multiple-conformer representation of the paramagnetic probe affords a means to successfully exploit the PRE information, provided that the sampling space of the conformers is estimated before the protein backbone is allowed to move during dynamics. Indeed, we show that if degrees of freedom are given simultaneously to both the paramagnetic probe and the peptide backbone at the linker region of GlnBP, the single-conformer representation of the probe yields more accurate structures than the multiple-conformer approach. Although this has been possibly inferred in previous work concerned with the application of PRE to the investigation of dynamical processes (for a review see ref 8), to the best of our knowledge, neither has this issue been addressed in the context of structure calculation, nor has its effect been studied in detail.

Figure 1.

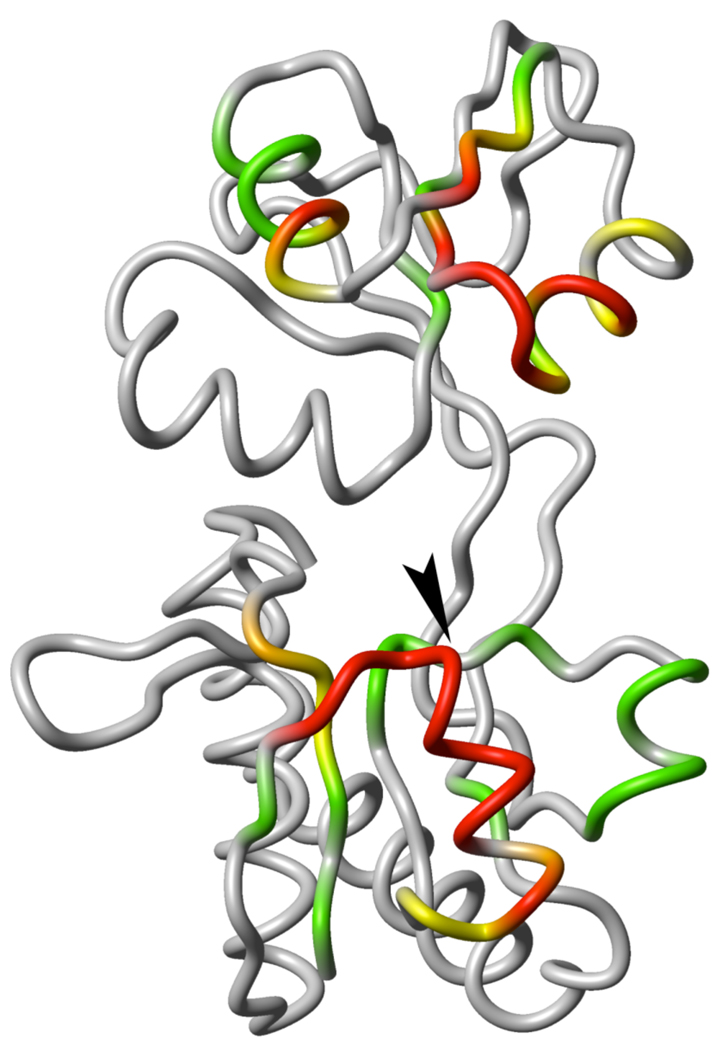
Ligand-free, open conformation of GlnBP (PDB ID: 1GGG). The large domain is displayed at the bottom and the small domain on top. The color scheme indicates H^N-PRE values observed on the bound GlnBP S51C sample: red, PRE > 40 s⁻¹ or completely broadened peak; orange, 40 ≥ PRE > 30 s^{– 1}; yellow, 30 ≥ PRE > 20 s⁻¹; green, 20 ≥ PRE > 10 s⁻¹; grey, PRE ≤ 10 s⁻¹ or missing due to overlapped/unassigned peak. An arrowhead indicates the position of the S51C point mutation. All molecular graphics were generated with MOLMOL.⁹

Materials and Methods

Sample Preparation

A single cysteine was introduced into GlnBP at position S51 using the pJ133 plasmid¹⁰ as a template, and the QuickChange site-directed mutagenesis kit (Stratagene). pJ133 S51C was transformed into BL21-Gold (DE3) E. coli host cells (Stratagene), and the uniformly ¹⁵N-labeled mutant was over-expressed in minimal medium using ¹⁵NH₄Cl as sole nitrogen source; induction was achieved with 1 mM IPTG. Protein extraction was performed by chloroform-shock treatment¹¹ followed by purification via anion exchange (DEAE) and gel filtration (Superdex-75) columns (GE Healthcare), as described by Shen et al.¹⁰ All buffers were 2 mM in dithiothreitol (DTT). The protein was subsequently concentrated and incubated for two hours in 20-fold molar excess DTT to ensure complete cysteine reduction, followed by desalting on a PD-10 column (GE Healthcare) using DTT-free 0.1 M potassium phosphate, pH 7.2.

Nitroxide spin-labeling was performed immediately after the PD-10 step by adding to the protein a 10-fold molar excess of MTSL (Toronto Research Chemicals Inc.) from acetonitrile stock. An extra 10-fold molar excess of MTSL was added after 30 min., followed by overnight incubation. The spin-labeled protein was purified by reverse-phase HPLC using a C4 column (Vydac), which produces ligand-free GlnBP as denaturation occurs in the organic solvent environment. Following liophylization, the protein was re-dissolved overnight in NMR buffer (0.1 M potassium phosphate, pH 7.2) to a final concentration of ∼ 0.5 mM; when present L-Gln was in a 3-fold molar excess. Spin-labeling was confirmed by LC-MS.

PRE Measurements

The transverse PRE rate is given by the difference in the R₂ relaxation rate between the paramagnetic and diamagnetic state of the protein. The diamagnetic state was generated by reducing the nitroxide spin label with the addition of 10-fold molar excess ascorbic acid to the paramagnetic NMR sample. PRE rates were measured for backbone H^N protons using a two-time-point (0 and 15 ms) ¹⁵N–HSQC-based interleaved experiment.³ Measurements were performed at 41 °C on a Bruker Avance 800-MHz spectrometer equipped with a cryo-probe and Z-pulsed field gradient. Spectra were processed with NMRPipe¹² and analyzed with PIPP.¹³

Simulated Annealing Calculations

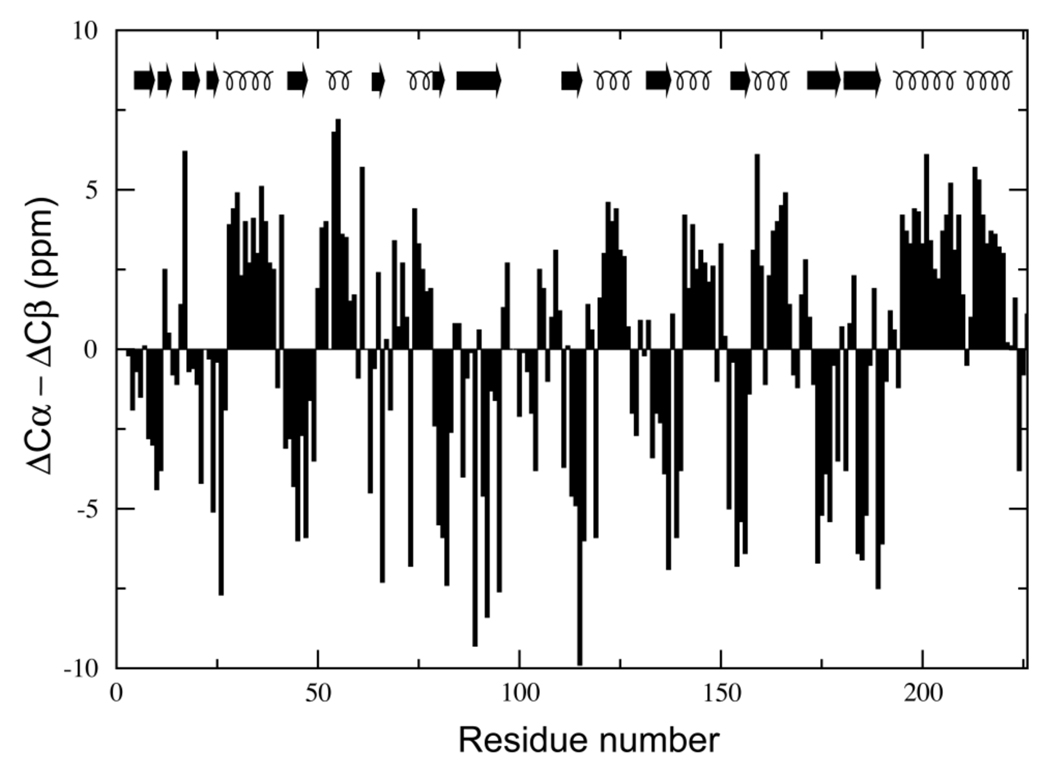
The Xplor-NIH package¹⁴ was used for all molecular dynamics calculations, which differed in at least one of the following: (i) starting coordinates (open or closed GlnBP), (ii) torsional degrees of freedom allowed to the hinge region and paramagnetic probe side chains (all or none), (iii) representation of probe side chains (single- or multiple-conformer), and (iv) experimental restraints enforced (all PREs, only intra-domain PREs, etc.). Despite these differences, a common underlying simulated annealing scheme was shared by all molecular dynamics calculations. Specifically, the scheme comprised a high-temperature (3000 K) 10-ps-long stage, subject to a PRE pseudo-potential⁴ (k_PRE = 0.05 kcal mol⁻¹ s²), a van der Waals-like repulsive term (k_VDW = 1.0 kcal mol⁻¹ Å⁻⁴; only C^α–C^α interactions active), and a torsion-angle database potential of mean force¹⁵ (k_DB = 0.02 kcal mol⁻¹ rad⁻²); where k_X represents the force constant of term X. Along a subsequent cooling (3000 → 25 K) 24-ps-long stage, k_PRE, k_VDW, and k_DB were increased 0.05 → 10.0 kcal mol⁻¹ s², 0.004 → 4.0 kcal mol⁻¹ Å⁻⁴ (all interactions active), and 0.02 → 1.0 kcal mol⁻¹ rad^–2, respectively. Unless otherwise stated, additional restraints were used during calculations of ligand-bound GlnBP structures, where full torsional degrees of freedom were given to the hinge region (residues 85–89 and 181–185). Such restraints involved the central hinge portion, and consisted in TALOS-derived dihedral angles,¹⁶ and hydrogen bonds between residues 88 and 183. The latter were introduced to preserve the integrity of the β-sheet conformation of the hinge, as the two anti-parallel peptide linkers are predicted as β- strand by both TALOS and the difference between C^α and C^β secondary chemical shifts¹⁷ (Figure 2). In all calculations, the two domains of GlnBP (Figure 1) were treated as rigid bodies, and the backbone coordinates of the large domain (residues 1–84 and 186–226) were kept fixed in space. The above-described simulated annealing protocol was based on that previously used for the refinement of a protein/DNA complex.⁴

Figure 2.

Difference between C^α and C^β secondary chemical shifts (ΔC^α–ΔC^β) for bound GlnBP versus residue number. The secondary structure of ligand-free GlnBP is indicated by arrows (β-strand) and curls (α-helix).

Protons were attached to GlnBP X-ray structures with the program REDUCE.¹⁸ The MTSL moiety was modeled as previously described,¹⁹ and represented by either one or three conformers.⁴ In all cases, the correlation time for the internal motion of the paramagnetic probe, τ_i, was assumed negligible against the correlation time τ_c (τ_i << τ_c). The latter was optimized within an 8–15 ns range.⁴ Accuracy of PRE-derived structures was judged relative to the crystallographic reference, excluding the 98–110 residue stretch from RMSD scoring as comparison of the ligand-free and bound X-ray models reveals structural differences for this loop segment.

Results and Discussion

Spin-labeling Strategy

GlnBP is a single-chain, 226-residue protein that consists of two globular domains, designated the large domain (residues 1–84 and 186–226) and the small domain (residues 90–180), connected by two linker segments (residues 85–89 and 181–185).⁵ In contrast to ligand-free GlnBP, which adopts an open conformation⁵ (Figure 1), the bound state exhibits a closed structure where the interface between the domains forms the binding cleft.²⁰ Here, we test the feasibility of a structure calculation strategy that assumes the ligand-free conformation of the protein is known, the goal being the determination of the bound structure. Only changes in the relative position and orientation of the domains upon binding are considered, a reasonable assumption for a periplasmic binding protein.² Further support for the above premise may be obtained as a byproduct of the resonance assignment stage, required for the ligand-bound state (structure assumed unknown) but not for the ligand-free state (structure assumed known). The difference in C^α and C^β secondary chemical shifts¹⁷ (ΔC^α–ΔC^β) of bound GlnBP shows excellent correlation with the secondary structure of the free conformation (Figure 2), thus reinforcing the assumption that the domains behave largely as rigid bodies.

With the above considerations in mind, a single cysteine mutation, S51C, was introduced into GlnBP for derivatization with MTSL. Based on the structure of free GlnBP, residue 51 sits on the solvent-exposed side of an α-helix in the large domain, at the periphery of a (potential) domain–domain interface created upon ligand binding (Figure 1). Furthermore, the selected site is placed opposite to the linker segments, appropriate for probing any possible hinge-twist motion. The effect of spin-labeling on the structure was assessed by analysis of ¹⁵N–HSQC spectra of free and bound GlnBP. In both cases, changes in chemical shifts relative to the wild-type spectra were minimal and localized around the mutation site, which suggests the structure is not significantly altered. In Figure 1, the PRE data on bound GlnBP S51C are graphically displayed on the ligand-free GlnBP structure. Large inter-domain PREs suggest the proximity of the domains in the bound conformation.

Structure Calculation by Simultaneous Optimization of Paramagnetic Probe and Polypeptide Backbone

Conjoined rigid-body/torsion-angle simulated annealing calculations^6,7 against all PREs were performed as described in Materials and Methods, starting from the open GlnBP conformation⁵ (PDB ID: 1GGG; Figure 1), giving the hinge region and all side chains, including that of the paramagnetic probe, full torsional degrees of freedom. Structural statistics are summarized in Table 1.

Table 1.

Statistics for PRE-based, Bound GlnBP Structures Calculated via Different Simulated Annealing Protocols^a

Optimization type	Simultaneousb		Sequentiac
Probe representation	1 conformer	3 conformers	3 conformers
Overall Q (163)d	0.25 ± 0.00	0.23 ± 0.00	0.22 ± 0.00
Intra-domain Q (86)d	0.25 ± 0.01	0.22 ± 0.01	0.20 ± 0.00
Inter-domain Q (67)d	0.24 ± 0.00	0.23 ± 0.01	0.23 ± 0.00
RMSD (Å)e	2.9 ± 0.6	6.5 ±0.9	2.5 ± 0.2
51–117 distance (6.6) (Å)f	8.3 ±0.4	10.4 ± 0.7	7.2 ±0.2
51–138 distance (7.7) (Å)f	9.0 ± 0.4	12.2 ±0.5	9.2 ±0.2
Rgyr(17.5)(Å)g	17.9 ±0.1	18.2 ±0.1	17.8 ±0.1

^aThe 10 lowest-PRE energy structures out of 200 are considered.

^bSimultaneous optimization of paramagnetic probe conformer(s) and protein backbone.

^cOptimization of paramagnetic probe conformations, followed by optimization of protein backbone.

^dAverage PRE Q-factor for corresponding data set (number of restraints indicated in parenthesis).

^eAverage pairwise backbone (N, C^α, C’) RMSD of the small domain relative to the X-ray coordinates of the bound conformation (PDB ID: 1WDN), after superimposition of the large domain. RMSD calculation excludes residue segment 98–110 (see text).

^fAverage H^N–H^N separation distance of indicated residues (target value from 1WDN coordinates indicated in parenthesis).

^gAverage radius of gyration calculated from backbone (N, C^α, C’) atoms (target value from 1WDN coordinates indicated in parenthesis).

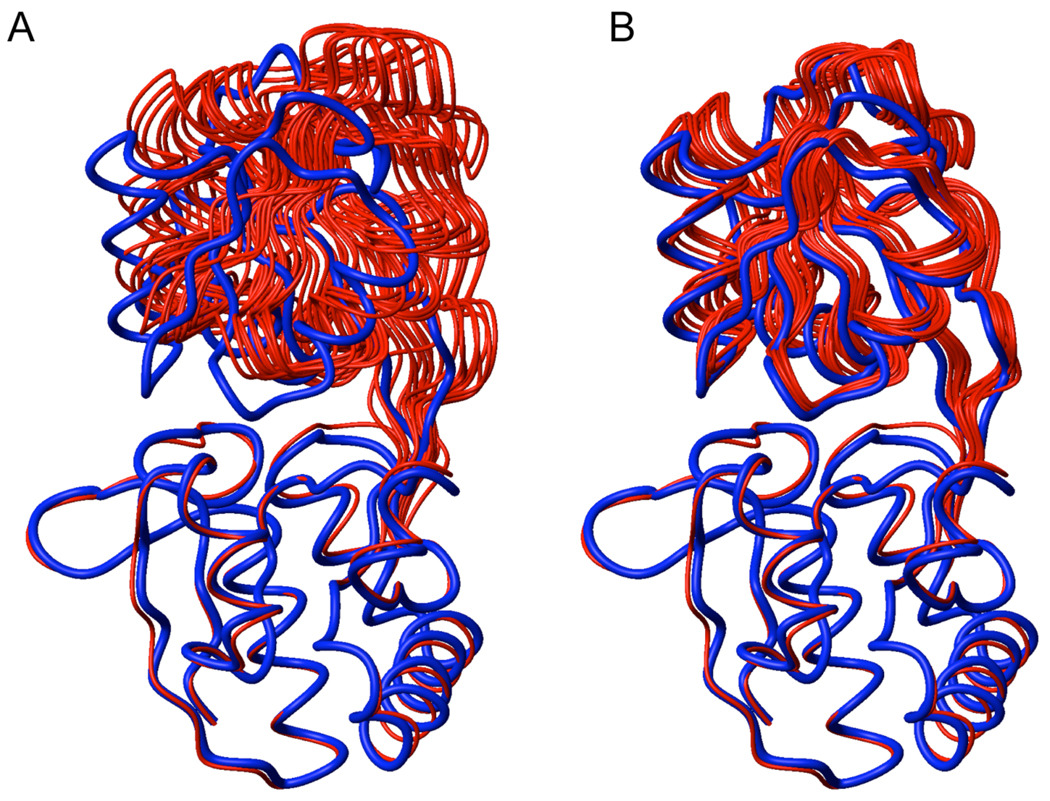
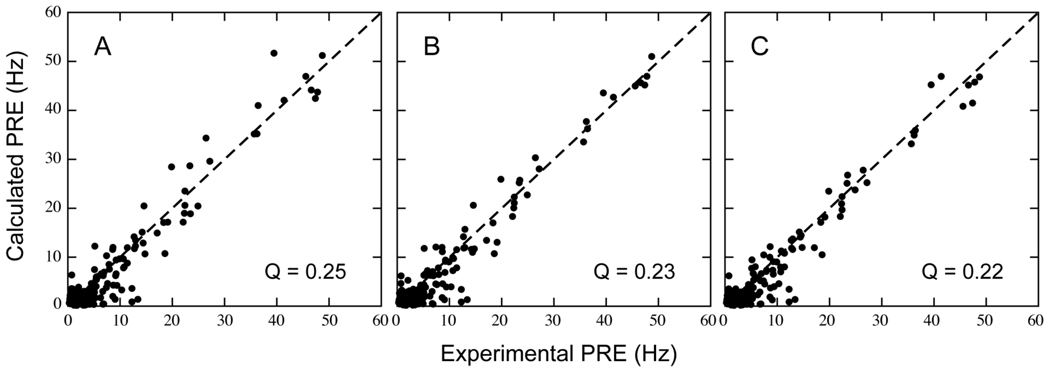
When representing the paramagnetic probe side chain by a 3-conformer ensemble, final structures (Figure 3A) show a good fit between experimental and back-calculated PREs, with an average overall Q-factor of 0.23 (Figure 4B). However, structural accuracy is poor, as indicated by a large 6.5-Å backbone RMSD for the small domain relative to the X-ray model of bound GlnBP (PDB ID: 1WDN),²⁰ after superimposing backbone coordinates of the large domain. This structural discrepancy can be largely attributed to failure of the small domain to completely close the gap between the open and closed configurations in the course of simulated annealing. Indeed, this can be visually appreciated in Figure 3A, and quantified by the overall compactness in terms of the average (N, C^α, C’)-based radius of gyration of the computed structures, 18.2 Å, which is larger than the 17.5 Å of the crystallographic counterpart. Furthermore, average H^N–H^N distances between residue 51 (in the large domain) and residues 117 and 138 (both in the small domain) are, respectively, 10.4 and 12.2 Å, and fall short of the corresponding X-ray-based values of 6.6 and 7.7 Å, respectively. These distances exhibit a large change between the open and closed X-ray models (21.7 → 6.6 Å for residue pair 51–117, and 23.1 → 7.7 Å for residue pair 51–138), and will be used henceforth as a measure of inter-domain proximity.

Figure 3.

PRE-based structures of bound GlnBP (red) superimposed to the X-ray model (blue; PDB ID: 1WDN) via the large domain (bottom). (A) Structures calculated by simultaneous optimization of probe conformers and protein backbone. (B) Structures calculated with previously optimized paramagnetic probe conformers using intra-domain PRE data on the fixed, open backbone coordinates. The 10 lowest-PRE energy structures (out of 200) are shown.

Figure 4.

Correlation between experimental and calculated ¹H^N-PRE values for structures computed via optimization of the protein backbone with simultaneous (A and B) or previous (C) optimization of the paramagnetic probe conformer(s). Plot A stems from a single-conformer probe representation, while plots B and C result from a three-conformer ensemble. The average overall Q-factor is indicated. See Table 1 for details.

If the above-described simulated annealing protocol is implemented with a 1-conformer representation of the paramagnetic probe, final structures yield a slightly worse PRE fit, with an average overall Q-factor of 0.25 (Figure 4A). Surprisingly, coordinate accuracy is significantly improved, with the backbone RMSD of the small domain decreasing to 2.9 Å, i.e., less than half that of structures generated with the 3-conformer representation. RMSD improvement is concomitant with a decrease in the inter-domain separation, as indicated by H^N–H^N distances of 8.3 and 9.0 Å for residue pairs 51–117 and 51–138, respectively.

Conformational Sampling of the Paramagnetic Probe

The above results are in contrast to previous observations that showed a multiple-conformer treatment of dT-EDTA-Mn²⁺ probe flexibility provided significant accuracy gains, relative to the single-conformer approach, in the refinement of a DNA/protein complex.⁴ The possibility that our particular MTSL-based PRE data is better described by a single probe conformer can be readily assessed by optimizing the probe side chain against all PREs, while fixing the peptide backbone at the known, X-ray-derived, bound GlnBP coordinates, target of the PRE-based structure calculation. As shown in Table 2, use of a 3-conformer ensemble yields a better fit to experiment (overall Q-factor = 0.22) than the 1-conformer approach (overall Q-factor = 0.29), a strong indication that the former representation affords a more suitable description of our data.

Table 2.

Correlation Between Experimental PREs and Those Calculated from Paramagnetic Probe Side Chains Optimized on the Fixed Backbone X-ray Coordinates of Bound GlnBP^a

	1 conformerb	3 conformersb
Overall Q (163)c	0.29 ± 0.00	0.22 ± 0.00
Intra-domain Q (86)c	0.29 ± 0.00	0.23 ± 0.00
Inter-domain Q (67)c	0.28 ± 0.00	0.22 ± 0.00

^aStatistics on the 10 lowest-PRE energy structures out of 200.

^bRepresentation of paramagnetic probe.

^cAverage PRE Q-factor for corresponding data set (number of restraints indicated in parenthesis).

Figure 5 sheds light into the problem by showing the location of the oxygen atom in the nitroxide group, superimposed to the backbone conformation of bound GlnBP’s X-ray structure. Oxygen positions that stem from the 3-conformer probe refinement against all PREs, fixing the backbone in the bound X-ray coordinates represent the “real” sampling space of the probe, as sensed by the PRE data (Figure 5, green spheres). It is evident that simultaneous optimization of the three probe conformers and the hinge backbone, as described in the previous section, results in a distortion of the probe sampling space (Figure 5, red spheres). In particular, the space is elongated towards the small domain: the flexible probe conformers reach towards the small domain to maximize the PRE fit, thus discouraging full inter-domain closure during simulated annealing. Furthermore, if similar structure calculations are performed using only the PRE term as experimental restraint—i.e. removing dihedral angle and hydrogen bond restraints on the hinge to avoid competition with these other observables—similar results are obtained with an average total PRE energy slightly lower than that achieved by optimizing the probe sampling space on the target bound conformation (not shown). This indicates that structures with sufficiently closed domains are hard (if not impossible) to reach by simultaneous refinement of the 3-conformer probe ensemble and the polypeptide backbone.

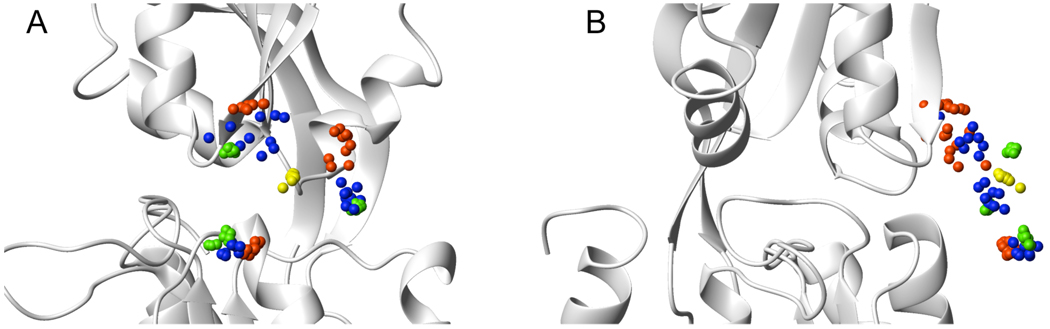
Figure 5.

Paramagnetic probe sampling as sensed by the PRE data during different simulated annealing protocols. Only the oxygen atom of the nitroxide group is shown (sphere), against the backbone conformation of bound, closed GlnBP (PDB ID: 1WDN), displayed with the large domain at the bottom. In green are atomic positions optimized assuming the fixed closed conformation. In yellow and red are positions optimized with a flexible hinge, using a 1- or 3-conformer representation of the probe, respectively. All PREs were used (green, yellow, and red). In blue are positions optimized with intra-domain PREs only, assuming a fixed, open conformation. In all cases, results of the 10 lowest PRE energy optimizations are shown (out of 200). Views A and B differ by a 90° rotation.

On the other hand, despite the 1-conformer probe representation affords a less accurate treatment of the PRE data (see Table 2), its use during structure calculations yields more accurate structures because the single oxygen has to satisfy both intra- and inter-domain PREs at the same time (Figure 5, yellow spheres). Consequently, if the probe moves towards the opposite domain to satisfy inter-domain PREs, the intra-domain fit suffers, and vice-versa. This leaves no other option than for the domains to close via the hinge.

Structure Calculation via Prior Estimation of Paramagnetic Probe Sampling Space

The observations made in the previous section suggest a different approach for structure computation. If the probe sampling space is determined before the actual structure calculation is attempted, then the conformers can be fixed in their optimal positions, subsequently allowing the polypeptide backbone to move during simulated annealing. Such an approach would prevent the distortion of the probe sampling space, and force the domains to breach the gap in order to fit the PRE data. Support for this strategy comes from a control calculation where the probe side chains are held fixed at the lowest PRE energy conformation on the “real” sampling space (Figure 5, green spheres; see previous section). Relative to the reference X-ray model, final structures had a small-domain backbone RMSD (after superimposition of the large domain) of 1.0 ± 0.2 Å. Average H^N–H^N distances for residue pairs 51–117 and 51–138 were 6.9 ± 0.2 and 7.7 ± 0.2 Å, respectively.

In the context of the structure determination of bound GlnBP given the free state, the question arises on how to determine the probe sampling space without a priori knowledge of the structure. Fortunately, a reasonable estimate of the sampling space can be achieved by fixing the protein backbone at the starting coordinates (open conformation), followed by optimization of the 3-conformer probe ensemble against intra-domain PREs only. The resulting probe conformations (Figure 5, blue spheres) are thus unaffected by the other domain—responsible for the previously observed distortions—and lie closer to the sampling space determined on the reference bound structure using the complete PRE data set (Figure 5, green spheres). The lowest (intra-domain) PRE energy structure was selected, and used in a subsequent simulated annealing run where the probe conformers were held fixed, and the hinge torsion angles allowed to move under the influence of non-intra-domain PREs (and additional experimental restraints; see Materials and Methods). Final structures (Figure 3B) fit the PRE data with an overall Q-factor of 0.22 (Table 1, Figure 4C). Relative to the simultaneous optimization of backbone and probe side chain, using both the 1- and 3-conformer approach, structural accuracy is significantly improved, as judged by a decrease in the small-domain backbone RMSD against the X-ray reference to 2.5 Å, and a decrease in H^N–H^N distances for residue pairs 51–117 and 51–138, to 7.2 and 9.2 Å, respectively (Table 1). The improvement of structural quality is also visually obvious in Figure 3. Application of the above approach to the 1-conformer representation of the probe yields structures of similar quality, with a small-domain backbone RMSD relative to the X-ray reference of 2.5 ± 0.3 Å. However, the PRE fit is slightly worse with an average overall Q-factor of 0.24.

Conclusions

Appropriate treatment of paramagnetic relaxation enhancement arising from a flexibly attached spin label calls for an ensemble representation of the probe’s side chain, in order to account for the concomitantly large sampling space.⁴ In doing so, however, a different problem may arise during structure calculation, such as the fit of the PRE data via trivial, or non-realistic conformational changes of the probe, at the expense of structural accuracy. Indeed, as shown here with the determination of the bound state of GlnBP, this problem may cause the ensemble probe representation to yield worse results than a non-ensemble approach, when implemented via a standard structure calculation protocol aimed at the simultaneous optimization of both probe conformers and protein backbone, thus contradicting previous observations.⁴ This problem, however, can be mitigated by initially resorting to a subset of the total PRE information (intra-domain PREs), and only partial structural information (domain structure), which allows for a more reliable estimation of the probe conformational sampling space. The latter subsequently leads to the calculation of improved structures. Therefore, the above-mentioned differences with a previous study⁴ become reconciled, and the multiple-conformer approach, with its already reported benefits,⁴ may be generalized to include problematic cases such as the one encountered in the present work. Nevertheless, there might be systems that do not afford a reasonably accurate estimation of the probe sampling space as a result, for example, of sparse PRE data. In such cases, the single-conformer probe representation may indeed be the most appropriate option, preferably implemented via the two-stage, sequential approach introduced in this study. Alternatively, the sequential strategy may benefit from advances in molecular dynamics (MD) simulations to independently determine likely probe conformers. This has been recently demonstrated in the context of electron spin resonance spectral prediction, where extensive MD calculations involving MTSL-derivatized cysteine side chains on the known structure of T4 lysozyme allowed the identification of five major conformers for two different labeling sites.²¹ Interestingly, use of a 5-conformer representation in our calculations with GlnBP yielded results similar to those obtained with the 3-conformer approach.

Although, to the best of our knowledge, the two-stage approach of probe refinement followed by backbone optimization proposed here has not been used in the slow exchange regime of the PRE, similar strategies have been implemented under fast exchange conditions.⁸ For instance, multiple non-specific DNA/protein complexes have been studied by fixing the paramagnetic probe conformations to those previously determined from the known structure of a different slow-exchanging DNA/protein complex.²² More closely related to our work, the structure of a minor ligand-free closed species of a periplasmic binding protein, MBP, in dynamic equilibrium with the major open conformer, has been recently determined.²³ During simulated annealing, probe sampling in the minor “free-hinged” species may have been biased to likely conformations by forcing them to be similar to those simultaneously optimized on the backbone-fixed, open major species.²³ Even though this issue related to probe flexibility might have been inferred in those previous studies, it is very important to quantify and evaluate its effects in detail, especially as the use of PRE in NMR structural studies is expected to become more common.