Abstract
Relapse following alcohol treatment is a major problem for individuals who are alcohol dependent, yet little is known about the course of drinking after the initial lapse. In the current study, discrete-time survival analysis and latent growth mixture modeling were used to evaluate the time to first lapse and the trajectories of postlapse drinking in a sample of 563 individuals who received community alcohol treatment. Results showed a decreasing risk of lapsing over time. After the initial lapse, 3 trajectory subgroups provided a parsimonious representation of the heterogeneity in postlapse drinking frequency and quantity, with the majority of individuals reporting light, infrequent drinking. Covariate analyses incorporating demographics, distal risk factors, time to first lapse, and coping behavior as predictors of time to lapse and postlapse drinking trajectories indicated that alcohol dependence and coping behavior were the strongest predictors of lapsing and postlapse drinking behavior.
Keywords: alcohol treatment outcomes, relapse, growth mixture modeling, posttreatment drinking trajectories, alcohol dependence
Approximately 17.6 million Americans meet criteria for alcohol abuse or dependence (Grant et al., 2004), and 12.5% of individuals who meet criteria for alcohol abuse or dependence (2.2 million Americans) will receive treatment for an alcohol problem (National Institute of Alcohol Abuse and Alcoholism [NIAAA], 1998). Of those who receive treatment, the majority of individuals will have at least one drink in the first 12 months following treatment (Maisto, Pollock, Cornelius, Lynch, & Martin, 2003), yet few studies have examined what happens after the initial posttreatment lapse (Stout, 2000). To our knowledge no empirical studies have systematically quantified individual patterns of drinking following the initial posttreatment drinking episode. Considering the majority of individuals do lapse following treatment, it is important to gain a better understanding of the drinking patterns following an initial lapse. Furthermore, can the frequency and severity of drinking following a lapse episode be predicted from pretreatment characteristics?
Understanding Alcohol Lapses
The high likelihood of a lapse following treatment has been described by several authors (Donovan, 1996; Hunt, Barnett, & Branch, 1971; Sutton, 1979). Detailed investigations of the relapse process have highlighted the large variation in drinking behavior between individuals (Delucchi, Matzger, & Weisner, 2004), as well as the erratic drinking behavior within individuals over time (Warren, Hawkins, & Sprott, 2003). Yet very little is known about the variation in postlapse drinking patterns and how these patterns may be predicted from pretreatment characteristics.
Several biological, physiological, and psychosocial factors have been put forward as potential risk factors in the relapse process. Shiffman (1989) and others (Donovan, 1996; Witkiewitz & Marlatt, 2004) have classified risk factors on the basis of their timing and mechanisms of action in predicting lapses. Distal risks are factors that present an underlying susceptibility to heavy drinking, including family history of alcohol use disorders (Craig, Krishna, & Poniarski, 1997), age at first drink (McGue, Iacono, Legrand, Malone, & Elkins, 2001), and severity of physical dependence (Heather, Stallard, & Tebbutt, 1991). Unlike distal risks, which are stable over time and present a constant level of risk, proximal risks are considered malleable and often act as a catalyst or immediate trigger of alcohol craving, alcohol seeking, or alcohol use (Brownell, Marlatt, Lichtenstein, & Wilson, 1986; Chung, Langenbucher, Labouvie, Pandina, & Moos, 2001; Marlatt & Gordon, 1985; Shiffman, 1989; Witkiewitz & Marlatt, 2004). One proximal risk factor, ineffective coping behavior, is particularly troubling because individuals who are unable to implement effective coping strategies are more likely to use alcohol as a means to cope with a variety of high-risk situations (e.g., negative affective states, social pressure to drink, the presence of alcohol cues; see Chung et al., 2001; Cooper, Frone, Russell, & Mudar, 1995; Litt, Kadden, Cooney, & Kabela, 2003; Timko, Finney, & Moos, 2005). The importance of coping behavior in preventing relapse has led to the implementation of coping skills training as a major component of nearly all empirically supported treatments for alcohol use disorders (Kadden & Cooney, 2005). Yet there is scant evidence that implementation of effective coping strategies following coping skills training is a mediating mechanism of improved outcomes (e.g., Litt et al., 2003; Morganstern & Longabaugh, 2000). Given these discrepant findings, it is critical to gain a better understanding of individual variation in the coping–drinking relationship following treatment.
Identifying Heterogeneity in the Lapse Process
Over the past decade social scientists have moved in the direction of using advanced longitudinal data analytic techniques (Collins & Sayer, 2001) to investigate the course of human behavior across time. Recently, methodology has been developed that allows researchers great flexibility in the parameterization of population heterogeneity beyond the conventional mixed-effects models. Unlike structural equation models, these new models combine both person-centered and variable-centered approaches (Bates, 2000; B. Muthén, 2000; Nagin & Tremblay, 2001). Longitudinal variable-centered approaches describe the relationships between variables in the prediction of outcomes modeled as a function of time and covariates. Longitudinal person-centered approaches describe the relationships between people by exploring the similarities and differences in response patterns over time across individuals. Latent growth mixture modeling (B. Muthén, 2001; B. Muthén & Shedden, 1999) provides a combined modeling focus by identifying discrete typologies of mean growth trajectories in the population (using a categorical latent variable with categories often referred to as latent classes or mixture components) as well as individual heterogeneity within each trajectory type (using continuous latent variables as random effects). Furthermore, measured covariates of both trajectory type and variability within type can be investigated (B. Muthén, 2001), although covariates are not needed to fit the model. Growth mixture modeling has been applied to several areas of clinical psychology, such as delinquency (Raskin-White, Bates, & Buyske, 2001), conduct disorder (Schaeffer, Petras, Ialongo, Poduska, & Kellam, 2003), and substance abuse (Colder, Campbell, Ruel, Richardson, & Flay, 2002; Hill, White, Chung, Hawkins, & Catalano, 2000; Jackson & Sher, 2006; Li, Duncan, & Hops, 2001; Orlando, Tucker, Ellickson, & Klein, 2004; Raskin-White, Johnson, & Buyske, 2000).
The current study aims to delineate patterns in posttreatment drinking behavior using a sample of individuals who reported on monthly alcohol consumption during the first 12 months following community alcohol treatment. The first goal of the present study was to use discrete-time survival analysis to assess the time to first lapse following alcohol treatment. The second goal was to use latent growth mixture modeling to investigate common patterns and individual differences in trajectories of drinking after the initial posttreatment drink. The third goal was to describe differences in time to lapse and postlapse drinking trajectories using relapse risk factors as predictors within a general latent variable framework (B. Muthén, 2001). In the current investigation we used growth mixture models to identify common trajectories (each with its own normally distributed growth process) and then investigated hypotheses that individual membership in trajectory subgroupings as well as the individual variability in level and shape of the trajectories would be associated with distal risk factors, time to first lapse, and coping behavior.
Method
The data for this study are from the Relapse Replication and Extension Project (RREP; Lowman, Allen, Stout, & the Relapse Research Group, 1996), which was sponsored by the NIAAA and conducted by researchers at three research sites: Brown University (Providence, RI), the Research Institute on Addictions (RIA; Buffalo, NY), and the University of New Mexico (UNM; Albuquerque, NM). All three sites met the shared design elements requested by the NIAAA, including identical assessment measures and the inclusion of research participants treated in standard treatment programs.
Participants
In order to be eligible for participation in the RREP, recruited individuals needed to meet the following criteria: be at least 18 years of age (21 at RIA), meet diagnostic interview survey criteria for alcohol abuse or dependence within the past 6 months without more severe concurrent drug diagnoses, not have used intravenous drugs within the past 6 months, not have major comorbid psychiatric diagnoses, and provide informed consent to participate.
The total sample size of the RREP was 563 participants. Brown recruited 300 participants from six facilities in the Providence area, RIA recruited 142 participants from eight programs in the Buffalo area, and UNM recruited 121 participants from one outpatient program in the Albuquerque area. Combined across all three sites, the participants were 41.2% female and 58.8% male, ranged in age from 18 to 64 years old (M = 34.33, SD = 8.72), and identified as Caucasian (67.3%), African American (16.0%), Hispanic (8.9%), American Indian (2.6%), or other race/ethnicity (5.2%).
Measures
Baseline assessments were conducted during the admission process, and the assessment intervals were based on a postadmission timeline. Drinking frequency was assessed bimonthly for 12 months following admission. Demographics and distal risk factors (e.g., family history of abuse) were assessed at baseline only, and proximal risk factors (e.g., coping skills) were assessed at baseline, 6 months, and 12 months following admission. Only the instruments described below were included in the primary analyses for the current study.
Pre- and posttreatment drinking behavior was assessed using the Form 90: A Structured Assessment Interview for Drinking and Related Behaviors (Miller, 1996), which gathers self-reported information on daily alcohol use between each assessment interval, beginning at 3 months preadmission and assessed bimonthly for 12 months following treatment. Frequency of drinking (percentage of drinking days; PDD) and quantity of drinking (drinks per drinking day; DDD) were both derived from the Form 90. The reliabilities of PDD and DDD in the total sample were adequate (PDD, α = .94; DDD, α = .90).
Individuals in the RREP received different lengths of treatment and reported their first lapse at various times during the 12-month follow-up assessment period. Starting the growth model at intake would present a treatment length bias, and starting the growth model at the end of treatment would present a time to first lapse bias. Thus, it was determined that calendar time did not provide an appropriate time scale for the growth models; rather, time was defined as the amount of time since the first lapse. Consequently, the first time of measure for the growth process of interest was the 1st month following the month of first lapse. The last time of measure for the growth process was defined as the 7th month following the month of the initial lapse. The selection of the 7th postlapse month was based on the frequency of lapsing in the first 5 months following treatment (61%) and thus the high frequency of individuals providing data throughout the 7 months following their initial lapse. Prior to running the growth models, we estimated the time to first lapse for all participants using a discrete-time survival model, as described below.
Demographic characteristics (age, gender, ethnicity, and years of education) and several distal risk factors (family history of alcoholism, age at first drink, and drinking history) were assessed by self-report, forced-choice, and binary items on the Comprehensive Drinker Profile (Miller & Marlatt, 1984). Alcohol dependence was assessed with the Alcohol Dependence Scale (ADS), a 25-item measure of alcohol dependence symptoms (Skinner & Horn, 1984). Coping was assessed with the Coping Behaviors Inventory (CBI; Litman, Stapleton, Oppenheim, & Peleg, 1983), a measure with four subscales (Positive Thinking, Negative Thinking, Avoidance or Distraction, and Seeking Social Support) representing the frequency with which individuals used each type of coping behavior in order to prevent drinking. The CBI was administered at baseline, 6 months, and 12 months and produced reliable scores at all three administrations (αs= .95, .94, and .95, respectively). All subscales of the CBI were averaged into a single coping composite measure for each time of administration, with higher scores indicating more frequent use of coping strategies. Each coping composite was then entered into an initial growth model with the baseline coping scores estimated as the random intercept. This coping intercept (coping at baseline) was used as a covariate in the discrete-time survival models. For the growth mixture models we estimated a second growth model of the coping scores by using time scores that estimated a random intercept at the month of first lapse. We then entered the change between the two intercepts (coping at 1st month of lapse subtracted from coping at baseline) as a covariate in the growth mixture models.
Data Analyses
Model estimation
The software program Mplus (Version 4.2; L. Muthén & Muthén, 2006) was used to estimate the discrete-time survival and growth mixture models. Mplus utilizes full information maximum likelihood (FIML) estimation under the assumption of data missing at random (MAR) with robust standard errors (called the MLR estimator in Mplus). Automatically generated starting values with random perturbations (100 random sets of starting values with 50 full optimizations) were used to increase confidence in the final maximum likelihood value, which was replicated in the optimized runs for all reported models (Hipp & Bauer, 2006; L. Muthén & Muthén, 2006).
For the discrete-time survival models, we were interested in estimating the hazard probabilities for first lapse corresponding to each 1-month time period beginning at treatment intake. The hazard probability for a given time period (t) is estimated by the proportion of individuals under observation who are known to have not experienced any drinking lapse prior to time period t that then experienced their first drinking lapse during time period t. We were further interested in testing the effects of covariates on the hazard probabilities. Initially, we estimated a conditional model where the log hazard odds (i.e., logit hazard probabilities) varied as a linear function of the covariates. This is sometimes referred to as the proportional hazard odds model. We also assessed evidence for time-varying effects of each covariate by relaxing the proportional hazard odds constraint and using a scaled likelihood ratio test to compare fit relative to the proportional hazard odds model. (For more on discrete-time survival analysis in a latent variable framework, see B. Muthén & Masyn, 2005.)
For the growth mixture models, we assessed the relative fit of models with varying numbers of classes using the two most accepted and widely cited methods (Bauer & Curran, 2003a; B. Muthén, 2003). First, we compared models with differing numbers of classes using the sample-size adjusted Bayesian information criterion (aBIC; Sclove, 1987), which is a criterion for assessing relative model fit on the basis of the log-likelihood of the estimated model given the observed data as well as the complexity of the model based on both the number of parameters and sample size. In a recent study the aBIC was shown to be the best likelihood-based indicator of model fit for latent variable mixture models (Henson, Reise, & Kim, 2007). Second, the bootstrapped likelihood ratio test (BLRT) and adjusted likelihood ratio test (LRT) were used to test the fit of k − 1 classes against k classes, with a significant p value indicating that the null hypothesis of k − 1 classes should be rejected in favor of at least k classes (Lo, Mendell, & Rubin, 2001; McLachlan & Peel, 2000; Nylund, Asparhouhov, & Muthén, 2007). In addition, we evaluated the classification precision as indicated by estimated posterior class probabilities, summarized by the entropy measure given by Ramaswamy, DeSarbo, Reibstein, and Robinson (1993). Entropy values closer to 1.0 indicate higher classification precision. Finally, models with varying numbers of classes were evaluated and compared according to substantive utility, distinctiveness, and interpretability of the resultant class sets.
Missing data
We included missing data in the discrete-time survival and growth mixture modeling specification using the FIML estimator with robust standard errors (MLR). Mplus (Version 4.2) allows for missing data that is MAR in endogenous variables. For the discrete-time survival models, hazard probabilities for the entire sample (N = 563) were included via MLR under the MAR assumptions, and the models with covariates included those individuals with complete data on all covariates (n = 439). For the growth mixture models, observed drinking at each time point was endogenous to the latent growth factors; therefore, the complete data of those who lapsed (n = 395) were included via MLR under the MAR assumptions. For the conditional growth mixture models, two methods were used to handle missing data in the covariates. First, the complete case data on covariates were included in the growth mixture models, with a total sample size of 331. Second, the multiple imputation methods developed by Schafer (1997) were incorporated into a growth mixture model in Mplus, in which covariate values were imputed where missing. We combined five imputed data sets into a single set of parameter estimates using the average of the squared standard errors across data sets and the variation in between-analysis parameter estimation (L. Muthén & Muthén, 2004; Schafer, 1997). The differences between the models estimated using complete case data and the parameters estimated with multiply imputed values were negligible, and the results from the complete case data are reported below.1 There were no significant differences on any of the study variables between those individuals with missing data and those with complete data.
Hypothesis testing
The first stage of the analyses for the current study involved estimating discrete-time survival models to determine the average hazard probabilities over time, to test the proportional hazard odds assumption for the covariate effects, and to test the significance of the covariate effects.
The second stage of the analyses consisted of estimating a series of unconditional two-part parallel-process growth mixture models for the two drinking outcomes, with one model for each class enumeration (i.e., estimating one- through five-class models). The two-part modeling strategy was used because the majority of individuals were not drinking at any given time point, even following the first lapse; thus two parts needed to be estimated: drinking versus not drinking and how much/often drinking occurs, when drinking. Essentially, a two-part model allows the researcher to simultaneously estimate a logistic growth model of binary indicators (i.e., drinking or not drinking) with a growth model for the continuous outcomes among those who reported drinking at the time of measurement. As described by Olsen and Schafer (2001),
it is natural to view a semi-continuous response as a result of two processes, one determining whether the response is zero and the other determining the actual level if it is non-zero. The two processes are distinct and may be influenced by covariates in different ways. (p. 730)
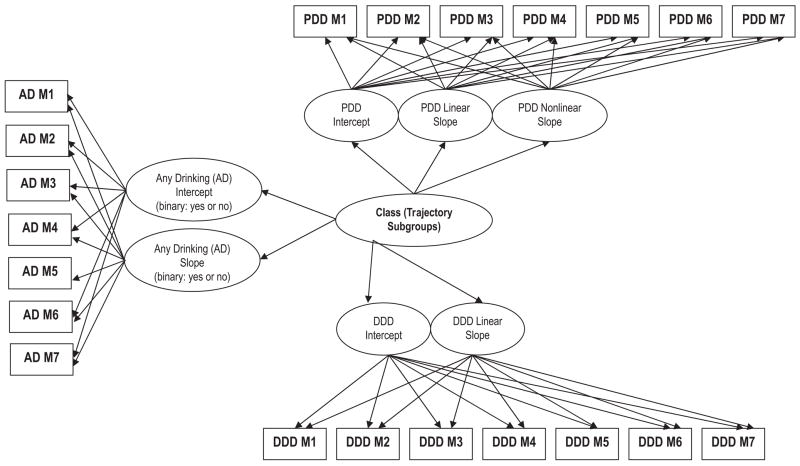
Figure 1 provides a reduced version of the unconditional two-part parallel-process model (in the estimated model all observed variables included residual variances, and latent variable variances and covariances were estimated as described in this section). The quantity and frequency outcomes were linked at zero (a zero value for PDD necessarily indicated a zero value for DDD); thus, only one logistic growth model was estimated for the binary indicators (any drinking vs. none). Two growth models for the continuous quantity and frequency indicators were estimated in parallel (growth models for PDD and DDD). For both DDD (quantity outcome) and the binary drinking indicator outcomes, the linear slope was sufficient to explain a significant amount of variation, but for PDD (frequency outcome) the quadratic slope was also significant and greatly improved the fit of the model to the observed data. For each class we evaluated the direction and significance of the means and variances of the random intercepts and slopes to gain a better understanding of the trajectory forms across classes. For the frequency outcomes, the variance on the quadratic factor as well as the covariances between the quadratic factor and the intercept and slope factors were fixed at zero. For the binary outcomes, variance of the slope was fixed at zero for model identification, which is often a necessary constraint in two-part models. The variances of the intercepts and linear slope factors as well as the covariance between the intercepts and linear slope factors were constrained to be class invariant for all three processes. For all analyses, we incorporated the treatment site into the analyses by adjusting the standard errors using a sandwich estimator for the within-site dependence of observations (L. Muthén & Muthén, 2006). Intraclass correlation coefficients for the site effect ranged from .007 to .026 for drinking quantity (DDD) and from .005 to .037 for drinking frequency (PDD).
Figure 1.
Unconditional two-part parallel-process growth mixture model. PDD = percentage of drinking days; M = model; DDD = drinks per drinking day.
The third stage of analyses was designed to test specific hypotheses about the relationship between distal risk, coping, and time to first lapse in the prediction of drinking trajectories and trajectory class membership. The goals of the covariate analyses were twofold: (a) to assess the degree to which baseline measures and distal risk predicted trajectory class membership and (b) to evaluate the associations of distal risk and baseline risk factors with drinking frequency and quantity within trajectory classes. We tested the overall significance of each covariate in predicting class membership using a scaled likelihood ratio test,2 comparing the log-likelihood difference in the (null) model, which had a zero path from the covariate to the latent class variable, with the (alternative) model, which had a freely estimated path from the covariate to the latent class variable. A multinomial logistic regression was used to estimate the associations between the covariate and latent class membership, so each covariate association was characterized by K − 1 regression coefficients, where K is the number of latent classes. Each coefficient represented the change in the log odds of being in a given class, k (k = 1,…, K − 1), relative to the reference class (K) for a one-unit change in the covariate. The significance of the separate regression coefficient was tested by calculating the estimated coefficient divided by its standard error and then comparing that ratio to the standard z-distribution. The sign and significance of the coefficients as well as the corresponding odds ratios and class probabilities were calculated for each covariate. In addition, we incorporated covariates as predictors of within-class variation in growth trajectories using standard linear regression. In these models, the relationship between covariates and the intercept and slope random effects were evaluated by the significance of the Wald statistic and the 95% confidence interval for each regression coefficient.
In comparison to previous longitudinal analyses of posttreatment drinking (see Godley, Dennis, Godley, & Funk, 2004; Miller, Westerberg, Harris, & Tonigan, 1996), the growth mixture modeling approach provided several advantages. Of primary focus to the current study, these models allowed for more flexible estimation of population heterogeneity in postlapse drinking trajectories through a finite mixture of random effects, with each mixture component (latent class) representing an empirically dominant pattern of drinking behavior among a subgroup of individuals. In addition, by estimating covariate effects on the latent growth factors, rather than the drinking indicators themselves, the attenuation caused by time-specific and measurement error in observed drinking outcomes is reduced.
Results
Discrete-Time Survival Model
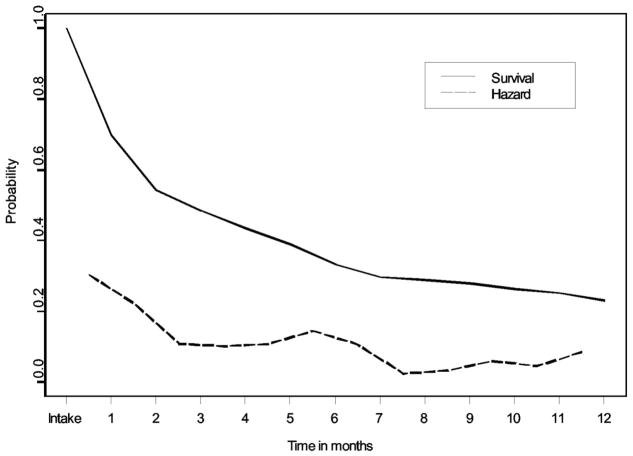
For these analyses, the outcome event was the month in which the first lapse occurred, which was defined as the 1st follow-up month where PDD and DDD were greater than zero. For the unconditional survival model, the marginal hazard probabilities were highest in the first 2 months of follow-up (0.21–0.28), then they were 0.08–0.13 for the 3rd through the 7th month, and they dropped to the range 0.03–0.06 for the remaining months. For the conditional survival model, none of the covariates individually showed significant time-varying effects, so the conditional model under the proportional hazard odds assumption was retained. Model results are given in Table 1. Only ADS total score and the estimated coping intercept score at baseline were significant predictors of time to first lapse. The confidence interval for the odds ratio of the ADS score included 1.00, indicating a potentially null effect of ADS on time to first lapse. Higher coping scores at intake corresponded to lower hazard probabilities of lapsing during the 1st year of follow-up (hazard odds ratio = 0.39). Figure 2 displays the estimated mean hazard and survival probabilities from the conditional model; as seen in the figure, there is a decreasing risk of lapsing over time. Time of first lapse was included as a covariate in the growth mixture models, as described next.
Table 1.
Hazard Odds Ratios (hOR) and 95% Confidence Intervals (CI) for Time to First Lapse
| Covariate | hOR | 95% CI |
|---|---|---|
| Gender | 1.15 | 0.89, 1.49 |
| Family history | 0.99 | 0.98, 1.01 |
| Years of drinking problem | 1.02 | 1.00, 1.03 |
| ADS total scores | 0.99* | 0.97, 0.99 |
| Coping at baseline | 0.39* | 0.21, 0.71 |
Note. Log-likelihood = −862.25; no. of free parameters = 17.
p < .05.
Figure 2.
Estimated mean hazard and survival probabilities for time to first lapse.
Latent Growth Mixture Models
All analyses were first conducted with demographic characteristics as predictors of class membership and random effects within class. Gender was significantly related to class membership and was included in all models as a covariate. No other demographic variables were related to drinking trajectories. We estimated one- to five-class two-part trajectory models using Mplus. As shown in Table 2, the three-class model appeared to strike the best balance between parsimony and fit, providing a significantly better fit than the two-class model based on the LRT/BLRT. The rate of decrease in the aBIC slows considerably when comparing differences from two to three classes (ΔaBIC = 126.56) versus three to four classes (ΔaBIC = 38.09). The three-class model had the highest entropy of all class enumerations. Also, the four-class model did not fit significantly better than the three-class model based on the LRT ( p= .26) or BLRT ( p= .67). The five-class model also did not provide a better fit than the four-class model based on the LRT/BLRT. Based on these empirical results, along with an assessment of each of these models with regard to substantive distinctness of the resultant classes, the results from the three-class models are presented below.3
Table 2.
Model Fit for Two-Part Parallel-Process Latent Growth Mixture Models
| Outcome | Log-likelihood (no. of free parameters) | Entropy | aBIC | LRT | Scaling Factor | BLRT p value | Scaled χ2 difference vs. Conditional Model 1 (df) |
|---|---|---|---|---|---|---|---|
| k-class model | |||||||
| 1-class | −6,942.38 (32) | 13,985.84 | |||||
| 2-class | −6,853.77 (40) | .66 | 13,833.90 | 173.78, p < .0005 | 177.21, p < .0005 | ||
| 3-class | −6,777.86 (48) | .80 | 13,707.34 | 154.88, p = .005 | 157.94, p < .0005 | ||
| 4-class | −6,746.18 (56) | .70 | 13,669.25 | 72.35, p = .26 | 73.78, p = .67 | ||
| 5-class | −6,698.79 (64) | .71 | 13,599.72 | 104.86, p = .08 | 106.93, p = .67 | ||
| Nested model comparisons | |||||||
| Conditional Model 1 | −5,402.18 (90) | .85 | 11,041.07 | 1.49 | |||
| Conditional Model 2 | −5,451.29 (60) | .85 | 11,060.39 | 1.78 | 107.93 (30), p < .0005 | ||
| Conditional Model 3 | −5,420.68 (78) | .83 | 11,046.51 | 1.52 | 28.57 (12), p = .005 | ||
| Conditional Model 4 | −5,478.89 (48) | .84 | 11,084.02 | 1.80 | 135.09 (42), p < .0005 | ||
Note. For the sample size adjusted Bayesian information criterion (aBIC), smaller values indicate a better fitting model. Conditional Model 1 includes both class membership and growth factors regressed on covariates; Conditional Model 2 includes only class membership regressed on covariates; Conditional Model 3 includes only growth factors regressed on covariates; for Conditional Model 4 the regression coefficients of the growth factors and the between class membership on the covariates were constrained to zero. Scaled χ2 difference testing for nested conditional models based on formulas given by Satorra and Bentler (1999), see http://www.statmodel.com/chidiff.shtml (last accessed June 17, 2007) for details. LRT = adjusted likelihood ratio test; BLRT = bootstrapped likelihood ratio test.
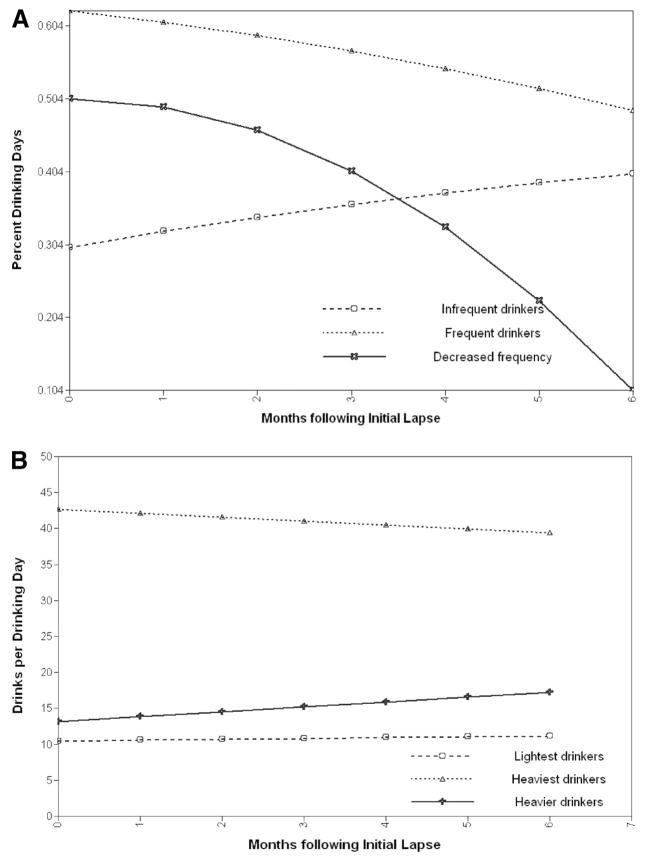
Shown in Figures 3A and 3B, the estimated trajectories for the three classes can be described as (a) a frequent heavy drinking trajectory (6%), (b) a “prolapsing” trajectory characterized by frequent drinking following the first lapse and a return to less frequent drinking (12%), and (c) an infrequent moderate drinking trajectory (82%).4
Figure 3.
A: Trajectory subgroups for three-class growth mixture model—percentage of drinking days. B: Trajectory subgroups for three-class growth mixture model—drinks per drinking day.
It is important to note that the two-part model identifies any nondrinking as a missing observation, and therefore the continuous drinking trajectories are based on an individual’s potential drinking outcomes, observed for those that are drinking during those time periods and unobserved for those not drinking. The data proportions for the binary (drinking vs. not drinking) part of the two-part model indicate that roughly a quarter of those people who had an initial lapse are abstinent at any given time point (ranging from 18% abstinent in the 1st postlapse month to 26% in Months 5 and 6). These rates of abstinence are in addition to the 30% of individuals who continuously abstained during the 12 months following treatment.
Risk Factors and Lapse Trajectories: Conditional Growth Mixture Models
Four conditional three-class growth mixture models incorporating the covariates (month of first lapse, gender, family history, ADS total scores, years of drinking problem, and coping) were estimated with a variety of between-class and within-class variable constraints. In Conditional Models 1 and 2, we used a multinomial logistic regression model within the Mplus program to regress class membership on month of first lapse, gender, family history, years of drinking problem, ADS total scores, and coping. This model expressed the probability that individual i is a member of class k as a function of the covariate x. Setting one of the classes as a reference class allows for estimation of the log odds of class membership for each covariate. Conditional Model 1 also included regressions of the growth parameters on the covariates, with the regression coefficients constrained to be invariant across classes. This model served as the full conditional model, which was compared to several alternative models (described below) in which parameters were systematically constrained to zero.
Overall fit and model comparisons for Conditional Models 1–4 are shown in Table 2, and the individual parameter estimates for the covariate effects are shown in Table 3. Conditional Model 1 provided the best fit to the data in comparison to the other conditional models on the basis of the aBIC and the scaled χ2 difference tests. In Conditional Model 2 the regression paths of the growth factors on the covariates were constrained to zero, providing a test of within-class differences on covariates. Conditional Model 2 fit significantly worse than Conditional Model 1, scaled χ2 diff (Δ df = 30) = 107.93, p < .0005, indicating the importance of including the growth factor regressions in the model. Conditional Model 3 constrained the between-class regressions to zero, which provided a test of the growth factors regressed on covariates without covariates predicting class membership. Model 3 also fit significantly worse than Model 1, scaled χ2 diff (Δ df = 12) = 28.57, p = .005. For Model 4 the regression coefficients of the growth factors and the between class membership on the covariates were constrained to zero. Model 4 fit significantly worse than Model 1, scaled χ2diff (Δ df = 42) = 135.09, p < .0005.
Table 3.
Parameter Estimates for Growth Factors Regressed on Covariates
| Continuous process
|
Categorical process
|
||||
|---|---|---|---|---|---|
| Covariate | PDD intercept B (SE) | PDD slope B (SE) | DDD intercept B (SE) | DDD slope B (SE) | Intercept B (SE) |
| Gender | −0.04 (0.04) | −0.01 (0.01) | −2.94 (1.13)* | −0.08 (0.26) | −0.28 (0.36) |
| Family history | 0.002 (0.003) | −0.001 (0.001) | 0.004 (0.05) | −0.02 (0.01) | −0.01 (0.02) |
| Years of drinking | 0.00 (0.002) | 0.00 (0.001) | −0.002 (0.07) | 0.00 (0.02) | 0.01 (0.02) |
| ADS total scores | 0.003 (0.003) | 0.001 (0.001) | 0.22 (0.08)* | 0.03 (0.02)* | 0.03 (0.02) |
| Month of lapse | 0.02 (0.01)* | −0.002 (0.003) | −0.01 (0.22) | 0.07 (0.08) | 0.11 (0.08) |
| Coping | −0.09 (0.02)* | −0.004 (0.01) | 0.41 (0.58) | −0.28 (0.16)* | −0.87 (0.22)* |
Note. PDD = percentage of drinking days; DDD = drinks per drinking day.
p < .05.
Given all comparisons, Conditional Model 1 was chosen as the best representation of the observed data. As shown in Table 3, the results from Model 1 indicated several significant relationships between the covariates and the within-class growth factors. ADS score was significantly related to the within-class intercept and slope of the quantity (DDD) growth processes, indicating that higher alcohol dependence is related to heavier drinking in the 1st month following lapse and a greater increase in drinking quantity over time. Time to first lapse was significantly related to the intercept of the frequency process, suggesting that individuals who lapse earlier are drinking more frequently in the 1st postlapse month. Gender was significantly related to the intercept of the quantity process, such that males reported drinking greater amounts in the month following lapse. The change in coping over time was significantly related to the intercept of drinking frequency and the slope of drinking quantity in the negative direction, suggesting that a decrease in coping scores from baseline to the month following the first lapse was associated with more frequent drinking and a greater increase in drinking quantity over time following the first lapse. Likewise, coping was negatively related to the intercept of the categorical process, indicating a decrease in coping is related to increased likelihood of drinking. All other covariate predictions were nonsignificant.
Results from the multinomial logistic regression of class membership regressed on the covariates indicated some differences between classes based on covariates. The odds ratios for the covariates effects on class membership from Conditional Model 1 (which controlled for covariate effects on the growth factors) are provided in Table 4. Earlier lapse was associated with membership in the prolapsing class of individuals, who were drinking frequently initially and then decreased their drinking frequency over time. Individuals with higher alcohol dependence were most likely to be classified in the frequent heavy drinking class.
Table 4.
Odds Ratios (95% Confidence Intervals) for Comparisons Between Three Trajectory Subgroups
| Covariate | Infrequent moderate drinking vs. prolapse drinking reference group | Frequent heavy drinking vs. prolapse drinking reference group | Infrequent moderate drinking vs. frequent heavy drinking reference group |
|---|---|---|---|
| Gender | 1.34 (0.60, 2.99) | 0.55 (0.10, 3.06) | 2.47 (0.52, 11.58) |
| Family history | 0.98 (0.93, 1.03) | 0.99 (0.92, 1.06) | 0.99 (0.94, 1.04) |
| Years of drinking problem | 1.00 (0.95, 1.06) | 0.99 (0.91, 1.08) | 1.01 (0.94, 1.08) |
| ADS total scores | 1.02 (0.97, 1.07) | 1.12 (1.02, 1.23)* | 0.91 (0.84, 0.98)* |
| Month of first lapse | 1.67 (1.24, 2.25)* | 1.61 (1.10, 2.37)* | 1.03 (0.80, 1.34) |
| Coping | 0.82 (0.47, 1.41) | 1.03 (0.46, 2.31) | 0.79 (0.39, 1.58) |
p < .05.
Discussion
The current study evaluated the time to lapse and individual trajectories of drinking frequency and quantity following an initial posttreatment drinking episode. We observed three common patterns of postlapse drinking, which could be characterized as infrequent moderate drinking, prolapse drinkers (heavier drinking with decreased frequency over time), and frequent heavy drinking. The estimated postlapse drinking trajectory class prevalence suggested that the majority of individuals were best classified as infrequent moderate drinkers or abstainers following treatment. Only a small percentage (6%) of individuals displayed a frequent heavy drinking trajectory. Another small subset of individuals returned to less frequent drinking after an initial period of sustained frequent drinking (12%). Thus, the majority of individuals reported a return to abstinence or infrequent drinking following the initial lapse, and only a small percentage of individuals could be reliably classified as continuously frequent heavy drinkers following treatment.
The effects of distal risk, gender, and coping scores were incorporated into the model and provided added insights into the time to lapse and postlapse drinking process. Distal coping, as measured by the intercept of coping scores following treatment, was not related to the drinking growth processes within class, but did predict time to first lapse. Proximal coping, assessed by the change in coping following treatment, was significantly related to within-class drinking frequency at the time of the first lapse and the change in quantity of drinking following the first lapse in the negative direction. That is, better coping skills over time were related to less frequent drinking at the time of first lapse and lighter drinking over time following the first lapse.
Alcohol dependence scores were predictive of time to first lapse, drinking quantity at the time of initial lapse, and increase in drinking quantity over time, as well as class membership. Individuals with higher alcohol dependence scores experienced earlier lapses, had the worst drinking outcomes within class, and were most likely classified as the heaviest, most frequent drinkers. Because the hazard probability of first lapse was influenced by baseline coping skills and alcohol dependence scores, there is evidence of additional indirect effects of ADS total scores and coping skills on postlapse drinking outcomes mediated by the timing of first lapse.
Time to first lapse was related to class membership: Individuals who lapsed earlier had a higher probability of being classified as individuals who initially drank heavily and frequently and then reported decreased drinking frequency over time. Years of drinking problem duration and family history were not significantly related to the within-class drinking outcomes and did not predict class membership. An optimistic interpretation of this finding is that individuals who have a family history or who have been suffering from a drinking problem for many years are not doomed to have the worst outcomes following treatment, although the extent to which these distal risk factors are also related to alcohol dependence is important to consider.
Implications and Limitations
The results from these analyses support a conceptualization of the relapse process as highly variable between and within individuals. Further, these results contradict the conceptualization of alcoholism as a relapsing condition (Litman, 1986). In all models the largest class could be described as an infrequent drinking class, and only a very small proportion of the sample represented a stable frequent drinking trajectory. The results from the covariate analyses of the estimated drinking classifications are consistent with clinical intuition and previous empirical findings.
Both baseline coping and the change in coping following treatment were related to posttreatment drinking outcomes. Baseline coping predicted the time to first lapse, and the change in coping from baseline to the month of first lapse predicted drinking frequency in the 1st postlapse month and the change in drinking quantity over time. These findings highlight the importance of teaching effective coping skills during treatment, as well as the need to provide follow-up/aftercare sessions that emphasize the importance of coping skill acquisition and utilization. As described by McLellan (2002), “many of those who develop addiction disorders suffer multiple relapses following treatments and are thought to retain a continuing vulnerability to relapse for years or perhaps a lifetime” (p. 249). McLellan suggested that alcohol dependence and addiction, in general, may be more accurately treated using a chronic illness model, in which continuing care is necessary to maintain long-term successful outcomes. The findings from the current study support the observations of McLellan and others (Maisto, Sobell, & Sobell, 1980) who have emphasized the importance of posttreatment aftercare.
On the basis of the current study and previous research, we suggest coping skills training be a major focus of aftercare interventions. McKay, Maisto, and O’Farrell (1996) identified coping strategies as being critical in the promotion of abstinence and termination of lapses in a sample of alcohol-dependent males followed for 30 months. Coping has also been shown to be a predictor of stable remission from an alcohol use disorder over a 16-year period (Moos & Moos, 2005, 2006).
One limitation of the current study is the reliance on the information provided by the RREP data. The self-report instruments used in the RREP to assess the domains of relapse risk factors and drinking outcomes may not provide the most accurate depiction of the complex forces interacting within a relapsing system. For example, the Form 90 uses retrospective information for measuring drinking behavior, and studies have shown that an individual’s reconstruction of behavior may contain biases (Bradburn, Rips, & Shevell, 1987). It is possible that some variability in drinking trajectories could be explained by self-report bias.
The results from the growth mixture analyses presented in this study need to be interpreted with a certain amount of caution (Bauer & Curran, 2003a, 2004). In general, we regard our modeling approach as exploratory, and all of the estimated models need to be replicated in a new data set, preferably by different investigators. One of the main limitations of mixture modeling, as well as other statistical techniques, is the inability of researchers to ever know the true underlying distribution in the population (Cudeck & Henly, 2003). Rather, growth mixture models can be used to approximate the true structure of the data, but the resulting model will always be making an approximation. We view the analyses conducted in the current study as one approach of many that may prove useful in studying drinking patterns over time, and as stated by Bauer and Curran (2003b), “All of our models are wrong, and it is quite possible that there is no ‘right’ model to discern whatsoever. The real task at hand is to decide which model is most useful” (p. 388). The goal of the current analyses was to summarize and evaluate models of posttreatment drinking behavior. The growth mixture models presented in this study provide an interesting and potentially useful representation of the population heterogeneity in the relapse process. The usefulness of these results does not hinge on whether the trajectory subgroups we reported reflect true or actual subpopulations of postlapse drinkers. Furthermore, these results are consistent with theories of relapse (Donovan, 1996) and provide directions for future research.
Future Directions
This study focused specifically on drinking frequency and quantity; however, models of drinking-related problems could also be estimated with growth mixture models. An important extension of the current study is to examine other substances and nonsubstance relapse using growth mixture modeling. There are many methodological possibilities for future research using the analytic techniques presented in this study. For example, these techniques could be applied to momentary data, where a single individual is measured over several time points on multiple days. Modeling relapse using a general latent variable modeling framework allows for researchers to test several additional hypotheses using a variety of different model specifications. For example, piecewise growth mixture modeling could be used to measure discontinuity in growth trajectories (see Colder et al., 2002), which would allow for a test of drinking trajectories that is consistent with the hypotheses of discontinuous models of alcohol relapse (Hufford, Witkiewitz, Shields, Kodya, & Caruso, 2003).
In summary, growth mixture modeling techniques can help identify multiple trajectory profiles of posttreatment drinking based on relapse risk factors. On the basis of these results, coping skills training should continue to be a major focus of relapse prevention and aftercare interventions. Individuals with higher alcohol dependence scores should either be provided more intensive treatment and/or more aftercare options or advised of the potential for a poor prognosis given their alcohol dependence. With a basic consideration of the dynamic relationship between risk factors and relapse vulnerability, researchers and clinicians may design experimental studies and treatments accordingly.
Acknowledgments
This research was supported by National Institute of Alcohol Abuse and Alcoholism Grant RO3 AA016322 01.
Footnotes
Results from the multiple imputation are available from Katie Witkiewitz.
A scaled likelihood ratio test is necessary when testing the difference in log-likelihoods from nested models estimated using robust maximum likelihood procedures (L. Muthén & Muthén, 2006).
Results from the 1-, 2-, 3-, and 5-class models are available from Katie Witkiewitz.
The moderate drinking trajectory was defined as a midpoint between the infrequent and frequent drinking trajectories and does not necessarily reflect the definition of moderate drinking provided by the NIAAA (see Dufour, 1999) or the Department of Health and Human Services (U.S. Department of Health and Human Services & U.S. Department of Agriculture, 1995).
Contributor Information
Katie Witkiewitz, University of Illinois at Chicago.
Katherine E. Masyn, University of California, Davis
References
- Bates ME. Integrating person-centered and variable-centered approaches in the study of developmental courses and transitions in alcohol use: Introduction to the special section. Alcoholism: Clinical and Experimental Research. 2000;24:878–881. [PubMed] [Google Scholar]
- Bauer DJ, Curran PJ. Distributional assumptions of growth mixture models: Implications for over-extraction of latent trajectory classes. Psychological Methods. 2003a;8:338–363. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Curran PJ. Over-extracting latent trajectory classes: Much ado about nothing? Reply to Rindskopf (2003), Muthén (2003), and Cudeck and Henly (2003) Psychological Methods. 2003b;8:384–393. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
- Bauer DJ, Curran PJ. The integration of continuous and discrete latent variable models: Potential problems and promising opportunities. Psychological Methods. 2004;9:3–29. doi: 10.1037/1082-989X.9.1.3. [DOI] [PubMed] [Google Scholar]
- Bradburn NM, Rips LJ, Shevell SK. Answering autobiographical questions: The impact of memory and inference on surveys. Science. 1987 April;236:157–161. doi: 10.1126/science.3563494. [DOI] [PubMed] [Google Scholar]
- Brownell KD, Marlatt GA, Lichtenstein E, Wilson GT. Understanding and preventing relapse. American Psychologist. 1986;41:765–782. doi: 10.1037//0003-066x.41.7.765. [DOI] [PubMed] [Google Scholar]
- Chung T, Langenbucher J, Labouvie E, Pandina RJ, Moos RH. Changes in alcoholic patients’ coping responses predict 12-month treatment outcomes. Journal of Consulting and Clinical Psychology. 2001;69:92–100. doi: 10.1037//0022-006x.69.1.92. [DOI] [PubMed] [Google Scholar]
- Colder CR, Campbell RT, Ruel E, Richardson JL, Flay BR. A finite mixture model of growth trajectories of adolescent alcohol use: Predictors and consequences. Journal of Consulting and Clinical Psychology. 2002;70:976–985. doi: 10.1037//0022-006x.70.4.976. [DOI] [PubMed] [Google Scholar]
- Collins LM, Sayer A. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. [Google Scholar]
- Cooper ML, Frone MR, Russell M, Mudar P. Drinking to regulate positive and negative emotions: A motivational model of alcohol use. Journal of Personality and Social Psychology. 1995;69:990–1005. doi: 10.1037//0022-3514.69.5.990. [DOI] [PubMed] [Google Scholar]
- Craig TJ, Krishna G, Poniarski R. Predictors of successful vs. unsuccessful outcome of a 12-step inpatient alcohol rehabilitation program. American Journal of Addictions. 1997;6:232–236. [PubMed] [Google Scholar]
- Cudeck R, Henly SJ. A realistic perspective on pattern representation in growth data: Comment on Bauer and Curran (2003) Psychological Methods. 2003;8:378–383. doi: 10.1037/1082-989X.8.3.378. [DOI] [PubMed] [Google Scholar]
- Delucchi KL, Matzger H, Weisner C. Dependent and problem drinking over 5 years: A latent class growth analysis. Drug and Alcohol Dependence. 2004;74:235–244. doi: 10.1016/j.drugalcdep.2003.12.014. [DOI] [PubMed] [Google Scholar]
- Donovan DM. Marlatt’s classification of relapse precipitants: Is the Emperor still wearing clothes? Addiction. 1996;91(Suppl):131–137. [PubMed] [Google Scholar]
- Dufour MC. What is moderate drinking? Alcohol Research and Health. 1999;23:5–14. [PMC free article] [PubMed] [Google Scholar]
- Godley SH, Dennis ML, Godley M, Funk R. Thirty-month relapse trajectory cluster groups among adolescents discharged from out-patient treatment. Addiction. 2004;99:129–139. doi: 10.1111/j.1360-0443.2004.00860.x. [DOI] [PubMed] [Google Scholar]
- Grant BF, Dawson DA, Stinson FS, Chou SP, Dufour MC, Pickering RP. The 12-month prevalence and trends in DSM-IV alcohol abuse and dependence: United States, 1991–1992 and 2001–2002. Drug and Alcohol Dependence. 2004;74:223–234. doi: 10.1016/j.drugalcdep.2004.02.004. [DOI] [PubMed] [Google Scholar]
- Heather N, Stallard A, Tebbutt J. Importance of substance cues in relapse among heroin users: Comparison of two methods of investigation. Addictive Behaviors. 1991;16:41–49. doi: 10.1016/0306-4603(91)90038-j. [DOI] [PubMed] [Google Scholar]
- Henson JM, Reise SP, Kim KH. Detecting mixtures from structural model differences using latent variable mixture modeling: A comparison of relative model fit statistics. Structural Equation Modeling. 2007;14:202–226. [Google Scholar]
- Hill KG, White HR, Chung IJ, Hawkins JD, Catalano RF. Early adult outcomes of adolescent binge drinking: Person and variable-centered analyses of binge drinking trajectories. Alcoholism: Clinical and Experimental Research. 2000;24:892–901. [PMC free article] [PubMed] [Google Scholar]
- Hipp JR, Bauer DJ. Local solutions in the estimation of growth mixture models. Psychological Methods. 2006;11:36–53. doi: 10.1037/1082-989X.11.1.36. [DOI] [PubMed] [Google Scholar]
- Hufford MH, Witkiewitz K, Shields AL, Kodya S, Caruso JC. Relapse as a nonlinear dynamic system: Application to patients with alcohol use disorders. Journal of Abnormal Psychology. 2003;112:219–227. doi: 10.1037/0021-843x.112.2.219. [DOI] [PubMed] [Google Scholar]
- Hunt WA, Barnett LW, Branch LG. Relapse rates in addiction programs. Journal of Clinical Psychology. 1971;27:455–456. doi: 10.1002/1097-4679(197110)27:4<455::aid-jclp2270270412>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Jackson KM, Sher KJ. Comparison of longitudinal phenotypes based on number and timing of assessments: A systematic comparison of trajectory approaches II. Psychology of Addictive Behaviors. 2006;20:373–384. doi: 10.1037/0893-164X.20.4.373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadden RM, Cooney NL. Treating alcohol problems. In: Marlatt GA, Donovan DM, editors. Relapse prevention: Maintenance strategies in the treatment of addictive behaviors. 2. New York: Guilford Press; 2005. pp. 65–91. [Google Scholar]
- Li F, Duncan T, Hops H. Examining developmental trajectories in adolescent alcohol use using piecewise growth mixture modeling analysis. Journal of Studies on Alcohol. 2001;62:199–201. doi: 10.15288/jsa.2001.62.199. [DOI] [PubMed] [Google Scholar]
- Litman GK. Alcoholism survival: The prevention of relapse. In: Miller WR, Heather N, editors. Treating addictive behaviors: Processes of change. New York: Plenum Press; 1986. pp. 391–405. [Google Scholar]
- Litman GK, Stapleton J, Oppenheim AN, Peleg M. An instrument for measuring coping behaviors in hospitalized alcoholics: Implications for relapse prevention and treatment. British Journal of Addiction. 1983;78:269–276. doi: 10.1111/j.1360-0443.1983.tb02511.x. [DOI] [PubMed] [Google Scholar]
- Litt MD, Kadden RM, Cooney NL, Kabela E. Coping skills and treatment outcomes in cognitive–behavioral and interactional group therapy for alcoholism. Journal of Consulting and Clinical Psychology. 2003;71:118–128. doi: 10.1037//0022-006x.71.1.118. [DOI] [PubMed] [Google Scholar]
- Lo Y, Mendell NR, Rubin DB. Testing the number of components in a normal mixture. Biometrika. 2001;88:767–778. [Google Scholar]
- Lowman C, Allen J, Stout RL the Relapse Research Group. Replication and extension of Marlatt’s taxonomy of relapse precipitants: Overview of procedures and results. Addiction. 1996;91(Suppl):51–71. [PubMed] [Google Scholar]
- Maisto SA, Pollock NK, Cornelius JR, Lynch KG, Martin CS. Alcohol relapse as a function of relapse definition in a clinical sample of adolescents. Addictive Behaviors. 2003;28:449–459. doi: 10.1016/s0306-4603(01)00267-2. [DOI] [PubMed] [Google Scholar]
- Maisto SA, Sobell MB, Sobell LC. Predictors of treatment outcome for alcoholics treated by individualized behavior therapy. Addictive Behaviors. 1980;5:259–264. doi: 10.1016/0306-4603(80)90048-9. [DOI] [PubMed] [Google Scholar]
- Marlatt GA, Gordon JR. Relapse prevention: Maintenance strategies in the treatment of addictive behaviors. New York: Guilford Press; 1985. [Google Scholar]
- McGue M, Iacono WG, Legrand LN, Malone S, Elkins I. Origins and consequences of age at first drink: I. Associations with substance use disorders, disinhibitory behavior and psychopathology, and P3 amplitude. Alcoholism: Clinical and Experimental Research. 2001;25:1156–1165. [PubMed] [Google Scholar]
- McKay JR, Maisto SA, O’Farrell TJ. Alcoholics’ perceptions of factors in the onset and termination of relapses and the maintenance of abstinence: Results from a 30-month follow-up. Psychology of Addictive Behaviors. 1996;10:167–180. [Google Scholar]
- McLachlan G, Peel D. Finite mixture models. New York: Wiley; 2000. [Google Scholar]
- McLellan TA. Have we evaluated addiction treatment correctly? Implications from a chronic care perspective. Addiction. 2002;97:249–252. doi: 10.1046/j.1360-0443.2002.00127.x. [DOI] [PubMed] [Google Scholar]
- Miller WR. Form 90: A Structured Assessment Interview for Drinking and Related Behaviors: Test manual, Project MATCH monograph series. Vol. 5. Bethesda, MD: National Institute of Alcohol Abuse and Alcoholism; 1996. [Google Scholar]
- Miller WR, Marlatt GA. Manual for the Comprehensive Drinker Profile. Odessa, FL: Psychological Assessment Resources; 1984. [Google Scholar]
- Miller WR, Westerberg VS, Harris RJ, Tonigan JS. What predicts relapse? Prospective testing of antecedent models. Addiction. 1996;91(Suppl):155–172. [PubMed] [Google Scholar]
- Moos RH, Moos BS. Sixteen-year changes and stable remission among treated and untreated individuals with alcohol use disorders. Drug and Alcohol Dependence. 2005;12:337–347. doi: 10.1016/j.drugalcdep.2005.05.001. [DOI] [PubMed] [Google Scholar]
- Moos RH, Moos BS. Rates and predictors of relapse after natural and treated remission from alcohol use disorders. Addiction. 2006;101:212–222. doi: 10.1111/j.1360-0443.2006.01310.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morganstern J, Longabaugh R. Cognitive–behavioral treatment for alcohol dependence: A review of evidence for its hypothesized mechanisms of action. Addiction. 2000;95:1475–1490. doi: 10.1046/j.1360-0443.2000.951014753.x. [DOI] [PubMed] [Google Scholar]
- Muthén B. Methodological issues in random coefficient growth modeling using a latent variable framework: Applications to the development of heavy drinking. In: Rose J, Chassin L, Presson C, Sherman J, editors. Multivariate applications in substance use research. Hillsdale, NJ: Erlbaum; 2000. pp. 113–140. [Google Scholar]
- Muthén B. Second-generation structural equation modeling with a combination of categorical and continuous latent variables: New opportunities for latent class-latent growth modeling. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 289–322. [Google Scholar]
- Muthén B. Statistical and substantive checking in growth mixture modeling. Psychological Methods. 2003;8:369–377. doi: 10.1037/1082-989X.8.3.369. [DOI] [PubMed] [Google Scholar]
- Muthén B, Masyn K. Discrete-time survival mixture analysis. Journal of Educational and Behavioral Statistics. 2005;30:27–58. [Google Scholar]
- Muthén B, Shedden K. Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics. 1999;55:463–469. doi: 10.1111/j.0006-341x.1999.00463.x. [DOI] [PubMed] [Google Scholar]
- Muthén L, Muthén B. Mplus user’s guide. 3. Los Angeles: Author; 2004. [Google Scholar]
- Muthén L, Muthén B. Mplus user’s guide. 4. Los Angeles: Author; 2006. [Google Scholar]
- Nagin DS, Tremblay RE. Analyzing developmental trajectories of distinct but related behaviors: A group-based method. Psychological Methods. 2001;6:18–34. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- National Institute of Alcohol Abuse and Alcoholism. Drinking in the United States: Main findings from the 1992 National Longitudinal Alcohol Epidemiologic Survey. Bethesda, MD: U.S. Department of Health and Human Services; 1998. [Google Scholar]
- Nylund K, Asparhouhov T, Muthén BO. Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural Equation Modeling. 2007;14:535–569. [Google Scholar]
- Olsen MK, Schafer JL. A two-part random effects model for semi-continuous longitudinal data. Journal of the American Statistical Association. 2001;96:730–745. [Google Scholar]
- Orlando M, Tucker JS, Ellickson PL, Klein DJ. Developmental trajectories of cigarette smoking and their correlates from early adolescence to young adulthood. Journal of Consulting and Clinical Psychology. 2004;72:400–410. doi: 10.1037/0022-006X.72.3.400. [DOI] [PubMed] [Google Scholar]
- Ramaswamy V, DeSarbo W, Reibstein D, Robinson W. Empirical pooling approach to marketing mix elasticities with PIMS data. Marketing Science. 1993;12:103–124. [Google Scholar]
- Raskin-White H, Bates ME, Buyske S. Adolescence-limited versus persistent delinquency: Extending Moffitt’s hypothesis into adulthood. Journal of Abnormal Psychology. 2001;110:600–609. doi: 10.1037//0021-843x.110.4.600. [DOI] [PubMed] [Google Scholar]
- Raskin-White H, Johnson V, Buyske S. Parental modeling and parenting behavior effects on offspring alcohol and cigarette use: A growth curve analysis. Journal of Substance Abuse. 2000;12:287–310. doi: 10.1016/s0899-3289(00)00056-0. [DOI] [PubMed] [Google Scholar]
- Satorra A, Bentler PM. A scaled difference chi-square test statistic for moment structure analysis. 1999. Unpublished manuscript. [Google Scholar]
- Schaeffer CM, Petras H, Ialongo N, Poduska J, Kellam S. Modeling growth in boys’ aggressive behavior across elementary school: Links to later criminal involvement, conduct disorder, and antisocial personality disorder. Developmental Psychology. 2003;39:1020–1035. doi: 10.1037/0012-1649.39.6.1020. [DOI] [PubMed] [Google Scholar]
- Schafer J. Analysis of incomplete multivariate data. London: Chapman & Hall; 1997. [Google Scholar]
- Sclove LS. Application of model-selection criteria to some problems in multivariate analysis. Psychometrics. 1987;52:333–343. [Google Scholar]
- Shiffman S. Conceptual issues in the study of relapse. In: Gossop M, editor. Relapse and addictive behavior. New York: Tavistock; 1989. pp. 149–179. [Google Scholar]
- Skinner HA, Horn JL. Alcohol Dependence Scale user’s guide. Toronto, Ontario, Canada: Addiction Research Foundation; 1984. [Google Scholar]
- Stout RL. What is a drinking episode? Journal of Studies on Alcohol. 2000;61:455–461. doi: 10.15288/jsa.2000.61.455. [DOI] [PubMed] [Google Scholar]
- Sutton SR. Interpreting relapse curves. Journal of Consulting and Clinical Psychology. 1979;47:96–98. doi: 10.1037//0022-006x.47.1.96. [DOI] [PubMed] [Google Scholar]
- Timko C, Finney JW, Moos RH. The 8-year course of alcohol abuse: Gender differences in social context and coping. Alcoholism: Clinical and Experimental Research. 2005;29:612–621. doi: 10.1097/01.alc.0000158832.07705.22. [DOI] [PubMed] [Google Scholar]
- U.S. Department of Health and Human Services & U.S. Department of Agriculture. Home and Garden Bulletin No. 232. 4. Washington, DC: U.S. Department of Agriculture; 1995. Nutrition and your health: Dietary guidelines for Americans. [Google Scholar]
- Warren K, Hawkins RC, II, Sprott JC. Substance abuse as a dynamical disease: Evidence and clinical implications of nonlinearity in a time series of daily alcohol consumption. Addictive Behaviors. 2003;28:369–374. doi: 10.1016/s0306-4603(01)00234-9. [DOI] [PubMed] [Google Scholar]
- Witkiewitz K, Marlatt GA. Relapse prevention for alcohol and drug problems: That was Zen, this is Tao. American Psychologist. 2004;59:224–235. doi: 10.1037/0003-066X.59.4.224. [DOI] [PubMed] [Google Scholar]