A neural network model to predict lung radiation-induced pneumonitis

Abstract

A feed-forward neural network was investigated to predict the occurrence of lung radiation-induced Grade 2+ pneumonitis. The database consisted of 235 patients with lung cancer treated using radiotherapy, of whom 34 were diagnosed with Grade 2+ pneumonitis at follow-up. The network was constructed using an algorithm that alternately grew and pruned it, starting from the smallest possible network, until a satisfactory solution was found. The weights and biases of the network were computed using the error back-propagation approach. Momentum and variable leaning techniques were used to speed convergence. Using the growing/pruning approach, the network selected features from 66 dose and 27 non-dose variables. During network training, the 235 patients were randomly split into ten groups of approximately equal size. Eight groups were used to train the network, one group was used for early stopping training to prevent overfitting, and the remaining group was used as a test to measure the generalization capability of the network (cross-validation). Using this methodology, each of the ten groups was considered, in turn, as the test group (ten-fold cross-validation). For the optimized network constructed with input features selected from dose and non-dose variables, the area under the receiver operating characteristics (ROC) curve for cross-validated testing was 0.76 (sensitivity: 0.68, specificity: 0.69). For the optimized network constructed with input features selected only from dose variables, the area under the ROC curve for cross-validation was 0.67 (sensitivity: 0.53, specificity: 0.69). The difference between these two areas was statistically significant (p=0.020), indicating that the addition of non-dose features can significantly improve the generalization capability of the network. A network for prospective testing was constructed with input features selected from dose and non-dose variables (all data were used for training). The optimized network architecture consisted of six input nodes (features), four hidden nodes, and one output node. The six input features were: lung volume receiving >16 Gy (V₁₆), generalized equivalent uniform dose (gEUD) for the exponent a=1 (mean lung dose), gEUD for the exponent a=3.5, free expiratory volume in 1 s (FEV₁), diffusion capacity of carbon monoxide (DLCO%), and whether or not the patient underwent chemotherapy prior to radiotherapy. The significance of each input feature was individually evaluated by omitting it during network training and gauging its impact by the consequent deterioration in cross-validated ROC area. With the exception of FEV1 and whether or not the patient underwent chemotherapy prior to radiotherapy, all input features were found to be individually significant (p<0.05). The network for prospective testing is publicly available via internet access.

I. INTRODUCTION

Radiation-induced pneumonitis is a major dose-limiting toxicity in thoracic radiotherapy,^1-9 occurring in approximately 5-15% of patients who undergo radiotherapy to the thorax. To minimize toxicity to the lung associated with thoracic radiotherapy, it is necessary to understand the correlation between the risk of radiation-induced pneumonitis and treatment parameters such as dosimetric factors, biological factors, and baseline pulmonary function tests. Several studies have correlated dosimetric factors to the incidence of radiation-induced pneumonitis.^2,10-25 These studies suggest that radiation pneumonitis may be linked to V₂₀ (lung volume receiving >20 Gy),^2,10-16,20 mean lung dose,^{2,12,13,16-19,25} V₃₀,^10,15,17 V₁₅,¹⁰, V₄₀,¹⁵ and V₅₀.¹⁵ Non-dose factors (such as age, tumor lobe location, etc.) have also been shown to correlate to radiation pneumonitis.^{11,13,15,17,23,24}

Most of these studies focus on univariate correlation, whereas it is possible that much greater correlation may be obtained by appropriately combining variables into a predictive model. In addition, most of these studies modeled the normal tissue complication probability (NTCP) based solely on dosimetric factors. For example, Seppenwoolde et al.²⁵ assumed a sigmoid relationship between the complication probability and mean lung dose in the Lyman²⁶ NTCP model. These models may not be ideal for modeling lung injury since they assume that radiation response depends on dose alone. Non-dose factors may play an important role in inducing and even enhancing lung injury. For example, chemotherapeutic drugs have been shown to enhance radiation-induced lung injury.²⁷ Lind et al.¹¹ found that the predictive ability of lung V₂₀ was substantially improved for the subset of patients under 55 years of age. To account for the synergistic interaction between dose and non-dose patient factors, it appears imperative that a powerful, yet robust, model is required to predict for the incidence of radiation-induced pneumonitis. In this work, predictive modeling using feed-forward neural networks²⁸ is investigated. Neural networks, unlike simpler models, have the potential to model the synergistic interaction between variables using a flexible nonlinear relationship.²⁸

Two prior analyses from our group have considered neural networks and concluded that their predictive capabilities are equivalent²⁹ or better³⁰ than other commonly used dosimetric models.^31,32 However, these earlier works were limited, since the network was constructed with a fixed number of nodes in the hidden layer,²⁹ they lacked a selection process for input features,³⁰ and input features did not include non-dose variables.³⁰ In addition, issues such as overfitting and the correlation of input features were not studied. Therefore, there is an opportunity to improve upon these prior efforts and potentially enhance the model robustness and predictive accuracy.

In this work the neural network was constructed using a growing/pruning methodology^33,34 that incorporated a unique strategy to reduce overfitting during training and feature selection. The possibility of overfitting was reduced by training the network using one portion of the training group and stopping training when the prediction error on the remaining portion of the training group does not improve (or deteriorates). This same strategy was also used for feature selection—one portion of the training group was used for identifying potential features, and the remaining portion was used for selecting from the potential features based on robustness.

The neural network was constructed from a database of 235 patients with lung cancer treated using radiotherapy (compared to 97 patients²⁹ and 142 patients³⁰ in prior neural network analyses from our group). Neural network input features were selected from dose and non-dose patient variables. The network was tested using ten-fold cross-validation, wherein one tenth of the patients were tested, in turn, using a network constructed from the remaining patients. The significance of each of the selected features was statistically evaluated. The network is made publicly available through internet access.

II. MATERIALS AND METHODS

II.A. Patient variables

This study was based on data from 235 patients with lung cancer treated with external beam radiotherapy at Duke University Medical Center. Of these patients, 34 were diagnosed with Grade 2 or higher lung pneumonitis at followup. Radiation-induced pneumonitis was graded from 0 to 4, as follows. Grade 0: no increase in pulmonary symptoms due to radiotherapy; Grade 1: radiotherapy-induced symptoms not requiring initiation or increase in steroids and/or oxygen; Grade 2: radiotherapy-induced pulmonary symptoms requiring initiation or increase in steroids; Grade 3: radiotherapy-induced pulmonary symptoms requiring oxygen; Grade 4: radiotherapy-induced pulmonary symptoms requiring assisted ventilation or causing death. The details of patients and radiotherapy treatments are described in a previous publication.³⁵ In brief, all patients were treated as part of a prospective study to assess radiotherapy-induced lung injury. Patients were treated using three-dimensional conformal radiotherapy to doses ranging from 40 to 86.4 Gy (median 66 Gy). Radiation pneumonitis was prospectively assessed by the treating physician at followups every 3-4 months post-treatment. The cases in which a diagnosis of radiation pneumonitis was uncertain were classified as “hard-to-score”³⁶ and not considered in this analysis.

Inputs for the neural network (features) were selected from 93 dose and non-dose variables. The dosimetric variables consisted of the dose-volume histogram (DVH, the percentages of normal lung volume above doses ranging from 6 to 60 Gy, in increments of 2 Gy), mean heart dose, and 37 lung generalized equivalent uniform doses (gEUD)³⁷ (gEUD is calculated as $\mathrm{gEUD}={({\Sigma }_i{V}_i{D}_i^a∕{\Sigma }_i{V}_i)}^{1∕a}$, where V_i is the lung volume receiving dose D_i) for the exponent a ranging from 0.4 to 4 in increments of 0.1. Note that for a=1, gEUD is equivalent to the mean lung dose. Non-dosimetric variables consisted of race, age, sex, tumor stage, tumor location, chemotherapy schedule, histology type, surgery (yes or no), once or twice daily radiotherapy, pre-radiotherapy FEV₁ (forced expiratory volume in 1 s), FEV₁% (as percentage of predicted normal), pre-radiotherapy DLCO (Carbon Monoxide diffusion capacity in lung), and pre-radiotherapy DLCO% (as percentage of predicted normal). In patient cases where a certain variable was not collected (missing variable), the variable was assigned the average of non-missing values. This method of imputing missing values is frequently employed in work on machine learning.^28,34

A characteristic of the data is that the dose variables tend to be highly correlated. Dose variables that are related to each other with a >95% correlation were identified. During network construction, variables satisfying this criterion were forbidden from being selected as neural network input features at the same time. Once a variable was selected as an input feature by the neural network, all other highly correlated variables were removed from contention in subsequent feature selection. This ensured a high degree of independence between the input features selected by a network.

II.B. Feed-forward neural network

An example neural network is shown in Fig. 1. The nodes in the first layer (input layer) take in the inputs X (X₁, X₂,...) and nodes in the last layer (output layer) produce the output f(X). Each node in the hidden and output layer sums (Σ) over all the weighted inputs, which is then passed through an activation function (σ) that outputs a response. The activation function used here is sigmoid: σ(v)=1/(1+e^-v),²⁸ where v is the input and σ is the response. The choice of sigmoid activation function was based on its popularity in neural networks, and also because it is exactly equivalent to the softmax function used in classification problems.²⁸

Fig. 1.

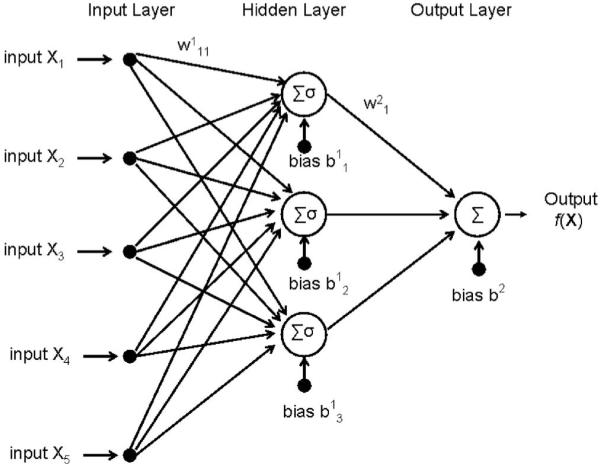
Typical architecture of a three-layer feed-forward neural network. Σ indicates the summation over the bias and weighted inputs (sample weights are indicated above arrows leading between nodes), and σ indicates a linear or nonlinear activation function.

The generalization capability of a neural network can be estimated by predicting outcome on data that are not used during training. Due to the small size of the overall dataset, a cross-validation²⁸ method was used to estimate network generalization capability rather than rigidly partitioning the data into a separate training set (used to build the network) and validation set (used to test the network). In the ten-fold cross-validation^28,34 testing scheme adopted here, the data were broken into ten approximately equal partitions, and each partition was tested using network(s) built using the nine remaining partitions as the training data.

A shortcoming of neural networks is their tendency to assume that “weak” trends and idiosyncracies in the training data are generalizable.²⁸ This shortcoming is generally referred to as overfitting. In this work, the tendency to overfit was reduced by adopting two measures: (1) An input feature was added only if it is judged robust by a subset of the training data (training-validation data) that was not used to select the feature, and (2) network weights and biases were progressively optimized (trained) only as long as the error in the training-validation data continued to decrease.

II.B.1. Neural network training and cross-validation

Given the data 〈(x₁, y₁)...(x_N, y_N)〉, where x_i is the vector of inputs and y_i is the outcome, for patient i, the neural network was trained by adjusting weights and biases to minimize the difference between the network outputs (f) and the known outputs (y). In this work, the error was defined as the regression formulation²⁸

$$R=\sum _{i=1}^N{(y_i-f\left(x_i\right))}^2,$$ (1)

where i labels the N training cases, x_i is the vector of input features, and y_i is 1 (pneumonitis Grade 2 or above) or 0 (pneumonitis Grade 1 or lower).

The error R was minimized by the back-propagation iterative learning procedure.³⁸ The weights and biases at the (r+1)st iteration were updated as follows:

$${\beta }^{(r+1)}={\beta }^{\left(r\right)}+m({\beta }^{\left(r\right)}-{\beta }^{(r-1)})-(1-m)\gamma \frac{\partial R}{\partial {\beta }^{\left(r\right)}},$$ (2)

where β denotes weights or biases, γ is the learning rate, and m is a momentum parameter^39,40 term used to accelerate learning. The learning rate γ and momentum parameter m were adaptively adjusted based on the change of error with iterations. The learning rate γ was varied during the course of iterations, starting from γ=0.01. During the iterative process, the momentum parameter m was fixed at 0.9, and the learning rate γ was increased by a multiplicative factor of 1.04 if the new iteration error was smaller than the previous iteration error. If, on the other hand, the new iteration error was larger than the previous iteration error, m was reduced to zero, and γ was decreased by a multiplicative factor of 0.7.

Since the activation function σ(v)=1/(1+e^-v) used here increases with increasing v, the weights associated with certain variables were constrained to take on only either positive or negative values. This was essentially a precaution to prevent unrealistic results, such as a higher dose predicting for a lower probability of injury. While this constraint prohibits a complementary subtractive effect between two dose variables, it also safeguards against detrimental overfitting caused by the more flexible constraint-free condition. Thus, the constraint leads to a more conservative predictive model. All dose, age, and stage features were allowed to have only positive weights, while pre-radiotherapy FEV₁, FEV₁%, pre-radiotherapy DLCO, and pre-radiotherapy DLCO% were allowed to have only negative weights. All other features were allowed positive or negative weights.

To avoid converging to the local minimum of the error function,²⁸ the network was trained five times with different initializations of weights and biases. The solution with the lowest error was chosen. At the global minimum of the training error R, the neural network can potentially detrimentally overfit to the training data (overtraining), i.e., the network could assume that “weak” trends in the training data are generalizable.²⁸ To avoid overfitting, an early stopping strategy was used.²⁸ This strategy stops network training before convergence to the global minimum. In this technique, patients with and without pneumonitis were randomly split into ten groups of approximately equal size. Eight groups of data were used as the training-construction data set to select input features and optimize the network weights and biases (network training). One group of data was used as the training-validation data set to monitor the evolution of a realistic estimate of error with training iterations and, thereby, signal early stopping in the training. Together, the training-construction and training-validation sets constitute the training set. During network training, the training-construction error can be expected to continuously decrease with iterations, whereas the training-validation error can be expected to initially decrease and then increase when the network starts overfitting. Network training was stopped (early stopping) when $E^{\left(r\right)}∕E_{\mathrm{opt}}^{\left(r\right)}>1.03$ (Prechelt⁴¹), where E^(r) is the training-validation error at iteration r, and $E_{\mathrm{opt}}^{\left(r\right)}$ is the lowest training-validation error obtained up to iteration r.

The one group remaining outside of the training set was used for cross-validation, to obtain a realistic estimate of model predictive capability. Each of the ten groups was treated as the cross-validation set, in turn. For each cross-validation set, the nine remaining groups were used as the training set. The training set was used to create nine neural networks, with each network using eight of nine groups for training-construction and the one remaining training set group for training-validation (early stopping). The nine neural networks associated with each training set possessed the same architecture and input features, but with different weights and biases (optimized for the particular training-construction set). The selection of input features for the nine neural networks was based solely on the characteristics of the training set. This selection process, explained in the next subsection, includes safeguards to reduce the possibility of overfitting. The results of testing on a cross-validation set were averaged over all nine networks. The combined results from all ten cross-validation groups were used to assess model predictive capability.

II.B.2. Neural network construction algorithm

The neural network was synthesized using an algorithm that combined constructive^33,34 and pruning⁴² approaches. The initial network consisted of one input node, one hidden layer with three nodes, and one output node. During the course of network building, three major steps were followed in sequence: pruning, substitution, and addition. Decrease in a mean-squared-error metric was used as an indicator of the success of a step in improving neural network (NN) predictive capability

$${\mathrm{mse}}_{\mathrm{S}}^{\mathrm{NN}}=\frac{1}{\mid \mathrm{S}\mid }\sum _i{(y_i-f\left(x_i\right))}^2,$$ (3)

where the summation i is over all the patients in a set S (|S| is the number of patients). In the pruning step, input and hidden node(s) were removed if the error metric improved (input node is equivalent to input feature). In the substitution step, an input feature was substituted with another unused variable if the error metric improved. In the addition step, an input node or hidden node was added if the error metric improved. The order of the “operators” involved in these steps is as follows: (1) Remove one input node; (2) remove one hidden node; (3) substitute one input node feature with another input feature selected from the unused variables (unused variables that have <0.95 correlation with all current input features); (4) add one input node; (5) add one hidden node.

Two algorithms for network construction are detailed next—Algorithm A: network construction for cross-validated testing (to obtain a realistic estimate of model predictive capability), and Algorithm B: network construction for prospective testing (testing on patients outside the database used in this work). Thus, the neural networks built with Algorithm A used nine tenths of the data for training, while those built with Algorithm B used all data for training (no data were reserved for testing). Operator_k refers to the kth operator in the order above; TV and TC refer to the training-validation and training-construction sets, respectively.

Algorithm A: Network construction for cross-validated testing

Step 1: Do for each cross-validation set i=1, ...,10.

Step 2: Let the initial network be denoted as ${\mathrm{NN}}_1^{ij}$ (one input node, three hidden nodes), for training-validation set j=1, ...,10 (j ≠ i).

Step 3: do for each Operator k=1, ...,5

1. ${\mathrm{NN}}_2^{ij}={\text{Operator}}_k\left({\mathrm{NN}}_1^{ij}\right)\text{for}j=1,\dots ,10(j\ne i)$;

2. Train the network ${\mathrm{NN}}_2^{ij}$ on its training-construction set (all patient groups except i and j)

3. $\begin{array}{c}\text{If}\frac{1}{9}{\sum }_{j=1,j\ne i}^{10}({\mathrm{mse}}_{{\mathrm{TV}}_{ij}}^{{\mathrm{NN}}_2^{ij}}+{\mathrm{mse}}_{{\mathrm{TC}}_{ij}}^{{\mathrm{NN}}_2^{ij}})<\frac{1}{9}{\sum }_{j=1,j\ne i}^{10}({\mathrm{mse}}_{{\mathrm{TV}}_{ij}}^{{\mathrm{NN}}_1^{ij}}+{\mathrm{mse}}_{{\mathrm{TC}}_{ij}}^{{\mathrm{NN}}_1^{ij}}),\hfill \\ {\mathrm{NN}}_1^{ij}\leftarrow {\mathrm{NN}}_2^{ij}\mathrm{for}j=1,\dots ,10(j\ne i)\hfill \end{array}$.

4. if k=5 and ${\mathrm{NN}}_1^{ij}$ were not replaced, stop construction.

Step 4: Test networks ${\mathrm{NN}}_1^{ij}(j=1,\dots ,10;j\ne i)$ on cross-validation set i.

Step 5: Average the nine test results for cross-validation set i.

When there was only one input node, Operator₁ (remove one input node) was skipped.

In Algorithm B, all ten groups were used for training. Each of the ten constructed networks used nine groups for training-construction and the remaining group for training-validation. The ten networks share a common architecture and input features but with weights and biases optimized to the corresponding training-construction set (the training-validation set is used for early stopping). The neural network prediction for a prospective patient is the average of the results from all ten networks.

Algorithm B: Network construction for prospective testing

Step 1: Let the initial network be denoted as ${\mathrm{NN}}_1^j$ (one input node, three hidden nodes), for training-validation set j=1, ...,10.

Step 2: Do for each Operator k=1, ...,5

1. ${\mathrm{NN}}_2^j={\text{Operator}}_k\left({\mathrm{NN}}_1^j\right)\text{for}j=1,\dots ,10$;

2. train the network ${\mathrm{NN}}_2^j$ on it’s training-construction set (all patient groups except j);

3. $\text{If}\frac{1}{10}{\sum }_{j=1}^{10}({\mathrm{mse}}_{{\mathrm{TV}}_j}^{{\mathrm{NN}}_2^j}+{\mathrm{mse}}_{{\mathrm{TC}}_j}^{{\mathrm{NN}}_2^j})<\frac{1}{10}{\sum }_{j=1}^{10}({\mathrm{mse}}_{{\mathrm{TV}}_j}^{{\mathrm{NN}}_1^j}+{\mathrm{mse}}_{{\mathrm{TC}}_j}^{{\mathrm{NN}}_1^j}),{\mathrm{NN}}_1^j\leftarrow {\mathrm{NN}}_2^j\mathrm{for}j=1,\dots ,10$;

4. if k=5 and ${\mathrm{NN}}_1^j(j=1,\dots ,10)$ were not replaced, stop construction.

Step 3: Output the networks ${\mathrm{NN}}_1^j(j=1,\dots ,10)$.

II.C. Model comparison

Two neural network ensembles were constructed, one (NN_dose) with input features selected only from the 66 lung dose variables and the other (NN_all) with input features selected from all 93 variables. These two networks were compared to each other by comparing their corresponding receiver operator characteristic (ROC) curves⁴³ for cross-validated testing (Algorithm A). The ROC curve plots true positive fraction versus 1-true negative fraction for varying values of the threshold measure of injury separating cases with and without predicted injury. The area under the ROC curve (AUC) was used to assess the predictive capability of the models—a larger area suggests a more accurate model. ROCKIT software⁴⁴ from the Department of Radiology, University of Chicago, was used to determine if the AUC difference between the two models was statistically significant. This software calculates the statistical significance of the difference between two ROC areas using a univariate z score test. (Null hypothesis: the datasets arose from binormal ROC curves with equal areas beneath them.)

II.D. Evaluation of significance of input features

To evaluate the significance of any one input feature selected in the prospective model (Algorithm B), the corresponding input node was removed, following which the network was retrained and tested. The exclusion of an input feature could result in some degradation of predictive ability, reflected as a decrement of the area under the cross-validated ROC curve. The statistical significance⁴⁴ of the ROC area decrement, resulting from feature exclusion, was used to evaluate the importance of the feature.

III. RESULTS AND DISCUSSION

III.A. Neural network construction

III.A.1. Cross-validated testing (Algorithm A)

The neural network was programmed in-house, using MATLAB (Mathworks, Natick, MA). The training time differed slightly for networks with different numbers of hidden nodes and input features. For the network with six input features and four hidden nodes, the training time was approximately 160 s on a dual-processor laptop (Intel CPU T7200, 200 GHz, with 2 GB of RAM).

Each of the ten sets of neural networks constructed for cross-validated testing (nine neural networks in each set) naturally selected input features that were different from each other. However, the input features selected by the different neural network sets were highly correlated. For example, the ten sets of networks constituting NN_all selected as one of the input features V₂₄, V₁₂, V₁₂, V₁₆, V₁₈, V₁₆, V₂₀, V₁₆, V₂₀, and V₁₆, respectively. The correlation coefficient between these features is ≥0.95.

Table I summarizes the sensitivity, specificity, and ROC area for training-construction, training-validation and cross-validation, for NN_all and NN_dose. Sensitivity and specificity are defined as the correctly predicted fraction of cases with and without injury, respectively. For the network NN_all, Fig. 2 shows the ROC curves for training-construction, training-validation, and cross-validation. The cross-validated area under the ROC curve of the network was 0.76, with sensitivity and specificity of 0.68 and 0.69, respectively. The network accuracy on the training-construction data was not perfect (ROC area: 0.85, sensitivity: 0.76, specificity: 0.76), due to the overfitting precautions taken during network training. The overfitting precautions used a mean-squared-error criterion that combined training-construction and training-validation errors (rather than training-construction error alone; see step 4 in Algorithm A) and employed early stopping to terminate network training at the minimum of the training-validation error (ROC area: 0.86, sensitivity: 0.82, specificity: 0.75). Figure 3 shows an example of the evolution of the training-construction error and training-validation error with training iterations, for the final architecture of one neural network (i=1, j=2 in Algorithm A). The training-construction error continuously decreases with increasing iterations, whereas the training-validation error increases beyond approximately 500 iterations. For the network NN_dose, Fig. 4 shows the ROC curves for training-construction, training-validation, and cross-validation. The trend is as for the network NN_all, albeit with lower ROC areas and sensitivity/specificity (Table I), suggesting that variables other than dose can improve predictive ability.

Table I.

The area under ROC curve (AUC), sensitivity, and specificity of network NN_all and NN_dose on training data, training-validation data, and cross-validation data, respectively

		NNall	NNdose
Training data	AUC	0.85	0.78
	Sensitivity	0.76	0.74
	Specificity	0.76	0.74
Training-validation data	AUC	0.86	0.77
	Sensitivity	0.82	0.65
	Specificity	0.75	0.78
Cross-validation data	AUC	0.76	0.67
	Sensitivity	0.68	0.53
	Specificity	0.69	0.69

Fig. 2.

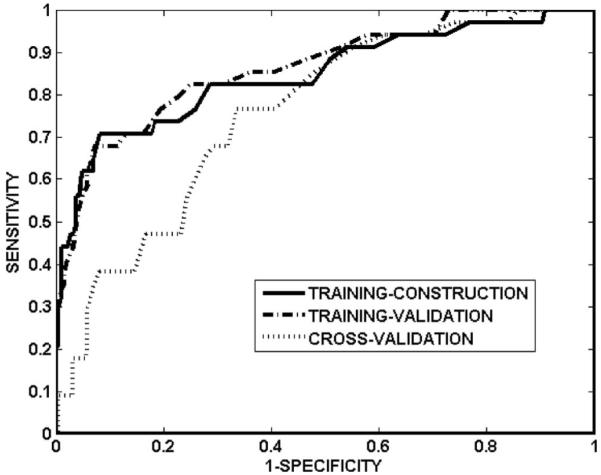
ROC curves of network NN_all on training-construction data, training-validation data, and cross-validation data. The corresponding areas under the ROC curves are 0.85, 0.86, and 0.76, respectively.

Fig. 3.

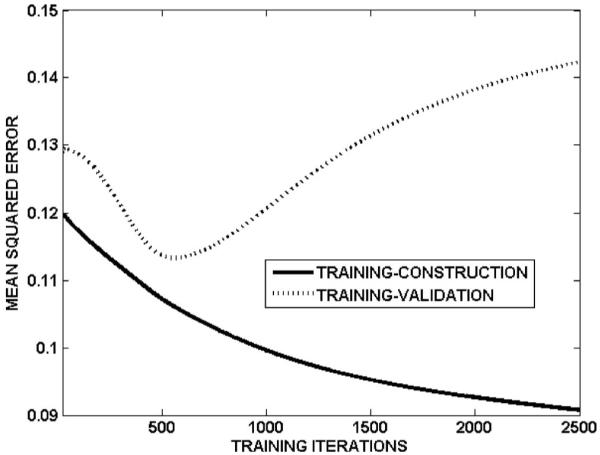
An example of the evolution of the training-construction and training-validation errors with training iterations. This example corresponds to i=1 and j=2 in Algorithm A for constructing NN_all. The training-construction error continuously decreases with increasing number of training iterations. The training-validation error, however, initially decreases and then increases beyond approximately 500 iterations. To avoid overfitting, network training was stopped at the point of the minimum training-validation error.

Fig. 4.

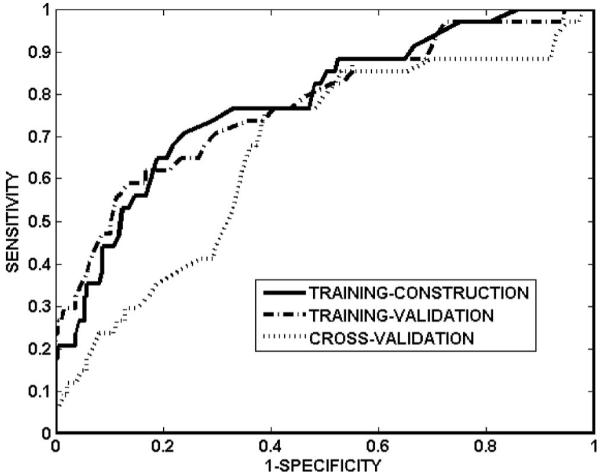
ROC curves of network NN_dose on training-construction data, training-validation data, and cross-validation data. The corresponding areas under the ROC curves are 0.78, 0.77, and 0.67, respectively.

The ROC analysis results are consistent with the two prior neural network analyses^29,30 from our group. Su et al.³⁰ constructed the neural network with input features selected only from lung dose variables. The network was trained with a randomly selected two thirds of 142 patients and tested on the remaining patients. The cross-validated ROC area of 0.68 agrees well with our results (cross-validated ROC area=0.67 for NN_dose, Table I). Munley et al.²⁹ constructed the neural network with 97 patients, and considered dose and non-dose variables. The cross-validated ROC area was not attempted, but the ROC area for training-validation (0.83) is similar to the corresponding ROC area (0.86) in this work. Although the same technique (neural network) was applied in this work and prior works, a number of improvements were made to enhance model robustness and predictive accuracy. The main differences can be described as follows: (1) 235 patients were studied in this work, (2) the network was constructed using a growing/pruning approach, (3) overfitting was reduced by using training-validation data, (4) highly correlated variables were forbidden from being input features at the same time, and (5) the network was tested using ten-fold cross-validation. Thus, the more optimistic results in Su et al.³⁰ are likely attributable to two major differences with the current work:

1. The number of patients is substantially higher in this work: 235 versus 142. The patients in Su et al.³⁰ are a subset of those in this study. This difference in numbers could naturally lead to differences in the model test results. The larger number of patients, in conjunction with the more robust feature selection and testing strategy, suggests that the current results are closer to being asymptotic.

2. The testing methodology is more comprehensive in this work: The neural network was tested on all data using ten-fold cross-validation, while Su et al.³⁰ tested their network on one third of the data. This ten-fold testing methodology also implies that the models used in testing are more representative, in this work, since they are based on a larger fraction of the total number of patients: nine tenths versus two thirds. For small datasets, K fold cross-validation is considered more accurate than testing on a separate set, as explained on page 214 of Hastie et al.²⁸: “Ideally if we had enough data, we would set aside a validation set and use it to assess the performance of our prediction model. Since data are often scarce, this is usually not possible. To finesse the problem, K-fold cross-validation uses part of the available data to fit the model, and a different part to test it.”

The impact of missing variables on neural network performance was evaluated as follows. Among the selected input features, FEV₁ and DLCO% were not collected for approximately 20% of the patients. They were assigned the average of non-missing values during the process of network building and cross-validated testing. The impact of these missing values was gauged by the extent of variation in the cross-validated test results for 10 000 sets of random values assigned to the missing FEV1 and DLCO% (randomly assigned within the range of non-missing values from other patients). The mean of the cross-validated ROC areas was 0.756±0.002, ranging from 0.746 to 0.762. This small variation implies that the neural networks built here are only minimally affected by the missing values.

III.A.2. Network construction for prospective use (Algorithm B)

The optimized architecture had six input features, four hidden nodes, and one output node. Figure 5 steps through Algorithm B to demonstrate the progress of constructing the network for prospective testing. The input features selected using Algorithm B are shown in Table II. Among these features, gEUD a=1 (mean lung dose) frequently appears as a strong predictor of radiation pneumonitis in the literature.^{2,12,13,16-19} Although V₁₆ does not often appear in other work, it is highly correlated with V₂₀.^2,10-16,20

Fig. 5.

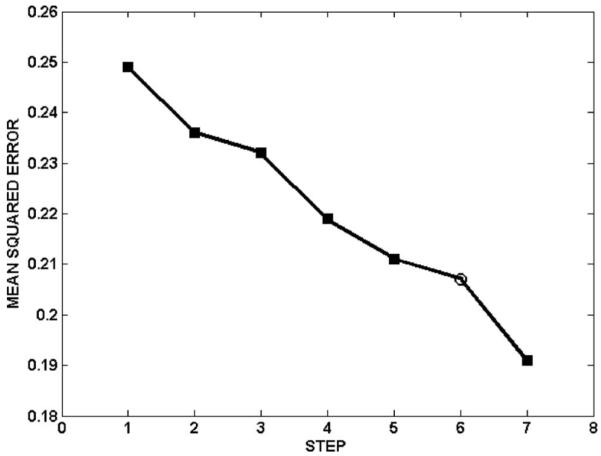
The progress of network construction for NN_all (Algorithm B for prospective testing). The symbols ■ and ○ indicate addition of an input feature and addition of a hidden layer node, respectively. The initial network architecture (step 1) consisted of one input node and three hidden nodes.

Table II.

The optimized architectures of neural network for prospective testing

Selected input features	Hidden nodes	Output nodes
Lung volume receiving >16 Gy	4	1
Lung gEUD a=3.5
Lung gEUD a=1
FEV1
DLCO%
Chemotherapy before radiotherapy

III.B. Model comparison

For networks NN_all and NN_dose constructed using Algorithm A, the areas under the ROC curves for cross-validated testing were 0.76 and 0.67, respectively (Table I). The difference between these two areas was significant (p=0.020). Thus, the generalization capability of the network was significantly improved by adding non-dose features.

III.C. Evaluation of significance of input features

The ROC areas and p values for significance testing of the deterioration are shown in Table III. The extent of deterioration of the ROC area was feature dependent. Input features corresponding to significant (p<0.05) deterioration were: gEUD a=3.5, DLCO%, gEUD a=1 (mean lung dose), and V₁₆. Note that this evaluation is limited to the individual exclusion of features. The nature of the selection process for input features (step 3 in Algorithm A, step 2 in Algorithm B) is such that it exploits the synergistic interaction between features to improve model prediction. This implies that a certain combination of input features could have greater influence, when removed, than the sum of their individual influences.

Table III.

Evaluation of significance of input features by single exclusion

Input feature excluded	AUC	p value
None	0.76	NA
gEUD a=3.5	0.65	<10-4
DLCO%	0.66	0.001
gEUD a=1	0.69	0.020
Lung volume receiving >16 Gy	0.71	0.037
FEV1	0.71	0.053
Chemotherapy before radiotherapy	0.75	0.059

III.D. Model publication

The neural network for prospective use, constructed from dose and non-dose features (Algorithm B), is available for download from http://www.radonc.duke.edu/modules/div_medphys/index.php?id=24. The required input features are shown in Table II. The input file (an example is available on the website) is required to include the entire lung DVH, DLCO%, FEV₁, and whether or not the patient was treated with chemotherapy prior to radiotherapy. Missing variables are indicated as negative values in the input file. The program internally computes two of the input features from the lung DVH: gEUDs with a=1 and a=3.5. The network outputs are two sets of metrics: A discriminant value that is a measure of the extent of injury (>0 indicates predicted pneumonitis, <0 indicates no predicted pneumonitis), and the number of patients in the Duke training database with a higher discriminant than the prospectively tested patient. The latter value ranks the prospectively evaluated patient in the context of the Duke population.

IV. CONCLUSIONS

In this work, two neural network ensembles (NN_all and NN_dose) were constructed using input features selected from all variables and only dose variables, respectively. A comparison of the cross-validated generalization capability of these two models showed that adding non-dose features significantly improved predictive accuracy (p=0.020). The selected input features, arranged in order of decreasing significance were: gEUD a=3.5 (p<10^-4), DLCO% (p=0.001), mean lung dose (p=0.020), V₁₆ (p=0.037), FEV₁ (p=0.053), and chemotherapy prior to radiotherapy (p=0.059). The optimized neural network for prospective use is available for public use via internet access.