The multiscale coarse-graining method. IV. Transferring coarse-grained potentials between temperatures

Abstract

This work develops a method for the construction of multiscale coarse-grained (MS-CG) force fields at different temperatures based on available atomistic data at a given reference temperature. The validity of this theory is demonstrated numerically by applying it to construct MS-CG models of the Lennard-Jones liquid and simple point charge water model systems.

INTRODUCTION

Molecular dynamics (MD)^{1, 2} is a powerful method for understanding a wide variety of physical phenomena in complex systems. It is a fundamental computational technique for investigating the equilibrium dynamics of proteins^{3, 4, 5, 6, 7} and related biomolecular ensembles,⁸ as well as for analyzing the properties of condensed phase systems.⁹ However, a fundamental issue faced by MD simulation methods is the problem of sampling. Typical systems of interest involve the dynamics of hundreds to many thousands of molecules and a correspondingly large number of degrees of freedom. MD methods estimate equilibrium statistical ensemble properties by propagating each molecule’s degrees of freedom using Newton’s equations of motion augmented by thermo- and∕or barostats. Consequently, the computational cost of MD methods grows as the number of particles involved in the physical processes of interest. In addition to this, the equilibrium dynamics of many physical systems of interest span multiple time and length scales. For example, biologically relevant properties of many proteins involve dynamics over the millisecond or greater time scales.^{10, 11, 12, 13} Self-assembly processes involving proteins occur over even longer time scales and length scales, as in the assembly of viral capsids,^{14, 15, 16, 17} which involves thousands of proteins self assembling to form structures tens of nanometers in length,¹⁴ over a time period of minutes.^{16, 17}

Although the ability to compute the equilibrium properties of these systems would be of tremendous value, atomistic MD techniques are generally unable to do so. The fundamental problem of adequate ensemble sampling of these systems is further exacerbated by the large disparity in the time scales characterizing the physical processes involved in these dynamical phenomena themselves. If these processes were dynamical processes evolving on only a few time scales, it might be possible to adapt MD simulations to model them, by choosing a suitable multiple time step algorithm by which to propagate the MD trajectories. However, the dynamics of most physical systems of interest involve multiple time scales, ranging from hydrogen bond fluctuations, which occur on a subpicosecond time scale, to the collective dynamics of the system, which could take place on a millisecond time scale or even much longer. It is this inherent hierarchy of time scales and the coupling between them that make sampling the equilibrium ensemble of complex condensed phase systems an intractable problem in practice.

Strategies to overcome this problem involved the construction of reduced [“coarse-grained” (CG)] descriptions of the physical system being studied.^{18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42} The general philosophy behind these approaches is to reduce the hierarchy of time and length scales present in the atomistic dynamics by incorporating fast time scale dynamics into the effective CG degrees of freedom. This approach enables the construction of reduced models that approximate only the relevant large scale dynamics. The reduction in the hierarchy of time and length scales in turn enables better sampling, either through MD simulations or by other methods, performed with the CG models to access physical processes at time and length scales, which would be inaccessible to conventional atomistic MD sampling methods.

Recently, a systematic multiscale approach has been developed for the construction of reduced CG models to represent a system’s large scale dynamics.^{32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42} This multiscale CG (MS-CG) method enables the construction of a CG potential function that is rigorously equivalent to the atomistic many body potential of mean force defined for the CG degrees of freedom.^{40, 41} Due to the rigorous thermodynamic averaging procedure, the MS-CG method can, in principle, guarantee the exact evaluation of ensemble averaged mechanical quantities through the analysis of the MS-CG model. Furthermore, the MS-CG construction can be derived as a minimal solution obtained from a variational principle. In practice, for a specified basis set expansion of the MS-CG potential energy function, the CG force field obtained from the MS-CG variational principle can be shown to be an optimal approximation to the many body mean force field determined by the atomistic equilibrium ensemble.^{40, 41}

Even though the CG force fields constructed by this MS-CG procedure provide a statistical mechanical description of the system that is consistent with properties derived directly from the atomistic ensemble, they may not be completely transferable across different thermodynamic conditions, i.e., CG potential functions constructed at a given set of conditions (thermodynamic or otherwise) cannot be directly applied in the modeling of the underlying atomistic system placed in a different set of conditions.⁴³ Generically, the construction of reduced CG models depends on the conditions under which the specific phenomena of interest are being studied and hence the models may be poorly transferable across different physical conditions.^{44, 45} For the CG models constructed from the MS-CG approach, the lack of transferability across thermodynamic conditions arises because contributions from the atomistic degrees of freedom being averaged are dependent on the thermodynamic conditions of the atomistic system. Hence, this lack of transferability is a direct consequence of the statistical mechanical averaging procedure that is used to construct the MS-CG force fields.

Indeed the development of transferable potentials for CG models remains a significant challenge within the modeling community. Several groups employed thermodynamic properties to parametrize CG potentials.^{22, 46, 47, 48, 49} In some cases CG models employing the resulting potentials semiquantitatively reproduced the structure of atomistic models under different conditions and for multiple systems. However, these methods have not been formulated to provide quantitative consistency with any particular atomistic model. Recent research has also demonstrated that the potentials calculated to ensure structural consistency between a particular atomically detailed model and a CG model of the same system can demonstrate significant and nontrivial dependence upon the particular thermodynamic state point used to parametrize the potentials.^{44, 45, 50, 51, 52, 53, 54, 55, 56}

This research indicates that achieving complete transferability⁴³ of CG model parameters across different conditions is intrinsically in conflict with the CG modeling approach because constructing a reduced representation of an atomically detailed system inevitably involves including some amounts of information regarding its thermodynamic state into the CG representation. Partial transferability of a given set of model parameters can possibly be achieved, but at the cost of sacrificing quantitative consistency. Thus, an alternative strategy for addressing this inherent lack of transferability in CG model parameters without sacrificing quantitative consistency with underlying atomistic models would be to devise rigorous methods for transforming CG potentials that have been determined to provide quantitative consistency at a given thermodynamic state point into new potentials that provide quantitative consistency with the underlying atomistic system at different thermodynamic state points. It is important to note that this strategy does not attempt to construct a single set of completely transferable CG potential functions, but is rather aimed at generating different sets of CG potentials, each of which is designed to quantitatively model the underlying atomistic system at a single thermodynamic state point. This work presents such a strategy to generate sets of MS-CG model potentials each of which correspond to different thermodynamic state points, given information about ensemble averages at a single given state point. A systematic framework for deriving CG potentials, which can easily be transferred across thermodynamic conditions and ensure structural consistency between atomically detailed and CG models at each state point, will significantly advance the promise of computationally efficient low resolution models. In this work, a formally exact statistical mechanical method is presented by which a MS-CG force field that is an optimal approximation to the many body potential of mean force at a temperature, T, can be constructed through the use of ensemble averages calculated at a reference temperature, T₀.

The present work extends the MS-CG variational principle for transferring MS-CG force fields across different temperatures using a simple procedure. The variational principle is used to derive a rescaling technique to transfer CG thermodynamic averages across different temperatures. This method, implemented using the normal MS-CG equations,^{40, 57, 58} is used to demonstrate the transferability of MS-CG force field parameters across different temperature regimes. Numerical calculations illustrate this procedure for the case of a simple condensed phase system for which the MS-CG potential is assumed to be pairwise decomposable. However, the proposed method is derived and may be numerically implemented for more complex potentials.

THEORY

A variational principle for temperature transferability of CG observables is derived in this section and applied to generalize the variational principle for the construction of MS-CG potentials. The notation to be used is as follows. An atomically detailed configuration with n atoms is described by the set of Cartesian vectors rⁿ={r₁,r₂,⋯r_n}. Similarly, a CG configuration with N CG sites is described by the set of Cartesian vectors R^N={R₁,R₂,…,R_N}. The atomistic n particle potential energy function is denoted as u(rⁿ) and the corresponding force on atom i is given byf_i(rⁿ)=−∂u(rⁿ)∕∂r_i. In the following it will be assumed that the atomistic potential function is temperature independent and that no rigid intramolecular constraints are included in either the atomistic or the CG model.

Variational principle

The dynamics of a system coupled to a thermostat that maintains a fixed temperature generates a canonical ensemble of structures if the dynamical trajectories are long enough for a sufficient sampling of the phase space of the system.^{1, 2} In mathematical terms, if A(rⁿ;t) is the value of an observable A at time t, then the time average of A is defined by

$${⟨A\left({\mathbf{r}}^n\right)⟩}_t=\frac{1}{t}{\int }_0^{t}d\tau A_{\tau }\left({\mathbf{r}}^n;\tau \right).$$ (1)

For a canonical ensemble at a given temperature T, with the assumption of adequate sampling, the following relationship is satisfied:

$$\underset{t\to \infty }{\text{lim}}{⟨A\left({\mathbf{r}}^n\right)⟩}_t={⟨A\left({\mathbf{r}}^n\right)⟩}_T.$$ (2)

The average in the right hand side of this equation is taken with respect to the canonical probability distribution, p_r(rⁿ;T), for the temperature T. The canonical probability distribution at a given temperature corresponding to the atomistic potential function is given as

$$p_r\left({\mathbf{r}}^n;T\right)=\frac{1}{z\left(T\right)}\text{exp}\left(-\frac{u\left({\mathbf{r}}_n\right)}{k_{B}T}\right).$$ (3)

The normalization factor z(T) is the canonical configurational integral given by

$$z\left(T\right)=\int d{\mathbf{r}}^n{e}^{-u\left({\mathbf{r}}^n\right)∕k_{B}T},$$ (4)

where the integral in Eq. 4 and in the following represents an integral over the relevant configuration space. The hypothesis expressed in Eq. 2 is central to the validity of the MD method wherein single, long trajectories of a given, thermostatted system are generated using Newtonian dynamics and equilibrium averages estimated through the use of the ergodic hypothesis.^{1, 2} Consider a set of N collective (CG) variables defined by the mapping,

$${\mathbf{R}}^N={\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\equiv \left\{{\mathbf{M}}_{{\mathbf{R}}_1}\left({\mathbf{r}}^n\right),\dots ,{\mathbf{M}}_{{\mathbf{R}}_N}\left({\mathbf{r}}^n\right)\right\}.$$ (5)

Here, the collection of N position vectors, R^N, is the collection of position vectors for the N CG sites, with CG site I having a position given by the vector R_I, which is determined as a function of the atomically detailed configuration, rⁿ, by the mapping operator M_RI(rⁿ). This mapping maps linear combinations of atomistic positions into an associated CG position vector. With the CG site positions determined by the atomistic configuration, a conditional probability distribution for the atomistic configuration given a fixed CG configuration and a temperature T is defined as

$$p_{r\mid R}\left({\mathbf{r}}^n\mid {\mathbf{R}}^N;T\right)=p_r\left({\mathbf{r}}^n;T\right)\delta \left({\mathbf{R}}^N-{\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)∕p_R\left({\mathbf{R}}^N;T\right),$$ (6)

where

$$p_R\left({\mathbf{R}}^N;T\right)={⟨\delta \left({\mathbf{R}}^N-{\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)⟩}_T$$ (7)

is the equilibrium CG coordinate distribution determined by the atomistic equilibrium distribution given by Eq. 3 and the CG mapping defined in Eq. 5, and $\delta \left({\mathbf{R}}^N-{\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)$ is the product of N delta functions, each of the form δ(R_I−M_RI(rⁿ)). Given this conditional probability distribution, one can compute a set of reduced observables that are determined by this distribution. For a general observable, γ(rⁿ), a corresponding reduced variable is defined as

$$\Gamma \left({\mathbf{R}}^N;T\right)=\int d{\mathbf{r}}^n{p}_{r\mid R}\left({\mathbf{r}}^n\mid {\mathbf{R}}^N;T\right)\gamma \left({\mathbf{r}}^n\right).$$ (8)

Corresponding to such a reduced observable, a functional is defined for arbitrary real continuous functions of the CG configuration, G(R^N), as follows:

$${\chi }_T^2\left[G\right]=\int d{\mathbf{r}}^n{p}_r\left({\mathbf{r}}^n;T\right){\mid G\left({\mathbf{M}}_{\mathbf{R}}^N\left({\mathbf{r}}^n\right)\right)-\gamma \left({\mathbf{r}}^n\right)\mid }^2.$$ (9)

The functional defined above is always non-negative,

$${\chi }_T^2\left[G\right]\ge 0.$$ (10)

Furthermore, ${\chi }_T^2$ has a stationary point in the vector space of real continuous functions, G(R^N). Since ${\chi }_T^2$ is quadratic in G, the stationary point corresponds to its unique minimum. The stationary point is determined by the equation

$$\frac{\delta {\chi }_T^2\left[G\right]}{\delta G}=0.$$ (11)

When this condition is evaluated, Eq. 9 implies that

$$G_{\text{min}}\left({\mathbf{R}}^N\right)=\Gamma \left({\mathbf{R}}^N;T\right),$$ (12)

where Γ(R^N;T) is the reduced observable given by the conditioned expectation value of γ(rⁿ) and defined in Eq. 8. For arbitrary G(R^N)

$${\chi }_T^2\left[G\right]={\chi }_T^2\left[\Gamma \right]+{\Vert G\left({\mathbf{R}}^N\right)-\Gamma \left({\mathbf{R}}^N;T\right)\Vert }_T^2,$$ (13)

where Eq. 13 introduces a temperature dependent norm

$${\Vert G\left({\mathbf{R}}^N\right)-\Gamma \left({\mathbf{R}}^N;T\right)\Vert }_T^2=\int d{\mathbf{R}}^N{p}_R\left({\mathbf{R}}^N;T\right){\mid G\left({\mathbf{R}}^N\right)-\Gamma \left({\mathbf{R}}^N;T\right)\mid }^2,$$ (14)

and p_R(R^N;T) is defined in Eq. 7. The first quantity on the right hand side of Eq. 13 is independent of G, while the second quantity on the right hand side is a non-negative quantity describing the difference between the arbitrary trial function, G, and the thermally averaged CG observable, Γ. From Eqs. 12, 13, it is clear that the CG observable Γ(R^N;T) provides the unique minimum of the functional defined in Eq. 9 for the temperature T. Therefore the minimization of the functional ${\chi }_T^2$ defined in Eq. 9 provides a variational principle for calculating the CG observable at a thermodynamic temperature T using data sampled from simulations at the same temperature. Moreover, by using the norm identified in Eq. 14 to define a “distance” between two real continuous functions of the CG configuration, R^N, then the function that minimizes ${\chi }_T^2$ within a given subspace also provides an optimal approximation to Γ within that subspace, in the sense that the optimal approximation minimizes the norm given by Eq. 14. Therefore, this variational principle also provides a systematic means for computing an optimal approximation to the CG observable within a given vector subspace of functions of the CG configuration.

Thermal transferability

It is evident that, in the canonical ensemble, the probability of observing a given atomistic configuration at temperature T^′ is related to the probability of observing the same configuration at temperature T by

$$p_r\left({\mathbf{r}}^n;T^{\prime }\right)=\omega \left(T^{\prime },T\right)\mu \left({\mathbf{r}}^n;T^{\prime },T\right)p_r\left({\mathbf{r}}^n;T\right).$$ (15)

The factor ω corresponds to a ratio of configuration integrals at T^′ and T, while μ corresponds to a ratio of Boltzmann factors, such that

$$\omega \left(T^{\prime },T\right)={\left(z\left(T^{\prime }\right)∕z\left(T\right)\right)}^{-1},$$ (16)

and

$$\mu \left({\mathbf{r}}^n;T^{\prime },T\right)=\text{exp}\left[-u\left({\mathbf{r}}^n\right)\left(1∕k_B{T}^{\prime }-1∕k_{B}T\right)\right].$$ (17)

With these definitions, the canonical average of a function a(rⁿ) at a given temperature, T^′, may be evaluated from sampling the ensemble at a different temperature, T,

$${⟨a\left({\mathbf{r}}^n\right)⟩}_{T^{\prime }}=\int d{\mathbf{r}}^n{p}_r\left({\mathbf{r}}^n;T^{\prime }\right)a\left({\mathbf{r}}^n\right)=\omega \left(T^{\prime };T\right){⟨\tilde{a}\left({\mathbf{r}}^n;T^{\prime },T\right)⟩}_T,$$ (18)

where $\tilde{a}\left({\mathbf{r}}^n;T^{\prime },T\right)=\mu \left({\mathbf{r}}^n;T^{\prime },T\right)a\left({\mathbf{r}}^n\right)$. Consequently, it is convenient to define a generalized functional

$${\tilde{\chi }}_T^2\left[G;T^{\prime }\right]={⟨\mu \left({\mathbf{r}}^n;T^{\prime },T\right){\mid G\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)-\gamma \left({\mathbf{r}}^n\right)\mid }^2⟩}_T.$$ (19)

This functional is expressed as a canonical ensemble average of the atomistic configuration space evaluated at a reference temperature T. The arguments of the functional are the trial function of the CG configuration, G(R^N), and also a target temperature T^′. According to Eq. 18${\tilde{\chi }}_T^2$ is directly proportional to ${\chi }_{T^{\prime }}^2$,

$${\tilde{\chi }}_T^2\left[G;T^{\prime }\right]=\frac{1}{\omega \left(T^{\prime },T\right)}{\chi }_{T^{\prime }}^2\left[G\right].$$ (20)

Consequently it follows that the function G(R^N) that minimizes ${\tilde{\chi }}_T^2\left[G;T^{\prime }\right]$ for a given target temperature T^′ also minimizes ${\chi }_{T^{\prime }}^2\left[G\right]$. This provides a variational principle for computing the CG observable at a target temperature T^′ using data sampled from simulations at a reference temperature, T. For a given T^′, Γ(R^N;T^′) provides the unique global minimum of ${\tilde{\chi }}_T^2\left[G;T^{\prime }\right]$. Moreover, using the distance metric defined in Eq. 14, an optimal approximation to Γ(R^N;T^′) within a given vector subspace of functions of the CG configuration can be obtained by minimizing ${\tilde{\chi }}_T^2\left[G;T^{\prime }\right]$ within that subspace. It is also evident from the above analysis that similar transferability can be achieved with respect to other thermodynamic parameters when the probability densities at two different values of the parameters can be related by an equation of the form of Eq. 15. This method of transferring CG quantities across different thermodynamic conditions may therefore be rather general. Similar approaches are quite common within the context of thermodynamic perturbation theory.² In particular, the atomistic sampling method developed by Ferrenberg and Swendsen utilizes a very similar rescaling approach.⁵⁹

Although the procedure described above is formally exact, there are practical limitations to its applicability. A significant limitation is that the sampled regions of phase space at the given simulation conditions must have significant overlap with the regions of phase space that may be sampled at the desired conditions to which the CG quantities are to be transferred. This limitation is common to many other classical simulation techniques.

MS-CG variational principle

The variational procedure developed in Sec. 2A can be applied to construct a CG force field, which correctly averages the forces derived from an atomistic ensemble. If an atomistic system is modeled with N CG sites, then the total “atomistic” force acting on a CG site I, F_I, is given by the sum of atomistic forces, f_i(rⁿ), from particles, i, which are mapped into the CG site. Mathematically, the atomistic force on CG site I is defined as

$${\mathcal{F}}_I\left({\mathbf{r}}^n\right)=\sum _{i∊I}{\mathbf{f}}_i\left({\mathbf{r}}^n\right).$$ (21)

Here the set i∊I indicates the set of atomistic particles, i, that are mapped into the given CG site and it has been assumed that each atomistic particle is mapped into not more than one CG site. The MS-CG variational principle,^{32, 33} which has recently been analyzed and generalized by Noid et al.,^{40, 41} can be obtained from the considerations leading to Eq. 13. If the function γ(rⁿ) in Eq. 8 is chosen to be the atomistic force, F_I, the appropriate averaged CG observable Γ(R^N;T) is

$${\mathbf{F}}_I\left({\mathbf{R}}^N;T\right)=\int d{\mathbf{r}}^n{p}_{r\mid R}\left({\mathbf{r}}^n\mid {\mathbf{R}}^N;T\right){\mathcal{F}}_I\left({\mathbf{r}}^n\right),$$ (22)

which is a many-body mean force defined by the conditioned expectation value of the atomistic force field.⁴¹ The MS-CG functional may be considered the appropriate generalization of the functional defined in Eq. 9,

$${\chi }_T^2\left[\mathbf{G}\right]=\frac{1}{3N}{⟨\sum _{I=1}^N{\mid {\mathbf{G}}_I\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)-{\mathcal{F}}_I\left({\mathbf{r}}^n\right)\mid }^2⟩}_T,$$ (23)

where G={G₁(R^N),…,G_N(R^N)} is an arbitrary trial CG force field specified by a set of N vector valued functions that determine the force on each of the N CG sites as a function of the CG configuration R^N. Because each element in the force field G is varied independently, it immediately follows from Eq. 13 that

$${\chi }_T^2\left[\mathbf{G}\right]={\chi }_T^2\left[\mathbf{F}\left(T\right)\right]+{\Vert \mathbf{F}\left(T\right)-\mathbf{G}\Vert }_T^2,$$ (24)

which employs the norm in the vector space of CG force fields introduced by Noid et al.:⁴¹

$${\Vert \mathbf{F}-\mathbf{G}\Vert }_T^2=\int d{\mathbf{R}}^N{p}_R\left({\mathbf{R}}^N;T\right)\frac{1}{3N}\sum _{I=1}^{3N}{\mid {\mathbf{G}}_I\left({\mathbf{R}}^N\right)-{\mathbf{F}}_I\left({\mathbf{R}}^N;T\right)\mid }^2.$$ (25)

In Eq. 24, F(T) is the CG mean force field at the temperature T with elements {F₁(R^N;T),…,F_N(R^N;T)} given by Eq. 22 for each I=1,…,N. Consequently, the MS-CG functional in Eq. 23 has a minimal solution G_min that corresponds to the thermally averaged CG mean force field at temperature T, F(T), as defined by Eq. 22. In principle, this CG mean force field can be integrated to obtain a CG many body potential of mean force. The equilibrium canonical configurational probability distribution resulting from this potential of mean force is identical to the probability distribution, p_R(R^N;T), in Eq. 7. Therefore, this force field can be used to construct a CG coordinate distribution function, which is consistent with that derived for the CG configurations from the atomistic Boltzmann distribution.^{40, 41} The development of Sec. 2B may be employed to extend the MS-CG variational principle for computing the many-body mean force field at a temperature T^′ given data sampled from the canonical ensemble at a temperature T. A generalized MS-CG functional of a trial CG force field G and a temperature T^′ may be defined as

$${\tilde{\chi }}_T^2\left[\mathbf{G};T^{\prime }\right]=\frac{1}{3N}{⟨\mu \left({\mathbf{r}}^n;T^{\prime },T\right)\sum _{I=1}^N{\mid {\mathbf{G}}_I\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)-{\mathcal{F}}_I\left({\mathbf{r}}^n\right)\mid }^2⟩}_T,$$ (26)

where μ(rⁿ;T^′,T) has been defined in Eq. 17. It follows from Eq. 18 that

$${\tilde{\chi }}_T^2\left[\mathbf{G};T^{\prime }\right]=\frac{1}{\omega \left(T^{\prime },T\right)}{\chi }_{T^{\prime }}^2\left[\mathbf{G}\right].$$ (27)

Thus, the many-body mean force field determined by a conditional canonical average of the atomistic force field at a temperature T^′, F(T^′), provides the unique minimum of the functional ${\tilde{\chi }}_T^2$ defined by Eq. 26. Moreover, given a vector subspace of CG force fields, the optimal approximation within this subspace to the many-body mean force field at a temperature T^′ may be determined by minimizing ${\tilde{\chi }}_T^2$ using data sampling the canonical ensemble at the temperature T.

Numerical calculations: The normal MS-CG equations

It is assumed that the total MS-CG potential function U(R^N) may be expressed as a sum of simple CG potential functions, U_ζ, each of which is a function of a single scalar variable, ψ_ζ, which is itself a function of the coordinates for a set of CG particles, {R}_γ, and which describes a particular interaction among that set,

$$U\left({\mathbf{R}}^N\right)=\sum _{\zeta }\sum _{\gamma }{U}_{\zeta }\left({\psi }_{\zeta }\left({\left\{\mathbf{R}\right\}}_{\gamma }\right)\right).$$ (28)

Each of these potential functions, U_ζ, will be represented by a linear combinations of basis functions U_ζd with coefficients, ϕ_ζd,

$$U_{\zeta }\left(z\right)=\sum _d{\varphi }_{\zeta d}{U}_{\zeta d}\left(z\right).$$ (29)

The MS-CG force on site I, F_I, may then be expressed as a linear combination of basis functions that depend on the CG configuration, R^N, and whose coefficients will act as force field parameters:

$${\mathbf{F}}_I\left({\mathbf{R}}^N\right)=\sum _{\zeta }\sum _d{\varphi }_{\zeta d}{\mathcal{G}}_{I;\zeta d}\left({\mathbf{R}}^N\right),$$ (30)

where

$${\mathcal{G}}_{I;\zeta d}\left({\mathbf{R}}^N\right)=\sum _{\gamma }{F}_{\zeta d}\left({\psi }_{\zeta }\left({\left\{\mathbf{R}\right\}}_{\gamma }\right)\right)\frac{\partial {\psi }_{\zeta }\left({\left\{\mathbf{R}\right\}}_{\gamma }\right)}{\partial {\mathbf{R}}_I}$$ (31)

play the role of force field basis vectors for the variational calculation and

$$F_{\zeta d}\left(z\right)=-d{U}_{\zeta d}\left(z\right)∕dz$$ (32)

are the (negative) derivatives of the potential energy basis functions.^{41, 42} For notational simplicity the superindex D will be used to represent the combination of index ζ, indicating the particular type of interaction, and index d, indicating the particular coefficient describing the potential function governing that type of interaction. The CG force on site I in configuration R^N may then be re-expressed:

$${\mathbf{F}}_I\left({\mathbf{R}}^N;T\right)=\sum _D{\varphi }_D\left(T\right){\mathcal{G}}_{I;D}\left({\mathbf{R}}^N\right).$$ (33)

The set of force field basis vectors {G_D} included in Eq. 33 forms a basis that spans a particular vector subspace of CG force fields. As discussed above, the CG mean force field depends on the thermodynamic temperature, T, at which the ensemble averaging was performed. Thus, the CG force field within the subspace spanned by the given basis set and also the parameters determining this CG force field depend on the thermodynamic temperature, as explicitly indicated in Eq. 33. It is important to recognize that in Eqs. 30, 33F_I represents the MS-CG approximation to the many body mean force field defined in Eq. 22 and not the mean force field itself.

By employing the linear representation for the MS-CG force field at temperature T given in Eq. 33, the MS-CG functional defined in Eq. 23 reduces to a simple function of the force field parameters and the variational calculation may be performed as a linear least-squares problem. The parameters determining the CG force field that minimizes the MS-CG functional in Eq. 23 and that therefore provide an optimal approximation to the many-body mean force at a temperature T satisfy the normal MS-CG equations,^{40, 41, 42}

$$\sum _{D^{\prime }}{G}_{D{D}^{\prime }}\left(T\right){\varphi }_{D^{\prime }}\left(T\right)=b_D\left(T\right),$$ (34)

for each parameter ϕ_D included in the MS-CG force field, where the functions

$$G_{D{D}^{\prime }}\left(T\right)=\frac{1}{3N}{⟨\sum _{I=1}^N{\mathcal{G}}_{I;D}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)\cdot {\mathcal{G}}_{I;D^{\prime }}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)⟩}_T,$$ (35)

$$b_D\left(T\right)=\frac{1}{3N}{⟨\sum _{I=1}^N{\mathcal{G}}_{I;D}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)\cdot {\mathcal{F}}_I\left({\mathbf{r}}^n\right)⟩}_T,$$ (36)

are canonical ensemble averages evaluated at temperature T.

Analogously, the CG force field parameters that provide the optimal approximation to the many-body mean force field at a temperature T^′ may be determined by performing the variational calculation outlined above and solving the normal system of equations, Eq. 34, using correlation functions evaluated at temperature T^′. Alternatively the generalized MS-CG functional defined in Eq. 26 may be used to determine the force field parameters providing the optimal approximation to the many body mean force field at the temperature T^′ by reweighting configurations sampled from the canonical ensemble at temperature T. The optimal CG force field at the temperature T^′ may then be determined by solving the generalized set of normal MS-CG equations:

$$\sum _{D^{\prime }}{\tilde{G}}_{D{D}^{\prime }}\left(T^{\prime },T\right){\varphi }_{D^{\prime }}\left(T^{\prime }\right)={\tilde{b}}_D\left(T^{\prime },T\right),$$ (37)

where

$${\tilde{G}}_{D{D}^{\prime }}\left(T^{\prime },T\right)=\frac{1}{3N}{⟨\mu \left({\mathbf{r}}^n;T^{\prime },T\right)\sum _{I=1}^N{\mathcal{G}}_{I;D}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)\cdot {\mathcal{G}}_{I;D^{\prime }}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)⟩}_T,$$ (38)

$${\tilde{b}}_D\left(T^{\prime },T\right)=\frac{1}{3N}{⟨\mu \left({\mathbf{r}}^n;T^{\prime },T\right)\sum _{I=1}^N{\mathcal{G}}_{I;D}\left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)\cdot {\mathcal{F}}_I\left({\mathbf{r}}^n\right)⟩}_T,$$ (39)

are correlation functions evaluated using configurations sampled from a canonical ensemble at the temperature T.

In the following calculations, each molecule is represented by a single CG site that corresponds to the center of mass for that molecule. The CG potential energy function includes only central pair potentials that are represented by discrete delta function basis functions as described previously in Refs. ^{41, 44}. In this representation, the CG pair force is discretized on a grid of spacing δR and the force field parameter ϕ_D corresponds to the magnitude of the pair force between two CG sites separated by a distance R_D. The CG force field basis vector G_I;D then becomes

$${\mathcal{G}}_{I;D}\left({\mathbf{R}}^N\right)=\sum _{J\ne I}{\hat{\mathbf{R}}}_{IJ}{\delta }_D\left(R_{IJ}-R_D\right),$$ (40)

where ${\hat{\mathbf{R}}}_{IJ}$ is the unit vector pointing toward CG site I from CG site J and the discrete delta function,

$${\delta }_D\left(R-R_D\right)=\{\begin{array}{ll}1\hfill & R_D-\delta R∕2<R<R_D+\delta R∕2\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (41)

The correlation functions G and b then reduce to

$$G_{D{D}^{\prime }}\left(T\right)=\frac{1}{3N}{⟨\int d{\mathbf{R}}^N\sum _{I=1}^N\sum _{J,K\ne I}\left({\hat{\mathbf{R}}}_{IJ}\cdot {\hat{\mathbf{R}}}_{IK}\right){\delta }_D\left(R_{IJ}-R_D\right){\delta }_D\left(R_{IK}-R_{D^{\prime }}\right)\delta \left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)-{\mathbf{R}}^N\right)⟩}_T,$$ (42)

$$b_D\left(T\right)=\frac{1}{3N}{⟨\int d{\mathbf{R}}^N\sum _{I=1}^N\sum _{J\ne I}\left({\hat{\mathbf{R}}}_{IJ}\cdot {\mathcal{F}}_I\left({\mathbf{r}}^n\right)\right){\delta }_D\left(R_{IJ}-R_D\right)\delta \left({\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)-{\mathbf{R}}^N\right)⟩}_T,$$ (43)

where the mapping operation $\delta \left({\mathbf{R}}^N-{\mathbf{M}}_R^N\left({\mathbf{r}}^n\right)\right)$ in each correlation function has been used to express the basis vectors in terms of CG coordinates, R^N, and R_IJ=R_I−R_J, R_IJ=∣R_IJ∣, ${\hat{\mathbf{R}}}_{IJ}={\mathbf{R}}_{IJ}∕R_{IJ}$, and R_IK, R_IK, and ${\hat{\mathbf{R}}}_{IK}$ are defined analogously. The correlation functions ${\tilde{G}}_{D,D^{\prime }}\left(T^{\prime },T\right)$ and ${\tilde{b}}_D\left(T^{\prime },T\right)$ in this basis then immediately follow from Eqs. 42, 43 using the rescaling function μ(rⁿ;T^′,T).

METHODS

The method developed above for transferring CG potential functions between temperatures is applied and validated here for a Lennard-Jones (LJ) liquid and the simple point charge (SPC) water model.⁶⁰ In each case, MD simulations were performed in the constant NVT ensemble using an integration time step of 2 fs and employing the Nose–Hoover thermostat^{61, 62} to sample the canonical ensemble at the appropriate temperature. Electrostatic interactions were evaluated using the particle mesh Ewald method⁶³ with the real space contribution truncated at 0.9 nm for SPC water. In each case the k space contribution was evaluated using a maximum grid spacing of 0.08 and a sixth order interpolation between grid points. van der Waals interactions were truncated at 1.2 nm. For the LJ and SPC simulations, configurations, forces, and energies were sampled every 2 ps and 100 fs, respectively. All MD simulations and calculations of thermodynamic quantities were performed using the GROMACS 3.3 software package.⁶⁴

Simulations of 216 LJ particles were performed in a cubic box of volume (1.86 nm)³ at a temperature of T=298 K. Atomically detailed simulations of 216 SPC water molecules were performed in a cubic box of volume (1.86 nm)³ at T=278, 298, and 318 K. All bond lengths in the SPC molecules were constrained using the LINCS algorithm.⁶⁵ Initial configurations for SPC simulations at T=278 and 318 K were obtained by simulated annealing in which the temperature was changed from T=298 K during the course of 2 ns and data from the first 5 ns of each simulation were not included in the following calculations.

CG configurations were generated from each simulation by mapping the atomic coordinates for each molecule to the center of mass for that molecule. (In the case of LJ system, the CG mapping is the trivial identity map.) Radial distribution functions (RDFs) were then calculated from the mapped configurations for each system at each temperature. The coordinates and forces from each sampled configuration were next employed to evaluate the canonical ensemble averages in Eqs. 35, 36. Using these correlation functions, the normal MS-CG equations in Eq. 34 were solved to determine the pair forces providing the optimal approximation for the many-body mean force field for each system at each temperature.^{41, 42} The grid spacing for all calculations of the CG pair force was 0.001 nm. The resulting CG pair forces were then numerically integrated to obtain the pair potential. Additionally, the second derivative of the CG pair potential was approximated by evaluating the centered finite differences of the calculated pair force and then smoothing the resulting curve by performing a running average over five consecutive data points. The resulting pair potential and its second derivative were then employed in CG MD simulations at the same temperature and volume as the corresponding atomistic simulation. Averages and fluctuations in the potential energy and pressure as well as distribution functions for the CG sites were computed from configurations sampled from these CG MD simulations.

Additionally, for both systems, the configurations, energies, and forces sampled from simulations at temperatureT=298 K were employed to evaluate the correlation functions ${\tilde{G}}_{D{D}^{\prime }}\left(T^{\prime },T\right)$ and ${\tilde{b}}_D\left(T^{\prime },T\right)$ defined in Eqs. 38, 39 for T^′=278 and 318 K. These correlation functions evaluated using data from simulations at 298 K were then employed in the rescaled normal MS-CG equations in Eq. 37 to solve for the MS-CG pair force at 278 and 318 K. The pair force functions calculated from rescaling were compared with force functions calculated using data for the appropriate temperature. These rescaling calculations required significant sampling to obtain converged results and 45 ns worth of data were used in the SPC calculations. The pair potential and its second derivative were calculated from these forces as described above and were then employed in CG MD simulations at the temperature corresponding to the rescaling temperature T^′. Again, averages and fluctuations in the potential energy and pressure, as well as distribution functions for the CG sites, were computed from configurations sampled from these simulations and compared with those obtained from the CG MD simulations using the pair forces calculated without rescaling.

RESULTS

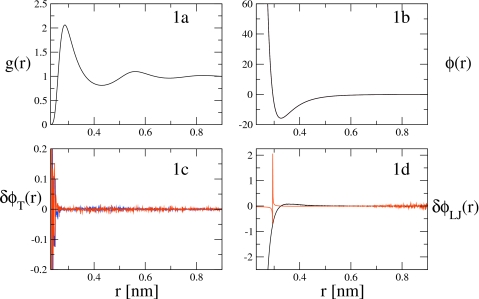
In Fig. 1 and in all subsequent figures, forces are presented in units of kJ∕(mol nm). Figure 1a presents the RDF, g(r), calculated from simulations of the LJ system at T=298 K. Figure 1b compares the true LJ pair force curve (black) with the pair force curves calculated from several MS-CG variational calculations. The dotted black curve in Fig. 1b corresponds to the pair force at T=298 K calculated from the normal MS-CG equations presented in Eq. 34. The red and blue curves in Fig. 1b correspond to the pair force curves at T^′=278 and 318 K, respectively, calculated from the rescaled normal MS-CG equations in Eq. 37, while using data from LJ simulations at T=298 K. Because the identity map has been used to define the “CG” system, the correct CG pair force equals the true LJ pair force and should be temperature independent. These calculations are therefore “control” simulations to test the validity of the temperature rescaling method. The four pair forces calculated presented in Fig. 1b are seen to be virtually indistinguishable on the scale of the figure. Figure 1c presents the absolute errors in the rescaling procedure for this simple control system as the difference between the pair force curves calculated for T^′=278 (blue curve) and 318 K (red curve) from the rescaled normal MS-CG equations, Eq. 37, using T=298 K data with the pair force curve calculated forT=298 K using the normal MS-CG equations, Eq. 34. Figure 1d presents the absolute (black) and percent error (red) in the LJ pair force curve calculated using the normal MS-CG equations as the absolute and relative difference between the pair force obtained from Eq. 34 and the true LJ pair force. The spike in the percent error curve (red) in Fig. 1d corresponds to the point at which the true pair force passes through zero. The magnitude of the absolute error curve (black) in Fig. 1d for r<0.3 nm corresponds to a small relative error in the magnitude of the pair repulsion at very short interparticle separations. In summary, the results of Fig. 1 clearly indicate that, for this simple control case, the MS-CG method accurately recovers the true LJ pair force and that the rescaling procedure accurately predicts the temperature independence of the MS-CG pair force for the LJ system over the temperature range from T=278 to 318 K using simulation data at T=298 K.

Figure 1.

Force and pair distribution curves plotted for the LJ liquid system: (a) is the RDF, g(r), plotted as a function of distance, r, and computed from a simulation at 298 K. (b) compares the true LJ pair force (black) at T=298 K with the pair forces calculated for the LJ system at T^′=318 K (red) andT^′=278 K (blue) using the rescaling procedure with simulation data from T=298 K and also with the pair force calculated using the normal equations at T=298 K (dotted black). (c) displays the absolute error in the rescaling procedure, δϕ_T, by plotting the difference between the LJ pair force computed from the MS-CG normal equations at T=298 K and the LJ pair forces at T^′=278 K (blue) and T^′=318 K (red) computed via the rescaling procedure and using simulation data from T=298 K. (d) presents the percentage error (red) and absolute error (black) in the LJ pair force, δϕ_LJ, calculated using the normal MS-CG equations compared to the true LJ pair force.

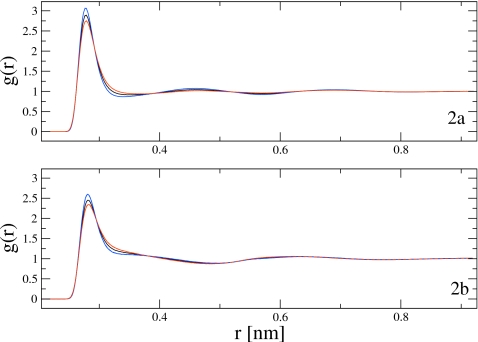
To further demonstrate the method, the temperature rescaling procedure was employed to determine the MS-CG pair forces for a system of 216 water molecules represented by the SPC water model.⁶⁰ Atomistic MD simulations at T=278, 298, and 318 K were performed for this system as described in Sec. 3. Atomistic configurations were sampled from these simulations and mapped onto one-site CG water configurations. From these mapped configurations, the site-site RDF was computed for each temperature. The resulting RDFs computed from atomistic simulations at T=278, 298, and 318 K are presented in Fig. 2a as the solid blue, black, and red curves, respectively. Over this temperature range the SPC water RDFs demonstrate relatively simple temperature dependence. With decreasing temperature, the SPC water system becomes increasingly ordered. In particular, the first peak of the SPC RDF becomes increasingly large and increasingly narrow, while the second peak demonstrates slightly more order at lower temperature. The third peak appears effectively temperature independent over this temperature range.

Figure 2.

Comparison of RDFs derived from MD simulations of all-atom and CG models of water at three different temperatures: (a) presents the RDFs calculated from all-atom MD simulations. The blue, black, and red solid curves correspond to RDFs calculated from all-atom MD simulations of SPC water at 278, 298, and 318 K, respectively. (b) presents RDFs calculated from CG MD simulations. The blue, black, and red solid curves correspond to RDFs calculated at 278, 298, and 318 K, respectively, using pair forces calculated via the normal MS-CG equations in Eq. 34. The blue and red dashed curves correspond to RDFs calculated from CG MD simulations at 278 and 318 K using pair forces calculated via the rescaled normal MS-CG equations in Eq. 37. The RDFs for the CG MD simulations at each temperature are indistinguishable on the scale of the figure.

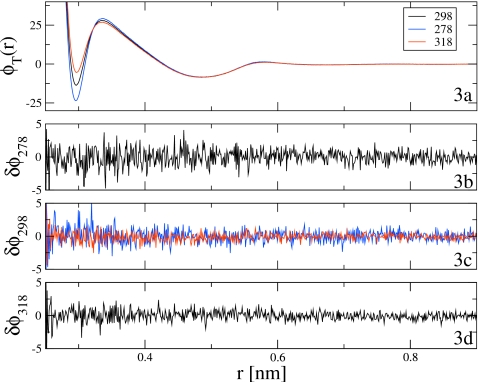
From the mapped configurations, the correlation functions G and b defined in Eqs. 35, 36 were computed for each temperature and the normal MS-CG equations in Eq. 34 for each temperature were numerically solved. The calculated MS-CG pair forces for T=278, 298, and 318 K are presented as the blue, black, and red curves in the top panel of Fig. 3, i.e., Fig. 3a. The MS-CG pair forces for the SPC system demonstrate significant temperature dependence in the first solvation shell, but appear to be essentially temperature independent for r>0.4 nm. At T=278 K, the MS-CG pair force is strongly attractive in the first solvation shell. However, for T=318 K the MS-CG pair force has almost no attraction between neighboring molecules. Moreover, with decreasing temperature, the MS-CG pair force demonstrates increasing structure as the repulsive maxima in the SPC pair force increases with decreasing temperature. As discussed earlier by Noid et al.⁴⁰ and in contrast with iterative CG procedures such as the reverse Monte Carlo method,^{9, 29} the MS-CG pair force is not determined completely by the RDF and reflects not only changes in pair correlations, but also changes in three-particle correlations in the SPC fluid with temperature.

Figure 3.

CG pair forces for the SPC water model calculated via the normal MS-CG equations in Eq. (34) and the rescaled normal MS-CG equations in Eq. 37. (a) presents the MS-CG pair force for 278 (blue), 298 (black), and 318 (red) K calculated via the normal MS-CG equations. (b) presents the absolute difference between the pair force at T=278 K calculated via the normal equations and the pair force at T^′=278 K calculated via the rescaled normal MS-CG equations using simulation data at T=298 K. (c) presents the absolute difference between the pair force at T=298 K calculated via the normal equations and the pair forces at T^′=298 K calculated via the rescaled normal equations using simulation data at T=278 K (blue) andT=318 K (red). (d) presents the absolute difference between the pair force at T=318 K calculated via the normal equations and the pair force atT^′=318 K calculated via the rescaled normal equations using simulation data at T=298 K.

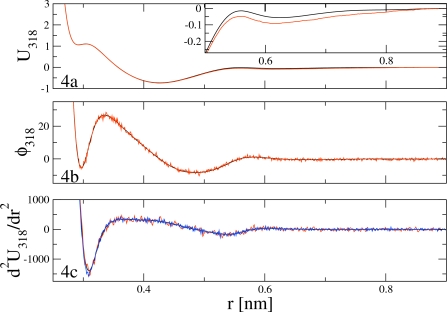
As discussed in Sec. 3, the CG pair potential and its second derivative were then computed from the calculated pair force. Figure 4 illustrates the numerical procedure for the CG pair interaction at T=318 K. The black curve in the central panel of Fig. 4 is the MS-CG pair force calculated from simulations at T=318 K. The potential obtained from integration is presented as the black curve in Fig. 4a. The second derivative which was used in the ensuing CG MD simulations is presented as the black curve in the lower panel. For comparison, the blue curve in Fig. 4c is the second derivative calculated directly from the pair force without any smoothing. Clearly, the running average effectively removed much of the statistical noise, allowing an accurate and smooth evaluation of the necessary numerical derivative.

Figure 4.

The MS-CG interaction at 318 K calculated via the normal MS-CG equations in Eq. 34 (black) and via the rescaled normal MS-CG equations in Eq. 37 using simulation data at 298 K (red). (a) presents the two pair potentials. The inset of (a) compares the two potentials for r between 0.4 and 0.9 nm. (b) presents the two calculated force curves. (c) presents the second derivatives of the pair potentials calculated as smoothed centered finite differences of the pair forces shown in (b). The blue curve in (c) presents the centered finite difference of the black curve in (b) without smoothing.

MD simulations of the one-site CG SPC model were then performed at each temperature using the MS-CG pair forces calculated for that temperature. The site-site RDFs were computed from the CG MD simulations at T=278, 298, and 318 K and are presented as the solid blue, black, and red curves, respectively, in Fig. 2b. It can be seen from Fig. 2b that the one-site MS-CG model for SPC water qualitatively reproduces structural features of the water model derived from all-atom simulations. For each temperature, the first peak of the CG RDF is at approximately the correct distance. However, although the relative ordering of the CG RDFs with temperature follows the same trend as the RDFs calculated for the atomistic model, the structure of the second solvation shell in the CG model and the temperature dependence of the CG RDFs are quantitatively different from the corresponding structural properties calculated for the SPC model. Since the objective of this work is to test the temperature transferability methodology, the quantitative accuracy of this CG model of SPC water is not a significant concern.

Using the CG configurations mapped from atomistic MD simulations at each temperature, the rescaled correlation functions $\tilde{G}$ and $\tilde{b}$ defined by Eqs. 38, 39 were computed. The rescaled normal MS-CG equations in Eq. 37 were then solved to determine (1) the MS-CG pair force at T^′=278 K using simulation data from T=298 K, (2) the MS-CG pair force at T^′=298 K using simulation data from T=278 K, (3) the MS-CG pair force at T^′=298 K using simulation data from T=318 K, and (4) the MS-CG pair force at T^′=318 K using simulation data from T=298 K. These four MS-CG pair forces calculated via the rescaling method were then compared with the MS-CG pair forces computed for each temperature from simulation data at the same temperature, which are presented in Fig. 3a and described above. Figures 3b, 3c, 3d then present the absolute numerical difference between the MS-CG pair force computed for each temperature (T=278, 298, and 318 K, respectively) from the normal MS-CG equations and the pair force computed for each temperature from the rescaled normal MS-CG equations. In particular, Fig. 3c presents the difference between the MS-CG pair force at T=298 K calculated from Eq. 34 and the pair forces at T^′=298 K calculated from Eq. 37 by rescaling simulation data from T=278 K and T=318 K simulations as the blue and red curves, respectively. In both cases, the pair force calculated from the rescaled normal equations agrees quite well with the pair force calculated directly from the normal equations. However, the statistical error in the pair force calculated by rescaling data from 278 K is slightly larger than the statistical error in the pair force calculated by rescaling data from 318 K. This is not unexpected, since simulations at a lower temperature can be expected to sample the Boltzmann distribution less efficiently than a high temperature simulation. As a result, a rescaling of simulation data down a temperature gradient (i.e., from a higher to a lower temperature) would be expected to be more efficient and reliable than a rescaling estimate performed for a given temperature using simulation data from a lower temperature. In summary, it is clear from Fig. 3 that, although the rescaled force curves are somewhat more noisy than the force curves calculated directly from simulation data at the appropriate temperature, the error in the rescaled force curves represents statistical error arising from lack of sampling and not systematic error. Within a relatively small statistical error, the current method accurately calculates the MS-CG pair force at a particular temperature by rescaling simulation data sampled from simulations at reference temperatures ±20 K from the target temperature.

As described in Sec. 3 and above, the pair forces calculated for each temperature via rescaling were then employed to obtain the CG pair potential and its second derivative. Figure 4 further compares the pair potential and its derivatives at T=318 K computed via the normal MS-CG equations (black) and the rescaled normal MS-CG equations (red). The direct comparison of the two force curves presented in Fig. 4b clearly demonstrates that the force curve calculated by rescaling simulation data from T=298 K provides an accurate, if somewhat noisy, approximation to the CG pair force at T=318 K. [The difference between these two force curves is presented in Fig. 3d.] The potentials computed from the two force curves are virtually indistinguishable on the scale of Fig. 4a. However, the inset, which compares the two pair potentials for r between 0.5 and 0.9 nm, demonstrates that the rescaled pair potential (red) slightly underestimates the true pair potential (black). Additionally, Fig. 4c demonstrates that, despite the statistical noise present in the rescaled force curve, upon performing a running average, the derivative of the rescaled force curve [red curve in Fig. 4c] provides a reasonably accurate approximation to the second derivative of the pair potential [black curve in Fig. 4c].

CG MD simulations were then performed at T^′=278 and 318 K using the pair potentials (and second derivatives) calculated by rescaling simulation data sampled at T=298 K. The RDF for the CG model at both temperatures was then computed from configurations sampled by these simulations. The RDFs computed from these CG MD simulations performed at T^′=278 and 318 K are presented as the dashed blue and red curves, respectively, in Fig. 2b. On the scale of Fig. 2b, the RDFs computed from simulations using the pair potentials calculated by rescaling are indistinguishable from the RDFs computed from simulations using the pair potentials calculated directly from the normal MS-CG equations shown as solid lines. Additionally, Table 1 presents the average and standard deviation of the potential and pressure calculated from these CG MD simulations. Table 1 indicates that simulations employing the pair potentials calculated by rescaling approximately reproduce the thermodynamic properties calculated from simulations employing the MS-CG pair potentials determined by the normal equations for the given temperature. The largest discrepancy arises in the potential energy at T=318 K and results from the slight error in the pair potential shown in the inset of Fig. 4a.

Table 1.

Comparison of thermal averages and root mean squared deviation (RMSD) fluctuations in the potential and pressure computed from CG MD simulations performed with the MS-CG pair forces of 278 and 318 K obtained from the (unscaled) normal and rescaled normal MS-CG equations.

T=278 K	Average	RMSD
Potential (kcal∕mol)
Unscaled	−75.96	23.26
Rescaled	−90.70	23.33
Pressure (bar)
Unscaled	7233.69	570.41
Rescaled	7180.92	575.90
T=318 K
Potential (kcal∕mol)
Unscaled	−73.73	25.60
Rescaled	−265.07	25.68
Pressure (bar)
Unscaled	8338.49	575.69
Rescaled	7843.17	577.25

DISCUSSION

The results presented above demonstrate that the thermal rescaling approach proposed in this work may provide a viable and systematic method by which MS-CG force fields can be transferred across different temperatures. As has been demonstrated from the model studies presented here, the rescaling procedure accurately determines the MS-CG force field at a particular target temperature by rescaling either from lower or higher temperatures than the target temperature. As noted in the results section, the rescaling calculations for the SPC system required extensive sampling at the reference temperature in order to rescale the force curve to the target temperature. Consequently, more careful numerical procedures using higher order basis functions,⁴² perturbation expansion approaches, and∕or numerical preconditioning techniques may be necessary for implementing the rescaling procedure for more complex biomolecular systems.

The results suggest that the rescaling method may be used in a symmetric fashion when the target temperature is either higher or lower than the reference temperature and may be extended to provide accurate approximations to CG force fields for other liquid systems, more generally for systems which can be well sampled over the time scale of the simulation trajectories. However, the rescaling method presented here is possibly an asymmetric method, with a rescaling downward from a higher temperature ensemble being potentially more accurate. This asymmetry is related to the fact that higher temperatures could enable a more exhaustive sampling of phase space.

The method presented in this work offers a promising approach to transferring CG potential functions across a range of thermodynamic conditions. Although this work provided a numerical demonstration of the method to transfer force parameters across temperatures, in principle, this method has more general applicability to the transferability of other thermodynamically averaged quantities. This can be seen clearly from the formulation of the generalized variational principle on which the method is based. However, this method becomes considerably simplified when applied to the transfer of force parameters. This simplification is made possible by the use of the normal MS-CG equations, Eqs. 34, 35, 36, which relate the CG forces directly to statistical mechanical distribution functions of the system and to simple kinetic equations for the liquid state.^{40, 57, 58} The strategy by which the variational principle is combined with the formal hierarchy for the distribution functions has considerable generality and promises to provide a powerful tool for the development of easily transferable MS-CG potentials for complex condensed phase systems, where the challenge of adequate sampling becomes especially severe.

APPENDIX: GENERALIZED THERMAL TRANSFERABILITY EQUATIONS

This appendix presents the thermal transferability equations in a general, matrix form. Let $\underset{͇}{G}\left(T\right)$ and $\underset{̱}{b}\left(T\right)$ be the temperature dependent matrix and vector of correlation functions determined for a temperature T with an associated vector of force parameters, $\underset{̱}{\varphi }\left(T\right)$. Then, the relation between $\underset{͇}{G}$, $\underset{̱}{b}$, and $\underset{̱}{\varphi }$ at two temperatures, T and T^′, is

$$\underset{͇}{G}\left(T\right)\underset{̱}{\varphi }\left(T\right)=\underset{̱}{b}\left(T\right),$$ (A1)

$$\underset{͇}{G}\left(T^{\prime }\right)\underset{̱}{\varphi }\left(T^{\prime }\right)=\underset{̱}{b}\left(T^{\prime }\right).$$

Define

$$\underset{̱}{\delta \varphi }=\underset{̱}{\varphi }\left(T^{\prime }\right)-\underset{̱}{\varphi }\left(T\right),$$ (A2)

$$\underset{͇}{G}\left(T^{\prime }\right)=\underset{͇}{{\Gamma }_G}\underset{͇}{G}\left(T\right),$$

$$\underset{̱}{b}\left(T^{\prime }\right)=\underset{͇}{{\Gamma }_b}\underset{̱}{b}\left(T\right).$$

Note that $\underset{͇}{G}$ is symmetric by definition and that $\underset{͇}{{\Gamma }_b}$ is a diagonal matrix with elements ${\left(\underset{͇}{{\Gamma }_b}\right)}_{D{D}^{\prime }}={\delta }_{D{D}^{\prime }}{b}_D\left(T^{\prime }\right)∕b_D\left(T\right)$. The quantities $\left(\underset{͇}{{\Gamma }_G},\underset{͇}{{\Gamma }_b}\right)$ contain the effects of a temperature change on the correlation functions, $\left(\underset{͇}{G},\underset{̱}{b}\right)$. From these definitions, Eq. A2 can be rewritten as

$$\underset{̱}{\delta \varphi }={\underset{͇}{G}}^{-1}\left(T\right)\underset{͇}{\Delta }\underset{̱}{b}\left(T\right),$$ (A3)

where

$$\underset{͇}{\Delta }=\underset{̱}{\underset{̱}{{\Gamma }_G^{-1}}}\underset{͇}{{\Gamma }_b}-\underset{̱}{\underset{̱}{1}}.$$ (A4)

The quantity $\underset{͇}{\Delta }$ is zero when T=T^′ and hence the right hand side of Eq. A3 represents the “perturbation” to the CG force resulting from changes in the temperature. Consequently, this form of the thermal transferability equations, Eq. A3, may be useful in constructing approximate perturbative treatments estimating the effect of changes in thermodynamic state on the MS-CG force fields.