Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2009 Jul 21;106(31):12735–12740. doi: 10.1073/pnas.0902169106

Predicting weakly stable regions, oligomerization state, and protein–protein interfaces in transmembrane domains of outer membrane proteins

Hammad Naveed 1, Ronald Jackups Jr 1, Jie Liang 1,1
PMCID: PMC2722334  PMID: 19622743

Abstract

Although the structures of many β-barrel membrane proteins are available, our knowledge of the principles that govern their energetics and oligomerization states is incomplete. Here we describe a computational method to study the transmembrane (TM) domains of β-barrel membrane proteins. Our method is based on a physical interaction model, a simplified conformational space for efficient enumeration, and an empirical potential function from a detailed combinatorial analysis. Using this method, we can identify weakly stable regions in the TM domain, which are found to be important structural determinants for β-barrel membrane proteins. By calculating the melting temperatures of the TM strands, our method can also assess the stability of β-barrel membrane proteins. Predictions on membrane enzyme PagP are consistent with recent experimental NMR and mutant studies. We have also discovered that out-clamps, in-plugs, and oligomerization are 3 general mechanisms for stabilizing weakly stable TM regions. In addition, we have found that extended and contiguous weakly stable regions often signal the existence of an oligomer and that strands located in the interfaces of protein–protein interactions are considerably less stable. Based on these observations, we can predict oligomerization states and can identify the interfaces of protein–protein interactions for β-barrel membrane proteins by using either structure or sequence information. In a set of 25 nonhomologous proteins with known structures, our method successfully predicted whether a protein forms a monomer or an oligomer with 91% accuracy; in addition, our method identified with 82% accuracy the protein–protein interaction interfaces by using sequence information only when correct strands are given.

Keywords: in-plug, membrane protein oligomerization, out-clamp, protein–protein interaction, weakly stable TM strand

Developing a general understanding of how proteins behave in membranes is of fundamental importance. β-barrel membrane proteins, one of the 2 major structural classes of membrane proteins, have been studied extensively. Currently, structures of 70 β-barrel membrane proteins have been resolved, and much has been learned about their thermodynamic stability (1), folding kinetics (2–4), biogenesis (5), and biological functions (6). These membrane proteins are thought to have very regular structures, with the basic principles of their architectural organization well understood (7). An overwhelming structural feature is the existence of an extensive regular hydrogen bond network between the transmembrane (TM) β-strands, which is thought to confer extreme stability on the proteins (8).

However, β-barrel membrane proteins have diverse structures and often deviate significantly from the standard barrel architecture. For example, there are often small α-helices and β-strands, called in-plugs, found inside the β-barrel (9). Non-barrel-embedded helices are also found to pack against the TM β-strands (10). In addition, some β-barrel membrane proteins exist in monomeric form, whereas others form oligomers as their biological functional unit (9). These structural irregularities and diversity often play important functional roles for β-barrel membrane proteins, such as voltage-sensing (11), flux control of metabolites, and ion-sensing (9).

Computational studies have also contributed much to the understanding of β-barrel membrane proteins, including the identification of β-barrel membrane proteins from sequences of many microbial genomes, the prediction of their topological orientations, and the characterization of their structural features (12, 13). In addition, numerous spatial and sequence motifs and ensemble properties of the TM domains have also been studied (13–18). As models and algorithms improve, it is natural to ask whether computational studies can reveal further insight on the structural organization of β-barrel membrane proteins.

In this study, we explore whether an empirical energy function and a minimalistic structural model of β-barrel membrane proteins (15, 17) can reveal the structural organizing principles of non-barrel elements in the TM domain. We also study whether the oligomerization state of the TM domains can be predicted and whether there exist unstable or weakly stable regions in TM strands, despite the existence of extensive H-bond networks.

First, we describe a computational approach for identifying unstable or weakly stable regions of β-barrel membrane proteins. We define such regions as TM strands with energy by an empirical potential function significantly higher than expectation. Using the PagP enzyme for which NMR and mutant data are available, we show that the predicted weakly stable region and the identified key residue contributing to the instability are consistent with experimental observations. We have further identified several general strategies where β-barrel membrane proteins employ non-barrel elements to stabilize weakly stable regions, including out-clamps (19), in-plugs, and oligomerization. We then describe the calculated melting temperature, Tm, of the TM domains of the proteins. In addition, we found that there are often extensive and contiguous weakly stable regions in many β-barrel membrane proteins that can be used to accurately determine whether a membrane protein exists primarily in a monomeric or oligomeric state, and to identify the interface regions for protein–protein interactions in the TM domain. Our method can be generalized so that oligomerization state and interaction interfaces can be predicted from sequence information alone, without the knowledge of the three-dimensional structures.

Results

The physical model for membrane-embedded β-strands is discrete and minimalistic. It assumes neighboring strands register and interact through canonical strong H-bonds, weak H-bonds, and side-chain interactions. Details of this model and an empirical statistical potential function can be found in refs. 15 and 17 and are described in Methods and in supporting information (SI) Appendix.

Detecting Weakly Stable Regions by Empirical Potential Function.

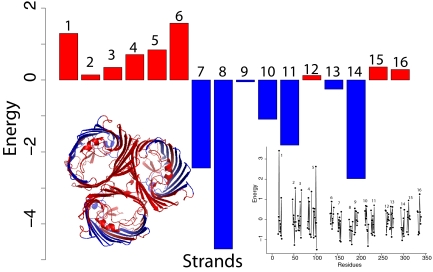
To demonstrate the utility of the empirical potential function, we first illustrate the detection of weakly stable regions in the TM domain of the protein OmpF. OmpF is a homotrimeric TM protein in which each subunit forms a pore that allows diffusion of small polar solutes across the outer membrane. After summing up the energetic contribution of individual TM residues, we found that the 8 strands with the highest overall energies are strands 1–6, 15, and 16, and are predicted as the weakly stable strands. It turns out that the strands involved in oligomerization are strands 1–5 and strand 16 (Fig. 1). Collectively, the weakly stable strands detected by the empirical potential function form the oligomerization interface (see also Fig. S2 in SI Appendix for other proteins). From the calculated energy profile of the protein OmpF, residues that contribute significantly to the strand instability include K16 in strand 1 and R100 in strand 5 (Fig. 1 Right Inset). These results provide an indication of the effectiveness of the empirical energy function and the correlation of weakly stable regions with structural characteristics of β-barrel membrane proteins.

Fig. 1.

Fig. 1.

Open in a new tab

The expected energy values of strands in the TM domain of OmpF. OmpF exists in trimeric form, with strands 1–5 and strand 16 forming the interaction surface. (Left Inset) The trimeric structure of OmpF. (Right Inset) The energetic contributions of individual residues. Among the 16 strands, strands 1–6 and strands 15 and 16 are found to have the highest overall energy values. These strands coincide with the protein–protein interaction interface.

Weakly Stable Regions in the TM Domain and Stabilization by Out-Clamps in PagP and α-Hemolysin.

PagP enzyme is a β-barrel outer membrane protein from Escherichia coli. It catalyzes the palmitate transfer from a phospholipid to a glucosamine unit of a lipid in the outer leaflet and reinforces the outer leaflet to protect E. coli from a host's immune response (19–21). PagP remains dormant when the outer membrane permeability barrier is intact but can respond adaptively and instantaneously to perturbations to restore the permeability barrier (22).

An important structural feature of PagP is its short amphipathic N-terminal α-helix, which closely packs against the TM strands (23). Both x-ray and NMR studies have shown strong interactions between the α-helix and the TM strands (10, 23). Although deletion of the helix does not affect the formation of a fully active protein in vivo, folding studies showed that the helix–strand interaction makes a major contribution to stabilize PagP (19). The N-terminal helix has been proposed to act as a postassembly clamp to the exterior of the barrel (we call it “out-clamp” here) to lock the protein in its native form once folding and insertion are complete (19).

Using a full space-filling atomic model of the structure (see SI Appendix and ref. 24 for details), we found that this helix interacts predominantly with strands B and D, instead of with strands B and C as reported in refs. 10 and 19, in which only the backbone ribbon diagram is considered. Among these, contacts with R59, L69, and Y87 account for the majority of the atomic interactions of barrel strands with the helix

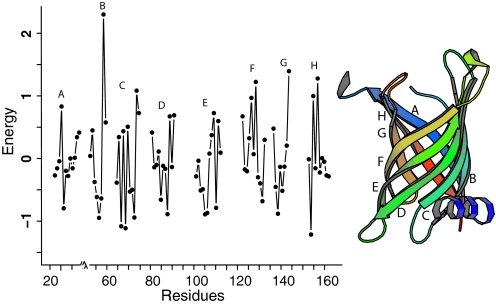
To assess the extent to which this helix stabilizes the TM strand, we quantify the stability of the strands using our empirical potential function. Fig. 2 shows the energy contribution at different positions of the TM strands in PagP. Our calculation indicates that strand B is the most unstable strand and has the highest energy, with the single-body energy term of residue R59 contributing most to its instability, despite the modest stabilizing effect of pairwise interactions involving R59.

Fig. 2.

Fig. 2.

Open in a new tab

The energy level of residues in the TM domain of PagP. Strand B has the highest overall energy and therefore is detected as the weakly stable strand. In wild-type PagP, this strand is stabilized by interactions with the N-terminal helix. Residue R59 contributes most to its instability, which is consistent with experimental results in ref. 19, in which it was found that, when R59 is mutated to L, the stabilizing interaction between strand B and the helix is largely abolished and the overall stability change is similar to the mutant when the N-terminal helix is truncated.

Experimental evidence is consistent with this result. Mutagenesis studies by Huysmans et al. (19) showed that the stability of the R59L mutant is similar to that of the mutant Δ(1–19), in which the entire helix is truncated. Our atomic model showed that residue R59 forms the strongest interactions with the N-terminal helix through hydrogen bonding with N12 and T16.

We found that the strategy of stabilizing the weakly stable region in the TM domain by barrel out-clamping is also used in α-hemolysin, a 14-strand barrel formed by 7 identical chains of strand hairpins. Among the top 4 most unstable residues in the hairpin, 2 (K110 and Y148) are stabilized by a barrel out-clamp through extensive H-bond interactions with the N-terminal of the soluble domain (K110 with Q150B and N173B; Y148 with N178B).

Stabilization of Weakly Stable Regions by In-Plug Domains.

PagP is uniquely endowed with a local strategy for stabilizing the weakly stable strand B. The sequentially neighboring N-terminal helix can effectively interact and stabilize this β-strand. We hypothesize that the need to stabilize weakly stable regions is not restricted to PagP. When the high energy region is more extensive and involves additional strands, a local solution using a single helix in the vicinity of the strands may not be possible.

Our energy model suggests that some of the TM strands of the ferric hydroxamate uptake receptor protein [FhuA; Protein Data Bank (PDB) ID code 2FCP] are weakly stable regions. Although FhuA does not have any barrel out-clamps, a distinctive characteristic of FhuA is the large in-plug domain formed by a mixture of two α-helices and a 4-strand β-sheet. This in-plug domain most likely provides interactions to stabilize the TM β-strands. In this case the interactions required for stabilization are extensive and can only be satisfied by an in-plug domain of significant size, unlike the local solution in PagP.

In-plugs are common in β-barrel membrane proteins and are important for controlling the transport of hydrophobic substrates (25). In-plugs are often formed by interstrand loops and the N terminus, and they occlude the interior of the barrel proteins and define the barrier characteristics of the cell wall. Our study here suggests there exists yet another general role for in-plug domains, namely, to stabilize the otherwise unstable TM domains.

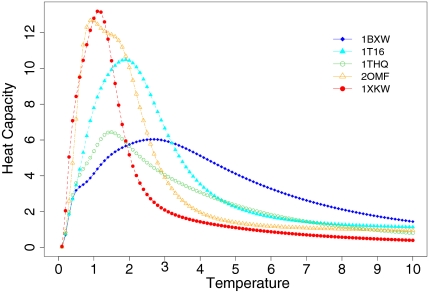
A more accurate indicator of protein stability than energy value is the relative melting temperature, Tm, which can be calculated by using a statistical mechanics model. Tm is computed as the temperature at which the heat capacity reaches its maximum (see Methods and SI Appendix). Fig. 3 shows the calculated heat capacities of several β-barrel membrane proteins at different relative temperatures. From calculated melting temperatures, we find, in addition to FhuA, that FepA (PDB ID code 1FEP), BtuB (PDB ID code 1NQE), transporter FecA (PDB ID code 1KMO), and FadL (PDB ID code 1T16) from E. coli, as well as FptA (PDB ID code 1XKW) from Pseudomonas aeruginosa and NalP (PDB ID code 1UYN) from Neisseria meningitidis show instability in their TM domains (Table S1 in SI Appendix). The in-plug domains found in these proteins are important in stabilizing their respective protein's strands.

Fig. 3.

Fig. 3.

Open in a new tab

Calculated heat capacities of OmpA (PDB ID code 1BXW), FadL (PDB ID code 1T16), PagP (PDB ID code 1THQ), OmpF (PDB ID code 2OMPF), and FptA (PDB ID code 1XKW) proteins at different temperature. These values are for the strands in the TM domain and are obtained based on the calculation of the partition function of the barrel assuming a simplified conformational state model. The temperature at which heat capacity reaches maximum corresponds to the melting temperature, Tm.

Extended Weakly Stable Regions and Interfaces of Protein–Protein Interactions.

Yet another possibility for stabilization of proteins with extensive high-energy regions in their TM domains is to interact with another membrane protein, i.e., by interacting with a similarly unstable region on a partner protein. Oligomerization or other types of protein–protein interactions in the membrane domain, as shown in the example of OmpF (Fig. 1) occur due to this type of stabilization.

We have examined the 7 oligomers among the set of 25 β-barrel membrane proteins studied. Altogether, we found that there are 57 strands with energy higher than the average strand energy of the protein. Among these strands, 38 (66.6%) are found to be located in interfaces of protein–protein interactions. For the 59 stable strands with a below-protein-specific average energy value, 48 (81.3%) are found to be located outside the protein–protein interface (Fig. S2 in SI Appendix). Overall, we found that strands with higher-than-average energy have greater deviation from protein-specific averages for oligomers (mean = 1.59) than for monomers (mean = 1.12). These observations further indicate that variation in strand energy correlates with preference for protein–protein interaction.

Stability of TM β-Barrels as Measured by Tm.

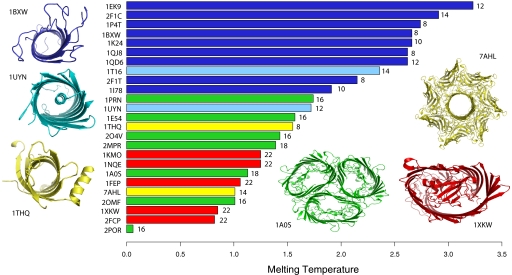
We have calculated the relative melting temperatures Tm as a measure of overall protein stability of the TM domains of the 25 β-barrel membrane proteins with known structures. These proteins have <32% pairwise sequence identity. Our results (shown in Fig. 4) indicate that these membrane proteins show clear patterns in Tm. We find that oligomeric proteins are less stable (i.e., Tm is lower), with Tm < 1.8. In contrast, all proteins with Tm > 1.8 are monomers. In addition, with the exception of FadL (PDB ID code 1T16), all monomers stabilized by in-plugs (light blue and red in Fig. 4) and out-clamps (yellow in Fig. 4) are unstable by the criterion of Tm < 1.8.

Fig. 4.

Fig. 4.

Open in a new tab

The relative stabilities of 25 nonhomologous β -barrel membrane proteins are measured by computed melting temperature, Tm, of the TM strands. The Tm values are plotted against the PDB names of the proteins. The number of TM strands in each protein is labeled at the end of the bar. Monomers that are stable without the aid of out-clamps and in-plugs are in dark blue and are represented by OmpA (PDB ID code 1BXW). Monomers with small in-plugs are in light blue (represented by NalP; PDB ID code 1UYN). Monomers stabilized by out-clamps are in yellow. They include PagP (PDB ID code 1THQ) and α-hemolysin (PDB ID code 7AHL). Outer-membrane proteins stabilized by oligomerization are green (e.g., ScrY; PDB ID code 1A0S). Monomers stabilized by large in-plugs are red (e.g., FptA; PDB ID code 1XKW). All stable monomers have Tm > 1.8. With the exception of FadL (PDB ID code 1T16), unstable monomers requiring stabilization by out-clamps or large in-plugs all have lower stability, with Tm < 1.8. Oligomeric outer-membrane proteins can be further distinguished from unstable monomers requiring either out-clamps or in-plugs.

Prediction of Oligomerization State and Interface for Protein–Protein Interaction.

We have further developed a computational method to identify β-barrel membrane proteins that oligomerize. Our method can distinguish them from other β-barrel membrane proteins with barrel out-clamps or in-plugs. Briefly, we calculate an index ϱ that summarizes the energy deviation of unstable strands from the overall expected energy value 𝔼(E): ϱ = √[Σi Ei − 𝔼(E)]2/nu, where Ei is the energy of unstable strand i, and nu is the number of unstable strands (see Methods for more details). Index ϱ essentially describes the average deviation of energy values of unstable strands from the mean energy of all strands. ϱ is formulated based on the observation that high energy strands in oligomers have an overall large deviation from the average strand energy (see Fig. S3 in SI Appendix). If ϱ > 2.5, we predict that the protein in question forms an oligomer. Using this improved criterion over the simple energy value, we find that 38 among the 50 TM strands (76%) structurally located in protein–protein interfaces are correctly identified, and 53 among 66 noninterface strands (80.3%) are correctly identified.

We have carried out a leave-one-out test to evaluate our prediction method. We take each of the 25 proteins out in turn as the test protein and construct an empirical energy potential function using the remaining 24 nonhomologous protein structures (15, 17). In this test, all known oligomers are correctly predicted. Only 1 monomer, ferric hydroxamate uptake receptor (FhuA; PDB ID code 2fcp) from E. coli, is incorrectly predicted as an oligomer. The other 17 monomers, including those containing in-plugs or out-clamps, are predicted correctly. This prediction has an accuracy of 96%, a sensitivity of 100%, and a specificity of 94%. Because these predictions are results of leave-one-out tests, the achieved accuracy indicates that our approach does not depend on the specific choice of data used in constructing the energy function, and our prediction results are unlikely to change if another β-barrel membrane protein structure is added to the data set.

To predict the interface of protein–protein interactions in oligomers, we use a slightly modified strand energy model to identify the largest set of consecutive strands with Ei ≥ 𝔼(E) (see SI Appendix). These strands are then predicted to form the interacting interface. Our results from the leave-one-out test (Table 1) show an overall prediction accuracy of 78% in identifying the correct interfacial strands, with a sensitivity of 76% and a specificity of 80% (see SI Appendix for definitions).

Table 1.

Prediction results

PDB ID code Structure
 Sequence
PPI TP Non-PPI TN PPI TP Non-PPI TN
2MPR 8 7 10 9 8 6 10 10
2OMF 7 7 9 6 7 6 9 8
1E54 9 7 7 7 9 8 7 7
2POR 7 7 9 8 5 5 9 7
2O4V 6 4 10 7 6 4 14 13
1A0S 8 6 10 10 7 4 11 11
1PRN 5 0 11 6 5 1 11 7
Total 50 38 66 53 47 34 71 63
Open in a new tab

Prediction of protein–protein interfaces (PPI) in the oligomers of β-barrel membrane proteins based on leave-one-out tests from structures and from sequences. When only sequence information is used, the strands predicted by the ProfTMB method to be in the TM domain are included. These strands may not be the same as the ones in the solved structure. TP, strands in interface predicted correctly; TN, strands not in interface predicted correctly. Using structure information, accuracy is 78%, sensitivity is 76%, and specificity is 80%. Using sequence information only of correctly given strands, accuracy is 82%, sensitivity is 72% and specificity is 88%. The overall accuracy using sequence information is 80% (accuracy in correctly predicting strand sequences by ProfTMB) × 82% = 66%.

Prediction of Oligomerization State and Interface from Sequence.

In our calculation, we assume the canonical strand interaction model (15, 17, 26, 27) (also see SI Appendix) and require only knowledge of the start position of the TM strands. Because the amount of required structural information is very small, our method can also predict oligomerization state and identify the interface for protein–protein interaction by using sequence information only. In this case, we use the estimated strand start position from the ProfTMB server (12).

Among the 24 β-barrel membrane proteins with known structures, the oligomerization states of 22 are correctly predicted in leave-one-out tests, with all of 7 oligomers correctly identified. An exception is PagP, which was not identified as a β-barrel membrane protein by the ProfTMB server and therefore was not included. Only 2 monomers (PDB ID codes 2FCP and 1UYN) are misclassified. Among these 2, the output TM sequences for NalP (PDB ID code 1UYN; N. meningitidis) from ProfTMB contain 2 non-β-strand sequence segments, which increased the overall energy of the protein significantly, leading to misclassification. Overall, our prediction has an accuracy of 92%, a sensitivity of 100%, and a specificity of 88%.

Using the sequences of the 7 proteins predicted to be oligomers, we are able to identify 72% of the strands at the oligomerization interfaces (Table 1). In the poorest prediction (porin from Rhodopseudomonas blastica), 1 of 5 interfacial strands and 7 of 11 noninterfacial TM strands are correctly identified (Table 1). The strand misclassification in this protein is due to the fact that the large in-plug domains interact strongly with strands located outside the interface but only weakly with interfacial strands. Overall, if predictions of TM strands by the ProfTMB server are correct, our prediction accuracy for interfacial strands is 82%. Combined with an estimated accuracy of 80% for strand prediction by ProfTMB, the overall accuracy of our prediction of interface strands using only sequence information is 66%.

Discussion

Weakly Stable Regions in β-Barrel Membrane Proteins.

Although the specifics are unclear, recent experimental studies on multiple conformations and the transient opening of membrane enzyme PagP can be interpreted as strongly suggesting the existence of unstable regions in membrane proteins (10, 19, 28). This dual nature of high energy on the one hand and conformational adaptability on the other may be general for the biological function of membrane proteins, which often require conformational changes (22, 28, 29). Although these conformational changes are initiated by exogenous perturbations, such as ligand binding, membrane depolarization, and limitation of divalent cations, the ability to adapt to such changes is already built into the protein structures in the form of weakly stable regions. Our results indicate that these unstable regions can be detected computationally for β-barrel membrane proteins. In addition, we find that proteins employ barrel out-clamps, in-plugs, and oligomerization as general strategies to stabilize unstable TM regions in the ground state.

Oligomerization of Membrane Proteins.

In complex cellular machineries required for biological processes, such as allosteric catalysis, signal transduction, and transcription regulation, oligomerization and other forms of protein–protein interactions play central roles (30). The importance of the oligomerization of integral membrane proteins is well-recognized, because most membrane protein domains are encoded by separate polypeptide chains (31). However, compared with soluble proteins, we are at a very early stage in the study of membrane protein oligomerization (32). In this work, we show that oligomerization in the TM domain of outer membrane proteins can be elucidated computationally through recognition and characterization of weakly stable regions, and the oligomerization interfaces can often be predicted.

The connection between unstable regions and protein–protein interactions has been clearly established in previous studies of soluble proteins. Global computational studies of known protein structures based on empirical energy functions showed that the interfacial regions on protein surfaces have abnormally high energy values when the binding partners are absent but become stabilized when the partners are added (33, 34). These studies suggest that the interface regions of protein–protein interactions are often intrinsically high energy, although they may not necessarily be fully disordered. Our results indicate that high-energy regions in the TM domain are also often implicated as surfaces for protein–protein interaction. In the TM domains, the loss of side-chain entropy upon binding will be less significant than that in soluble proteins, and therefore the stabilizing effect upon binding will be more pronounced.

In studies on the origin of symmetric homooligomeric protein assembly, Lukatsky et al. (35) and André et al. (36) suggested that for large protein assemblies to contribute to fitness, the primordial protein complexes must be significantly populated to be available for extensive optimization and to contribute to function during evolution. These complexes therefore must have their energy reduced upon binding. Extensive simulation of protein–protein docking indicates that symmetric protein–protein complexes predominate in low-energy assemblies, and this bias toward low energy is sufficient for the emergence of protein–protein interactions (36, 37). Our study suggests that reducing the energy of weakly stable regions may be a general physical driving force for the primordial protein complex to be highly populated in membrane proteins, which leads to the eventual emergence of modern membrane protein complexes.

Computationally Derived Energetic Models of Membrane Proteins.

Studying membrane proteins poses a significant challenge because it is difficult to obtain purified membrane fractions and to derive high-resolution structures (32). Our current understanding of the physical determinants governing membrane protein structures is not yet complete. For example, despite numerous successes (6, 12, 13, 15–18, 38, 39), we cannot yet accurately predict the full three-dimensional structures of β-barrel membrane proteins from sequence information alone. Further challenges come from the fact that functional membrane proteins are often the result of the assembly of multiple subunits, each consisting of one or more polypeptide chains. The problem of finding the correct protein–protein interactions is reminiscent of the protein–protein docking problem, a well known difficult problem despite recent progress (40).

A promising approach is to bootstrap ourselves through these difficulties by developing physical models, with parameters estimated from bioinformatic analysis of known sequences and structures to gain insight on the important physical factors and to make testable predictions. The success of this approach is illustrated by the work of Hessa et al. (41), in which the chemical code for α-helical membrane protein translocation was independently obtained from elegantly designed experimental studies and from bioinformatic estimation. In our computational study, we have developed models characterizing the stability and other thermodynamic properties (such as melting temperature) of the TM domain. The approach developed in this study requires a detailed energy function that goes beyond coarse-grained models, such as the Gaussian network model. Although we have simplified our model by adopting a reduced conformational space, the improved prediction using melting temperature over energy value is significant. This simplified model and the enumeration of conformations, including nonnative ones, can capture key factors determining the native state of β-barrel membrane proteins, even though the energy function is not yet perfect.

Our results show that the key stabilization interactions in PagP can be detected, the weakly stable regions in outer membrane proteins can be identified, and the oligomerization state and interfaces of protein–protein interaction can be predicted from either structure or sequence. These predictions are based on a very simple physical model that does not account for the existence of non-barrel structural elements explicitly. This model's detection of high-energy regions leads to the recognition of the existence of non-barrel elements. Such predictions can aid in the identification of the biological forms of β-barrel membrane proteins, which may require quaternary interactions between monomers. In addition, the involvement of non-barrel elements may facilitate understanding of the biological functions of β-barrel membrane proteins, as in the case of the out-clamp in PagP (22) and the latching loop L2 for ion selectivity in OmpF (9). Furthermore, it is envisioned that improvement in the crystallization of membrane proteins may be achieved if mutations at selected sites can be made such that these proteins are stabilized. Because predictions can be made from sequences alone, such applications can be made for a large number of β-barrel membrane proteins.

Challenges and Future Development.

Our current computational model is based on many simplifying assumptions. It is likely that the overall topology, orientation, and structure of a membrane protein are not only determined by the sequence of the β-barrel membrane protein but are also influenced by other factors of the organism in which the protein is expressed. For example, interactions between amino acid residues and the correct lipids of the outer membrane are important for determining the topology and the assembly of the membrane protein (42). The formation of a stable OmpLA dimer is possible only with the presence of a substrate molecule located in the interface (43). Furthermore, interactions of β-barrel membrane proteins with chaperone proteins, translocons, and the β-barrel assembly machinery during the biogenesis process may also play an important role in deciding the final protein structure. In addition, whether two predicted interfaces directly interact, the numeric state or distribution of states of the oligomerization, the number of monomeric units involved, and how they are docked against each other remain challenging problems. Computational models currently do not accurately account for these factors, and much work remains before our understanding is complete.

Materials

We take 25 β-barrel membrane proteins with known structures as our data set. Each pair of proteins has <32% pairwise-sequence identity (see SI Appendix). For simplification, we take the canonical model of membrane β-strands based on the physical model of β-strand interactions described in refs. 15, 17, 26, and 27. A strand is assumed to have a length of 16 residues located in 8 different regions (see SI Appendix). The energetic contribution of each residue E(i) has 4 components: energy of the individual residue located in the specific environment, E1; the interaction energy with a neighboring strand through the backbone strong H-bond, ESH; the side-chain interaction, ESC; and the backbone weak H-bond, EWH.

Assuming a reduced conformational space that each strand can slide up or down ≤3 positions, a strand can have 7 different registrations with its neighbor. We can exhaustively enumerate all conformations for proteins with up to 14 strands. For larger proteins, we have developed an approximate method to compute their thermodynamic properties (see SI Appendix). To calculate the expected energy values of a central strand, we calculate the energy of its 7 × 7 = 49 possible registrations with its 2 neighbors and take the expected energy value. The relative melting temperature, Tm, of the TM β-barrel strands is computed as Tm = arg maxT Cv = arg maxT [{𝔼(E2) − 𝔼(E)2}/T2 ]. Additional details can be found in SI Appendix.

Supplementary Material

Supporting Information
supp_106_31_12735__index.html (865B, html)

Acknowledgments.

We thank Drs. Larisa Adamian, William Dowhan, Linda Kenney, Renhao Li, Kevin MacKenzie, and Zhifeng Shao for helpful discussions; Dr. R. Scott Prosser for sharing NMR data on PagP; Hsiao-Mei Lu for help; and Michael Montesano for reading the manuscript. This work was supported by National Institutes of Health Grants GM079804-01A1 and GM081682, National Science Foundation Grants DBI-0646035 and DMS-0800257, and Office of Naval Research Grant N00014-09-1-0028. H.N. was supported by a Fulbright Fellowship and the Higher Education Commission of Pakistan.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/cgi/content/full/0902169106/DCSupplemental.

References

  • 1.Hong H, Joh N, JU B, LK T. Methods for measuring the thermodynamic stability of membrane proteins. Methods Enzymol. 2009;455:213–236. doi: 10.1016/S0076-6879(08)04208-0. [DOI] [PubMed] [Google Scholar]
  • 2.Tamm L, Arora A, Kleinschmidt J. Structure and assembly of β-barrel membrane proteins. J Biol Chem. 2001;276:32399–32402. doi: 10.1074/jbc.R100021200. [DOI] [PubMed] [Google Scholar]
  • 3.Tamm LK, Hong H, Liang B. Folding and assembly of β-barrel membrane proteins. Biochim Biophys Acta. 2004;1666:250–263. doi: 10.1016/j.bbamem.2004.06.011. [DOI] [PubMed] [Google Scholar]
  • 4.Burgess N, Dao T, Stanley A, Fleming K. Beta-barrel proteins that reside in the Escherichia coli outer membrane in vivo demonstrate varied folding behavior in vitro. J Biol Chem. 2008;283:26748–26758. doi: 10.1074/jbc.M802754200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Gentle I, Burri L, Lithgow T. Molecular architecture and function of the Omp85 family of proteins. Mol Microbiol. 2005;58:1216–1225. doi: 10.1111/j.1365-2958.2005.04906.x. [DOI] [PubMed] [Google Scholar]
  • 6.Wimley WC. The versatile β-barrel membrane protein. Curr Opin Struct Biol. 2003;13:404–411. doi: 10.1016/s0959-440x(03)00099-x. [DOI] [PubMed] [Google Scholar]
  • 7.Schulz GE. The structure of bacterial outer membrane proteins. Biochim Biophys Acta. 2002;1565:308–317. doi: 10.1016/s0005-2736(02)00577-1. [DOI] [PubMed] [Google Scholar]
  • 8.Haltia T, Freire E. Forces and factors that contribute to the structural stability of membrane proteins. Biochim Biophys Acta. 1995;1228:1–27. doi: 10.1016/0005-2728(94)00161-w. [DOI] [PubMed] [Google Scholar]
  • 9.Phale P, et al. Stability of trimeric ompf porin: The contributions of the latching loop l2. Biochemistry. 1998;37:15663–15670. doi: 10.1021/bi981215c. [DOI] [PubMed] [Google Scholar]
  • 10.Evanics F, Hwang P, Cheng Y, Kay L, Prosser R. Topology of an outer-membrane enzyme: Measuring oxygen and water contacts in solution NMR studies of PagP. J Am Chem Soc. 2006;128:8256–8264. doi: 10.1021/ja0610075. [DOI] [PubMed] [Google Scholar]
  • 11.Van Gelder P, et al. Voltage sensing in the phoe and ompf outer membrane porins of escherichia coli: Role of charged residues. J Mol Biol. 1997;269:468–472. doi: 10.1006/jmbi.1997.1063. [DOI] [PubMed] [Google Scholar]
  • 12.Bigelow H, Rost B. PROFtmb: A web server for predicting bacterial transmembrane beta barrel proteins. Nucleic Acids Res. 2006;34:W186–W188. doi: 10.1093/nar/gkl262. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Randall A, Cheng J, Sweredoski M, Baldi P. TMBpro: Secondary structure, beta-contact and tertiary structure prediction of transmembrane beta-barrel proteins. Bioinformatics. 2008;24:513–520. doi: 10.1093/bioinformatics/btm548. [DOI] [PubMed] [Google Scholar]
  • 14.Wimley WC. Toward genomic identification of β-barrel membrane proteins: Composition and architecture of known structures. Protein Sci. 2002;11:301–312. doi: 10.1110/ps.29402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Jackups R, Jr, Liang J. Interstrand pairing patterns in beta-barrel membrane proteins: The positive-outside rule, aromatic rescue, and strand registration prediction. J Mol Biol. 2005;354(4):979–993. doi: 10.1016/j.jmb.2005.09.094. [DOI] [PubMed] [Google Scholar]
  • 16.Jackups R, Jr, Cheng S, Liang J. Sequence motifs and antimotifs in beta-barrel membrane proteins from a genome-wide analysis: The Ala–Tyr dichotomy and chaperone binding motifs. J Mol Biol. 2006;363:611–623. doi: 10.1016/j.jmb.2006.07.095. [DOI] [PubMed] [Google Scholar]
  • 17.Jackups R, Jr, Liang J. Combinatorial analysis for sequence and spatial motif discovery in short sequence fragments. IEEE/ACM Trans Comp Biol Bioinform. 2008 doi: 10.1109/TCBB.2008.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Waldispuhl J, Donnell C, Devadas S, Clote P, Berger B. Modeling ensembles of transmembrane beta-barrel proteins. Proteins. 2008;71:1097–1112. doi: 10.1002/prot.21788. [DOI] [PubMed] [Google Scholar]
  • 19.Huysmans G, Radford S, Brockwell D, Baldwin S. The N-terminal helix is a post-assembly clamp in the bacterial outer membrane protein PagP. J Mol Biol. 2007;373:529–540. doi: 10.1016/j.jmb.2007.07.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Bishop R, et al. Transfer of palmitate from phospholipids to lipid A in outer membranes of gram-negative bacteria. EMBO J. 2000;19:5071–5080. doi: 10.1093/emboj/cdd507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Bishop R, Lo E, Khan M, El Z, Jia W. Enzymology of lipid A palmitoylation in bacterial outer membranes. J Endotoxin Res. 2004;10:107–112. doi: 10.1179/096805104225004004. [DOI] [PubMed] [Google Scholar]
  • 22.Bishop R. Structural biology of membrane-intrinsic beta-barrel enzymes: Sentinels of the bacterial outer membrane. Biochim Biophys Acta. 2008;1778:1881–1896. doi: 10.1016/j.bbamem.2007.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Ahn V, et al. A hydrocarbon ruler measures palmitate in the enzymatic acylation of endotoxin. EMBO J. 2004;23:2931–2941. doi: 10.1038/sj.emboj.7600320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Adamian L, Liang J. Helix-helix packing and interfacial pairwise interactions of residues in membrane proteins. J Mol Biol. 2001;311:891–907. doi: 10.1006/jmbi.2001.4908. [DOI] [PubMed] [Google Scholar]
  • 25.van den Berg B. The FadL family: Unusual transporters for unusual substrates. Curr Opin Struct Biol. 2005;15:401–407. doi: 10.1016/j.sbi.2005.06.003. [DOI] [PubMed] [Google Scholar]
  • 26.Wouters M, Curmi P. An analysis of side chain interactions and pair correlations within antiparallel β-sheets: The differences between backbone hydrogen-bonded and non-hydrogen-bonded residue pairs. Proteins. 1995;22:119–131. doi: 10.1002/prot.340220205. [DOI] [PubMed] [Google Scholar]
  • 27.Ho B, Curmi P. Twist and shear in β-sheets and β-ribbons. J Mol Biol. 2002;317:291–308. doi: 10.1006/jmbi.2001.5385. [DOI] [PubMed] [Google Scholar]
  • 28.Hwang P, Bishop R, Kay L. The integral membrane enzyme PagP alternates between two dynamically distinct states. Proc Natl Acad Sci USA. 2004;101:9618–9623. doi: 10.1073/pnas.0402324101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Li R, et al. Activation of integrin alphaIIbbeta3 by modulation of transmembrane helix associations. Science. 2003;300:795–798. doi: 10.1126/science.1079441. [DOI] [PubMed] [Google Scholar]
  • 30.Marianayagam N, Sunde M, Matthews J. The power of two: Protein dimerization in biology. Trends Biochem Sci. 2004;29:618–625. doi: 10.1016/j.tibs.2004.09.006. [DOI] [PubMed] [Google Scholar]
  • 31.Liu Y, Gerstein M, Engelman D. Transmembrane protein domains rarely use covalent domain recombination as an evolutionary mechanism. Proc Natl Acad Sci USA. 2004;101:3495–3497. doi: 10.1073/pnas.0307330101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Elofsson A, von Heijne G. Membrane protein structure: prediction versus reality. Annu Rev Biochem. 2007;76:125–140. doi: 10.1146/annurev.biochem.76.052705.163539. [DOI] [PubMed] [Google Scholar]
  • 33.Bastolla U, Farwer J, Knapp EW, Vendruscolo M. How to guarantee optimal stability for most representative structures in the protein data bank. Proteins. 2001;44:79–96. doi: 10.1002/prot.1075. [DOI] [PubMed] [Google Scholar]
  • 34.Hu C, Li X, Liang J. Developing optimal non-linear scoring function for protein design. Bioinformatics. 2004;20:3080–3098. doi: 10.1093/bioinformatics/bth369. [DOI] [PubMed] [Google Scholar]
  • 35.Lukatsky D, Shakhnovich B, Mintseris J, Shakhnovich E. Structural similarity enhances interaction propensity of proteins. J Mol Biol. 2007;365:1596–1606. doi: 10.1016/j.jmb.2006.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.André I, Strauss C, Kaplan D, Bradley P, Baker D. Emergence of symmetry in homooligomeric biological assemblies. Proc Natl Acad Sci USA. 2008;105:16148–16152. doi: 10.1073/pnas.0807576105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Levy E, Erba E, Robinson C, Teichmann S. Assembly reflects evolution of protein complexes. Nature. 2008;453:1262–1265. doi: 10.1038/nature06942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Fariselli P, Martelli P, Casadio R. A new decoding algorithm for hidden Markov models improves the prediction of the topology of all-beta membrane proteins. BMC Bioinformatics. 2005;6:S12. doi: 10.1186/1471-2105-6-S4-S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Marani P, et al. New Escherichia coli outer membrane proteins identified through prediction and experimental verification. Protein Sci. 2006;15:884–889. doi: 10.1110/ps.051889506. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Mendez R, Leplae R, Lensink M, Wodak S. Assessment of CAPRI predictions in rounds 3–5 shows progress in docking procedures. Proteins. 2005;60:150–169. doi: 10.1002/prot.20551. [DOI] [PubMed] [Google Scholar]
  • 41.Hessa T, et al. Molecular code for transmembrane-helix recognition by the Sec61 translocon. Nature. 2007;450:1026–1030. doi: 10.1038/nature06387. [DOI] [PubMed] [Google Scholar]
  • 42.Bogdanov M, Heacock P, Dowhan W. A polytopic membrane protein displays a reversible topology dependent on membrane lipid composition. EMBO J. 2002;21:2107–2116. doi: 10.1093/emboj/21.9.2107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Stanley A, Chuawong P, Hendrickson T, Fleming K. Energetics of outer membrane phospholipase A (OMPLA) dimerization. J Mol Biol. 2006;358:120–131. doi: 10.1016/j.jmb.2006.01.033. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_106_31_12735__index.html (865B, html)
0902169106_Appendix_PDF.pdf (405.4KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES