Feasibility of Using Limited-Population-Based Average R₁₀ for Pharmacokinetic Modeling of Osteosarcoma Dynamic Contrast-Enhanced MRI Data

Abstract

Retrospective analyses of clinical dynamic contrast-enhanced (DCE) MRI studies may be limited by failure to measure the longitudinal relaxation rate constant (R₁) initially, which is necessary for quantitative analysis. In addition, errors in R₁ estimation in each individual experiment can cause inconsistent results in derivations of pharmacokinetic parameters, K^trans and v_e, by kinetic modeling of the DCE-MRI time course data. A total of 18 patients with lower extremity osteosarcomas underwent multislice DCE-MRI prior to surgery. For the individual R₁ measurement approach, the R₁ time course was obtained using the two-point R₁ determination method. For the average R₁₀ (pre-contrast R₁) approach, the R₁ time course was derived using the DCE-MRI pulse sequence signal intensity equation and the average R₁₀ value of this population. The whole tumor and histogram median K^trans (0.57 ± 0.37 and 0.45 ± 0.32 min⁻¹) and v_e (0.59 ± 0.20 and 0.56 ± 0.17) obtained with the individual R₁ measurement approach are not significantly different (paired t test) from those (K^trans: 0.61 ± 0.46 and 0.44 ± 0.33 min⁻¹; v_e: 0.61 ± 0.19 and 0.55 ± 0.14) obtained with the average R₁₀ approach. The results suggest that it is feasible, as well as practical, to use a limited-population-based average R₁₀ for pharmacokinetic modeling of osteosarcoma DCE-MRI data.

Introduction

T₁-weighted dynamic contrast-enhanced (DCE) MRI has in recent years been widely utilized in studies of many different types of cancer (1), frequently for purposes of diagnosis (2–5) and assessment of the effectiveness of antiangiogenic therapies (6–10). For interpretation of the DCE-MRI signal time course, there are generally three approaches (11): a) qualitative assessment of the curve shape, such as wash-out, plateau, and persistence; b) empirical quantitation, such as maximum slope, percent signal intensity change; and c) analytical pharmacokinetic modeling. The results from the first two approaches depend on DCE-MRI pulse sequence parameters, contrast agent dose and injection rate, magnetic field strength, and vendor platform, etc (11–13). These data acquisition details vary greatly between institutions, thus limiting DCE-MRI study reproducibility and comparability between different imaging sites. The analytical approach is more sophisticated, and also the more desirable. Unlike the first two approaches, analytical modeling of DCE-MRI data extracts pharmacokinetic parameters that are in principle independent of data acquisition details mentioned above. This data analysis method, therefore, should improve study reproducibility, enable meaningful comparison of results from different groups, and be especially important for multi-center trial studies. The extracted pharmacokinetic parameters from analytical modeling of DCE-MRI time course data are usually variants of: K^trans, a rate constant for contrast agent plasma/interstitium transfer, and v_e, the interstitial space volume fraction (the putative contrast agent distribution volume).

Using a semi-quantitative approach, we reported that the histogram amplitude of initial slope of DCE-MRI signal time course correlated significantly with necrosis percentage of osteogenic and Ewing sarcoma, which is an important indicator of the effectiveness of chemotherapy (14). For pharmacokinetic modeling of DCE-MRI data, both the determination of arterial input function (AIF) and the measurement of longitudinal relaxation rate constant, R₁ (= 1/T1) [either region of interest (ROI) or pixel by pixel R₁], time course are critical to the accuracy of absolute quantitation of K^trans and v_e (11–13). In a previous study (11), we have shown that it is feasible and practical to use a limited-population-based average AIF for kinetic modeling of osteosarcoma DCE-MRI data of a larger population. For R₁ measurement, two methods are often used: a) two-point R₁ determination method (15, 16) by comparing signal intensities of the T1-weighted DCE-MR_I images with those of the proton density images acquired prior to contrast injection or b) multiple flip angle method (17). In the former approach, however, proton density images are sometimes not collected due to time constraints in the clinical setting or poor planning for a clinical DCE-MRI study. This results in great difficulty in retrospective quantitative analysis of DCE-MRI data. Furthermore, possible patient motion between the acquisitions of the proton density and the DCE-MRI series may cause errors in R₁ estimation or require motion correction when comparing signal intensities of the two image series. In the latter approach, any inconsistency between flip angle images such as scale factor mis-calibration or motion can lead to major systematic errors in R₁ measurement (18). A recent study (18) demonstrates that fixing the pre-contrast R₁, R₁₀, makes it possible to obtain more stable measures of the vascular properties using DCE-MRI, while still yielding pharmacokinetic results consistent with those when actual R₁₀ values were measured.

In this study, R₁₀ values were measured using the two-point R₁ determination method in a limited population of patients with osteosarcomas. We sought to assess the feasibility of calculating R₁ values of the DCE-MRI time course using a limited-population-based average R₁₀ for the purpose of pharmacokinetic modeling of osteosarcoma DCE-MRI data of a larger population.

Materials and Methods

Patients

Prior to definitive surgery, 18 patients (mean age: 16 years, range: 10–29 years) with osteosarcomas in the lower extremity underwent a routine clinical MRI protocol, in which a DCE-MRI scan was added for the purpose of evaluating the efficacy of chemotherapy in inducing tumor necrosis. The DCE-MRI study was conducted under an Institutional Review Board-approved protocol, and the written consent was obtained from each patient prior to the DCE-MRI scan.

Data Acquisition

All the MRI studies were performed with a 1.5T GE Excite system (General Electric Medical Systems, Milwaukee, WI, USA). An extremity knee coil was used for RF transmission and reception. Before the DCE-MRI study was conducted, a standard clinical MRI exam was performed through the tumor. Axial T₁-weighted and fat-suppressed fast spin-echo T₂-weighted images were obtained with as small a field of view (FOV) as possible. Longitudinal (coronal and/or sagittal) T₁-weighted and fat-suppressed fast spin-echo T₂-weighted images through the entire bone were also obtained with a small FOV. These were followed by proton density MRI and the T₁-weighted DCE-MRI study in the sagittal plane, and then post-contrast axial fat-suppressed T₁-weighted MRI. For DCE-MRI data acquisition, a fast multiplanar spoiled gradient echo sequence was employed with a 30o flip angle (α), 2.9 ms TE, 7.5–9.0 ms TR, 20–24 cm FOV, and 256×128 matrix size zero filled to 256×256 during image reconstruction. The entire tumor was imaged with 8–11 sagittal slices of 10–12 mm thickness and zero gap. The total DCE-MRI acquisition time was about 5–10 min with 7–10 sec temporal resolution and 30–60 time course data points. At the beginning of the sixth image set (data point) acquisition, Gd-DTPA contrast agent (Magnevist; Berlex Laboratories, Wayne, NJ, USA) at a dose of 0.1 mmol/kg was administered intravenously at a rate of 1 cc/sec or 2 cc/sec by an MR-compatible programmable power injector (Spectris; Medrad, Indianola, PA, USA). The patient often arrived at the MRI suite with the IV catheter already in place because he/she was undergoing other clinical procedures during the same visit. The injection rate was determined according to the location and the size of the IV catheter. Proton density images were acquired for the purpose of determining R1 for each DCE-MRI data point, using the same pulse sequence with a 30o flip angle, 2.0 ms TE, 350 ms TR, and DCE-MRI-matching slice number, thickness and location.

DCE-MRI Data Analysis

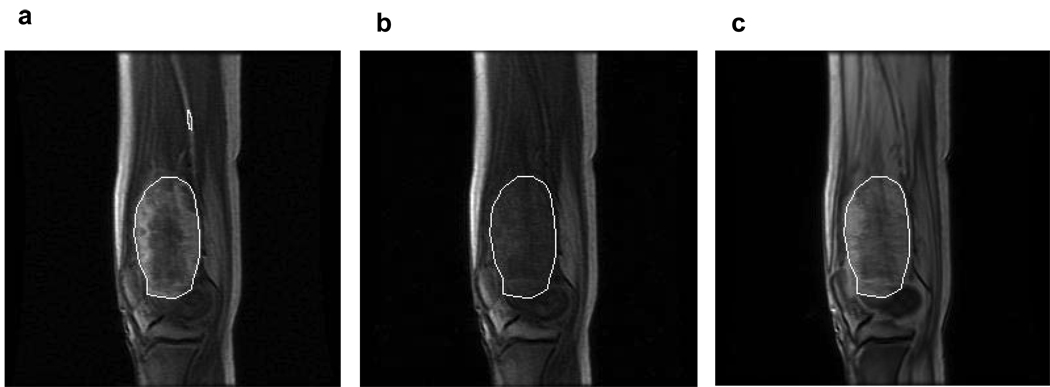
One ROI was manually drawn by an experienced radiologist (DMP) on each post-contrast DCE-MRI image slice that showed contrast enhancement in the tumor region (white ROI in Figure 1a). The ROI circumscribed the entire contrast-enhanced tumor area and was positioned in the same spatial location on the corresponding pre-contrast (baseline) DCE-MRI image slice (Figure 1b), as well as the proton density image slice (Figure 1c). If needed, motion corrections were performed by aligning the images based on anatomic features of skin, bone, and knee joint. The signal intensity from each pixel within the ROI was obtained from the proton density images and the five pre-contrast DCE-MRI images. The average of the latter was considered as the single pre-contrast intensity value. Assuming TE << T2, the signal intensity (S) of a spoiled gradient echo sequence is given by (19):

$$S=S_0\sin \alpha \frac{1-\text{exp}(-TR\cdot R_1)}{1-\cos \alpha \text{exp}(-TR\cdot R_1)}$$ [1]

where S0 is a constant proportional to the proton density of the sample. By comparing the corresponding pixel S values between the pre-contrast DCE-MRI and the proton density images, pixel R₁₀ values can be theoretically calculated using Eq. [1]. To correct for possible errors in T₁ calculation likely caused by imperfect slice profile, a calibration curve of signal intensity ratio of T₁-weighted image over proton density image versus T₁ was constructed using a method introduced by Parker et al (15). Twelve agar gel phantoms doped with various concentrations of Gd-DTPA were imaged with the same pulse sequence and acquisition parameters as those used for DCE and proton density MRI. The T₁ values for each phantom were first measured using an inversion recovery spectroscopy sequence, covering a range of 105 to 2224 msec. The twelve data points were empirically fitted with a biexponential function with offset (15) to generate the calibration curve. The pixel R₁₀ (1/T10) values within the multi-slice tumor ROIs were obtained from the calibration curve. The average of these values gave the average R₁₀ value for one tumor region. Measurement of tumor R₁₀ for each of the 18 patients resulted in R₁₀ = 0.87 ± 0.29 s⁻¹ (mean ± SD) for this population of lower extremity osteosarcomas with a range of 0.58 to 1.62 s⁻¹ . For pharmacokinetic modeling of the DCE-MRI data, the R1 value for each time course data point, R₁(t), was converted to Gd-DTPA concentration using the following linear equation:

$${\mathrm{R}}_1(\mathrm{t})={\mathrm{r}}_1\cdot {\mathrm{C}}_{\mathrm{t}}(\mathrm{t})+{\mathrm{R}}_{10}$$ [2]

where C_t(t) is the tumor tissue Gd-DTPA concentration at time t, and r1 is the contrast agent relaxivity which was taken to be 4.1 sec⁻¹ (mmol/L)⁻¹ at 1.5T (20).

Figure 1.

Sagittal images from a patient with an osteosarcoma in the distal femur: (a) A post-contrast image extracted from a multi-slice dynamic contrast-enhanced (DCE) MRI acquisition, with the white ROI circumscribing the contrast-enhanced tumor. The yellow ROI was placed within the adjacent femoral artery for arterial input function (AIF) data sampling. (b) The pre-contrast image from the same DCE-MRI series with the same location as in panel a. (c) A proton density image acquired prior to DCE-MRI with the same location and slice thickness as panels a and b. The white ROIs in panels b and c were positioned in the same spatial location as in panel a.

For the individual R₁ measurement approach, the R₁ values for all the DCE-MRI time course data points, including both pre- and post-contrast phases, were obtained with the two-point R₁ determination method (15, 16) by comparing signal intensities of the DCE-MRI images with those of the proton density images and using the T₁ calibration curve. For the average R₁₀ approach, the R₁ value for each DCE-MRI time point was calculated using the following equation derived from Eq. [1], assuming for each patient R₁₀ was uniformly equal to the average value, 0.87 s⁻¹ , for each ROI and each pixel within the ROI:

$$\frac{S}{Spre}=\frac{\left\{\left[1-\text{exp}(-TR\cdot R_1)\right]\left[1-\text{exp}(-TR\cdot R_{10})\cdot \cos \alpha \right]\right\}}{\left\{\left[1-\text{exp}(-TR\cdot R_{10})\right]\left[1-\text{exp}(-TR\cdot R_1)\cdot \cos \alpha \right]\right\}}$$ [3]

where S_pre is the pre-contrast S.

The biexponential AIF was constructed from data sampled in a ROI placed within a femoral artery (yellow ROI in Figure 1a) that was adjacent to the tumor (11). The C_t(t) time course (obtained through either the individual R₁ measurement or the average R₁₀ approach) and an average AIF [obtained from individual measurements in five patients, Figure 2 of (11)] based on 2 cc/sec contrast injection rate were subjected to kinetic modeling using the Toft’s model (21). We have shown that it is feasible and reasonable to use limited-population-based average AIF for quantitative analysis of lower extremity osteosarcoma DCE-MRI data obtained with either 1 or 2 cc/sec contrast injection rate (11). An in-house IDL (6.0 version; Research Systems, Boulder, CO, USA) program was used to fit the C_t(t) time course for the extraction of the K^trans and v_e parameters, as shown in the following Kety-Schmidt type of rate law equation:

$${\mathrm{C}}_{\mathrm{t}}(\mathrm{t})={\mathrm{K}}^{\text{trans}}{\displaystyle \underset{0}{\overset{t}{\int }}{\mathrm{C}}_{\mathrm{p}}(\mathrm{t}’)\text{exp}(-{\mathrm{K}}^{\text{trans}}{{\mathrm{v}}_{\mathrm{e}}}^{-1}(\mathrm{t}-\mathrm{t}’))\text{dt}’}$$ [4]

where C_p(t’) is the plasma Gd-DTPA concentration time course, i.e. AIF. The term that includes plasma volume fraction (v_p), v_pC_p(t), is ignored on the right hand side of this equation. Generally, v_e is significantly greater than v_p. Simulations have shown that, for a relatively long DCE-MRI acquisition, such as the one in this study, the signal change during the DCE time course is affected mostly by the K^trans and v_e terms (22). The v_p term contributes mainly only to the early signal rising part of the time course and becomes important for curve fitting when the DCE time course is short (22). Further, it has been shown that when there is sufficient contrast agent extravasation from plasma to interstitium, such as in tumor tissue, the K^trans and v_e parameters are adequate for pharmacokinetic modeling of DCE-MRI data (22). Whole tumor K^trans and v_e values were calculated by averaging ROI K^trans and v_e values on each image slice, respectively, weighted by the number of pixels in each ROI. Histogram analyses (14) of the pixel K^trans and v_e values within the entire tumor were also performed and the median values of these parameters were calculated.

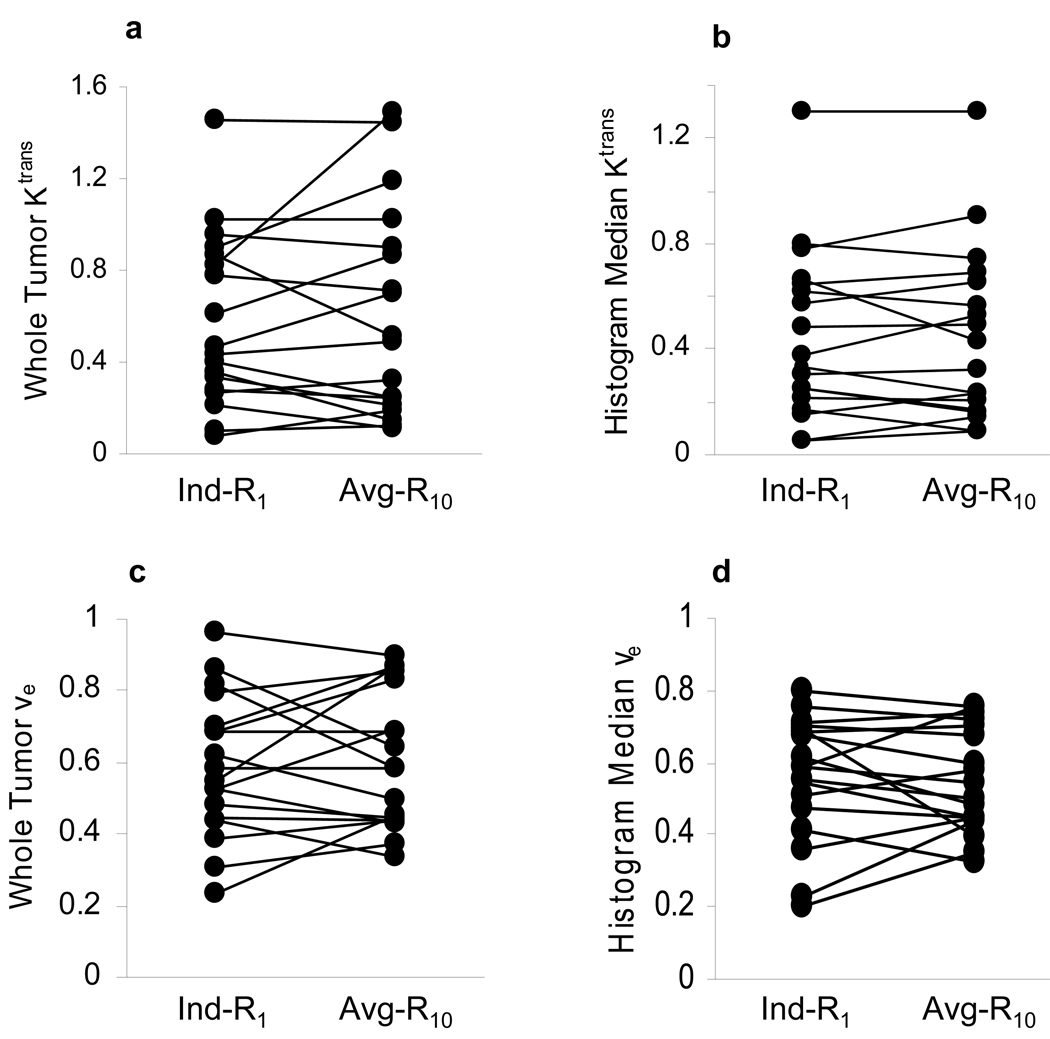
Figure 2.

Scatter plots of K^trans (min⁻¹) and v_e parameters obtained from pharmacokinetic modeling analyses of DCE-MRI data from eighteen patients with lower extremity osteosarcomas. Kinetic analyses with the individual R₁ measurement (Ind-R₁) approach and the average R₁₀ (Avg-R₁₀) approach were performed for each study, yielding whole tumor ROI K^trans (a) and v_e (c), and median values from histogram analyses of pixel K^trans (b) and v_e (d) parameters within the tumor. The straight lines connect data points from the same patient.

Student paired t test was used to evaluate differences in pharmacokinetic parameters resulted from the individual R1 measurement approach and the average R₁₀ approach.

Simulations

To further validate the average R₁₀ approach, simulations were performed for kinetic modeling of the DCE-MRI signal time courses from three patients. The measured tumor R₁₀ values for the two patients were 0.58 s⁻¹ and 1.62 s⁻¹, respectively, representing the lowest and highest ends of the R₁₀ range for the study population. The R₁₀ value for the other patient was 0.92 s⁻¹, approximately the average R₁₀ (0.87 s⁻¹) of the group. The time course data from each patient was fitted with the fixed average AIF and assumed R₁₀ values varied from 0.58 s⁻¹ to 1.62 s⁻¹ with 0.04 s⁻¹ increment. Whole tumor K^trans and v_e values were derived for each assumed R₁₀ value.

Results

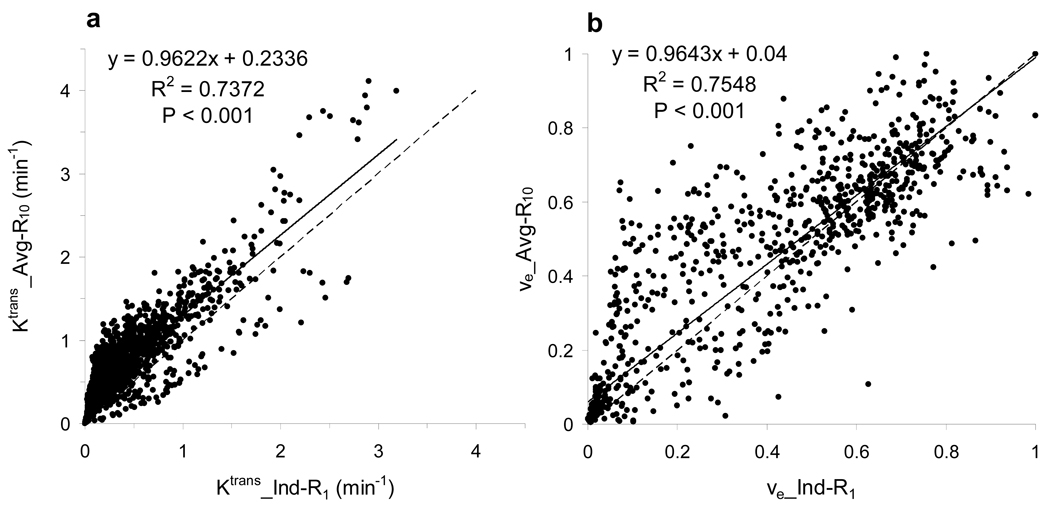
Figure 2 shows scatter plots of (a) whole tumor K^trans, (b) histogram median K^trans, (c) whole tumor v_e, and (d) histogram median v_e. The left column represents the parameter values derived from kinetic modeling of the DCE-MRI data with the R₁ time courses measured individually (Ind-R₁) using the two-point R₁ determination method, while the right column represents those obtained with the R₁ time courses calculated from Eq. [3] using the average R₁₀ (Avg-R₁₀). The straight lines connect the data points from the same patient. There are no statistically significant differences between K^trans parameters derived with the Ind-R₁ approach and those derived with the Avg-R₁₀ approach (p = 0.55 for whole tumor K^trans and 0.87 for histogram median K^trans, paired t test). The same conclusion applied to the v_e values (p = 0.64 for whole tumor v_e and 0.72 for histogram median v_e, paired t test). The comparisons are summarized in Table 1. No significant changes in K^trans and v_e parameters occurred when the Avg-R₁₀ approach was used for R₁ time course determination. Figure 3 displays the representative graphs from one patient study, showing pixel K^trans (a) and v_e (b) values within the whole tumor obtained with the Avg-R₁₀ approach plotted against those obtained with the Ind-R₁ approach. There were a total of 2174 pixels within the whole tumor. Both plots demonstrate significant linear correlations (p < 0.001) with the slope values close to one (0.962 for the K^trans plot and 0.964 for the v_e plot). Similar results were obtained from the other seventeen patients. The above results indicate that the use of Avg-R₁₀ for R₁ time course determination works equally well for both ROI and pixel-by-pixel data analyses.

Table 1.

Comparisons of K^trans and v_e Obtained with Ind-R₁ and Avg-R₁₀ Approaches

R1 Determination	Ind-R1	Avg- R10
Whole Tumor Ktrans (min−1)	0.57 ± 0.37	0.61 ± 0.46a
Histogram Median Ktrans (min−1)	0.45 ± 0.32	0.44 ± 0.33b
Whole Tumor ve	0.59 ± 0.20	0.61 ± 0.19c
Histogram Median ve	56 ± 0.17	0.55 ± 0.14d

Mean ± SD; Student paired t test for K^trans and v_e values obtained with the Ind-R₁ and the Avg-R₁₀ approaches:

^ap=0.55

^bp=0.87

^cp=0.64

^dp=0.72.

Figure 3.

Scatter plots of pixel (a) K^trans and (b) v_e parameters from one patient with lower extremity osteosarcoma. The K^trans and v_e parameters derived with the average R₁₀ (Avg-R₁₀) approach are plotted against those derived with the individual R₁ measurement (Ind-R₁) approach. The analyzed pixels (n = 2174) are within the contrast-enhanced tumor tissue region. The solid straight lines represent linear correlations, while the dashed ones are lines of identity.

Table 2 lists the whole tumor K^trans and v_e ranges and the standard deviations (SDs) of the study population obtained with the Ind-R₁ approach, and the simulation results of the time course data from the three tumors. Compared to the experimental results, the K^trans and v_e ranges and SDs from simulations with presumed R₁₀ value across the entire R₁₀ range were much smaller, whether the actually measured R₁₀ was at the lowest or highest end of the spectrum, or near the mean.

Table 2.

Experimental and Simulation Results for Whole Tumor Pharmacokinetic Analysis

	Ind-R1	Simulation 1	Simulation 2	Simulation 3
Ktrans range (min−1)	0.08–1.45	0.09–0.44	0.53–1.28	0.30–1.02
Ktrans SD (min−1)	0.37	0.11	0.23	0.22
ve range ve	0.24–0.96	0.27–0.62	0.70–0.94	0.46–0.79
SD	.20	0.10	0.07	0.10

SD: standard deviation; Simulations 1, 2, and 3 represent simulations performed with the DCE-MRI time course data from the tumors with measured R₁₀ values of 0.58, 0.92, and 1.62 s⁻¹, respectively.

Discussion

Using the two-point R₁ determination method (15, 16), individual R₁₀ values were measured from 18 patients with lower extremity osteosarcomas. Post-surgical pathology analyses of this patient population revealed a wide range of tumor necrosis percentage, 10 – 100%. Consequently, the measured R₁₀ values had a relatively broad range: 0.58 – 1.62 s⁻¹. This is expected, as the more solid tumor tissue and the more fluid-like necrotic region can have quite different R₁ values. However, the results of this study show that pharmacokinetic modeling of the DCE-MRI data yielded pharmacokinetic parameters that were not significantly different whether individual R₁ value was measured or a fixed R₁₀ (average R₁₀) was used to calculate the R₁ value for the DCE-MRI time course. The experimental results were further validated by simulations of the time course data from three tumors whose measured R₁₀ values were at the lowest and highest ends of the R₁₀ range, and near the mean, respectively. With smaller SDs, the K^trans and v_e ranges from the simulations were smaller than, and within those obtained from the individual R₁ measurement approach. Therefore, both the experimental and simulation results indicate the feasibility of using a fixed, limited-population-based average R₁₀ for pharmacokinetic modeling (ROI or pixel-by-pixel analysis) of lower extremity osteosarcoma DCE-MRI data from a larger population.

In pharmacokinetic modeling of the DCE-MRI data, the tumor C_t(t) time course is submitted to quantitative analysis along with the AIF. As shown in Eq. [2], C_t(t) is determined by ΔR₁(t) which is [R1(t) - R₁₀]. Therefore, the accuracy of AR₁(t) determination directly affects the accuracies of derived pharmacokinetic parameters. With the average R₁₀ approach, R₁(t) is calculated from Eq. [3] using a fixed average R₁₀ value. For an individual DCE-MRI study of one specific tumor, the difference between the actual R₁₀ and the average R₁₀ could be quite substantial, potentially causing significant errors in calculated R₁(t). However, the errors in both R₁(t) and R₁₀ determinations may originate from the same source and therefore partially negate each other when ΔR₁(t) is calculated. This possibly explains why the pharmacokinetic parameters obtained with the individual R₁ measurement and the average R₁₀ approaches are not significantly different from each other. This study was conducted in a population of 18 patients with lower extremity osteosarcomas, and with one specific set of flip angle (α) and TR for DCE-MRI acquisition. Further validation of the average R₁₀ approach with different types of cancer and different data acquisition parameters is desirable. In a breast DCE-MRI study (23), Tofts et al. pointed out the importance of R₁₀ measurement for kinetic modeling of the signal time-course data, showing that errors in assumed parameter values, such as R₁₀, r₁, TR, α, contrast dose, caused propagational errors in derived K^trans and v_e values. Thus, the rigorous approach of R₁₀ measurement should always be adopted when reliable measurements can be carried out. However, in that study the TR (50 ms) and α (60°) values used in simulation and actual data acquisition are quite different from those used in this study. The types of cancer studied are also different. Our simulation and experimental results show that with the set of acquisition parameters employed for this study, the errors in estimations of K^trans and v_e caused by the use of average R₁₀ in place of measured individual R₁₀, if any, are not significant. It is worth noting that a breast DCE-MRI study using a fixed average R₁₀ for pharmacokinetic modeling has been showing consistent and promising results of discriminating malignant and benign breast tumors using the K^trans parameter (4, 24, 25).

Using multiple flip angle method for R₁ measurement, Haacke et al. (18) demonstrated, with both simulated data and actual liver and muscle DCE-MRI data, that noise in the experiments led to spread of R₁₀ estimates and unstable C_t(t) curves, which could be effectively eliminated by forcing R₁₀ to a fixed value. These authors have also shown that fixing R₁₀ not only yields more consistent results when evaluating DCE-MRI data, but also is useful in analyzing data collected with wrong flip angle scale factors or patient motion prior to DCE-MRI data acquisition. The results from this study are consistent with such findings even though the two-point R1 determination method was used instead of the multiple flip angle approach. In our osteosarcoma DCE-MRI protocol, the proton density images are acquired immediately before the DCE-MRI series. Any inconsistency in flip angle scaling between the two acquisitions can lead to errors in R1 estimation. Furthermore, since the tumor cannot be easily delineated on proton density image, any slight patient movement, which is more likely to happen between scans than during a scan, can cause difficulty in spatially registering the tumor ROI on the proton density and the DCE-MRI images for the purpose of measuring R₁ by comparing signal intensity in the same ROI or pixel. This will result in errors in R₁ measurement as well. Thus, it is quite reasonable, and sometimes necessary to use the average R₁₀ approach for determination of the R₁(t) time course.

DCE-MRI examination is often included in clinical MRI protocols to study cancer. In such clinical studies, data collection schemes are usually planned solely for the purpose of qualitative or semi-quantitative analysis of DCE-MRI data. Thus, data may not be available for actual R₁ measurement. One clear advantage of the average R₁₀ approach is to enable retrospective pharmacokinetic modeling of such data by using a fixed average R₁₀ and Eq. [3] if a spoiled gradient echo type of sequence was used for DCE-MRI acquisition. However, it is important to identify the appropriate situation to use a fixed average R₁₀ value for DCE-MRI data analysis. For instance, in a longitudinal DCE-MRI study to evaluate the effects of chemotherapy through monitoring the changes in tumor necrosis, the individual R₁ measurement approach may be a wiser choice if can be done accurately, as R₁₀ values can be quite different pre- and post-treatment. Use of the average R₁₀ approach may lead to errors in estimating changes of pharmacokinetic parameters in such a study.