Longitudinal associations between lead dose and renal function in lead workers

Abstract

Background

Existing research on the lead dose range associated with nephrotoxicity in the occupational setting is inconsistent and primarily cross-sectional in design.

Objective

To determine if lead dose predicts change in renal function in a large population of current and former lead workers.

Methods

Three evaluations were performed between 1997 and 2001. Lead dose was assessed with blood and tibia lead. Renal outcomes included blood urea nitrogen, serum creatinine, and calculated creatinine clearance. We used generalized estimating equations to model change in renal function between each evaluation in relation to tibia lead at the beginning of each follow-up period and concurrent change in blood lead, while adjusting for baseline lead dose and other covariates.

Results

At baseline, mean (SD) age and duration of occupational lead exposure were 42.0 (9.3) and 8.8 (6.3) years, respectively, in 537 current and former lead workers followed over a mean of 2.1 years. Mean (SD) blood and tibia lead were 31.3 (14.4) μg/dL and 35.0 (37.8) μg/g bone mineral, respectively. Women (25.9%) were older and more likely to be former lead workers than men. In males, serum creatinine decreased and calculated creatinine clearance increased over the course of the study. Mean blood lead was not significantly different between evaluations 1 and 3 in either sex, however, tibia lead decreased in women. Blood and tibia lead were significantly associated with change in renal function. In males, serum creatinine decreases and calculated creatinine clearance increases were greatest in participants whose blood lead declined.

Conclusions

Both acute and chronic occupational lead dose measures were associated with change in renal function measures prospectively.

INTRODUCTION

Inorganic lead is a nephrotoxicant at high levels of exposure (blood lead levels > 70 – 80 μg/dL). An increasing body of literature in both general and patient populations indicates adverse renal effects at much lower levels (< 10 μg/dL), particularly in susceptible populations, such as those with hypertension, diabetes mellitus and chronic kidney disease (CKD) from causes other than lead nephropathy (Ekong et al., 2006). In contrast, data on risk for adverse renal effects at the moderate lead dose levels currently found in occupational settings in developed countries (20 – 50 μg/dL) are inconsistent. The challenges inherent in this research, such as the healthy worker effect (which is exacerbated by medical surveillance practices often mandated in lead industries), may be explanatory factors (Ekong et al., 2006). In addition, lead dose assessment that relies solely on blood lead may result in misclassification since blood lead has a relatively short half-life (Hu et al., 1998) and can fluctuate greatly if occupational exposure does. Further, with the exception of two small (n≤ 30) studies (Coratelli et al., 1988; Hsaio et al., 2001), prior occupational research has been cross-sectional whereas longitudinal data allow individuals to serve as their own controls thus mitigating problems, such as selection bias, encountered in cross-sectional analyses. In addition, longitudinal data allow an assessment of factors involved in change in renal function over time. Finally, inverse associations (e.g., higher lead dose positively associated with lower serum creatinine and/or higher creatinine clearance) may be involved. These relations have been reported in Korean (Weaver et al., 2003), Belgian (Roels et al., 1994) and Chinese (Hsaio et al., 2001) lead workers.

We have been following a large cohort of Korean lead workers since 1997. In our cross-sectional analysis of first evaluation data, we observed that both blood and tibia lead levels were associated with worse renal function, primarily in older workers (Weaver et al., 2003). In younger workers, associations in the opposite direction were observed. Herein, we report the analysis of prospective data collected in this cohort from 1997 to 2001. To our knowledge, this is the first study to examine associations of blood and tibia lead with change in renal function longitudinally in a large cohort of workers with current and past occupational exposure to inorganic lead.

MATERIALS AND METHODS

Study population and design

We conducted a longitudinal study to evaluate the adverse health effects of inorganic lead exposure in current and former workers employed at 26 lead-using facilities in South Korea. Three evaluations were performed between October 1997 and June 2001. Detailed descriptions of the study population and design have been reported previously (Schwartz et al., 2001; Weaver et al., 2003). No medical exclusionary criteria (e.g., hypertension, renal disease) were applied. Study participants were not occupationally exposed to other known renal toxicants. The study protocol was approved by Institutional Review Boards at the SoonChunHyang University School of Medicine and the Johns Hopkins University Bloomberg School of Public Health. Participation in the study was voluntary. All participants provided written, informed consent.

Data collection and laboratory methods

Data collection and laboratory methods have been previously described (Schwartz et al., 2001; Weaver et al., 2003). Information on demographic variables, medical and occupational history, blood pressure, and a blood specimen (for blood lead, blood urea nitrogen [BUN], and serum creatinine) were obtained at each evaluation. Height and weight were measured at evaluations one and three and the average was used for evaluation two. BUN and serum creatinine were measured via the same Automatic Chemical Analyzer (Toshiba TBA 40FR Biochemical Analyzer, Tokyo, Japan) over the study period. Serum creatinine was assayed with a kinetic Jaffe method. Two levels of serum creatinine controls (1.21 and 5.70 mg/dl) and one urine creatinine control (1.05 mg/ml) were run each day. Twice per year the lab successfully participated in the quality assurance program of the Korean Clinical Pathology Association. Creatinine clearance was calculated using the Cockcroft-Gault equation (Cockcroft and Gault, 1976). Blood lead was measured via atomic absorption spectrophotometer and, in evaluations one and two, tibia lead concentration was measured via K-shell X-ray fluorescence using ¹⁰⁹Cd.

Statistical analysis

The primary goal of our analysis was to evaluate longitudinal associations between measures of lead dose and renal function (BUN, serum creatinine and calculated creatinine clearance) in current and former lead workers. We focused on associations between change in renal function over each follow-up interval in relation to: 1) tibia lead concentration (as a measure of cumulative lead dose) at the beginning of each follow-up interval and 2) concurrent change in blood lead (as a measure of current lead dose) while adjusting for initial blood and tibia lead and other covariates. This approach to modeling lead dose was formulated a priori in accordance with our understanding of lead kinetics and toxicity to facilitate biologic interpretations and minimize chance associations. For example, change in tibia lead was not modeled due to the long half-life of that measure.

Models were parameterized in a modified Distributed Lag Model (DLM) framework (Zanobetti et al., 2000) with time-varying and baseline effects. Our approach decomposes an explanatory variable’s effects into “longitudinal” (within-subject) and “cross-sectional” (between-subject) components (Diggle et al., 2002). The DLM formulation accommodates inclusion of additional evaluations which will be useful for the ongoing component of this longitudinal study. This method is also a simple reparameterization of the cross-sectional (C) -historical (H) - longitudinal (L) (CHL) modeling approach used by Schwartz et al. (2005) to examine lead dose effects on cognitive outcomes. It can be thought of as ‘adjusting’ the effects of a variable that changes over time for its baseline value (where the trajectory begins).

The statistical appendix contains a detailed description of this model and parameter interpretations. Briefly, letting ‘i’ denote the i^th participant, ‘1’ denote the baseline evaluation, and ‘j’ the j^th longitudinal evaluation on that participant, for a given renal outcome (RO), blood lead (PbB) and tibia lead (lnTibia) we specify a regression model:

$$E({\text{RO}}_{ij})={\theta }_0+{\beta }_1({\text{PbB}}_{i1})+{\beta }_{\text{L}}({\text{PbB}}_{ij})+{\alpha }_{\text{C}}({\text{lnTibia}}_{i1})+{\alpha }_{\text{H}}\sum _{\text{m}=1}^{(\text{j}-1)}{\text{lnTibia}}_{i\text{m}}+\text{adjustors}$$

The primary parameters of interest are the terms, β_L and α_H, for blood and tibia lead, respectively. The association between a longitudinal change in blood lead and renal outcome (e.g., between evaluations 1 and 2) within a participant for a given set of adjustors, is estimated by β_L:

$$E(\mathrm{\Delta }{\text{RO}}_{i(2-1)})=E({\text{RO}}_{i2}-{\text{RO}}_{i1})={\beta }_{\text{L}}({\text{PbB}}_{i2}-{\text{PbB}}_{i1})={\beta }_{\text{L}}(\mathrm{\Delta }{\text{PbB}}_{i(2-1)})$$

Similarly, the historical effects of cumulative lead dose (as measured by tibia lead at the beginning of a follow-up interval) on longitudinal change in renal outcome over that interval (again using evaluations 1 and 2) for a participant with a given set of adjustors is estimated by α_H:

$$E(\mathrm{\Delta }{\text{RO}}_{i(2-1)})=E({\text{RO}}_{i2}-{\text{RO}}_{i1})={\alpha }_{\text{H}}({\text{lnTibia}}_{i1})$$

Under this formulation, α_C represents the cross-sectional effect of tibia lead at baseline, (describing associations between RO and tibia lead across different subjects at baseline), and β₁ represents the baseline effect of blood lead. Covariate selection for final regression models involved adding variables separately into a priori models (age, sex, body mass index [BMI defined as weight in kilograms divided by the square of height in meters], and evaluation number). Covariates assessed for inclusion in models included systolic and diastolic blood pressure, hypertension and diabetes mellitus (both based on participant report of physician diagnosis or medication use), current/former lead worker status, time since retirement, factory of employment, outcome at the beginning of each follow-up interval, smoking status (current, ex, never), alcohol ingestion status (current, ex, never), and current analgesic use (based on participant report).

Men and women differed in several important respects that could influence the results of the analysis (see Table 1). Therefore, these groups were initially analyzed separately and gender interaction terms were used in final combined models to accurately replicate differences observed in the stratified models. Close agreement between stratified and combined interaction model estimates was observed (shown in Figures 1 and 2). Tibia lead distributions were skewed and were natural log-transformed to achieve better model fits and minimize overly influential data points at extreme levels. XRF measurements in two plants in the first evaluation were subsequently determined to be invalid due to measurement interference from background lead contamination in the examination room. These 35 participants were excluded, leaving 537 participants in this analysis. Parameter estimates were obtained using generalized estimating equation techniques to account for correlations among repeated measures within subjects. Results are reported using robust (Huber-White sandwich) variance estimates derived from an exchangeable working correlation model. Sensitivity analyses towards the working correlation structure were conducted and similar results were obtained. Diagnostics included examining added variable residual plots (Weisberg, 1985) and leverage and Cook’s D values (Cook, 1977; 1979) to evaluate linearity, influential points, and homoscedasticity in the final models. When warranted, models were repeated without outliers. Models were also assessed for collinearity by examining variance inflation factors. Statistical analysis was performed using SAS 9.1 software (SAS Institute, Inc., Cary, NC, USA).

Table 1.

Demographic, exposure and health outcome measures in 537 current and former lead workers. Baseline (evaluation 1) data are shown except where indicated.

	All		Males		Females
	N = 537		N = 398		N = 139		p-value*
Variables	N	%	N	%	N	%
Hypertensives	43	8.0	28	7.0	15	10.8	0.16
Diabetics	3	0.6	3	0.75	0	0	NA
Current smokers	274	51.0	273	68.6	1	0.7	<0.01
Ex-smokers	62	11.6	60	15.1	2	1.4	<0.01
Current alcohol users	334	62.2	300	75.4	34	24.5	<0.01
Analgesic users	17	3.2	6	1.5	11	7.9	<0.01
Former lead workers
Evaluation 1	69	12.9	11	2.8	58	41.7	<0.01
Evaluation 2	95	17.7	25	6.3	70	50.4	<0.01
Evaluation 3	146	27.2	63	15.8	83	59.7	<0.01
	Mean	SD	Mean	SD	Mean	SD	p-value
Age, years	42.0	9.3	39.7	9.1	48.6	6.4	<0.01
Body mass index, kg/m2	23.1	3.0	22.5	2.6	24.6	3.4	<0.01
Diastolic blood pressure, mm Hg	76.4	11.8	76.5	11.5	76.2	12.6	0.85
Systolic blood pressure, mm Hg	123.4	16.9	123.0	15.4	124.4	20.6	0.47
Blood lead level, μg/dL
Evaluation 1	31.3	14.4	35.1	13.8	20.4	9.6	<0.01
Evaluation 2	32.6	15.4	36.8	14.5	20.7	10.8	<0.01
Evaluation 3	31.4	16.3	35.5	15.9	19.7	10.8	<0.01
Tibia lead, μg Pb/g bone mineral
Evaluation 1	35.0	37.8	37.6	42.2	27.6	19.3	<0.01
Evaluation 2	33.0	39.4	36.2	43.6	23.5	20.5	<0.01
Lead job duration, years	8.8	6.3	9.2	6.7	7.6	4.8	<0.01
BUN, mg/dL
Evaluation 1	14.4	3.6	14.8	3.6	13.4	3.4	<0.01
Evaluation 2	14.2	3.7	14.5	3.6	13.4	3.9	<0.01
Evaluation 3	14.2	3.8	14.7	3.6	12.9	3.8	<0.01
Serum creatinine, mg/dL
Evaluation 1	0.89	0.14	0.94	0.11	0.74	0.10	<0.01
Evaluation 2	0.88	0.14	0.92	0.12	0.75	0.12	<0.01
Evaluation 3	0.87	0.14	0.91	0.12	0.75	0.11	<0.01
Creatinine clearance, ml/min
Evaluation 1	93.2	19.8	95.5	18.8	86.5	21.0	<0.01
Evaluation 2	94.3	21.0	97.3	19.8	85.3	21.8	<0.01
Evaluation 3	95.2	21.6	98.7	21.1	84.8	17.7	<0.01

^*p-value for comparison between males and females using Chi-square or t-test, as appropriate

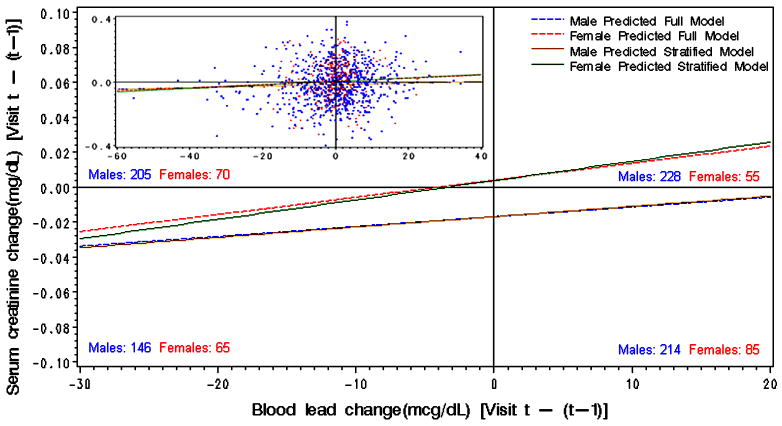
Figure 1.

Linear regression of the association between interval change in blood lead and predicted values of serum creatinine for males and females plotted over the observed (unadjusted) data. Numbers indicate males and females in each quadrant based on observed data.

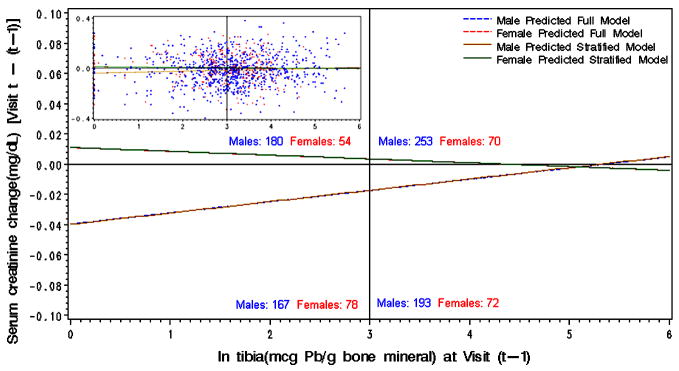
Figure 2.

Linear regression of the association between tibia lead and subsequent interval change in predicted values of serum creatinine for males and females plotted over the observed (unadjusted) data. Numbers indicate males and females in each quadrant based on observed data.

RESULTS

Selected Demographic, Exposure, and Health Outcome Measures

A mean (SD) of 1.03 (0.22) years elapsed between evaluations 1 and 2, and 1.09 (0.4) years between evaluations 2 and 3 for the 537 current and former lead workers in the longitudinal study. Mean blood lead at baseline was 31.3 μg/dL (Table 1); blood and tibia lead level ranged from 4.3 to 76.1 μg/dL and −7.4 to 290.8 μg/g bone mineral, respectively. At baseline, 69 (12.9%) of all participants were no longer employed in the lead industry. An additional 77 workers left the lead industry during the two-year study due primarily to plant closures related to the difficult economic conditions encountered in the Republic of Korea in the late 1990s. Female participants comprised 25.9% of the study population. Significant differences in most measures were observed between male and female participants (Table 1). Women were more likely to be former lead workers, non-smokers, non-drinkers, analgesic users, and older; they also had higher mean BMI and lower mean lead dose measures and lead job duration. Renal function also differed; lower BUN, serum creatinine and calculated creatinine clearance were observed in women.

Longitudinally, in both men and women, mean blood lead was stable over the course of the study (i.e., mean blood lead levels at evaluations 1 and 3 were not statistically different). However, in males, mean blood lead at evaluation 2 was statistically different when compared to means at evaluations 1 and 3 (p < 0.001 and 0.05, respectively). In females, mean blood lead at evaluation 3 was significantly lower than at evaluation 2 (p = 0.03). Mean tibia lead declined in women (p < 0.001). Renal function in women declined over the course of the study but this did not reach statistical significance. In contrast, in males, serum creatinine decreased and calculated creatinine clearance increased during study follow-up (p < 0.001 comparing evaluation 1 and 3 means for both outcomes).

Longitudinal Associations Between Lead Dose and Renal Function

After controlling for baseline blood and tibia lead and other covariates (listed in Table 2), change in blood lead was positively associated with concurrent change in serum creatinine and negatively associated with concurrent change in calculated creatinine clearance (Table 2). The beta coefficient was similar in both male and female workers in models of serum creatinine but the association was limited to male workers in models of calculated creatinine clearance. As shown in Figure 1 (lower left quadrant), declining blood lead over the follow-up interval was associated with decreasing serum creatinine in both males and females. In females, a longitudinal increase in blood lead was associated with an increase in serum creatinine (Figure 1; upper right quadrant). However, in men, an increase in blood lead was still associated with a decrease in serum creatinine; the magnitude of the decline was less than in male participants whose blood lead decreased (Figure 1; lower right quadrant).. The same pattern was observed with calculated creatinine clearance in men (i.e., calculated creatinine clearance increased but less if blood lead increased compared to participants in whom blood lead decreased).

Table 2.

Associations between lead dose and change in renal outcomes, modeled with generalized estimating equations, in 537 lead workers^a

	Males (n = 398)			Females (n = 139)
	β coeff	95 % CI	p-value	β coeff	95 % CI	p-value
Change in Calculated Creatinine Clearance
Interval change in blood lead, μg/dL/int.b	−0.1197	(−0.2221, −0.0183)	0.02	−0.0339	(−0.3296, 0.2618)	0.82
Ln tibia lead preceding each follow-up interval, μg Pb/g bone mineral	−1.4366	(−2.2229, −0.6503)	<0.01	−0.3556	(−1.8668, 1.1556)	0.64
Calculated creatinine clearance preceding each follow-up interval, ml/min	0.0231	(−0.0235, 0.0697)	0.33	−0.0757	(−0.1567, 0.0053)	0.07*
Calculated Creatinine Clearance
Intercept	57.9380	(46.4271, 69.4489)	<0.01
Baseline blood lead, μg/dl	0.1172	(−0.0133, 0.2478)	0.08	−0.1115	(−0.4790, 0.2560)	0.55
Baseline ln tibia lead, μg Pb/g bone min.	2.7889	(0.6519, 4.9260)	0.01	−1.2436	(−4.7093, 2.2220)	0.48*
Female	−0.0615	(−20.0445, 19.9215)	0.99
Baseline age, years	−1.2196	(−1.3735, −1.0657)	<0.01
Baseline body mass index, kg/m2	3.4999	(3.0617, 3.9381)	<0.01	3.9192	(3.2098, 4.6286)	<0.01
Evaluation 2	4.6649	(−0.8655, 10.1953)	0.10	6.8712	(−1.8362, 15.5785)	0.12
Evaluation 3	8.5573	(−2.3104, 19.4251)	0.12	14.0172	(−2.8921, 30.9265)	0.10
Hypertension	−1.0685	(−4.5638, 2.4267)	0.55
Former lead worker	−3.5780	(−7.8412, 0.6851)	0.10	0.7439	(−4.2504, 5.7381)	0.77
Time since retirement, years	−0.5770	(−1.3763, 0.2223)	0.16
Factory of employment	−0.7343	(−2.9411, 1.4725)	0.51
Current smoker	4.4216	(1.4865, 7.3568)	<0.01
Ex-smoker	2.6593	(−1.0763, 6.3949)	0.16
Analgesic use	−4.7746	(−9.1231, −0.4260)	0.03
Change in Serum Creatinine
Interval change in blood lead, μg/dL/int.b	0.0010	(0.0001, 0.0019)	0.03	0.0014	(−0.0009, 0.0036)	0.23
Ln tibia lead preceding each follow-up	0.0075	(0.0010, 0.0140)	0.02	−0.0037	(−0.0158, 0.0083)	0.54 *
interval, μg Pb/g bone mineral
Serum creatinine preceding each follow-up interval, mg/dl	0.0209	(−0.0241, 0.0658)	0.36	−0.0435	(−0.1464, 0.0594)	0.41
Serum Creatinine
Intercept	0.8233	(0.7333, 0.9133)	<0.01
Baseline blood lead, μg/dl	−0.0006	(−0.0017, 0.0006)	0.33	0.0007	(−0.0018, 0.0032)	0.58
Baseline ln tibia lead, μg Pb/g bone min.	−0.0203	(−0.0367, −0.0038)	0.02	0.0108	(−0.0166, 0.0381)	0.44*
Baseline age, years	0.0002	(−0.0008, 0.0012)	0.74
Female	−0.1294	(−0.2683, 0.0096)	0.07
Baseline body mass index, kg/m2	0.0059	(0.0026, 0.0092)	<0.01	−0.0016	(−0.0056, 0.0025)	0.45*
Evaluation 2	−0.0653	(−0.1138, −0.0168)	<0.01	0.0498	(−0.0327, 0.1322)	0.24*
Evaluation 3	−0.1251	(−0.2180, −0.0321)	<0.01	0.0884	(−0.0697, 0.2465)	0.27*
Hypertension	0.0156	(−0.0165, 0.0477)	0.34
Former lead worker	0.0274	(−0.0041, 0.0589)	0.09	−0.0033	(−0.0382, 0.0315)	0.85
Time since retirement, years	0.0057	(−0.0004, 0.0118)	0.07
Factory of employment	0.0343	(0.0163, 0.0522)	<0.01
Current smoker	−0.0166	(−0.0391, 0.0060)	0.15
Ex-smoker	−0.0204	(−0.0504, 0.0097)	0.18
Analgesic use	0.0748	(0.0409, 0.1088)	<0.01
Change in BUN
Interval change in blood lead, μg/dL	−0.0013	(−0.0254, 0.0228)	0.91	−0.0503	(−0.1136, 0.0129)	0.12
Ln tibia lead preceding each follow-up interval, μg Pb/g bone mineral	0.0480	(−0.1240, 0.2199)	0.58	0.3513	(0.0129, 0.6897)	0.04*
BUN preceding each follow-up interval, mg/dl	−0.0458	(−0.0943, 0.0028)	0.06	−0.0196	(−0.1098, 0.0705)	0.67
BUN
Intercept	9.9517	(7.2865, 12.6170)	<0.01
Baseline blood lead, μg/dl	−0.0120	(−0.0449, 0.0209)	0.48	0.1024	(0.0326, 0.1722)	<0.01*
Baseline ln tibia lead, μg Pb/g bone min.	0.2197	(−0.2258, 0.6652)	0.33	−0.5019	(−1.2758, 0.2720)	0.20
Baseline age, years	0.0970	(0.0643, 0.1297)	<0.01
Female	−2.1710	(−7.0345, 2.6926)	0.38
Baseline body mass index, kg/m2	0.0128	(−0.0900, 0.1156)	0.81	0.0169	(−0.1425, 0.1763)	0.84
Evaluation 2	0.1803	(−0.6851, 1.0457)	0.68	−0.7393	(−2.1029, 0.6242)	0.29
Evaluation 3	0.8399	(−0.7737, 2.4535)	0.31	−1.7808	(−4.3436, 0.7820)	0.17*
Hypertension	0.3781	(−0.4474, 1.2036)	0.37
Former lead worker	−0.5011	(−1.4572, 0.4549)	0.30	−0.8559	(−1.8957, 0.1839)	0.11
Time since retirement, years	0.0004	(−0.2264, 0.2272)	0.99
Factory of employment	1.2667	(0.6987, 1.8347)	<0.01
Current smoker	0.0217	(−0.7207, 0.7641)	0.95
Ex-smoker	−0.3655	(−1.3486, 0.6177)	0.47
Analgesic use	0.5837	(−0.4707, 1.6381)	0.28

^aAssociations of change in renal outcome were examined for three variables: interval change in blood lead; ln tibia lead preceding each follow-up interval; and renal outcome preceding each follow-up interval. Adjustment for other co-variates involved associations between each renal outcome at each evaluation and the co-variate. Effect modification by sex was assessed by interaction models using cross-product terms with sex for body mass index, evaluation indicator, current/former lead worker status, and lead dose variables. For clarity, the beta coefficients shown in the Table are the actual slopes of these associations for both sexes;

^bint. indicates interval between each evaluation or approximately one year;.

^*p-value ≤ 0.1 for sex interaction term

Tibia lead at the beginning of the follow-up interval was positively associated with change in serum creatinine and negatively associated with change in calculated creatinine clearance in male workers. However, serum creatinine declined over most of the tibia lead dose range (Figure 2). Therefore, the negative beta coefficient is due to smaller declines in serum creatinine in workers with higher tibia lead levels at the beginning of the follow-up interval compared to workers with lower tibia lead levels. Similarly, in males, calculated creatinine clearance increased over the tibia lead range but the increase was less at higher tibia lead doses. In female workers, tibia lead was positively associated with change in BUN over the follow-up period. When blood and tibia lead variables were entered into separate models (e.g., longitudinal and baseline blood lead without tibia lead) the beta coefficients were similar to those in the combined model, thus indicating independent effects of each lead dose measure (data not shown).

As discussed in an earlier publication (Weaver et al., 2005), several of the variables in our analyses are biologically inter-related and adjustment presents unique challenges. In our data, none of the blood pressure measures (hypertension status, systolic and diastolic blood pressure) was associated with the renal outcomes. Outcome at the beginning of the follow-up period was borderline significant in models of BUN in males and of calculated creatinine clearance in females. We also analyzed the models in Table 2 without adjustment for hypertension and outcome preceding each follow-up interval; the results were unchanged (data not shown).

DISCUSSION

In this longitudinal analysis of data from 537 current and former lead workers followed over a two year period, we used generalized estimating equations (GEE) in a modeling approach developed to separate the effects of recent dose (as estimated by blood lead) from the chronic effects of cumulative dose (as estimated by tibia lead). We evaluated associations between change in renal function over each follow-up interval (time between each evaluation) in relation to concurrent change in blood lead and tibia lead at the beginning of the follow-up interval; while controlling for baseline blood and tibia lead. This allowed us to separate the baseline effects of lead dose at study onset from subsequent longitudinal effects. Both current (blood lead) and cumulative (tibia lead) lead dose were associated with change in renal function. Results were robust to adjustment for hypertension status and previous renal function and with different tibia transformations. Mean renal function measures remained normal; classical lead nephropathy, characterized by chronic interstitial nephritis associated with hypertension and gout after prolonged high-level lead exposure, is not common in this population.

Interpretation of beta coefficients in longitudinal data analysis in which both exposure and outcome measures can increase or decrease is greatly facilitated by plotting. For example, in models of serum creatinine, the positive association between change in blood lead and serum creatinine can be observed if increasing blood lead is associated with increasing serum creatinine, indicative of worse renal function. In fact, this was observed in plots in females (Figure 1). However, although the beta estimate in males is similar, serum creatinine did not increase longitudinally in this group, even when blood lead did. The longitudinal decrease in serum creatinine (and increase in calculated creatinine clearance) was greatest in the males whose ages are in the youngest tertile (data not shown). This is similar to our cross-sectional analysis of first evaluation data in this cohort, in which higher lead dose was associated with lower serum creatinine in younger workers (Weaver et al., 2003). The mechanism for these inverse associations may be a factor in the longitudinal associations observed in males as well and effect modification by age will be evaluated in analyses of data from all 6 evaluations in this ongoing longitudinal study. Other explanations for longitudinal change in outcome include regression to the mean with a floor effect due to the lower end of the serum creatinine normal range; bias from longitudinal drift in measurement and secular trends in Korea during the time of the study. The sex and potentially age-related pattern of the change suggests that the latter two reasons are less likely.

Significant longitudinal associations between lead dose and renal function, although noted in both sexes, were more common in males. Age may be one explanation, given the older age of women and the changes in renal function observed in younger men. Several other factors must also be considered. Lack of power related to smaller sample size and more restricted lead dose range in women is one factor as evidenced by similar beta coefficients for the association between change in blood lead and serum creatinine in males and females but different statistical significance. Differences by sex could be involved. In addition, former lead worker status differs by sex. Specifically, in the first evaluation, 42% of the 139 women who completed all three evaluations were retired or had otherwise left the lead industry compared to only 3% of the males. By the third evaluation, 60% of the females were no longer occupationally exposed compared to 16% of the males. Thus, although our model adjusts for lead worker status, the small number of male former lead workers, particularly early in the study, raises concern regarding residual confounding. The dataset from 6 evaluations will include a larger number of male former lead workers followed over a longer period which will allow additional analysis to assess this potential explanatory factor.

To our knowledge, this study is the largest longitudinal analysis of renal function in current and former lead workers. We are aware of only two studies in which renal function was evaluated longitudinally in lead workers. Coratelli et al. (1988) reported a decline in urinary N-acetyl-β-D-glucosaminidase (NAG) over a 1 month period of decreased occupational exposure in 20 lead battery factory workers followed over a 1 year period. NAG increased when exposure resumed. However, no association was observed between NAG and blood lead (mean blood lead at study onset was 47.9 μg/dL) and clinical renal function measures were not obtained. Hsiao et al. (2001) analyzed 8 years of annual medical surveillance data in 30 lead battery workers in Taiwan. Lead dose was assessed with blood lead; renal outcome with serum creatinine. Levels of both measures declined early in the course of the study; blood lead decreased from approximately 60 μg/dL to 30–40 μg/dL. Associations between the two were analyzed using GEE; relevant results for our analyses include a cross-sectional model of associations between blood lead and serum creatinine from each evaluation and a longitudinal model of concurrent change in blood lead and serum creatinine between evaluations. All models were adjusted for age and sex; the longitudinal model also controlled for creatinine level at the beginning of each follow-up period. Higher blood lead was associated with lower serum creatinine in the cross-sectional model. This is similar to associations we have observed in our cross-sectional analyses in younger workers (Weaver et al., 2003). However, in contrast to the longitudinal data we report herein, Hsaio et al. (2001) found that change in blood lead was negatively associated with concurrent change in serum creatinine (p = 0.07). The authors hypothesized that bone lead could explain this unexpected association. Although unmeasured, bone lead could not have declined substantially due to its long half-life.

Two longitudinal general population studies are relevant. Kim et al. (1996) studied 459 men who had periodic examinations conducted every 3–5 years during 1979–1994. Mean blood lead and serum creatinine levels, at baseline, were 9.9 μg/dL and 1.2 mg/dL, respectively. With random-effects modeling, ln-transformed blood lead was associated (p = 0.05) with change in serum creatinine over the subsequent follow-up period in the 428 participants whose highest blood lead level was ≤25 μg/dL. A subsequent study, in which bone lead was also measured in the Normative Aging population, reported no significant associations between lead dose measures (blood, tibia, and patella lead) and change in serum creatinine in 448 participants studied over an average of 6 years from 1991 to approximately 2001 (Tsaih et al., 2004). However, significant positive associations between blood and tibia lead and change in serum creatinine were observed in susceptible populations including diabetics and hypertensives. Finally, smaller studies in populations of patients with chronic kidney disease from causes other than lead nephropathy have reported that chelatable and/or blood lead are significant predictors of subsequent decline in renal function even after adjustment for a broad range of renal risk factors (Yu et al., 2004).

In conclusion, these results support the inference that both acute and chronic occupational lead exposure affect renal function. The associations between lead dose and change in renal function are complex and analysis of additional longitudinal data from this ongoing study will be important as will assessment of effect modification by factors, such as age and/or job duration, that may alter the impact of lead on the kidney in workers. From a public health perspective, significant associations could be obscured if lead has opposing effects on the kidney that are dependant on age or duration of exposure. Finally, it is noteworthy, in light of the tibia lead associations observed in these data, that surveillance of cumulative lead dose is not currently required under either OSHA lead standard (OSHA 29 Code of Federal Regulations 1926.62 and 1910.1025).

Abbreviations

BUN

blood urea nitrogen

BMI

body mass index

CI

confidence interval

CKD

chronic kidney disease

SD

standard deviation

Statistical Appendix

This appendix contains an in-depth description of the regression equations corresponding to the model specified in the statistical analysis section. Letting ‘i’ denote the i^th participant, ‘1’ denote the baseline evaluation, and ‘j’ the j^th longitudinal evaluation on that participant, and for a given renal outcome (RO), blood lead (PbB) and tibia lead (lnTibia) we formulate:

$$E({\text{RO}}_{ij})={\theta }_0+{\beta }_1({\text{PbB}}_{i1})+{\beta }_{\text{L}}({\text{PbB}}_{ij})+{\alpha }_{\text{C}}({\text{lnTibia}}_{i1})+{\alpha }_{\text{H}}\sum _{m=1}^{(j‐1)}{\text{lnTibia}}_{i\text{m}}+\text{adjustors}$$

From this model we have (for any given set of adjustors):

For evaluation 1:

$$E({\text{RO}}_{i1})={\theta }_0+{\beta }_1({\text{PbB}}_{i1})+{\beta }_{\text{L}}({\text{PbB}}_{i1})+{\alpha }_{\text{C}}({\text{lnTibia}}_{i1})$$ (1)

For evaluation 2:

$$E({\text{RO}}_{i2})={\theta }_0+{\beta }_1({\text{PbB}}_{i1})+{\beta }_{\text{L}}({\text{PbB}}_{i2})+{\alpha }_{\text{C}}({\text{lnTibia}}_{i1})+{\alpha }_{\text{H}}({\text{lnTibia}}_{i1})$$ (2)

For evaluation 3:

$$E({\text{RO}}_{i3})={\theta }_0+{\beta }_1({\text{PbB}}_{i1})+{\beta }_{\text{L}}({\text{PbB}}_{i3})+{\alpha }_{\text{C}}({\text{lnTibia}}_{i1})+{\alpha }_{\text{H}}({\text{lnTibia}}_{i1}+{\text{lnTibia}}_{i2})$$ (3)

Contrasts of interest are threefold: comparing outcomes between-subjects (“cross-sectional” effects, denoted C); comparing changes in outcomes within-subjects over time (“longitudinal” effects, denoted L); and comparing changes in outcomes within-subjects over time across initial cumulative (tibia) lead doses (“historical” effects, denoted H). The cross-sectional tibia effect (α_C) can be thought of as the expected difference in outcomes between subjects with differing baseline tibia concentrations. The cross-sectional PbB effect (β_C) at baseline is constructed from two parameters in the model above as β_C = (β₁ + β_L), since the longitudinal PbB term in the model above requires inclusion of the baseline PbB measurement in the model. The longitudinal PbB effect (β_L) describes how a within-subject change in PbB over an interval is associated with a within-subject change in outcome over the same interval, and is obtained by subtracting either equation 1 from equation 2, or equation 2 from equation 3 as follows:

For average change from evaluation 1 to evaluation 2:

$$\text{Avg}({\text{RO}}_{i2}‐{\text{RO}}_{i1})={\beta }_{\text{L}}({\text{PbB}}_{i2}‐{\text{PbB}}_{i1})+{\alpha }_{\text{H}}({\text{lnTibia}}_{i1})$$ (4)

For average change from evaluation 2 to evaluation 3:

$$\text{Avg}({\text{RO}}_{i3}{‐\text{RO}}_{i2})={\beta }_{\text{L}}({\text{PbB}}_{i3}‐{\text{PbB}}_{i2})+{\alpha }_{\text{H}}({\text{lnTibia}}_{i2})$$ (5)

Note that the expected longitudinal change in outcome is adjusted for the value of a subject's tibia lead measurement at the previous evaluation. Thus, equations (4) and (5) also show that the historical coefficient α_H summarizes the additional prediction of change in renal outcomes from time t to time t + 1 (evaluation 1 to 2 or evaluation 2 to 3) by tibia lead at time t, after accounting for longitudinal PbB effects.