From causal diagrams to birth weight-specific curves of infant mortality

Abstract

This report explores the low birth weight paradox using two graphical approaches: causal directed acyclic graphs (DAGs), and the empirical curves of the birth weight distribution and birth weight-specific mortality. The birth weight curves are able to represent the associations quantitatively, while the corresponding causal DAGs provide a set of plausible explanations for the findings. Taken together, these two approaches can facilitate discussion of underlying biological mechanisms.

Low birth weight (LBW) is strongly associated with increased neonatal mortality (NM) [1]. However, LBW infants in groups exposed to a prenatal factor that increases LBW typically have a lower mortality rate than unexposed LBW infants. For example, LBW infants born to mothers who smoke have lower mortality rates than LBW infants born to nonsmoking mothers [2], and LBW infants born at high altitude have lower mortality rates than LBW infants born at low altitude. This phenomenon is known as the “birth weight paradox” [1].

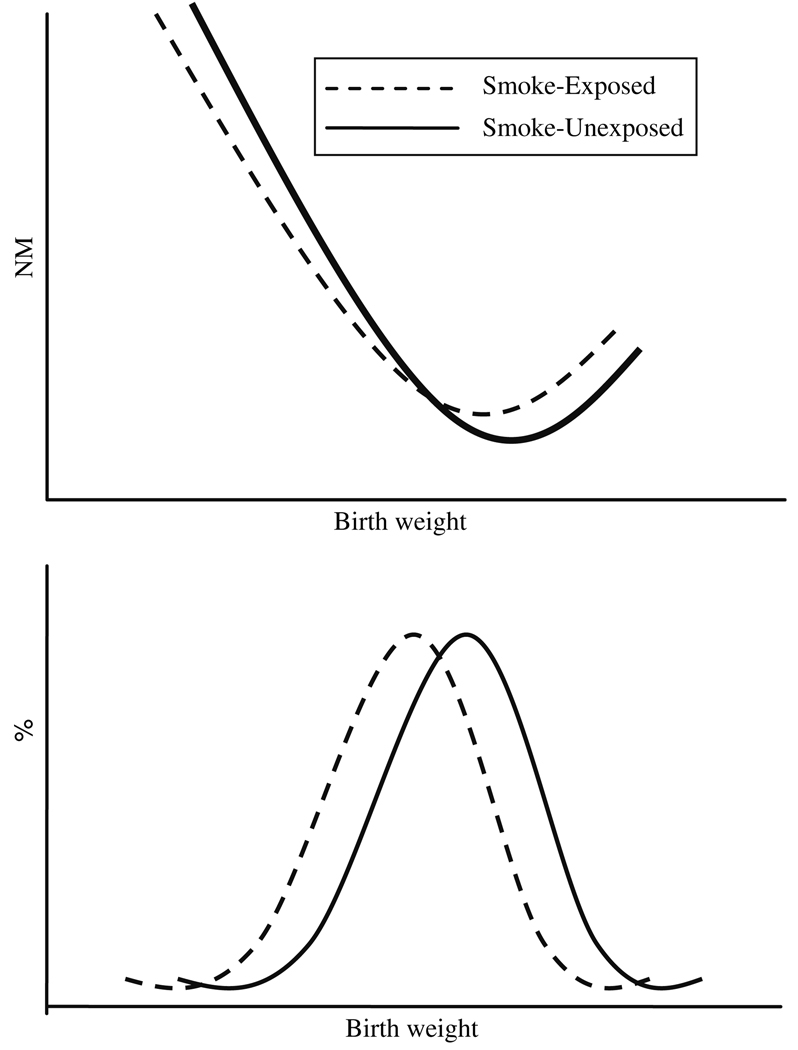
Since the early 80’s, Wilcox and coworkers have discussed the birth weight paradox by using the empirical curves of the birth weight distribution and birth weight-specific mortality [1]. The forms of these curves are highly consistent across populations, with a near-Gaussian distribution of birth weight and a reverse-J shaped pattern of weight-specific mortality (on a log scale). The typical relationship among these curves for a prenatal exposure (e.g., maternal smoking) that decreases birth weight is shown in Fig. 1. That is, as the birth weight curve shifts, so does its weight-specific mortality curve. Wilcox et al. interpret this shift of the mortality curve as calling into question the existence of a direct effect of birth weight on mortality [1, 3].

Fig. 1.

Birth weight-specific neonatal mortality (NM) curves and birth weight distribution for smokers and non-smokers

More recently, Hernández-Díaz and coworkers have proposed the use of causal directed acyclic graphs (DAGs) as a conceptual framework in which to discuss the birth weight paradox [4]. Causal DAGs comprise variables (nodes) linked by arrows (directed edges) that represent direct causal effects (protective or causative) of one variable on another [5, 6]. Using causal DAGs, these authors proposed that the apparent paradox could be the result of selection bias due to stratification on a variable (birth weight) that is affected by the exposure of interest (smoking), and that shares common causes with the outcome (infant mortality) [7–9].

In this article we present the correspondence between Wilcox et al.’s curves and causal DAGs under several hypothetical scenarios. We will show that these two representations of the problem are complementary and that the curves may be used to inform the construction of causal DAGs. We use maternal smoking as an example of prenatal exposure. Figure 1 represents the empirical findings for maternal smoking, birth weight, and neonatal mortality. For example, the birth weight distribution of smoke-exposed babies is always shifted to lower weights, in the manner seen in Fig. 1, probably because smoking reduces birth weight (i.e., there is an arrow from smoking to weight) [9]. We accept this as a basic assumption in all our scenarios below. To simplify the subsequent figures, this shift of the weight distributions is assumed and not shown.

It is also true empirically that smoking is associated with increased neonatal mortality in analyses not conditioned on birth weight. This will enter into discussions of the scenarios below. For simplicity, we assume that the analysis is conducted within strata of all confounders of the effect of smoking on mortality, i.e., there is no unmeasured factor with an arrow to both smoking and mortality.

Scenario 1: “Neither smoking nor birth weight have an effect on mortality”

The simplest causal DAG to describe this scenario is depicted in Fig. 2. The DAG implies no association between birth weight and mortality, which would make the mortality curve flat.

Figs. 2–9.

Proposed causal structures (DAGs; directed acyclic graphs) and corresponding birth weight-specific neonatal mortality curves under several hypothetical scenarios

However, the causal DAG must be incomplete because we know that the empirical birth weight-specific mortality curves have a steep slope (see Fig. 1), showing the strong association between birth weight and mortality. This association could in principle be explained by an effect of birth weight on mortality (which is ruled out in this scenario), or by the existence of common causes of lower birth weight and mortality (U) as shown in Fig. 3. Some examples of these common causes U are known to exist (e.g., congenital abnormalities). The variables U guarantee that the mortality curves will not be flat as in Fig. 2. To determine the actual shape of the curves requires information about the distribution of U that is beyond the qualitative information encoded by the causal DAG. Hernández-Díaz et al. [4] argued that the birth weight paradox mortality curves of Fig. 1 can be qualitatively explained by the presence of unmeasured common causes U, but they did not specify the conditions under which that would occur. Basso and Wilcox [3] used simulations of hypothetical variables U to identify some sufficient conditions. The causal DAG in Fig. 3, however, cannot be correct because it implies that smoking and mortality are not associated in analyses that do not condition on birth weight. This predicted lack of association is not consistent with the well-known (unconditional) association between smoking and mortality typically found in epidemiologic studies.

Scenario 2: “Birth weight, but not smoking, has a direct effect on mortality”

The simplest structure for Scenario 2 is depicted in the causal DAG of Fig. 4. In this scenario, lower birth weight causes mortality, and thus the mortality curve is not flat. However, conditional on birth weight, there is no association between smoking and mortality. The mortality curve is the same for smokers and non-smokers. In other words, the (unconditional) association between smoking and mortality is mediated entirely through the smoking effect on birth weight. Note that the specific shape of the mortality curve in Fig. 4 is not (and cannot be) determined by the qualitative information encoded in the causal DAG. To increase the plausibility of this scenario, we again need to add to the causal DAG the known common causes of lower birth weight and mortality (U) (Fig. 5). The variables U induce an association between smoking and mortality conditional on birth weight [4]. Thus, it is possible under Scenario 2 to produce lower mortality for the exposed babies—the birth weight paradox.

Scenario 3: “Both smoking and birth weight have a direct effect on mortality”

Figure 6 shows the simplest causal DAG for this scenario. As in Scenario 2, Scenario 3 assumes an effect of birth weight on mortality, and the mortality curve is therefore sloped. By adding a direct effect of smoking on mortality, the mortality curve for smokers is also shifted upwards across all birth weight levels. The particular curves we chose for Fig. 6 also show that smoking increases mortality uniformly at all levels of birth weight, i.e., that the effect of smoking is not modified by birth weight. This lack of effect-measure modification is not necessarily implied by the causal DAG. In fact, the causal DAG of Fig. 6 could also be consistent with the intersecting mortality curves of Fig. 7 if there were a qualitative interaction between smoking and birth weight in which smoking reduced mortality at some birth weights and increased mortality at other weights.

In the absence of such qualitative interaction, intersecting mortality curves could also be explained by the addition of common causes (U) to the causal DAG as in Fig. 7. The common causes U induce a new source of association between smoking and mortality conditional on birth weight, which may result in intersecting mortality curves, even under the assumption that smoking increases mortality at all levels of birth weight.

Scenario 4: “Smoking, but not birth weight, has a direct effect on mortality”

Figure 8 shows the simplest causal DAG for this scenario. Under this causal DAG, there is no association between birth weight and mortality conditional on smoking, and thus the mortality curves are flat. Because of the direct effect of smoking on mortality, the smokers’ mortality curve is shifted upwards. The mortality curves incorporate the assumption (not necessarily implied by the causal DAG) that smoking increases mortality at all levels of birth weight.

By adding the common causes (U) of lower birth weight and mortality (Fig. 9) we induce an association between birth weight and mortality (slope of the curves), as well as an additional association between smoking and mortality conditional on birth weight (shown by the crossing). Thus, this scenario is also able to replicate an intersection of mortality curves (and the birth weight paradox), even under the assumption that smoking increases mortality at all levels of birth weight.

Discussion

In this article we have discussed the birth weight paradox in the context of causal diagrams and the empirical curves of birth weight and weight specific mortality. This exercise demonstrates the correspondence between causal diagrams and mortality curves. Causal DAGs are qualitative models that do not encode the magnitude and direction of the effects. For this reason, a single causal DAG can be consistent with several mortality curves, and vice versa. That is, no causal DAGs necessarily imply a crossover of the curves, but some causal DAGs describe structures that are consistent with the crossover. Given the empirical crossover of the mortality curves for smokers and non smokers, a possible interpretation might be that the effect of smoking on mortality varies with birth weight, i.e., that there is a qualitative interaction between the effects of smoking and birth weight on mortality. However, causal DAGs provide alternative explanations for the crossover, showing that such intersection of mortality curves is possible even in the absence of a qualitative interaction, or in the absence of any effect of birth weight on mortality.

The choice of causal DAGs is informed by both the observed data and subject-matter knowledge. Thus the causal DAGs in Figs. 2–4, 6, and 8 can be ruled out because they are inconsistent with the observed data (in some cases combined with the assumption of no qualitative modification of the effect of smoking on mortality). Under the generally-accepted assumption that smoking has direct effects on mortality not mediated through birth weight, the causal DAG in Fig. 5 is also ruled out. The use of causal DAGs clearly shows that the subject-matter discussion revolves around the existence of a direct effect of birth weight on mortality (Figs. 7 vs. 9). If subject-matter experts believe that there is a qualitative interaction of the effects of smoking and birth weight on mortality risk (an interaction that cannot be generally encoded by the causal DAG), then Fig. 6 could be added to the debate. Figure 6 would be consistent with the crossing of the curves if smoking reduced the mortality risk among low birth weight infants and increased the risk in larger infants.

Wilcox and his colleagues have proposed that the causal DAG in Fig. 9 is the one that most likely explains the birth weight paradox. They rule out the causal DAG in Fig. 7 because it states that birth weight has a direct effect on mortality. Such an effect of birth weight seems to be at odds with the observation that moderate reductions of birth weight are not necessarily associated with increased mortality [1].

In summary, the DAG-based approach is a helpful complement to the empirical curves-based approach developed by Wilcox and colleagues. Causal DAGs can be used 1) to enhance communication among researchers by representing the biological explanations proposed by experts in the field, and 2) to propose less obvious explanations to apparently surprising findings such as the “birth weight paradox.” The birth weight and mortality curves can represent more quantitative information (e.g., the magnitude of the associations)—something DAGs are not able to capture. While causal DAGs can facilitate discussion among subject-matter experts, they do not provide the final answer.