Lightweight comparison of RNAs based on exact sequence–structure matches

Abstract

Motivation: Specific functions of ribonucleic acid (RNA) molecules are often associated with different motifs in the RNA structure. The key feature that forms such an RNA motif is the combination of sequence and structure properties. In this article, we introduce a new RNA sequence–structure comparison method which maintains exact matching substructures. Existing common substructures are treated as whole unit while variability is allowed between such structural motifs.

Based on a fast detectable set of overlapping and crossing substructure matches for two nested RNA secondary structures, our method ExpaRNA (exact pattern of alignment of RNA) computes the longest collinear sequence of substructures common to two RNAs in O(H·nm) time and O(nm) space, where H ≪ n·m for real RNA structures. Applied to different RNAs, our method correctly identifies sequence–structure similarities between two RNAs.

Results: We have compared ExpaRNA with two other alignment methods that work with given RNA structures, namely RNAforester and RNA_align. The results are in good agreement, but can be obtained in a fraction of running time, in particular for larger RNAs. We have also used ExpaRNA to speed up state-of-the-art Sankoff-style alignment tools like LocARNA, and observe a tradeoff between quality and speed. However, we get a speedup of 4.25 even in the highest quality setting, where the quality of the produced alignment is comparable to that of LocARNA alone.

Availability: The presented algorithm is implemented in the program ExpaRNA, which is available from our website (http://www.bioinf.uni-freiburg.de/Software).

Contact: {exparna@informatik.uni-freiburg.de,backofen@informatik.uni-freiburg.de}

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Ribonucleic acids (RNAs) are associated with a large range of important cellular functions in living organisms. Moreover, recent findings show that RNAs can perform regulatory functions formerly assigned only to proteins. Likewise to proteins, these functions are often associated with evolutionary conserved motifs that contain specific sequence and structure properties. Examples for such regulatory RNA elements, whose functions are mediated by sequence–structure motifs are selenocysteine insertion sequence (SECIS) elements (Huttenhofer et al., 1996) (see Fig. 1 for an example), iron-responsive elements (IREs) (Hentze and Kuhn, 1996), different riboswitches (Serganov and Patel, 2007) or internal ribosomal entry sites (IRESs) (Martineau et al., 2004). Therefore, the detection of similar structural motifs in different RNAs is an important aspect for function determination and should be considered in pairwise RNA comparison methods. Although this problem is addressed in sequence–structure alignment methods, these approaches are often very time-consuming and do not necessarily preserve functionally important common substructures in the alignment (Jiang et al., 1995, 2002).

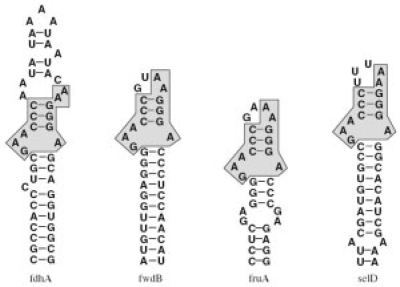
Fig. 1.

Putative SECIS elements in non-coding regions of Methanococcus jannaschii according to Wilting et al. (1997). The indicated substructure represents a common substructure, i.e. a local motif.

In this article, we propose a new lightweight, motif-based method for the pairwise comparison of RNAs. Instead of computing a full sequence–structure alignment, our approach efficiently computes a significant arrangement of sequence–structure motifs, common to two RNAs. For the sake of algorithmic complexity and applicability in practice, we neglect higher order interactions like pseudoknots. This allows to describe sequence–structure motifs with nested RNA secondary structures, as shown in Figure 1.

Our ExpaRNA (exact pattern of alignment of RNA) method uses as a pre-processing step a fast O(nm) time and space algorithm from Backofen and Siebert (2007) for the identification of isolated common substructures for the two given RNAs of lengths n and m with nested secondary structures. More precisely, this method identifies the complete, but overlapping set of exact common substructures. Our approach makes use of these common substructures and computes the longest collinear, non-overlapping sequence of substructures common to two RNAs in O(H·nm) time and O(nm) space, where H ≪ n·m for real RNA structures. Herein after, we call this the Longest Common Subsequence of Exact Pattern Matchings problem (LCS-EPM).

The LCS-EPM requires known or predicted structure. We have compared our approach with two other alignment methods that work with given RNA structures, namely RNAforester and RNA_align. The results are in good agreement, but can be obtained in a fraction of running time, in particular for larger RNAs.

Since in many practical applications, there is no known structure, and structure prediction would lead to wrong results, we have also setup a pipeline that combines ExpaRNA with a state-of-the-art Sankoff-style algorithm for simultaneous alignment and folding (Sankoff, 1985). Albeit Sankoff-like approaches are currently the gold standard for RNA alignment, it has the drawback of a high computational complexity. Basically, we predict a longest common subsequence of exact pattern first, and then use LocARNA (Will et al., 2007) to fill the unaligned space between the exact pattern matchings. This amounts to calculate a constraint alignment by LocARNA, which restricts the search space and thus speeds up LocARNA. Moreover, the speedup increases with the extent of information calculated by ExpaRNA. However, this normally implies that the quality is decreased. Hence, there is a trade-off between the speedup resulting from this combined pipeline, and the quality of the produced alignment. However, we get a speedup of 4.25 even in the highest quality setting, where the quality of the produced alignment is comparable to that of LocARNA alone. In application scenarios where optimal quality is not strictly required, we obtain a speedup up to 8.25. Note that this pipeline could also be used in combination with other Sankoff-like tools that are in principle able to profit from alignment constraints, e.g. Dynalign, PMComp and FoldalignM (Hofacker et al., 2004; Mathews and Turner, 2002; Torarinsson et al., 2007).

Related work:

existing approaches addressing the sequence–structure comparison problem for RNA molecules can be distinguished by the given structural information and their representation. The standard alignment-based comparison approach employs the computation of edit distances between given RNA secondary structures (Bafna et al., 1995; Jiang et al., 2002). In (Evans, 1999) the author introduced the problem of finding the longest arc-preserving common subsequence (LAPCS). However, even for two nested RNA secondary structures, both problems remain NP-hard (Blin et al., 2003; Lin et al., 2002). With some restrictions to the scoring scheme, the time complexity for determination of the edit distance can be lowered to polynomial time (Jiang et al., 2002).

If the nested secondary structure is represented as a tree, comparison methods exist for the edit distance between two ordered labeled trees (Zhang and Shasha, 1989) as well as for the alignment of trees (Jiang et al., 1995). An improved version of the tree alignment method with extension to global and local forest alignments is given in Höchsmann et al. (2003) and implemented in the program RNAforester. The MiGaL (Allali and Sagot, 2005) approach extends the tree edit distance model by the two new tree edit operations and is especially efficient due to its usage of different abstraction layers.

The article is organized as follows. In Section 2, we describe the way in which exact common substructures can be used for pairwise sequence–structure comparison. In addition, we explain how sequence–structure alignment methods can profit from anchor constraints. Sections 3 and 4 present the results for two applications of our tool ExpaRNA.

2 METHODS

RNA is a macro molecule described formally by a pair ℛ=(S, B) of a primary structure S and a secondary structure B. A primary structure S is a sequence of nucleotides S=s₁s₂…s_n over the alphabet {A, C, G, U}. With |S| we denote the length of sequence S. S[i] indicates the nucleotide at position i in sequence S. With S[i…j] we define the substring of S starting at position i until j for 1≤i<j≤|S|. A secondary structure B is a set of base pairs B={(i, i′) | 1≤i<i′≤|S|} over S, where each base takes part in at most one base pair. A secondary structure B is called crossing if there are two pairs (i, i′),(j, j′)∈B with i<j<i′<j′. Otherwise it is called non-crossing or nested.

For the definition of local RNA motifs, we represent an RNA ℛ=(S, B) as undirected labeled graph G=(V, E), called the structure graph of ℛ. Its set of vertices V is the set of positions in S, i.e. V={1,…, |S|}. Its set of edges E comprises all backbone bonds and all base pairs, i.e. E={(i, i+1)∣1≤i<|S|}∪B. An RNA pattern in ℛ is a set of positions 𝒫⊆{1,…, |S|}, such that the pattern graph for 𝒫 in G, defined as the subgraph G′=(V′, E′) of G, where V′=𝒫 and E′={(i, i′)∈E | i∈𝒫 and i′∈𝒫}, is connected. By this definition, an RNA pattern corresponds to a local motif, i.e. a substructure consisting of neighbored nucleotides according to a neighborhood that is induced by the backbone bonds and base pairs within a fixed secondary structure (cf. Fig. 1).

2.1 Exact pattern matchings of two RNAs

In the following, we consider two fixed, non-crossing RNAs ℛ₁=(S₁, B₁) and ℛ₂=(S₂, B₂). Their corresponding structure graphs are G₁=(V₁, E₁) and G₂=(V₂, E₂), respectively. We will define an exact pattern matching as a special ordered matching of V₁ and V₂, i.e. as a set ℳ⊆V₁ × V₂, where for all (p, q), (p′, q′)∈ℳ it holds that p<p′ implies q<q′ and p=p′ iff q=q′.

According to an ordered matching ℳ of V₁ and V₂, we merge the graphs G₁ and G₂ into a matching graph 𝒢_ℳ=(ℳ, E_ℳ), where E_ℳ={((p, q),(p′, q′))∈ℳ×ℳ∣(p, p′)∈E₁ and (q, q′)∈E₂}. A pair (p, q)∈ℳ is called admissible if it satisfies the following conditions: (i) S₁[p]=S₂[q] and (ii) STRUCT₁(p)=STRUCT₂(q). Here, function STRUCT_i(j) yields one of the three possible structural types for a nucleotide at position j in structure i: single stranded, left paired or right paired. Furthermore, exact pattern matchings need to preserve all base pairs. A matching ℳ satisfies this iff ∀(p, q), (p′, q′)∈ℳ : (p, p′)∈B₁ ⇔ (q, q′)∈B₂. Then, an exact pattern matching 𝒫ℳ is an ordered matching where G_𝒫ℳ is connected, all (p, q)∈𝒫ℳ are admissible and all base pairs are preserved.

Hence, an exact pattern matching 𝒫ℳ describes the matching between sets of positions in the two RNAs ℛ₁ and ℛ₂, namely the projections π₁𝒫ℳ={p|(p, q)∈𝒫ℳ} and π₂𝒫ℳ={q|(p, q)∈𝒫ℳ}. Note that π₁𝒫ℳ and π₂𝒫ℳ are patterns in ℛ₁ and ℛ₂, respectively, i.e. in particular they correspond to the connected pattern graphs G^p₁ and G^p₂. Note further, although we require that an exact pattern matching 𝒫ℳ is an isomorphism on base pairs, 𝒫ℳ does not necessarily describe an isomorphism on backbone edges in the pattern graphs G^p₁ and G^p₂, since for (p, q),(p′, q′)∈𝒫ℳ where p and p′ form an edge in G^p₁, q and q′ do not necessarily form an edge in G^p₂. For details and proofs we refer to Backofen and Siebert (2007).

For our algorithm, we utilize only maximal exact pattern matchings, i.e. ∀𝒫ℳ′ : 𝒫ℳ⊆𝒫ℳ′⇒𝒫ℳ′=𝒫ℳ. In the following, we abbreviate the term maximal exact matching pattern by EPM. Similar to the minimal word size as e.g. used in BLAST (Altschul et al., 1997), it is reasonable to consider a minimal size γ for EPMs. Hence, the set of all maximal exact pattern matchings ℰ over two RNAs ℛ₁ and ℛ₂ is defined as

Note that each EPM is an arc-preserving common (but not longest common) subsequence as defined in Evans (1999) for the LAPCS problem. Since EPMs have in addition the above described properties, the detection of all EPMs is a computationally light problem, compared to LAPCS, which is NP-complete even for nested sequences (Blin et al., 2003). Using the dynamic programming approach described in Backofen and Siebert (2007), the set of all EPMs can be found in O(nm) time and O(nm) space, making this approach applicable for fast sequence–structure comparisons. Now recall that each EPM is maximal. This implies that any two exact pattern matchings are disjoint and therefore a pair (p, q)∈ℰ∈E^1,2_γ is unique in E^1,2_γ and part of at most one EPM. The number of EPMs contained in E^1,2_γ is bounded by n·m, with n=|S₁| and m=|S₂|.

E^1,2_γ can be seen as a ‘library’ of all common motifs between two RNAs that can be utilized for a pairwise comparison method. Thus, the main idea of our approach will be to take a subset EPMs from E^1,2_γ that in combination will cover a large portion of both RNAs. The EPMs in E^1,2_γ differ in their size and shape as well as in their structural positions in both RNAs. Simply selecting two or several of these substructures for combination would probably lead to overlapping or crossing structures (Fig. 2). Hence, the set of all EPMs is not a solution for the LAPCS problem since the combination of several EPMs is not necessarily arc-preserving. Clearly, a meaningful subset of common substructures excludes overlapping and crossing patterns. This guarantees that the backbone order of matched nucleotides as well as base pairs of the given RNAs are preserved. Compatible EPMs are called non-crossing. Formally, two EPMs ℰ₁ and ℰ₂ are non-crossing if ℰ₁∪ℰ₂ is an ordered matching. Figure 2 shows an example of a possible set E^1,2_γ. A ‘good’ subset to describe the similarity between the two RNAs would probably exclude the EPMs indicated in red.

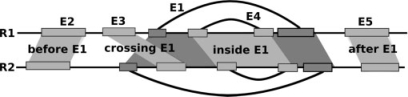
Fig. 2.

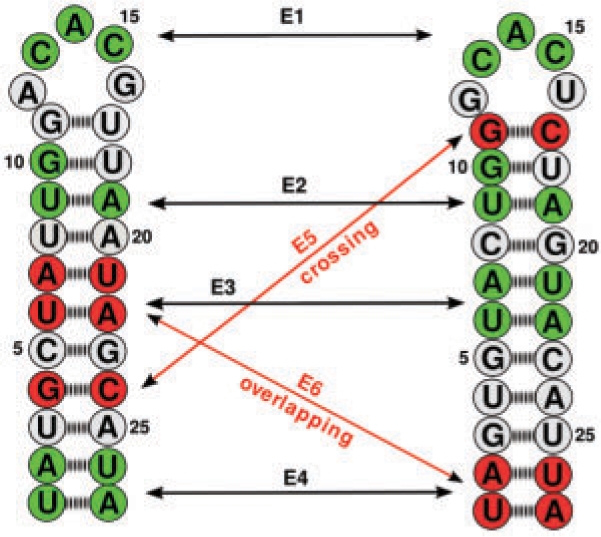
A possible set E^1,2_γ for two RNAs ℛ₁, ℛ₂. The set {ℰ₁, ℰ₂, ℰ₃, ℰ₄} can be used for a comparison, whereas {ℰ₅, ℰ₆} should be excluded. ℰ₅ is crossing ℰ₂ and ℰ₃, whereas ℰ₆ is overlapping with ℰ₃ in ℛ₁ and with ℰ₄ in ℛ₂. Note that not all possible EPM s are indicated.

2.2 Combining EPMs for comparing RNAs: problem definition and algorithm overview

The formulation of LCS-EPM is motivated by the fact that similar RNAs with fixed secondary structures share identical structural elements in a similar arrangement. Examples are shown in our result section for the comparison of thermodynamically folded as well as experimentally verified secondary structures. The knowledge of such a ‘common core’ of identical substructures in two RNAs is interesting for different tasks.

For our global approach, we are interested in a maximal possible arrangement of substructures shared by two RNAs. If the motifs are given in the form of exact pattern matchings, we call this the LCS-EPM problem. Basically, we search for a maximal combination of EPMs that form a common subsequence. Note that albeit the problem shares some similarity with LAPCS, it is restricted in such a way that an efficient solution is possible.

Formally, LCS-EPM is defined as follows. Given two nested RNAs ℛ₁, ℛ₂ and a set of exact pattern matchings E^1,2_γ of these two RNAs, find an ordered matching ℳ_EPM consisting of a subset of EPMs from E^1,2_γ that has maximal cardinality. Thus, ℳ_EPM is defined as the union 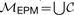of a subset 𝒞⊆E^1,2_γ, where all EPMs contained in 𝒞 are mutually non-crossing. Note that this implies that the found subsequence is a common subsequence since ℳ_EPM is an ordered matching. The common base pairs are induced by the EPM s itself.

Given a library of EPMs, our algorithm works by singling out the best combination of compatible EPMs. This task is performed efficiently by dynamic programming. The main idea is to recursively reduce the problem of solving the EPM puzzle for the EPMs enclosed in subsequences S¹[i…j] and S²[k…l] to the problem for smaller subsequences. For our recursion scheme, we exploit the special structure of EPMs, which span matchings of certain subsequences of consecutive nucleotides. Between the boundaries of these matched consecutive subsequence, EPMs can omit subsequences; thereby they contain holes.

Figure 3 illustrates this structure of EPMs and shows how, given a single EPM ℰ, the relative position of the other EPMs to ℰ can be distinguished. Formally, this is defined via the boundaries and holes of a single EPM.

Fig. 3.

Ordering of exact pattern matchings relative to EPM ℰ₁ (indicated in dark gray). The cases before, inside and after do not violate the non-crossing condition. Only EPM ℰ₃ crosses ℰ₁. Note that an arc denotes a base pair within an EPM.

2.3 Algorithmic concepts: boundaries and holes

The nucleotide positions of a pattern 𝒫 of size k can be written as an increasing sequence. Similarly, an EPM ℰ of size k over two RNAs is given with its corresponding patterns 𝒫₁ in ℛ₁ and 𝒫₂ in ℛ₂ and their increasing sequences 𝒫₁=〈p₁, p₂,…, p_k〉 and 𝒫₂=〈q₁, q₂,…, q_k〉.

2.3.1 Boundaries of EPMs

In the view of the secondary structure, the elements (p₁, p_k) and (q₁, q_k) determine the outside borders of the EPM. Therefore, we call them outside-boundaries and write them as 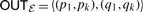. In the view of an arc-annotated sequence, we call (p₁, q₁) left-outside-boundaries and (p_k, q_k) right-outside-boundaries and denote them as LEFT_ℰ and RIGHT_ℰ.

If an EPM contains base pairs, the structural shape is more complex and the outside-boundaries are not sufficient to describe all structural borders. If not all enclosed nucleotides of a base pair are part of the EPM, then there exist two positions in each RNA that form an additional structural border inside the range of the outside-boundaries. In addition, if a pattern contains several independent base pairs (e.g. in a multi-loop), there can be several such inside borders (cf. Fig. 4). The set of all such borders is called inside-boundaries and is defined as 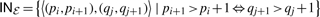. Note that outside-boundaries always exists, whereas the set inside-boundaries can be empty. For example, assume an EPM that comprises only unpaired nucleotides or a complete hairpin including the closing bond. If an EPM consists of only one base pair in each sequence, then inside-and outside-boundaries are identical. With the superscript index for the RNA we retrieve the boundaries for a single RNA. For example LEFT_ℰ¹=p₁.

Fig. 4.

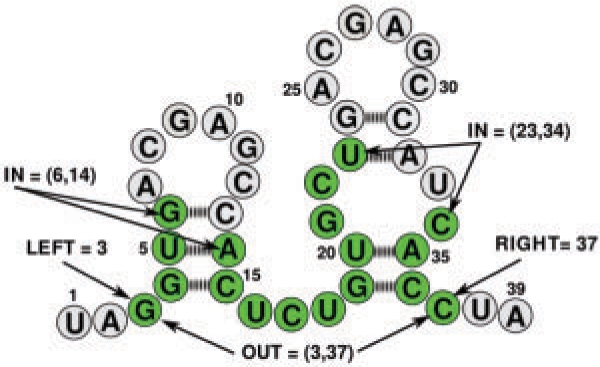
A pattern of an EPM in one RNA (green nucleotides). The different boundaries are indicated.

2.3.2 Holes

Holes are directly related to inside-boundaries and describe the subsequences which are not the part of the subsequence S_i[LEFT_ℰⁱ, RIGHT_ℰⁱ] of an EPM ℰ. For a given EPM ℰ with its set of inside-boundaries IN_ℰ, the set of holes with minimal size γ is defined as HOLES_ℰ={〈(l¹, r¹), (l², r²)〉 | r¹≥l¹ + γ ∧ r²≥l² + γ}. We introduce the notations h^L1, h^R1, h^L1 and h^R2 to refer to l¹,r¹,l² and r² of a hole h=〈(l¹, r¹),(l², r²)〉, respectively. For each h∈HOLES_ℰ there exists a pair of inside-boundaries with 〈(h^L1−1, h^R1+1),(h^L2−1, h^R2+1)〉∈IN_ℰ. Clearly, a hole spans a substring S₁[h^L1…h^R1] in the first RNA and a substring S₂[h^L2…h^R2] in the second RNA. With γ we refer to the same size as indicated by E^1,2_γ.

According to the length of the induced subsequences S_i[h^Li…h^Ri], we can sort all holes in one RNA. Let h_i∈HOLES_ℰi and h_j∈HOLES_ℰj two holes for any two ℰ_i, ℰ_j∈E^1,2_γ. We define an ordering in ℛ₁ if and only if h_i is of smaller size than h_j or of equal size in ℛ₁, i.e. .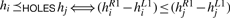

2.4 Dynamic programming recursion for LCS-EPM

The essential difference of LCS-EPM to other alignment-based RNA comparison problems (including LAPCS) is that it treats a common substructure (i.e. an exact pattern matching) as a whole, unbreakable unit. This means that a solution of LCS-EPM either completely includes or completely excludes the edges (p, q) of each EPM. Following this idea, we want to compute the longest collinear sequence of EPMs which does not contain any crossing and overlapping EPMs.

The overall solution for LCS-EPM is constructed by a bottom-up approach from the comparison of substructures that are covered by the subsequences S₁[i…j] and S₂[k…l]. In principle, this requires a four-dimensional matrix, denoted as D(i, j, k, l), which contains the maximal score for combining EPMs that match only bases in S₁[i…j] and S₂[k…l]. However, we can restrict ourselves to two-dimensional matrices using our notions of boundaries and holes for an exact pattern matching ℰ. For each hole, we introduce one two-dimensional matrix of entries D^h(j, l), such that D^h(j, l) is D(h^L1, j, h^L2, l) of our imaginary four-dimensional matrix.

Finding non-crossing regions relative to an EPM is achieved as follows: all nucleotides before LEFT_ℰ, i.e S_i[1, LEFT_ℰⁱ−1], as well as all nucleotides after the RIGHT_ℰ, i.e. S_i[RIGHT_ℰⁱ+1, |S_i|] fulfill the non-crossing condition. This means that any EPM with its outside-boundaries OUT_ℰ in these regions is non-crossing relative to the considered EPM. Similarly we handle EPM s that contain base pairs with the introduced notion of HOLES_ℰ. All EPMs that are located inside any hole of ℰ cannot cross or overlap with ℰ.

The recursion scheme for a dynamic programming algorithm is as follows. Any ℰ is handled only once at its right-outside-boundary RIGHT_ℰ. The score of ℰ is composed of the score before ℰ (Fig. 3), given at the position LEFT_ℰ−1, plus the size of ℰ itself, denoted by the function ω, plus possible scores between inside-boundaries, given recursively by the computation for scores for holes h∈HOLES_ℰ. This last recursion case recurses to possible substructures and therefore suggests the use of a four-dimensional matrix. However, it suffices to use only quadratic space, since (1) all the scores for EPM s are stored in a vector with entries S_ℰ and (2) the score of each hole of an EPM can be computed using only a two-dimensional matrix. By ordering all holes according to , we guarantee that all necessary scores are already computed and stored, whenever an EPM is considered. Due to this order, the recursion starts with the smallest holes and goes on to the larger ones. Note that the two holes of the same size can be treated in any order.

For the formal description of the recursion, fix a hole h. The following recursion scheme works for any h^L1≤j≤h^R1 and h^L2≤l≤h^R1.

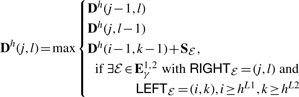After filling the matrices, the best score is computed from treating the whole sequence as hole. With a standard traceback technique the set of EPMs that form the LCS-EPM are found.

2.5 Complexity

Let n=|S₁| and m=|S₂| denote the lengths of the sequences. The time complexity depends primarily on the total number of holes. The set E^1,2_γ contains maximal n · m different holes which is estimated with O(nm). The proof is omitted. For each hole, we fill a two-dimensional matrix with a size of at most |S₁[l¹, r¹]|≤|S₁|=n and |S₂[l², r²]|≤|S₂|=m. Consequently, for all holes we need O(n²m²) time as worst case complexity. For real RNAs, a more appropriate time complexity can be given as O(H·nm) with H as the number of holes, since H ≪ n·m. This explains the fast running time of our algorithm on RNA. The space complexity is only O(nm) because for each hole, after computing its score contribution and adding the score to its EPM, the space for the corresponding matrix D^h is recycled.

We summarize the complexity of solving the LCS-EPM problem as follows. Given two nested RNAs ℛ₁=(S₁, B₁) and ℛ₂=(S₂, B₂). The problem to determine the longest common subsequence of exact pattern matchings (LCS-EPM), including computation of E^1,2_γ, is solvable in total O(n²m²) time and O(nm) space.

2.6 Speeding up RNA alignment by EPMs

One important application of LCS-EPM is the use of the predicted alignment edges ℳ_EPM as anchor constraints for sequence–structure alignment methods (Bauer et al., 2007; Havgaard et al., 2007; Will et al., 2007). The idea of this combined alignment approach is to first solve the LCS-EPM for two given RNAs and then hand over the obtained result to an (usually much more expensive) sequence–structure alignment algorithm. This algorithm is used to fill the unaligned space between the exact pattern matchings in ℳ_EPM in order to produce a complete alignment, i.e. an alignment that also includes all the bases that do not occur in exact pattern matchings.

In general, anchor constraints restrict the space of possible alignments. Thus any alignment algorithm can be sped up by the use of such constraints. Therefore, one expects a speed up of the existing sequence–structure alignment tools that support anchor constraints, when one combines them with the preprocessing by ExpaRNA that generates anchor constraints. Thus, the proposed combination will result in an accelerated RNA alignment approach compared to the underlying RNA alignment approach alone, which will work for any available alignment method.

In particular, we modified the LocARNA algorithm for simultaneous folding and alignment of two RNA sequences S₁ and S₂ in order to profit from anchors. As a Sankoff-style algorithm, LocARNA essentially evaluates the recursion

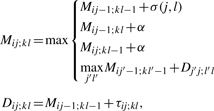where i, j, k, l are sequence positions, i.e. 1≤i<j≤n=|S₁| and 1≤k<l≤m=|S₂|, α is the gap cost, σ is a base similarity function and τ is a base pair similarity function τ, which reflects Turner's RNA energy model (Hofacker et al., 2004; Mathews et al., 1999). An entry M_ij;kl contains the maximal score of alignments of S₁[i..j] with S₂[k..l], whereas for the entries D_ij;kl the alignments additionally have to match the base pairs (i, j) and (k, l). In consequence, D_ij;kl are only required when (i, k) and (j, l) can be alignment edges of some alignment at all. For computing all entries D_ij;kl with a common (i, k), the algorithm fills the matrix slice M_i·;k·, which is the main load of the algorithm.

Given anchors, the algorithm can be modified to require less entries in D_ij;kl, namely only those where (i, k) and (j, l) are compatible with the anchors. Particularly, this implies that it needs to compute only entries M_ij;kl where (i, k) is compatible with the anchor constraints.

For example, assume that we have a single anchor constraint (n/2, m/2) (w.l.o.g. n and m even). Because only alignment edges (i, k) with i≤n/2 and k≤n/2 or i>n/2 and k>n/2 are compatible with the anchor, the algorithm computes only entries in M_ij;kl for those (i, j), i.e. only half of the entries compared to the unconstrained algorithm.

3 RESULTS

We implemented the algorithm for finding the longest common subsequence of exact RNA patterns (i.e. LCS-EPM) in the tool ExpaRNA. The algorithm to determine all EPM s is implemented according to Backofen and Siebert (2007). ExpaRNA is implemented in C++.

We see at least two main application areas for ExpaRNA. First, given two RNAs along with their known or predicted secondary structure, the result of ExpaRNA comprises the optimal set of compatible exact common substructures. In biology, this can be used to get a good, first overview of existing similarities. Second, due to the fast running time of ExpaRNA, it is very attractive to use ExpaRNA for high-throughput RNA analysis tasks. We designed scenarios for both applications to study the different uses of our tool in detail.

3.1 Comparative structural analysis of large RNAs

Here, we study the application of ExpaRNA for analyzing large RNAs that are very costly to compare by other sufficiently accurate tools and where ExpaRNA elucidates information about identical structural motifs, which is not directly addressed by these tools and therefore may remain hidden. To enable an evaluation of our results, the experiments are performed on medium-sized and large RNAs where sequence–structure alignment tools are still applicable.

We have chosen two pairs of RNAs: (a) two IRES RNAs from hepatitis C virus, which belong both to the Rfam family HCV_IRES for IRESs (Griffiths-Jones et al., 2005). GenBank: AF165050 (bases 1–379) and D45172 (bases 1–391). The secondary structures were predicted by RNAfold (Hofacker et al., 1994). (b) Two 16S rRNAs. The first RNA is from Escherichia coli and is 1541 bases long. The second RNA of length 1551 stems from Dictyostelium discoideum (GenBank codes: J01859 and D16466). The secondary structures were taken from the Comparative RNA Web (CRW) site (Cannone et al., 2002).

Table 1 shows the results for both pairs of RNAs. The solution of LCS-EPM is depicted as annotation of the secondary structures in Figure 5 for the IRES RNAs and in Figure 6 for the 16S rRNAs. These figures are directly produced by ExpaRNA using the Vienna RNA Package (Hofacker et al., 1994) for the structure layout. For the IRES RNAs, the numbers mark the five largest EPM s from the set E^1,2_γ and correspond to the manually marked EPM s in Backofen and Siebert (2007). LCS-EPM predicts all of them automatically. In the case of the 16S rRNAs, the result of ExpaRNA shows significant similarities in nearly all stem and loop regions. Note that the set E^1,2_γ was computed with γ=2 for both examples.

Table 1.

Comparison of the number of exactly matching alignment edges found by LCS-EPM and two alignment methods

Methods	IRES RNAs			16S rRNAs
	No. of matches	Coverage (%)	Time (s)	No. of matches	Coverage (%)	Time
ExpaRNA	175	45	0.97	875	57	16.9 s
RNA_align	192	50	62.1	861	56	1 h 35 m
RNAforester	128	33	5.41	847	55	7 m 25 s
Comparison		IRES RNAs		16S rRNAs
		No. of common matches		No. of common matches
ExpaRNA and RNA_align		159 (82.8%)			688 (79.9%)
ExpaRNA and RNAforester		103 (80.5%)			700 (82.6%)

In the lower part, no. of common matches defines the number of identical aligned nucleotides of ExpaRNA and the other methods.

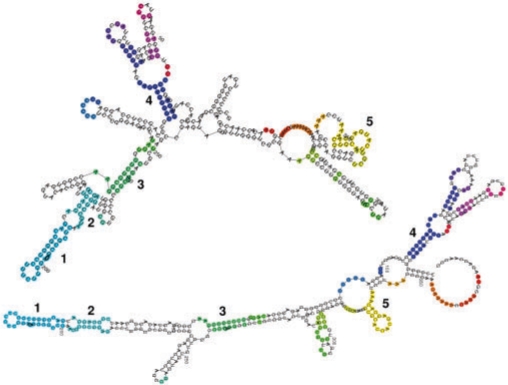
Fig. 5.

LCS-EPM approach applied to two hepatitis C virus IRES RNAs. The colored nucleotides represent the found LCS-EPM with a coverage of 45% (175 nt). Each EPM is shown in a different color. The numbers indicate the five largest EPM s from E^1,2_γ. GenBank: D45172 (upper RNA), AF165050 (lower RNA).

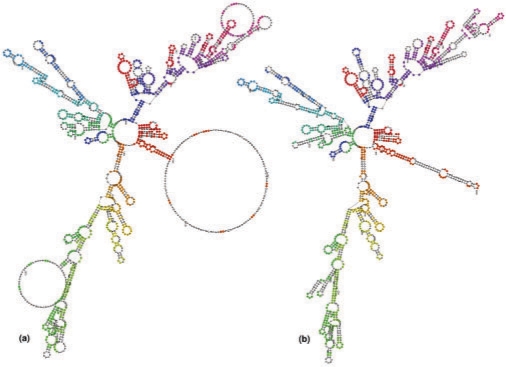
Fig. 6.

LCS-EPM approach applied to two 16S RNAs. The colored nucleotides represent the found LCS-EPM with a coverage of 57% (875 nt). Each EPM is shown in a different color. (a) D. discoideum 16S rRNA (D16466), (b) E. coli 16S rRNA (J01859).

We compare our results with the output of RNA_align and RNAforester. The first method computes sequence-structure alignments according to the general edit distance algorithm (Jiang et al., 2002). The RNAforester program of Höchsmann et al. (2003) is built upon the tree editing algorithm for ordered trees of Jiang et al. (1995) and extends it to calculate forest alignments. We compare us with these tools since both tools cover the state-of-the-art in RNA alignment that is based on fixed structures. The general edit distance algorithm is a classic editing type algorithm for RNA comparison, whereas RNAforester represents the class of tree alignment-based algorithms, which can be due to their working principle much faster, but are less accurate than editing algorithms.

We compared the methods by the number of common realized alignment edges. Therefore, we have first computed the alignments for both RNA pairs. Next, we have counted all positions with exact sequence–structure matchings in these alignments and also determined the intersections with LCS-EPM. Note that the time for ExpaRNA in Table 1 includes the time to determine all EPM s for the two IRES RNAs (0.44s) and for the two 16S rRNAs (1.2s). The given sequence coverage rate is twice the number of predicted exact matches divided by the sum of the two sequence lengths.

3.2 Speeding up RNA alignment for large-scale analysis

Here, we study the performance of ExpaRNA for high-throughput RNA analysis. In Section 2.6, we showed by which means sequence–structure alignment algorithms can profit from anchor constraints and suggested to combine such tools with ExpaRNA that yields EPM s as anchor constraints in the form of a pre-computation step.

In order to assess the possible speedup by this combination, we tested ExpaRNA in combination with the LocARNA algorithm (Otto et al., 2008; Will et al., 2007).

The accuracy of our combined approach (called ExpLoc) was evaluated with the Bralibase 2.1 benchmark (Gardner et al., 2005; Wilm et al., 2006). The Bralibase 2.1 consists of a collection of hand-curated sets of RNA alignments. Because we are interested in the performance of pairwise alignment, we choose the k2 dataset with 8976 pairwise alignments. For each reference alignment, we compute the corresponding ExpLoc alignment and determined its sum of pair scores (SPS)/Compalign score (Bahr et al., 2001; Gardner et al., 2005; Wilm et al., 2006) that measures the accuracy of reproducing the reference alignment. Furthermore, we recorded the running times of ExpLoc and LocARNA for each k2 alignment.

For the computation of a single ExpLoc alignment, we first computed the mfe structure with RNAfold of each sequence and input the two RNAs to ExpaRNA. Afterwards, the ExpaRNA output is used as anchor constraints for LocARNA in order to obtain the complete alignment of the two RNAs.

To test the performance of the two approaches, we carried out five experiments. First, we examined the accuracy of LocARNA alone. The other four experiments evaluate the performance of the combined approach ExpLoc. Here, we assessed the resulting alignment quality for different values γ=7,8,9 and 10 for the ExpaRNA algorithm.

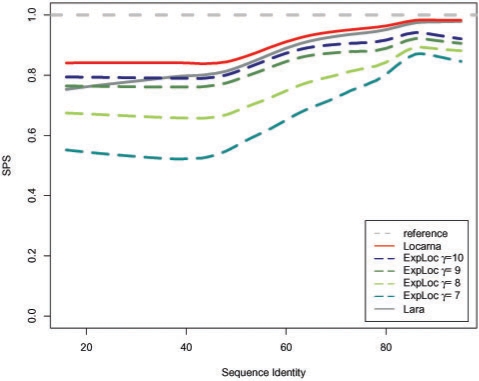
Figure 7 shows the achieved SPS scores at different levels of sequence identity for all five experiments. In addition, we included the performance of the Lara sequence–structure alignment algorithm (Bauer et al., 2007).

Fig. 7.

Obtained alignment qualities for different minimal EPM sizes γ in comparison to LocARNA and Lara on Bralibase 2.1 k2 dataset.

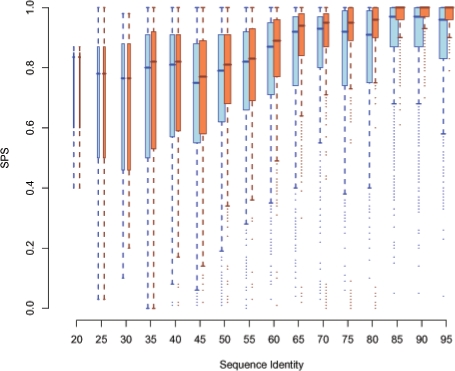
Figure 8 shows a boxplot (also called box-and-whisker plot) visualizing min-values, max-values, medians and quartiles of the SPS/Compalign score distribution for varying pairwise sequence identities.

Fig. 8.

Comparison of the quality of obtained results for exploc (light blue) and LocARNA (orange). The boxplot shows distributions of sum-of-pairs scores (SPS) on the y-axis for different sequence identities on the x-axis for all 8976 pairwise alignments from Bralibase 2.1 and an minimal EPM size of γ=10. To compute distributions, alignments were grouped according to their APSI in intervals of width 5.

The obtained speedup factors shown in Figure 9 are calculated relative to the LocARNA algorithm. The shown values correspond to the experiments in Figure 7. The overall running time of LocARNA was 19 h 26 min. All computations were carried out on a Pentium 4 with 3.2 GHz.

Fig. 9.

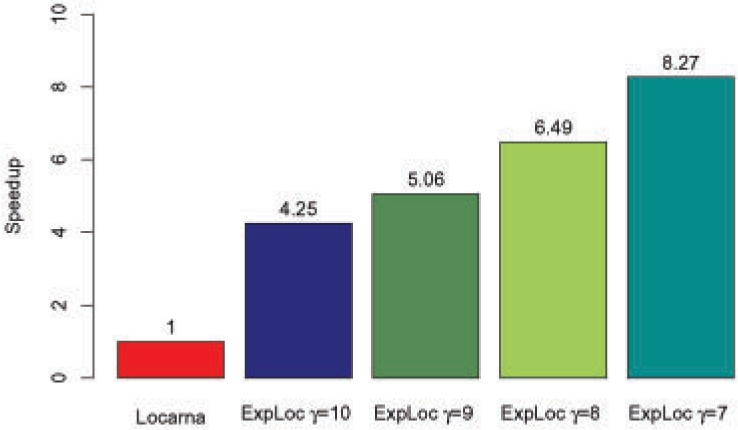
Achieved speedup of ExpLoc with respect to LocARNA running time when using different minimal EPMsizes γ. Total times were measured for both methods when applied to all alignments of the Bralibase 2.1 k2 dataset.

4 DISCUSSION

Our results indicate that ExpaRNA can be advantageous in different application scenarios. In comparative RNA analysis, the results of ExpaRNA exhibit the existing similarities between RNA structures in a nice way. Existing relationships can be detected in a fraction of runtime without using a full alignment procedure.

Due to the availability of more and more large-scale datasets from modern pyro-sequencing techniques, high-throughput analysis methods for thousands of RNAs are needed. We analyzed the contribution of ExpaRNA for such tasks with the Bralibase benchmark. In general, our combined approach yields comparable results like other sequence–structure alignment algorithms. We observed a scaleable tradeoff between speedup and resulting alignment quality according to the selected minimal EPM size γ (Figs 7 and 9). By using different γ parameters our combined approach ExpLoc can be nicely balanced. This is important for problems with large datasets in which often a lower quality setting is sufficent. Moreover, our results show that anchor constraints are able to speedup Sankoff-style alignment algorithms in general (see Section 2.6).

A more fine-grained picture of the achieved accuracy of ExpLoc with γ=10 is shown in Figure 8. In the <70% sequence identity the differences are small. The lowered quality especially in region with a high sequence identity can be explained by the used mfe structures for ExpaRNA. Only slight differences in the sequence result in wide changes of the secondary structure which in turn leads to wrong predicted anchors. However, pure sequence alignment programs are sufficent here. For low sequence identities (≤30%), there are nearly no differences. Here, ExpaRNA often does not find anchors which result in a standard LocARNA alignment. However, these cases are rare, which is also indicated by the width of the boxes in Figure 8.

The different speedups of ExpLoc for different γ values can be explained by the number of predicted anchor points. For γ=7 there exists more anchors than for γ=10. Further, we observe from our data speedups for short as well as for long alignments (Supplementary Figs 1 and 2). In particular, the speedup for long alignments is higher than for small ones, but also the majority of small alignments are accelerated. For longer RNAs we observe speedups around 100. We also look into the distribution of the speedups over different sequence identity classes. In general, sequences with a high sequence identity gain a higher speedup, but we also observe high speedups for classes between 35% and 65% sequence identity. This range is especially relevant for sequence–structure alignment methods, as pure sequence alignment methods will fail here.

Finally, we also observe 336 alignments for ExpLoc with γ=10 (447 for γ=7) resulting in a better SPS score than LocARNA alone.

5 CONCLUSION

We have developed a new algorithm for the pairwise sequence–structure comparison of RNAs and implemented it in the program ExpaRNA. Our approach utilizes common substructures for the detection of global similarities between two RNAs. We have applied the presented dynamic programming algorithm to two different kinds of application. In comparative sequence analysis, ExpaRNA can be used as good overview of existing similarities between two RNAs. Especially for large RNAs, ExpaRNA produces fast meaningful results without the need for usually more expensive alignment methods. In addition, we tested the performance of ExpaRNA in large-scale data analysis. Here, the main idea is to use the predicted LCS-EPM, i.e. an optimal set of compatible substructures, as anchor constraints for Sankoff-style alignment algorithms in order to compute a complete gapped global alignment. We tested ExpaRNA in combination with the LocARNA algorithm on the Bralibase benchmark. In our experiments, we observe a trade-off between quality and speedup according to the chosen parameter γ. However, we get a speedup of 4.25 even in the highest tested quality setting, where the quality of the produced alignment is comparable to other sequence–structure alignment methods. The achieved results also suggests further exploration of the full potential of the ExpaRNA and ExpLoc approach for a variety of RNA structure comparsion-based applications.

Funding: German Research Foundation (DFG grant BA 2168/2-1 SPP 1258); Federal Ministry of Education and Research (BMBF grant 0313921 FORSYS/FRISYS).

Conflict of Interest: none declared.